Radiation and Diffraction Waves of a Ship at Forward Speed
M.Ohkusu, G.Wen (Kyushu University, Japan)
Abstract
An improved method to measure diffraction and radiation waves around a ship model running in waves at forward speed is proposed. With this technique we are able to view the diffraction and/or radiation waves which are usually invisible in tank tests due to the existence of other effects such as incident waves and steady Kelvin waves. Measured wave pattern especially with blunt bow and shallow draft ships is used to investigate validity of an analytical method to predict the diffraction and radiation waves and added resistance of a ship.
1
Introduction
We are developing more and more sophisticated analytical method to understand and predict realistic nonlinear hydrodynamics of ships in waves. Validity of those methods is still tested, however, with traditional way of comparing the theoretically predicted and experimentally measured global hydrodynamic force on ships. The global force is an integrated effect and the implication of the test results is not always clear. The more sophisticated the analytical methods are, the more strict and direct experimental test such as the comparison of fluid pressure without any integration effect will be necessary to prove their advantage over traditional heuristic approaches. This kind of test is also plausible from practical point of view because ship designers do need analytical tool accurate enough to predict local sea loads as well as global sea loads.
The present author proposed (Ohkusu (1984)) to make careful observation of radiation and/or diffraction wave form generated by a ship running in waves and to compare them with the theoretically predicted ones. The purpose is to prove by more direct manner validity or invalidity of our current analytical methods to predict the flow and the pressure regarding the ships in waves. Measurement of the flow and the pressure themselves naturally serves better practically as well as academically this purpose. Reason of the wave observation instead is that it undergoes less integration effect than the global force. Moreover the measurement is easier in terms of experimental instrumentation and its accuracy is much more reliable than that of the flow or pressure measurement.
Investigations based on this idea have already produced some successful results. A large discrepancy, for example, found between added resistance measured as a force and one directly derived from measured wave energy leads to an idea of breaking of the diffraction waves in front of the ship bow and new method has been developed to predict extra added resistance due to the breaking of the diffraction waves (Naitoh et al. (1987)). Yet we found recently that the difference is unusually large with hull forms of shallow draft or at ballast condition corresponding to the shallow draft (SR211(1993)). No theoretical explanation is available now for this large difference.
We have some to be improved in the original technique proposed by the present author to measure diffraction and radiation waves. It gave only wave distribution on a line parallel to the track of a ship model running in experimental tank. One can not construct two dimensional image of the wave pattern by those data alone. This was one reason to derive the amplitude function of the component wave composing the diffraction and radiation waves from the data and to reconstruct the global wave characteristics. This process is possible only when we can assume a mathematical expression of the waves, a linear superposition of component waves satisfying dispersive relation corresponding to its direction of propagation. Therefore some part of wave energy will not possibly be captured with this process. So it is plausible if we could measure two dimensional wave pattern and compare them without any processing with theoretical prediction. It is also desirable to separate the first and second order wave components to compare the former with the predicted by linear theories.
In this report we return to the present author's old approach of measuring waves but we attempt to improve it in order that we can obtain directly the global image of the diffraction and radiation waves at forward speed and separate them into the first and sec-
ond order parts. We investigate various information on the diffraction and radiation waves observed by the improved technique of wave measurement particularly for seeking any explanation of the discrepancy of added resistance of shallow draft ships.
We then propose a linear analytical approach to predict the fluid pressure on ships particularly due to the diffraction wave. This approach accounts effectively for nonuniform steady flow which is prominent in the vicinity of the blunt bow and is supposed to have large influence on accurate prediction of the wave pressure on the bow part.
We test the accuracy of our analytical approach by comparing the diffraction wave field predicted with the measured with our improved technique. We presume that if the prediction of the diffraction wave elevation around the bow is accurate, then the prediction of wave pressure on the bow part will be accurate and the added resistance, on which the wave loads at the bow is the most influential, will be predicted accurately.
2
Measurement of Radiation and Diffraction Waves
Neither radiation wave nor diffraction wave field generated by a ship advancing in waves is visible at tank test because of the coexistence of other waves such as steady wave generated by the forward speed of the ship on otherwise a calm water and incident waves. So we need a technique to separate each of those waves.
It is relatively simple to exclude the effect of the incident waves. We measure them upstream where they are not yet disturbed by a ship model and extrapolate them to near it. The extrapolated incident waves are subtracted from the measured wave.
Another problem is that instantaneous distribution of wave elevation around the model is not a full information of the radiation and the diffraction waves. One can obtain a complete picture of the radiation and the diffraction waves only when the distribution of the amplitude and the phase of the wave motion is measured.
Our method to overcome this at tank test is to place several wave probes on fixed positions to the water tank and on a line parallel to the track of the ship model with an equal spacing Δx. When the ship model advances in the tank, each wave probe comes to a location relative to the ship model at different time instant. In other words the wave probes record the wave elevation at every location on the line parallel to the ship model's track on several different time
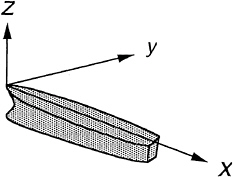
Figure 1: Coordinate System
instants whose interval is Δx/U. U is the speed of the ship model.
Temporal and spatial variation of the diffraction or radiation waves generated by the ship model running at forward speed in the monochromatic incident waves or sinusoidally oscillating is given to the second order by
ζ(x,y,t)=η0(x,y)+η1(x,y)eiωt+η2(x,y)ei2ωt (1)
where the coordinates fixed to the average position of the ship model are defined as a right-hand system shown in Fig.1.
The first term on the right of (1) is the steady wave elevation corresponding to the Kelvin wave pattern. Naturally it includes the second order steady component. The second term is the linear oscillatory part and the third the second order oscillatory component.
If the interval Δx/U is small enough and the number of the wave probes is large enough, we fit measured wave elevation on several different time instants with equation (1) at every x of the line y=constant to determine η0, η1 and η2. Fig.2 is an example of the fitting of the wave motion in the vicinity of a ship model at midship; this example is the radiation waves of a Series 60 model of CB=0.8 at ballast condition forced to heave at relatively large amplitude (amplitude-to-draft-ratio is 0.9). We used
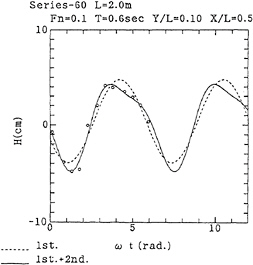
Figure 2: Time Series of Wave Elevation
twelve wave probes in this experiment and the number of the measured data represented by circles is naturally twelve. Introduction of the second harmonic terms in equation (1) is apparently appropriate and the η1 determined is the complex amplitude distribution of linear radiation wave.
Replace the wave probes to another y and repeat the procedure described above, we have η0,1,2 on various y values. With them we can compose the pattern of the radiation or diffraction waves as shown in Fig.3 and Fig.4.
Fig.3 is the diffraction wave η1(x,y)eiωt and η2(x,y)ei2ωt at a time instant of ωt=0 for OHS hull form(a bulk carrier's hull form of CB=0.80, L/B=5.48) at ballast condition. The relative position of the ship is drawn by a slender rectangle. Magnitude of η2 to η1 (about 20%) in this example is found to be much larger than the second harmonic component of the incident waves (less than 5%) which is inevitably contained. We may conclude that the most part of η2 is generated not by the second harmonic component of the incident waves but by some nonlinear interaction of waves and body.
Several features of the diffraction wave shown in Fig.3 and 4 are:
-
Energy of other wave component than the component of the fundamental frequency is apparently very small. This means that added resistance due to the wave component other than the linear one may not be considerable.
-
The second harmonic component is significant at the fore front of the diffraction wave pattern where naturally the wave steepness is the largest. Amplitude of the second harmonics is as large as 10 % of that of the incident waves. It might suggest the wave breaking at the front of the diffraction waves.
-
No significant difference between the diffraction waves at full load and ballast conditions is observed.
Free wave component of η1(x,y) that is predominant away from the hull surface is expressed by
(2)
where
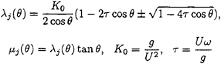
The direction θ of the component wave for which real value of λj does not exist is to be excluded from the integral (2).
A technique is already established of obtaining experimentally the function Fj(θ) with a Fourier transform of the measured waves on a line of y=constant (Ohkusu (1996)). Practically an extrapolation of the measured wave record to the location of x larger than some value is necessary since the record far behind the ship model is affected by the tank wall reflection and not to be used as the data for the transform. The expression (2) of the wave elevation is asymptotic one which is correct when |x| is sufficiently large but |y| is kept constant. Possible error in Fj(θ) due to a Fourier transform of the measured wave at a finite x was investigated by making use of theoretical wave elevation (Ohkusu and Iwashita (1986)). No considerable error was found especially for the dominant F2(θ).
At higher Froude number the diverging wave part of diffraction and radiation waves will prevail; the diverging wave components propagate into the directions θ close to π/2 and their wave length 2π/λj in the x direction is very long. Naturally the x-wise Fourier transform of η1(x, y) will not give accurate amplitude Fj(θ) of those components. In such cases the y-wise transform of η1(x,y) is plausible. This transverse transform is possible when the measured wave data as shown in Fig.3 and 4 are available. The wave pattern in Fig.3 and 4 exemplifies that diffraction waves vanish rapidly as y become larger; the transverse transform is more convenient for one may terminate the transform at a finite y.
Two wave components propagating into two different directions θ and θ* have an identical wave number in the y direction:
µ=µ1(θ)=µ1(θ*)
for µ>4(ω2/g)sin[cos–1(1/4τ)]
µ=µ1(θ)=µ2(θ*)
for 0<µ<4(ω2/g)sin[cos–1(1/4τ)]
Consequently the Fourier transform of η1 into y direction provides a linear sum of F1(θ) and F1(θ*) or F2(θ*) dependent on the value of µ as given in equation (3) and (4).
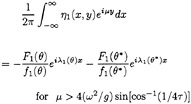
(3)
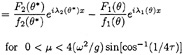
(4)
where
(5)
In order to determine F1(θ) and F2(θ) we repeat the transform (3) and (4) for the data η1(x,y) at more than two different x. We compute the left hand side of equation (3) and (4) with η1(xp,y) at several locations of xp(p=1,2,3,···,M) that distribute at an equal spacing along the length (2π/λ2(π)) from some distance behind the stern. We determine Fj(θ) such that equation (3) and (4) fit those values at different xp with the least error. For µ, for example, in 0<µ<(ω2/g)sin[cos–1(1/4τ)], the following is a simultaneous equation to determine F1(θ) and F2(θ*):
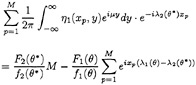
(6)
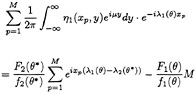
(7)
For µ>4(ω2/g)sin[cos–1(1/4τ)], F1(θ) and F1(θ*) will be determined in a similar manner with equation (4).
Fj(θ) that is determined by the transverse transform must be accurate for the component propagating into the direction θ ~ π/2. It is, however, supposed to be less accurate for the components whose crest lines are parallel or almost parallel to the y axis. However this is improved in our method by using the data at several xp covering the length 2π/λ2(π), the wave length of the component with the crest line parallel to the y axis.
Fj(θ) determined by the y-wise transform will give the wave structure behind the ship model because it uses the measured wave behind the stern. On the other hand x-wise transform is on the waves measured close to the bow. We expect that comparison of Fj(θ) for the components propagating forward of the ship obtained by both transforms will possibly give some information on the difference of far and near field wave characteristics.
In Fig.5 and 6 we compare relative magnitude of F1,2(θ) obtained by the x-wise and the y-wise transforms. They are of the diffraction waves due to a Series 60 model presented in the previous section. In those figures the abscissa β represents the angle of θ–α0 where α0 is the critical angle cos–1(1/4τ). F2(θ) is plotted to the right direction from β=0 but F1(θ) to the left direction. F1(θ) is negligibly small for larger angle θ. Naturally F1(α0)=F2(α0) as known from µ1(α0)=µ2(α0) and both curves are continuous at β=0. Reason of the plotting F2(β) for relatively small range of β is that only this part prevails in the contribution to added resitance. It is seen clearly that F1(θ) is very small compared with F2(θ)
Agreement of Fj(θ) by the x-wise and y-wise transforms is considerable except that the latter seems to represent more details of it. This is not surprising since the latter is supposed to give more accurate F2(θ) of the diverging waves (θ ~ α0 ~ π/2). The agreement of regardless of the full load (Fig.5) or ballast condition (Fig.6). This agreement suggests that our linear model of the wave given by equation (2) is correct in describing diffraction waves around a ship.
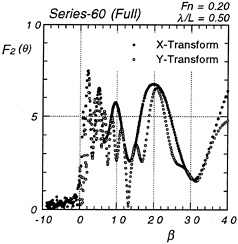
Figure 5: Fj(θ) of diffraction waves (full load)
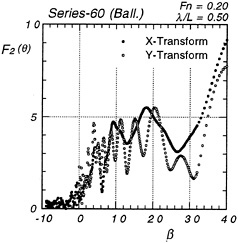
Figure 6: Fj(θ) of diffraction waves (ballast)
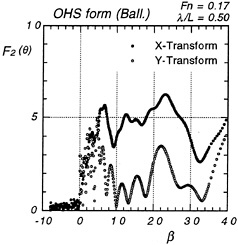
Figure 7: Fj(θ) of diffraction waves (ballast)
Fig.7 is a similar comparison with the diffraction waves of OHS form st ballast condition. The hull form has a big bulbous bow. Added resitance of this hull form particularly in head waves of short wave length and at ballast condition is unusually large as shown later. We see significant difference between Fj(θ) by the x and y-wise transforms. The disagreement suggests anomaly in the wave pattern of this hull form one can not describe by equation (2). However we can not find any considerable feature suggesting this anomaly of the wave in Fig.3. We may conjecture the the wave energy is disspated during its propagation from near to behind the ship. But we can not conclude definitely so and we can not either say that this anomaly of the wave is the cause of unusually large added resistance of this ship.
3
Computation of Diffraction and Radiation Waves
Full nonlinear treatment of radiation or diffraction waves generated by a running ship is not straightforward. Even linear or qusi-linear theory is not so easy to be numerically implemented (Sclavounos (1996), Iwashita et al. (1994)). A panel method using 3D Green function satisfying a full linear free surface condition at forward speed, for example, needs formidable computer time and the results are some-
time ambiguous when we compute the fluid pressure close to the free surface or the wave elevation close to the hull surface. We should develop a theoretical method robust as well as rational in predicting the diffraction waves particularly close to the ship bow.
We give the first priority to accurate prediction of the diffraction wave, the divergent wave component in particular, close to the bow part. We suppose the diffraction wave at the bow almost determines the fluid pressure that decides added resitance of the ship in the incident waves of short wave length. Moreover the divergent waves propagating into the direction θ~α0 to π/2 contribute much more to the added resistance than the transverse waves progressing into the direction θ~π. The divergent wave prevails at the bow part and therefore is to be accurately predicted. We must consider interacting effect by nonuniform steady flow close to the bow of the ship.
Consider a ship running at forward speed U in incident regular waves on deep water. Let (x, y, z) be a right-handed coordinate system fixed to the mean position of the ship; the z is vertically upward through the fore end of the ship, –x is in the direction of forward motion and the origin is in the plane of the undisturbed free surface. Here we restrict ourselves to diffraction waves for brevity of explanation.
The problem is formulated in terms of potential flow theory. The total velocity potential is expressed by
Φ=Ux+![]() S(x,y,z)+
S(x,y,z)+![]() 0(x,y,z)eiωt+
0(x,y,z)eiωt+![]() (x,y,z)eiωt (9)
(x,y,z)eiωt (9)
where ω is the circular frequency of encounter of the ship with the regular incident waves. ![]() S is the velocity potential of the steady flow due to the ship forward velocity,
S is the velocity potential of the steady flow due to the ship forward velocity, ![]() 0eiωt the velocity potential of the incident waves and
0eiωt the velocity potential of the incident waves and ![]() eiωt the velocity potential of the first harmonics of the diffraction waves.
eiωt the velocity potential of the first harmonics of the diffraction waves.
The boundary value problem for ![]() is simplified by introducing the slenderness parameter ε which represents the order of magnitude of the ratio of the beam or the draft to the ship length.
is simplified by introducing the slenderness parameter ε which represents the order of magnitude of the ratio of the beam or the draft to the ship length.
Faltinsen and Zhao (1991) gave a boundary value problem for the radiation wave ![]() derived from the assumptions ∂f/∂x=O(fε–1/2) ∂f/∂y, z=O(fε–1) in some region near the ship, where f is any flow variable caused by the ship. The first assumption is quite appropriate when we are concerned with the flow close to a relatively bluff bow, where the flow variation down the ship length is supposed to be not so small. The governing equation of
derived from the assumptions ∂f/∂x=O(fε–1/2) ∂f/∂y, z=O(fε–1) in some region near the ship, where f is any flow variable caused by the ship. The first assumption is quite appropriate when we are concerned with the flow close to a relatively bluff bow, where the flow variation down the ship length is supposed to be not so small. The governing equation of ![]() near the ship is two dimensional Laplace equation:
near the ship is two dimensional Laplace equation:
(10)
Their free surface condition is complicated one and must be satisfied on the steady water surface displaced from z=0. The relatively high steady wave elevation resulting from the first assumption for f does not admit the free surface condition of ![]() transferred onto z=0. This free surface condition, though it is linear with respect to
transferred onto z=0. This free surface condition, though it is linear with respect to ![]() , apparently produces an intricate situation for the diffraction wave; the incident waves coming far upstream which is usually assumed linear will be diffracted on the displaced free surface and the ship surface. Numerical implementation of this formulation has not been successful for the diffraction waves.
, apparently produces an intricate situation for the diffraction wave; the incident waves coming far upstream which is usually assumed linear will be diffracted on the displaced free surface and the ship surface. Numerical implementation of this formulation has not been successful for the diffraction waves.
Their formulation is yet attractive because it can deal with the bow flow rather correctly but by simpler way. It can account for the interaction effect of steady wave elevation considerable at the bow part on the diffraction wave. We introduce a rather inconsistent and simpler approach similar to it. Our simpler approach considers only weak interaction with the steady flow. Despite ∂f/∂x=O(fε–1/2) we assume the steady wave elevation is not so high and the free surface condition for ![]() is transferred to z=0. While we ignore
is transferred to z=0. While we ignore ![]() terms, we retain almost all other terms even if they are redundant. It yields the free surface condition when the ship is in head waves:
terms, we retain almost all other terms even if they are redundant. It yields the free surface condition when the ship is in head waves:
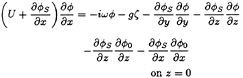
(11)
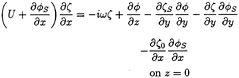
(12)
where ζeiωt represents the wave elevation due to ![]() eiωt, ζ0eiωt the elevation of the incident wave and ζS the steady wave elevation by
eiωt, ζ0eiωt the elevation of the incident wave and ζS the steady wave elevation by ![]() S.
S.
The difference of this free surface condition from usual linear free surface condition is the inclusion of the nonuniform steady flow and wave elevation represented by the terms of ![]() S and ζS. They will represent partly the effect of the steady flow on the unsteady wave making. The terms including ∂
S and ζS. They will represent partly the effect of the steady flow on the unsteady wave making. The terms including ∂![]() S/∂x
S/∂x
and ∂ζS/∂x are all retained in our formulation because they are likely to be numerically of considerable magnitude, though they are the redundant terms of higher order of magnitude in the formalism of our pertubation scheme.
![]() 0=iζAg/(ω–KU) exp(Kz–iKx) (K: wave number) satisfies linear free surface conditions without the terms including
0=iζAg/(ω–KU) exp(Kz–iKx) (K: wave number) satisfies linear free surface conditions without the terms including ![]() S and ζS:
S and ζS:
(13)
(14)
Nevertheless ![]() +
+![]() 0 must satisfy the free surface condition retaining the nonuniform steady flow and wave elevation represented by
0 must satisfy the free surface condition retaining the nonuniform steady flow and wave elevation represented by ![]() S and ζS. As a consequence the diffraction wave
S and ζS. As a consequence the diffraction wave ![]() involves a part to correct the difference of the actual free surface condition from (13) and (14). This part might be called a diffraction of
involves a part to correct the difference of the actual free surface condition from (13) and (14). This part might be called a diffraction of ![]() 0 by the nonuniform steady flow close to the ship. The last two terms of the right side of equation (11) and the last of equation (12) represent this effect. In other wave conditions than head seas some more terms appear to represent the effect.
0 by the nonuniform steady flow close to the ship. The last two terms of the right side of equation (11) and the last of equation (12) represent this effect. In other wave conditions than head seas some more terms appear to represent the effect.
The boundary value problem posed by equation (10), (11), (12) and the body boundary condition is solved starting from an appropriate condition at the bow to downstream. Equation (11) is used to forward the value of ![]() on z=0 into x direction with the right hand side computed on the current x; equation (12) updates the elevation ζ at new x value. The body boundary condition is imposed at the contour of a cross section at new x.
on z=0 into x direction with the right hand side computed on the current x; equation (12) updates the elevation ζ at new x value. The body boundary condition is imposed at the contour of a cross section at new x.
Condition imposed at |y|=∞ is two dimensional flow due to a vertical dipole at the center of the cross section. This condition is derived by the behavior at | y|=∞ with keeping x constant of a linear solution that satisfies the conditions (13) and (14) without the terms including ![]() S and ζS. The linear solution is given in the form of impulsive source distribution on the cross sectional contour (Ohkusu and Faltinsen (1990)). The flow at |y|=∞ and x constant due to an impulsive source is asymptotically the flow due to a vertical dipole (Stoker (1957)) and so is its distribution.
S and ζS. The linear solution is given in the form of impulsive source distribution on the cross sectional contour (Ohkusu and Faltinsen (1990)). The flow at |y|=∞ and x constant due to an impulsive source is asymptotically the flow due to a vertical dipole (Stoker (1957)) and so is its distribution.
One implicit assumption of this approach is that the flow downstream does not affect that upstream. It is well recognized (Ogilvie (1977)) that the flow by this approach does not contain the transverse waves. It does not, however, cause a trouble since our current concern is accurate prediction of divergent waves which are predominant in the vicinity of the bow; this method can account readily for the effect of the nonuniform steady flow which is also considerable close to the bow.
The steady flow ![]() S and wave elevation ζS to be substituted in equation (11) and (12) are linear solutions of almost the identical boundary problem given by equation (10), (13), (14) and the body condition.
S and wave elevation ζS to be substituted in equation (11) and (12) are linear solutions of almost the identical boundary problem given by equation (10), (13), (14) and the body condition.
The initial condition for ![]() will be generally one weak point in this approach if we wish to account for the flow around the blunt bow. Presumably true nonlinear and three dimensional flow in the vicinity of the bow is required for it, because the three dimensionality and the nonlinearity are supposed to be the strongest there. Generally this flow is not available.
will be generally one weak point in this approach if we wish to account for the flow around the blunt bow. Presumably true nonlinear and three dimensional flow in the vicinity of the bow is required for it, because the three dimensionality and the nonlinearity are supposed to be the strongest there. Generally this flow is not available.
We tried two alternatives for the initial condition: one is the zero condition as for ![]() and ζ, and another is a three dimensional solution at x=0 given by 3D panel method based on a linear free surface condition.
and ζ, and another is a three dimensional solution at x=0 given by 3D panel method based on a linear free surface condition.
(15)
However the results are almost identical regardless of two alternatives.
On the fluid plane of each section we employ the method described by Faltinsen (1983) for numerically solving 2D flow; the Green's second identity was used to represent the velocity potential ![]() in the plane in terms of a distribution of fundamental 2D source and dipole over the closed surface consisting of the body surface, the free surface z=0 and a control surface away from the body. Straight line segments were used to approximate all the control surface; constant value of the velocity potential and its normal derivatives were assumed over each segment. The contribution to the velocity potential from the control surface away from the body is zero because we assume no waves exist there. But the contribution from the free surface far away from the body is approximated by the flow due to a single vertical dipole at the center of the body section.
in the plane in terms of a distribution of fundamental 2D source and dipole over the closed surface consisting of the body surface, the free surface z=0 and a control surface away from the body. Straight line segments were used to approximate all the control surface; constant value of the velocity potential and its normal derivatives were assumed over each segment. The contribution to the velocity potential from the control surface away from the body is zero because we assume no waves exist there. But the contribution from the free surface far away from the body is approximated by the flow due to a single vertical dipole at the center of the body section.
Data for numerical computation: For OHP form at the ballast condition, in which a large bulbous bow protrudes in front of the bow, the initial point of the calculation is its leading tip and the step Δx to forward the solution is 0.002 of the ship length L and the size of the free surface to the control surface is selected as large as 3.2 L. The free surface is divided into the segments of 0.007 L size at the least. We need not such fine mesh particularly for x of a Series 60 model which is less bluff at the bow. Actually
we found Δx=0.0033L gives sufficiently stable solutions.
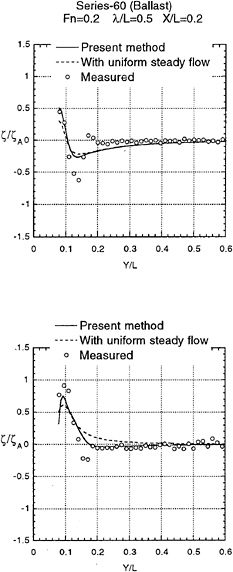
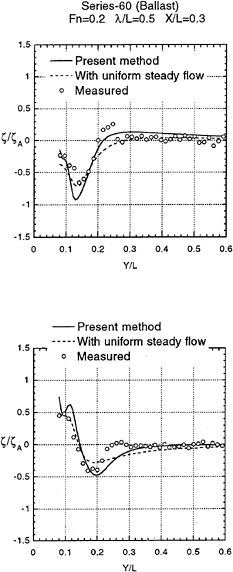
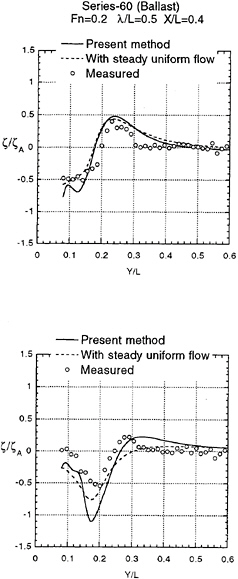
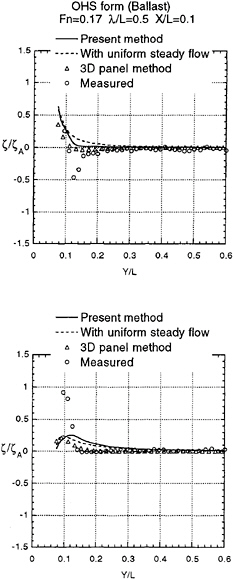
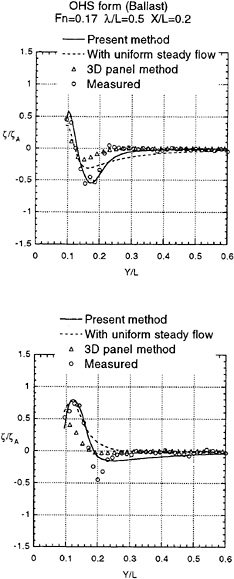
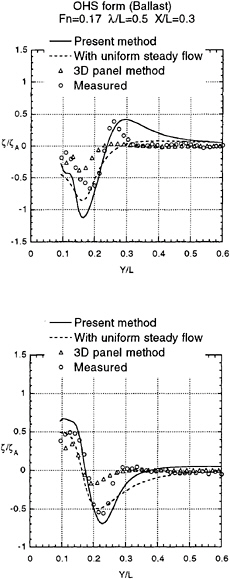
Validity of our approach is tested by comparing the computed wave form with the measured as shown in Fig.3 and 4. Variation into y direction of ζ at ωt=0 and at ωt=π/2 of the diffraction wave is plotted in Fig.8 to 15 at several positions down the ship length x/L=0.1,0.2,0.3 and 0.4. Fig.8 to Fig.11 for a Series 60 (CB=0.8) and in Fig.12 to 15 for OHS form. Both are at ballast condition. ζA is the amplitude of the incident waves.
Numerical results with uniform steady flow U with ignoring the terms of ![]() S and ζS on the right side of equation (11) and (12) are compared. The results by 3D panel method based on the free surface condition (15) (Iwashita (1996) private communication) are plotted too. The present method is the best in terms of the correlation with the measured wave.
S and ζS on the right side of equation (11) and (12) are compared. The results by 3D panel method based on the free surface condition (15) (Iwashita (1996) private communication) are plotted too. The present method is the best in terms of the correlation with the measured wave.
With closer look of the results we conclude:
-
Our method considering the effect of nonuniform steady flow demonstrates better agreement closer to the bow.
-
3D panel method gives the better results than others when we come further down stream. This is natural because it account for the effect of the transverse wave correctly. However at the location very close to the hull surface 3D panel method does not always give good result. It might be due to the difficulty of numerical implementation of the method at the intersection of the free surface and the hull surface.
-
The predicted wave elevation at x/L=0.1 is much lower than the measured. The worse correlation at the place closer to the bow is of course due to our unappropriate initial condition (
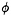 =ζ=0). In order to obtain the better result at this location we need real three dimensional solution at x=0 for the initial condition which is valid on nonuniform steady flow in front of the bow.
=ζ=0). In order to obtain the better result at this location we need real three dimensional solution at x=0 for the initial condition which is valid on nonuniform steady flow in front of the bow. -
∂
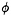 S/∂x affects the computational results consididerably. It is due to its substantial magnitude at closer to the bow. Apparently inclusion of this term improves numerically the correlation with the measured. This is rather contradicting however because if the steady flow velocity in x direction is large enough to make U+∂
S/∂x affects the computational results consididerably. It is due to its substantial magnitude at closer to the bow. Apparently inclusion of this term improves numerically the correlation with the measured. This is rather contradicting however because if the steady flow velocity in x direction is large enough to make U+∂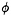 S/∂x small, then the diffraction wave propagates upstream and the present method assuming no effect from downstream to upstream is invalidated.
S/∂x small, then the diffraction wave propagates upstream and the present method assuming no effect from downstream to upstream is invalidated.
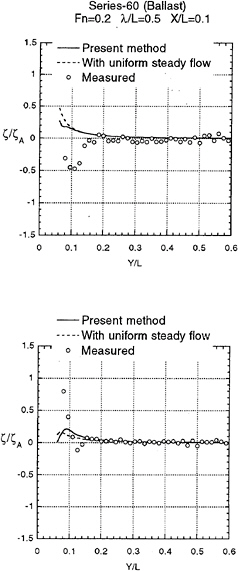
Figure 8: Wave Elevation at ωt=0 (upper) and ωt=π/2 (lower)
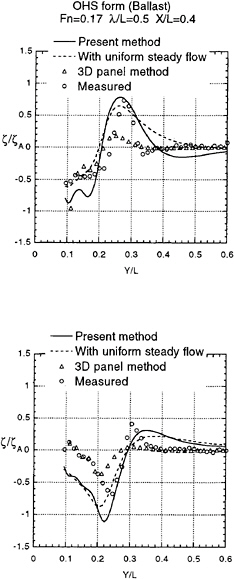
Figure 15: Wave Elevation at ωt=0 (upper) and ωt=π/2 (lower)
Figure 16: Added Resitance of OHS form
4
Added Resistance
One purpose of this study is an improvement of the accuracy of added resitance prediction. Very large added resitance of shallow draft and blunt bow ships at short wvae length is reported (SR211(1993)).
In waves of small length the ship does not oscillate. Consequently one can ascribe the larger added resitance to the diffraction wave supposed to be larger for the blunt bow hull forms. If it is true, the present method which we confirmed is able to compute the diffraction waves more correctly than other approaches may possibly predict added resitance of those hull forms more correctly.
We integrate x component of fluid pressure given by the present theory on the hull surface correct to the second order O(![]() 2) and take its time average to obtain added resitance ΔR due to the wave diffraction:
2) and take its time average to obtain added resitance ΔR due to the wave diffraction:
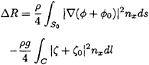
(16)
The first integral is over the wetted surface of the ship S0 below z=0 and the second integral over the water line contour C. nx is x component of the vector normal to the hull surface and directing into the fluid.
Other way to compute added resistance is to integrate Fj(θ) of the diffraction and radiation waves multiplied with a weighting function with respect to θ. Integration of the measured Fj(θ) will give added resitance directly derived from the measured wave energy. Added resitance, for example, in head seas is given by
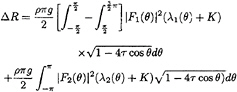
(17)
where K is the wave number of the incident waves. The range of α0<θ<α0 is to be excluded from the integration. In our numerical computation the integral on F1(θ) was carried out only for α0<θ<π/2 and the contribution from other θ was ignored. Reason is that the measured F1(θ) is genarally very s mall and actually the contribution to the total added resitance is negligible. Moreover F1(θ) is the amplitude of the wave component of so small length that any kind of experimental technique may not have enough resolution.
Added resitance plotted in Fig.16 by rectangles is the resitance measured as a force on the ship model (OHS form) in head waves and at ballast condition. Magnitude of added resitance of this hull form particularly in the range of small wave length is unusually large. It naturally includes the effect of heave and pitch in large wave length, say λ/L>0.75. But in smaller wave length the ship does not move and the motions will have no effect on added resitance; at such wave length, for example at λ/L=0.5 ~ 0.6, added resitance is supposed to be due to the diffractopn wave alone.
Solid line represents added resitance due to the diffraction wave which was computed by substituting the velocity potential and wave elevation obtained by the present theory into equation (16). Two circles in this figure are the value obtained by equation (17) with the measured Fj(θ) of the diffraction wave.
Despite accurate prediction of the wave elevation and accurate correlation with the added resitance obtained from the measured wave elevation, the present theory cannot account for such a large added resitance value of OHS form at ballast condition. One thing which the present theory does not consder will be the wave generated in front of the bow. This weak-point was already guessed from the disagreement observed in the wave close to the bow part (Fig.8 and 12). Presumably the high wave in front of the bow will be steep and have higher harmonic component. Nevertheless we found its energy is not considerable.
5
Summary
We have presented an improved technique to measure the radiation and diffraction wave field generated by a ship running in waves at forward speed. Attempt was focussed on capturing complete energy of the waves without letting the energy of the second harmonics escape. We have succeeded in showing the whole picture of the radiation and diffraction wave based on the data obtained at tank test. It is usually invisible at tank test. With experiment by new technique we found the energy of the second harmonics of the diffraction wave is not considerable.
We proposed an analytical method, simple for numerical implementation but considering the interaction of the steady and unsteady flow prominent at the bow of the ship, to predict the elevation of radiation and diffraction wave and resulting fluid pressure. We tested the present analytical method on the comparion of the predicted wave elevation with the measured one by our new technique and confirmed its accuracy. However the present theory is not sucessful in predicting large added resitance of a shallow draft ship. More work on the wave formation in front of the bow will be required.
References
Faltinesen, O. and Zhao, R.: “Numerical Predictions of Ship Motions at High Forward Speed”, .Trans. Royal Soc. London A. 1991
Iwashita, H. and Ohkusu, M.: “The Green Function Method for Ship Motions at Forward Speed” Ship Technology Research 39(2) 1991
Iwashita, H., Okada, T., Itoh, A., Ohkusu, M., Takaki, M. and Mizoguchi, S.: “Wave Forces Acting ona Blunt Ship with Forward Speed in Oblique Sea ”, J. Society of Naval Architects Japan vol.176 1994
Naitoh, S., Nakamura, S. and Nishiguchi, A.: “Added Resistance in Regular Head Waves of a Ship with Blunt Bow”, Proc. 3rd Symp. on Practical Design of Ships and Mobil Units, Trondheim, 1987
Ohkusu, M: “Added Resistance in Waves of Hull Forms With Blunt Bow” Proc. of 15th Symp. on Naval Hydrodynamics 1984
Ohkusu, M. and Iwashita, H.: “Radiation and Diffraction Wave Pattern of Shps with Forward Speed ”, Trans. West-Japan Society of Naval Architects 73 1986
Ohkusu, M. and Faltinesen, O.: “Prediction of Radiation Forces on a Catamaran at High Froude Number ”, Proc. 18th Symp. on Naval Hydrodynamics 1990
Ohkusu, M: “Hydrodynamics of Ships in Waves”, Advances in Marine Hydrodynamics, Computational Mechanics Publications 1996
Ogilvie, T.F.: “Singular Perturbation Problems in Ship Hydrodynamics”, Advances in Applied Mechanics 17 Academic Press 1977
Sclavounos, P.: “Computation of Wave Ship Interaction” Advances in Marine Hydrodynamics, Computational Mechanics Publication 1996
SR211: “Study on Improvement of Middle Size Bulk Carriers Performance”, Report of Japan Ship Research Association 1993
Stoker, J.J.: “Water Waves”, Interscience Publishers 1957
DISCUSSION
C.M.Lee
Pohang Institute of Science and Technology, Korea
This paper presents one of the most fundamental aspects of the problems associated with the wave-excited ship motion. In the process of validating analytical methods, it is very important to check how accurately we are predicting the individual components of waves generated by a ship moving in waves. In this regard, this paper shows the proper direction in which we have to focus our investigations.
I would like to suggest that we should validate our panel codes by comparing with the results presented in this paper for each component of waves generated by a ship, i.e., the waves generated by the forward translation, diffracted waves, and radiated waves. We may then be able to find out where the deficiencies are with our panel codes.
AUTHOR'S REPLY
NONE RECEIVED