A Multigrid Velocity-Pressure-Free Surface Elevation Fully Coupled Solver for Calculation of Turbulent Incompressible Flow Around a Hull
B.Alessandrini, G.Delhommeau (Ecole Centrale de Nantes, France)
1.
ABSTRACT
This paper deals with the calculation of free surface flow of viscous incompressible fluid around the hull of a boat moving with rectilinear motion. An original method to avoid a large part of the theoretical problems connected with free surface boundary conditions in three-dimensional Navier-Stokes-Reynolds equations is proposed here.
The linearised system of convective equations for velocities, pressure and free surface elevation unknowns is discretised by finite differences and two methods to invert the resulting matrix are presented here.
A k-ε model solving two transport equations is used for the calculation of turbulent viscosity.
Numerical results are presented on the Series 60 CB=0.60 ship model.
2.
INTRODUCTION
Today most of the computing codes solving Navier-Stokes equations, including free surface effects, take their numerical algorithms in double model theory [1] [2] [3] [4]. The method is based on uncoupling of velocity and pressure unknowns on one side and free surface elevation calculated using kinematic condition on the other side. This evolution of hydrodynamic softwares seems reasonable but free surface boundary conditions reveal some unpredictable difficulties.
The use of kinematic equation for free surface height calculation when velocity field is known necessarily involves adding of non physical boundary conditions which do not allow neither resolution of tangential dynamic conditions nor introduction of viscosity or surface tension effects. This phenomenon takes of course more consequences when the discrete free surface elevation is located on nodes of the grid, setting unknowns on the singularity of kinematic condition at free surface and hull intersection. Moreover, in this case, pressure Dirichlet condition and continuity equation under free surface cannot be satisfied together. This formulation leads at last to a software inefficient in taking into account the complete free surface boundary conditions particularly near the hull and unable to verify the global conservation of mass.
Theoretical and numerical resolution of these problems seems essential and constitutes the present objective of this study. We propose to solve the Three Dimensional Navier-Stokes Reynolds equations, with Newtonian closure, written in the convective form in a curvilinear computational space, fitted at each time to the hull and the free surface.
A k-ε model solving two transport equations for kinetic energy and turbulence dissipation is used. Near the hull a Jones-Launder low Reynolds formulation [5] has been developed. The main boundary conditions are the no-slip condition on the hull and the fully non-linear free surface conditions written on the real position of the surface.
A dual unknown location on the volumic grid associated to the Rhie & Chow interpolation technique is used for the construction of pressure equation. The three components of velocity are located on the nodes of the grid, pressure at the centre of elementary volumes and free surface elevation at the centre of free surface interfaces.
Transport equations are written on the nodes of the mesh, the pressure equation is solved at the centre of elementary volumes and normal dynamic free surface condition at the centre of the free surface interfaces. The two tangential dynamic conditions and the kinematic condition form the set of velocity boundary conditions on the free surface.
The fully linear system obtained by second order finite difference schemes for the velocity components, the pressure and the free surface unknowns is solved at each iteration using a multigrid method with three levels of grid. A generalised Rhie & Chow technique is used to ensure the invertibility of the pressure block.
Numerical results concerning the free surface, the velocity and the pressure field around a Series 60 CB=0.60 (Rn=4.5.106, Fn=0.316) show a good agreement with experiments. The problem of singularity of kinematic condition on the hull is well solved and we can calculate the formation of unsteady meniscus near the wall in the whole boundary layer.
Efficiency of k-ε model, in spite of free surface conditions, waves, pressure and velocity fields are presented here, for the steady state and also during the unsteady phase.
3.
EQUATIONS
Navier-Stokes-Reynolds equations are written under a convective form for a three-dimensionnal turbulent flow in a Newtonian incompressible fluid. The 3 components of velocity (ui), pressure (p) including the gravitational effects (ρgx3) and turbulent kinetic energy (2/3ρk) are the dependant unknowns. Independent unknowns are the 3 directions of curvilinear co-ordinates (ξi) and the time (t), (xi) is the Cartesian basis and Ua the forward velocity, the curvilinear system is chosen to simplify boundary conditions on the hull and on the free surface. ξ2=0 et ξ3=0 are the equation of wetted part of the hull and of the free surface respectively at each time.
A partial four-dimensionnal transformation of the Cartesian space moving with time in a curvilinear computation space is then applied. The metric of this transformation uses covariant basis (ai) and contravariant basis (ai), contravariant metric tensor (gij), control grid functions (fi) and deformation velocities of the computational domain ![]() . Transport equations in the frame moving with the hull are written:
. Transport equations in the frame moving with the hull are written:
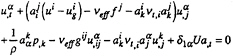
(1)
and the continuity equation:
(2)
A classical k-ε model is given for completely developed turbulent flow and does not allow to describe parietal flow where the turbulent viscosity is negligible versus molecular viscosity. The Jones and Launder' s model [7] allows to integrate transport equations up to the wall. It gives the damping function, describing attenuation of turbulence, as a function of turbulent Reynolds number ![]() In the curvilinear space (ξi,t) the two transport equations for k and
In the curvilinear space (ξi,t) the two transport equations for k and ![]() are:
are:
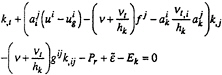
(3)
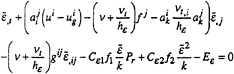
(4)
Turbulent viscosity is given by:
(5)
f1, f2 and fµ are given as functions of turbulent Reynolds number:
f1=1, f2=1–0,3exp(–Rt2)
fµ=exp(−2,5/(1+Rt/50)) (6)
The production term and the two other source terms are given by the following expression, n being the normal at the hull and Vt the tangential velocity:
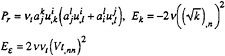
(7)
Numerical values of constants are:
Cµ=0,09, Cε1=1,44, Cε2=1,92
hk=1, hε=1,3 (8)
4.
BOUNDARY CONDITIONS
The previous formulation implies to have boundary conditions for the velocity field, the kinetic energy and the turbulence dissipation. But no other equation is needed to give pressure or free surface elevation on the boundaries. Particularly, there is no algebraic interpolation in the vicinity of the wall. We note Γc the hull, Γe the external boundary, Γa the symmetry plane and Γs the free surface.
We use on k and ![]() the following boundary conditions:
the following boundary conditions:
(9)
It is known by experiments [3] that the turbulent viscosity is greatly damped on the free surface. This fact justifies the boundary conditions given by (9). However, the decrease is very local and its influence on the results presented in this paper is weak.
Boundary conditions for the velocity field on other boundaries than Γs are given by:
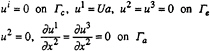
(10)
Boundary conditions on Γs are one kinematic condition, two dynamic tangential conditions and one normal dynamic condition. The kinematic condition, coming from the continuity hypothesis, expresses that the fluid particles of free surface stay on it. To write this condition in a curvilinear frame, we must remark that h is only a function of two independent variables on the surface. Noting (bi) the contravariant basis of the metric bidimensionnal transformation, we have:
(11)
Numerical difficulties at the intersection of the hull with free surface come from this equation. We have to satisfy both no-slip condition and free surface condition on the intersection. If we put directly no-slip condition into free surface equation without care, one can deduce that ∂h/∂t=0. This conclusion is not verified by experiment and shows the singular numerical behaviour of kinematic condition on the intersection. Mathematically, the only way for the free surface to move is to become tangential to the hull. In this case, the value of the Jacobian of the transformation is zero and kinematic condition cannot be used on the hull.
Dynamic conditions are given by the continuity of strains at the free surface. If we suppose that pressure is constant above the free surface, normal dynamic condition is:
(12)
where γ is the superficial tension coefficient and r the free surface medium curvature radius. The tangential dynamic conditions are simply given by a linear combination of first velocities derivatives:
(13)
5.
DISCRETISATION OF EQUATIONS
The discrete components of velocity ![]() kinetic energy (Ki) and turbulence dissipation (Ei) are located along the curvilinear co-ordinates lines defining the volumic grid (Ω), which allows to write easily the boundary conditions on (∂Ω). Pressure unknowns (Pk) are located at the centre of elementary volumes (Ωv) to ensure mass conservation without special treatment at the boundaries. Free surface elevation (Hk) is located at the centre of free surface interfaces (∂Ωsi) avoiding the singularity of kinematic free surface condition. ∂Ωs are the points of Ω belonging to the free surface only and ∂Ωb is the complementary of ∂Ωs in ∂Ω.
kinetic energy (Ki) and turbulence dissipation (Ei) are located along the curvilinear co-ordinates lines defining the volumic grid (Ω), which allows to write easily the boundary conditions on (∂Ω). Pressure unknowns (Pk) are located at the centre of elementary volumes (Ωv) to ensure mass conservation without special treatment at the boundaries. Free surface elevation (Hk) is located at the centre of free surface interfaces (∂Ωsi) avoiding the singularity of kinematic free surface condition. ∂Ωs are the points of Ω belonging to the free surface only and ∂Ωb is the complementary of ∂Ωs in ∂Ω.
All numerical schemes used in the remaining part of this chapter are second order schemes.
5.1
Discretisation of transport equations
This discretisation needs a linearisation of equations: convection velocities and a part of turbulence terms are computed at the previous time step. Convection terms are computed with an upward second-order scheme and need a 13 points grid. Diffusion terms need a 7 points grid and the cross second derivatives are in the source terms. Pressure gradient is computed on the nodes with a 8 points grid. So we have at node i:
(14)
5.2
Discretisation of transport equations for kinetic energy and turbulence dissipation
Transport equations for k and ε have the same form after the linearisation as the convection-diffusion equations, the fundamental difference coming from the linear coupling between k and ε. The terms in factor of Cε1 and Cε2 are not in the source terms, but are implicit when ε is introduced in the convection terms. Discretisation with second-order scheme gives:
(15)
5.3
Discretisation of free surface conditions
Uncoupled methods use classically kinematic equation to compute free surface elevation and dynamic normal condition, without viscous terms, as a Dirichlet condition on the pressure. The problem of these methods has been described, so we use here a completely different algorithm. The two tangential dynamic conditions associated with kinematic condition give the 3 boundary conditions on the velocity at the free surface and normal dynamic condition allows to compute the free surface elevation.
With this formulation, we linearise the kinematic condition as a implicit relation between the 3 velocity components and the free surface elevation:
(16)
Spatial derivatives of free surface elevation in the terms Ai are expressed with second-order centred schemes on a 4 points grid. Unsteady term is computed by a 3 points non-centred scheme. ![]() is the free surface elevation on the nodes of free surface given by interpolation of H, so the discrete expression of kinematic condition is:
is the free surface elevation on the nodes of free surface given by interpolation of H, so the discrete expression of kinematic condition is:
(17)
Discretisation of the two tangential dynamic conditions on a 6 points grid can be written:
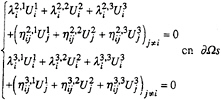
(18)
The three equations (17) and (18) are free surface velocity field boundary conditions.
To obtain a well-conditioned system, we solve analytically, on each node, the linear system of 3 equations (17) and (18) for the unknowns Ui. The boundary conditions are solved together and become:
(19)
It must be noted that a better conditioning of equation (19) is obtained by avoiding to centre the derivatives of the tangential dynamic conditions in the way to maximise the absolute value of coefficients λii.
Discretisation of normal dynamic condition gives no problem. Viscous terms are explicit in the RHS. The only point to note is that the pressure is known at the centre of control volumes and the free surface at the centre of free surface interfaces. Pressure at free surface is linearly extrapolated with 2 points.
Hk+(χsp)kjPj=fhk on ∂Ωsi (20)
5.4
Discretisation of continuity equation, use of a generalised Rhie and Chow method to obtain pressure equation
The Rhie and Chow method is commonly used to obtain, from continuity equation, a pressure equation without spurious modes. This method gives for the double model an infinity of solutions differing by a constant and numerical solution needs the compatibility of RHS. In the case of free surface problem, the new boundary conditions ensure invertibility of linear coupled system and unicity of the solution. Unfortunately, due to the pressure block, numerical convergence is poor. A method giving an invertible and well conditioned pressure block is used. All free surface conditions are explicitly introduced into the continuity equation for calculation of the divergence. The symbols with a ~ or a line above are respectively interpolated on the nodes of the mesh or at the centre of free surface interfaces.
Free surface elevation is eliminated of equation (19) using normal dynamic condition (20):
(21)
If we introduce the secondary unknowns ![]() the 3 transport equations and 3 free surface conditions can be expressed at the centre of each interface (Ωi) under the following form:
the 3 transport equations and 3 free surface conditions can be expressed at the centre of each interface (Ωi) under the following form:
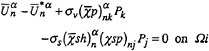
(22)
with:
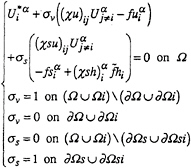
(23)
Pressure equation is obtained by cancellation of the divergence on the control volumes. The case σs=0 is the classical Rhie and Chow method and gives an ill-conditioned system. Introduction of boundary conditions for the divergence calculation under free surface (σs≠0) corrects the previous equation and
gives a system easy to solve numerically. Pressure equation becomes:
(24)
6.
COUPLED SOLUTION
The coupled linear system matrix is:
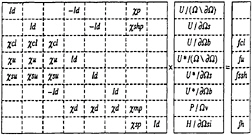
The linear system allowing to obtain kinetic energy and the dissipation of turbulence is solved independently. So it is necessary to summarize the equations at each step to obtain the velocity, the pressure and the free surface elevation. The transport equation is written on Ω\∂Ω (14), the relation between the main and secondary unknowns on Ω\∂Ω (23), the kinematic and tangential dynamic conditions on ∂Ωs (21), the implicit definition of secondary unknowns compatible with the values taken by σv and σs on ∂Ωs (23), boundary conditions on velocities and the implicit relations for secondary velocity unknowns on ∂Ω, the normal dynamic condition on ∂Ωsi and the pressure equation on Ωv (24). It is important to note that no condition on pressure or free surface elevation is needed.
The main interest of the discretisation of the present method is that the velocities-pressure block is uncoupled with the free surface in the linear system. The solution for velocities and pressure can be obtained independently from free surface elevation, which can be computed at the end of each time step by the normal dynamic condition.
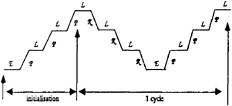
Figure 1 presents the general resolution algorithm of unsteady Navier-Stokes equation. The most expensive step concerns the resolution of linear systems for k-ε solver on one side and for velocities, pressure and free surface unknowns on other side.
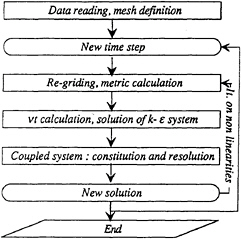
Figure 1, General resolution algorithm
7.
SOLUTION OF LINEAR SYSTEM
Linear system for turbulence kinetic energy and turbulence dissipation issued from k-ε model is first solved.
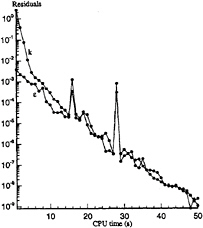
Figure 2, Convergence of k-ε system
This system is well conditionned and easily invertible by a classical CGSTAB (accelerated and stabilised bi-conjugate gradient) without any preconditioning.
Unfortunately the fully coupled linear system for the velocities, pressure and free surface elevation unknowns is very ill-conditionned, particulary the χmp block concerning the incompressible pressure equation, that means the mass conservation. So classical iterative methods are not available to solve this very large system. Two up to date iterative methods have been tested in this paper.
First method consists on the amelioration of CGSTAB algorithm using matrix preconditioning. The second method is based on linear multigrid algorithms.
7.1
Preconditioning of CGSTAB algorithm
Preconditionning CGSTAB algorithm consists in multiplying the system matrix A and the right side of discrete equations f by the same matrix M in order to decrease the conditioning number of the resulting matrix. The system becomes:
Ax=f ⇔ (MA)x=(Mf) (25)
If M=Id (identity matrix), it is clear that there is no preconditioning. M=A−1 is the more effective theoretical preconditioning, but in this case A−1 is still to be computed. A classical way to calculate the preconditioning matrix M is to express it under an approximation form of A−1 by an incomplete LU decomposition [1]. This decomposition is very easy to perform on a multi-diagonal matrix but here the matrix structure is much more complicated. Moreover a large part of sub-system is well-conditionned. The pressure equation (χmp block) only is ill-conditionned and gives the divergence of single CGSTAB algorithm. So incomplete LU decomposition on the full matrix is not very suitable because of the algorithm complexity and the excessive cpu time increase. The solution proposed here is to perform an incomplete LU decomposition on the multi-diagonal pressure block only. The conditioning matrix becomes:
where LUp is the incomplete LU decomposition of χmp block. The figure 3 present the performance of this iterative method to solve the fully linear system during a current iteration of flow calculation around a Series 60 CB=0.60.
7.2
The Full Multi-Grid algorithm
In order to improve the cpu time a second fully coupled system solver has been tested: the linear multi-grid method and its improvement, the Full Multi-Grid algorithm.
Iterative relaxation methods (Jacobi, Gauss-Seidel, SLOR) to solve linear system work very well in smoothing hight spatial frequencies of the error but fail in smoothing low frequencies. So the principle of bi-grid method is:
-
to smooth the hight frequencies of the error on the fine grid using iterations of relaxation method
-
to restrain the residuals (essentially low frequencies on the fine grid) on a coarse grid
 and compute the error system exact solution to eliminate low frequencies
and compute the error system exact solution to eliminate low frequencies 
-
to prolong the error system in order to correct the solution on the fine grid
Multi-grid algorithms are defined recursively using multi-grid algorithm to solve the linear system on the coarse grid (step (ii)). So linear multi-grid method are entirely given by:
-
The smoothing method on the fine grid
-
The restriction operator of residuals on the coarse grid
-
The linear solver on the coarser grid
-
The prolongation operator on the fine grid
A classical cycle of multi-grid algorithm (4 grids) can be presented like this:
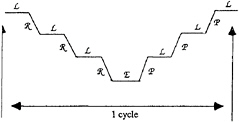
The smooting method is based on a Jacobi algorithm. However, because of the very large mesh stretching in one direction (normal to the body) the smothing of the error on the hull parallel planes is not very efficient. So the CGSTAB+ILU method is used before that in order to decrease all the components of the residuals.
The restriction operators allow to calculate the coarse grid residuals with the fine grid residuals. The classical injection is used for the unknowns located on the nodes of the grid (velocities). Concerning the unknowns located at the centre of each elementary volume an algebraic interpolation with the height adjacent nodes on the fine grid is necessary.
The solution on the fine grid is corrected using prolongation of coarse grid residuals. Generally algebraic interpolations work well but in the case of boundary unknowns located at the centre of each cells (the pressure in this case) an extrapolation between the coarse grid and the fine grid is necessary. This extrapolation on the boundaries is a major problem because of important errors generation on the fine grid solution.
There are two classical ways to obtain the linear operator on the coarse grids. First way is the construction of operator using prolongation and restriction operations (Galerkin method) and second way is to apply a new discretisation on the coarse grid. Galerkin method is very effective when the linear system is basic but in the present calculation fully coupled matrix is very complicated and Galerkin method seems very hard to code. So a new discretisation on the coarse grid has to be chosen.
The exact solution on the coarser grid is obtained using CGSTAB+ILU process described in the previous paragraph.
Full Multi-Grid algorithm (FMG) is a very efficient way to initialize multigrid algorithm. Initial solution on the fine grid is computed by successive prolongation and smoothing of the exact solution calculated ont the coarser grid. This method is very easy to apply when prolongation and smoothing operators are coded. FMG algorithm can be presented like this:
The convergence of FMG and CGSTAB+ILU algorithm are compared on the figure 3 for velocity residuals.
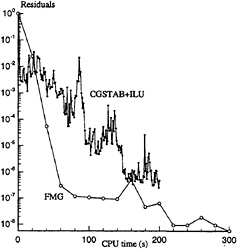
Figure 3, velocity residuals with FMG and CGSTAB+ILU
First FMG cycles (white symbols) are very efficient and the residuals decrease very quickly but after 5 or 6 cycles the convergence slows down due to saturation of smoothing process. I think Galerkin method could improve this situation and should be a new research orientation.
8.
NUMERICAL RESULTS
Numerical results of this method are presented here. The calculations are performed on a Series 60 CB=0.6 hull for a Reynolds number Rn=Ua.l/v=4.5.106, a Froude number ![]() and a Bond number Bn=ρgl2/γ=1.33.106. Two O-O topology grids are compared: a coarse grid with 190 905 nodes (89×65×33) and a fine grid with 314 265 nodes (105×73×41).
and a Bond number Bn=ρgl2/γ=1.33.106. Two O-O topology grids are compared: a coarse grid with 190 905 nodes (89×65×33) and a fine grid with 314 265 nodes (105×73×41).
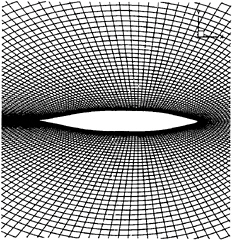
Figure 4, free surface view of the volumic mesh
Figures 4 and 5 show two different views of the coarse volumic mesh around the Series 60 hull. Three zones are considered on the grids. The first one, which first calculation point is located at 1.10−5 of the hull is streched on the whole boundary layer to take into account no-slip condition without wall function, a second zone without stretching with a non-dimensional radius R=1 well to compute the gravitational effects (waves propagation) and a third zone with a non-dimensional radius R′=15 very stretched to damp the waves up to the external boundary

Figure 5, lateral view of the volumic mesh
To obtain a steady state 300 time iterations are necessary. A non dimensional time step τ=0.020, corresponding to a non-dimensional final duration T=6, are necessary. The CPU time is about 30 hours in a HP-J200 workstation.
Starting calculation with the final boat speed is physically the same as suddenly introducing a hull in a water-circulating channel. A shock is created on the free surface and this requires an important sub-relaxation of the velocity field and free surface elevation to converge. In order to avoid this problem the calculation simulates an uniform acceleration to reach the final speed. The unsteady boat speed is computed according to the figure below.
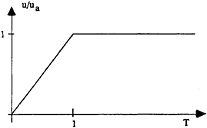
Figure 6, unsteady boat speed
8.1
Turbulence model
It has been shown in a previous paper [2] that Baldwin-Lomax model is efficient for non free surface flows but very unstable combined with free surface boundary conditions. The calculation of ymax parameter presents important instabilities which reflect on the turbulent viscosity calculation. So general iterative process converges with a lot of difficulties. Moreover, the vorticity increase on the crests and on the hollows of free surface induces an increase of turbulent viscosity not in accordance with experimental values. So this model has been given up in favor of two transport equation of k-ε model.
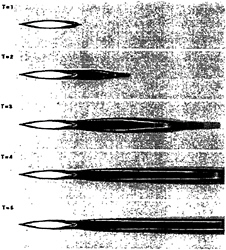
Figure 7, turbulent viscosity during the simulation
This last turbulence formulation allows to avoid all the numerical problems which appear with the Baldwin-Lomax model. The evolution of turbulent viscosity in space and in time is very smooth and does not produce divergence in the general process.
Figure 7 presents turbulent viscosity just under the free surface for various time steps during the simulation on the fine grid and figure 8 shows the same scalar in the x/l=0.4 section. We can see the hight regularity of turbulent viscosity which comes from k-ε model. Of course this argumentation is not complete and turbulent values have to be comparated with experiments. Unfortunately it seems that this experiments does not exist on the Series 60 CB=0.60. So, efficiency of turbulence model has to be evaluated through comparison on velocity profiles.
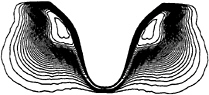
Figure 8, turbulent viscosity on the x/l=0.4 section
8.2
Free surface field
The originality of the method is its ability to take into account the exact free surface conditions in the whole space and particularly near the hull. Additional non physical boundary conditions, like Neumann conditions, are not required and the kinematic condition is solved, without smoothing, up to the first free surface elevation control point next to the body. Of course interpolation are necessary to compute free surface elevation on the nodes of the mesh and the contact line elevation requires an extrapolation but this is only for re-griding operation and the coupling with unknowns of the problem is very weak.
Figure 9 shows computed free surface field around the Series 60 hull for the two meshes. We can see good accordance between the two calculations. However a weak damping is noticeable on the coarse mesh and it seems that the convergence relative to the mesh is not yet obtained. Our opinion is that calculation on finer grid (aroud 500 000 nodes) is necessary to have a good grid convergence (that is to say independency of solution with the grid for the present Froude an Reynolds numbers).
The same conclusion can be made on figure 10 which presents free surface elevation along the hull located between x/l=–0.5 (bow) and x/l=+0.5 (stern). Numerical calculations on the two grids are
compared with experimentals results. We can observe a good accordance between computed and experimental values. The free surface crests on the bow and on the stern are well predicted but a light damping (of course more important on the coarse grid) can be noticed.
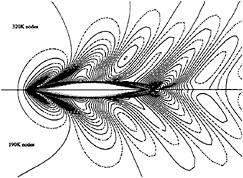
Figure 9, free surface field calculations on two grids
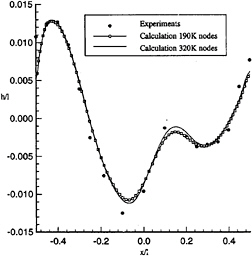
Figure 10, free surface elevation along the hull
Figure 11 present a comparison between measured and computed free surface field on the fine grid. Exploitation of this figure is quite difficult because of the noise in measurements. However experiment and calculation are in quite good agreement. Kelvin dihedron is more perceptible on the experimental values due to numerical damping of the calculation.

Figure 11, Comparison between measured and computed free surface field
8.4
velocity field
Figure 12 shows the calculated pressure fited on the wet part of the hull. We can see the difference between initial mesh and final mesh which defines fluid domain only. Wall streamlines are presented also in this picture. They correspond to the limit of velocity direction when the distance to the hull decreases to zero.

Figure 12, pressure and wall streamlines on the hull
The topology of wall streamlines shows accumulation lines near the kell on the stern which is very common on this kind of hull and traduces open
separation when the flow crosses the bilge. An accumulation is also present on the first crest on the bow and explains important dificulties to calculate the solution at this place.
It has been shown that the influence of grid size on free surface elevation is light despite a small damping of oscillations for the coarse grid. On the contrary the grid size is very important to compute well the velocity profiles connected to a good calculation of turbulent values in the boundary layer. The figure 13, 14 and 15 presents isolines of longitudinal velocity for the coarse grid (on the left) and the fine grid (on the right). In a section located at the bow (figure 13) numerical results are very similar but for the sections located at the stern, where viscous effects are more important, (figure 14 and 15) differences are very important. The influence of open separation on the accumulation line is much more noticeable with coarse grid calculation and the boundary layer is much more thick. Fortunately, Comparisons with experiment given below (figure 19 and 20), show that best results are obtained with finest grid calculation. Moreover the turbulent kinetic energy, the turbulent dissipation and, of course, the turbulent viscosity are very different in the two calculation.
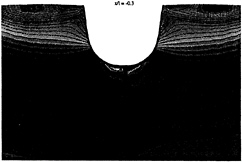
Figure 13, longitudinal velocity in x/l=–0.3 section for the coarse grid (left) and the fine grid (right)
Our opinion is that good calculation of turbulent quantities with a k-ε model and law Reynolds formulation and furthermore velocity components requires a lot of nodes in the boundary layer. In fact, regarding to turbulence phenomena finest grid is still too coarse.
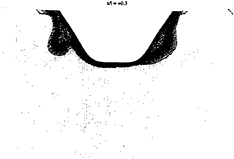
Figure 14, longitudinal velocity in x/l=+0.3 section for the coarse grid (left) and the fine grid (right)
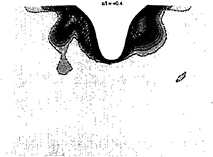
Figure 15, longitudinal velocity in x/l=+0.4 section for the coarse grid (left) and the fine grid (right)
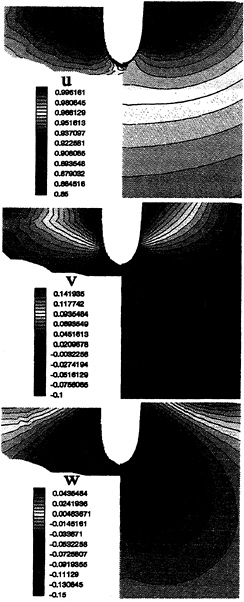
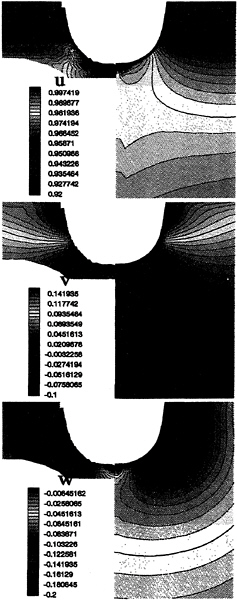
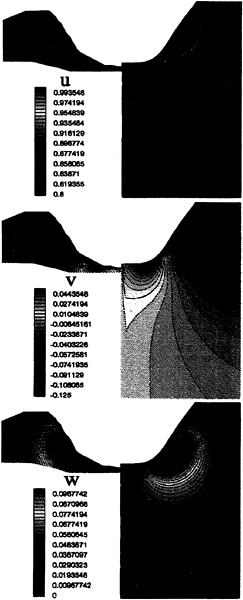
Figures 16 to 21 show the 3 cartesian components of velocity field in various fluid domain sections at the bow of Series 60 hull (x/l=–0.5, –0.4 and –0.3) and at the stern (x/l=+0.3, +0.4 and +0.5). The calculations on the fine grid are on the right of each picture and experimental data on the left. Agreement is very good for the three components particularly on the bow.
Stern numerical results are good too in spite of a light boundary layer thickness overestimate (figure 19, 20 and 21 at the top) and a vertical component underestimate (figure 20 at the bottom).
9.
CONCLUSION
The results presented here show the ability of fully coupled method to take into account the exact free surface conditions and to solve the kinematic condition near the hull in spite of the singularity of equations at free surface and hull intersection. However the finest grid size seems too coarse to compute well free surface elevation, pressure velocity field and especially turbulent quantities.
The continuation of this work will consist in perform calculation with finer mesh to obtain grid independency results (perhaps around 500 000 or 600 000 nodes). After this step it will be possible to consider the problem of turbulence modelisation and the influence of various schemes.
Short-dated study will concern comparisons between k-ε and k-ω turbulence model. Calculations on yawed hull and turning hull will be the long-dated work.
10.
ACKNOWLEDGMENTS
The authors express their thanks to the french Direction des Recherches et Etudes Techniques (DRET) of the Délégation Générale pour l'Armement (DGA) and the Institut du Développement et des Ressources en Informatiques Scientifique (IDRIS) of the CNRS which are supporting this work.
11.
REFERENCES
1. B.ALESSANDRINI, G.DELHOMMEAU, “Simulation of three-dimensional unsteady viscous free surface flow around a ship model”, International Journal for Numerical Methods in Fluids, vol 19, August 1994.
2. B.ALESSANDRINI, G.DELHOMMEAU, “Numerical calculation of three-dimensional viscous free surface flow around a Series 60 CB=0.6 ship model”, CFD WORKSHOP, Tokyo, March 1994.
3. I.CELIK, W.RODI, M.S.HOSSAIN, “Modelling of free surface proximity effects on turbulence”, Proc. Refined Modelling of Flows, Paris, 1982.
4. H.C.CHEN, W.L.LIN, K.M.WEEMS, “Interactive zonal approach for ship flows including viscous and nonlinear wave effects”, 6th international Conference on Numerical Ship Hydrodynamics, Iowa City, August 1993.
5. E.B.DUSSAN V, “On the spreading of liquids on solids surfaces: static and dynamic contact lines”, Ann. Rev. Fluid Mech., vol 11, 1979.
6. J.FARMER, L.MARTINELLI, A.JAMESON “Multigrid solutions of the Euler and Navier-Stokes equations for a series 60 Cb=0,6 ship hull for Froude numbers 0,160, 0,220 and 0,316”, CFD Workshop, Tokyo, March 1994.
7. W.P.JONES, B.E.LAUNDER, “The prediction of low Reynolds number phenomena with a two equation model of turbulence”, International Journal of Heat Mass Transfer, vol 16, 1972.
8. E.E.MARKOVITCH, “Effect of free surface tension on the free outflow of a wetting fluid from a horizontal tube”, Traduction of Mekhanika Zhidkosti i Gaza, No 2, March–April 1988.
9. Y.TAHARA, F.STERN, “A large domain approach for calculating ship boundary layers and wakes for nonzero Froude number”, CFD Workshop, Tokyo, March 1994.
10. Y.TODA, F.STERN, J.LONGO, “Mean-flow measurements in the boundary layer and wake and wave field of a Series 60 Cb=0,6 ship model for Froude numbers 0,16 and 0,316 ”, IIHR report No 352, August 1991.
11. Y.TODA, F.STERN, I.TANAKA, V.C.PATEL, “Mean-flow measurements in the boundary layer and wake and wave field of a Series 60 Cb= 0,6 ship model with and without propeller”, Journal of Ship Research, Vol 34, December 1990.
12. H.A.VORST, “Bi-CGSTAB: a fast and smoothly converging variant of Bi-CG for the solution of nonsymetric linear systems”, J. Sci. Stat. Comp. vol 13, 1992.
DISCUSSION
M.Peric
University of Hamburg, Germany
This is an interesting and certainly original approach to solving fluid flow problems with free surface. Both the solution method and the obtained results are worth reporting in the conference proceedings.
The use of finite difference (FD) method and structured grids limits the applicability of the method to geometries which are not too complicated; otherwise, highly distorted grids would result (e.g., for ships with more complicated bow and stern shapes than in the case of the Series 60 hull). This is where the method has disadvantages compared to finite volume (FV) methods, which can use block-structured and unstructured grids with cell-wise local refinement. Especially the local refinement capability is essential if a high accuracy is to be achieved in calculating flows around ship hulls, since very fine grid is needed close to the hull and in the wake while much coarser grid can be used elsewhere.
The strong point of the algorithm presented by the authors is the coupled solution for velocity and pressure. Only after the second reading I recognized that the explicit calculation of the free surface elevation at the end of each time step is not a drawback, since the dependence of velocities on H has been taken into account implicitly by combining Eqs. (20) and (19).
The authors are solving linear systems for κ-ε, and ε velocity-pressure coupling sequentially and are iterating within each time step to account for nonlinearities and coupling of the two systems (velocities depend on κ and ε through v, and κ and ε depend on the velocity field through the production rate and the convective terms). However, they seem to be solving these two systems to a tight tolerance for each “outer” iteration, as indicated in Figs.2 and 3. I doubt that is really necessary, since the residuals increase each time the matrix and source terms are updated; the reduction of residual levels for a fixed matrix and right-hand side by one to two orders of magnitude should normally suffice. No information was given about the required number of iterations on nonlinearities and the criterion used to control them (usually, the residual norm calculated after the matrix and source terms are updated is used as a measure of convergence). Also, no information is given about the decision on when the steady state is reached (usually, if the residuals do not increase above certain level when the matrices and source terms at the new time level are calculated, the changes in the time can be considered negligible).
The full multigrid method is applied only to the linear velocity-pressure system. The efficient sequential solution methods use multigrid to accelerate also (or only) the outer iterations, so I would expect that it would be beneficial to do so in this case too. This would mean performing iterations on non-linearities on each grid level using a non-linear (full approximation) multigrid scheme. It is difficult to predict what reduction of computing time would result in the case of free surface flows, but for a fixed free surface shape this is certainly the most efficient way to calculate steady flows. The comment that the multigrid method “saturates” after few V-cycles is not appropriate; a properly implemented multigrid method is supposed to converge at a constant rate up to machine accuracy.
A few words about the presented solutions: The grid refinement from 190,000 to 320,000 nodes is not a substantial refinement in 3 dimensions, less than 20% more nodes in each direction. To assess the discretization errors reliably, a systematic refinement is most appropriate (halving mesh spacing in all directions, at least in the regions where large errors are expected, e.g., near ship hull and in the wake). One can then use Richardson extrapolation to estimate the “grid-independent ” solution.
The contours of Ω in Figs.13, 16, 18, and 21 show high gradients normal to the symmetry plane; this should not happen, as the symmetry plane must have zero gradient in the normal direction (zero shear stress). Either the boundary conditions are not properly implemented in the code, or the grid is severely distorted in this region. Otherwise, the results seem to agree well with experimental data. However, it would be necessary to quantify the discretization errors as noted above in order to be able to judge the performance of the turbulence model, since the model errors and discretization errors tend to sometimes partially cancel out.
AUTHORS' REPLY
Figures 2 and 3 show the convergence of various iterative algorithms to solve linear problems with the zero machine accuracy. For practical calculations we reduce the linear residuals by two orders.
In the present paper only steady state is compared with experiments so only one non-linear iteration is made at each time step. Concerning the obtaining of steady state, free surface flow problem is much more complicated than zero Froude number problem. Because of the propagation of wave field, convergence on the whole calculation domain takes a long time. In fact we test only the convergence on a sphere near the full (R/1=1) and we reduce the non-linear residuals by two order of magnitude (non-linear residuals are obtained after the matrix and source terms are updated).
The multigrid algorithm converges up to the machine accuracy at a constant rate on elementary case but in 3-D for the fully coupled system the convergence depends strongly of prolongation and restriction operators and of smoothing operator. A bad smoothing leads to the divergence. Here the small wave lengths of the error induced by prolongation procedure are very difficult to smooth under the saturation level.
The grid refinement is not a “substantial refinement” but the solutions on the two grids are very different (figure 14). The conclusion is that small variation of grid size can induce strong differences on the solution due certainly to turbulence behavior.
DISCUSSION
W.W.Schultz
University of Michigan, USA
The rolling motion (tangency condition) you require at the free surface singularity makes matters worse for the second fluid (air in this case). It has been shown that the singularity has to be relieved in a different way. E.B.Dussan [(1979) Ann. Rev. Fluid Mech.] shows that slip is observed and material on the surface is mapped into the interior! Ting & Perlin [(1995) J. Fluid Mech.] shows similar behavior for high Reynolds number, oscillatory flow.
AUTHORS' REPLY
The purpose of our work is to propose a numerical formulation to solve Navier-Stokes equations coupled with classical boundary conditions (no-slip conditions on the wall, kine-matic and dynamic conditions on the free surface). It is well known that the wetting problem cannot be solved by these macroscopic equations. The physics does not follow the continuity hypothesis, and particularly the kinematic condition seems to be unverified. The problem is not to predict the meniscus and the dynamic contact angle at a very small scale, but to ensure the contact line progression with classical boundary conditions. In this case, mathematically, free surface has to be tangent to the wall.
DISCUSSION
H.Raven
Maritime Research Institute, The Netherlands
Your figures 10 and 11 compare calculated and measured wave patterns. The bow wave at the hull is well predicted, the wave profile is fair, but the diverging bow wave system is completely absent. Using a nonlinear free surface condition and a paneling like shown in figure 4, a panel method would probably give a better result for the waves. Does the use of Navier-Stokes equations have a greater amount of numerical damping than a panel method and does it therefore require a finer free surface discretization? Or are there other effects leading to this difference.
AUTHORS' REPLY
We have compared Navier-Stokes formulation with Rankine panel method for the same grid refinement (except in the boundary layer zone). It appears clearly that Navier-Stokes formulation has a greater amount of numerical damping. In fact to obtain similar results we have to use more or less a two times finer grid in each direction in the Navier-Stokes formulation. The explanation is that in the panel method a part of the solution (the mass conservation, that is to say the continuity equation) is mathematically exact and does not proceed from a discretization as in the Navier-Stokes formulation.