Water Entry of Arbitrary Two-Dimensional Sections with and Without Flow Separation
R.Zhao, 1 O.Faltinsen,2 J.Aarsnes1
(1MARINTEK, 2Norwegian University of Science and Technology, Norway)
1
ABSTRACT
Two different theoretical methods for predicting slamming loads on two-dimensional sections have been developed. One of the methods is a fully nonlinear numerical simulation, that includes flow separation from knuckles or fixed separation points of a body with continuously curved surface. The other method is an extension of Wagner's solution(1932). It is an approximate solution and does not include flow separation. The numerical methods are validated by comparing with new experimental results from drop tests of ship cross-sections.
2
INTRODUCTION
Many experimental, analytical and numerical studies of slamming loads have been reported since the pioneering works by von Karman(1929) and Wagner(1932). A strip theory approach is common to use in the analyses of slamming loads on ship hull sections. This is also implicitly assumed in this paper. Three-dimensional flow effects are present in reality. However the many challenging physical and numerical problems are obviously easier to study properly by a two-dimensional method. This will also give guidance on how to treat the three-dimensional flow properly during water entry. Two different two-dimensional methods are presented together with new experimental results. One of the methods represents a fully nonlinear solution. This is a further development of the work by Zhao and Faltinsen(1993). They studied slamming loads on two-dimensional symmetrical sections without the effect of flow separation. The problem was solved as an initial value problem. The exact body boundary condition and fully nonlinear free-surface conditions without gravity were used in the numerical analysis. A local jet flow was introduced near the intersections between the body and the free-surface. The method was verified by Zhao and Faltinsen(1993) by comparing with analytical and asymptotic solutions for water entry of symmetrical wedges with deadrise angles from 4° to 81°. Faltinsen(1993) applied the method with good results for a bow flare section. The numerical method of Zhao and Faltinsen(1993) is in this paper extended to general asymmetric bodies. Flow separation from knuckles and bodies with continuously curved surfaces has been included. When separation occurs from a continuously curved surface, the separation points are determined empirically. The separation mechanism has to be better understood in this case. Viscous boundary layer effects are not believed to be important. Some insight can be gained by studying solutions for steady cavity flow past cylinders.
An approximate solution based on a generalization of Wagner's solution(1932) is also presented. The effect of flow separation is not included. The problem is solved numerically in the time domain by using Green's second identity for each time step. The body boundary condition is satisfied exactly. The piled-up water around the intersection between the free surface and the body surface is calculated by a similar approach as Wagner(1932) used. The dynamic free-surface condition is zero velocity potential on horizontal lines that go through the intersection points between the free surface and body surface. The approximate solution has been compared with the similarity solution for wedges and the fully nonlinear numerical solution. Satisfactory prediction of the maximum pressure and total slamming loads are documented. This approximate solution is fast to calculate and more easy to use for non-experienced users than the complete nonlinear numerical solution.
The numerical methods are validated by comparing with new drop test experiments of a wedge and a bow flare sec-
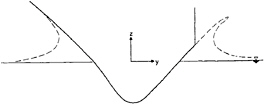
Figure 1: The (y,z) coordinate system, and the water entry of a body with flow separation on the right side and no separation on the left side.
tion. Each section has knuckles. The pressure and the total slamming forces are measured for the whole period of water entry. Systematic comparisons between the numerical and experimental results have been carried out. The three-dimensional flow effects in the drop tests have been theoretically estimated. The maximum estimated three-dimensional effect represents a 20% reduction of the two-dimensional results. This method of estimating three-dimensional flow effects can in a qualitative way be used to analyze an error source in strip theory predictions of bow flare slamming. It is shown that the common method of estimating bow flare impact forces based on fluid momentum conservation and infinite frequency added mass coefficients as a function of submergence relative to undisturbed free surface, gives too low maximum force and wrong time history of the force.
3
FULLY NONLINEAR SOLUTION
A general two-dimensional asymmetric body with time dependent vertical downwards velocity, is forced through initially calm water. The problem is solved as an initial value problem. Since viscous effects are neglected, the problem can be solved by potential theory. The effects of compressibility of the water and air cushions between the water and the structure are neglected. Gravity is not included in the analysis. This has a negligible effect in the initial phase of water entry of a blunt body, but will be more important at a later stage after flow separation has occurred. Hydroelastic effects are disregarded. This can be significant when the slamming loads are large, like for wetdeck slamming(Faltinsen(1996), Kvålsvold et al.(1995)). Cavitation and ventilation can also occur in the latter case.
The reference coordinate system yz is fixed in space. The origin of the coordinate system is in the plane of the undisturbed water surface. The z-axis is positive upwards(see figure 1). The velocity potential ![]() satisfies the Laplace
satisfies the Laplace

Figure 2: The free-surface elevation and pressure(p) distribution on the body surface during water entry of a symmetric wedge with constant velocity V. Deadrise angle α=30°. pa is atmospheric pressure. The results are based on a similarity solution(Zhao and Faltinsen(1993)).
equation
(1)
in the fluid domain. The dynamic free-surface condition on the exact free surface can be written as
(2)
D/Dt means the substantial derivative and t is the time variable. The kinematic free-surface condition is that a fluid particle remains on the free surface. Hence the free surface can be found by convecting particles on the free surface with the local fluid velocity. The body boundary condition on the wetted body surface is satisfied on the instantaneous body surface. It can be written as
(3)
where Vn is the body velocity in the normal direction ![]() on the body surface. Positive direction of
on the body surface. Positive direction of ![]() is into the fluid domain. The initial conditions are zero velocity potential and free-surface elevation.
is into the fluid domain. The initial conditions are zero velocity potential and free-surface elevation.
The problem without flow separation will be studied first. A jet flow is created at the intersection between the free surface and the body surface. A similarity solution can be found for a symmetrical wedge with constant vertical impact velocity(Dobrovol'skaya(1969), Zhao and Faltinsen(1993)). Figure 2 shows the similarity solution for the free-surface elevation and pressure distribution during water entry of a symmetrical wedge with deadrise angle 30°. Figure 2 illustrates that the thin jet will not contribute much to the total force on the body. The part of the jet, where the pressure is close to atmospheric pressure, can therefore be neglected. This makes it unnecessary to find the intersection point between the body
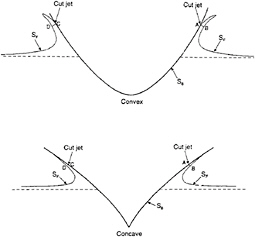
Figure 3: The water entry of bodies with convex and concave shapes. The jets are cut at AB and CD in the numerical simulations. SF is the free surface.
and free surface. This angle is very small for bodies with small deadrise angles and will cause numerical problems(Greenhow(1987)). The geometry of the body may be either convex or concave around the spray root of the jet flow(see figure 3). Part of the jet will leave the body for a convex shape. This can be observed from experimental tests(see for instance Faltinsen(1990)). One should cut the jet before it leaves the body in the numerical simulations(see figure 3). The thin jet will follow the body surface for a body with concave shape (see figure 3), but it will give a small force on the body surface. Therefore one may cut the most part of the jet.
An instantaneous fluid domain Ω that does not contain the whole jet flow, is defined. The jet flow is cut at AB and CD(see figure 3). The velocity potential ![]() for the flow inside the fluid domain is represented by Green's second identity, i.e.
for the flow inside the fluid domain is represented by Green's second identity, i.e.
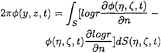
(4)
where r=[(y–η)2+(z–ζ)2]0.5. ![]() means derivative in the normal direction of S. Positive direction is into the fluid domain. The surface S consists of AB, CD, SB, SF and SC. Here SB is the instantaneous wetted body surface below A and C, SF is the instantaneous free surface outside B and D, SC is a control surface infinitely far away from the body. The contribution from integrating over SC in equation (4) is zero. The contribution from the free surface far away from the body can be rewritten. The velocity potential
means derivative in the normal direction of S. Positive direction is into the fluid domain. The surface S consists of AB, CD, SB, SF and SC. Here SB is the instantaneous wetted body surface below A and C, SF is the instantaneous free surface outside B and D, SC is a control surface infinitely far away from the body. The contribution from integrating over SC in equation (4) is zero. The contribution from the free surface far away from the body can be rewritten. The velocity potential ![]() for |y|>b(t), where b(t) is large relative to the cross-dimensions of the hull, can be expressed as a vertical dipole(symmetrical part) and a multipole(asymmetrical part) in infinite fluid. The reason is that the free surface condition is
for |y|>b(t), where b(t) is large relative to the cross-dimensions of the hull, can be expressed as a vertical dipole(symmetrical part) and a multipole(asymmetrical part) in infinite fluid. The reason is that the free surface condition is ![]() =0 on z=0 from a far-field point of view.
=0 on z=0 from a far-field point of view. ![]() can then be written as
can then be written as
(5)
where C1(t) and C2(t) are unknowns that are found as a part of the solution. Using equation (5) in equation (4) makes it possible to analytically express the integrals from b to ∞ and from –∞ to –b. The angle between the body surface and AB(CD) is 90°, while the angle between the free surface and AB(CD) is close to 90°(see figure 3). The line AB (CD) is in the area where the jet starts and where the pressure can be approximated by atmospheric pressure.
An integral equation based on equation(4) is set up by letting (y,z) approach points on S for each time step. The free surface SF inside |y|=b(t), and the body surface SB, are divided into a number of straight line segments in the numerical evaluation of this integral equation. One straight line element is used to represent AB and CD. ![]() and ∂
and ∂![]() /∂n are set constant on each element, except on AB and CD, where
/∂n are set constant on each element, except on AB and CD, where ![]() has a linear variation over the element. For each element on the free surface inside |y|=b(t), and on AB and CD,
has a linear variation over the element. For each element on the free surface inside |y|=b(t), and on AB and CD, ![]() is known and ∂
is known and ∂![]() /∂n is unknown. The instantaneous position of these elements and the values of
/∂n is unknown. The instantaneous position of these elements and the values of ![]() follow from the free-surface conditions. Special care is necessary in describing the motion of the free surface in order to satisfy conservation of fluid mass. A second order description of the free surface is used in areas with large curvature. On the body surface
follow from the free-surface conditions. Special care is necessary in describing the motion of the free surface in order to satisfy conservation of fluid mass. A second order description of the free surface is used in areas with large curvature. On the body surface ![]() is unknown and ∂
is unknown and ∂![]() /∂n is known. In addition there are two unknowns which come from the representation of the far field solution, namely C1(t) and C2(t). The total number of unknowns is NB+NF+2, where NB is number of elements on the body surface and NF is number of elements on the free surface and on AB and CD. The integral equation resulting from equation (4) is satisfied at the midpoint of each element on SB, SF, AB, CD and at two control points in the fluid domain with |y|-value larger than b(t). One obtains then a system of linear equations with the same number of equations as the number of unknowns. The linear equations are solved by a standard procedure. AB and CD(see figure 3) are not used in the initial phase. When the free surface at the intersection with the body is
/∂n is known. In addition there are two unknowns which come from the representation of the far field solution, namely C1(t) and C2(t). The total number of unknowns is NB+NF+2, where NB is number of elements on the body surface and NF is number of elements on the free surface and on AB and CD. The integral equation resulting from equation (4) is satisfied at the midpoint of each element on SB, SF, AB, CD and at two control points in the fluid domain with |y|-value larger than b(t). One obtains then a system of linear equations with the same number of equations as the number of unknowns. The linear equations are solved by a standard procedure. AB and CD(see figure 3) are not used in the initial phase. When the free surface at the intersection with the body is
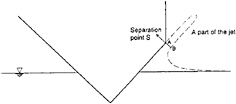
Figure 4: The water entry of a body with flow separation at the knuckles. When the spray root of the jet reaches the separation point S, a part of the jet is introduced in the numerical simulation.
close to the slope of the body surface, AB and CD are introduced.
It will now be described how to solve the problem when the flow separates from a knuckle(or a fixed separation point). When AB(or CD) reaches the separation point S, a part of the previously neglected jet is introduced. The computational domain will then include a larger part of the jet(see figure 4). The reason for doing this is to avoid numerical difficulties. The thin jet, which has been introduced here, is assumed to have the same thickness and constant velocities in the y and z-direction for the whole jet. The length of the introduced jet part is about 6 times the length of AB. In reality the thickness will not be the same. For instance the angle at the intersection between the water and the body surface is about 1.8° during water entry with constant velocity of a wedge with deadrise angle 30°(see figure 2). The length of the total jet is almost the same as the length of the wetted body surface when the wetted surface is defined as the distance from the keel to the spray root of the jet. The introduced jet part is therefore a small portion of the whole jet. It is a good approximation to assume constant jet thickness in this part of the jet. The numerical results are not sensitive to the length of the introduced jet part. A hemicircle is used at the end of the jet. This is advantageous in the time stepping of the solution.
A Kutta condition is applied at the separation point S. This implies that the flow leaves tangentially at the knuckle and the velocities at point S are finite. In a small region near the knuckle the behaviour of the velocities can be studied by a local analysis.
Here a local polar coordinate system (rθ) and a local Cartesian coordinate system (s,n) is used (see figure 5). A local solution of the velocity potential ![]() loc, that satisfies the body boundary condition, can be written as
loc, that satisfies the body boundary condition, can be written as
(6)
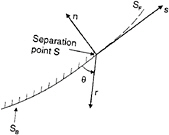
Figure 5: The local polar coordinate system (r,θ) and the local Cartesian coordinate system (s,n). S is the separation point, SB the body surface and SF the free surface. The s-coordinate coincides with the tangent of the body surface at the separation point S.
The velocity potential ![]() loc satisfies the free-surface condition
loc satisfies the free-surface condition
(7)
This leads to the following approximation for small r
(8)
The lowest order term in equation (8) is
(9)
This equation says simply that the pressure is atmospheric at the separation point. This is automatically satisfied as a part of the solution. The next term in equation (8) gives
2U Annrn–1cosnπ=0 (10)
Possible values of n are ![]() cannot be a solution since it leads to a singular velocity. Choosing
cannot be a solution since it leads to a singular velocity. Choosing ![]() is consistent with that r2(n–1) should be a smaller term then rn–1. This means that the solution in the vicinity of the separation point can be written as
is consistent with that r2(n–1) should be a smaller term then rn–1. This means that the solution in the vicinity of the separation point can be written as
(11)
Equation (11) implies that the tangential velocity at the free surface is U(t). Close to the separation point, the tangential velocity at the body surface can be written as
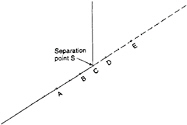
Figure 6: Element distribution and midpoints A, B, D, and E of the elements near the separation point S.
(12)
The free surface near the separation point can be found by equation (11). It can be shown that the flow leaves the knuckle tangentially. Very small elements are used near the knuckle in the numerical calculations. The length of the segments used near the knuckle on the body and free surface is about 0.3% of the length of the wetted body surface for the wedge with deadrise angle 30°. Therefore the tangential velocity for the segments closest to the knuckle on the body can be approximated by the particle velocity on the free surface closest to the knuckle. This means that the last term in equation (12) is neglected. The numerical details of the implementation of the conditions at a separation point are described below.
Figure 6 shows the element distribution around a knuckle. Based on the velocity potentials at points A,B and D, the tangential velocity at point B can be estimated. Based on the velocity potentials at points B, D and E the tangential velocity at point D can be estimated. These two velocities are set equal. This gives a linear relationship between unknown velocity potential values on the body surface and known potential values of the free surface near the separation point. In addition the normal derivative ![]() of the potential near the knuckle is set equal on the body and the free surface. These two relationships implies that two equations in the linear equation system that follows from the integral equation based on equation (4) must be excluded. This is done by not satisfying the integral equation at the closest segments to the knuckle on the body and free surface. The same procedure can be used for flow separation from the other side of the body.
of the potential near the knuckle is set equal on the body and the free surface. These two relationships implies that two equations in the linear equation system that follows from the integral equation based on equation (4) must be excluded. This is done by not satisfying the integral equation at the closest segments to the knuckle on the body and free surface. The same procedure can be used for flow separation from the other side of the body.
When the solution is stepped from time ti to ti+1, the free surface location and velocity potential on the free surface for ti+1 are obtained by using the kinematic and the dynamic free-surface conditions. Because the velocities on the body and free surface for the elements closest the separation point are the same, the element closest to the separation point on the free surface will always be located on the tangential continuation of the body surface from the separation point.
The front part of the jet has larger velocities than the rest of the fluid in the beginning of flow separation from the knuckle. Number of elements to represent the jet must therefore be increased as time goes. It is also found that the free surface can be unstable at the front part of the jet. This problem can be suppressed for a long time by cutting the front part of the jet. It has been checked that this does not affect the pressure on the body surface. The particle velocities near the original jet flow will be strongly reduced at a late stage. This means that it is not really a jet flow anymore. It should also be noted that the acceleration of fluid particles will not be much larger than the gravitational acceleration at a late stage of the flow. The effect of gravitation should therefore be included in the numerical simulation at this stage. This has not yet been studied.
The pressure p on the body surface is calculated by Bernoulli's equation, which can be written as
(13)
Here the hydrostatic pressure is neglected. pa is atmospheric pressure and ρ is the mass density of the fluid. The term ![]() is found by generalizing the concept of substantial derivative. One introduces
is found by generalizing the concept of substantial derivative. One introduces
(14)
where ![]() is the change in
is the change in ![]() when one follows the midpoint of a segment, that moves with velocity
when one follows the midpoint of a segment, that moves with velocity ![]()
The numerical results have been checked by changing number of elements and time step and by checking conservation of mass, momentum and energy. The expressions can be found in Zhao and Faltinsen (1993) and are valid both with and without flow separation.
4
SIMPLIFIED SOLUTION
Wagner (1932) developed an asymptotic solution for water entry of two-dimensional bodies with small local deadrise angles. The flow was studied in two fluid domains. The inner flow domain contains a jet flow at the intersection between the body and the free surface. In the outer flow domain the body boundary condition and the dynamic free-surface condition ![]() =0 were transformed to a horizontal
=0 were transformed to a horizontal
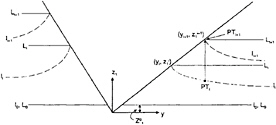
Figure 7: The coordinate system (y,z1), the real free surface l and the horizontal lines L used in the numerical simulation for time steps t0, ti and ti+1 in the simplified solution.
line. The kinematic free-surface condition was used to determine the intersection between the free surface and the body in the outer flow domain. Zhao and Faltinsen(1993) presented a composite solution for the pressure distribution in the outer and inner flow domain and showed satisfactory agreement with similarity solutions for wedges with deadrise angles smaller than 20°.
A generalization of Wagner's solution to larger local deadrise angles is presented in the following text. Only the outer flow domain solution is analyzed. A main difference from the Wagner theory is that the exact body boundary condition is satisfied at each time instant. The wetted body surface is found by integrating in time the vertical velocities of fluid particles on the free surface and finding when the particles intersect the body surface. Wagner did also that, but he could use analytical solutions because of the simplified body boundary condition. The dynamic free-surface condition will be the same as Wagner used. The pressure is calculated by the complete Bernoulli's equation without gravity. It has not been possible to find an inner flow solution near the spray roots that matches the outer flow solution. This would have made it possible to exclude in a rational way the large negative pressures that occur at the intersection points in our outer flow solution. The procedure is now simply to neglect the negative pressure.
The problem is solved as an initial value problem. The velocity potential satisfies two-dimensional Laplace equation in the fluid domain. A boundary value problem is solved by using equation (4) for each time step. The numerical procedure is similar as the fully nonlinear problem. A coordinate system yz1 which follows the vertical motion of the body is used(see figure 7). The dynamic free surface condition ![]() =0 is satisfied on horizontal lines that starts at the intersection points between the body and the free surface on each side of the body (see figure 7). The dynamic free surface condition implies that fluid particles on the free surface have only vertical velocities. The instantaneous z1-coordinate of the intersection points on the two sides of the body are different for water entry of an asymmetrical body.
=0 is satisfied on horizontal lines that starts at the intersection points between the body and the free surface on each side of the body (see figure 7). The dynamic free surface condition implies that fluid particles on the free surface have only vertical velocities. The instantaneous z1-coordinate of the intersection points on the two sides of the body are different for water entry of an asymmetrical body.
The numerical simulation starts at time t0. The submergence of the body is ![]() at t0(see figure 7). The effect of free-surface elevation is neglected initially, so the free surface l0 is horizontal. In the numerical computation, t0 is set equal to 0.15tpout, where tpout is the time instance when one needs the pressure distribution and slamming forces as output. This procedure has been tested against the Wagner solution for a water entry of a circle at an early stage and water entry of a wedge with small deadrise angles. Satisfactory predictions of the pressure distribution and the slamming forces were obtained.
at t0(see figure 7). The effect of free-surface elevation is neglected initially, so the free surface l0 is horizontal. In the numerical computation, t0 is set equal to 0.15tpout, where tpout is the time instance when one needs the pressure distribution and slamming forces as output. This procedure has been tested against the Wagner solution for a water entry of a circle at an early stage and water entry of a wedge with small deadrise angles. Satisfactory predictions of the pressure distribution and the slamming forces were obtained.
Figure 7 illustrates the free surface li and li+1 at two time instances ti and ti+1. The free-surface conditions are satisfied on the horizontal lines Li and Li+1 at ti and ti+1. An integral equation following from equation (4) is used at each time step ti to find the velocity potential on the body surface and the vertical velocities at Li. It is assumed that the vertical velocity on Li for a given y-value is the same as the vertical velocity on li. The solution can be stepped from t=ti to t=ti+1 in the following way. The procedure is first to decide the intersection point ![]() for positive y-values at time ti+1 and then find what Δt= ti+1–ti must be. By knowing Δt, the intersection point for negative y-values at ti+1 is determined afterwards. Δt is found in details as follows. One can write
for positive y-values at time ti+1 and then find what Δt= ti+1–ti must be. By knowing Δt, the intersection point for negative y-values at ti+1 is determined afterwards. Δt is found in details as follows. One can write
(15)
where ΔP=PTi+1–PTi(see figure 7) and W is the relative vertical velocity of a point between PTi and PTi+1 with y-coordinate yi+1. W depends on c(t) which is the y-coordinate of the intersection point between the free surface and the body surface at time t. Equation (15) can be written
(16)
This is evaluated numerically by using an average value ![]() for
for ![]() W is expressed in terms of a local solution. Here a local polar coordinate system (r2θ2) is used(see figure 8). W can be written as
W is expressed in terms of a local solution. Here a local polar coordinate system (r2θ2) is used(see figure 8). W can be written as
(17)
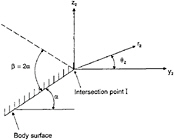
Figure 8: Local polar coordinate system (r2,θ2) and local Cartesian coordinate system (y2,z2). I is the intersection point between the body and the free surface. The local deadrise angle is α. The free surface condition is satisfied on the y2-axis in the numerical simulation of the simplified method.
Here r2 is (yi+1–c(t)). β is defined in figure 8 and is assumed constant from ti to ti+1. D is found from the global solution and an average value is used from ti to ti+1. This is found for a symmetric body by solving the global problem for ti and ti+1, and use an average value Dm for D at these two time instances. The procedure for an asymmetric body will be explained later. Equation(16) can now be written as
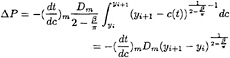
(18)
This means that
(19)
Δt is now determined as
(20)
If the body is asymmetric, Dm is determined as follows. An estimate of the horizontal line Li+1 on the left hand side of the body (see figure 7) is based on the rate of change with time of the intersection point from the previous time step. Dm is then again determined as the average value at ti and ti+1. Δt can then be determined by equation (20) and equation (19).
Knowing Δt, the intersection point on the left hand side of the body can be determined by linear interpolation. This has been done by using similar equations, as used for the right hand side of the body, to calculate the times it takes for points on the left hand free surface to move up to the body surface. Then one can determine the y-coordinate of the intersection point by linear interpolation.
After the velocity potential on the body surface has been determined, the pressure distribution on the body can be found from equation (13). Special care is shown near the intersection between the body and the free surface. Since the velocity is infinite there, the last term in equation (13) will be negative infinite. It can be shown that the first term is positive infinite at the intersection point, and that the last term is more singular than the first term. Therefore the total pressure is negative infinite. But this is an integrable singularity. Let us define the integrated vertical force for the part with negative pressure as FN, and from the part with positive pressure as FP. It can be shown that FN/FP goes to zero when the deadrise angle goes to zero. For small deadrise angles, the maximum pressure(positive) is obtained near the intersection point. The maximum pressure obtained from the outer solution is the same as the maximum pressure from the composite solution based on Wagner's solution(Zhao and Faltinsen(1993)) when the deadrise angle goes to zero.
5
VERIFICATION OF THE SIMPLIFIED METHOD
Figure (9) compares predicted pressure distributions by the simplified solution and the similarity solution. Wedges with deadrise angles 10°, 30°, 45°, 60° and 81° are analyzed. The negative pressures in the simplified solution have been omitted. The maximum pressure occurs near the spray root for small deadrise angles. When the deadrise angle is larger than approximately 40°, the maximum pressure is located at the keel of the wedge. For small deadrise angles there are good agreement between the simplified and similarity solution in the region near the spray root of the jet. The agreement is less satisfactory near the spray root for large deadrise angles. But from a design point of view this has no consequence for the total slamming loads and the maximum pressure, because the pressure is relatively low compared with the average pressure on the body surface.
Numerically predicted total slamming force and maximum pressures on a wedge with different deadrise angles are presented in figure 10. There are good agreement between the simplified and the similarity solution. The results from Wagner's solution and von Karman's solutions are also presented in figure 10a. A von Karman solution means that the local up-rise of the water is not accounted for. The dynamic free-surface condition is the same as in
Wagner's solution. Two different von Karman solutions are presented in figure 10a. One is based on a flat plate solution, similar as Wagner did. The other von Karman solution is obtained by using the exact body boundary condition and the principle of conservation of momentum. The vertical force is expressed by
(21)
where A33 is the infinite frequency added mass in heave as a function of submergence. V is the drop velocity. This is referred to as the von Karman-momentum solution. Figure 10a shows that the Wagner solution clearly over-predicts the slamming loads for larger deadrise angles. The von Karman solution based on the flat plate solution clearly under-predicts slamming loads for relatively small deadrise angles. The von Karman-momentum solution with exact body boundary condition clearly under-predicts slamming loads. The latter approach is common to use in practical nonlinear ship motion and sea load computations during water entry of a bow flare section. The results in figure 10 illustrate unsatisfactory predictions based on this method.
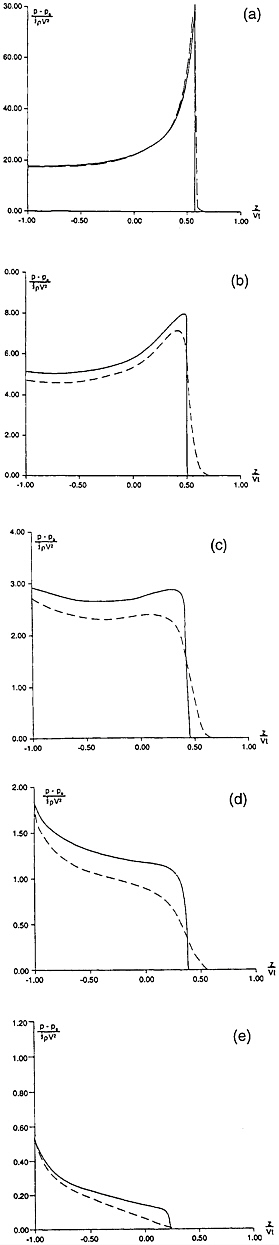
Figure 9: Pressure(p) distribution on symmetric wedges during water entry with constant vertical velocity V. ———, simplified solution; – - –, similarity solution. pa is atmospheric pressure, α is deadrise angle, ρ is mass density of the fluid, z is vertical coordinate, t is time variable and Vt is the instantaneous draft relative to calm water. (a) α=10°; (b) α=30°; (c) α=45°; (d) α=60°; and (e) α=81°.
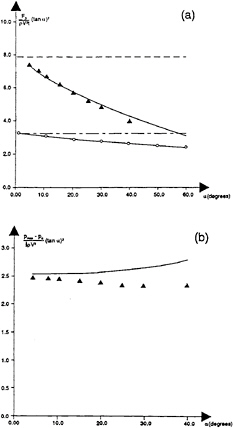
Figure 10: The vertical slamming force F3 and maximum pressure pmax on symmetric wedges during water entry with constant vertical drop velocity V. pa is atmospheric pressure, α is deadrise angle, ρ is mass density of the fluid, t is time variable and Vt is the instantaneous draft relative to calm water.
(a) the vertical slamming force, ———, simplified solution; ∆ ∆ ∆, similarity solution;------, Wagner solution; – - –, von Karman; o – o – o, von Karman-momentum.
(b) the maximum pressure, ———, simplified solution; ∆ ∆ ∆, similarity solution.
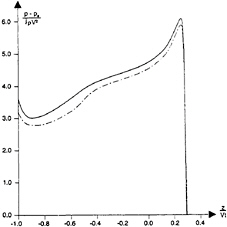
Figure 11: Numerically predicted pressure(p) distribution during water entry of a bow flare section. The vertical velocity V is constant pa is atmospheric pressure and ρ is mass density of the fluid. The geometry of the body is shown in figure 13b. The numerical results are presented for the time instance just before the spray roots of the jets reach the knuckles. z is vertical coordinate on the body surface, t is time variable and Vt is the instantaneous draft relative to calm water. ———, simplified solution; – -–, fully nonlinear solution.
The simplified and the fully nonlinear solution have been compared for different ship sections. Figure 11 shows the predicted pressure distribution for the bow flare section, which was used during the drop tests(see figure 13b). The vertical velocity of the section is constant. The time instance is just before the spray roots of the jets reach the knuckles. The comparison between the theories and the experimental results will be shown in section 7. Figure 11 shows satisfactory agreement between the two different methods.
The general conclusion is that the simplified theory represents a reasonable approximation of the total slamming force and the local slamming loads.
6
DESCRIPTION OF DROP TESTS
6.1
THE MODEL
Drop tests have been carried out at MARINTEK. The objective was to validate the theoretical methods. A sketch of the free-falling rig used in the tests is shown in figure 12. The rig consists of four different parts; the vertical guide rails, the trolley, a rotatable horizontal beam and the test
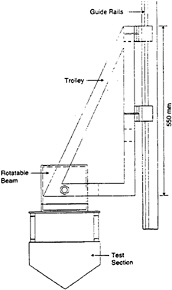
Figure 12: The free-falling rig used in the drop tests.
sections. The rotatable beam is connected to the trolley using one bolt at each end of the beam. The beam can be rotated in intervals from zero to a maximum roll angle of 28 degrees. Only results for non-rotated sections will be presented. The ballast weights are located within the rotatable beam. The trolley is engaged with the vertical guide rails. The test sections are mounted directly to the horizontal, rotatable beam. The tests sections are connected to the trolley during the entire drop. Any rotation of the test sections are in this way suppressed during the impact. The total length of the test sections are L=1.0 m. The breadth B of the test sections can vary from 0.25 to 0.60 m. The maximum drop height for this rig is about 2.0 m. The trolley is raised using a winch fitted with a quick-release hook. The hook is connected to an automatic release mechanism. After the test section has hit the water surface, the trolley is stopped using two elastic ropes.
Both a V-shaped section with 30 degrees deadrise angle and a typical ship bow section were tested. The shape of the two different sections are shown in figure 13. The total test section was divided into three parts, one measuring section with a dummy section on each side (see figure 13). No vertical end plates were used. The measuring section was connected to the rig using two force transducers. The main data for the test setup for the two different sections can be summarized as follow:
Table 1. The main data of the test sections.
|
V shape |
bow flare |
|
|
Breadth of section |
0.50 m |
0.32 m |
|
Vertical distance from keel to knuckles |
0.29 m |
0.203 m |
|
Length of measuring sections |
0.20 m |
0.10 m |
|
Length of each dummy sections |
0.40 m |
0.45 m |
|
Total length |
1.00 m |
1.00 m |
|
Weight drop rig (without ballast) |
141 kg |
161 kg |
|
Ballast weight |
100 kg |
100 kg |
|
Total weight of drop rig |
241 kg |
261 kg |
|
Weight of measuring section |
14.5 kg |
6.9 kg |
The total weight of the measuring section represents the total weight of the section connected underneath the vertical force transducers.
6.2
INSTRUMENTATION
The instrumentation in the tests is shown in figure 13 and the following parameters were measured:
-
Pressures in 4–5 points using pressure cells of piezoresistive type with resonance frequency of 500 kHz. The cell diameter is 4 mm. The positions of the pressure cells are shown in figure 13.
-
The vertical force using two force transducers connected to the ends of the measuring section.
-
Wetted surface measurements using wave gauges tape.
-
Vertical acceleration of the drop rig using an accelerometer.
-
The vertical drop velocity was measured using an optical sensor. The time development of the drop velocity was obtained by using this value in combination with the measured vertical acceleration of the drop rig.
The sections were dropped against calm water. At least two drops were performed for each test condition.
7
COMPARISONS BETWEEN THEORY AND EXPERIMENTS
Only the fully nonlinear method can be used to predict the pressure distribution on bodies after flow separation occurs. An example with water entry of a wedge with deadrise angle 30° and with knuckles is presented in figure 14. The vertical velocity is constant. The pressure distribution and free surface elevation for different time instances after the spray roots separate from the knuckles are presented. Figure 14a shows that the maximum pressure is located near the spray root of the jet before separation occurs. After the flow separates, the maximum pressure near the separation point drops fast and the maximum pressure moves to the keel of the wedge. Figure 14b
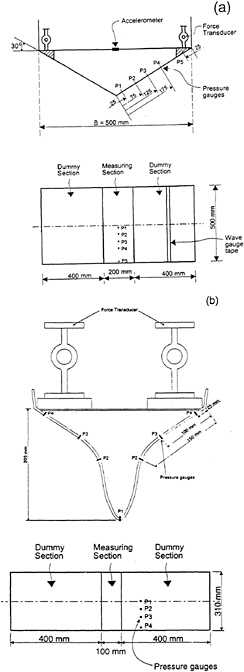
Figure 13: The geometry of the test section and the locations Pi of the pressure gauges.
(a) the wedge section; (b) the bow flare section.
shows the free-surface elevation after the flow separation. Greenhow and Lin(1983) studied experimentally water entry of a wedge with deadrise angle 30°. One of the pictures showed the water elevation after flow separation. Figure 14c shows both experimental and theoretical predictions of the free-surface elevation. The agreement seems satisfactory. However information on the variation of the experimental drop velocity was not available. Deceleration of the test section will effect the free-surface elevation.
Fig.15a compares numerical and experimental time histories of the vertical hydrodynamic force on the symmetrical wedge with deadrise angle 30 ° described in figure 13. The fully nonlinear method is used. The measured vertical drop velocity of the body during water entry is presented in figure 15b. The same velocity has been used in the numerical simulations. There is good agreement between numerical and experimental results initially. The differences are larger at a later stage. A main reason is three-dimensional flow effects.
The three-dimensional effects can approximately be explained by combining Meyerhoff's(1970) calculations of added masses of thin rectangular plates with a generalization of Wagner's theory to three-dimensional flow. This implies that at each time step, the cross-flow around a flat plate of local beam 2B and length 2L in infinite fluid is solved. The coordinates B and -B represents an approximation of the local intersection between the instantaneous free surface and the exact body surface. This has to be find by an integral equation in a similar way as Wagner(1932) did for two-dimensional flow. However by applying Meyerhoff's(1970) results, we are assuming the same wetted surface at each cross-section. This procedure can only be applied up to the time instant when the spray roots are in the vicinity of the knuckles.
The vertical force per unit length on the measurement section can then be written as
(22)
where ![]() accounts for three-dimensional flow effects. The value of
accounts for three-dimensional flow effects. The value of ![]() for different values of
for different values of ![]() can be found by using Meyerhoff's(1970) results. The three-dimensional effect f3D=F3/F32D have been estimated for
can be found by using Meyerhoff's(1970) results. The three-dimensional effect f3D=F3/F32D have been estimated for ![]() and 0.5. It is found that f3D(0.25)= 0.95, f3D(0.40)=0.87 and f3D(0.5)=0.80. Here F32D is the two-dimensional vertical force valid when B/L goes to zero. B/L=0.5 represents the situation when the spray roots are at the knuckles. It means that three-dimensional effects cause a 20 % reduction in the vertical force at the stage when the spray roots reach the knuckles. Including these three-dimensional effects clearly improve the numerical predictions relative to the experiments(see
and 0.5. It is found that f3D(0.25)= 0.95, f3D(0.40)=0.87 and f3D(0.5)=0.80. Here F32D is the two-dimensional vertical force valid when B/L goes to zero. B/L=0.5 represents the situation when the spray roots are at the knuckles. It means that three-dimensional effects cause a 20 % reduction in the vertical force at the stage when the spray roots reach the knuckles. Including these three-dimensional effects clearly improve the numerical predictions relative to the experiments(see
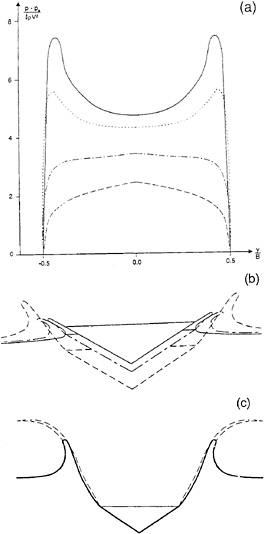
Figure 14: The pressure(p) distribution and free-surface elevation during the water entry of a wedge with deadrise angle 30° and knuckles. Calculated by the fully nonlinear solution. V is constant drop velocity, pa is atmospheric pressure, ρ is mass density of the fluid and B is breadth of the wedge. y is horizontal coordinate on the body surface. to is the time instance when the spray roots of the jets reach the separation points.
(a) pressure distribution, ———, t=t0; - - - - - -, t= 1.1t0; – - – , t=1.3t0; – – –, t=2.0t0.
(b) free-surface elevation, ———, t=t0; – - –, t= 1.3t0; – – –, t=2.0t0.
(c) comparison of free-surface elevation between theory and experiments, t=2.9t0(Greenhow and Lin(1983)). ———, theory; – – –, experiment.
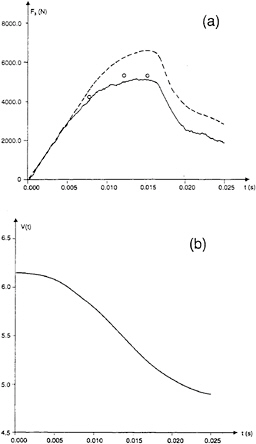
Figure 15: The vertical slamming force F3 on a wedge with deadrise angle 30° and knuckles(see figure 13a) during water entry. t is time variable and V(t) is measured vertical drop velocity of the wedge. (a) the vertical slamming force ———, experimental results; – – – –, fully nonlinear solution; ooo, fully nonlinear solution with three-dimensional corrections; (b) experimental drop velocity.
figure 15a). When there is a drop in the vertical force and later on, Wagner 's procedure does not apply. However the body is also non-slender during this stage of the flow. It is therefore qualitatively speaking believed that three-dimensional effects are at least as important as when B/L=0.5. Figure 15a shows that the slamming force reduces quickly in the beginning after flow separation, then decay more slowly. If equation (21) is used to predict the vertical hydrodynamic force, V is assumed constant and infinite frequency added mass values are calculated for different submergences, it follows that the force is zero after separation. If the deceleration of model is accounted for, the vertical force based on equation (21) will be negative after flow separation. Since the maximum force(see figure 10) and the time rate of change of the wetted area in a von Karman type of solution will be clearly lower than in our predictions, the time history of the force will also be quite different before flow separation.
At a late stage of the water entry, it is of interest to compare the numerical results of vertical force with theoretical drag coefficients for steady symmetric cavity flow past a wedge. These values are a function of the cavitation number. Knapp et al.(1970) defines the cavitation number as
(23)
for water entry. Here V is the velocity of the body, po is pressure in undisturbed fluid at the depth of the nose of the entering body, pB is the cavity pressure. The cavity pressure is the same as atmospheric pressure in our case. According to Knapp et al(1970), CD=0.745 for two-dimensional symmetric steady supercavitating flow(K=0) past a wedge with interior angle 120° at the nose. CD is defined as CD=F/(0.5ρV2B). Here F is the total force and B is the maximum breadth of the section.
Since gravity is neglected in the numerical computations, the water entry force on the wedge should approach the results for supercavitating flow when the submergence goes to infinity and the drop velocity is constant. The different force components are plotted in figure 16a as a function of Vt/B, where B is breadth of the body and Vt is the submergence of the keel relative to calm water. The force term associated with the pressure term D′![]() /D′t in equation (14) should go to zero and the sum of the rest of the terms should approach 0.745 when the submergence goes to infinity. The results show that the D′
/D′t in equation (14) should go to zero and the sum of the rest of the terms should approach 0.745 when the submergence goes to infinity. The results show that the D′![]() /D′t-term of the force reduces slowly after a rapid decrease just after flow separation from the knuckles. The results are plotted as a function of b/(Vt) in figure 16b. This makes it easier to estimate asymptotic values when Vt goes to infinity. Figure 16b indicates that the computed CD-value approaches an asymptotic value close to 0.745 when Vt goes to infinity.
/D′t-term of the force reduces slowly after a rapid decrease just after flow separation from the knuckles. The results are plotted as a function of b/(Vt) in figure 16b. This makes it easier to estimate asymptotic values when Vt goes to infinity. Figure 16b indicates that the computed CD-value approaches an asymptotic value close to 0.745 when Vt goes to infinity.

Figure 16: Different components of the numerical predicted slamming force F3 on a symmetric wedge with deadrise angle 30° and knuckles during water entry. Fully nonlinear method is used. V is constant vertical drop velocity, ρ is mass density of the fluid, t is time variable, Vt is the instantaneous draft relative to calm water and B is breadth of the body. ———, total slamming force; – – – –, force due to ![]() – - –, force due to
– - –, force due to ![]()
(a) the horizontal axis is Vt/B, (b) the horizontal axis is B/(Vt).
The numerical simulations should ideally have been continued for larger submergences, but numerical difficulties were encountered. Our computations indicate that the cavity becomes infinitely long when Vt goes to infinity. It is expected that the cavity will be finite if gravity is included. The deceleration of the section will also affect the solution.
The numerical and experimental pressure distribution for three time instances are plotted in figure 17. Good agreement between theory and experiments are documented at an early stage of the water entry. The differences are larger at a later stage, but this is mainly due to three-dimensional effects in the experiments. Figure 17c corresponds to a time instant after the spray roots have separated from the knuckles. The pressure level is then low and spatially uniform over the body surface. The vertical force found by integrating the measured pressure are in good agreement with the measured vertical force presented in figure 15. Figure 18 shows a comparison of numerical and experimental values of slamming loads on the bow flare section. The measured vertical velocity of the body during water entry is presented in figure 18b. The fully nonlinear solution is used. Good agreement between the numerical results and the experiments are obtained. The ratio B/L is 0.31 when the spray roots reach the knuckles in this case. The previous simplified analysis shows that three-dimensional effect causes 8% reduction of the force relative to the two-dimensional force when the spray roots of the jets reached the knuckles.
The pressure distributions for the bow flare section are plotted for three time instances in figure 19. A comparison is made between the fully nonlinear solution and the experimental results. There are quite good agreement between the results. Generally speaking, the experimental results give lower values than the numerical results. By comparing the measured pressures with measured force presented in figure 18, it appears that the measured force is somewhat higher than the force obtained by pressure integration. This indicates measurement errors.
8
CONCLUSIONS
A fully nonlinear numerical method that predicts slamming loads on a general two-dimensional body is presented. Two-dimensional Laplace equation is solved by a boundary element method. The jet flows at the intersection between the body surface and the free surface are approximated. The fully nonlinear free-surface conditions without gravity and the exact body boundary condition are satisfied. The effect of flow separation is incorporated by a Kutta condition. The numerical method is validated by comparing with new experimental results from drop tests of a wedge and a bow flare section. Both sections have knuckles. Satisfactory agreement is documented for the
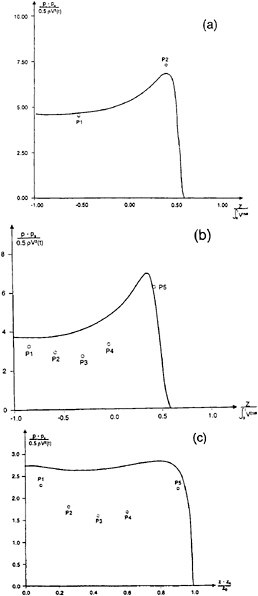
Figure 17: The pressure distribution(p) at three time instances during water entry of a wedge with deadrise angle 30° and knuckles(see figure 13a). V(t) is the drop velocity, which is shown in figure 15b, pa is atmospheric pressure, ρ is mass density of the fluid, t is time variable, t=0 corresponds to that the keel touches the water surface, z is vertical coordinate on the body surface, zk is vertical coordinate of the keel and zD is the draft of the body. o, experimental results; ———, fully nonlinear solution.
(a) t=0.00435 s; (b) t=0.0158 s; (c) t=0.0202 s.
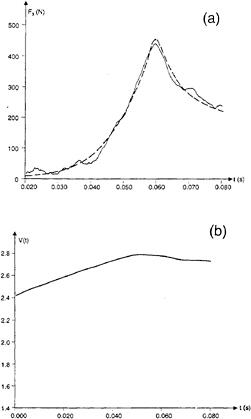
Figure 18: The vertical slamming force F3 on a bow flare section with knuckles(see figure 13b) during water entry. t is time variable. t=0 corresponds to that the keel touches the water surface. V(t) is measured vertical drop velocity.
(a) the vertical slamming force ———, experimental results; – – – –, fully nonlinear solution.
(b) experimental drop velocity
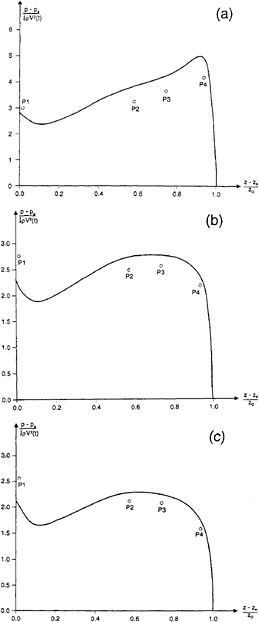
Figure 19: The pressure distribution(p) at three time instances during water entry of a bow flare section with knuckles(see figure 13b). V(t) is the measured drop velocity (see figure 18b), pa is atmospheric pressure, ρ is mass density of the fluid, t is time variable, t=0 corresponds to that the keel touches the water surface, surface, z is vertical coordinate on the body surface, zk is vertical coordinate of the keel and zD is the draft of the body. o, experimental results; ———, fully nonlinear solution.
(a) t=0.06 s; (b) t=0.07 s; (c) t=0.08 s.
whole period of water entry including when separation from the knuckles occurs. Three-dimensional flow effects in the experiments are theoretically estimated. A simplified method to predict slamming load is also presented. This is based on a generalization of the Wagner(1932) approach. The exact body boundary condition is satisfied. No flow separation is accounted for. It is demonstrated that the simplified solution gives reasonable results. The commonly used method to calculate forces on bow flare sections based on von Karman method and conservation of momentum gives too low maximum force and a wrong time history of the force.
9
ACKNOWLEDGEMENT
This work is carried out as a part of the DYNAMIC ANALYSIS SUPPORT SYSTEM PROJECT, DASS-Project. The project is a 5-years cooperative project between The Royal Norwegian Navy and The US Naval Sea System Command, Norwegian and US research institutes and universities, and the Norwegian industry.
10
REFERENCES
Dobrovol'skaya, Z.N. ”On some problems of similarity flow of fluid with a free surface, ” J.Fluid Mech. Vol.36, pp.805–829, 1969
Faltinsen, O.M. ”Sea loads on ships and offshore structures,” Cambridge University Press, 1990.
Faltinsen, O.M. ”On seakeeping of conventional and high-speed vessels,” 15th Georg Weinblum Lecture, Journal of Ship Research, Vol.37, no.2, June 1993.
Faltinsen, O.M. ”The effect of hydroelasticity on ship slamming,” to be published in Phil. Trans. R. Soc. Lond., 1996.
Greenhow, M. and Lin, W.M. ”Nonlinear free surface effects: experiments and theory,” Department of Ocean Engineering, MIT, report no.83–19, 1983.
Greenhow, M. ”Wedge entry into initially calm water,” Appl. Ocean Res., Vol.9, pp.214–223, 1987.
Knapp, R., Daily, J,W., Hammitt, H.F.G. ”Cavitation,” McGraw-Hill Book Company, 1970.
Kvålsvold, J., Faltinsen, O.M., Aarsnes, J.V. ”Effect of structural elasticity on slamming against multihull vessels, ” In Proc. 6th. Int. Symp. on the Practical Design of Ships and Offshore Mobile Units(PRADS), pp.1684–1699, Seoul. 1995.
Meyerhoff, W.K., ”Added masses of thin rectangular plates calculated from potential theory,” Journal of Ship Research, pp.100–111, June 1970.
von Karman, T., ”The impact of seaplane floats during landing,” N.A.C.A. TN321, Washington, 1929.
Wagner, H., ”Über stoss- und Gleitvergänge an der Oberflache von Flüssigkeiten,” Zeitschr. f. Angew. Math. und Mech., Vol. 12, No. 4, pp.193–235, 1932.
Zhao, R., Faltinsen, O.M., ”Water entry of two-dimensional bodies,” J.Fluid Mech., Vol. 246, pp.593–612, 1993.
















