Nonlinear Ship Motions and Wave-Induced Loads by a Rankine Method
D.Kring, Y.-F.Huang, P.Sclavounos (Massachusetts Institute of Technology, USA), T.Vada, A.Braathen (Det Norske Veritas, Norway)
Abstract
This paper presents the computation, by a three-dimensional Rankine Panel Method, of nonlinear ship motions and structural loads induced by steep ambient waves. Founded upon a thoroughly validated model of the linear seakeeping problem for realistic ship hulls, the nonlinear extension presented in this study accounts for various nonlinear effects in the seakeeping problem. These include the variable wetness of the ship hull, the nonlinear hydrostatic effects and Froude Krylov exciting forces, and the treatment of the radiation and diffraction wave disturbances according to the “weak scatterer” hypothesis. Computations are presented of the vertical motions and structural loads for a Series 60 and the Snowdrift hull, and an assessment is carried out of the importance of nonlinear effects in the motion and load predictions.
1
Introduction
The simulation of steady and unsteady ship flows, wave induced motions, and structural loads by three-dimensional Rankine Panel Methods (RPM 's) has enjoyed rapid growth and considerable success over the past ten years. Such CFD (Computational Fluid Dynamics) methods have evolved into valuable and trusted analysis and design tools which are today used routinely for the design and optimization of hull forms and the assessment of their safety in severe sea states.
Since the mid-80's an RPM method known as SWAN (ShipWaveANalysis) has been under development at MIT. During the early stages of this research program the fundamental numerical properties of the method were studied and an algorithm was derived capable of accurately treating ship flows over a broad range of Froude numbers and wave frequencies. Early versions of SWAN treated the linear steady and seakeeping problems in the frequency domain [7],[12]. More recently the method was extended to solve the same problems in the time domain [6],[8], paving the way towards the treatment of the nonlinear seakeeping problem which is the focus of the present paper. The performance of the linear versions of SWAN for naval, commercial, twin-hull ships, and America's Cup sailing yachts is surveyed in [13].
The structural design of a ship requires the evaluation of its motions and wave induced pressure distributions over the hull in severe sea states. In order to estimate the importance of extreme events, a nonlinear seakeeping solution must simulate, with sufficient accuracy and efficiency, the seakeeping behavior of a ship in steep random wave trains that may be several hours long in duration. With this goal in mind, the development of the nonlinear extension of SWAN was initiated.
In order of importance, nonlinearities affecting the ship seakeeping problem are: a) the steepness of the ambient wave train; b) the nonlinear hydrostatic and Froude Krylov forces re
sulting from the interaction of a steep wave train with the ship hull; c) roll damping mechanisms arising from viscous separation, viscous lift forces from appendages and transom sterns; d) slamming and e) nonlinearities in the radiated and diffracted wave disturbance. The simultaneous treatment of all these nonlinear effects, even by a potential flow computational method, leads to a prohibitively expensive seakeeping simulation of little use in ship design. The strategy was therefore adopted to treat the nonlinearities outlined above progressively and to assess their importance before proceeding towards a more complete treatment.
This paper treats the seakeeping problem in head waves, therefore only the surge, heave and pitch motions and wave loads are considered. The ambient wave train is modeled independently of the seakeeping problem using the techniques of perturbation theory to first, second, and, if necessary, higher orders, along the lines of [11] and [14]. This approach allows the efficient generation of long wave records designed to correspond to a given sea spectrum, indepedently of the computation of the wave ship interaction which represents the bulk of the seakeeping simulation.
The nonlinear hydrostatic and Froude Krylov effects are treated by introducing a time dependent panel mesh over the ship wetted surface defined by the intersection of the ambient wave profile with the ship hull. Upon integration of the hydrostatic and ambient wave hydrodynamic pressure over the ship hull, the nonlinear hydrostatic and Froude Krylov exciting forces are obtained. Efficient meshing algorithms have been developed which allow the discretization of realistic hull shapes with cruiser or transom sterns in ambient wave trains of high steepness.
The ship wave disturbance arising from its forward translation, the surge, heave, and pitch oscillatory motions, and the interaction with the ambient wave, are initially treated by linear theory. Heave and pitch motion simulations are carried out by combining the nonlinear treatment of the hydrostatic and Froude-Krylov effects and the linear solution of the surface wave disturbance. Comparisons with experimental measurements reveal that a significant portion of the nonlinearity is accounted for by these effects.
The nonlinear coupling of the ambient-and ship-wave disturbances is next treated according to the “weak scatterer” hypothesis. It is postulated that the ship wave disturbance is small compared to the ambient waves and therefore can be linearized about the ambient wave profile, an assumption justified by observations of seakeeping experiments in steep waves. Evidently the weak scatterer hypothesis is violated in the vicinity of the ship waterline where strong spray roots are often seen to form, caused by the ship forward motion or slamming. These effects and slamming in particular, are however not treated in the present study.
Boundary value problems have been derived for the ship wave disturbance and stated around the time-varying (but a priori known) ambient wave profile. The body boundary condition is stated exactly over the instantaneous position of ship hull, therefore the need to introduce the so-called m-terms of linear seakeeping theory is avoided. Assuming potential flow, integral equations are derived for the unknown velocity potential over the ship hull and the ambient wave profile, using the Rankine source as the Green function. The set-up and solution of the integral equation is carried out along lines similar to those in the linear time-domain problem discussed in [8]. The radiation condition is satisfied as in the linear problem via an absorbing beach located at some distance from the ship, and designed to dissipate the energy carried by the ship wave disturbance. An outline of the solution algorithm and a brief review of the linear problem are given in Section 2.1. The weak scatterer hypothesis and corresponding boundary value problem is presented in Section 2.3.
An important component of a nonlinear seakeeping simulation is the enforcement of the exact body boundary condition. In Section 2.3
computations are presented of the heave and pitch hydrodynamic coefficients by the body-nonlinear algorithm and comparisons are carried out of the same quantities computed by the linear method which makes use of the so-called m-terms. The agreement between these two methods is found to be very satisfactory for a Series 60 hull over a broad range of forced oscillation amplitudes, confirming the need for the presence of the m-terms in the linear problem and their absence when the exact body boundary condition is satisfied.
Heave and pitch motion simulations are presented in Section 2 in head regular waves of variable steepness of the Series 60 and the Snowdrift hull. Experimental measurements are compared to heave and pitch motion simulations obtained from; a) linear theory and b) nonlinear hydrostatic and Froude Krylov effects coupled with a linear computation of the ship wave disturbance. Consistent with the stated objectives of this study, the purpose of these comparisons is to assess the nature and importance of nonlinear effects in the prediction of the heave and pitch motions in head waves.
Computations of the vertical bending moment and shear force distributions along the ship length are presented in Section 3.1, along lines similar to the ship motion simulations presented in Section 2. Since wave induced structural loads are obtained by integration of the hydrodynamic pressure over a portion of the ship hull, end effects, and, therefore, nonlinearities play a more important role than in the prediction of the ship motions. This is also born out of experience with the measurement and computation of the midships peak hogging and sagging moments in steep waves which are often found to differ by as much as a factor of two, when linear theory predicts that they must be equal in a regular wave. The prediction of the structural loads by the linearized seakeeping method and its nonlinear extensions are compared to a nonlinear strip theory method and experiments in Section 3.1.
The paper concludes with a discussion on how a nonlinear, time-domain, ship motion and structural load simulation might be used to determine the extreme value statistics needed in ship structural design. In order to detect a sufficient number of extreme events, a seakeeping simulation several hours long is necessary, a quite challenging task with a nonlinear seakeeping method. These issues are discussed in Section 3.2 where possible ways of coupling a linear with a nonlinear simulation method for the study of the extreme statistics are addressed.
2
Nonlinear Ship Motions
Consider a ship advancing with constant forward speed and a Cartesian coordinate system, ![]() fixed to the mean, translating position of the ship with the origin on the calm free surface, x-axis pointing upstream and z-axis pointing upwards. A second Cartesian system,
fixed to the mean, translating position of the ship with the origin on the calm free surface, x-axis pointing upstream and z-axis pointing upwards. A second Cartesian system, ![]() s fixed to the body is also introduced. The two coordinate systems coincide when the ship is in its equilibrium position and are related by translation and nonlinear rotation,
s fixed to the body is also introduced. The two coordinate systems coincide when the ship is in its equilibrium position and are related by translation and nonlinear rotation,
(1)
where ![]() T are the translations (ξ1,ξ2,ξ3) in surge, sway, and heave, and the matrix T is a function of the Eulerian rotation angles (ξ6,ξ5,ξ4) for yaw, pitch, and roll. The order of the Eulerian angles have been deliberately chosen in descending order.
T are the translations (ξ1,ξ2,ξ3) in surge, sway, and heave, and the matrix T is a function of the Eulerian rotation angles (ξ6,ξ5,ξ4) for yaw, pitch, and roll. The order of the Eulerian angles have been deliberately chosen in descending order.
Newton's Law expressed relative to the body-fixed frame lead to the following equation of motion for the six rigid body modes of motion, ![]() (t),
(t),
(2)
where ![]() D are the hydrodynamic forces,
D are the hydrodynamic forces, ![]() S are the hydrostatic forces, and M is the inertia matrix. It is important to note that, in this form, only the linear inertia terms are retained. Even
S are the hydrostatic forces, and M is the inertia matrix. It is important to note that, in this form, only the linear inertia terms are retained. Even
in realistic waves of large steepness, the effect of the nonlinear inertia terms is expected to be small when compared to the nonlinear hydrostatic, Froude-Krylov and hydrodynamic forces. These inertia terms will not be included in the present study.
In order to obtain the hydrodynamic wave forces, ![]() D for the freely floating body, a potential flow boundary-value problem is solved. In general, viscous forces do not contribute appreciably to ship motions and loads, especially in head seas. A possible exception occurs in the presence of a transom stern of large draft where unsteady flow separation may contribute appreciably to the heave and pitch damping. Also, viscous and lifting effects are known to be important for roll, sway, and yaw motion, therefore the present framework will be extended to incorporate these in the future.
D for the freely floating body, a potential flow boundary-value problem is solved. In general, viscous forces do not contribute appreciably to ship motions and loads, especially in head seas. A possible exception occurs in the presence of a transom stern of large draft where unsteady flow separation may contribute appreciably to the heave and pitch damping. Also, viscous and lifting effects are known to be important for roll, sway, and yaw motion, therefore the present framework will be extended to incorporate these in the future.
The flow is assumed to be governed by a total velocity potential, Ψ(![]() ,t), which satisfies the Laplace equation in the fluid domain and is subject to the kinematic and dynamic free surface conditions,
,t), which satisfies the Laplace equation in the fluid domain and is subject to the kinematic and dynamic free surface conditions,
(3)
(4)
imposed at the instantaneous position of the free surface, ζ(x,y,t).
On the wetted surface of the ship hull, a no-flux body boundary conditions states,
(5)
where ![]() is the component of the ship instantaneous velocity normal to the wetted surface of the hull. To close the exact problem, initial conditions are posed for
is the component of the ship instantaneous velocity normal to the wetted surface of the hull. To close the exact problem, initial conditions are posed for ![]() and the body displacement and velocity. Also, the gradients of the disturbance potential must decay infinitely far from the ship for finite time.
and the body displacement and velocity. Also, the gradients of the disturbance potential must decay infinitely far from the ship for finite time.
2.1
Linear Foundation
The study of a linearized model for seakeeping simulation allows a better understanding of any proposed nonlinear model. A nonlinear method will only be successful if the underlying linear theory is well understood.
This paper presents two nonlinear extensions to the linear formulation and numerical implementation summarized in this section. Both the nonlinear restoring and Froude-Krylov effects and the Weak Scatterer hypothesis are direct extensions of this linear foundation.
2.1.1
Linear formulation
Assuming that the total velocity potential, Ψ, consists of a dominant double-body component, Φ, and a perturbation correction, φ, the linear form of the kinematic and dynamic free surface conditions reduce to the form,
(6)
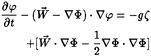
(7)
applied on z=0, where is the ![]() mean translational velocity of the ship. A further decomposition of the perturbation potential into instantaneous and memory components is used to obtain a stable form for the integration of the equations of motions, as discussed in [6].
mean translational velocity of the ship. A further decomposition of the perturbation potential into instantaneous and memory components is used to obtain a stable form for the integration of the equations of motions, as discussed in [6].
For an ambient wave steepness and ship motions that are sufficiently small, linear theory allows the decomposition of the incident, radiated and diffracted wave disturbances. The linear radiation body boundary conditions become,
(8)
applied on the mean wetted surface of the hull. Here, the m-terms, mj, provide a coupling between the steady basis flow and unsteady ship motion. They have been shown in [7] to contribute appreciably to the hydrodynamic coefficients and therefore must be included in a linear formulation. The diffraction body boundary condition merely states that the normal velocity of the sum of the incident and diffraction velocity potentials vanishes over the hull mean position.
The Laplace equation is enforced in the fluid domain by a distribution of Rankine sources and dipoles over the free surface and wetted hull surface. Application of Green's second identity leads to a boundary integral formulation for the perturbation potential,
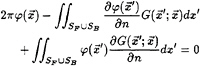
(9)
where ![]() is the Rankine source potential, SF is the mean position of the free surface, and SB is the mean position of the hull.
is the Rankine source potential, SF is the mean position of the free surface, and SB is the mean position of the hull.
2.1.2
Numerical implementation
A full discussion of the linear formulation, numerical method, and applications can be found in [7], [10], and [12], for frequency domain solutions [5], [6], and [8], for time domain motion solutions, so the basic numerical algorithm for the linear problem is only summarized in this section. The algorithm for the nonlinear problem is a direct extension of this implementation.
The three unknowns in the formulation are the velocity potential, φ, the wave elevation, ζ, and the normal velocity, φn. To solve for these unknowns, the free surface conditions (6) and (7), which form a pair of evolution equations, and the integral equation (9) are satisfied numerically by a time-domain Rankine panel method.
The Rankine panel method discretizes the hull surface and a finite portion of the free surface lying near the ship. Each of the unknowns is approximated independently by a set of biquadratic spline functions that provide continuity of value and first derivative across panels.
The evolution equations employ an explicit Euler integration to satisfy the kinematic free surface condition and an implicit Euler integration to satisfy the dynamic free surface condition. This scheme is based on the numerical stability analysis for time-domain panel methods found in [16]. Higher order schemes are also considered.
This stability analysis quantifies the numerical solution in terms of ship speed, panel size and aspect ratio, and time-step size, allowing for an optimal choice for the parameters of the numerical algorithm. An important result of this analysis is the discrete dispersion relation. This relation demonstrates that, for wavelengths less than four panels long, the discrete group velocity contains significant errors. A low-pass, spatial filtering scheme removes these erroneous short waves without affecting the consistency and convergence of the method. The filter does have some effect on the local, nonradiating free surface disturbance, but this problem is minimized since the filter is not applied at every time-step. The local disturbance can recover its proper equilibrium position between consecutive applications of the filter.
A numerical, wave-absorbing beach has been designed to satisfy the radiation condition, since only a finite portion of the free surface is covered by the panel method. This beach, based on the studies of [1] and [2], is applied on an outer zone of free surface panels and has an effect that is similar to a Rayleigh viscosity in the equivalent frequency domain formulation. The particulars of this beach are discussed in [8]. A key feature of the beach is that it can treat the case of zero speed and the ![]() critical frequency problem.
critical frequency problem.
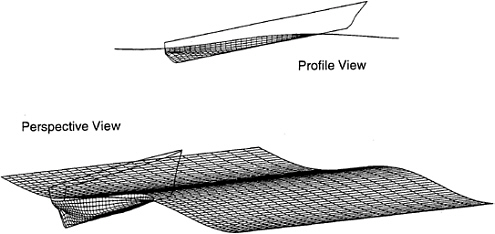
Figure 1: Snapshot of computational mesh for the Snowdrift hull at Froude number 0.325 in head seas.
The Rankine panel method produces a solution for the wave flow, but the equation of motion (2) for the ship must also be integrated at each time step in this simulation. This integration is delicate due to the presence of wave memory effects, but the numerical stability analysis of [6] provides an appropriate numerical integration scheme and time-step size.
2.2
Nonlinear Restoring and Froude-Krylov Forces
This first extension to the linear solution adds nonlinear restoring and Froude-Krylov forces to the equation of ship motion. These forces are considered to have a significant nonlinear contribution for ships with overhanging sterns or bows, or large degrees of flare.
This extension retains the linear results for radiation and diffraction forces, but replaces the linear restoring and Froude-Krylov forces. The hydrostatic and Froude-Krylov incident wave pressures are integrated on the exact, wetted hull surface, to produce the nonlinear forces. At each time step, the intersection of the a priori known ambient wave profile and the ship hull defines this exact wetted surface. Figure 1 shows a snapshot of such a time-varying wetted surface for the Snowdrift hull.
In this study, motions and loads have been investigated for two ships, the Snowdrift and the Series 60, Cb=0.7. The Series 60 is a ship that is very nearly wall-sided at the design waterline so the motions are predicted well by linear theory. The Snowdrift, which was examined in its ballast condition, manifests important nonlinear effects in its motions because of an overhanging stern that is neglected by linear theory. Linear, nonlinear restoring and Froude-Krylov, and Weak Scatterer motion simulations will be compared with experiments for these two hulls in section 2.4.
2.3
Weak Scatterer HypothesisAfter establishing the validity and limitations of the time-domain Ranking Panel Method in the linear seakeeping problems and investigating the importance of the nonlinear hydrostatic and Froude-Krylov forces, a more exact formulation has been examined. In this study, the so-called weak scatterer hypothesis [9] is adopted. The Weak Scatterer approach relaxes two of the restrictions of linear theory. The incident wave and body motions are allowed to be large, but the ship wave disturbance due to its forward translation and its interaction with the ambient wave is considered to be small.
This relaxation is physically justifiable. The incident wave driven by the environmental conditions cannot be reasonably restricted in magnitude, but observation often shows ship-generated waves to be relatively small. This stems from the fact that most ships are designed to be slender and, hence, do not produce steep wave disturbances even for large wave motion. Those large disturbances that do exist, spray for instance, do not contribute significantly to global forces. Under this observation, the ship-generated disturbance can be formally linearized about a steep incident wave using an Eulerian formulation.
The advantage of this approach is that it offers a more exact solution, but one that is still simplified enough to retain computational efficiency and numerical control. The solution of the fully nonlinear potential solution could be undertaken by a Mixed Eulerian-Lagrangian (MEL) scheme, for instance, but this might be prohibitively expensive.
Under the weak scatterer assumptions, we introduce the total disturbance potential, Ψ, and the decomposition:
where Φ is a time-dependent basis flow, satisfying a no-flux condition on the instantaneous incident wave surface and wetted hull. The impulsive flow, ![]() , governs the instantaneous impulse response of the ship to the surrounding fluid flows. Its introduction is motivated by the stability constraints [6] determined from the linear problem. φ0 is the incident wave potential and φ is the disturbance potential excluding the impulsive part
, governs the instantaneous impulse response of the ship to the surrounding fluid flows. Its introduction is motivated by the stability constraints [6] determined from the linear problem. φ0 is the incident wave potential and φ is the disturbance potential excluding the impulsive part ![]() . The total wave elevation η is decomposed into the incident wave elevation ζ0 and the disturbance wave elevation ζ.
. The total wave elevation η is decomposed into the incident wave elevation ζ0 and the disturbance wave elevation ζ.
The weak scatterer hypothesis assumes that the disturbance quantities φ and ζ are small, so only the first order terms are retained upon linearization about the ambient wave profile. Under this decomposition, the kinematic and dynamic conditions become,
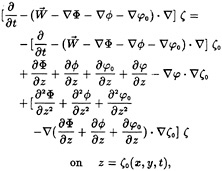
(11)
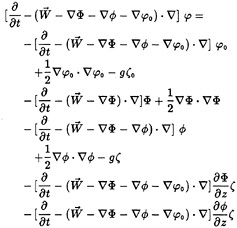
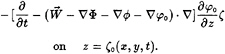
(12)
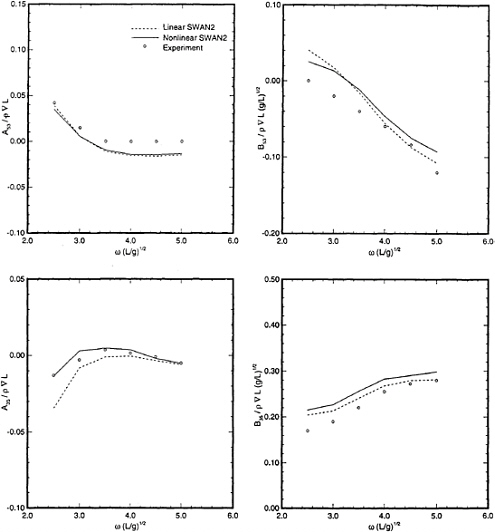
A no-flux, body boundary condition is applied over the instantaneous nonlinear position of the ship wetted surface. The need to evaluate the so-called m-terms of linear theory is circumvented. To validate the consistency of the linearized and nonlinear enforcement of the body boundary conditions, the heave and pitch hydrodynamic coefficients were computed for the Series 60 Cb=0.7 hull using the linear and nonlinear methods. In the limit of small oscillation amplitudes the two methods are expected to agree, confirming the proper evaluation of the m-terms in the linear problem and of the correct enforcement of the exact body boundary condition in its nonlinear counterpart.
Figure 2 show the comparison among the linear, nonlinear, and experimental coefficients. For this relatively wall-sided ship and for sufficiently small oscillation amplitudes all results were expected to be in good agreement. The correlation is indeed very satisfactory, demonstrating that the m-terms resulting from the linearization of the body boundary conditions are accounted for by the present body nonlinear approach.
In the presence of a specified ambient wave profile, the boundary value problem obtained from the weak scatterer hypothesis is solved by discretizing the instantaneous position of the ship wetted surface and ambient free surface. The panel arrangement is illustrated in in Figure 1 which shows a typical snapshot of the computational mesh for the Snowdrift hull in free motion. As in the linear solution, a dissipative beach is included on an outer layer of panels in order to absorb the outgoing ship wave disturbance as in the linear problem.
Computations of the heave and pitch motions of the Series 60 hull predicted by the linear solution and the weak scatterer hypothesis are presented and discussed in Section 2.4.
An important step in the weak scatterer formulation, involves the evaluation of the Eulerian time derivative of the velocity potential which enters in the free surface condition and the evaluation of the hydrodynamic pressure over the ship hull. The direct approach of extracting the Eulerian time derivative from the Lagrangian derivative of the velocity potential, has been found to introduce numerical instability and to therefore lead to an excessive restriction of the time-step size.
Therefore, a more robust method has been devised. A boundary value problem may be posed for the Eulerian time derivative, ∂Ψ/∂t, which is a harmonic function. Therefore, Green's theorem is directly applicable, as for the velocity potential, leading to the statement
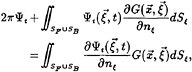
(13)
where the subscript t denotes the partial time derivative. A similar equation may be posed for the Eulerian derivative of the basis flow potential Φ. The numerical properties of this algorithm of evaluating the Eulerian time derivatives of the unknown potentials appear to be very promising and are under study. A similar treatment of the time derivative has been proposed by [17].
2.4
Linear and Nonlinear MotionsThis section compares linear, nonlinear restoring and Froude-Krylov, and Weak Scattering motion simulations to experiments for two ships, the Series 60, Cb=0.7, and the Snowdrift.
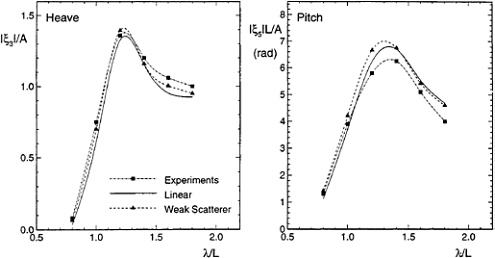
Experiments for the Series 60 [3] are compared in Figure 3 with the results from the linear and Weak Scatterer nonlinear simulations. The nonlinear simulations were conducted in regular head seas of varying wave-
length with a wave amplitude equal to one percent of the ship length. The reported motion amplitudes are half the difference between the maximum and minimum values for the nonlinear results. It is evident that the linear theory is in good agreement with the experiments, and that the nonlinear results from the Weak Scatterer simulation provide only a small correction. This was expected since the Series 60 is wallsided at its design waterline.
A series of experiments in regular waves were carried out for the Snowdrift hull (L=160m) at a Froude number of 0.325 in head seas. These experiments were conducted as a cooperative program between the U.S. Navy and Det Norske Veritas. They include measurements of the ship motions, but also of the global loads which will be presented later.
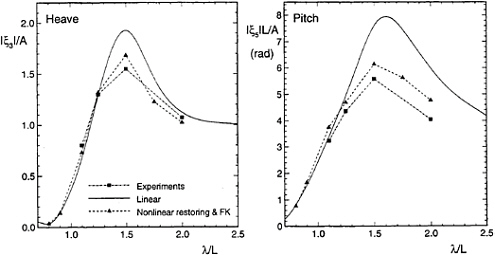
In ballast condition (T=8m), there is an overhanging stern above the waterline that is neglected by linear theory but was observed to submerge in the tests. Experiments clearly demonstrated nonlinearity with increasing wave steepness.
Figure 4 compares the linear to the experimental results. Results for the nonlinear restoring and Froude-Krylov predictions in regular waves of 3.2 meter wave amplitude are also presented in this figure.
Figure 4 clearly demonstrates that nonlinear effects are significant for the Snowdrift hull and that the nonlinear restoring and Froude-Krylov extension provides a good prediction for the motions.
In all the simulations, both linear and nonlinear, for motions and loads, steady sinkage and trim effects were included. The choice of running condition has a significant effect on motions.
3
Global Loads3.1
Global Loads in Regular WavesThis section presents results for the computation of global loads on the Snowdrift hull. The computations are carried out by linear theory and by linear theory with the non-linear hydrostatic and Froude-Krylov forces extension. Global load computations by the weak scatterer method have not yet been performed.
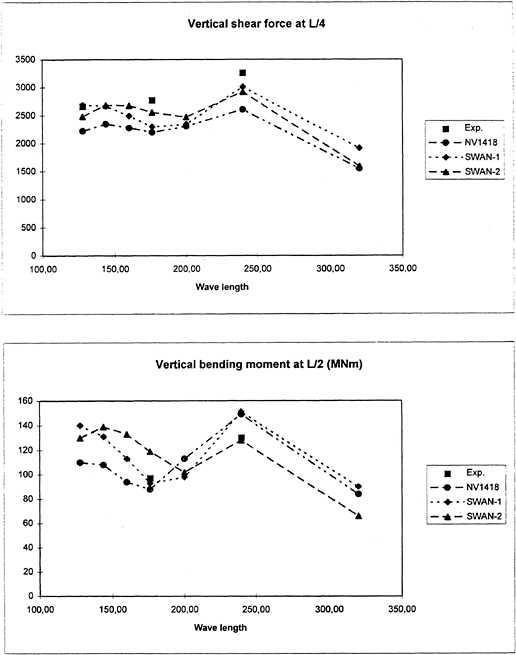
The computed results are compared with experimental data and with results from the computer program NV1418 which is a nonlinear strip theory program. Computations are carried out for the Snowdrift in both the ballast condition (T=8m) and a loaded condition (T=11.4m) in head seas. Results will be presented for the vertical shear force at L/4 (i.e. 1/4 ship length aft of the fore perpendicular) and vertical bending moment at L/2 (i.e. midship).
The global loads are computed by integration of forces from the bow to the section across which the load is computed.
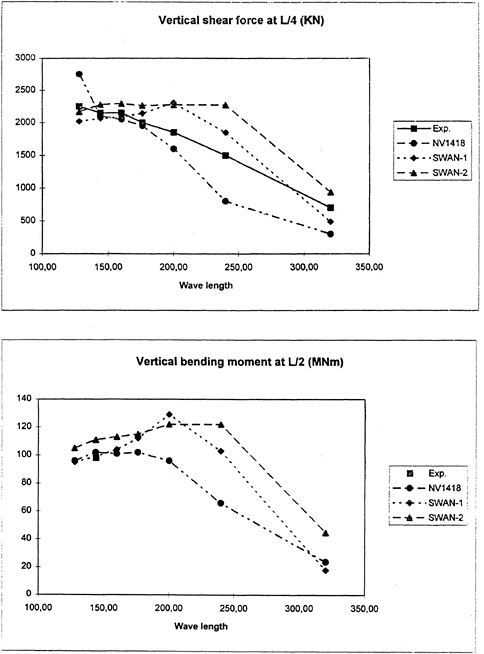
Both the experimental data and the NV1418 time records are non-linear. The linear component of the signals can be extracted by numerical techniques. The method used is based on Volterra functional analysis, [4]. In Figures 5 and 6 these results are compared with results from the linear time domain code SWAN-2 and the corresponding frequency domain code, SWAN-1.
The results from non-linear strip theory is expected to be better for the low speed than for the high speed, and better for long waves than for short waves. For the shortest waves and the highest speed we are definitely outside the applicability region for the non-linear strip theory.
Results from SWAN-1 and SWAN-2 should be expected to agree well since they are obtained for very similar, although not identical, theories. The agreement is fairly good in most
cases, but the difference between the two types of simulation is significant in many cases. With the exception of the combinations where strip theory is not valid, and the high speed/ballast condition case, the general impression is, however, that all three simulations show reasonable agreement, but that the agreement with the experiments is not always good. For the ballast condition (i.e. 8m draft) and Fr=0.325 the codes differ dramatically around resonance with the experimental data lying between the SWAN and NV1418 results.
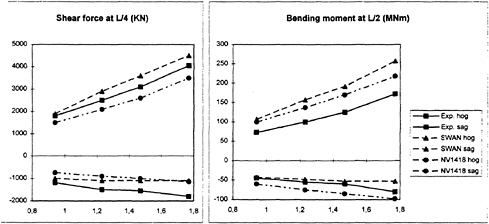
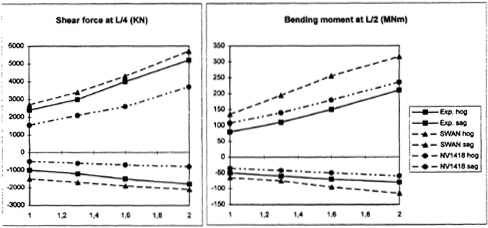
Figures 7 through 10 show a comparison between the experiments, non-linear strip theory and SWAN-2 with non-linear hydrostatic and Froude-Krylov forces. Positive values correspond to sag loads, negative values to hog loads. The sag and hog values are computed as deviations from the still water loads, which have been computed by SWAN-2 as well. The results clearly illustrate the expected result that the loads are much more non-linear than the motions.
With the sign conventions used in SWAN the hog situations will correspond to maxima on the curve for the shear force and minima on the curve for the bending moment. The wave amplitude is in both cases modest, but still the difference between the two results is large. For the full load condition (11.4m draft) the signal from the non-linear code looks quite harmonic, but the comparison still reveals strong non-linear effects with the results shown in Figures 7 through 10. In some cases SWAN is much closer to the experimental data than strip theory is, in other cases it is the other way around. At the 8m draft SWAN predicts larger sag bending moments than the experiments does. At the 11.4m draft the predicted hog loads for the high speed case are small compared to the experiments. In the latter case strip theory agrees very well with the experimental data.
The reasons for the deviations are yet unknown. The fact that non-linear strip theory is better in those cases where SWAN fails might indicate that non-linear added mass effects may be important. In the weak scatterer version of SWAN this is included, since the radiation problem is always solved for the instantaneous wetted hull, so the results may improve.
3.2
Extreme Value StatisticsThe prediction of extreme responses (loads and motions) is critical in the structural design of a ship. If the incoming waves have a Gaussian distribution then the response based on linear theory will also be Gaussian, and the response statistics can be calculated by well established methods. On the other hand, if nonlinear hydrodynamic effects are introduced, the response will be, in general, non-Gaussian which may require a simulation of considerable duration.
By extending the model for ship motions and global loads beyond linear theory, the physical accuracy of the simulation is reduced for a given deterministic input (i.e. reduced model uncertainty), but the computational requirements may become prohibitive. Even with the promise of “real time” simulation, the simulations may be too long to consider practically. So, this decrease in model uncertainty is offset by an increase in statistical uncertainty arising from the difficulty in producing sufficiently long records.
In order to overcome these problems, a method [15] which incorporates a well founded strategy for the selection of the inputs to the nonlinear simulations has to be used. The adoption of such a method will avoid impractical computational burdens by using the more exact physical model only when it is justified within time windows of extreme motion. A “critical wave episode” within a give sea-state will require initial conditions for the nonlinear simulation for this time window. A collection of these short duration episodes provides a basis for the estimation of the (short term) extreme value statistics. Statistical methods can then be applied to obtain an optimal choice for the necessary sea-state, the number of episodes, and the
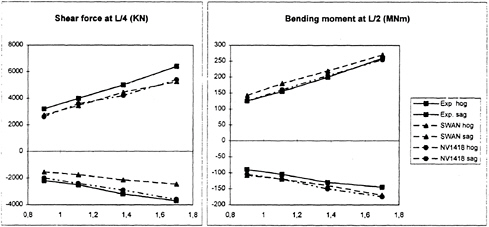
Figure 9: Sag (positive) and hog (negative) loads for Snowdrift (T=11.4m) at Froude number 0.145 and 160m wavelength as a function of wave amplitude(m).
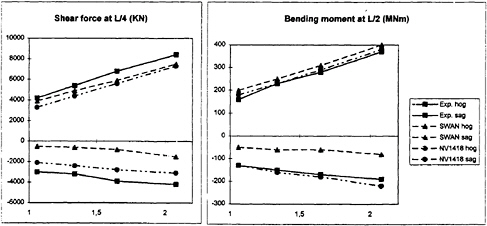
Figure 10: Sag (positive) and hog (negative) loads for Snowdrift (T=11.4m) at Froude number 0.325 and 240m wavelength as a function of wave amplitude(m).
number of repeated realizations of each of these episodes.
For the vertical bending moment of a container ship, for instance, an estimation of the extreme response with less than five percent statistical uncertainty can be based on simulations of only one percent of what would be needed for a direct time domain simulation.
4
ConclusionsA nonlinear seakeeping method has been presented for the simulation of the ship motions and wave induced loads in steep random waves. The method is based on a potential flow model which is treated by a Rankine Panel method based on the distribution of sources and dipoles over a mesh of panels placed on the instantaneous positions of the ship hull and the a priori known ambient wave profile. The computational method reflects an evolution of a host numerical algorithms developed for the solution of the linear seakeeping problems in the frequency and time domains, which have been developed from first principles and designed to be numerically stable, robust and efficient.
Computations of the hydrodynamic forces and motions of a wall-sided Series 60 hull and the flared Snowdrift hull in head regular waves of variable steepness, confirm the accuracy of linear theory for the Series 60 and the need for nonlinear corrections for the Snowdrift hull. In particular, accounting for nonlinear hydrostatic and Froude Krylov effects for the Snowdrift hull leads to a significant reduction of the heave and pitch motion amplitudes in head waves of moderate steepness, found to be in very good agreement with experiments.
Predictions of the bending moment and shear force distributions on the Snowdrift hull in head regular waves have been compared to experiments and a nonlinear strip theory method. The nonlinear loads reported in this study are based on the nonlinear computation of the hydrostatic and Froude Krylov effects and the linearized ship wave disturbance. They have been found to be in satisfactory agreement with experiments and to reveal a clear sensitivity upon the ambient wave steepness, as expected. Discrepancies between the predictions and measurements of the global loads were identified and attributed to nonlinear effects which are presently not included in the method.
Future extensions of the method will incorporate missing nonlinear effects in the motion and global load computations, based upon the weak scatterer approximation. The extension of the method is also planned in oblique waves, where models for the roll, sway and yaw damping mechanisms will be developed for ships with appendages and transom sterns. Finally means to further improve the computational efficiency of the method will be investigated in order for the study of the ship motion and global load extreme statistics to become feasible.
5
AcknowledgementsThe development of SWAN has been funded by the Office of Naval Research and Det Norske Veritas.
References
[1] Baker, G.H., Meiron, D.I., and Orszag, S.A., “Application of a Generalized Vortex Method to Free Surface Flows”, 3rd International Conference on Numerical Ship Hydrodynamics, 1981.
[2] Cointe, R., “Nonlinear Simulations of Transient Free Surface Flows”, 5th International Conference on Numerical Ship Hydrodynamics, 1989.
[3] Gerritsma, J., Beukelman, W., and Glansdorp, C., “The Effects of Beam on the Hydrodynamics Characteristics of Ship Hulls”, 10th Symposium on Naval Hydrodynamics, 1974.
[4] Korbijn, F.: “Analysis of the sag to hog regular wave model test results and comparison with results from available nonlinear theory”, DNVC Rep. No. 91–0134, DNV Jan. 1991.
[5] Kring, D.C. “Time Domain Ship Motions by a Three-Dimensional Rankine Panel Method ”, PhD Thesis, MIT, Cambridge, MA, 1994.
[6] Kring, D.C., and Sclavounos, P.D., “Numerical Stability Analysis for Time-Domain Ship Motion Simulations ”, Journal of Ship Research, Vol.39, No.4, Dec. 1995.
[7] Nakos, D.E., and Sclavounos, P.D., “Steady and Unsteady Ship Wave Patterns”, Journal of Fluid Mechanics, Vol.215, 1990.
[8] Nakos, D.E., Kring, D.C., and Sclavounos, P.D. “Rankine Panel Methods for Transient Free Surface Flows”, Proceedings of the 6th International Conference on Numerical Ship Hydrodynamics, Iowa City, Iowa, 1993.
[9] Pawloski, J., “A Nonlinear Theory of Ship Motions in Waves”, Proceedings of 19th Symposium on Naval Hydrodynamics, Seoul, Korea, 1992.
[10] Sclavounos, P.D., and Nakos, D.E., “Stability Analysis of Panel Methods for Free Surface Flows with Forward Speed”, 17th Symposium on Naval Hydrodynamics, The Hague, The Netherlands, 1988.
[11] Sclavounos, P.D., “On the Quadratic Effect of Random Gravity Waves on a Vertical Boundary ”, Journal of Fluid Mechanics, Vol.242, 1992.
[12] Sclavounos, P.D., Nakos, D.E., and Huang, Y., “Seakeeping and wave induced loads on ship with flare by a Rankine Panel Method” Proceedings of the 6th International Conference on Numerical Ship Hydrodynamics, Iowa City, Iowa, 1993. 62
[13] Sclavounos, P.D., “Computation of wave ship interactions” Advances in Marine Hydrodynamics, edited by M.Ohkusu, Computational Mechanics Publications, 1995.
[14] Tick, L.J., “A Non-linear Random Model of Gravity Waves”, Journal of Maths Mech., Vol.8, 1959.
[15] Torhaug, R., Braathen, A., and Winterstein, S., “Non-Linear Ship Loads: Stochastic Models for Extreme Response.”, to be published.
[16] Vada, T., and Nakos, D.E., “Time Marching Schemes for Ship Motion Simulations”, 8th International Workshop on Water Waves and Floating Bodies, 1993.
[17] van Daalen, E.F.G. “Numerical and Theoretical Studies of Water Waves and Floating Bodies ” PhD Thesis, University of Twente, Enschede, The Netherlands, 1993.
DISCUSSION
C.M.Lee
Pohang Institute of Science and Technology, Korea
This paper shows a definite improvement in predicting the motion and wave loads of ships. I would like to congratulate the authors for the excellent work presented here
My long-held assertion is that the validity of the methods in predicting ship motion in waves should be proved by checking the relative vertical motion of a ship with respect to waves, rather than checking the absolute motion alone with the corresponding experimental results. I would like to know how good the present theory is in this regard.
AUTHORS' REPLY
You are correct in that any method should be validated against as many experimental results as possible. However, due to the difficulty in obtaining relative wave elevations from experiments, few of these results can be found in the open literature. We have compared our relative wave elevation predictions to one set of experiments for the commercial design, TGC's FASTSHIP, and found a favorable comparison.
Also, for the purposes of global load predictions presented in this paper, the quantity of relative wave elevation is not directly relevant, since we have not examined slamming. When this quantity is evaluated there is also a question of physical significance. Exactly at the intersection of the wave and ship, the wave profile is difficult to measure due to localized effects such as jet formation and spray. In these loads, the relative wave elevation may be measured at some small distance away from this exact line of intersection. In this case a potential based method will perform well.