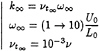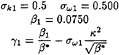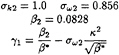Evaluation of Eddy Viscosity and Second-Moment Turbulence Closures for Steady Flows Around Ships
G.Deng, M.Visonneau (Ecole Centrale de Nantes, France)
1
Introduction
The flow around the so-called HSVA Tanker hull, experimentally studied by Dr. J.Kux [1] at the Institute of Shipbuilding in Hamburg, is considered by the hydrodynamical community as one of the best documented testcases among all the available experimental ship flow databases. Despite the relative geometric simplicity of the body, the flowfield around this hull is the result of many complicated features involving convergence and divergence of streamlines, a strong thickening of the boundary layer due to rapid changes in cross-sectional shape leading to the development of an intense longitudinal vortex which is slowly relaxed in the wake at large distances downstream from the ship. A more accurate understanding of the flow is provided by the analysis of the limiting streamlines (Figure 1 from [1]). This figure indicates the existence of two lines of convergence located in the aftpart of the hull. The first S-shaped line delimits a vertical wall flow region and a limited zone of flow reversal. The second line of convergence is almost rectilinear and situated slightly above the keel plane of symmetry. It indicates the existence of a region characterized by a large normal velocity which, in that case, is correlated with the development of an intense longitudinal vortex. Figure 2 from [1] shows the axial velocity contours at x/L=0.978. It enables a complementary interpretation of the print provided by the previous figure. The longitudinal velocity contours are characterised by a “hook” shape in the central part of the wake illustrating the interaction between the velocity and vorticity fields, the longitudinal isovels being significantly distorted by the longitudinal vorticity.
Considering the complexity of this physical configuration, the simulation of such a flow is a considerable challenge for the numerical methods. The availability of a remarkable experimental data base gives us a formidable opportunity to assess the rel-

Figure 1: HSVA Tanker–Re=5.0106.
Experimentally observed wall flow.
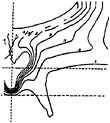
Figure 2: HSVA Tanker–Re=5.0106.
Experimental isowake contours at x/L=0.978
ative influences and respective merits of discretisation algorithms and turbulence models. It is why this database was chosen as one of the two test cases of the 1990 SSPA-CTH-IIHR Workshop on Viscous Flow held at Goteborg [2], and again selected for the 1994 CFD Workshop held at Tokyo [3].
The results obtained during the first workshop held at Goteborg [ 2], indicated that most of the methods based on Reynolds Averaged Navier-Stokes Equations were able to simulate the gross features of the flowfield and predicted the shape and location of the wake. However, neither the central region of the wake (the now famous “hook” shaped contours) nor the details of the wall flow were simulated by the methods used at that time. Actually, most of compared methods produced essentially the same too diffusive flow, particularly in the near wake region. Insufficient grid resolution, especially on such complex three-dimensional configurations, spatial discretisation errors, limited convergence on non-linearities are the usual reasons put forward to justify the bad performances of a numerical simulation. Even if these reasons are to be considered, and this paper will draw attention to another one (the influence of inlet conditions), the authors noticed [4] that the turbulence models used at that time were mainly responsible for the bad representation of longitudinal vortex. A systematic comparison of the respective influences of various discretisation schemes and grids was conducted and used to quantify the consequences of adhoc modifications of the turbulent viscosity in the central region of the wake. This systematic analysis established that the modifications of eddy-viscosity distribution were the only ones responsible of dramatic improvments of the iso- velocity contours. The aim of this previous study [4] was obviously not to promote such a-posteriori alterations, but rather to underline the likely weaknesses of an eddy-viscosity based turbulence closure for such a complex flow in order to stimulate the validation and assessments of more complex turbulence models in the context of complex geometries.
One year later, during the 1994 CFD Workshop held at Tokyo [3], a session was again devoted to the same test cases, namely the HSVA and Dyne Tankers. Although many contributors employed again algebraic zero equation models (Cebeci-Smith or Baldwin-Lomax models), the results were significantly improved since the “hook-shape” behaviour was often captured, at least to some extent, by an increased number of participants. Those results are somewhat difficult to understand since the same Baldwin-Lomax turbulence models used in 1990 and 1994 did not provide the same results. An analysis of eddy-viscosity contours in the near wake conducted by Sotiropoulos and Patel suggests that “the apparent success of methods using the Baldwin-Lomax model is mainly due to the arbitrary restriction of the computed eddy-viscosity level in the central part of the wake”. Therefore, this unexpected and undesirable consequence of [4] can be considered as a not-always-confessed illustration of the major role played by the turbulence closure in the representation of such complicated afterbody flows.
During this last workshop and for the first time in the context of naval hydrodynamics, two research teams tried to use second-moment turbulence closures ([5], [6]). Sotiropoulos & Patel [5] employed the near-wall second-moment transport closure of Shima [7]. Comparisons with results obtained with the two-layer k–ε turbulence model of Chen & Patel [8] revealed that the second-moment closure was able of reproducing most of the features observed in the measurements and particularly the S-like structure of the isovels in the central part of the wake. However, a closer examination of their results revealed that the longitudinal vorticity in the near wake was noticeably overestimated, the computed rate of decay of secondary motion in the wake being also slower than its measured counterpart. Chen et al. [6] employed a second-moment closure based on the pressure-strain correlations of Speziale, Sarkar and Gatski [9] in the fully turbulent flow regions whereas the low Re near-wall closure of Shima [10] was used to provide the necessary viscous damping in the laminar sublayer and buffer layer. Here again, their results clearly established the superiority of second-moment closures over simpler isotropic eddy viscosity models for this kind of applications, even if, on the contrary of the previous contributors, the longitudinal vorticity appeared to be slightly underestimated.
The objectives of the present study are twofold:
-
The analysis in the first part will be conducted under the general context of isotropic eddy viscosity turbulence closures. New turbulence closures based on the k–ω model and its recent variants developped in the aerodynamical context will be examined. The influence of inlet conditions will be examined in order to determine if full-body computations provide mechanisms for generating longitudinal vorticity that would be absent or underestimated when computations start at mid-body.
-
The second part will be devoted to the assessment of a second-moment closure with near-wall low-Re formulation [7] which was successfully employed by Sotiropoulos and Patel. Numerical implementation of this new approach in the difficult context of implicit pressure Poisson equations will be described. Comparisons between this promising second-moment closure and the more robust and validated eddy-viscosity models will conclude this paper.
2
The Numerical Method
Our CFD Group has developped a code (HORUS) which is used for the validations presented in this paper. This code is based on a partial transformation,
for which the curvilinear space coordinates are used
as independent variables and the cartesian compo
nents of velocity and pressure are retained as dependent variables. Many turbulence models are already implemented ranging from eddy-viscosity based models (one equation: Baldwin & Barth's model [11]; two equations: k–ε models (Chen & Patel [8], Nagano & Tagawa [12], Deng & Piquet [13]), k–ω models (Wilcox, Menter BSL and SST modified versions [14], [15])) to models requiring the solution of Reynolds Stress Transport Equations (Shima's model [7], Craft & Launder's model presently in test [16]). To avoid any wall-function boundary conditions which turn out to be unacceptable when three-dimensional flows are considered, near-wall low-Reynolds number treatments are sytematically implemented in the aforementionned turbulence models.
A structured cell-centered layout is used in which the pressure, turbulence and velocity unknowns share the same location. The momentum and continuity equations are coupled through the PISO procedure with the help of the Rhie & Chow flux interpolation procedure and several implicit second order accurate schemes are implemented for the space and time discretisations.
Preconditionned conjugate gradient solvers (CGS, CGSTAB) are used to solve the linear systems.
This code can be used with almost any kind of mathematical boundary conditions and additional no-slip condition can be added inside the computational domain to enable the computation of configurations of intermediate complexity (afterbody+nozzle, for instance) without having recourse to a multiblock approach. However, a multiblock extension, currently based on point-to-point coincident blocks, has been developped and is under validation before the more promising “Chimera approach ”, based on overlapping grids, which is now under development.
This code is included into a modelisation chain comprising a multiblock mesh generator (ICEMCFD) able to read CAO formats, a X-MOTIF interface facilitating the use of RANSE solver and a three-dimensional interactive graphic post-processor.
3
The Isotropic Eddy Viscosity Closures
3.1
The k–ω Models
Among the two-equation models, the k–ε models are by far the most validated today in the hydrodynamical domain. However, even if they are relatively robust, they are known for their lack of sensitivity to adverse pressure-gradients. The models tend to underpredict the separation region or to delay its development. Moreover, if low-Reynolds number k–ε formulations are employed, the additional non-linearities introduced by the damping functions often deteriorate the overall convergence of the algorithm. The k–ω model of Wilcox [14], [17] employs one equation for the turbulent kinetic energy k and a second equation for a specific turbulence frequency ω. This model is known to perform better than the k–ε models under adverse pressure-gradient conditions and, moreover, since its formulation does not employ damping functions in the viscous sublayer, it is characterised by an increased numerical robustness. However, the results of this model depend strongly on the freestream values ωf that are prescribed outside the shear-layer [18]. In order to remove this unacceptable sensitivity, Menter [15] proposed two variants, the BSL and SST formulations, which result from a blending between the original k–ω model in the inner region of a boundary layer and a transformed version of the k–ε model in the outer wake region.
3.1.1
The Original k–ω Model
The eddy-viscosity is defined by;
(1)
and the turbulence transport equations are defined by:
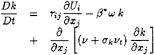
(2)
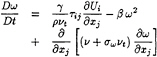
(3)
with:
(4)
The various constants are defined by:
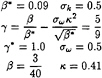
(5)
The boundary conditions for ω, [14], are given by:
3.1.2
BSL variant from Menter
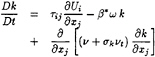
(6)
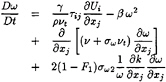
(7)
![]() 1 represents the constant relative to the original model (σk1,…),
1 represents the constant relative to the original model (σk1,…), ![]() 2 the corresponding constant in the transformed k–ε model (σk2,…) and
2 the corresponding constant in the transformed k–ε model (σk2,…) and ![]() the constant associated to the new k–ω BSL model (σk,…). The relation between these constants is given by:
the constant associated to the new k–ω BSL model (σk,…). The relation between these constants is given by:
(8)
with the following two sets of constants:
and:
κ=0.41 et β*=0.09 (11)
The blending function F1 is built to be one in the near-wall region and zero away from the body. It is defined by:
(12)
with
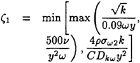
(13)
where:
(14)
4
The Second Moment Closures
Difficulties encountered by eddy-viscosity models in modelling complex flows are most often related to models' inability to account for the selective amplification or attenuation of different Reynolds stresses by curvature-related strain components. These limitations are principally rooted in the fact that the eddy-viscosity models have been designed to provide the correct level of shear stress in flows in which only this stress is influential. The eddy-viscosity models are not able to modelize separately the normal
turbulent stresses, since only the kinetic turbulent energy is taken into consideration. Therefore, the essential inability of eddy-viscosity closures to simulate anisotropic turbulence can explain their bad performances on flows containing recirculating regions or intense vortices, since the turbulence anisotropy strongly influences the magnitude of longitudinal vorticity ([19]). With the need to resolve anisotropy taken for granted, the main choice is between nonlinear eddy-viscosity models and second-moment closures. The non-linear eddy-viscosity models are very attractive because they can be seen as the natural and painless evolution from linear eddy-viscosity models. It is now difficult to evaluate the potentialities of such models in complex three-dimensional flows. However, we believe that they will perform better than linear eddy-viscosity models only on a limited range of flows characterised by a weak turbulent anisotropy. On complex three-dimensional flows, second-moment closures will be probably superior because of the exact representation of stress production which enables realistic interactions between normal stress anisotropy and shear-stress components.
Here and there, very promising computational studies employing second-moment closures on highly complex three-dimensional flows are emerging ([ 5], [6], [20], [21]). In the same time, new proposals of low-Reynolds number near-wall second-moment closures make it possible the eviction of wall-function boundary conditions, what is for us a prerequisite for validating them on three-dimensional flows.
4.1
The Shima Model
This model [7] is defined by the following transport equations:
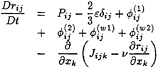
(15)
where the source terms corresponding to production, dissipation, transfer and diffusion are modelled by by:
(16)
(17)
(18)
where:
(19)
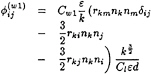
(20)
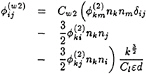
(21)
(22)
with Cs=0.22 and Cl=2.5.
The coefficients are given by:
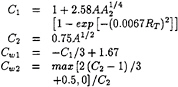
(23)
where:
(24)
A2=aijaij (25)
A3=aijajkaki (26)
(27)
(28)
where d is the distance to the wall.
A transport equation for ε must also be solved:
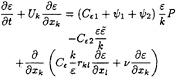
(29)
with:
(30)
Ψ1=1.5A(P/ε–1) (31)
ψ2=0.35 (1–0.3A2) exp [–(0.002RT)1/2] (32)
The additional constants take their usual values: Cε1=1.45, Cε2=1.9 and Cε=0.18.
4.2
Numerical Implementation
Second-moment closures are particularly difficult to include into a time-implicit RANSE solver because of:
-
the absence of the numerically stabilising eddy viscosity,
-
the strong coupling between anyone stress and strains other than the ones linked to that stress via the Boussinesq relations,
-
the predominant influence in the momentum transport equations of equilibrium between several strong and opposite source terms, namely, the pressure and Reynolds-stress gradients,
-
the complexity of second-moment transport equations through added non linearities introduced by the actual low-Reynolds near-wall formulations. In particular, the practical impossibility of obtaining theoretically or numerically realisable turbulence in complex configurations makes it difficult to reach a safe numerically converged state.
Moreover, the incorporation of second-moment closures into solvers designed for flows around complex geometries is considerably complicated by the mandatory use of colocated variable arrangment. Different numerical strategies have been designed to enhance stability in this context. Some authors, [20], enforce stability by extracting apparent turbulent viscosity from the source terms of second-moment transport equations. On the other hand, [22] developped a fully coupled implicit resolution of momentum and second-moment transport equations to avoid velocity-turbulence decoupling. More recently, several authors, [5], [21], have employed explicit time-marching procedures, often based on a four stage Runge-Kutta scheme for the mean flow equations, without reporting any severe stability problem.
Actually, if one wants to include a second-moment closure into an existing time-implicit solver based on the resolution of a Poisson equation for the pressure, many problems of stability may be expected. In the momentum equations, the predominant role played by the source terms in absence of turbulent viscosity makes it necessary deep modifications of the original numerical algorithm. When the Reynolds stress is treated implicitly in the momentum equations when using eddy-viscosity models, it appears explicitly when second-moment closures are used. This situation is particularly difficult for the normal velocity component when it is integrated down to the wall. In fact, in the wall region, due to the rapid growth of normal Reynolds stress, its gradient becomes a predominant term which is balanced only by the normal pressure gradient, both appearing explicitly in the momentum source term. It is why the main idea behind the present proposed modifications of the original algorithm is the obligation of treating the turbulent and pressure gradients in the same way if we want to maintain the regularity of small magnitude velocity components. We think that the main source of irregularity is not necessarily the absence of turbulent viscosity but the discrete disequilibrium between several strong and opposite gradients which would provide, if perfect balance was achieved, a regular solution of small magnitude. To enforce this discrete equilibrium is not a trivial task because of the numerous source terms interpolations which are carried out if the popular Rhie & Chow interpolation practice is used to build the mass fluxes in the general context of a pressure equation method on non-staggered variable arrangment. The only physical tool able to restore this equilibrium is the pressure and it is why it is perhaps more justified to speak of a pressure-turbulence-velocity coupling instead of the conventional pressure-velocity coupling.
In a pressure equation RANS solver, the three fundamental steps are the prediction step, the solution of pressure equation and the correction step. Each step must be somewhat revised in order to maintain a strict discrete equilibrium between the dominant source terms, namely, the pressure and turbulent correlations gradients. These generalisations which are designed to enforce the regularity of discrete fields and consequently the stability of the numerical algorithm, are now described on a 2D curvilinear example.
4.2.1
A pressure-turbulence equation
The RANS equations are defined by:
(33)
where ![]() Once discretised, the momentum equations can be written as:
Once discretised, the momentum equations can be written as:
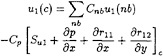
(34)
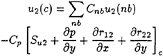
(35)
where Cnb and Cp are the usual influence coefficients.
Once expressed with the curvilinear coordinates, the momentum equations become:
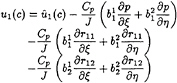
(36)
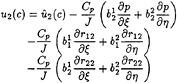
(37)
where J is the jacobian of the transformation and ![]() are the usual j components of
are the usual j components of ![]()
The contributions of neighboring points and source term (except the pressure and turbulent stress gradients) are incorporated into the pseudo-velocity ûl:
(38)
(39)
To build a pressure equation, the continuity equation is written under its fully conservative form on the mass control volume:
[JU1]d–[JU1]u+[JU2]n–[JU2]s=0 (40)
with ![]() The contravariant velocity components
The contravariant velocity components ![]() have now to be rebuilt at the interfaces and this reconstruction must avoid chequer-board pressure oscillations and maintain the discrete link between pressure and turbulent gradients. The mass flux at the interface d is rebuilt through the following interpolation of velocity components:
have now to be rebuilt at the interfaces and this reconstruction must avoid chequer-board pressure oscillations and maintain the discrete link between pressure and turbulent gradients. The mass flux at the interface d is rebuilt through the following interpolation of velocity components:

(41)

(42)
where the overlined quantities are linearly interpolated in the computational domain, the pressure and turbulent stress gradients being rediscretised at the interface. Once the contravariant components are expressed with the help of the previous interpolations, a pressure equation is obtained which is somewhat different because the contributions of turbulent stresses are explicit instead of being accumulated (and linearly interpolated) in the source terms.
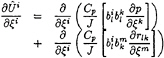
(43)
where:
(44)
With this special treatment of turbulent stresses gradients in the pressure equation source term, the discrete link between pressure and turbulence gradients is enforced, and a first source of numerical oscillations is avoided when pressure and turbulent correlations gradients compete in the momentum equations.
4.2.2
The correction step
Since the source terms of momentum equations do not contain any turbulent contribution, it is necessary to devise a slightly modified correction step:
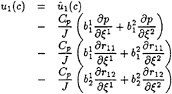
(45)
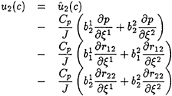
(46)
where the turbulent stresses gradients are explicitly computed and combined with the new pressure gradients. Here, it is important to point out the role of pressure relaxation factor for maintaining the discrete balance between pressure and turbulence. If the pressure is under-relaxed after solving the pressure equation as:
pcorr.=αppsol+(1–αp)p(n–1) (47)
where pcorr., psol and p(n–1) stand for, respectively, the under-relaxed pressure used in the correction step, the current solution of pressure equation and the previous pressure field, it is necessary to under-relaxe similarly the turbulent correlations before adding their contributions in the correction step as:
(48)
This joint under-relaxation of pressure and turbulent stresses will maintain the discrete equilibrium for which the pressure is designed in the modified pressure equation.
4.2.3
The overall coupling algorithm
Since the pressure is the only variable which is able to account for the turbulent gradients to promote numerical regularity, the conventional organisation of the coupling algorithm must be modified.
Conventional coupling algorithm Non-linear iteration 1
Solve momentum equations:
(49)
Solve the pressure equation:
(50)
Correction step:
(51)
Solve the second-moment transport equations:
(52)
Non-linear iteration 2
Solve momentum equations:
(53)
where M.E., P.E., C.S. and T.E. stand for momentum equations, pressure equation, correction step and turbulence equations.
It is clear that the pressure p(1) which was devised to maintain regularity with respect to ![]() can not cope with the new turbulent field
can not cope with the new turbulent field ![]() That is a strong source of oscillations because the discrete equilibrium is broken.
That is a strong source of oscillations because the discrete equilibrium is broken.
It is the reason why the overall algorithm must be modified in order to restore the link between turbulence and pressure:
Modified coupling algorithm Non-linear iteration 1
Solve momentum equations:
(54)
Solve the second-moment transport equations:
(55)
Solve the pressure equation:
(56)
Correction step:
(57)
Non-linear iteration 2
Solve momentum equations:
(58)
4.2.4
An appropriate pressure boundary condition
In the same order of idea, we have devised a special wall boundary condition for the pressure which links pressure and turbulence in the immediate vicinity of the walls. Let us suppose that the wall is located
at η=cste. The transport equation for the normal contravariant component ![]() is given by:
is given by:
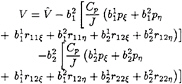
(59)
The η derivatives are the only prominent terms near the wall, leading to the equilibrium:
(60)
which is used as generalised wall boundary condition for the pressure.
5
Results
The first part of this section is devoted to the comparison of the aforementionned turbulence closures, all the others characteristics (grid, numerical schemes, level of convergence) being kept unchanged. These computations have been carried out on an O-O grid topology. The flow domain is defined by 0.5<x/L< 5.0 and rs<r/L<4.0 (L being the length between perpendiculars and rs the radius of the hull's surface). This domain is covered by 65×81×34 nodes in the streamwise, radial and girthwise directions respectively. The first coordinate surface is situated at y+ ≈ 1.0. Each eddy-viscosity solution necessitated about 5000 non-linear iterations and the Rij–ε solution, which was initialised by several hundred non-linear iterations using eddy-viscosity models, needed 1000 additional non-linear iterations to reach a not enough converged state.
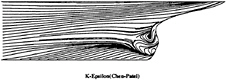
Figure 3: Chen & Patel k–ε model—Computed wall flow
Figures 3, 4, 5 and 6 show the limiting streamlines on the hull with the various turbulence closures. The

Figure 4: Wilcox k–ω model—Computed wall flow
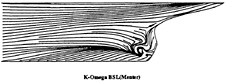
Figure 5: BSL k–ω model—Computed wall flow
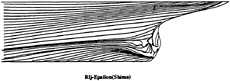
Figure 6: Shima Rij–ε model—Computed wall flow
limiting streamlines are found to be very sensitive to turbulence model. Previous comparisons [4] with Chen & Patel k–ε model underestimated the separation region compared with the present results shown in figure 3. We believe that it is due to numerical stiffness. In the present computations, convergency is ensured by checking the convergence of wall shear stress which is quite slow to establish in the separation region. Several thousands iterations were found to be necessary to achieve convergence. The k–ε and BSL k–ω models (at a lesser degree) provide a too diffusive flow even if the limiting streamlines exhibit the main characteristics indicated by the experiments. For the k–ε models, the behaviour of computed wall flow has been found independent from near-wall low-Reynolds number treatments which are present in our code ([12], [13], [8]). This analysis is confirmed by the isovels at x/L=0.978 (Figs.7, 9) although the BSL model performs slightly better than the Chen & Patel closure. The k–ω and Rij–ε models simulate a very accurate location of the first rectilinear convergence line near the keel, behaviour which is confirmed by the isovels (Figs.8, 10) which indicate that the flow in the near-wake is more rotational. Moreover, the k–ω predicts a weak longitudinal vortex near the waterplane, which is not the case with other closures. However, Figure 10 show that the simulated longitudinal vorticity is now too intense. These results exaggerate the tendancies already present in the previous computations of [5] obtained with a totally different numerical methodology. It is important to notice that the iso-velocity contours are regular, which confirms the efficiency of the proposed modifications, except near the symmetry plane where computational grid is not fine and regular enough to capture rapid changes of flow field due to the longitudinal vortex.
These conclusions are illustrated more convincingly by Figures 11, 12, 13, 14, 15 and 16 which show the axial and vertical velocity profiles at different longitudinal stations and depths. The Rij–ε model overpredicts the secondary motion and its rate of decay is slower than indicated by the measurements. These results are also in accordance with [5].
The second part of the results is devoted to the influence of inlet condition. To determine if a significant amount of longitudinal vorticity is created at the fore part of the ship, complementary computations using a full body domain have been carried out. The flow domain is defined by –3.0<x/L<5.0 and rs<r/L<4.0. This domain is covered by 120×81×34 nodes in the streamwise, radial and
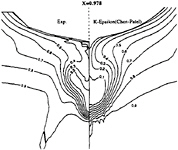
Figure 7: Chen & Patel k–ε model—Comparison between experimental and computed isowakes at x/L=0.978
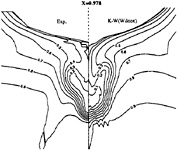
Figure 8: k–ω model—Comparison between experimental and computed isowakes at x/L=0.978
girthwise directions respectively. The after part of this grid (i>55) is identical to the above grid, so that uncertainty related to grid resolution can be excluded in the following comparisons. Computations were started with U=1 as initial conditions everywhere (except at the wall) which were different from above computations where prescribed inlet conditions were used as initial conditions. No special transition treatment was employed except that the production of turbulent kinetic energy is bounded by 20 times the dissipation as proposed by [15], that is Pk=min(Pk, 20ε).
Figures 17, 18, 19, 20, 21 and 22 show the longitudinal and vertical velocity profiles at several stations and depths for the original k–ω model and its BSL variant. It is clear that we can not exclude the
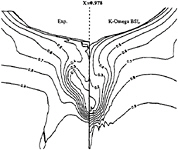
Figure 9: BSL k–ω model—Comparison between experimental and computed isowakes at x/L=0.978
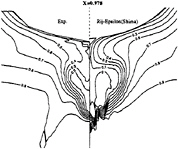
Figure 10: Shima Rij–ε model—Comparison between experimental and computed isowakes at x/L=0.978
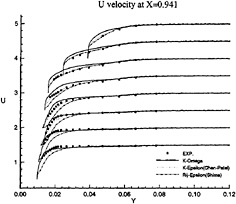
Figure 11: Half-body—Axial velocity profiles at x/L=0.941 as functions of y for several depths: symbols are from measurements
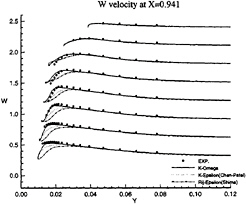
Figure 12: Half-body—Vertical velocity profiles at x/L=0.941 as functions of y for several depths: symbols are from measurements
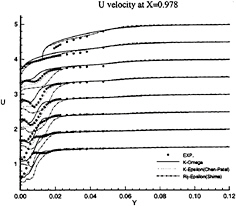
Figure 13: Half-body—Axial velocity profiles at x/L=0.978 as functions of y for several depths: symbols are from measurements
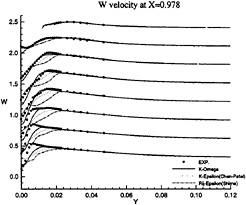
Figure 14: Half-Body—Vertical velocity profiles at x/L=0.978 as functions of y for several depths: symbols are from measurements
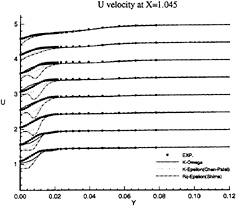
Figure 15: Half-Body—Axial velocity profiles at x/L=1.045 as functions of y for several depths: symbols are from measurements
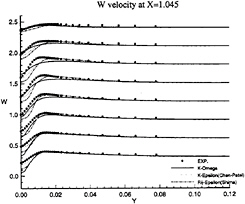
Figure 16: Half-Body—Vertical velocity profiles at x/L=1.045 as functions of y for several depths: symbols are from measurements
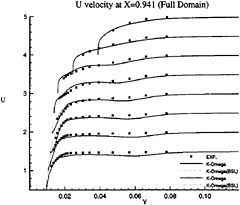
Figure 17: Full-body—Axial velocity profiles at x/L=0.941 as functions of y for several depths: symbols are from measurements
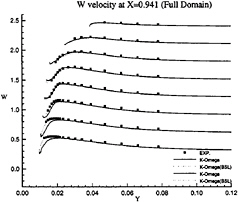
Figure 18: Full-body—Vertical velocity profiles at x/L=0.941 as functions of y for several depths: symbols are from measurements
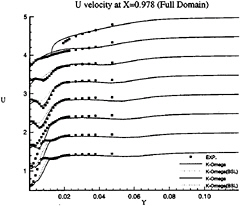
Figure 19: Full-Body—Axial velocity profiles at x/L=0.978 as functions of y for several depths: symbols are from measurements
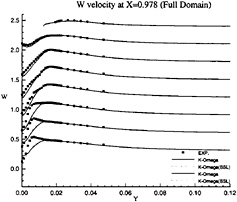
Figure 20: Full-Body—Vertical velocity profiles at x/L=0.978 as functions of y for several depths: symbols are from measurements
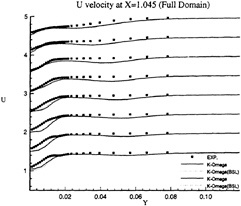
Figure 21: Full-Body—Axial velocity profiles at x/L=1.045 as functions of y for several depths: symbols are from measurements
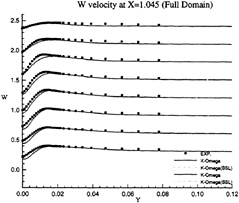
Figure 22: Full-Body—Vertical velocity profiles at x/L=1.045 as functions of y for several depths: symbols are from measurements
influence of inlet conditions since the full-ship computations provide a better simulation of the velocity profiles at the experimental stations even if the boundary conditions on turbulent quantities at the inlet plane (half-domain) are Neumann conditions. The superiority of k–ω model over k–ε closure can be observed not only the separation region, but also in the attached boundary layer under adverse pressure gradient. At the section x/L=0.941 where no separation occurs, k–ω model yields a better prediction, especially on the vertical velocity component (fig.18). Although longitudinal velocity component is somewhat overpredicted near the waterline with half-domain computations (fig.11) in this section, it is equally well predicted with full-domain computations (fig.17). Sensitivity to free stream values of ω is not observed in this configuration, but influence of inlet conditions seems to be important for k–ω model when we compare U velocity component given at x/L=0.978 (figs 13 and 19). For the sake of brevity, no comparisons are presented with the k–ε model but additional computations have not indicated such a sensitivity to inlet conditions for this closure.
6
Concluding Remarks
Several eddy-viscosity models and a second-moment closure have been employed to calculate the flow around the HSVA Tanker. Deep modifications of the original algorithm have been designed to maintain the discrete equilibrium between the various source terms involved in the momentum equations. These modifications made it possible to implement a second-moment closure into a Poisson pressure RANSE solver without introducing any apparent turbulent viscosity. The results obtained for this complex geometry, illustrate the potentialities of this approach. The Shima Rij–ε closure is very promising but yields a too intense secondary flow in the near wake. However, in that case, it is still necessary to improve the robustness of second-moment closures when strong variations of physical quantities are present in the flow field. Actually, we consider that the k–ω models offer, till now, the best compromise for this particular class of flows since the best simulation of the flow around the HSVA Tanker is provided by the original Wilcox model with a full-domain computation.
7
Acknowledgments
Thanks are due to the Scientific Committee of IDRIS and the DS/SPI for attributions of Cpu on the Cray C98.
References
[1] K.Wieghardt and J.Kux. Nomineller nachstrom auf grund von windkanal versuchen. Jahrb. der Schiffbau Technischen Gesellschaft (STG), 1980.
[2] In L.Larsson, V.C.Patel, and G.Dyne, editors, Proc. of 1990 SSPA-CTH-IIHR Workshop on Ship Viscous Flow. Flowtech Int. Report 2, 1990.
[3] In Ship Research Institute, editor, Proc. CFD Workshop for Improvement of Hull Form Designs —Tokyo, 1994.
[4] G.B.Deng, P.Queutey, and M.Visonneau. Navier-stokes computations of ship stern flows: A detailed comparative study of turbulence models and discretisation schemes. In V.C.Patel and F.Stern, editors, Proc. 6th Int. Conf. on Numerical Ship Hydrodynamics, pages 367–386. National Academy Press, 1993.
[5] F.Sotiropoulos and V.C.Patel. Second moment modelling for ship-stern and wake flows. In Ship Research Institute, editor, Proc. CFD Workshop for Improvment of Hull Form Designs —Tokyo, pages 187–198, 1994.
[6] H.C.Chen, W.M.Lin, and K.M.Weems. Second moment rans calculations of viscous flows around ship hulls . In Ship Research Institute, editor, Proc. CFD Workshop for Improvment of Hull Form Designs—Tokyo, pages 275–284, 1994.
[7] N.Shima. Prediction of turbulent boundary layers with a second moment closure . Journal of Fluids Engineering, 115:1–27, 1993.
[8] H.C.Chen and V.C.Patel. Practical near-wall turbulence models for complex flows including separation. AIAA-87–1300, 1987.
[9] C.G.Speziale, S.Sarkar, and T.B.Gatski. Modeling the pressure-strain correlation of turbulence: An invariant dynamical systems approach. Journal of Fluid Mechanics, 227:245– 272, 1991.
[10] N.Shima. A reynolds-stress model for near-wall and low-reynolds-number regions . Journal of Fluids Engineering, 110:38–44, 1988.
[11] B.S.Baldwin and T.J.Barth. A one equation turbulence transport model for high reynolds number wall-bounded flows. In AIAA 29th Aerospace Sciences Meeting, AIAA Paper 91– 0610, 1991.
[12] Y.Nagano and M.Tagawa. An improved k– ε model for boundary layers flows. Journal of Fluids Engineering, 100:33–39, 1990.
[13] G.B.Deng and J.Piquet. k–ε turbulence model for low-reynolds number wall-bounded shear flow. In Proc. 8th Turbulent Shear Flows, 26–2, 1991.
[14] D.C.Wilcox. Reassessment of the scale-determining equation for advanced turbulence models. AIAA Journal, 26:1299–1310, 1988.
[15] F.R.Menter. Zonal two-equations k–ω turbulence models for aerodynamic flows. In AIAA 24th Fluid Dynamics Conf., AIAA Paper 93– 2906, 1993.
[16] T.J.Craft and B.E.Launder. Improvments in near-wall reynolds stress modelling for complex flow geometries. In Proc. 10th Turbulent Shear Flows, 20–25, 1995.
[17] D.C.Wilcox. Turbulence Modeling for CFD. DCW Industries, 1993.
[18] F.R.Menter. Influence of freestream values on k–ω turbulence model prediction. AIAA Journal, 30–6, 1992.
[19] C.G.Speziale. On turbulent secondary flows in pipes of non circular sections. Int. J. Eng. Sci., 20:863–872, 1982.
[20] F.S.Lien and M.A.Leschziner. Computational modelling of multiple vortical separation from streamlined body at high incidence. In Proc. 10th Turbulent Shear Flows, 4–19, 1995.
[21] L.Davidson. Reynolds stress transport modelling of shock-induced separated flow . Computers & Fluids, 24–3:253–268, 1995.
[22] S.Sebag, V.Maupu, and D.Laurence. Non-orthogonal calculation procedures using second moment closure . In Proc. 8th Turbulent Shear Flows, 20–3, 1991.
DISCUSSION
F.Sotiropoulos
Georgia Institute of Technology, USA
This is a very careful and useful numerical study in line with the authors previous significant contributions in the area of viscous ship hydrodynamics. It is very encouraging that they were able to successfully employ a full, near-wall, Reynolds-stress transport closure and essentially reproduce previous results for the same case obtained with an entirely different numerical methodology (Sotiropoulos and Patel, 1995). Their work underscores the significance of the turbulence lengthscale equation and demonstrates the potential of ω-based closures for modeling flows of practical interest. Studies like this, which carefully eliminate grid-related and other numerical uncertainties, are essential for meaningful assessment of advanced turbulence closures and should continue.
I have two comments/questions:
-
The propeller-plane isowakes obtained with the Reynolds-stress closure of Shima are very similar to the results reported by Sotiropoulos and Patel (1995) who employed the same turbulence model on a somewhat coarser computational mesh. The corresponding limiting streamline patterns (Figure 6), however, are markedly different than those obtained by Sotiropoulos and Patel. On the other hand, the limiting streamline patterns produced by the two-layer κ–ε model, shown in Figure 3, are essentially identical to the Reynolds-stress results of Sotiropoulos and Patel. I suspect that two figures were switched by mistake, that is the Shima predictions are actually those shown in Figure 3 while the κ–ε predictions are shown in Figure 6.
-
Sotiropoulos and Patel (1995) showed that the Launder-Shima model resolves with remarkable accuracy several velocity harmonics at the propeller plane of the modified HSVA tanker. Have the authors compared their various predictions in terms of velocity harmonics? Such a comparison would be very interesting, particularly in light of the very encouraging results obtained with the standard κ–ε model.
REFERENCE
Sotiropoulos, F., and Patel, V.C. ( 1995) “Application of Reynolds-Stress Transport Models to Stern and Wake Flows,” J. Ship Research, Vol. 39, No. 4, pp. 263–283.
AUTHORS' REPLY
-
Actually, the figures 3 & 6 are put in correct order. Shima's model does not yield satisfactory results for this particular flow configuration. A marked tendency towards relaminarization has been observed here as on several other geometries previously tested by the authors. This incorrect behavior is mainly due to the near-wall modeling of the transport equation for turbulent dissipation through: (i) the use of O(ε;≤) to damp the destruction term which is numerically dangerous on complex geometries and highly-stretched non-orthogonal grids, (ii) the introduction of Ψ1 which can take strong negative values in some regions of the flow.
-
We have not compared our simulation in terms of velocity harmonics. However, this is a very useful suggestion and we will give in the future this element of comparison which is a good indicator for possible computations of propeller-hull interactions.
DISCUSSION
L.Larsson
Chalmers University of Technology, Sweden
The authors have again presented a paper which could become a milestone in the development of CFD for stern flows (the first one was in 1993). A quite interesting and surprising outcome of their investigation is the fact that an isotropic eddy viscosity model (the κ–ω model) seems to be superior to the much more advanced Reynolds stress model. The authors correctly stress in the introduction that an isotropic model is not likely to work well in a vortical flow since the turbulence anisotropy influences the longitudinal not vorticity. Still the isotropic model is the best. Any explanation for this?
AUTHORS' REPLY
The modelization of Reynolds Stress Transport equations requires the development of closures for several complicated turbulent correlations (pressure-strain, diffusion, and dissipation correlations) mainly based on a local turbulence homogeneity hypothesis. Moreover, near-wall low Reynolds number closures are still under development and not yet enough validated. In our opinion, the Reynolds Stress closures are probably the missing link between the classical
and robust isotropic eddy-viscosity based turbulence models and the future Large Eddy Simulations, as long as high Reynolds number flows on complex geometries are considered. But, it is still difficult to evaluate their actual potentialities because of a lack of counter-validations on flows in realistic configurations.