Self-Propelled Maneuvering Underwater Vehicles
H.McDonald (Pennsylvania State University, USA), D.Whitfield (Mississippi State University, USA)
ABSTRACT
A physics-based computational method is presented for the trajectory prediction of fully appended self-propelled underwater vehicles, including a rotating propeller. The approach is to interactively couple the numerical solution of the three-dimensional unsteady incompressible turbulent Navier-Stokes equations with a six-degree-of-freedom (6-DOF) computational method. The Navier-Stokes equations are solved using a multiblock multigrid scheme with relative motion structured subblocks for handling the rotating propellers. The computational methods, including the Navier-Stokes/6-DOF coupled code, has been validated using numerous examples. Two fully appended configurations that include sail, sail plane, and four stern appendages are presented, one with a body force propulsor and the other with an actual rotating propulsor.
1.0
INTRODUCTION
Maneuvering characteristics of undersea vehicles are determined from, or at least based on, results from large scale model tests. Experimental information from these tests are used to investigate maneuverability directly, or the information is used to develop correlations that in turn are used in dynamic motion codes to perform semi-empirical maneuvering predictions. This experimental-based approach is a necessary, but expensive, method of determining maneuvering characteristics of sea-going vehicles. Also, this approach frequently has to be used outside the regime corresponding to the experimental data on which it is based, such as the particular flow conditions, geometric configuration, and propulsor device. It might be that the experimental configuration used may have even lacked a suitable propulsor. This experimentalbased approach also has the disadvantage that the Reynolds number of an actual submarine, for example, is much larger than can be simulated in experimental test facilities. Therefore, the Office of Naval Research (ONR) initiated a research program that had as it's objective the development of a physics-based method for the maneuvering prediction of self-propelled underwater vehicles.
In conjunction with the development of this physics-based maneuvering prediction method the experimental-based maneuvering results will be of major importance with regard to validation of the physics-based approach. The idea would be to use the strengths of each approach to supplement the other, and thereby, produce a physics-based computational approach that can be used for various flow conditions, geometric configurations, and propulsor devices that can be used outside the regime of available experimental data and yet has been validated to the extent possible. The approach to developing this physics-based maneuvering prediction of self-propelled underwater vehicles is to solve the three-dimensional time-dependent incompressible turbulent Navier-Stokes equations and interactively couple these numerical results with a six-degree-of-freedom (6-DOF) computational code.
This work on maneuverability has been a team effort between the Computational Fluid Dynamics Laboratory of Mississippi State University and the Applied Research Laboratory of Penn State University. Close contact among the researchers at each Laboratory was maintained at all times during the development of these computational tools. The researchers included faculty members, research engineers, post docs, graduate students, and undergraduate students.
This paper is organized as follows. The numerical approach used to solve the three-dimensional time-dependent Navier-Stokes equations is discussed in Section 2; Two propulsor treatments are available, a body force propulsor and an actual rotating propulsor, and these two propulsor treatments are described in Section 3. The 6-DOF computational approach is discussed in Section 4, turbulence modeling in Section 5, and results and concluding remarks are given in Sections 6 and 7.
|
NOTE: This research was sponsored by the Office of Naval Research (ONR) with James A.Fein as the first technical monitor, and Dr. Pat Purtell as the present technical monitor. This support is gratefully acknowledged. |
2.0
NUMERICAL APPROACH
The approach of this physics-based research aimed at maneuvering predictions of self-propelled underwater vehicles is to solve the three-dimensional time-dependent incompressible turbulent Navier-Stokes equations. Because of the magnitude of the problem size with regard to resolving full configurations that include sail, sail planes (or bow planes), stern appendages, and rotating propulsor, the numerical solution of the Navier-Stokes equations is carried out on dynamic relative motion multiblock structured grids. The Reynolds numbers of these flows are extremely large and the viscous regions are resolved to y+ values of near one. This places severe demands on the numerical solution scheme in terms of stability and accuracy. Moreover, the flow is both three dimensional and unsteady in the sense of the Reynolds averaged mean flow. To make the computation of these high Reynolds number unsteady flow problems practical in terms of the total CPU time required, the time step needs to be restricted by the physics of the problem being solved and not the numerics of the scheme used to solve the equations. The equations, numerical flux formulation, and the solution algorithm used to solve the equations and achieve the physics-based time restriction is discussed in this section.
2.1
Navier-Stokes Equations
The three-dimensional time-dependent Navier-Stokes equations are first transformed to a time-dependent curvilinear coordinate system. The artificial compressibility idea of Chorin [1] is then introduced [2, 3, and 4]. The use of artificial compressibility permits the experience gained in the numerical solution of compressible flow problems to be exploited in the numerical solution of incompressible flow problems [5]. The artificial compressibility form of the three-dimensional time-dependent Navier-Stokes equation in general curvilinear coordinates is
(1)
where
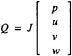
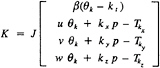
and
θk=kt+kxu+kyv+kzw
K=F, θk=U for k=ξ
K=G, θk=V for k=η
K=H, θk=W for k=ζ
In these equations, β is the artificial compressibility coefficient, with a typical value of 5~10; p is static pressure; u, v, and w are the velocity components in Cartesian coordinates x, y, and z. U, V, and W are the contravariant velocity components in curvilinear coordinate directions ξ, η, and ζ, respectively. Terms ![]() where k=ξ, η, and ζ, are the viscous flux components in curvilinear coordinates. J is the Jacobian of the inverse transformation, and kx, ky, kz, and kt with k=ξ, η, and ζ are the transformation metric quantities [4], where a subscript denotes differentiation.
where k=ξ, η, and ζ, are the viscous flux components in curvilinear coordinates. J is the Jacobian of the inverse transformation, and kx, ky, kz, and kt with k=ξ, η, and ζ are the transformation metric quantities [4], where a subscript denotes differentiation.
In this work, the thin-layer approximation is introduced to simplify the full Navier-Stokes equations, an algebraic turbulence model [ 6], a k–ε model and a nonlinear k–ε model [7] were implemented within the code and used for the turbulent flow computations. The details of treating the viscous terms is explained in the work of Gatlin [8]. In addition, improvements have been made by Chen [9] with regard to the computation of the wall shear stress by improving the computation of the tangential velocity derivatives normal to a solid surface. This improvement is simple to implement and works extremely well on grids that may be highly skewed [9].
2.2
Numerical Flux Vector
Equation (1) is discretized into a cell-centered finite-volume form which for one-dimensional flow, for example, can be written as
(2)
where the index i corresponds to a cell center and indices i±1/2 correspond to cell faces. In this expression, the dependent variable vector Q is considered to be constant throughout the cell whereas the flux ![]() is assumed to be uniform over each surface of the cell. A flux vector is therefore needed at each cell face.
is assumed to be uniform over each surface of the cell. A flux vector is therefore needed at each cell face.
There are numerous ways of developing this flux vector, and the formulation used early on [4] in this maneuvering underwater vehicle research was the flux difference split scheme of Roe [10] for the first-order contribution and a hybrid numerical flux vector for the higher-order contribution that was patterned after the flux vector developed for compressible flow [11]. An advantage of this hybrid flux is that the formulation leads more or less naturally to the limiting of characteristic variables which is important for compressible flows
with discontinuities. However, perhaps because two of the eigenvalues never change sign in this artificial compressibility formulation [12], limiting the characteristic variables for these incompressible flow computations has not been required. Therefore, some considerable time after the first version of this incompressible code was written it was determined to investigate the sort of results that could be obtained for second and third-order flux vectors by the more classical van Leer MUSCL-type of numerical flux vector formulation [13]. The nonlimited form of the dependent variable extrapolation method of Anderson, Thomas, and van Leer [14] was found to work rather well for this incompressible formulation and the numerical results were found to be extremely close to the results provided by the hybrid numerical flux vector [12]. The numerical flux currently used [12] is based on Roe's approximate Riemann solver [10], which in the interest of reduced floating point operation count is written for this one-dimensional example (Eq. (2)) in the form [11]
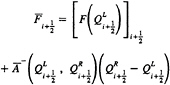
(3)
where ![]() is the Roe matrix given by
is the Roe matrix given by
(4)
The eigenvalue matrix, ![]() contains only the nonpositive eigenvalues of
contains only the nonpositive eigenvalues of ![]() and the similarity matrix, Rξ, has the right eigenvectors of
and the similarity matrix, Rξ, has the right eigenvectors of ![]() as columns. The matrix
as columns. The matrix ![]() consists of the Roe averaged variables [12], and all metric quantities occurring in Eq. (3) are evaluated at cell face i+1/2.
consists of the Roe averaged variables [12], and all metric quantities occurring in Eq. (3) are evaluated at cell face i+1/2.
The numerical scheme is made higher order by using the MUSCL approach of van Leer [13]. Anderson, Thomas, and van Leer [14] used a MUSCL-type approach in flux vector split schemes. Following [14], the dependent variables just to the right of the cell face, QR, located at i+1/2 and just to the left of the same cell face, QL, are written as
(5a)
(5b)
For ![]() =0 in Eqs. (5) the numerical scheme would be first-order in space. For higher order schemes set
=0 in Eqs. (5) the numerical scheme would be first-order in space. For higher order schemes set ![]() =1. With x=–1 only points to the right of the cell face are used for QR and only points to the left of the cell face are used for QL, and a second-order scheme results. With x=1/3 two points to the right and one point to the left of the cell face are used for QR, and two points to the left and one point to the right of the cell face are used for QL. The resulting scheme is referred to as third-order upwind-biased [14]. Note that the third-order upwind-biased scheme depends on information from the same number of points as the second-order scheme. All numerical results presented here were obtained with x=1/3.
=1. With x=–1 only points to the right of the cell face are used for QR and only points to the left of the cell face are used for QL, and a second-order scheme results. With x=1/3 two points to the right and one point to the left of the cell face are used for QR, and two points to the left and one point to the right of the cell face are used for QL. The resulting scheme is referred to as third-order upwind-biased [14]. Note that the third-order upwind-biased scheme depends on information from the same number of points as the second-order scheme. All numerical results presented here were obtained with x=1/3.
2.3
Solution Algorithm
The normal procedure for the solution of Eq. (2) would be to linearize the spatial difference terms, move the terms not containing ΔQn to the right-handside of the equations, and solve for ΔQn. This is particularly true for problems expected to have steady state solutions because the sum of the spatial difference operator terms as well as ΔQn would both go to zero. However, for unsteady flow, the ideal situation would be to find Qn+1 such that Eq. (2) is satisfied. That is, find Qn+1 such that [15]
(6)
One way of attempting to solve this problem is to use Newton's method. Newton's method [16] for the function ![]() would be
would be
(7)
where m=1, 2, 3,…and is the Jacobian ![]() matrix of the vector
matrix of the vector ![]() In principle the generated sequence Qn+1,m+1 converges to Qn+1 and, hence, Eq. (6) is satisfied. For the one-dimensional example
In principle the generated sequence Qn+1,m+1 converges to Qn+1 and, hence, Eq. (6) is satisfied. For the one-dimensional example
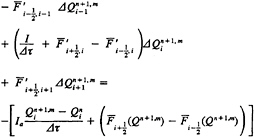
(8)
In this expression, ![]() is the Jacobian of the numerical flux vector, with the first subscript representing the position of the cell face of the numerical flux vector and the second subscript representing the position of the dependent variable vector that the numerical flux vector is differentiated with respect to. Ia is an identity matrix, except the first diagonal element is zero in order to satisfy the true incompressible continuity equation.
is the Jacobian of the numerical flux vector, with the first subscript representing the position of the cell face of the numerical flux vector and the second subscript representing the position of the dependent variable vector that the numerical flux vector is differentiated with respect to. Ia is an identity matrix, except the first diagonal element is zero in order to satisfy the true incompressible continuity equation.
A linear system of equations must be solved at each iteration of Newton's method. For three-dimensional problems a direct solution seems to be impractical [17] and in this work symmetric Gauss-Seidel relaxation is used. Because the flux Jacobian of the flux vector based on Roe's formulation is difficult to obtain analytically in three dimensions, and also in the interest of simplicity, the flux Jacobian is obtained numerically [18]. The solution scheme is referred to as discretized Newton-relaxation [16], or the DNR scheme [17]. Multigrid is used to accelerate the numerical solutions [19]. This multigrid scheme has been extended to multiblock [20] and unsteady flow [21]. The solution process is, therefore, a multigrid scheme for three-dimensional unsteady viscous flow on dynamic relative motion multiblock grids.
3.0
PROPULSOR TREATMENTS
From the beginning of the program it was determined that there needed to be two methods of handling the propulsor. One was to be a simulation of the propulsor using a relatively simple model that was computationally efficient, and the other was to incorporate the capability of handling the actual rotating propulsor. Both methods were developed, have been included in the code, and are discussed below.
3.1
Body Force Propulsor
The model selected that satisfies the conditions of simplicity and efficiency was one that has been used for a number of years for similar simulations such as open propellers [22] and ducted fans [23]. The basic approach is explained in [22] and consists of including body forces in Eq. (1) which operate on the fluid in a manner similar to the way an actual propulsor operates on the fluid. All three components of the body force vector were taken into account and consequently thrust, swirl, and their radial distributions can be included in the computations. In any given situation this force data may be obtained from conventional propulsor design tools or data bases. Here this information is based on thrust and torque coefficient data which were obtained from an actual marine propulsor. A description of the experiment and the measured results are reported in [24]. This coefficient information was used to determine the components of the body force vector and then distribute these components to the center of the cells in this cell-centered finite volume scheme in the region where the propulsor was located.
3.2
Actual Rotating Propulsor
The method used to include an actual rotating propulsor is one that has been continually developed and also used for a number of years, primarily for compressible flows [25–31]. The approach is to use relative motion blocks with structured grids, whereby the blocks that include the rotating blades move relative to adjacent blocks with a region of the blocks near the relative motion interface being treated using the localized grid distortion technique introduced by Janus [31]. This method of handling relative motion blocks insures the continuity of grid lines (although they do change partners periodically, or “click”) and restricts the maximum distortion of the grid to be of the order of the distance between grid points which for viscous grids is, of course, small. This approach eliminates the need to interpolate the solution vector from one grid to another. The cell volumes do change in time, however, and the geometric conservation law must be satisfied [31].
4.0
DYNAMIC MOTION OF THE VEHICLE
The trajectory of the body at any instant of time is described by its linear velocities u, v, w, and by its angular velocities p, q, r, in the body fixed frame of reference and its position and orientation in an inertial frame of reference. The governing six-degree-of-freedom (6-DOF) Equations Of Motion (EOM) can be written as:
Axial Force
Lateral Force
Normal Force
Rolling Moment
Pitching Moment
Yawing Moment
where
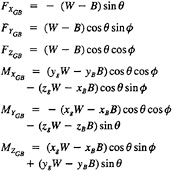
and
W=vehicle weight
B=vehicle buoyancy
xg,yg,zg=position of the cg in the body-axis system
XB,yB,zB=position of the cb in the body-axis system
![]() , θ=vehicle roll and pitch Euler angles with respect to an inertially fixed reference frame, here taken to be Earth-fixed
, θ=vehicle roll and pitch Euler angles with respect to an inertially fixed reference frame, here taken to be Earth-fixed
The hydrodynamic forces ![]() and moments
and moments ![]() are determined by integrating the pressure field and viscous stresses, obtained from the Navier-Stokes solver, over the body.
are determined by integrating the pressure field and viscous stresses, obtained from the Navier-Stokes solver, over the body.
Since the frame of reference adopted for the equations of motion is fixed to the body, and moves with it, the position and orientation of the body cannot be described relative to it. Seven more equations are needed to describe the vehicle's orientation and position in an inertial reference frame. This frame of reference is taken to be fixed on the surface of the Earth (neglecting the Earth's rotation), with X-axis pointing to North, Y-axis pointing East and Z-axis pointing towards the center of the Earth. The orientation of the vehicle with respect to this frame is defined by four quaternions e0, e1, e2, e3, as follows:
where
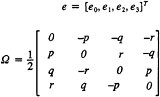
The Euler angles (![]() , θ, ψ) are related to e as follows:
, θ, ψ) are related to e as follows:
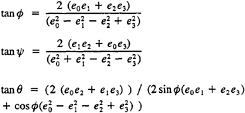
Finally, the position of the vehicle in the inertial frame of reference is derived from:
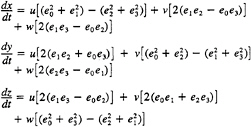
The final result is a set of 13 O.D.E.'s in 13 unknowns. These are:
-
—Six strongly coupled, highly nonlinear O.D.E.'s for the motion in the body-fixed frame of reference. Solution of these equations yields the linear velocities of the vehicle u, v, w and the angular velocities of the vehicle p, q, r in the body fixed frame of reference.
-
—Four strongly coupled, nonlinear O.D.E.'s for the body orientation in the inertial frame of reference. Solution of these equations yields the four quaternions e0,e1,e2,e3, from which Euler angles can be derived.
-
—Three linear (not coupled) O.D.E.'s for the body position in the inertial frame of reference whose solution yields the position of the body in the inertial frame of reference.
The above 13 vehicle dynamics O.D.E.'s are numerically integrated using a fourth-order accurate Runge-Kutta technique. The assembly and solution of the vehicle dynamics equations was implemented directly from the vehicle simulation code TRJv [ 32].
The coupled Navier-Stokes flow solver and the 6-DOF equations of motion solver was successfully used to simulate a free falling sphere (Re=1000) and a 6:1 ellipsoid (Re=7500) prior to the SUBOFF calculation presented later in this paper.
5.0
TURBULENCE MODEL
Turbulence models used in this work include the Baldwin-Lomax mixing length model [6] the Launder-Sharma Low-Reynolds number k–ε model and a Low-Reynolds number nonlinear k–ε model based on the work of Nisizima and Yoshizawa, Speziale, and Myong and Kasagi [7].
The bulk of the initial work was done with the algebraic mixing length model typified by the eddy viscosity
Here, a representative length scale is determined empirically, and it is combined with vorticity, ω, to provide a representative velocity scale.
A more general model uses two transport equations to find the representative length and velocity scales of the flow. In this work, the Launder-Sharma model was used to find the turbulent kinetic energy, k, and the turbulent energy dissipation rate, ε. The resulting velocity scale is k1/2 while the length scale is provided by k3/2/ε, so that the turbulent viscosity is given by
Damping functions, including one for the eddy viscosity, are used to allow integration of the flow directly to the wall. Both of the above models rely on the Boussinesq approximation, which provides for an isotropic eddy viscosity and so fails to capture important anisotropic effects. For this reason, the k–ε model was extended by a nonlinear Reynolds stress assumption of the form
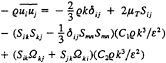
where Sij and Ωij represent the mean strain and rotation tensors, respectively, and k and ε continue to be determined by the Launder-Sharma Low-Reynolds number k–ε model. The standard model is recovered when C1 and C2 are set to zero. However, the nonlinear effects provided by this new Reynolds stress assumption prove to be dramatic. Calculation in a three-dimensional square duct, shown in Fig.1, demonstrates secondary flow which is absent when a standard two-equation model is used. Additionally, it has been shown that the model greatly improves the prediction of the normal Reynolds stresses in highly three-dimensional flows, such as the flow over a 6:1 prolate spheroid at 10° angle of attack. Results, compared to the experimental data of Reference [33], are shown in Figs.2–5.
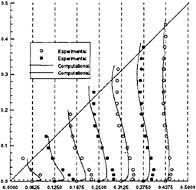
Fig. 1 W/Ur Profiles in the Square Duct.
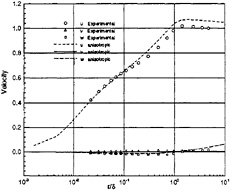
Fig. 2 Boundary Layer Velocity Profile, x/L=0.4, Φ=100°, Anisotropic Model, Re=4.2×106, α=10°.
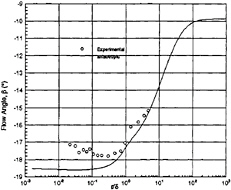
Fig. 3 Flow Angle β=tan–1(W/U), Anisotropic Model, Re=4.2×106, α=10°.
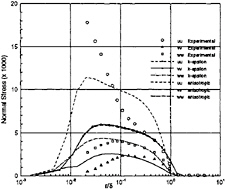
Fig. 4 Boundary Layer Normal Stress Profiles, x/L=0.4,Φ=100°, Anisotropic Model, Re=4.2×106, α=10°.
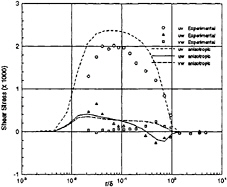
Fig. 5 Boundary Layer Shear Stress Profiles, x/L=0.4,Φ=100°, Anisotropic Model, Re=4.2×106, α=10°.
6.0
RESULTS
Throughout this research effort, computations were carried out in order to validate the code as each additional computational capability and improvement was added. These test cases have ranged from steady state laminar flow over a flat plate to unsteady turbulent flow about a fully appended submarine configuration that included sail, sail plane, four stern appendages, and an actual rotating propeller; and, the coupling of this unsteady flow computation to the 6-DOF computation in order to predict the trajectory of the submarine. The computations performed between these two extremes were cases where analytical solutions or experimental data were available for comparison whenever possible. The solutions were carried out on multiblock grids with structured subgrids, and nearly all of these grids were built using EAGLEView [34]. Moreover, all of the grids were tight with y+ values near surfaces of order one.
6.1
Validation Computations
The ultimate objective of this work, which was the prediction of the trajectory of fully appended self-propelled maneuvering vehicles, involved more complicated flow fields and configurations than those corresponding to the experiments for which measured data were available. Nevertheless, the approach taken, whenever data and time permitted, was to perform rather critical comparisons with the experimental data that were available. For steady state flows, comparisons have been made between numerical results and experimental data that include one or more of the measurements of pressure, skin friction, and/or boundary-layer velocity profiles for geometric configurations that include SUBOFF [35], inflected stern [36], 6:1 prolate spheroid [37], and wing-body junction [38]. These numerical and experimental comparisons are included in [ 4, 18, 19, 20, 39, and 40]. For unsteady flows, comparisons with experimental pressure and velocity measurements have been made with the so-called flapping foil experiment [41]. the 6:1 prolate spheroid in pitch, plunge, and roll maneuvers [42 and 43], an impulsively started cylinder [44], and isolated rotating propellers [45 and 46]. These numerical and experimental comparisons are included in [ 21, 39, 47, 48, and 49]. The quality of agreement for all of the steady and unsteady flow comparisons have been considered reasonable to excellent.
The computations mentioned above that have been carried out for comparisons with experimental data have involved an enormous number of calculations and essentially all of these calculations were performed on workstations that included SGI 75 MHz R8000 processors and IBM RS/6000 Model 560 and 590 processors. Examples of processing speed are given in [20] and include an example of the computation of a
submarine configuration that was gridded using 12 blocks with a total of 2.5 million points and was carried to a steady state solution in 200 multigrid cycles in 45 hours on an IBM Model 590 using 512 MB of memory. Versions of the UNCLE code have now been parallelized by Pankajakshan and Briley [50] and are just beginning to be used for routine calculations. However, the computations mentioned above and the results presented below have been obtained on workstations in serial mode.
The validation comparisons sited in the references above have involved, primarily, comparisons with pressure and flow field velocity data and to a lesser extent skin friction and velocity profile experimental data. Since the trajectory of a vehicle depends on the forces and moments produced by the flow on the vehicle, these comparisons do not indicate the accuracy to which the resulting forces and moments can be computed. Roddy [51] has reported experiments that include measurements of forces and moments of the SUBOFF bare hull with and without appendages. These data were used in what might be considered component form, that is, with the various appendage combinations, to determine how accurately the forces and moments on the body with these isolated appendages could be predicted. As has been the case in times past, it was found that excellent agreement between the computations and the experimental data could be obtained by “tuning” the turbulence model for each data point. This, however, does not seem to be appropriate for the problem in general. Therefore, computations are being carried out where the turbulence model is frozen in the sense that computations for the various appendage combinations have the same turbulence model. An example of these results for the SUBOFF bare hull with four stern appendages is given in Fig.6. Numerical and experimental comparisons are presented in Fig.6 for various angles of drift and the results indicate that the computed forces and moments are essentially within the error bars of the experimental data. Of course this is a simplified configuration compared to the fully appended configuration with a rotating propulsor, but it is an example of the type of validation computations that have been, and are being, performed.
6.2
Maneuvering Predictions
Maneuvering predictions of two self-propelled vehicles are presented. The vehicles are fully appended with sail, sail plane, four stern appendages, and propulsor. The vehicles differ only in that their propulsor units differ. One vehicle has a body force propulsor and the other an actual rotating propulsor. The hull, sail, and four stern appendages were taken from the standard SUBOFF configuration. The sail plane was constructed from viewing various published pictures of
submarines and although it was not designed by marine designers it is thought to be representative of a typical sail plane. The body force propulsor was located at 98.7% of the body length. The actual rotating propulsor was located in the same region and was scaled for the SUBOFF geometry by ARL personnel who have experience in marine propeller design.
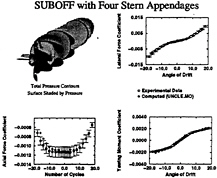
Fig. 6 Comparison of Computed and Experimental Force and Moment Coefficients for SUBOFF with Four Stern Appendages.
The computed trajectory of the body force propelled vehicle was carried out by first computing the steady state flow field about the vehicle at zero degrees angle of attack and drift. The ballast tanks were then blown and the Navier-Stokes/6-DOF computation was initiated. The resulting trajectory is presented in Fig.7. At first the vehicle rises and then this motion is followed by the pitching moment causing a nose down attitude which causes the propelled vehicle to descend at a rather steep angle as shown in Fig.7. The trajectory calculation was carried out for five body lengths. These computations were performed on an IBM Model 590 workstation with 512 MB of RAM and took 100 hours of CPU time. The grid consisted of a total of 1.4 million points and 36 blocks.
The computation of the trajectory of the fully appended vehicle with an actual rotating propulsor was carried out in the same fashion as the trajectory calculation for the body force propelled vehicle, except in this case a complete steady state solution does not exist due to the rotating propulsor. Rather, a periodic solution at zero angle of attack and drift is first obtained and then the Navier-Stokes/6-DOF computation was initiated. An example of the multiblock grid used for this calculation is given in Fig.8. The grid consists of a total of 1.6 million points and 51 blocks. It turns out that the rotation of the propeller was such that the vehicle initially had more drag than thrust and consequently the rotation rate of the propeller was increased to compensate for this imbalance of axial force. With this adjustment, the drag and thrust were much more in
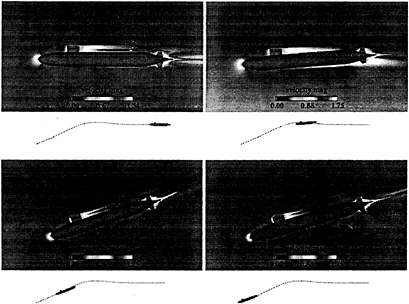
Fig. 7 Trajectory and Flow Field about SUBOFF Configuration with Sail, Sail Planes, and Stern Appendages with Body-Force Propulsor.
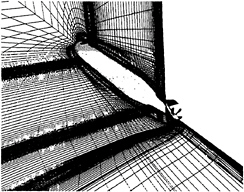
Fig. 8 Multiblock Grid for SUBOFF Configuration with Sail, Sail Planes, Stern Appendages, and Propeller.
balance and the rapid deceleration of the vehicle was eliminated. This trajectory computation continues to be carried out but the additional CPU time required for the rotating propulsor computation limits the number of body lengths that can be computed in a reasonable amount of computer time. It is estimated that 1000 CPU hours on the IBM Model 590 is required to complete five body lengths of travel. Whereas, this is a large amount of computer time, it is anticipated that a five body length computation can be carried out overnight using the parallel version of the code. The parallel computation of this trajectory calculation is just now being initiated. The vehicle trajectory that has been computed thus far is shown in Fig.9.
All of the above calculations were performed using an algebraic turbulence model and are currently being repeated using k–ε and nonlinear k–ε turbulence models.
7.0
CONCLUDING REMARKS
A physics-based method was presented for the maneuvering prediction of self-propelled underwater vehicles. The method is based on coupling the numerical solution of the three-dimensional time-dependent incompressible turbulent Navier-Stokes equations with the numerical solution of the equations of motion of the vehicle. The computational methods were previously verified independently on numerous test cases, and also verified in the coupled mode. The Navier-Stokes/6-DOF coupled code was applied to the trajectory calculation of two fully appended submarine configurations that differed only in their propulsor units. One had a body force propulsor and the other had an actual rotating propeller.
This research effort was of three and one-half years duration and was sponsored by the Office of Naval
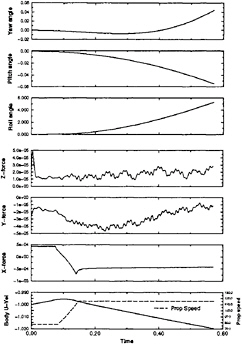
Fig. 9 Forces on the Body, Angles of the Body, Streamwise Velocity, and Propeller Speed for the SUBOFF Configuration with Sail, Sail Planes, Stern Appendages, and Rotating Propeller.
Research (ONR). The work involved a team of rather significant size that was composed of researchers at both the Applied Research Laboratory at Penn State University and the Computational Fluid Dynamics Laboratory at Mississippi State University. Close contact among the researchers was maintained throughout the effort. Credit for all involved in this research program would involve a list of more than twenty people. The two authors of this paper are not to be considered the leaders of this effort, rather servants to the faculty, research engineers, postdocs, graduate students, and undergraduate students who so admirably carried out the real work involved in putting ONR's idea of a physics-based maneuvering prediction method on a firm foundation.
ACKNOWLEDGEMENTS
The authors are indebted to their colleagues at the Engineering Research Center, Mississippi State University and the Applied Research Laboratory, Pennsylvania State University for their contribution to this project. Special thanks are due to Mr. James Fein of the Office of Naval Research for his ideas, advocacy, and support.
REFERENCES
1. Chorin, A.J., “A Numerical Method for Solving Incompressible Viscous Flow Problems , Journal of Computational Physics, Vol. 2, 1967, pp. 12–26.
2. Pan, D. and Chakravarthy, S., “Unified Formulation for Incompressible Flows”, AIAA Paper No. 89–0122, January 1989.
3. Rogers, S.E. and Kwak, D., “Upwind Differencing for the Time-Accurate Incompressible Navier-Stokes Equations”, AIAA Journal, Vol. 28, No. 2, 1990, pp. 253–262.
4. Taylor, L.K., “Unsteady Three-Dimensional Incompressible Algorithm Based on Artificial Compressibility,” Ph.D. Dissertation, Mississippi State University, May 1991.
5. Whitfield, D.L., “Perspective on Applied CFD,” AIAA Paper No. 95–0349, AIAA 33rd Aerospace Sciences Meeting and Exhibit, Reno, NV, January 9–12, 1995.
6. Baldwin, B.S. and Lomax, H., “Thin-Layer Approximation and Algebraic Model for Separated Turbulent Flows,” AIAA Paper No. 78–0257, January 1978.
7. Boger, D.A., and McDonald, H., “Observations on Non-linear k–ε Models of Turbulent Transport,” 1996, to appear.
8. Gatlin, B., “An Implicit, Upwind Method for Obtaining Symbiotic Solutions to the Thin-Layer Navier-Stokes Equations,” PhD Dissertation, Mississippi State University, August 1987.
9. Chen, J.P., “Unsteady Three-Dimensional Thin-Layer Navier-Stokes Solutions for Turbomachinery in Transonic Flow,” PhD Dissertation, Mississippi State University, December 1991.
10. Roe, P.L., “Approximate Riemann Solvers, Parameter Vector, and Difference Schemes, ” Journal of Computational Physics, Vol. 43, 1981, pp. 357–372.
11. Whitfield, D.L., Janus, J.M., and Simpson, L.B., “Implicit Finite Volume High Resolution Wave-Split Scheme for Solving the Unsteady Three-Dimensional Euler and Navier-Stokes Equations on Stationary or Dynamic Grids,” Engineering and Industrial Research Station Report MSSU-EIRS-ASE-88 –2, Mississippi State University, Mississippi State, MS, February 1988.
12. Whitfield, D.L., and Taylor, L.K., “Numerical Solution of the Two-Dimensional Time-Dependent Incompressible Euler Equations,” MSSU-EIRS-ERC-93–14, April 1994.
13. van Leer, B., “Towards the Ultimate Conservative Difference Scheme. V. A Second Order Sequel to Godunov's Method.” Journal of Computational Physics, Vol. 32, 1979, pp. 101–136.
14. Anderson, W.K., Thomas, J.L., and van Leer, B, “Comparison of Finite Volume Flux Vector Splittings for the Euler Equations,” AIAA Journal, Vol. 24, No. 9, September 1986, pp. 1453–1460.
15. Whitfield, D.L., “Newton-Relaxation Schemes for Nonlinear Hyperbolic Systems,” Engineering and Industrial Research Station Report MSSUEIRS-ASE-90 –3, Mississippi State University, Mississippi State, MS, October 1990.
16. Ortega, J.M. and Rheinboldt, W.C., Iterative Solution of Nonlinear Equations in Several Variables. Academic Press, Inc., New York, 1970.
17. Vanden, K.J., and Whitfield, D.L., “Direct and Iterative Algorithms for the Three-Dimensional Euler Equations, ” AIAA Journal, Vol. 33, No. 5, May 1995, pp. 851–858.
18. Whitfield, D.L. and Taylor, L.K., “Discretized Newton-Relaxation Solution of High Resolution Flux-Difference Split Schemes,” AIAA Paper No. 91–1539, June 1991.
19. Sheng, C., Taylor, L.K., and Whitfield, D.L., “Multigrid Algorithm for Three-Dimensional Incompressible High-Reynolds Number Turbulent Flows,” AIAA Journal, Vol. 33, No. 11, November 1995, pp. 2073–2079.
20. Sheng, C., Taylor, L.K., and Whitfield, D.L., “Multiblock Multigrid Solution of Three-Dimensional Incompressible Turbulent Flow About Appended Submarine Configurations,” AIAA Paper No. 95–0203, AIAA 33rd Aerospace Sciences Meeting and Exhibit, Reno, NV, January 9–12, 1995.
21. Sheng, C., Taylor, L.K., and Whitfield, D.L., “A Multigrid Algorithm for Unsteady Incompressible Euler and Navier-Stokes Flow Computations,” Sixth International Symposium on Computational Fluid Dynamics, September 4–8, 1995, Lake Tahoe, Nevada, USA .
22. Whitfield, D.L. and Jameson, A., “Euler Equation Simulation of Propeller-Wing Interaction in Transonic Flow,” Journal of Aircraft, Vol. 21. No. 11, November 1984, pp. 835–839.
23. Pankajakshan, R., Arabshahi, A., and Whitfield, D.L., “Turbofan Flowfield Simulation Using Euler Equations with Body Forces, ” AIAA Paper No. 93–1978, AIAA/SAE/ASME/ASEE 29th Joint Propulsion Conference and Exhibit, Monterey, CA, June 28–30, 1993.
24. Yang, C.I., Hartwich, P.M., and Sundaram, P., “A Navier-Stokes Solution of Hull -Ring Wing- Thruster Interaction, ” Eighteenth Naval Hydrodynamics Symposium, University of Michigan, Ann Arbor, MI, August 1990.
25. Whitfield, D.L., Swafford, T.W., Janus, J.M., Mulac, R.A., and Belk, D.M., “Three-Dimensional Unsteady Euler Solutions for Propfans and Counter-Rotating Propfans in Transonic Flow,” AIAA Paper No. 87–1197, June 1987.
26. Janus, J.M. and Whitfield, D.L., “A Simple Time-Accurate Turbomachinery Algorithm with Numerical Solutions of an Uneven Blade Count Configuration,” AIAA Paper No. 89–0206, January 1989.
27. Janus, J.M., Whitfield, D.L., Horstman, H., and Mansfield, F., “Computation of the Unsteady Flowfield About a Counter Rotating Propfan Cruise Missile,” AIAA Paper No. 90–3093, August 1990.
28. Janus, J.M., Horstman, H.Z., and Whitfield, D.L., “Unsteady Flowfield Simulation of Ducted Prop-Fan Configurations,” AIAA Paper No. 92–0521, January 1992.
29. Chen, J.P. and Whitfield, D.L., “Navier-Stokes Calculations for the Unsteady Flow Field of Turbomachinery, ” AIAA Paper No. 93–0676, 31st AIAA Aerospace Sciences Meeting and Exhibit, Reno, Nevada, January 1993.
30. Webster, R.S., Chen, J.P., and Whitfield, D.L., “Numerical Simulation of a Helicopter Rotor in Hover and Forward Flight, ” AIAA Paper No. 95–0193, AIAA 33rd Aerospace Sciences Meeting and Exhibit, Reno, NV, January 9–12, 1995.
31. Janus, J.M., “Advanced 3-D CFD Algorithm for Turbomachinery,” PhD Dissertation, Mississippi State University, May 1989.
32. Smith, N.S. and Watkinson, K.W., “A Six-Degree-Of-Freedom Simulation Program For Underwater Vehicles With Significant Vortical Flow Effects,” V.C.T. Report No. 3; User's Manual for TRJv, Vehicle Control Technologies, Inc., August 1994.
33. Chesnakas, C.J., Simpson, R.L., and Madden, M M., “Three-Dimensional Velocity Measurements on a 6:1 Prolate Spheroid at 10° Angle of Attack,” Department of Aerospace and Ocean Engineering, Virginia Polytechnic Institute and State University, Report VPI-AOE-202, January 1994.
34. Jiang, M.Y., Remotigue, M.G., Stokes, M.L., and Thompson, J.F., “EAGLEView: Grid Enhancement and Applications,” AIAA Paper No. 94–0316, January 1994.
35. Huang, T.T., Liu, H-L., Groves, N.C., Forlini, T.J., Blanton, J.N., and Gowing, S., “Measurement of Flows Over an Axisymmetric Body with Various Appendages, ” Nineteenth Symposium on Naval Hydrodynamics, Seoul, Korea, August 24–28, 1992.
36. Huang, T.T., Groves, N.C. and Belt, G., “Boundary-Layer Flow on An Axisymmetric Body with An Inflected Stern, ” David W.Taylor Naval Ship Research and Development Center, Report No. DTNSRDC-80/064, August 1980.
37. Ahn, S., “An Experimental Study of Flow Over a 6 to 1 Prolate Spheroid at Incidence, ” Ph.D. Dissertation, Aerospace and Ocean Engineering Department, Virginia Polytechnic Institute and State University, October 1992.
38. Devenport, W.J. and Simpson, R.L., “An Experimental Investigation of the Flow Past an Idealized Wing-Body Junction: Final Report,” Department of Aerospace and Ocean Engineering, Virginia Polytechnic Institute and State University, Report VPI-AOE-172, July 1990.
39. Taylor, L.K. and Whitfield, D.L., “Unsteady Three-Dimensional Incompressible Euler and Navier-Stokes Solver for Stationary and Dynamic Grids,” AIAA Paper No. 91–1650, June 1991.
40. Sheng. C., Taylor, L.K., and Whitfield, D.L., “An Efficient Multigrid Acceleration for Solving the 3-D Incompressible Navier-Stokes Equations in Generalized Curvilinear Coordinates,” AIAA Paper No. 94–2335, 25th AIAA Fluid Dynamics Conference, Colorado Springs, CO, June 1994.
41. Kerwin, J., Keenan, D., Mazel, C., Horwich, E., and Knapp, M., “MIT/ONR Flapping Foil Experiment, Unsteady Phase,” unpublished data.
42. Hoang, N.T., Wetzel, T.G., and Simpson, R.L., “Unsteady Measurements Over a 6:1 Prolate Spheroid Undergoing a Pitch-Up Maneuver,” AIAA Paper No. 94–0197, January 1994.
43. Hoang, N.T., Wetzel, T.G., and Simpson, R.L., “Surface Pressure Measurements Over a 6:1 Prolate Spheroid Undergoing Time-Dependent Maneuvers,” AIAA Paper No. 94–1908, June 1994.
44. Bouard, R. and Coutanceau, M., “The Early Stage of Development of the Wake Behind an Impulsively Started Cylinder for 40<Re<104 ,” Journal of Fluid Mechanics, Vol. 101, Part 3, 1980, pp. 583–607.
45. Bushnell, P., “Measurement of the Steady Surface Pressure Distribution on A Single Rotation Large Scale Advanced Prop-Fan Blade at Mach Numbers from 0.03 to 0.78,” NASA Contract Report 182124, July 1988.
46. Jessup, S.D., “An Experimental Investigation of Viscous Aspects of Propeller Blade Flow,” Ph.D. Dissertation, The Catholic University of America, 1989.
47. Taylor, L.K., Busby, J.A., Jiang, M.Y., Arabshahi, A., Sreenivas, K., and Whitfield, D.L., “Time Accurate Incompressible Navier-Stokes Simulation of the Flapping Foil Experiment,” The Proceedings Sixth International Conference on Numerical Ship Hydrodynamics, Iowa City, Iowa, August 2–5, 1993, pp. 721–738.
48. Taylor, L.K., Arabshahi, A., and Whitfield, D.L., “Unsteady Three-Dimensional Incompressible Navier-Stokes Computations for a 6:1 Prolate Spheroid Undergoing Time-Dependent Maneuvers, AIAA Paper No. 95–0313, AIAA 33rd Aerospace Sciences Meeting and Exhibit, Reno, NV, January 9–12, 1995.
49. Arabshahi, A., Taylor, L.K., and Whitfield, D.L., “UNCLE: Toward a Comprehensive Time-Accurate Incompressible Navier-Stokes Flow Solver,” AIAA Paper No. 95–0050, AIAA 33rd Aerospace Sciences Meeting and Exhibit, Reno, NV, January 9–12, 1995.
50. Pankajakshan, R. and Briley, W.R., “Parallel Solution of Viscous Incompressible Flow on Multi-Block Structured Grids Using MPI.” Accepted for Parallel Computational Fluid Dynamics—Implementations and Results Using Parallel Computers, Edited by S.Taylor, A.Ecer, J.Periaux, and N.Satofuca, Elsevier Science, B.V. Amsterdam, 1995.
51. Roddy, R.F., “Investigation of the Stability and Control Characteristics of Several Configurations of the DARPA SUBOFF Model (DTRC Model 5470) from Captive-Model Experiments,” David Taylor Research Center Report DTRC/SHD-1298–08, September 1990.












