Numerical Simulation of Three-Dimensional Breaking Waves About Ships
A.Kanai, T.Kawamura, H.Miyata (University of Tokyo, Japan)
Abstract
Two types of numerical methods are developed for the simulation of three-dimensional breaking waves. One is a finite-difference-method approach (TUMMAC-VIII) for solving the incompressible Navier-Stokes equation employing orthogonal staggered grid system which is not fitted to the body surface. Body boundaries are treated by a porosity technique. The other is a finite-volume-method approach (WISDAM-VI) with the body-fitted curvilinear coordinate system to cope with viscous flows on the body boundary. Both methods employ density-function method for implementing free surface boundary conditions.
The finite-difference method can deal with arbitrary complicated bodies due to its simplicity of the grid system. Using this method simulations of bow waves around a wedge model and a simple parabolic-waterline model WM2 are conducted and the three-dimensional breaking wave is successfully simulated. Also the numerical results clarify the detail structure of the Free Surface Shock Wave (FSSW) generated around the bow and show good agreement with experiments.
The viscous effects are very important for the stern flow around a ship. The WISDAM-VI method is developed to simulate bow wave breaking and viscous stern flow simultaneously. Two cases of simulations are carried out for flows around a bulk carrier model and a tanker model. The computed wave patterns show good agreement with experiments, and it is noted that the loss due to wave-breaking is distributed near the free surface and that it effects on the formation of the wake.
INTRODUCTION
Wave breaking is one of the most nonlinear phenomena in fluid dynamics. It gives various significant influences on fluid flows and obstacles in many hydrodynamical problems. In the ship wave problem waves generated by an advancing ship are usually very steep ones called free surface shock wave (FSSW)[1][2][3], which gives great contribution to ship resistance. Hence the clarification of the breaking wave phenomenon is of essential importance for the progress in both marine structural dynamics and ship hydrodynamics represented by hull form design.
Some numerical simulations for the strongly nonlinear waves have been carried out by many researchers. In two-dimensional cases the boundary element method of irrotational free surface flows following the work by Longuet-Higgins & Cokelet (1976)[4] can explain the plunging wave breaker. However, it has difficulty in the explanation of wave motion after the stage of overturning which is only the beginning of the nonlinear behaviour of wave breaking. The finite-difference approach with the VOF method by Hirt & Nichols (1981)[5] and Ng & Kot (1992)[6] can be applicable to the bore or two-layer flows. Another finite-difference method by Miyata (1986)[7] and Miyata & Lee (1990)[8] have succeeded in the simulation of breaking waves including the impinging and the vortex generation processes. Since all above methods seem to be incapable of treating three-dimensional wave-breaking motions. A 3D finite-difference method for breaking is developed by Miyata et al. (1988)[9]. It employs the density-function method to cope with two-layer flows involving strongly interacting interface. The technique is very useful not only for the treatment of wave breaking but also for various engineering problems concerning interface of multi-phase or multi-layer flows. Some similar methods using the concept of the density-function method have been developed recently by Xiao & Yabe (1993)[10] and Brackbill, Kothe & Zemach (1992)[11].
In this paper two types of approach for 3D wave-breaking simulations are shown. One is the finite-difference method called TUMMAC-VIII[ 12] in the framework of a rectangular coordinate system that enables us to express complicated geometries without elaborate efforts of grid generation. And the other is the finite-volume method, WISDAM
VI[13], employing a boundary-fitted curvilinear coordinate system that is advantageous for resolving viscous flows near body boundaries. Both methods use the density-function method to implement the nonlinear kinematic free surface condition. Some applications of those methods to ship wave problems are explained.
NUMERICAL METHOD
Finite-difference Method
The modified marker-and-cell method called TUMMAC-VIII[12] is constructed by combining the free surface treatment of the TUMMAC-VI[ 9] method for a two-layer flow and the no-slip body boundary treatment and the porosity expression for geometries of the TUMMAC-VII method[ 14]. A rectangular grid system with variable spacing is employed and the velocity and pressure points are defined in a staggered manner.
The governing equations for the two-layer flow are the following incompressible Navier-Stokes equations and the continuity equation.
(1a)
(1b)
![]() · u=0 (2)
· u=0 (2)
where,
a = v![]() 2u + f (3)
2u + f (3)
Here, the subscripts ![]() 1
1![]() and
and ![]() 2
2![]() denote the fluids below and above the interface respectively. In the present study
denote the fluids below and above the interface respectively. In the present study ![]() 1
1![]() corresponds to the water region and
corresponds to the water region and ![]() 2
2![]() the air region. u is the velocity, p is the pressure, t is the time, v is the kinematic viscosity and f is the external force including the gravitational acceleration. The surface tension is ignored here since its effect can be considered to be very small in the problems described in this paper.
the air region. u is the velocity, p is the pressure, t is the time, v is the kinematic viscosity and f is the external force including the gravitational acceleration. The surface tension is ignored here since its effect can be considered to be very small in the problems described in this paper.
The above equations for each layer are quite separately solved at each time step of time-marching following the MAC-type algorithm. Firstly the pressure field in the air region is obtained by solving the Poisson equation and secondly in the water region. The Richardson 's method is used for the solution of the Poisson equation. The configuration of the interface is determined by the free surface condition described in the subsequent section.
For the time derivative of velocity forward differencing is used and second-order centered differencing is for the space derivatives excluding the convective terms for which third-order upwind differencing is used.
Finite-volume method
The WISDAM-VI method employs the coordinate system that is fitted to the body boundary but not to the free surface, so that the boundary layer around the body of arbitrary form and large free-surface deformation is simultaneously simulated. Since the numerical schemes of the WISDAM-VI method are based on the WISDAM-V method[15] except for the free-surface treatment, the computational method is briefly explained here.
The governing equations are the Navier-Stokes equation and the continuity equation in conservative form.
(4)
where,
(5)
Here I and Re is the unit matrix and Reynolds number respectively and ![]() is the normalized pressure without hydrostatic component defined as
is the normalized pressure without hydrostatic component defined as
(6)
where Fn is the Froude number. The continuity equation for incompressible fluid is written as
div u=0. (7)
Third order upwind-biased flux interpolation scheme for the convective term and second-order central interpolation scheme for the other terms is used for the finite-volume discritization of Eq.(4) and Eq.(7).
Since the MAC type solution algorithm is employed, the pressure term is separated from the other terms and thus, the velocity field of the (n+1) time level is written as
un+1=un+Δt·div T–Δt · ![]()
![]() , (8)
, (8)
where, the superscript n denotes the time level. Taking the divergence of Eq.(8), following Poisson equation for ![]() is obtained.
is obtained.
(9)
Eq.(9) is solved iteratively by use of the SOR method.
FREE SURFACE CONDITION
Density-function method
The density-function method is employed for the fulfilment of the kinematic free surface condition. The density-function plays the role of conserving mass and the determination of the interface location. Assuming that both viscous stresses and the surface tension on the free surface can be ignored, the dynamic free surface condition becomes the condition of pressure continuity between the two layers. Then the kinematic and dynamic free surface conditions are approximately implemented by the following equations.
(10)
![]() =
=![]() (11)
(11)
Here, M is the density-function, u,v,w are the velocity components in the x,y,z directions which represent the longitudinal, lateral and vertical coordinates, respectively, and ![]() and
and ![]() are the pressures of the water and air on the interface. For the time differencing in Eq.(10) the Adams-Bashforth method is used and the third-order MUSCL-type upwind scheme for the space differencing. Eqs.(1a) and (1b) are solved with constant value of density-for respective fluid and the location of interface is defined to be the surface on which the value of the density-function takes the value of
are the pressures of the water and air on the interface. For the time differencing in Eq.(10) the Adams-Bashforth method is used and the third-order MUSCL-type upwind scheme for the space differencing. Eqs.(1a) and (1b) are solved with constant value of density-for respective fluid and the location of interface is defined to be the surface on which the value of the density-function takes the value of ![]() , where
, where ![]() and
and ![]() are the density-function values initially set for the water and air regions, respectively. Due to the inherent numerical diffusion in the solution of Eq.(10) the sharpness of interface can be lost as calculation proceeds. However, it is demonstrated in the subsequent section that the degree of accuracy can be raised to a sufficient level in case a higher-order differencing scheme such as third-order upwind scheme used here is employed in a fine grid system.
are the density-function values initially set for the water and air regions, respectively. Due to the inherent numerical diffusion in the solution of Eq.(10) the sharpness of interface can be lost as calculation proceeds. However, it is demonstrated in the subsequent section that the degree of accuracy can be raised to a sufficient level in case a higher-order differencing scheme such as third-order upwind scheme used here is employed in a fine grid system.
After determining the interface location the dynamic free surface condition is implemented by the so-called “irregular star” technique[16] in the solution process of the Poisson equation. The length of leg in the irregular star technique is calculated using the density-function. The pressure on the interface is determined by extrapolating the pressure in the air region, in which the pressure is extrapolated with zero gradient in the horizontal direction while in the vertical direction the pressure difference due to the gravitation is considered. Since the velocity must be continuous between the two layers, the extrapolation of velocity from the water region to the air region is conducted by approximately satisfying zero normal gradient to the interface.
Accuracy examination
As described in the previous section the numerical diffusion takes place in the computation of the free-surface location and this should be solved to keep sufficient degree of accuracy. For the numerical test, regular periodic waves of finite-amplitude based on the linear theory is generated by the finite-difference method with density-function method and the accuracy of the generated waves is compared with the records of physically generated waves by a flap-type wave generator[ 17].
For the space derivative terms of the Eq.(10), a variety of schemes are tested. Three of them are represented as follows only for the first term for simplicity.
In the case of variable grid spacings, the values of ![]() and
and ![]() are determined as follows.
are determined as follows.
(18a)
(18b)
where,
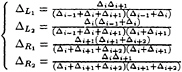
(19)
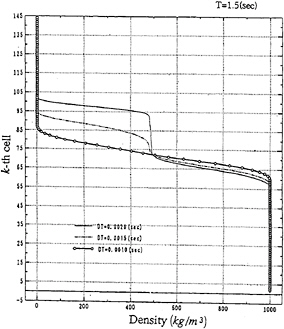
The schemes above are compared for the period of ten times of wave period (T) of the case of T=1.5sec, and the results are shown for the vertical variation of the density-function in Fig.1. It is obviously noted that the higher the order of derivative of the differencing error is, the less the density-function is diffused in the vertical direction. The smaller time increment (DT) is also very effective for suppressing the numerical diffusion. As shown in Fig.2 the discontinuity of the density-function disappears and a very sharp interface is obtained when the time increment is reduced to the half value of the original one for the third order upwind scheme. Therefore, the third order upwind scheme is employed hereafter.
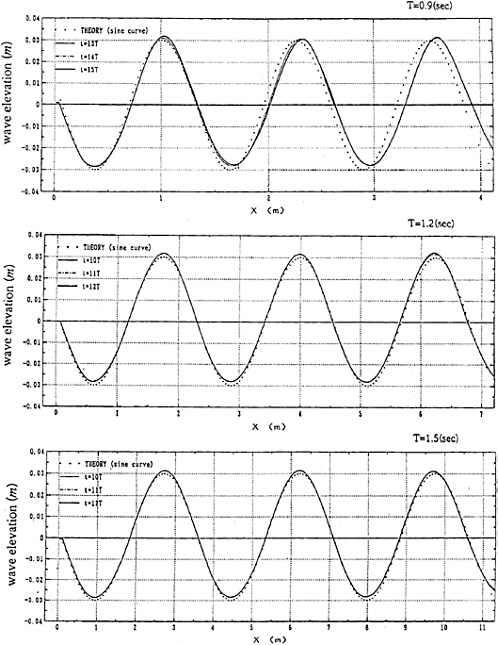
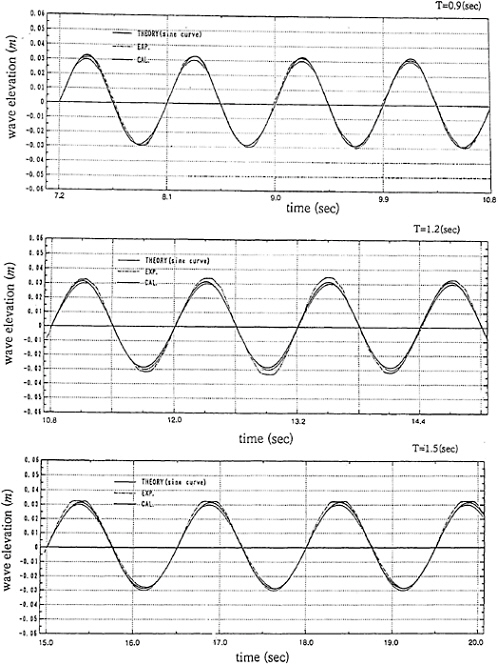
The simulated waves for three cases of wave period, T=0.9, 1.2 and 1.5sec, are presented in Figs.3 and 4, which indicate respectively the wave profile with a sine curve for each case and the time variation of wave height with measurements. It is demonstrated that at least ten waves are generated with sufficient degree of accuracy and the magnitude of the error due to the numerical modelling is of the same order with that of experiments. Therefore it may be safe to say that the density-function method employed here can have sufficient accuracy for simulating waves without special treatments for suppressing the numerical diffusion when it uses sufficiently fine grid spacing and small time increment.
FREE SURFACE SHOCK WAVE ABOUT A WEDGE MODEL
The nonlinear features of ship waves in the near field had been noticed in the 1970s and the detailed structure and mechanism of nonlinear bow waves are experimentally investigated by Miyata et al.[1][2][3]. It is elucidated that the nonlinear bow wave had a lot of common properties with supersonic shock waves and the nonlinear bow waves involving these properties are called free surface shock wave (FSSW). The typical properties of FSSW are (1) steepness of the wave slope, (2) discontinuity of velocities satisfying the shock wave condition, (3) free surface turbulence on and behind the wave front, (4) systematic change of the wave-front-angle depending on the Froude number (Fd) and the ship configuration and (5) dissipation of wave energy into momentum loss far behind the ship. Also the FSSW is limited in the thin layer near the free surface.
Although the above properties are recognized by experiments, the details of the FSSW structure had to be investigated by numerical simulations. However, due to the property of (1), wave breaking occurs at the wave-crest point, which makes the numerical simulation of FSSW significantly difficult. The finite-difference method mentioned in 2.1 with density-function method is applied to this problem and a wedge model of which half entrance angle is 20deg and draft is 0.1m is chosen for the simulation [20]. The simulations are carried out at three Froude numbers based on the draft, 0.8, 1.1 and 1.4, with normal grid spacing. The case of Fd=1.4 is also simulated with fine grid spacing of which minimum spacing is 1/4 of that for the former case. See the Ref.[20] for other details for computational conditions.
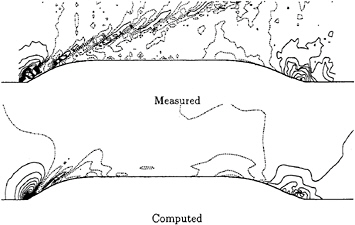
The systematic change of the wave-front-angle depending on the Froude number is realized showing good agreement with the experimental results and other properties of FSSW including 3D wave breaking phenomenon are recognized in the simulations by the finite-difference method. In this paper only the result of the case of Fd=1.4 with fine grid spacing is shown. The time-sequential overviews of the wave at Fd=1.4 are presented in Fig.5 The uniform flow is accelerated until dimensional time (T) reaches 1.77sec. Spilling breaker appears at T=1.564sec before the flow acceleration is ceased and the wave crest overturns at around T=1.932sec. The plunging wave front breaks at T=2.024sec and the wave again develops. The breaking wave front is laterally extended after T=2.208sec and the above process of breaking is periodically repeated. The secondary wave also shows breaking features in the vicinity of the body surface, however the accuracy is supposed to be inferior to the foremost wave due to the influence of the momentum deficient motions of the foremost wave.
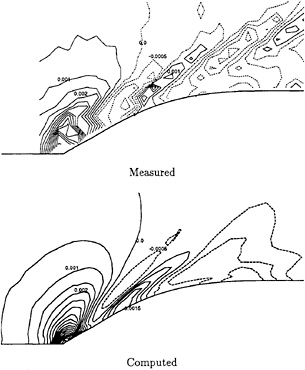
A typical plane vertical and parallel to the di
rection of uniform stream is chosen and the time-sequential development of the wave profile is shown as well as the contours of Lamb vector and helicity respectively in Figs.6 and 7 The Lamb vector indicates the magnitude of the tangential component of vortical motion and the helicity the longitudinal component. The vorticity that appears on the wave front is intensified when the breaking motion occurs, which shows the periodical generation of its own due to the periodical property of the wave breaking motion. It is, however, noted that the vortical layer is limited within the thin layer near the free surface.
BREAKING WAVES AROUND PRACTICAL HULLS
In the preceding section, it is shown that the TUMMAC-VIII method can simulate highly nonlinear free-surface wave by use of the density-function method. However, since the TUMMAC-VIII method employs the rectangular grid system, it can not accurately simulate the viscous phenomena such as growth and separation of the boundary layer, which contributes to the most significant part of resistance of a ship of practical hull forms. In a practical sence, the simultaneous simulation of nonlinear wave system and viscous flow around ships would give very useful information to hull form designers. Therefore, the WISDAM-VI method is developed in the framework of the curvilinear body fitted coordinate system. The treatment of the free surface condition is as described for rectangular coordinate system in the preceding section. However, since the WISDAM-VI method is based on the finite volume method Eq.(10) is written in conservative form as follows:
(20)
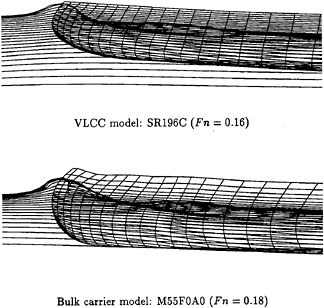
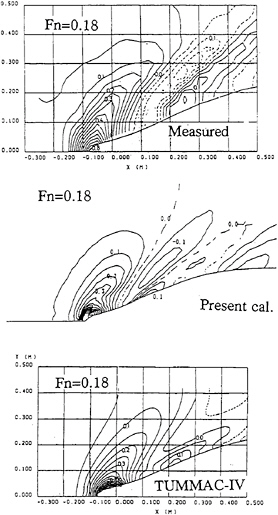
In this section the WISDAM-VI method is applied to the flow around a VLCC model SR196C and a bulk carrier model M55F0A0 in ballast condition. The number of the control volumes used in the simulation is about 85,000, and the Reynolds number is set at 1.0×106. The Froude number is set at 0.16 for the VLCC model and 0.18 for the bulk carrier model. The grid system is shown for the VLCC model in Fig.8.
Perspective view of computed waves are shown for both models in Fig.9, and computed wave contour maps are compared in Figs.10, 11 and 12. As shown in these figures, the bow waves observed in the experiments show the feature of the FSSW. The computed wave patterns agree well with the experiments in the near field, however because of the large grid spacing in the far field of the ship, dispersive wave sysmtem of low wave height observed in the experiments are dissipated in the computation. In Fig.12, the present computational result is compared with the experimental result and with a result of another computational method TUMMAC-IV[ 18]. The number of grid points in the two calculations are comparable, but it is clear that the present calculation shows much better agreement with the experiment.
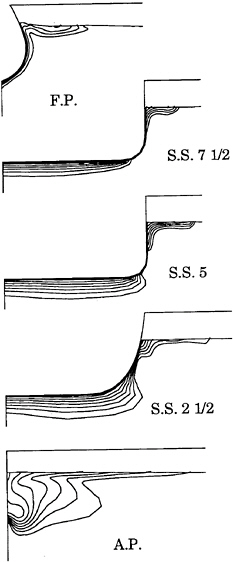
As Miyata and Inui[1] pointed out, dissipation of energy is one of the most important characteristics of FSSW. Baba[19] found that energy deficit due to bow wave breaking is observed in the wake far behind the ship. In order to discuss the energy loss due to bow wave breaking, distribution of total head H is shown at five transverse sections in Fig.13. The total head is defined as follows:
(21)
The energy deficit generated near the bow is convected downstream and distributed near the free surface. At the aft-part of the ship, the loss due to wave breaking is mingled with the loss due to viscous effect, and apparently has influence on the formation of the wake. However the above discussion remains qualitative, and further validation of accuracy is necessary for the qualitative discussion.
CONCLUDING REMARKS
The free-surface flow is of significant importance in a variety of fields, and some of the problems include high degree of nonlinearity. By use of the density-function method, numerical simulations of such highly nonlinear free-surface flow including three-dimensional breaking waves has been achieved. The new treatment of the free surface condition is introduced both into the two simulation techniques based on either the rectangular or curvilinear grid systems. Each type of the grid system has the advantages and the disadvantage, and the choice depends on the true nature of the problem.
On the whole the numerical results shown in this study demonstrate that we can accomplish qualitatively realistic reproduction of highly nonlinear free surface phenomena, but there are still greater demands for the improvement of qualitative accuracy. Breaking waves are dissipating in their nature, however, we still do not have clear understanding and modelling of free surface turbulence and we do not
have the free-surface condition that can cope with the turbulent free-surface. Further researches must be focused on the development of novel modelling of nonlinear free-surface motions.
References
[1] Miyata, H. and Inui, T., ”Nonlinear ship waves,” Advances in Applied Mechanics, Vol. 24, 1984, pp. 215–288.
[2] Miyata, H., Inui, T. and Kajitani, H., ”Free surface shock waves around ships and their effects on ship resistance, ” Journal of The Society of Naval Architects of Japan, Vol. 147, 1981, pp. 1–9.
[3] Takahashi, M., Kajitani, H., Miyata, H. and Kanai, M., ”Characteristics of free surface shock waves around wedge models,” Journal of The Society of Naval Architects of Japan, Vol. 148, 1980, pp. 1–9.
[4] Longuet-Higgins, M.S. and Cokelet, D., ”The deformation of steep surface waves on water, I. A numerical method of computation,” Proceedings of the Royal Society of London, A.350, 1976, pp. 1–26.
[5] Hirt, C.W. and Nichols, B.D., ”Volume of fluid (VOF) method for the dynamics of free boundaries, ” Journal of Computational Physics, Vol. 39, 1981, pp. 201–225.
[6] Ng, C.O. and Kot, S.C., ”Computations of water impact on a two-dimensional flat-bottomed body with a volume-of fluid method,” Ocean Engineering, Vol. 19, No. 4, 1992, pp. 377–393.
[7] Miyata, H., ”Finite-difference simulation of breaking waves,” Journal of Computational Physics, Vol. 65, No. 1, 1986, pp. 179–214.
[8] Miyata, H. and Lee, Y.G., ”Vortex motions about a horizontal cylinder in waves,” Ocean Engineering, Vol. 17, No. 3, 1990, pp. 279–305.
[9] Miyata, H., Katsumata, M., Lee, Y.G. and Kajitani, H., ”A finite-difference simulation method for strongly interacting two-layer flow,” Journal of The Society of Naval Architects of Japan, Vol. 163, 1988, pp. 1–16.
[10] Xiao, F. and Yabe, T., ”A method to trace sharp interface of two fluids by one grid with density function,” Proceedings of the 5th International Symposium on Computational Fluid Dynamics, Vol. 3, 1993, pp. 337–342.
[11] Brackbill, Journal of U., Kothe, D.B. and Zemach, C., ”A continuum method for modeling surface tension,” Journal of Computational Physics, Vol. 100, 1992, pp. 335–354.
[12] Park, J.C. and Miyata, H., ”Numerical simulation of the nonlinear free-surface flow caused by breaking waves,” ASME, FED-Vol. 181, Free-Surface Turbulence, 1994, pp. 155–168.
[13] Kawamura, T. and Miyata, H., ”Simulation of nonlinear shipflows by density-function method,” Journal of The Society of Naval Architects of Japan, Vol. 176, 1994, pp. 1–10.
[14] Miyata, H. and Yamada, Y., ”A finite difference method for 3D flows about bodies of complex geometry in rectangular co-ordinate systems,” International Journal of Numerical Methods in Fluids, Vol. 14, 1992, pp. 1261– 1287.
[15] Miyata, H., Zhu, M. and Watanabe, O., ”Numerical study on a viscous flow with free-surface waves about a ship in steady straight course by a finite-volume method,” Journal of Ship Research, Vol. 36, No. 4, 1992, pp. 332– 345.
[16] Chan, R.O.C. and Street, R.L., ”A computer study of finite amplitude water waves,” Journal of Computational Physics, Vol. 6, 1970, pp. 68– 94.
[17] Park, J.C., Zhu, M. and Miyata, H., ”On the accuracy of numerical wave making techniques,” Journal of The Society of Naval Architects of Japan, Vol. 173, 1993, pp. 35–44.
[18] Miyata, H., Nishimura, S. and Masuko, A., ”Finite difference simulation of nonlinear waves generated by ships of arbitrary three-dimensional configuration,” Journal of Computational Physics, Vol. 60, No. 3, 1985, pp. 391– 436.
[19] Baba, E., ”A new compenent of viscous resistance,” Journal of The Society of Naval Architects of Japan, Vol. 125, 1969, pp. 23–34.
[20] Kanai, A. and Miyata, H., ”Elucidation of the structure of free surface shock waves about a wedge model by finite-difference method,” Journal of The Society of Naval Architects of Japan, Vol. 177, 1995, pp. 147–159(in Japanese).
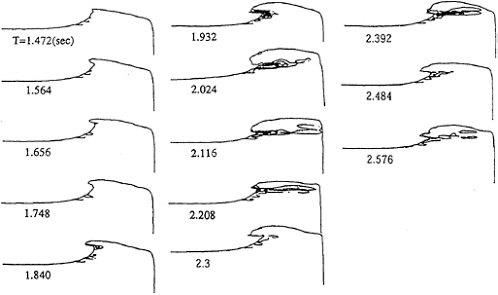
Figure 6: Time-sequential contour of the magnitude of Lamb Vector on the plane vertical and parallel to the direction of uniform stream. The distance from the center line to the plane is 0.0525m. The contour interval is 5. (T=1.472 2.576sec, Fd=1.4, fine grid)
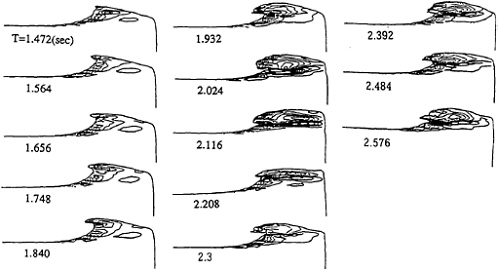
Figure 7: Time-sequential contour of helicity on the plane vertical and parallel to the direction of uniform stream. The distance from the center line to the plane is 0.0525m. The contour interval is 10. (T=1.472 2.576sec, Fd=1.4, fine grid)