A Method for the Optimization of Ship Hulls from a Resistance Point of View
C.Janson, L.Larsson (Chalmers University of Technology, Sweden)
Abstract
A method for optimizing ship hulls from a resistance point of view is presented. The SHIPFLOW program for computing the flow around ship hulls is linked to the OCTOPUS program for solving non-linear optimization problems. The resistance components including wave resistance from a potential-flow solution and viscous resistance from a boundary layer and a Navier-Stokes solution are included in the computation. In the optimization process a basic shape of the hull is given small disturbances and derivatives of the resistance and displacement with respect to the disturbances are computed. A linearized optimization problem can then be formulated and solved taking a displacement constraint into account. The optimized shape is used as a new basic shape and the procedure is iterated until convergence. Each iteration includes the generation of three computational models and a full resistance computation for the basic shape and every hull disturbance. The whole procedure is fully automatic and no user interference is needed during the optimization.
Experience from two examples shows that the optimization system works well from a computational point of view. The computed total resistance for the two cases was reduced by 11 and 9% respectively. However, experiments carried out for one of the examples did not confirm the improvements obtained in the computations. Three main reasons for the discrepancy between the computations and the experiments are discussed. The neglected viscous influence on the stern wave making seems to be the most important one.
Nomenclature
1.0
Introduction
Resistance is one of the important areas that has to be taken into account in ship hull development. Prediction of ship resistance is in most cases based on results from experiments at model scale. If the resistance requirements are not fulfilled a modification of the hull shape is undertaken and another model test is carried out. This process forms a system for “manual optimization”.
In recent years computational methods (CFD) have been introduced in the design process to predict the flow around the hull and in some cases also the resistance of the hull. Different design alternatives may be compared based on computed results and the best one is then selected for verification by model tests. In this way CFD methods may help to speed up the “manual optimization” process by reducing the number of “iterations” that are needed to find the final shape.
Another interesting possibility is to combine a CFD method and a mathematical optimization method together with a program for hull form variation. This system can then be used to find a hull form that is optimized with respect to properties computed by the CFD method, like the resistance, maximum wave height, velocity in the propeller plane, etc. One or more constraints, for instance displacement and hull main dimensions, must then be introduced to limit the modifications of the hull. This forms a system for “automatic optimization”.
Many interesting works on hull form optimization from a hydrodynamic point of view have been presented through the years. Systems for “automatic optimization” as described above have been presented by Kim (1), Nowacki (2, 3), Papanikolaou et al. (4), Hsiung (5), Wyatt and Chang (6), Maisonneuve (7) and others. Different levels of approximation for the flow prediction, from thin ship theory for wave resistance and a simple formula like the ITTC-57 line for the viscous resistance to more advanced computational methods, both for the inviscid and the viscous flow, have been used.
Research in viscous and inviscid flow calculations has been carried out at SSPA Maritime Consulting and FLOWTECH International AB in collaboration with Chalmers University of Technology since about 1970. The computational methods developed in this research work, Xia (8), Kim (1), Larsson (9) and Broberg (10) are used in the present work together with an optimization method developed at the Royal Institute of Technology and at ALFGAM Optimization AB, Svanberg (11, 12) and Esping et al. (13, 14) to form a system for “automatic optimization” of ship hulls.
2.0
The Zonal approach
A zonal approach is used in SHIPFLOW to compute the flow around the ship hull. The flow domain is divided into three zones, figure 1, and a computational method is developed for each zone. The first zone covers the entire hull and a part of its surrounding free-surface. A free-surface potential-flow method of Rankine-source type is used. The second zone is a thin layer at the hull surface and a boundary layer method of the momentum integral type is used. The momentum integral equations are solved along streamlines traced from the potential flow solution. Finally, the third zone includes the aft part of the hull and extends about half a ship length downstream of the hull. It also covers about half a ship length in the radial direction. A Navier-Stokes method of the RANS type using the k–ε model and a wall-law is used in zone three. The zones are computed in sequence and boundary conditions are generated for succeeding zones. The reason for the division of the flow field into zones is that the computational time may be reduced considerably compared to the global approach where the Navier-Stokes method is used in the entire computational domain.
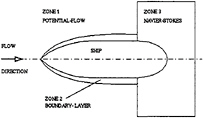
Fig. 1 The Zonal approach
2.1
The potential-flow method
Inviscid, irrotational flow is assumed and a velocity potential, whose gradient is equal to the local velocity may be defined. The potential is governed by the Laplace's equation which is an elliptic partial differential equation that requires boundary conditions on all boundaries of the computational domain. On the hull the flow in the hull surface normal direction must be zero and on the free-surface the flow must be tangent to the surface and the pressure must be constant. At infinity the disturbance due to the hull must vanish. One additional condition is also needed to prevent upstream waves. This condition is introduced together with the numerical method.
The potential-flow problem is non-linear and the free-surface boundary conditions have to be applied
on the wavy free-surface which is initially unknown. A linearization of the free-surface boundary conditions is therefore used and the conditions are applied to the undisturbed free-surface. To be able to make the linearization a known basic solution is required. A double-model solution as suggested by Dawson (15) is used as the basic solution in the present method. The exact non-linear problem can be solved as a series of linearized problems where the previous linear solution is used as the basic solution and the boundary conditions are applied on the wavy free-surface just obtained, Kim (1).
Quadrilateral panels are used to approximate the hull surface and part of the surrounding free-surface. The panels are of the Rankine-source type, Hess and Smith (16), and may be first order or higher order, Hess (17). The first order panels are flat having a constant source strength while the higher order panels are parabolic having a linear variation of the source strength. The source panels on the free-surface are in the present method positioned a small distance above the free-surface, a procedure that is known to improve the solution and to stabilize the non-linear computations, Xia (8), Raven (18) and Jensen et al. (19).
In their final form the free-surface boundary conditions contains second derivatives of the velocity potential. Two possibilities for computing the second derivatives are introduced in the present method. The first is to use an upstream four-point numerical operator as suggested by Dawson (15). The second is to use analytical formulas for the second derivatives as described by Jensen et al. (19) and Jensen (20). Upstream waves are automatically prevented when the upstream operator is used while a collocation point shift is introduced together with the analytical computation to fulfil this condition. Details of the potential-flow method is described in Kim (1), Janson (21), Larsson et al. (22) and (23).
2.2
The Boundary layer method
In a boundary layer the velocity changes from zero to approximately the ship speed across the boundary layer. If this is thin, the gradients in the hull surface normal direction dominate over the ones in the plane of the surface. It is thus possible to delete two of the stress derivatives in the Navier-Stokes equations. Since the velocity in the normal direction must be much smaller than the tangential velocities the equation for the normal velocity degenerates to the statement that the pressure is constant across the boundary layer. If the boundary layer is thin, it disturbs the potential flow very little, so the potential flow pressure distribution over the hull surface may be used for the pressure across the layer. The boundary layer equations are in the present method expressed in a curvi-linear orthogonal coordinate system. An integration of the equations in the normal direction gives the momentum integral equations. A further simplification of the equations is also introduced since the cross-flow in the boundary layer is assumed to be small. The resulting ordinary differential equations are then solved using a Runge-Kutta technique along the potential flow streamlines traced on the hull surface.
Laminar and turbulent boundary layers can be computed in the present method. The computation of the former is started from a stagnation point, obtained from backwards streamline tracing, and is continued until transition occurs. After transition, initial conditions are generated for the turbulent boundary layer and the computation is continued along the streamlines. Alternatively the turbulent boundary layer computation may be started from initial values estimated from flat plate formulas. Details of the boundary layer method are described in Larsson (9).
Boundary layer methods are very accurate and efficient and can be used for the viscous flow over a large part of the hull as long as the boundary layer assumptions are valid. The thick viscous region close to the stern of a conventional hull cannot, however, be computed. But, the boundary layer solution can be used to generate the upstream boundary conditions for the Navier-Stokes method.
2.3
The Navier-Stokes method
The time averaged Navier-Stokes equations for incompressible flow are solved in zone three, and if all terms are included, the equations are elliptic. A predominant flow direction is often present for the flow around a ship hull and a somewhat simplified set of equations can be used, assuming that the stress derivative in this direction is small. The equations for the velocities then becomes parabolic and a marching technique can be used for the solution. The pressure calculation is, however, elliptic and the method can be referred to as partially parabolic. A curvi-linear nonorthogonal coordinate system is used and both the independent and the dependent variables are transformed to this system.
Transport equations are solved for the turbulent kinetic energy, k, and its rate of dissipation, ε. A wall law represents the velocity distribution close to the hull surface and the k–ε model can then be used for obtaining the turbulent viscosity in the entire flow domain.
Numerically the problem is solved using a finite-difference method. In the cross-plane a finite-analytic scheme is used while a second order upwind scheme is used in predominant direction. The pressure-velocity coupling is based on the SIMPLER algorithm.
Upstream, the boundary conditions are obtained from the boundary layer solution and from the potential flow solution outside this layer. The potential flow solution is used as boundary condition at the outer edge of the domain and at the downstream boundary
zero derivatives are specified for the dependent variables. Symmetry conditions are specified at the undisturbed free-surface level and at the centre plane. The theory for the Navier-Stokes method is described in detail in Broberg (10) and Larsson et al. (22) and (23).
2.4
Computation of resistance
There are three types of resistance components that can be computed in the present method, wave resistance, friction resistance and viscous pressure resistance. The potential-flow method may also include lift forces and induced drag.
Wave resistance is obtained from an integration of the potential flow pressure over the body surface. The pressure integration is for first order panels carried out as a summation over flat panels where the pressure and the normal direction are assumed to be constant over each panel. A more accurate integration is used if the computation is carried out for higher order panels. The pressure is then assumed to vary linearly over the panel and the normal direction is varying over the parabolic panel.
In case of a linear computation, where the body is panelized up to the undisturbed free-surface level, a resistance correction using the double-model resistance can be introduced. According to the d 'Alemberts paradox the pressure integration over the double-model should be zero. This is however not true for a discretized body. A small resistance, positive or negative, is always obtained for the double-model. This double-model resistance should be small compared to the wave resistance if an accurate solution is to be obtained. A too high value of the double-model resistance indicates that the body is not well described by the chosen distribution of panels. The final wave resistance is then computed by subtracting the double-model resistance from the resistance obtained in the linear computation. It is thus assumed that the discretization error is the same in the free-surface and the double-model computations. The double-model correction can not be used for a non-linear computation since the body is panelized up to the wavy free-surface which excludes the possibility to compute a zero resistance case for comparison. A more accurate discretization of the body surface is therefore needed for non-linear computations.
Integration of the local skin friction coefficient over the hull surface is carried out to obtain the friction resistance. The local skin friction is computed as a part of the solution along the stream lines in the boundary layer method and from the wall shear stress of the wall law in the Navier-Stokes solution.
The potential-flow pressure over the stern part of the hull is changed due to viscous effects computed by the Navier-Stokes solution. An integration of the pressure including viscous effects gives the viscous pressure resistance. A form factor can also be computed from the viscous pressure resistance and the friction resistance if the ITTC-57 line is used as reference.
3.0
The Optimization method
Optimization of a ship hull from a resistance point of view forms a non-linear optimization problem. The objective function (i.e. resistance) and the constraint (i.e. displacement) are non-linear functions of the design variables (hull modifications). The optimization problem may include multiple minima and a general optimization method cannot be expected to find a global minimum for this case. An optimization method, the Method of Moving Asymptotes, MMA, for solving non-linear optimization problems, Svanberg (11, 12), is implemented in the optimization program OCTOPUS, Esping et al. (13, 14), which is used in the present work. In MMA the solution is computed as a sequence of linearized sub-problems, where each sub-problem is obtained through a Taylor series expansion of the objective function and the constraints about the previous design point. The MMA method was originally developed for structural optimization problems but can also be applied to CFD problems as long as the objective functions, constraints and their gradients with respect to the design variable changes can be computed.
The non-linear optimization problem can be formulated as
minimize: f0(γ) (1)
subject to: ![]() (2)
(2)
(3)
where γ is a vector of design variables.
An iterative approach for solving the non-linear optimization problem can be used if the function values and the gradients of the objective function and the constraints can be computed. The procedure is to select an initial design point (first iteration point) and compute the function values and the gradients. Then generate an explicit sub-problem that approximates the original problem. Find the optimal solution to the sub-problem with some suitable method and use the solution as the next iteration point. The iterations are continued until some convergence criterion is fulfilled.
The choice of approximating function is important for the success of the method and the approximating functions are preferably convex. The most obvious convex approximation is perhaps to use a first order Taylor expansion of the object function and the constraints.
minimize:
(4)
subject to:
(5)
(6)
This gives a linear programming problem which can be solved using the Simplex method. The convergence of the above method is, however, in some cases very slow.
In the MMA, both the objective function and the constraints are approximated by a first order Taylor expansion but the variables are in this case of the type
where the first is used if the derivative of the object function or the constraints with respect to the design variable is negative and the second is used for a positive derivative. Lj and Uj are the lower and upper asymptotes for γj and γj will always be somewhere in between. Lj and Uj are adjusted in each iteration according to the behaviour of the solution. If the solution is oscillating in a design variable, the distance between Lj and Uj is diminished and if the change of the variable is monotonous a larger distance between Lj and Uj is allowed.
The original non-linear problem is reduced to a sequence of approximate sub-problems which can be formulated
minimize:
(7)
or
subject to:
(8)
or
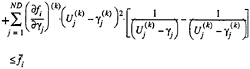
(9)
where the first summation in equations (7) and (8) is used for the terms having a negative gradient and the second is used if the gradient is positive.
The constraints in the MMA approximation are convex and the objective function is strictly convex which gives the possibility to use dual methods to solve each sub-problem. In some sense, the dual problem is equivalent to the original sub-problem and is for the present formulation easy to solve numerically. The optimal solution of the original sub-problem can then be obtained from the solution of the dual problem. A Lagrangian function corresponding to the approximating sub-problem is the starting point for the dual formulation.
(10)
Where λi are Lagrangian multipliers which are required to be non-negative. The Lagrange function is then strictly convex and there is a unique γ=γ(λ) which minimizes the Lagrange function. A dual objective function can be defined by minimizing the Lagrange function with respect to the design variables.
φ(λ) = minγ(L(γ,λ)) = L(γ(λ), λ) (11)
The dual problem corresponding to the original minimizing sub-problem is then:
maximize: φ(λ) (12)
subject to: λ≥0 (13)
A solution to the dual problem can be computed using methods for unconstrained problems, for instance conjugate gradient or Newton methods. Once the optimal solution, λ°, of the dual problem is found, the unique global optimum to the original sub-problem can be computed as γ(λ°). This correspondence
between the original and the dual problem holds because of the convexity of the constraints and the strict convexity of the objective function of the original approximating sub-problem.
4.0
A system for ship hull optimization
The SHIPFLOW code for computation of the flow around ship hulls and the program OCTOPUS for solving non-linear optimization problems are used to form a system for ship hull optimization, figure 2. Included in the system is also a geometry program ALADDIN. The optimization starts from an original shape defined by a set of offset-points on the hull surface. In the optimization procedure all or selected offset-points are attached to a design variable, figure 3, which represents the location of the point along a line, in the direction of which it is allowed to move (for instance the surface normal direction). The design variables may be either master or slave variables, the latter being determined as linear combinations of the former. Given the master and slave variable values the position of the offset-points on the surface is specified and so is the shape of the hull. Master and slave variables are attached to the offset-points in ALADDIN and a basic shape together with a number of variations are created. The variations are obtained through a small disturbance of the master variables, one at the time. SHIPFLOW then computes the resistance (objective function) for the basic shape and the derivative of the resistance with respect to the master variable variations. A computation of the displacement of the ship (constraint) together with the derivatives of the displacement with respect to the master variable variations is also performed. Enough information for creating and solving an approximate sub-problem of the optimization problem can then be formulated. The optimum of the sub-problem is computed in OCTOPUS and the new values of the design variables are computed and transferred to ALADDIN where a new basic shape together with variations are created. The process is iterated until the constraints are fulfilled and no further improvements are obtained within some convergence criteria.
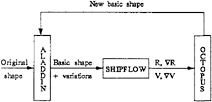
Fig. 2 The system for hull optimization
The coordinates of an offset-point, p, directly connected to a master variable, γj, are determined from
xp= x0p + αx.γj
yp= y0p + αy.γj
zp= z0p + αz.γj (14)
where (x0p, y0p, z0p) are the coordinates of the original position and αx, αy, αz are linking factors between the master variable and the point.
Other offset-points, q, where a slave variable is assigned are computed in a similar way.
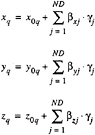
(15)
where (x0q, y0q, z0q) are the coordinates of the original position and βxj, βyj, βzj are linking factors between the offset-point and each of the master variables.
Once the hull surface is defined, grids suitable for the potential flow calculation, the boundary layer calculation and the Navier-Stokes calculation may be generated using grid generators developed for each computational method, figure 4, 5 and 6.
In the present version of the optimization system the only possible objective function is the resistance.
RT= RF+ RVP+ RW (16)
All or selected components of the resistance may be included in the total resistance depending on the number of zones that have been included in the flow computation. The only possible constraint is the displacement, V.
Gradients of the objective function and the constraint with respect to the master variable changes are obtained by numerical differentiation.
(17)
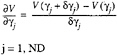
(18)
δγj is the small disturbance of the master variables generated in ALADDIN before the flow computations in each iteration.
The iteration procedure is terminated when the following two criteria are fulfilled.
(19)
(20)
![]() is the displacement of the original hull.
is the displacement of the original hull.
5.0
Optimization of the Series 60 hull
The optimization procedure was applied to the Series 60 CB=0.6 hull at a Froude number of 0.316 and a Reynolds number of 5.0 ×106. Sinkage and trim effects were not included. The hull was optimized with respect to the total resistance including wave resistance from a linear potential-flow solution and viscous resistance from boundary layer and Navier-Stokes solutions.
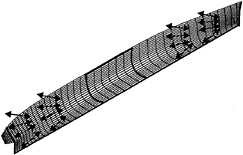
Fig. 3 Position of the master variables
A total of 16 master variables were used in the optimization model. The master variables were attached to four offset points at each of the stations x/Lpp=0.11, 0.22, 0.77 and 0.90 as shown in figure 3. Offset points located at the stem, stern and keel line were not allowed to move during the optimization. The midship section between x/Lpp=0.41 and x/Lpp=0.6 was also kept unchanged. Upper and lower limits for the master variable values were specified and the 16 attached offset points were allowed to move in the hull surface normal direction in the plane of the section. Slave variables, equation (15), were used to connect the neighbouring offset points to the master variables and the slave variable values varied linearly, both in the streamwise and girthwise directions, from a maximum value at the master variable in question to zero at the next master variable or fixed boundary.
Three computational models, one for each of the computational methods, were created for the basic shape and for each master variable change in each iteration which gives a total of 17 complete computations in each iteration. The computational model for the potential-flow solution, figure 4, included about 900 panels and a linear computation without sinkage and trim was performed. 10 potential-flow streamlines traced between 5% and 95% of the ship length, figure 5, were used for the boundary layer computation. A turbulent boundary layer was assumed at the starting point and the initial values were estimated from flat plate formulas. The computational model for the Navier-Stokes solution, figure 6, included 20000 points (50*20*20) and the mean value of the distance to the first point off the hull, y+, was about=80. All Navier-Stokes solutions were started from a converged solution for the original hull (first basic shape). Each succeeding computation was then executed 15 more iterations. No user interference is needed during the optimization process.
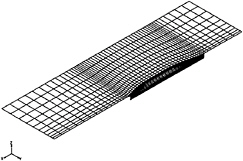
Fig. 4 Computational model for the potential-flow

Fig. 5 Potential flow streamlines for boundary layer solution
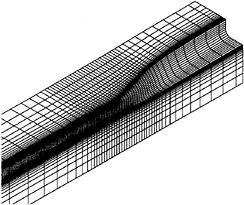
Fig. 6 Computational model for the Navier-Stokes solution
Two optimizations were carried out using different limitations, one larger and one smaller range, for the master variable changes. The constraint was in both cases that the displacement was not allowed to be smaller than for the original hull. The computed total resistance for the optimized hull was 11% less than for the original hull when the larger master variable range was used and 9% less for the smaller. Hull modifications outside the hull main dimensions were allowed for the larger range while the modifications were kept inside the main dimensions for the small range.
The original and optimized hulls for the large range are compared in figure 7 for the x/Lpp positions 0.1, 0.2 0.3 0.5 0.7 0.8 and 0.9. It is seen that the volume of the lower part of the fore body has increased dramatically and the fore body is now more bulb-shaped than the original one. The maximum draught is also increased at the fore body which indicates that the limits for the master variable changes close to the keel line are to wide, at least if the intention is to keep the hull main dimensions constant. The lines of the aft body are more U-shaped than the original ones and the volume close to the water line is decreased. Since the volume was constant during the optimization this means that volume was moved from the aft body close to the waterline to the lower part of the fore body and to the lower part of the aft body. The longitudinal position of the centre of buoyancy moved 1% forward and 0.15% of Lpp downwards.

Fig. 7 Original and optimized hull, large range
Thick lines—original hull
Thin lines optimized hull
A comparison of the original and optimized hulls for the small range is shown in figure 8 for the same positions as in figure 7 and the two optimized shapes are compared in figure 9. As can be seen in the figures the aft body modifications are very similar for the smaller and the larger range. The volume in the fore body was positioned closer to the free-surface for the smaller range and the water line angle becomes larger.
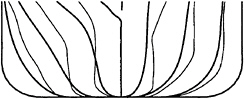
Fig. 8 Original and optimized hull, small range
Thick lines—original hull
Thin lines—optimized hull
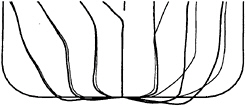
Fig. 9 Optimized hull
Thick lines—large range
Thin lines—small range
It is obvious that none of the two optimized hull forms are acceptable from a practical point of view but this can not be expected since the optimization system does not include any constraints on the hull modifications from a practical point of view or from a lines fairing point of view. The two optimizations also allowed for very large changes of the shape.
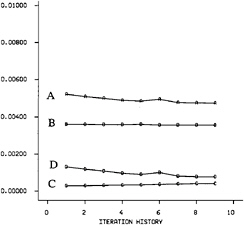
Fig. 10 Iteration history for the optimization
A—Total resistance
B—Friction resistance
C—Viscous pressure resistance
D—Wave resistance
The second case where the hull modifications were kept inside the main dimensions was selected for the discussion in the following sections. The iteration history of the resistance components, figure 10, shows that the main part of the reduction comes from the wave resistance, while the friction resistance is almost constant and the viscous pressure resistance increases. The reduction of the wave resistance is much larger than the increase of the viscous pressure resistance. A total reduction of 9% is obtained in 9 iterations.
The wave profile at a longitudinal cut close to the hull side is compared for the original and the optimized hull in figure 11. The bow wave is slightly larger for the optimized hull, but the stern wave is reduced considerably which explains the lower wave resistance. This may be in accordance with the hull modifications where the volume was moved from the upper part of the aft body to the fore body. The hull modifications gave a more U-shaped aft body. This may result in a more pronounced bilge vortex that can explain the increase in the viscous pressure resistance.
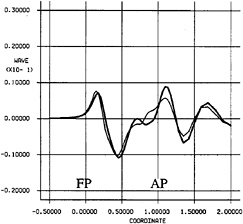
Fig. 11 Wave profile at y/Lpp=0.0755
Thick line—original hull
Thin line—optimized hull
Both a finer and a coarser computational grid than in the optimization were used for the original and optimized hull to verify the result and it was found that the improvement was the same within 1% for all grids. It was therefore believed that the improvement came from the modification of the hull shape and not from the rearrangement of the computational grid during the optimization process.
6.0
Experiments
To finally verify the optimization a model test was carried out for both the original and the optimized hull. Resistance measurements for a model free condi-
tion and wave profile measurements for a fixed condition were carried out at SSPA Maritime Consulting. The optimized hull was introduced in the hull design program NAPA and the lines were slightly modified to smooth the hull, but great care was taken to keep the main features of the optimized hull. A final computation was thereafter performed using the coordinates from the faired lines. This additional computation was to verify that the main features of the optimized hull were not changed and that the total resistance reduction was the same as before the lines fairing. The slightly modified hull showed about 1% higher resistance. The length of the models was Lpp=5.0 m.
The resistance measurements for the model free condition, figure 12, did not verify the resistance reduction obtained in the computations. Based on the computations the increased resistance at low speeds was expected due to the higher viscous pressure resistance and the larger form factor for the optimized hull, but the residuary resistance was expected to be much lower at speeds close to the Froude number 0.316.

Fig. 12 Resistance measurements, model free condition.
A—Total resistance coefficient, original hull
B—Residuary resistance coefficient, original hull
C—Total resistance coefficient, optimized hull
D—Residuary resistance coefficient, optimized hull
Since the optimization worked well from a computational point of view, the question is now why the computations failed to find the same difference between the original and the optimized hull as the experiments. Were there flow phenomena missing in the computational model or was the grid resolution not good enough or was it a combination of both?
The potential-flow solution was first investigated. A linear computation without sinkage or trim had been used in the optimization and the reduction of the wave resistance coefficient was 0.51×10–3. Non-linear computations without sinkage and trim were now carried out and a reduction of 0.36×10–3 was obtained if the same grid distribution was used. Another non-linear computation was also carried out using a finer grid and the reduction was then 0.37×10–3. It was therefore concluded that the absent non-linear effects can explain part of the discrepancy between computations and experiments. The grid refinement seems to be of minor importance.
In figures 13 and 14 a comparison of the computed and measured wave profiles is made close to the hull for the original and the optimized hull. The computed wave profiles agree well with the measurements but the bow wave amplitude is underpredicted. Both measurements and computations show a higher bow wave crest for the optimized hull and the irregular profile from the measurements indicates that wave breaking occurs for the optimized hull. The wave breaking, which cannot be captured in the potential flow model, was also observed in photos from the experiments. The reduction of the stern wave amplitude for the optimized hull is much more pronounced in the computations than in the measurements.
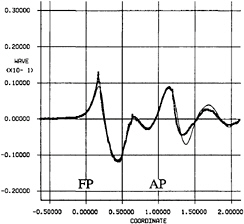
Fig. 13 Wave profile at y/Lpp=0.0755, original hull
line with circles—experiments
line without circles—computations
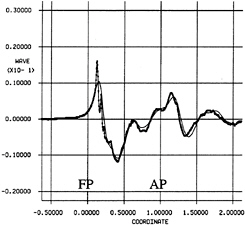
Fig. 14 Wave profile at y/Lpp=0.0755, optimized hull
line with circles—experiments
line without circles—computations
Non-linear computations including sinkage and trim were also executed using the finer grid. The reduction of the wave resistance was in this case 0.44×10–3 which indicates that the optimized hull performs slightly better in model free condition than in model fixed compared to the original hull.
All potential-flow computations showed a large reduction of the stern wave for the optimized hull. The reduction was much smaller in the experiments and the grid refinement did not improve the prediction. One attempt was therefore made to investigate if the interaction between the viscous flow and the wave making at the stern is of importance. The displacement thickness obtained from the boundary layer solution was used to represent the effect of the viscosity on the potential flow. The shape of the original and the optimized hulls was modified by adding the displacement thickness. To make it possible to add the displacement thickness also at parts covered by the wave in the non-linear computations, a boundary layer computation was performed for a draught larger than the design draught. The potential flow computations were then repeated using the modified hull shapes and the finest grid. This procedure can not be considered very accurate since the boundary layer assumptions are not valid in the stern part of the hull and the boundary layer method used is of first order. The results may, however, give an indication if there is a significant influence of the viscous flow on the wave making.
There is also a question how to represent the modified hull downstream of the stern were only the displacement thickness is present, Larsson and Chang (24). The hull was in the present computations closed downstream of the stern and three positions of the closure point were tested, 7.5%, 10% and 20% of Lpp downstream of AP. Only small differences were found for the three positions and 7.5% was selected for the final computations. A large reduction of the stern wave amplitude was obtained for both the original and optimized hull when the displacement thickness was added to the hull.
The wave resistance cannot be obtained from pressure integration over the hull surface when the displacement thickness is added since the modified surface does not represent the real shape of the hull. A longitudinal wave cut method described by Michelsen and Uberoi (25) and Lundgren and Åhman (26) was therefore used when the influence of the displacement thickness on the wave resistance was investigated. The difference between the original and the optimized hull was 0.52×10–3 without displacement thickness and 0.29×10–3 when the displacement thickness was included. It seems that the effect of including the displacement thickness is to reduce the influence of the hull modifications on the potential-flow solution. It was therefore concluded that in this case there is a significant influence between the viscous flow and the wave making at the stern but the magnitude of the influence cannot be determined from this investigation. The displacement effect was not included in the optimization and this is probably the main reason why a too large reduction of the stern wave was obtained.
The computation of the viscous forces was also investigated since the experiments showed an increase of the viscous forces by 7.7% for the optimized hull while the computations showed an increase of 2.3%. A grid refinement study was carried out and the finest grid including 75000 (120*25*25) points showed an increase of 3.5%. It was therefore concluded that only a small part of the difference can be referred to grid resolution. The form factor was in the experiments 0.07 for the original hull and 0.15 for the optimized hull while the computations for the finest grid showed 0.108 and 0.133 respectively. In general an overprediction of the form factor is obtained for slender hulls. The wakes for the original and optimized hull are plotted in figures 15 and 16. A more pronounced bilge vortex was obtained for the U-shaped aft body of the optimized hull. The strength of the vortex is probably underpredicted for both hulls which is a well known behaviour of the standard k-e model. See the discussion at the workshops (27) and (28). The k–ε model together with the wall law may form a too “stiff” computational model for predicting the magnitude of the vortex changes between the hulls. This is a likely reason why the increase of the viscous forces was underpredicted.

Fig. 15 Wake at AP, original hull
Isowakes for 0.5, 0.6, 0.7, 0.8 and 0.9
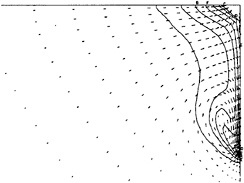
Fig. 16 Wake at AP, optimized hull
Isowakes for 0.5, 0.6, 0.7, 0.8 and 0.9
7.0
Conclusions
The optimization worked well from a computational point of view. Two optimizations were carried out for the Series 60 hull using different limits for the allowed hull modifications and the computed total resistance was reduced by 11 and 9% respectively.
The Method of Moving Asymptotes, MMA, for optimization of non-linear problems performed well for the present application. When searching for an optimum MMA takes large steps in the right direction in the first iterations. This is interesting from and engineering point of view since only a few iterations are required to come close to the optimum. The convergence is, however, slower as the optimum is approached.
Experiments carried out for the original and one of the optimized hulls did not verify the resistance improvements obtained in the computations.
Three main reasons for the discrepancy between the computations and the experiments are found:
-
The neglected non-linear effects on the waves gave a to small increase of the bow wave system for the optimized hull.
-
A too large reduction of the stern wave was obtained for the optimized hull, probably due to the neglected viscous effects on wave making.
-
The increase of the viscous resistance was under predicted, partly due to grid resolution, but the main reason is probably that the k–ε model and the wall law give a computational model that is insensitive to hull modifications. This may influence the strength of the predicted bilge vortex.
For the three points above it may noted that the computations predicted the right trends but the magnitude was wrong. The experiments showed a larger bow wave for the optimized hull. Linear computations of the waves, included in the optimization, showed a small increase of the bow wave and the increase was even more pronounced when the computations were repeated using non-linear free-surface boundary conditions. The stern wave was reduced in the experiments but the reduction was overpredicted in the computations. Both the experiments and the computations showed an increased viscous resistance but the increase was underpredicted.
In future work, parts of the optimization system must be improved. The most important improvement is a Navier-Stokes solver including the free-surface. Non-linear free-surface boundary conditions in the potential-flow solution may also improve the results. The routine for hull modifications must be improved to ensure hull forms of practical use.
Optimization from a wave resistance point of view must be restricted to fore body design until a Navier-Stokes method including the free-surface waves is introduced in the optimization system.
8.0
Acknowledgements
The authors would like to thank Dr. Keun-Jae Kim, who started the optimization work in the research group, for interesting discussions. Special thanks are also due to Dr. Björn Esping and Dr. Dan Holm at ALFGAM Optimization AB for the permission to use the OCTOPUS program and for their help when linking the SHIPFLOW and OCTOPUS programs. Thanks also to SSPA Maritime Consulting for carrying out the experiments and for manufacturing the optimized Series 60 model and to SVA, Potsdam, Germany, for lending us the original Series 60 model.
9.0
References
1. Kim, K.J., “Ship Flow Calculations and Resistance Minimisation,” PhD Thesis, 1989, Department of Marine Hydrodynamics, Chalmers University of Technology , Gothenburg.
2. Nowacki, H., “Hull Form Variation and Evaluation,” J. Kansai Society of Naval Architects, Japan, No 219, March 1993, pp. 173–184.
3. Nowacki, H., “Optimization Methods Applied to Viscous Drag Reduction,” Proceedings of the Osaka International Colloquium on Ship Viscous Flow, Osaka, Japan, 1985.
4. Papanikolaou, A., Zaraphonitis, G. and Androulakakis, M., “Preliminary Design of a High-Speed SWATH Passenger/Car Ferry,” Marine Technology, Vol. 28, No. 3, 1991, pp. 129–141.
5. Hsiung, C.C., He, Y.J. and Cong L.Z., “Optimal Ship Forms for Minimum Total Resistance With the Consideration of Boundary Layer and Wake,” 5th International Symposium on the Practical Design of Ships and Mobile Units, Newcastle upon Tyne, UK, Vol. 1, 1992, pp. 1.33–1.46.
6. Wyatt, D.C. and Chang, P.A., “Development and Assessment of a Total Resistance Optimized Bow for the AE-36,” Marine Technology, Vol. 31, No. 2, April 1994, pp. 149–160.
7. Maisonneuve, J.J., “Optimization Tools for Ship Resistance and Seakeeping Problems,” Proceedings of the Second International Conference on Fast Sea Transportation , Yokohama, Japan, Vol. 2, 1993, pp. 1465–1476.
8. Xia, F., “Numerical Calculation of Ship Flows, with Special Emphasis on the Free Surface Potential Flow,” PhD Thesis, 1986, Department of Marine Hydrodynamics, Chalmers University of Technology , Gothenburg, Sweden.
9. Larsson, L., “Boundary Layers of Ships (Three-dimensional Effects),” PhD Thesis, 1975, Department of Applied Thermo and fluid Dynamics, Chalmers University of Technology, Gothenburg, Sweden.
10. Broberg, L., “Numerical Calculation of Ship Stern Flow,” PhD Thesis, 1988, Department of Mechanics, Chalmers University of Technology, Gothenburg, Sweden.
11. Svanberg, K., “Convex Approximation Methods for Structural Optimization,” COMETT-Seminar on Computer Aided Optimal Structural Design, Castle of Thurnau, Germany, May 18–22, 1992.
12. Svanberg, K., “Method of Moving Asymptotes—A New Method for Structural Optimization,” International Journal for Numerical Methods in Engineering, Vol. 24, 1987. pp. 359–373.
13. “OASIS-ALADDIN User's Manual,” Chapter 9, 1990, ALFGAM Optimering AB, Stockholm, Sweden,
14. Esping, B., Clarin, P. and Romell, O., “OCTOPUS—A Tool for Distributed Optimization of Multi-Disciplinary Objectives ”, ALFGAM Optimering AB, Stockholm, Sweden.
15. Dawson, C.W., “A Practical Computer Method for Solving Ship-Wave Problems,” 2nd International Conference on Numerical Ship Hydrodynamics, Berkely, 1977, pp. 30–38.
16. Hess, J.L. and Smith, A.M.O., “Calculation of Non-lifting Potential Flow About Arbitrary Tree-Dimensional Bodies,” Douglas Report No. E S 40622, 1962.
17. Hess, J.L., “A Higher Order Panel Method for Three-Dimensional Potential Flow, ” Douglas Report N62269–77-C0437, 1979.
18. Raven, H.C., “A Practical Nonlinear Method for Calculating Ship Wavemaking and Wave Resistance,” 19th Symposium on Naval Hydrodynamics, Seoul, South Korea, 1992, pp. 349–364.
19. Jensen, G., Bertram, V. and Söding, H., “Ship Wave-resistance computations,” 5th International Conference on Numerical Ship Hydrodynamics, Hiroshima, Japan, 1989, pp. 593–605.
20. Jensen, P.S., “On the Numerical Radiation Condition in the Steady-State Ship Wave Problem,” Journal of Ship Research, Vol. 31, No. 1, 1987, pp. 11–28.
21. Janson, C.E., “A Method for the Prediction of Wave Resistance, Lift and Induced Drag,” Lic. Eng. Thesis, 1993, Department of Naval Architecture and Ocean Engineering, Chalmers University of Technology, Gothenburg, Sweden.
22. Larsson, L., Broberg, L., Kim, K.J. and
Zhang, D.H., “New Viscous and Inviscid CFD Techniques for Ship Flows,” 5th International Conference on Numerical Ship Hydrodynamics, Hiroshima, Japan, 1989.
23. Ohkusu, M., ed., Advances in Marine Hydrodynamics, Computational Mechanics Publications, Southampton, Boston, 1996, pp. 1–75.
24. Larsson, L., and Chang, M.S., “Numerical Viscous and Wave Resistance Calculations Including Interaction, ” 13th Symposium on Naval Hydrodynamics, Tokyo, Japan, 1980.
25. Michelsen, F.C. and Uberoi, S.B.S., “A Study of Wave Resistance Characteristics Through the Analysis of Wave Height and Slope Along a Longitudinal Track,” Report No. Hy-15, 1971, Hydro og Aerodynamisk Laboratorium, Lyngby, Denmark.
26. Lundgren, H. and Åhman, M., “Experimentell och numerisk bestämning av vågmotstånd för ett tankfartyg (Dynetankern),” Report No. X-94/58, 1994, Department of Naval Architecture and Ocean Engineering, Chalmers University of Technology, Gothenburg, Sweden. (In swedish).
27. Larsson, L., Patel, V.C. and Dyne, G., “Ship Viscous Flow,” Proceedings of 1990 SSPACTH-IIHR Workshop, Flowtech International AB, Gothenburg, Sweden, Report No. 2, June 1991.
28. Proceedings of CFD Workshop Tokyo 1994, Tokyo, Japan, March 1994.
DISCUSSION
L.J.Doctors
University of New South Wales, Australia
The authors are to be congratulated on working on such a difficult problem—the optimization with respect to resistance based on nonlinear viscous computations. To their credit, the authors pointed out clearly that the optimization unfortunately generated a hull with greater resistance. This was due to the computed changes in resistance being incorrect, even though the computed changes of components of the total resistance possessed the correct sign.
My question is that one might be better advised to use a simpler method, such as the linear theory of Mitchell for the computation of the wave resistance. Although the results for the resistance might be less accurate, perhaps the trends might be more precisely predicted and hence this approach might be more suitable for an optimizer.
AUTHORS' REPLY
Thank you for your comment on using a simpler method for the computation of wave resistance. Due to the large computational effort included in the optimization it may be of interest to consider a simpler and faster method, as the linear theory of Mitchell, for the wave resistance. This, however, requires that viscous effects and nonlinear wave effects are of minor importance and that the derivatives of the wave resistance with respect to the shape modifications are close to the derivatives computed by more accurate methods.
In the paper, both fore body and aft body modifications were included and the total resistance was considered for the optimization. It turned out that not only the trend but also the magnitude of the change of each resistance component was of importance. This indicates that more accurate methods must be used for the predictions. In the optimization, the magnitude of the wave resistance change was not correctly predicted due to neglected displacement effects. This prediction can probably not be improved by changing from a Rankine source method to the linear theory of Mitchell.
DISCUSSION
H.Raven
Maritime Research Institute, The Netherlands,
Inspired by this interesting paper, I have a question on which I would like to hear your opinion. What will be the best way ahead in ship hull form design—automatic optimization or an expert system?
AUTHORS' REPLY
For a hull type where an expert system (data base) exists, this can be used to find a good initial design point. If further improvements are required, the automatic optimization system can be used as a tool for the designer in a local form optimization. If no data base is available for the hull type, an optimization may first be carried out for the global hull parameters as design variables. As a second step, a local form optimization can then be carried out. In both cases, the result of the automatic optimization is only one source of information among others for the designer when the decision for the final design is made.
One advantage of optimization together with CFD is that it gives information on the pressure and velocity distribution and the wave pattern around the hull—information that can be used to understand why one hull form performs better than the other.
DISCUSSION
H.Nowacki
Berlin Technical University, Germany
The authors are presenting interesting new evidence on the contrasting conclusions from CFD hull form optimization and from experiments. Qualitatively I find their results very plausible and noncontradictory.
-
In potential flow analysis, whether by linear or nonlinear wave theory, it does appear promising to move displacement from a high region aft to a low region in the forebody. The optimization results are consistent with this.
-
In viscous flow, the stern wave system is weaker than calculated for both the original and the optimized hull. The removal of
-
displacement there must be less effective than calculated. “Something that is not there cannot go away.”
That much should be regarded as reassuring rather than disappointing.
Quantitatively it is more difficult to account for the differences. I agree that wave-viscous interaction effects may play a major role. Since trim and sinkage depend on viscous effects, this raises an open question. In the current study, trim and sinkage were not included in the optimization, but were later estimated apparently, as is customary, by pressure integration only in potential flow. How much did this sinkage and, in particular, trim differ from the measured results? If appreciably, as one might suspect in view of the viscous effects on the stern wave system, then this may be another cause for the observed discrepancies.
The displacement thickness approach does not seem to promise any hope. The displacement thickness is not defined to predict correct pressure distributions in way of the stern and it would be a miracle if it did.
In any case in optimization, I would tend to ensure realistic sinkage and trim as in a real fluid before proceeding to refine secondary flow and turbulence models.
Clearly, full Navier Stokes flow models with free surface hold much promise also for optimization. But before going to such extreme calculation effort, one should not neglect to examine approximate ways for indirectly, perhaps semi-empirically, allowing for viscous effects including trim and sinkage.
AUTHORS' REPLY
Thank you for pointing out the importance of sinkage and trim and the difference in sinkage and trim between potential flow and real fluid flow. For the 5-m models used in the measurements, the original hull showed a sinkage of 18.5 mm and a 7-mm trim on the bow while the computations showed a sinkage of 16 mm and a 6-mm trim on the stern. For the optimized hull, the measurements gave a sinkage of 15.5 mm and 7-mm trim on the bow while the computations gave a sinkage of 15 mm and 2-mm trip on the stern.
After preparation of the paper, additional resistance measurements were carried out for the model fixed condition to exclude sinkage and trim effects as a possibility for the discrepancy between computations and measurements. For the Series 60, the measured difference in resistance between the original and the optimized hull was approximately the same with and without sinkage and trim.
DISCUSSION
A.D.Papanikolaou, G.Tzabiras
National Technical University of Athens, Greece
The paper describes a fully automatic computer-aided method for optimization of ship hull forms from the resistance point of view. The method is based on the well-known code SHIPFLOW for the determination of the flow around the ship hull and the OCTOPUS code for the solution of the formulated nonlinear optimization problem. The application of the presented method to the optimization of a typical Series 60 hull form is satisfactory from the computational, but discouraging from the practical point of view when considering the validation of obtained theoretical-numerical results in comparison to model experimental data.
The discussors would like, at first, to commend the authors for the shown courage to present a “discouraging” case of application of their optimization system and not a straightforward one that could be easily produced, taking as reference a “bad” starting point. We should explore in the following the reasons for the shown discrepancies.
-
Optimization Methododology. The adopted methodology is briefly explained in chapter 4.0 and Fig. 2 of the paper. The method can be understood to address the last stage of hull form optimization (local form optimization), when adopting a multistage optimization strategy as, e.g., presented earlier in [4]. Therefore, we might first assume that the main dimensions and global characteristics of the hull form, to be optimized, are given and a refinement of the globally optimized hull is herein addressed. According to our experience, the geometric constraints set for the formulation of the optimization problem influence drastically the final result. Therefore, the proper formulation of these constraints seems to be the key for a
-
successful optimization procedure. Based on this, the following points are raised.
-
How far can the “automation” of an optimization code go, what is the responsibility of the code user and the designer?
-
The optimized hull forms, shown in Figs 7 and 9, suggest that the draft constraint has been implemented only at the ship's centerplane. The depicted “tunnel” bow sections cannot be justified both from the physical and the practical point of view.
-
The authors are optimizing the hull forms for the least total resistance. This is basically correct. However, it seems essential, before setting up the optimization procedure, to carefully consider the individual contributions of the viscous and wave components to the total resistance of the studied hull. In addition, with reference to propulsive aspects, the hull efficiency (wake and thrust deduction factors) of the stern should be taken into account, e.g., through specific geometric constraints. The rather U-shaped stern body suggests that possibly the studies will have not only increased viscous resistance, but possibly also inferior propulsive efficiency.
-
Resistance Algorithms. The authors show great courage to present the rather disappointing results of Fig 12, where the measured resistance of the original hull is below the corresponding one of the optimized hull. The above figure would greatly gain in clarity if the authors would add the computational results for the total resistance and its components for the original and the optimized hull. In any case, the conclusion is that the used resistance algorithms are partly problematic and the authors discuss several aspects for the shown discrepancies in their paper. Considering the complicated flow around a ship hull form, weaknesses in the employed resistance algorithms are to a certain degree acceptable. However, for a hull form optimization procedure, it is possibly of less importance the accurate prediction of the absolute value of the resistance and its components. Rathermore, it is the prediction of the relative value of resistance between hull alternatives that is essential. In the studies case, it seems that the theoretical predictions for the resistance of the optimized hull ore more “optimistic” than those for the original hull. This is the point that should be clarified, e.g., by checking the predictions for the individual resistance components step by step.
The authors discuss carefully many aspects and possible shortcomings of their potential (wave resistance) and viscous flow solution. The discussors agree with the authors that the shortcomings of the employed κ-ε model and the neglect of the influence of the free surface on the viscous calculations are the main points to be addressed in future work.
AUTHORS' REPLY
Thank you for discussing several aspects on hull form optimization. As you point out, the intention of the present optimization was a local form optimization, but the changes allowed were probably too large to be considered as local variations.
The authors agree that it is necessary to include more aspects on hull performance in the optimization both in the objective function and as constraints. But an optimization system of this kind can only serve as one tool among others for the designer since many areas of hydrodynamic hull performance as well as practical considerations must be taken into account in the decision of the final design. Some of the considerations are probably difficult to include in an automatic optimization system.
Our experience is that the resistance algorithms work well for slender hulls like the Series 60. The problem in this case was that the physics of the flow around the stern was not well captured due to the neglected displacement effects in the wave prediction. The resistance algorithms may be more problematic for the full hull forms.
We agree that ranking is more important than absolute resistance values for numerical computations and optimization. But in cases where the total resistance is obtained as a summation of several resistance components also, the absolute value of the change of each component is important if the ranking is different for the components.

















