On Ships at Supercritical Speeds
X.-N.Chen (University of Stuttgart, Germany), S.Sharma (Mercator University, Germany)
ABSTRACT
This paper deals with the problem of a ship moving at supercritical speeds. Following the idea of shallow channel superconductivity (zero wave resistance) proposed in Chen & Sharma (1995), we continue to look for more nonlinear superconductive solutions within an improved theoretical model. We begin our study with an extended KP equation (eKP) that holds to same precision as the Boussinesq equations. First, we reduce the problem of a ship moving at supercritical speeds in horizontally unbounded shallow water to an “initial” value problem of the KdV equation. This reduction enables various analytical solutions, specially an N-soliton solution. Second, we construct an eKP solution of the interaction of solitons (or any wave packets) moving in different directions. Third, we derive a fore-and-aft asymmetric superconductive hullform from the 2-KdV-soliton and the solution of the interaction between itself and its reflection from the channel sidewall. Finally, we propose a heuristic method for improving the precision of the shallow-water wave models by comparing their dispersion relations with the exact one for finite depth. In the concluding remarks we point out possible practical applications of our theory.
NOMENCLATURE
Dimensional variables carry a superscript asterisk*, all others are nondimensional.
A* typical wave amplitude
h* water depth
g*=9.80665m/s2 acceleration due to gravity
![]() circular wave number
circular wave number
Oxyz coordinate system moving with the ship, x pointing forward, z upward.
S(x)=S*(x*)/(εh*2) submerged cross sectional area of ship at section x
![]() depth Froude number
depth Froude number
U* ship speed
w* channel width
![]() horizontal coordinates
horizontal coordinates
ε=A*/h* smallness parameter for wave nonlinearity
![]() depth-averaged potential
depth-averaged potential
ζ=ζ*/(εh*) free surface elevation
INTRODUCTION
This paper deals with the problem of wave pattern and wave resistance of a slender ship moving steadily at supercritical speeds in shallow water. The critical speed is known to be ![]() and the depth Froude number U can be understood as the ratio of ship speed to critical speed. Supercritical ship speed means U>1.
and the depth Froude number U can be understood as the ratio of ship speed to critical speed. Supercritical ship speed means U>1.
The depth Froude number plays an important role in shallow water ship hydrodynamics that is almost the same as that of the Mach number in aerodynamics (Tuck 1978), except that there is a dispersion effect in shallow water waves. It is well-known that there is a favorable supercritical speed range in which the absolute value of wave resistance is smaller than that in the transcritical speed range, e.g. Graff, Kracht & Weinblum (1964). Nevertheless, supercritical ships are not as common as supersonic airplanes. Most inland or coastal ships plying in shallow water operate well below the
critical speed. Only recently can one observe a worldwide interest in the commercial exploitation of supercritical speeds for ships, especially ferries.
It is probably less well-known that the favorable effect of wave interference between twin hulls of a catamaran in shallow water, which diminishes total wave resistance, is more significant in the supercritical speed range than in the subcritical speed range (and, of course, in deep water). This phenomenon has been reported earlier by Eggers (1955, Figs.2 and 18) and Kirsch (1966, Figs.2–9). It was recently rediscovered by Chen & Sharma (1994a, Fig.5a) on the basis of a nonlinear theory and confirmed by model experiment. Even more exciting is the fact that when we tried to seek a fuller theoretical understanding of this interesting phenomenon, see Chen & Sharma (1995), we found that the wave resistance of a single-hull ship in a channel of suitable width can be made to vanish totally within the framework of a linear shallow-water wave approximation and, furthermore, also in a more accurate nonlinear theory, namely the standard KP equation. To put it simply in one sentence, the mechanism is that the bow wave after reflection from the channel sidewall hits the after-body and counteracts the stern wave so that the resultant wave in the ship wake disappears totally, if the hull geometry is adapted to ship speed and channel width according to certain rules. To our knowledge, this is a new type of ship and channel configuration marked by zero wave resistance. By analogy to electrical conductors, we have proposed the name “shallow channel superconductivity” for this phenomenon.
We would like to insert in the following three paragraphs a short review of shallow water wave theory as applied to ship hydrodynamics. The first relevant paper was by Tuck (1966) who developed a strictly linear technique of matched asymptotic expansions for a slender ship in shallow water. Lea & Feldman (1972) partly took account of nonlinearity and used an established transonic-flow numerical method for computing the transcritical motion of ships. Later on, Mei (1976) extended this work to include the dispersion effect in the near-critical speed range while still dealing with the steady problem. With due consideration to remarkable early towing tank experiment reports, e.g. Thews & Landweber (1935, 1936), Helm (1940), Kinoshita (1946), Graff (1962), and Graff, Kracht & Weinblum (1964), it may be stated that the recently revived interest in upstream solitons generated by a ship moving steadily at near-critical speeds stems from the experimental and numerical works by Huang et al. (1982) and Wu & Wu (1982). Since then various follow-up investigations have been done, e.g. Ertekin, Webster & Wehausen (1986) and Katsis & Akylas (1987) solved the 3-D free-surface pressure disturbance problem. Mei (1986), using matched asymptotic expansions, derived an inhomogeneous Korteweg-de Vries (KdV) equation for a slender ship moving at near-critical speed in shallow water and theoretically demonstrated solitons propagating upstream. Mei & Choi (1987) further developed this theory to calculate hydrodynamic forces on the ship but only crude agreement with experiments was obtained because this theory cannot predict the two-dimensional waves around a real ship and in its wake. So Choi & Mei (1989) improved their theory by using a Kadomtsev-Petviashvili (KP) equation in the far field to take account of the 2-D effect. More numerical results were reported in Choi, Bai, Kim & Cho (1990) with another finite element method.
Chen & Sharma (1992) pursued this method further with the aim of practical application. The slender body theory in the near-field was refined by taking account of local wave elevation, longitudinal disturbance-flow velocity and ship squat. Moreover, it was extended to the more general case of asymmetric motion. The KP equation in the far field was solved numerically by an efficient finite difference method, namely, a fractional step algorithm with Crank-Nicolson-like schemes in each half step. Very good agreement with towing tank experiments was achieved in wave resistance, sinkage, and trim for several ship models. Furthermore, Chen & Sharma (1994a) derived a KP equation from the Boussinesq equations by keeping a higher-order nonlinearity in the lateral direction, thus making it valid for a wider speed range. More numerical results from this modified KP equation for a ship in a wider speed range were reported in Chen & Sharma (1994b) and compared with old model experiments of Graff et al. (1964) on a Taylor Standard Series hull as well as with new tests on a Series 60 hull. It was concluded that the method based on nonlinear shallow-water wave theory holds enough precision for the practical ship problem if higher-order effects in the near field are taken into account as indicated above.
Extension of the theory to the case of asymmetric ship motion also proved useful. The corresponding computer codes enabled us to treat a ship moving parallel to the channel axis off-center and/or at a drift angle. With vertical sidewalk this configuration is mathematically equivalent to a catamaran moving in a channel of twice the width. Numerical results were reported in Chen & Sharma (1994a). The calculated wave resistance, lateral force, yaw moment, sinkage and trim agreed very well with towing tank measurements on a Series 60 model hull both in off-center and in oblique motion, except for the lateral force and yaw moment in oblique motion at higher speeds. Especially the significant wave resistance reduction in the supercritical off-center case led us on to the discovery of superconductive ship-channel geometries marked by no trailing waves and
zero wave resistance, see Chen & Sharma (1995). More calculations for a projected catamaran passenger ferry were earned out by Jiang, Sharma & Chen (1995) with the same computer program and satisfactory agreement with measurements previously done by Heuser (1973) in the Duisburg Model Tank was obtained for a wide range of speed.
The idea of shallow channel superconductivity is not merely of academic interest but also of practical value. One of the authors (XNC) further exploited the asymmetric theory and invented a catamaran form with cambered hulls that theoretically has zero wave resistance. The hulls are so designed that no waves exist in the outside domain and in the wake of the catamaran for a certain depth Froude number larger than unity. This 100% wave-resistance elimination is possible in shallow water independent of channel width and sidewalls. As regards absolute speed, a depth Froude number U=1.5 in inland or coastal waters of 5–20 m depth corresponds to ship speeds ranging from 37.8 to 75.6 km/h, which are well within the range of present technical feasibility and economic interest. A German patent for this concept has been applied for. Details will be reported separately in the future.
Here, a few comments on the exciting topic of zero wave resistance are in order. Naval architects have always striven for ships with little waves. It would be a dream to build a ship without waves. Bow bulbs and submerged wings attached to ship hulls are good examples of devices conceived to achieve mutual cancellation of waves originating from different sources. In principle, ship waves can be even completely eliminated within linear theory. Several interesting theoretical proposals have been made recently by Tuck (1989), Tuck & Tulin (1992), and Tulin & Oshri (1994). The experimental investigation of Mori (1993) is also worth mentioning. But to our knowledge the idea of superconductive ships in shallow water has never been demonstrated or proposed before, even in the linear regime. Intuitively speaking, since wave dispersion is weaker in shallow water, the interference between waves becomes more effective than in deep water, specially in the supercritical range, where there are even nonlinear characteristic wave solutions. In this sense zero wave-resistance ships in shallow water are more feasible.
In this paper, we still concentrate on theoretical studies and develop a shallow water wave theory specially for ships symmetrically moving at supercritical speeds. First, we summarize the linear and nonlinear concepts of a superconductive channel already described in detail by Chen & Sharma (1995). The nonlinear solution was constructed from a two-soliton solution of a standard KP equation (Mei 1976). Then we report several new developments. The standard KP equation is believed to be valid only in a near-critical speed range, so we begin our study here with an extended KP equation which holds for a wider speed range because higher-order transverse derivatives are taken into account. Although it lacks a useful property of the original KP equation, namely, an exact and explicit N-soliton solution, yet its single-soliton solution is still simple to find.
The main body of this paper comprises the following four steps: (i) For a ship in horizontally unbounded shallow water moving at supercritical speed, we reduce the ship wavemaking problem from the boundary value problem of the extended KP equation to an initial value problem of the KdV equation without loss of precision. The slowly varying transverse variable Y plays the same role as slowly varying time in the standard KdV equation. It is not surprising that for almost unidirectional free waves the stationary KP equation, or more generally the Boussinesq equations, can be reduced to a KdV equation. But it is rather astonishing that for arbitrary ship hulls the wave generation problem can be reduced to a KdV initial value problem, which can be solved so easily. (ii) The solution of interacting solitons moving in different directions is vital to the construction of superconductive ship hullforms. Fortunately, this interaction is weak in the sense of Miles (1977), which means that the interaction time is short. We show how to find an approximate solution. (iii) We construct a fore-and-aft symmetric superconductive hullform from the solution of two identical solitons in the same way as in the previous paper. Moreover, we construct a fore-and-aft asymmetric superconductive hullform from the N-soliton solution. (iv) Finally, we propose a heuristic method for improving the precision of various shallow-water wave models. Based on the fact that the wave pattern depends mostly on the dispersion relation, we compare the exact stationary dispersion relation in finite-depth water with the dispersion relations of various approximate shallow-water wave equations. As a consequence we introduce a speed-dependent coefficient into the equation and obtain a heuristic model whose dispersion relation is almost equal to the exact one. Hence, it is expected that this model will yield better results in applications to the ship wavemaking problem, specially in the superconductive mode.
RECAPITULATION OF PREVIOUS SOLUTIONS OF CHANNEL SUPERCONDUCTIVITY
Originally, the idea was inspired by the numerical cum experimental result that the wave resistance at supercritical speeds is significantly reduced as the ship track is moved off the centerline
and brought closer to one of the channel sidewalls. For the Series 60, block 0.6 hull at depth Froude number 1.3 the reduction of wave resistance reaches 30% in both calculation and experiment (Chen & Sharma 1994a). The mechanism of this effect becomes clear as we directly see the calculated ship wave pattern. The bow wave (elevation) on the near-wall side is reflected by the channel sidewall and almost cancels the stern wave (depression) on the far-wall side. Naturally, one is tempted to try moving the far wall also close to the ship so that the opposite pair of bow and stern waves would also nearly cancel itself. It works. By numerical experiment we obtained 75% wave resistance reduction in an optimal narrow channel for the Series 60 hull (Chen & Sharma 1995).
Stimulated by this success we sought a fuller theoretical understanding of this intriguing phenomenon and discovered (Chen & Sharma 1995) that the wave resistance of a ship at supercritical speed in a channel can be made to vanish totally not only in linear shallow-water wave approximation (Tuck 1966) but also in a more accurate nonlinear theory (Mei 1976). In the linear analysis we showed that the wave resistance becomes zero for a suitable combination of body speed, water depth and channel width if the afterbody geometry is adapted to an arbitrary forebody according to a simple geometric rule. Further, we extended the idea by considering the standard stationary Kadomtsev-Petviashvili equation (stationary 2D KdV equation, Mei 1976). By exploiting its well-known two-soliton solution we still obtained a zero-wave-resistance ship, albeit with strong restrictions on body geometry. Here, we present a new graph to show this solution.
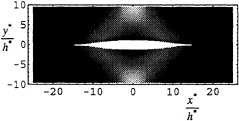
Fig. 1 The localized diamond-shaped wave pattern generated by a superconductive ship hull in the case of U=1.5, A=0.1 and x1=10 (Chen & Sharma 1995).
REDUCTION TO KdV EQUATION
We begin our study with the mathematical model as formulated in Chen & Sharma (1994a, Eq. 19). Here only the symmetric and steady flow is considered,
(1)
with the boundary condition at the ship location,
(2)
where ε is a smallness parameter that is defined as the ratio of typical wave amplitude to water depth. Eq. (1) is the stationary extended KP equation that holds for a wide speed range and is precise to the same order as the Boussinesq equations. If the higher order terms of the transverse derivatives are neglected, it becomes the standard KP equation (Mei 1976). In the boundary condition (2) the higher order terms are neglected for the sake of mathematical simplicity.
For supercritical speed U>1 and ![]()
![]() we can apply a characteristic transformation for y>0:
we can apply a characteristic transformation for y>0:
(3)
Then via
Equations (1) and (2) become
(4)
for Y >0, and
(5)
It is clear that the problem is a standard initial-value problem of the KdV equation if we set u=φξ. The variable Y plays exactly the same role as time in the original KdV equation. All solutions of the KdV equation are approximate solutions of the extended KP equation, specially the N-soliton solution.
This reduction is so wonderful that the problem can be solved even analytically for certain hullforms S(x) by the well-known inverse scattering method and, in any case, numerically for arbitrary hullforms without any difficulty. Specially the forebody of a ship can emit either single or multiple oblique solitons, while the afterbody generates undulating
dispersive waves. We directly employ some examples given in Drazin & Johnson (1989) to explain these phenomena. Via a transformation
Eq. (4) becomes the standard form of KdV (4.7) in Drazin & Johnson (1989). So now if the “initial condition” is taken as
i.e., the forebody is of the form:
then from this initial single-peak wave packet N oblique solitons will evolve asymptotically as Y→ ∞. From (4.36) in Drazin & Johnson (1989) we have the detailed solution for N=2 as xo =0:
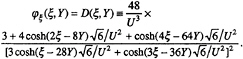
(6)
D(ξ,Y) here means a double-soliton solution of the KdV equation. Its asymptotic wave form for Y →+∞ can be given as
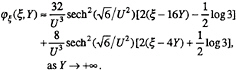
(6‘)
Mei (1976) found a forebody that generates a single oblique soliton. The method presented here will yield many forms that generate N solitons.
In the afterbody we have dS(x)/dx>0, so φξ(ξ,0)<0. Then the solution of the KdV equation (4) will develop without the emergence of a soliton. The initial wave packet will collapse and degenerate into a wave train which disperses into ξ<0. As an example we can see Fig.4.8 in Drazin & Johnson (1989, p.85). This is why we usually see dispersive undulating waves instead of a soliton in the wake.
We conclude that as a ship moves at supercritical speed in horizontally unbounded shallow water its forebody can generate oblique solitary waves which extend to infinity along their characteristic lines while its afterbody generates an undulating wave train which disperses into ξ<0.
APPROXIMATE SOLUTION OF WEAK INTERACTION OF SOLITONS
As is generally known, the KdV equation holds only for unidirectional waves. So the reduced KdV equation (4) is not valid for the interaction of waves in two different directions, specially for the reflection of a solitary wave by a channel sidewall. So we have to deal with such problems by means of the original Eq. (1). In the following, we develop a technique for constructing approximate solutions of arbitrary solitons moving in two different directions.
Since the interaction of solitons in two different directions is weak in the sense of Miles (1977), i.e., the interaction period is short, we can assume that the solution of (1) is of the form:
φ(x,y)=F(ξ+εσ1(η,Y),Y)+ G(η+εσ2(ξ,Y),Y), (7)
with
(8)
where F and G are solitons propagating in different directions and εσ1, εσ2 are the phase functions. Substituting (7) into (1) and neglecting higher order terms, intermediate calculation
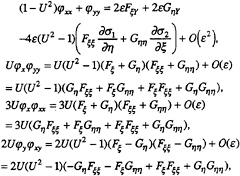
yields, within the precision of the original equation,
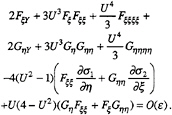
(9)
Since F(ξ,Y) and G(η,Y) are asymptotic soliton solutions, they satisfy the following KdV equations, respectively,
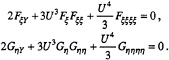
If the small phase shifts εσ1, εσ2 are inserted into F and G as in Equation (7), they are still approximate solutions of the above KdV equations, respectively. If we now choose
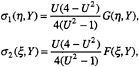
(10)
we have a complete approximate solution of (9) or (1) in the form (7).
σ1 and σ2 will change signs as U increases from U<2 to U>2. Specially at U=2, σ1=σ2=0, i.e., the solitons interact without phase shift. This is because the term φyφxy produces a negative phase shift during soliton interaction that cancels the positive phase shift caused by the terms φxφxx and φxφyy. To our knowledge, this is a new phenomenon in solitons. This may be due to the fact that one usually does not deal with the term φyφxy. We further note that F and G are not necessarily single soliton solutions, they can also be multiple solitons or even undulating dispersive wave solutions of the KdV equation.
We leave the task of solving for the N-soliton interaction to the next section and show here only the simplest example, namely, the two single-soliton interaction. The single-soliton solution of the KdV equations are:
Fξ(ξ,Y)=A sech2k1(ξ–aY)
and
So the approximate solution becomes
φx(x,y)=Fξ(ξ+εσ1(η,Y),Y)+Gη(η+εσ2(ξ,Y),Y)
=A sech2k1(ξ–aY+εσ1)+ B sech2k2(η+bY+εσ2),
where
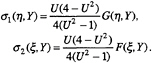
This solution is equivalent to the solution of weak interactions obtained by Miles (1977). The corresponding fore-and-aft symmetric hullform can be derived from the boundary condition (2).
SUPERCONDUCTIVE SHIP HULLFORM DERIVED FROM THE N-SOLITON INTERACTION SOLUTION
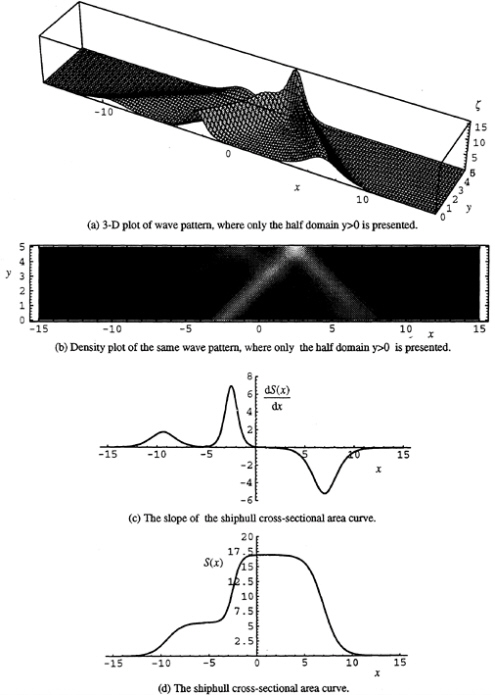
Now we construct a superconductive hullform and its associated wave pattern in terms of an N-soliton solution. For simplicity we take U=2, at which the phase shift is zero. Then according to (7)
φx(x,y)=Fx(x,y)+Gx(x,y) for U=2, (11)
where for y>0,
and D(ξ,Y) was given in (6). The wave elevation to first order is
ς(x,y)=Uφx(x,y). (12)
We can easily check that the boundary condition on the sidewall is satisfied, i.e.,
According to the boundary condition (2), the hullform can be expressed approximately as,
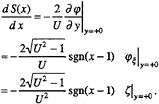
(13)
We select round parameter values ε=0.08, x1=7 and w=10 and display the results (12) and (13) in Fig. 2. The parameter values are so chosen that the phenomenon of interaction can be clearly observed. Consequently, the resulting ship length is very exaggerated. E.g., if we let L=3x1 here, then ![]() which is simply unrealistic. But it is not difficult to construct realistic hullforms by suitably selecting parameter values. In Fig.2 (a, b) we see that the wave hump at the forebody evolves into two solitons along a characteristic direction and the evolution is continued after reflection by the sidewall along another direction. Thus two solitons reach the afterbody. For an afterbody determined by (13) no additional waves are generated and radiated out. The slope of the sectional area curve and the cross-sectional area itself are shown in Fig.2 (c, d). The ship generates no waves in the wake; therefore, it does not experience any wave resistance.
which is simply unrealistic. But it is not difficult to construct realistic hullforms by suitably selecting parameter values. In Fig.2 (a, b) we see that the wave hump at the forebody evolves into two solitons along a characteristic direction and the evolution is continued after reflection by the sidewall along another direction. Thus two solitons reach the afterbody. For an afterbody determined by (13) no additional waves are generated and radiated out. The slope of the sectional area curve and the cross-sectional area itself are shown in Fig.2 (c, d). The ship generates no waves in the wake; therefore, it does not experience any wave resistance.
Unlike Chen & Sharma (1995), the present hullform is obviously fore-and-aft asymmetric. The original problem has a built-in mathematical symmetry which implies that if φ(x,y) is a solution of (1) and (2) for S(x), then –φ(–x,y) is a solution for S(–x). It means that the ship is superconductive going both ways, i.e., forward or backward. The paradoxical equality of wave resistance in forward and backward motion seems to apply to ideal-fluid wavemaking in general.
HEURISTIC IMPROVEMENT OF THE PRECISION OF SHALLOW-WATER WAVE MODELS
There are various shallow-water wave models available for the ship wavemaking problem. One might naturally ask which one is better than others. It is difficult to answer this question intuitively. For example, one may believe that the Boussinesq equations would be better than the KP equation since the KP equation is obtained from the former by neglecting higher order terms. But it is not really true according to our studies. The main deficiency of the shallow-water wave models in comparison to the exact finite-depth wave theory is the loss of higher order dispersion effect, which is not small in the off-critical cases. (On the other hand, higher order nonlinearities are also neglected; but this is permissible if the ship is really slender enough.) The wave pattern depends largely on the dispersion relation. Any deficiency will distort the wave pattern from its true form, which is crucial for superconductivity since it is required to predict the precise position where the reflected bow wave meets the afterbody. A reasonable method to determine which model is better in its linear part would be to compare the exact stationary dispersion relation in finite-depth water with the approximate dispersion relations of various linearized shallow-water wave equations. One can also heuristically introduce speed-dependent coefficients into the equation and obtain an even better model of which the dispersion relation is almost identical to the exact one.
Approximate and Exact Dispersion Relations
We study here two dispersion relations of stationary shallow-water wave models. One comes from the extended KP equation (1). This dispersion relation can be seen as Boussinesq's. The other comes from the standard KP equation, i.e., Eq.(1) without the term φxxyy. By setting the solution as a free-wave mode, i.e., φ ![]() exp(ikxx+ikyy), we can obtain dispersion relations from the linearized stationary equation (1) with and without the term φxxyy, respectively,
exp(ikxx+ikyy), we can obtain dispersion relations from the linearized stationary equation (1) with and without the term φxxyy, respectively,
U2 cos2θ=1/[1+εk2/3], (14)
U2 cos2θ=1/[1+(εk2/3)cos2θ]. (15)
where k is the circular wave number, U is the depth Froude number and θ is the direction of wave propagation measured from the x-axis, i.e. kx=kcosθ, ky=ksinθ.
The exact stationary dispersion relation in finite-depth water is known to be
(16)
The well-known Kelvin ship-wave pattern can be constructed from this dispersion relation by the method of stationary phase. The parameter ε just plays the role of a scale that has no sense in linear equations because if we transform the wave number
back to its dimensional form, i.e., ![]() ε is eliminated from (14–16). Equation (16) is now expanded as
ε is eliminated from (14–16). Equation (16) is now expanded as
U2 cos2θ=1/[1+εk2/3– ε2k4/45+2ε3k6/945–ε4k8/4725+–···].
We see that (14) and (15) are good approximations of (16) for small ε. Even if ![]() the error due to the remaining terms that stand in the lower line is only about 2%. But the wave number of elementary waves generated by a shiplike disturbance theoretically ranges from zero, or a certain positive value, up to infinity. The wave number is a function of U and varies with θ. When θ approaches its upper limit π/2, for so-called divergent waves, the wave number
the error due to the remaining terms that stand in the lower line is only about 2%. But the wave number of elementary waves generated by a shiplike disturbance theoretically ranges from zero, or a certain positive value, up to infinity. The wave number is a function of U and varies with θ. When θ approaches its upper limit π/2, for so-called divergent waves, the wave number ![]() will be much larger than one. Thus the approximate dispersion relations (14) and (15) will not be so good at large θ. Although the high-θ. waves contribute relatively little to wave resistance, the wave pattern itself would be somewhat distorted.
will be much larger than one. Thus the approximate dispersion relations (14) and (15) will not be so good at large θ. Although the high-θ. waves contribute relatively little to wave resistance, the wave pattern itself would be somewhat distorted.
Comparison of Dispersion Relations
Figs.3–6 show the numerical comparison. Surprisingly, we find that the KP dispersion relation is better than Boussinesq's in the subcritical range, as seen in Fig.3 and 4 for U=0.7 and 1, respectively. This is in line with the fact that in the subcritical range our numerical ship wave patterns based on the KP equation, i.e., on Eq. (1) without the term φxxyy, look more realistic than those based on the extended KP equation (1).
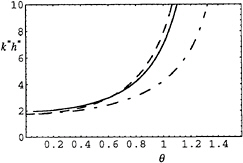
Fig. 3 Comparison of dispersion relations at U=0.7, where the exact one is represented by a solid line, KP's by a dashed line and Boussinesq's by a dot-dashed line.
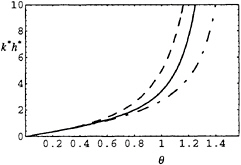
Fig. 4 Comparison of dispersion relations at U=1, where the exact one is represented by a solid line, KP's by a dashed line and Boussinesq's by a dot-dashed line.
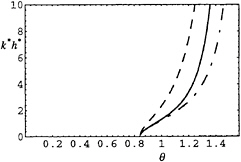
Fig. 5 Comparison of dispersion relations at U=1.5, where the exact one is represented by a solid line, KP's by a dashed line and Boussinesq's by a dot-dashed line.
Improvement of the extended KP equation
We introduce a coefficient to the term φxxyy in the following way,
(17)
This modification will yield a very good dispersion relation in the entire speed range compared with the exact one. The dispersion relation of the linear part of (17) is
U2 cos2θ=1/[1+(cos2θ+α sin2θ)εk2/3]. (18)
We choose a smooth function for α(U)
as depicted in Fig.6. This leads to the dispersion relation shown in Fig.7.
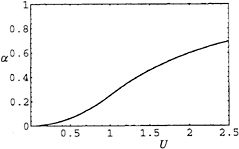
Fig. 6 The heuristically introduced coefficient α(U)
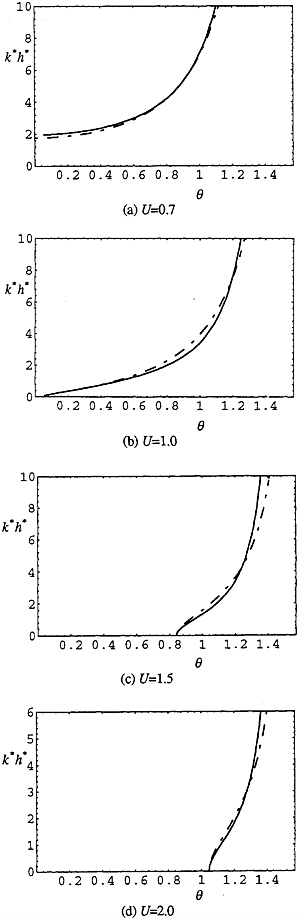
Fig. 7 The dispersion relation of the extended KP equation after introduction of a coefficient α(U) see (17), compared with the exact one, where the former is represented by dot-dashed lines and the latter by solid lines.
We believe that equation (17) will yield better results, specially less distorted wave patterns, than other shallow-water wave models. Certainly, one can also obtain superconductive solutions from it just by including the coefficient α appropriately.
CONCLUDING REMARKS
Although the superconductivity demonstrated here is only achieved for a monohull in a rather narrow channel, the idea can be further exploited to construct a more practical superconductive catamaran no longer dependent on sidewall reflection and channel width. A crucial feature is that although the catamaran as a whole is port-and-starboard symmetric, each individual hull has to be carefully cambered so that all waves are contained within the space between the two hulls. This requires our theory of asymmetric motion as presented at the last Symposium (Chen & Sharma 1994a). We hope to
undertake further efforts in this direction by analysis, computation and tank experiment.
ACKNOWLEDGMENT
One of the authors (X.-N. C.), who is being supported by a research grant of the German Federal Ministry of Research (BMBF Project SC7STU), thanks his supervisor Prof. Dr. K.Kirchgässner for his encouragement.
REFERENCES
Chen, X.-N. and Sharma, S.D. 1992 “A slender ship moving at a near-critical speed in a shallow channel, ” Presented at a poster-session of the 18th International Congress of Theoretical and Applied Mechanics, Haifa, Israel and published in Journal of Fluid Mechanics , Vol. 291 (1995), pp. 263–285.
Chen, X.-N. and Sharma, S.D. 1994a “Nonlinear theory of asymmetric motion of a slender ship in a shallow channel,” Twentieth Symposium on Naval Hydrodynamics, Santa Barbara, CA, Preprints of Tuesday Sessions, pp.134–154.
Chen, X.-N. and Sharma, S.D. 1994b “A slender ship moves in a shallow channel,” International Conference on Hydrodynamics, Wuxi, China.
Chen, X.-N. & Sharma, S.D. 1995 “Superconductivity of shallow channels for ships at supercritical speeds,” Submitted to J. Fluid Mechanics.
Choi, H.-S., Bai, J.-W. and Cho, I.-H. 1990 “Nonlinear free surface waves due to a ship moving near the critical speed in a shallow water,” Proceedings of 18th Symposium on Naval Hydrodynamics, Ann Arbor, pp. 173–189.
Choi, H.S. and Mei, C.C. 1989 “Wave resistance and squat of a slender ship moving near the critical speed in restricted water,” Proceedings of 5th International Conference on Numerical Ship Hydrodynamics, pp.439–454.
Drazin, P.G. & Johnson, R.S. 1989 Solitons: an Introduction. Cambridge University Press.
Eggers, K. 1955 “Über Widerstandsverhältnisse von Zweikörperschiffen,” Jahrbuch der Schiffbautechnischen Geselschaft, Vol. 49, pp. 516– 537.
Ertekin, R.C., Webster, W.C. and Wehausen, J.V. 1986 “Waves caused by a moving disturbance in a shallow channel of finite width,” Journal of Fluid Mechanics, Vol. 169, pp. 275–292.
Graff, W. 1962 “Untersuchungen über die Ausbildung des Wellenwiderrstandes im Bereich der Stauwellengeshwindigkeit in flachem, seitlich beschränktem Fahrwasser,” Schiffstechnik, Vol. 9, pp. 110–122.
Graff, W., Kracht, A. and Weinblum, G. 1964 “Some extensions of D.W.Taylor's Standard series,” Transactions of Society of Naval Architects and Marine Engineers, Vol. 72, pp. 374–401.
Helm, K. 1940 “Effect of canal depth and width on ship resistance (in German),” Hydrodynamische Probleme des Schiffsantriebs, Teil 2, Ed. G.Kempf, Verlag Oldenbrurg, Munich and Berlin, pp.144–171.
Heuser, H. 1973 “Systematic investigation of the resistance of twin-hull ships (in German),” Versuchsanstalt für Binnenschiffbau e.V Duisburg (VBD) Report, No. 661a.
Huang, D.B., Sibul, O.J., Webster, W.C., Wehausen, J.V., Wu, D.-M. and Wu, T.Y. 1982 “Ships moving in the transcritical range,” Proceedings of Conf. on Behaviour of Ships in Restricted Waters, Varna, Bulgaria, Vol.2, pp.26–1– 26–10.
Jiang, T., Sharma, S.D., and Chen, X.-N. 1995 “On the wavemaking, resistance and squat of a catamaran moving at high speeds in a shallow water channel,” Proceedings of Third Int. Conf. on Fast Sea Transportation, Lübeck-Travenmünde, Germany, Vol. 2, 1313–1325.
Katsis, C., and Akylas, T.R. 1987 “On the excitation of long nonlinear water waves by a moving pressure distribution. Part 2. Three-dimensional effects,” Journal of Fluid Mechanics, Vol. 177, pp. 49–65.
Kinoshita, M. 1946 “On the restricted-water effect on ship resistance,” Japan Society of Naval Architects, Vol. 150, pp. 181–187.
Kirsch, M. 1966 “Shallow water and channel effects on wave resistance,” Journal of Ship Research, Vol. 10, pp.164–181.
Lea, G.K., and Feldman, J.P. 1972 “Transcritical flow past slender ships,” Proceedings of 9th
Symposium on Naval Hydrodynamics, pp.1527–1542.
Mei, C.C. 1976 “Flow around a thin body moving in shallow water,” Journal of Fluid Mechanics, Vol. 77, pp. 737–752.
Mei, C.C. 1986 “Radiation of solitons by slender bodies advancing in a shallow channel, ” Journal of Fluid Mechanics, Vol. 162, pp. 53–67.
Mei, C.C. and Choi, H.S. 1987 “Forces on a slender ship advancing near the critical speed in a wide canal,” Journal of Fluid Mechanics, Vol. 179, pp. 59–76.
Miles, J.W. 1977 “Obliquely interacting solitary waves,” Journal of Fluid Mechanics, Vol. 79, pp.157–169.
Mori, K.-H. 1993 “Resistance and lifting force of a submerged body with a wing producing a downward lifting force,” Proc. 8th Int. Workshop on Water Waves and Floating Bodies, St. John's, Newfoundland, Canada.
Thews, J.G. and Landweber, L. 1935 “The influence of shallow water on the resistance of a cruiser model, ” US Experimental Model Basin, Navy Yard, Washington, DC, Rep. no. 408
Thews, J.G. and Landweber, L. 1936 “A thirty-inch model of the SS Clariton in shallow water,” US experimental Model Basin, Navy Yard, Washington, DC, Rep. no. 414.
Tuck, E.O. 1966 “Shallow water flows past slender bodies,” Journal of Fluid Mechanics, Vol. 26, pp. 81–95.
Tuck, E.O. 1978 “Hydrodynamic problems of ships in restricted waters,” Annual Review of Fluid Mechanics, Vol. 10, pp. 33–46.
Tuck, E.O. 1989 “A submerged body with zero wave resistance,” Journal of Ship Research, Vol. 33, pp.81–83.
Tuck, E.O. & Tulin, M.P. 1992 “Submerged bodies that do not generate waves,” Proc. 7th Int. Workshop on Water Waves and Floating Bodies, val de Reuil, France.
Tulin, M.P. & Oshri, O. 1994 “Free surface flows without waves; Applications to fast ships with low-wave resistance,” Twentieth Symposium on Naval Hydrodynamics, Santa Barbara, CA, pp. 74–86.
Wu, De-Ming and Wu, T.Y. 1982 “Three-dimensional nonlinear long waves due to moving surface pressure, ” Proceedings of 14th Symposium on Naval Hydrodynamics, Ann Arbor, Mich., pp.103–129.
DISCUSSION
L.J.Doctors
University of New South Wales, Australia
In the verbal presentation of the research, you displayed a graph comparing the resistance of a monohull and a catamaran as a function of the speed. Assuming the displacement of the two vessels is the same (implying that the beam of the demihull is one half that of the monohull), then the resistance of the catamaran should asymptotically approach one half that of the monohull at high speeds. However, this feature does not appear on the graph. Could you please clarify this point?
AUTHORS' REPLY
It is true that if you compare a catamaran with an affine monohull of equal length, draft, and displacement, but necessarily, twice the beam, then as the hull separation tends to infinity, which is effectively the case for infinite depth Froude number, the wave resistance of the catamaran in linear theory asymptotically approaches one-half that of the monohull. However, following Heuser (1973), we compared the specific resistance of our catamaran with that of a monohull identical to one of the component hulls so that the displacement of the catamaran was twice that of the monohull. In this case, as the depth Froude number and, hence, the effective separation tends to infinity, the specific wave resistance of the catamaran should asymptotically equal exactly that of the monohull, even in nonlinear theory since the interference effects disappear. The same should apply, approximately, also to the specific viscous resistance. Our measurements as well as calculations, as shown, for example, in Fig.7 of Jiang, Sharma, and Chen (1995) are compatible with this requirement. The practical implication is that the theoretical wave resistance reduction achieved for a finite design depth Froude number by exploiting the interference effect between the wave systems of the component hulls of a catamaran does not extend up to arbitrarily high depth Froude numbers.