Nonlinear Water Wave Computations Using a Multipole Accelerated, Desingularized Method
S.Scorpio, R.Beck (University of Michigan, USA), F.Korsmeyer (Massachusetts Institute of Technology, USA)
ABSTRACT
Nonlinear inviscid water wave computations are performed using an Euler-Lagrange approach to solve a boundary integral formulation. The integral equations are solved numerically at each time step using a desingularized method with multipole acceleration. Solutions obtained using multipole acceleration can require as little as O(N) effort and O(N) storage whereas conventional methods require O(N.2) effort and storage. Multipole methods are applicable to a variety of physical simulation problems in astrophysics, plasma physics, molecular dynamics, electrostatics, and fluid dynamics. The application of multipole methods to the numerical solutions of these problems has the potential of significantly improving computational efficiency.
INTRODUCTION
The Euler-Lagrange method is due to Longuet-Higgens and Cokelet (1976) who present results for inviscid free surface wave problems in two-dimensions. The method requires at each time step: 1) The (Eulerian) solution of a linear boundary value problem and 2) the (Lagrangian) time integration of the nonlinear free surface boundary conditions. In the implementation of this method, it is important to have an accurate and stable time stepping procedure. However, it is the solution of the linear boundary value problem which requires most of the computational effort. Green 's theorem is used to derive the indirect integral formulation of the problem. This equation is discretized by distributing fundamental singularities over a surface referred to as the “integration surface ” and enforced at collocation points on the physical surface of the computational domain referred to as the “control surface.” In conventional formulations, the integration and control surfaces coincide. This results in singular kernels which require special treatment by considering only their principal part. By moving the integration surface slightly off the control surface, the kernels are desingularized, hence the term “desingularized method.” This method, probably first introduced in panel methods by Webster (1975), has several computational advantages over the singular formulation. Because of the nonsingular kernels, no special treatment is needed when evaluating the integrals so that simple numerical quadratures may be used. This removes the necessity of evaluating transcendental functions which appear in the singular formulation. In fact, the desingularized formulation becomes even simpler by replacing the singularity distribution with isolated singularities. These can be sources or higher order singularities such as dipoles. When desingularized isolated singularities are used, the necessity to evaluate surface integrals is eliminated and is replaced by simple summations. This leads to fast, stable free surface computations. Examples of desingularized, fully nonlinear free surface computations are given in Cao et al. (1991), Beck et al. (1993), and Beck et al. (1994).
The numerical approximation of the integral equations results in a linear system of equations. For free surface problems, the linear system consists of a matrix of coefficients (representing the influence of sources on control points in the desingularized method) multiplied by a vector of unknown source strengths. The matrix/vector product must equal a known boundary condition. Solution of this linear system by an iterative method will require O(N2) work and storage for the tasks of filling the matrix once and applying the matrix to a vector at each iteration. With large numbers of unknowns, as is required to discretize three-dimensional domains (O(104)), solutions by iterative solvers are too expensive for practical computations on workstations. However, the efficiency of an iterative, solver can be im-
proved significantly when accelerated by a multipole algorithm.
Multipole expansions result when Laplace's equation is solved in spherical coordinates using the method of separation of variables. The multipole algorithm approximates the influence of groups of far field sources with expansions, thereby replacing the influence coefficient matrix. In a multipole-accelerated iterative solver, the matrix/vector product required at each iteration (normally O(N2) cost) is replaced by a multipole approximation (O(N) cost). Greengard (1987) presents an efficient algorithm for the application of multipole expansions to potential problems. Nabors et al. (1994) presents a slightly different approach developed for electrostatics problems, and Korsmeyer et al. (1993) extend that approach to Laplace problems in general, particularly the Green's theorem formulation of free surface problems.
In the following sections, we present formulations for the boundary value problem for the fluid velocity potential, the desingularized integral equations for the perturbation potential, a domain decomposition solution technique, and the multipole algorithm. These are followed by numerical results. The efficiency of the multipole algorithm is evaluated by solving a fictitious boundary value problem for the Rankine source strength using an iterative solver with and without multipole acceleration. Next, a new method for including fully nonlinear incident waves in the forward speed problem is introduced. Finally, these methods are applied to a submerged submarine moving with constant forward speed under incident waves.
PROBLEM FORMULATION
Boundary Value Problem for the Fluid Motion
The fluid is assumed inviscid and incompressible. The problem is started from rest so that the flow remains irrotational. This implies that the fluid velocity field can be described by a scalar potential, Φ. Consider a vessel floating on a free surface and translating with speed ![]() (t) with respect to a right handed space fixed coordinate system. The z=0 plane defines the calm water level and the x–z plane is coincident with the centerplane of the vessel. Since we are interested in ships, we want to concentrate on the “forward speed ” case which is
(t) with respect to a right handed space fixed coordinate system. The z=0 plane defines the calm water level and the x–z plane is coincident with the centerplane of the vessel. Since we are interested in ships, we want to concentrate on the “forward speed ” case which is ![]() (t)=(U(t),0,0) where U(t) is in the negative x direction. The total velocity potential describing the fluid motion is then,
(t)=(U(t),0,0) where U(t) is in the negative x direction. The total velocity potential describing the fluid motion is then,
(1)
where ![]() is the perturbation potential and
is the perturbation potential and ![]() =(x, y, z). Both potentials Φ and
=(x, y, z). Both potentials Φ and ![]() satisfy Laplace's equation in the fluid domain.
satisfy Laplace's equation in the fluid domain.
(2)
In order to define a well posed problem, boundary conditions must be specified on all surfaces surrounding the fluid domain. Since the forward speed part of the potential is known, the boundary conditions can be set up in terms of the unknown perturbation potential with respect to the translating coordinate system in the centerplane of the vessel. On the body wetted surface (SH) and on the bottom (SB) the boundary conditions are,
(3)
and
(4)
where ![]() is the unit normal out of the fluid. VB is the velocity of the body surface. On the far field surface at infinity (S∞) the boundary condition is,
is the unit normal out of the fluid. VB is the velocity of the body surface. On the far field surface at infinity (S∞) the boundary condition is,
(5)
Due to the fact that only a finite amount of the free surface can be modeled, this far field condition is usually treated by either an approximate radiation condition, an absorbing beach, walls, or, in some cases, it is ignored and the boundary is left open. If the far field surfaces are truncated with solid walls (SW), the far field boundary condition is then,
(6)
There are two boundary conditions on the free surface (SF), one kinematic and one dynamic. We use a special form of these conditions for following the temporal evolution of nodes on the free surface (see Beck et al. 1994). The kinematic condition is,
(7)
(8)
where z=η(x, y, t) is the free surface elevation. ![]()
![]() is the velocity of free surface nodes where u(t) and v(t) are prescribed horizontal velocities of the nodes. If
is the velocity of free surface nodes where u(t) and v(t) are prescribed horizontal velocities of the nodes. If ![]() then the free surface nodes become material nodes and move with the fluid velocity. Prescribing the horizontal plane motions of the free surface nodes can prevent certain numerical problems such as the piling up of nodes at stagnation points. The disadvantage is that spatial derivatives on the free surface are required. These normally have to be computed using some type of numerical differentiation which is difficult to accomplish accurately. The dynamic free surface boundary condition is,
then the free surface nodes become material nodes and move with the fluid velocity. Prescribing the horizontal plane motions of the free surface nodes can prevent certain numerical problems such as the piling up of nodes at stagnation points. The disadvantage is that spatial derivatives on the free surface are required. These normally have to be computed using some type of numerical differentiation which is difficult to accomplish accurately. The dynamic free surface boundary condition is,
(9)
where ρ is the fluid density, g is the gravitational acceleration, and Pa is the atmospheric pressure.
Mixed Boundary Value Problem for the Perturbation Potential
The boundary value problem defined above has a linear field equation with nonlinear boundary conditions. The method used for the numerical solution of this problem is an Euler-Lagrange time stepping technique. A desingularized boundary integral method is used to solve the mixed boundary value problem for the perturbation potential at each time step. The kinematic and dynamic free surface boundary conditions are then integrated in time.
The mixed boundary value problem for the perturbation potential is determined by solving the Laplace equation in the fluid domain. At each time step ![]() is known on the free surface and ∂
is known on the free surface and ∂![]() /∂n is known on solid boundary surfaces. The boundary conditions are satisfied by distributing Rankine sources on an integration surface. The integration surface is offset a small distance from the problem boundary, i.e. above the free surface and inside the body. Rather than using Green's theorem (the direct method) to from integral equations for the unknown potential, we use an indirect formulation where the potential anywhere in the fluid volume is defined by,
/∂n is known on solid boundary surfaces. The boundary conditions are satisfied by distributing Rankine sources on an integration surface. The integration surface is offset a small distance from the problem boundary, i.e. above the free surface and inside the body. Rather than using Green's theorem (the direct method) to from integral equations for the unknown potential, we use an indirect formulation where the potential anywhere in the fluid volume is defined by,
(10)
where ![]() = (x, y, z) is a point in the fluid domain,
= (x, y, z) is a point in the fluid domain, ![]() = (ξ, η, ζ) is a point on the integration surface, σ(
= (ξ, η, ζ) is a point on the integration surface, σ(![]() ) is the value of the source strength at
) is the value of the source strength at ![]() , G(
, G(![]() ;
; ![]() ) is the Rankine source Green function, and Ω is the integration surface. The Green function for three-dimensional problems is,
) is the Rankine source Green function, and Ω is the integration surface. The Green function for three-dimensional problems is,
(11)
In order to obtain the appropriate Dirichlet and Neumann boundary conditions, we simply enforce (10) on Dirichlet boundaries and multiply (10) by ![]() to obtain a form suitable for Neumann boundaries.
to obtain a form suitable for Neumann boundaries.
(12)
(13)
where,
|
|
= |
given potential on the free surface at |
|
SF |
= |
The free surface |
|
= |
given normal velocity on solid boundaries |
|
|
SB |
= |
all solid boundary surfaces |
After the integral equations are solved, the fluid velocities can be found without the need of numerical derivatives,
(14)
where,
(15)
SOLUTION TECHNIQUES
Domain Decomposition
When using desingularized Rankine sources, the integral equations 12 and 13 reduce to simple summations relating the influence of the source points (![]() ) on the node points (
) on the node points (![]() ) In this case, the integral equations can be written as,
) In this case, the integral equations can be written as,
A·Σ=B (16)
Where A is the influence matrix, Σ is the source strength and B is the appropriate Dirichlet or Neumann boundary condition. The individual terms of the influence matrix A are,
(17)
for nodes on the free surface. And,
(18)
for nodes on the body.
We use a domain decomposition technique to solve the linear system for the source strength Σ. The linear system is written as,
(19)
Here, for example, AFB would represent the influence of sources in the body (B) on nodes on the free surface (F). The decomposed linear system is solved by simply iterating between the solutions for the source strengths ΣF and ΣB.
(20)
There are several advantages to using domain decomposition. The free surface and body may have different grid densities. This will result in poor conditioning of the total A matrix. Whereas the individual matrices AFF and ABB will have better conditioning because they have relatively constant grid densities. For most ship-wave problems, the majority of the nodes are used to discretize the free surface. The number of nodes on the body is often small enough to use an iterative method without multipole acceleration, or even direct factorization. The free surface domain is solved using a multipole algorithm. For the computations contained herein, the multipole algorithm is tailored for solving the free surface domain. This strategy is used to simplify the coding of the algorithm. For problems where the body geometry is complicated requiring large numbers of nodes to resolve the details, it will be necessary to extend the multipole algorithm for use on the body domain.
Multipole Expansions
Writing the Laplace equation in spherical coordinates yields,
(21)
The solution of this equation by separation of variables results in a series of spherical harmonic terms,
(22)
![]() and
and ![]() are the moments of the expansion and
are the moments of the expansion and ![]() (θ,
(θ, ![]() ) are the spherical harmonics. Using the series solution to the Laplace equation, the far field potential due to a collection of near field sources can be expressed in a multipole expansion. Suppose there are k sources with coordinates (ρi,αi,βi), i=1,···, k and strengths σi. Consider a sphere of radius a containing the k sources. Let the center of a multipole expansion be defined as the center of this sphere. We can then express the potential due to the k sources at any point, P(r,θ,
) are the spherical harmonics. Using the series solution to the Laplace equation, the far field potential due to a collection of near field sources can be expressed in a multipole expansion. Suppose there are k sources with coordinates (ρi,αi,βi), i=1,···, k and strengths σi. Consider a sphere of radius a containing the k sources. Let the center of a multipole expansion be defined as the center of this sphere. We can then express the potential due to the k sources at any point, P(r,θ,![]() ), outside of the sphere,
), outside of the sphere,
(23)
where the coefficients of the expansion are given by,
(24)
Likewise, the near field potential due to a collection of far field sources can be expressed in a local expansion. Suppose the k sources now lay outside of the sphere of radius a centered at the origin. The center of a local expansion is defined by the center of the sphere inside which all of the evaluation points (P) lay. The potential due to these sources at any point, P(r,θ,ϕ), inside of the sphere is given by,
(25)
where the coefficients are given by,
(26)
Several theorems are used in the multipole algorithm which involve shifting the origins of multipole and local expansions and the conversion of multipole expansions into local expansions. See Greengard (1987) for the development of these theorems and their error bounds.
Multipole Acceleration
There is a wide variety of N log N algorithms for accelerating the evaluation of N potentials due to N sources, typically these are based on some form of hierarchical panel clustering. The underlying idea is that the potential due to a cluster of panels may be evaluated at some distant point xj by first accumulating the panel influences into a multipole expansion, and then evaluating the single expansion. It is the careful arrangement of the clusters of panels which leads to the N log N efficiency. The fast-multipole algorithm reduces the cost yet further, to order N, by a complementary arrangement of the evaluation points so that accumulated multipole expansions may be transformed to local expansions centered in the clusters of evaluation points, and these expansions are evaluated instead. More specifically, the use of multipole and local expansions is orchestrated by a tree-structured hierarchy of source clusters and evaluation point clusters; as shown in figure 1, multipole expansions for clusters of sources are accumulated from the leaves of the tree to the root, and local expansions are distributed from the root to the leaves for evaluation at collocation points. This is accomplished in order N operations while maintaining a uniform precision as shown by Greengard (1987).
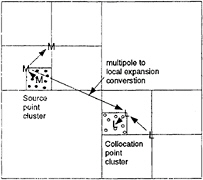
Figure 1: Multipole and local expansion manipulation
Local and multipole expansions must be carefully applied to insure that the potential is accurately approximated everywhere in the problem domain. The structure which makes this possible is the hierarchical partitioning of the domain. Consider the smallest cube which contains the entire domain, that is, all of the sources. We refer to this cube as the level 0 or root cube This parent cube is subdivided into eight child cubes, and the sources are divided among these level 1 child cubes. This process is repeated down to some finest level (the leaves), designated level L. The number of levels, L, is usually selected so that no finest level cube contains more than some fixed small number of sources. After setting up this hierarchical spatial decomposition, the fast multipole algorithm begins with the finest level, where each cube of sources is represented by a multipole expansion about the center of the cube. During an upward pass through the tree to the root, each child cube's multipole expansion is shifted to the child cube's parent's center, to generate a single expansion which represents all of the sources in the parent cube. In an interaction phase, at each level a local expansion is created for each cube by accumulating multipole expansions representing distant cubes at that level. In a downward pass, the local expansions in the parent cubes are shifted to the centers of their children. Finally, in an evaluation phase, the local expansions and direct contributions from nearby sources are evaluated at the points at which the potential is required: the collocation points.
For the computations herein, the multipole algorithm is applied only to the free surface domain. Since the free surface lies more or less in a plane with the elevations representing small deviations, the three-dimensional hierarchical tree structure can be collapsed into a two-dimensional “pancake”. This simplifies some of the logic required in partitioning the domain.
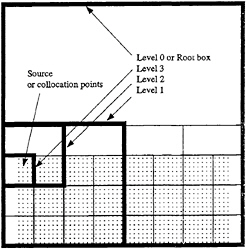
Figure 2: Typical hierarchical tree structure
Figure 2 shows a typical two-dimensional hierarchy. In the desingularized method, the source points are directly above (in the +z direction) the collocation points. This guarantees that a source point and its collocation point will be in the same box. Therefore, the source clusters and evaluation (or collocation) point clusters will have the same hierarchy. The “pancake” hierarchy is oriented in the x-y plane and positioned at the calm water level (z=0).
RESULTS
Multipole Efficiency
A sample problem is set up and solved for the purpose of studying the performance of multipole acceleration. A rectangular area is discretized with equally spaced nodes in the x-y plane. The z-coordinate of the nodes is given a small amplitude cosine distribution. Desingularized sources are placed a small distance (inversely proportional to the local node density) above the nodes. The potential at the nodes is prescribed with a cosine distribution. The source strengths for this fictitious problem are then solved using an iterative solver, GMRES.
For the direct solution, the linear system of equations (eqn. 16) is set up by assembling and storing the matrix of influence coefficients, A. With the right hand side (B=potential) given, the unknown source strength, Σ, is then solved using the GMRES solver. This solution procedure is an O(N2) method because the matrix, A, requires O(N2) storage on the computer and the linear system requires O(N2) computations to solve.
For the multipole solution, the “pancake” hierarchy is set up in the z=0 plane. Each iterate of the GMRES solution is then computed using the multipole algorithm. This solution procedure results in an O(N) method because the matrix A is no longer computed and stored and the multipole algorithm allows the linear system to be solved in O(N) computations.
There is a third alternative to these two solution procedures that might be considered. The linear system can be solved using the direct method without storing the matrix of influence coefficients. Every time an influence coefficient is needed it is simply recomputed. This solution procedure requires O(N) storage and O(N2) computational effort.
The following computations were performed on a DEC alphastation 600 5/266. Figure 3 shows the time required to arrive at the solution by the three methods versus the number of nodes (N) in the linear system. The direct method —no memory refers to the direct method without storing the influence, matrix. This
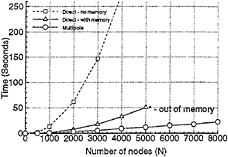
Figure 3: Time requirements
method has the advantage of using very little memory but the time requirements quickly become excessive. The direct method with memory is much faster but the memory requirements become larger than the available memory on the alphastation when N becomes greater than ~5000. The multipole solution is more efficient than either option when N>1000. Significant speed up is attained with multipole acceleration when N becomes very large (O(104)).
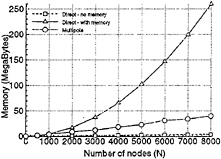
Figure 4: Memory requirements
Figure 4 shows the memory requirements of the three methods. The direct method —no memory requires very little memory but the time requirements ( figure 3) are unreasonable. The direct method—with memory requires the most memory which quickly becomes excessive as N becomes large. The multipole method requires a moderate amount of memory which increases approx-
imately linearly with N.
These results clearly show the advantages of using a multipole solver. The O(N2) methods are severely limited by time and memory requirements with large N. The time and memory requirements for the multipole method increase linearly with N. This allows large problems to be analyzed without a significant computational penalty.
While we have shown that the fast-multipole algorithm is an effective means to accelerating the solution of nonlinear free-surface problems, it should be noted that an apparently more efficient algorithm has been developed recently which may be useful for these problems as well. This algorithm, referred to as the pre-corrected-FFT algorithm, was developed for application to electrostatics problems (Phillips 1994). Rather than using multipole expansions, this algorithm represents distant influences at evaluation points by replacing a cube's cluster of sources with a small number of weighted point singularities located at the corners and on the faces of the cube. The evaluation of the matrix/vector product then consists of the following four steps: The sources distributed on the integration surface are replaced by a uniform grid of sources; the value of the potential is computed on this uniform grid by FFT; this potential is computed at the evaluation points by interpolation; and the nearby interactions are computed directly including the correction for the fact that they have been included inaccurately in the previous two steps. A complexity analysis of this algorithm shows that it has a higher asymptotic cost than the fast-multipole algorithm demonstrated here (Phillips 1995), however in applications using up to order 105 degrees of freedom its actual cost is lower (Nabors et al. 1995). This is due in part to the fact that carefully tuned FFT routines are available for many architectures and distributed computing environments.
Nonlinear incident waves at forward speed
Because boundary conditions are required on all enclosing surfaces for any boundary integral method, the problem of producing fully nonlinear incident waves on a ship moving at forward speed is not trivial. The difficulty arises because computational limitations allow only a portion of the free surface to be modeled. Therefore, a method must be contrived to introduce waves into the computational domain. This is achieved by producing waves in a two-dimensional tank relative to a fixed reference frame Xo-Yo. A small computational window, described in an x-y coordinate system moving relative to the fixed Xo-Yo coordinates, can then be moved through the waves by prescribing the upstream and downstream boundary conditions on the window.
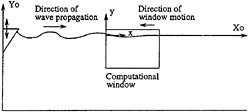
Figure 5: A two-dimensional wave making tank with a moving computational window
Figure 5 shows a two-dimensional tank with a plunger wave maker producing waves in the Xo-Yo reference frame. The plunger wave maker has a 30 degree wedge angle and a prescribed sinusoidal motion in the Yo direction. The computational window containing the ship is then moved through the incident wave field by prescribing ∂![]() /∂n on a vertical “wall” and
/∂n on a vertical “wall” and ![]() and η on the free surface for both the upstream and downstream boundaries. However, for problems where a body is present in the window, the waves passing through the downstream boundary are unknown a priori. Therefore, the downstream boundary condition cannot be specified exactly. In this case, the downstream boundary can be left unspecified, an approximate radiation condition can be applied, or some type of numerical beach strategy may be used. For computations presented here, the boundary is unspecified.
and η on the free surface for both the upstream and downstream boundaries. However, for problems where a body is present in the window, the waves passing through the downstream boundary are unknown a priori. Therefore, the downstream boundary condition cannot be specified exactly. In this case, the downstream boundary can be left unspecified, an approximate radiation condition can be applied, or some type of numerical beach strategy may be used. For computations presented here, the boundary is unspecified.
Figure 6 shows the results of this method in two-dimensions with no ship form included. The computational window is moved at a constant speed through the wave tank by specifying the upstream boundary condition and leaving the downstream boundary condition unspecified. Four cases are studied for windows translating through the incident wave field at varying speeds. The incident waves have wavelength λ and the speed of the computational window is defined by a Froude number based on wavelength, ![]() The wave elevations, η, in the moving window are compared with elevations in the stationary wave tank after the incident waves have been entering the moving window for some time. Because the downstream boundary condition is not applied in the moving window, the wave elevations do not agree exactly. They are, however, quite reasonable. If the downstream boundary had been specified, the waves in the window would agree with the waves in the tank to within graphical accuracy.
The wave elevations, η, in the moving window are compared with elevations in the stationary wave tank after the incident waves have been entering the moving window for some time. Because the downstream boundary condition is not applied in the moving window, the wave elevations do not agree exactly. They are, however, quite reasonable. If the downstream boundary had been specified, the waves in the window would agree with the waves in the tank to within graphical accuracy.
These results indicate that this method produces rea-
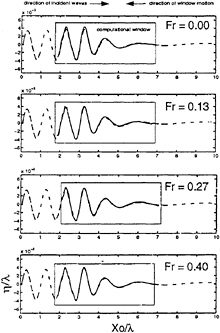
Figure 6: Incident waves in a moving computational window. Solid line—wave elevations in the computational window. Dashed line—wave elevations in the stationary wave tank
sonable waves inside a two-dimensional computational window with no body present. The question of whether the unspecified downstream boundary will produce acceptable results for a three-dimensional problem with a body present is the subject of the next section.
Wave forces on a submerged submarine with forward speed
Two-dimensional plane waves are introduced into a three-dimensional computational window via the method outlined in the previous section. The three-dimensional window is bounded by a vertical wall on the upstream boundary (on which the incident wave boundary conditions are applied), a vertical wall on the outer boundary, a plane of symmetry on y=0, and the free surface. The downstream boundary is left open and the fluid is infinitely deep. A small distance below the free surface an axisymmetric submarine hull form is translating with steady forward speed Uo.
The submarine hull form is described using the following formula from Jackson (1991). The local radius is defined as a function of position forward (rf) and aft (ra) of the parallel middle body.
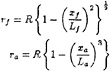
(27)
Where R is the radius of the parallel middle body, Lf and La are the lengths of the forward and after bodies respectively and xf and xa are local coordinates which run from zero at the parallel middle body up to Lf and La. Given the total length of the submarine is L, then the parameters used to describe the submarine are: Lf/L=0.167, La/L=0.389, and R/L=0.046.
The submarine is operating in infinitely deep water at a depth of submergence of Depth/R=2. It is translating in the opposite direction of the incident waves (head seas). Preliminary results for forward speed cases of Fr=0.1 and Fr=0.3 are presented here. The incident waves have frequency ![]() This wave frequency was selected because according to linear theory it produces the maximum mean second order diffraction moment about the center of buoyancy for the Fr=0.1 case.
This wave frequency was selected because according to linear theory it produces the maximum mean second order diffraction moment about the center of buoyancy for the Fr=0.1 case.
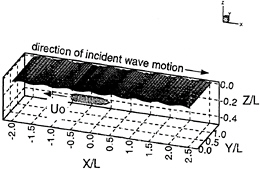
Figure 7: Incident waves with forward speed in a three-dimensional moving window
Figure 7 shows the three-dimensional computational domain. The submarine body is discretized with 251 nodes and the free surface with 2720 nodes. Not shown in the figure are the upstream and outer boundaries which are discretized with 320 and 500 nodes respectively resulting in a total of 3791 nodes. The non-dimensional time step for this problem is ∆t* = ![]()
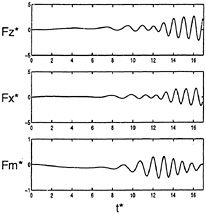
Figure 8: Exciting forces, ![]()
Figure 8 shows the time histories of the exciting forces and moment for the Fr=0.1 case. Here, the non-dimensional time, vertical force, horizontal force and pitch moment about the center of buoyancy are: ![]() Fz*=Fz/ρgA2L, Fx*=Fx/ρgA2L, and Fm*=Fm/ρgA2L2. ρ and g are the density and gravitational acceleration and A is the incident wave amplitude. For this case, linear theory predicts a maximum second order mean shift of
Fz*=Fz/ρgA2L, Fx*=Fx/ρgA2L, and Fm*=Fm/ρgA2L2. ρ and g are the density and gravitational acceleration and A is the incident wave amplitude. For this case, linear theory predicts a maximum second order mean shift of ![]() for the pitching moment due to wave diffraction. The mean shift for the total nonlinear pitching moment computed here is
for the pitching moment due to wave diffraction. The mean shift for the total nonlinear pitching moment computed here is ![]() The difference is due to the fact that in nonlinear computations, the diffraction force cannot be separated from the total force. Therefore, the total moment includes contributions from diffraction, incident waves and steady forward speed. This comparison gives an indication of the relative magnitudes of the total mean shift in the moment and the mean shift due only to diffraction.
The difference is due to the fact that in nonlinear computations, the diffraction force cannot be separated from the total force. Therefore, the total moment includes contributions from diffraction, incident waves and steady forward speed. This comparison gives an indication of the relative magnitudes of the total mean shift in the moment and the mean shift due only to diffraction.
The mean shift in the forces and moment due to steady forward speed in the absence of incident waves is expected to be small due to the low Froude number. For this speed the ratio of wavelength in the Kelvin wake to body length is λ/L ≈ 1/16. The free surface discretization shown in figure 7 is too coarse to resolve the waves accurately. The number of nodes required to adequately resolve the Kelvin wake would be very large. Since the forces resulting from steady forward speed are small relative to the Froude-Krylov forces due to incident waves, we used the coarse grid expecting a small error due to inadequate resolution of the Kelvin wake.
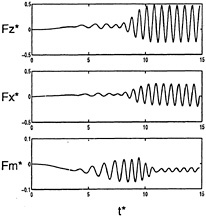
Figure 9: Exciting forces, ![]()
Figure 9 shows the exciting forces and moment for the Fr=0.3 case. Here we see that the increase in encounter frequency has resulted in a significant reduction in the exciting forces. This is expected since linear theory predicts a maximum at Fr=0.1. Notice that the maximum pitching moment occurs before the moment reaches its steady state oscillation. This occurs when the submarine is passing under the wave front. The length of the incident waves in the front are longer due to dispersion. These longer waves are closer to the ship length and therefore create a larger exciting moment.
The results presented for this problem serve to indicate the validity of using the two-dimensional incident waves in the three-dimensional moving window. They do not constitute a complete set of results for the problem of exciting forces on a submerged submarine. The analysis of this problem was not completed by the preprint deadline. We expect to have a more thorough set of results available for presentation at con-
ference time.
CONCLUSIONS
The desingularized method is well suited for computing nonlinear wave-body problems. When combined with a multipole algorithm, solutions can be obtained with a reasonable amount of computational effort and storage on a workstation level computer. This significant improvement in efficiency will help in advancing nonlinear free surface computations from a research project to a usable design tool.
A new method has been presented for introducing nonlinear incident waves into problems with forward speed. This method can be used to produce waves inside both two- and three-dimensional computational windows. The wave exciting forces on a submerged submarine with forward speed results are incomplete. We expect to have a complete set of results for presentation by conference time.
ACKNOWLEDGMENTS
This research was funded by the Office of Naval Research Grant Numbers N00014–93–1–0629, N00014–94–1– 0099 and N00014–95–1–0870 and the University of Michigan/Sea Grant/Industry Consortium on Offshore Engineering. Computations were made in part using a Cray Grant, University Research and Development Program at the San Diego Supercomputer Center.
REFERENCES
1. R.F.Beck, Y.Cao, and T.-H.Lee, “Fully nonlinear water wave computations using the desingularized method,” In Proceedings 6thInternational Conference on Naval Hydrodynamics, University of Iowa, 1993.
2. R.F.Beck, Y.Cao, S.M.Scorpio, and W.W. Schultz,” “Nonlinear ship motion computations using the desingularized method, ” In 20thSymposium on Naval Hydrodynamics, Santa Barbara, California, 1994.
3. Y.Cao, W.W.Schultz, and R.F.Beck, “A three-dimensional desingularized boundary integral method for potential problems,” International Journal of Numerical Methods in Fluids, 11:785–803, 1991.
4. L.F.Greengard, The rapid evaluation of potential fields in particle systems, The MIT Press, Cambridge, Massachusetts, 1987.
5. H.A.Jackson, Submarine design trends, MIT Department of Ocean Engineering, Cambridge, Massachusetts, 1991. Course Notes.
6. F.T.Korsmeyer, D.K.P.Yue, K.Nabors, and J.White, “Multipole-accelerated preconditioned iterative methods for three-dimensional potential problems,” In Proceedings of BEM, volume 15, pages 517– 527, Worcester, Massachusetts, 1993.
7. M.S.Longuet-Higgins and C.D.Cokelet, “The deformation of steep surface waves on water: I. a numerical method of computation,” In Proceedings of the Royal Society of London, volume A350, pages 1–26, 1976.
8. K.S.Nabors, F.T.Korsmeyer, F.T.Leighton, and J.White, “Preconditioned, adaptive, multipole-accelerated iterative methods for three-dimensional first-kind integral equations of potential theory,” SIAM Journal of Scientific Computation, 15(3):713–735, 1994.
9. K.Nabors, J.Phillips, F.T.Korsmeyer, and J.White, “Multipole and precorrected-FFT accelerated iterative methods for solving surface integral formulations of three-dimensional Laplace problems,” Domain-based Parallelism and Problem Decomposition Methods in Science and Engineering, D.E.Keyes, Y.Saad, and D.G.Truhlar, eds., SIAM, Philadelphia, 1995.
10. J.Phillips and J.White, ”A precorrected-FFT method for capacitance extraction of complicated 3-D structures,” Proceedings of the International Conference on Computer-Aided Design, Santa Clara, California, 1994.
11. J.Phillips, “Error and complexity analysis for a collocation-grid-projection plus precorrected-FFT algorithm for solving potential integral equations with Laplace or Helmholtz kernels,” Colorado Conference on Multigrid Methods, April, 1995.
12. W.C.Webster, “The flow about arbitrary, three-dimensional smooth bodies,” J. Ship Research, 19:206– 218, 1975.
DISCUSSION
C.M.Lee
Pohang Institute of Science and Technology, Korea
In the present morning session, we hear that the nonlinear ship motion theory cannot prescribe the radiation condition in the far field, and hence the numerical methods developed so far are based on the so-called “open boundary condition in the far field.” For the 3-D potential theory, the physical condition dictates that the diffracted and radiated waves should decay in the far field. We unfortunately do not know how far the far field should be in the numerical solutions. I would like to see somebody perform a careful experiment to provide as a guideline how we should impose the far-field conditions in our numerical solutions for the nonlinear water waves.
AUTHORS' REPLY
In wave radiation and diffraction problems where the fluid domain is infinite, a radiation boundary condition is required in the computational domain in order to make the problem well-posed. No one has yet been able to find exact radiation boundary condition for fully nonlinear wave problems. This necessitates the use of approximate radiation boundary conditions. In our problem we have steady flow in a box which is perturbed by the presence of a body or by the generation of incident waves. The box is unbounded below, bounded above the free surface and on the centerline by symmetry. The remaining boundaries upstream, downstream and side all require appropriate boundary conditions. The examples we have published here have all been for τ>1/4 so the upstream condition is defined by the steady flow or by incident waves. The side boundary is truncated with a vertical wall made with source and collocation points that extend down to a depth of one wavelength (defined by the incident wave or the boat speed). We have also tried absorbing beaches along the side boundary but they interfere with the propagation of the incident waves. Only the downstream boundary has the “open” boundary condition. In this case we justify its use because the waves are carried out of the problem domain by the natural downstream convection of the free surface nodes. This is an implied radiation boundary condition, not a rigidly defined boundary condition, and we provide no proof of its legitimacy. Our results indicate that the “open” boundary has little effect on the wave pattern of forces on the body relative to previously published experimental results. We agree with Dr. Lee that an experiment might be contrived to provide insight into this problem. We are still searching for the perfect far-field boundary.











