Effects of Tip-Clearance Flows
Y.-T.Lee,1 J.Feng,2 C.Merkle,2 M.Tse1
(1David Taylor Model Basin, 2Pennsylvania State University, USA)
ABSTRACT
Tip-leakage flows for a linear compressor cascade and a one-stage shrouded pump rotor are discussed in this paper. A numerical method solving the Reynolds averaged Navier Stokes equations is used to explore various detail features of the tip-leakage flows. Calculation results for the cascade provide an assessment for predicting flow past a non-rotating blade passage with zero and 2% chord clearances. On the other hand, the pump rotor configuration provides a swirling passage flow with the complication of a trailing-edge separation vortex mixed with the tip-clearance and passage vortices and produces a very complex three-dimensional flow in the rotor wake. The physical aspects of the tip-clearance flows are discussed including suction-side reloading and pressure-side unloading due to a tip clearance and formation and transportation of the tip-leakage vortex. Detailed velocity comparisons in the blade passage and the tip gap region are shown to indicate the difficulty of predicting tip-leakage flow. The pressure at the core of the tip vortex is also examined to evaluate the strength of the tip-leakage vortex.
NOMENCLATURE
|
c |
chord |
|
Cp |
pressure coefficient |
|
L.E. |
leading edge |
|
E,F,G |
defined in Eq. (2) |
|
Ev,Fv,Gv |
viscous terms |
|
H |
source term |
|
p |
static pressure |
|
Q |
defined in Eq. (2) |
|
s |
pitch |
|
S |
shear stress tensor |
|
t |
pseudo-time |
|
T.E. |
trailing edge |
|
TLF |
tip-leakage flow |
|
TLV |
tip-leakage vortex |
|
u |
velocity in x-direction |
|
v |
velocity in y-direction |
|
w |
velocity in z-direction |
|
U |
contravarient velocity in Eq. (3) |
|
UREF |
reference velocity |
|
V |
contravarient velocity in Eq. (3) |
|
Vx |
axial velocity |
|
Vt |
tangential velocity |
|
W |
contravarient velocity in Eq. (3) |
|
x,y,z |
physical coordinates |
|
β |
cascade inflow or outflow angle; artificial compressibility coefficient |
|
Γ' |
defined in Eq. (2) |
|
vt |
viscosity |
|
τ |
shear stress or tip gap size |
|
ωb |
blade rotational speed |
|
ξ,η,ζ |
transformed coordinates |
INTRODUCTION
Tip-leakage flow (TLF) past ducted or shrouded blade tips occurs in many turbomachinery applications including axial-flow machines, centrifugal impellers and ducted propulsors. Similarly, tip leakage occurs in the gap between stators and a rotating hub. Because of the relative movement between the blade tip and the adjacent wall, the gap flows in rotating machinery applications are typically driven by a combination of the pressure difference between the pressure and suction sides of the blade and the viscous forces arising from the relative motion between the adjacent surfaces. Depending on the parameters and
the geometries involved, either of these may be the primary driver in a given application. When the gap is large and the blade loading is high, the tip-gap flows are generally dominated by pressure effects, while very narrow gaps or low blade loading lead to gap flows that are more dependent on the relative movement between the blade tip and the casing. In general, however, inertial forces in this narrow gap region are sufficient to generate a tip-leakage vortex (TLV) on the suction side of the blade that not only produces substantial losses, but may also initiate blade surface cavitation [1]. Over the life span of a turbomachine, the machine efficiency and operating margin deteriorate due to the increase in tip gap spacing.
The engineering importance of tip gap flows, and the complexity of the physics they contain, has stimulated numerous previous studies of these phenomena. Recent studies of tip-leakage flow have involved various turbomachinery configurations, including linear cascades, compressors, turbines and pumps. Experimental studies of tip-gap flows in cascades have been reported by Kang and Hirsch [2,3], while Lakshminarayana et al. [4], Inoue et al. [5,6], Suder and Celestina [7], and Foley and Ivey [8], have conducted measurements in compressors. Tip-gap flows in turbines have been studied experimentally by Chan et al. [9], Yamamoto et al. [10], and DeCecco et al. [11] while pump flow experiments have been reported by Graham [12] and Zierke et al. [13, 14].
In addition to these experimental investigations, many analytical studies and numerical simulations of tip-gap flows have also been reported. Because our emphasis in the present paper is computational in nature we emphasize the latter here. Previous computational studies have included the simulations reported by Hah [15], Dawes [16], Crook [17], Adamczyk et al. [18], Copenhaver et al. [19], and Kang and Hirsch [20]. Of the numerous analytical studies, we here cite only the work of Chen et al. [21] who have developed a similarity scaling for the crossflow in the clearance region and a generalized description of the tip-leakage vortex based on inviscid-flow modeling. A comparison of our tip-leakage vortex trajectories with the model of Chen et al. [21] is presented later.
Although the experimental investigations and numerical simulations cited above have revealed many features of tip-leakage flows, many unsettled issues still remain. In general, the results to date have shown that several characteristic features tend to dominate the tip gap region in most cases. These include: (i) the formation, transport and trajectory of the tip-leakage vortex; (ii) the interaction of the tip-leakage flow with vortices generated by other mechanisms; and (iii) the size of the tip clearance and the blade loading. Despite these similarities, the detailed characteristics of the tip-leakage flow vary from one type of machine to another. For example, the relative motion between the blade tip and the shroud acts in an opposite direction in compressors and turbines. In compressor rotors, the relative movement between the blade tip and the casing or shroud tends to enhance tip leakage by dragging fluid through the gap region in the same direction as the pressure drop. By contrast, the relative motion in turbine rotors is in the opposite direction and tends to negate the effects of pressure drop. In fact, observations in turbines have been reported in which the tip gaps were so small that the leakage flow was reduced to zero by the relative movement [9].
The present study investigates the physical processes involved in the generation and transport of the tip-leakage vortex by means of numerical solutions of the three-dimensional Navier-Stokes equations. Results are presented for both a stationary cascade and a high Reynolds number axial rotor. The cascade geometry and operating conditions are chosen to match the low-speed compressor cascade experiments of Kang and Hirsch [2,3] who have provided a detailed map of the passage and tip-leakage flow at three different tip clearance conditions. The axial-flow rotor computations are chosen to match the conditions tested by Zierke et al. [13,14] who have furnished a reasonably complete outline of the wake of a pump rotor in the rotating frame including information on the transport of the tip-leakage vortex. The passage flow for this rotor has been investigated numerically by [22, 23, 24]. Dreyer and Zierke [23] quantitatively compared their predicted tip flow with the measured data at the design tip gap size. The cascade experiments were obtained with a stationary wall so that the gap flows are driven by pressure drop alone, while the pump rotor experiment involves the effects (in the relative frame) of a moving shroud. Thus, these two cases not only provide us with detailed experimental data against which we can check our computations, but they also represent an interesting comparison of the effects of the moving wall. Our emphasis therefore is on comparing the details of the tip gap flow in a cascade with a stationary wall with those in a rotating pump stage where there is relative motion between the blade and the casing.
In the following sections, we first present the numerical method along with the numerical gridding techniques with particular emphasis on the tip-clearance region. Then a brief summary of the experimental data used for comparison is given. The formation and the transport of the tip-leakage vortex for both cases are then examined in detail in the results section. In particular, we present numerical solutions for two tip gap clearances for both the cascade and the pump rotor.
NUMERICAL METHOD
Computational solutions of the Reynolds-averaged Navier Stokes equations were performed to explore the features of tip-leakage flow. The numerical flow solver used is designed to solve either compressible or incompressible flows. For the present incompressible applications, an artificial compressibility term is added to the continuity equation to facilitate convergence. A brief discussion of this numerical approach is given next.
Governing Equations and Turbulence Closure
The incompressible Reynolds-averaged Navier Stokes equations are formulated as
(1)
where
(2)
and
U=ξxu+ξyv+ξzw Ev=vtS·(ξx,ξy,ξz)T
V=ηxu+ηyv+ηzw; Fv=vtS·(ηx,ηy,ηz)T
W=ςxu+ςyv+ηzw Gv=vtS·(ςx,ςy,ςz)T
with
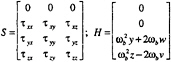
(4)
The inclusion of the time-derivative in the continuity equation changes the Navier Stokes equations from a partially elliptical system in time to a hyperbolical system. Thus a time marching scheme to update the primitive variables (p,u,v,w) is feasible. For steady state flows, the time derivative terms in the equations approach zero as the solution converges so that the converged solution satisfies the steady-state incompressible Navier Stokes equations.
The coefficient vt in Eq. (3) represents the effective viscosity which includes contributions from both the molecular viscosity and the turbulent viscosity. A standard two-equation k-ε turbulence model [25] was used to provide the turbulent viscosity closure in Eq. (3) for the computations presented in this paper. To facilitate resolution near the walls, a wall-function approach was used to enforce wall boundary conditions. In this wall-function procedure, the tangential velocity on the wall is determined by applying its normal derivative at the half grid point from the wall to satisfy the law of the wall. This finite wall velocity scheme was validated over a range of grid resolutions near the wall prior to conducting the present computations to verify its appropriateness.
Numerical Procedure
The combined Reynolds-averaged Navier Stokes equation and the two equation turbulence model in Eq. (1) were jointly solved by means of a four-stage Runge-Kutta time marching approach [26]. In the formulation, both viscous and inviscid spatial derivatives are computed by means of second-order central difference representations. Fourth-order artificial dissipation is applied to prevent odd-even splitting in the numerical solution. A local time step size is defined in conjunction with the artificial compressibility coefficient to obtain an optimal convergence rate. In regions of primarily inviscid flow, the convergence rate is controlled by the convective terms, and β in Eq. (2) is chosen to minimize the disparity among the system eigenvalues. In viscous-dominated regions where the convergence is mostly subject to the rate of viscous diffusion, the time step size is determined by viscous terms. β is then chosen such that an optimal time step size is still achievable for that part of the convective terms whose eigenvalue corresponds to the downstream-running acoustic characteristic.
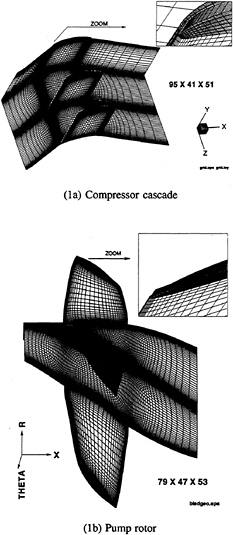
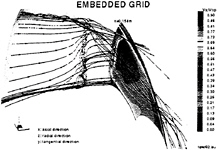
A multi-block structure is employed to model blade passages with tip clearance. As shown in Fig.1, the layout of the grid for both the cascade and the pump rotor consists of five H-type blocks. They include the inlet block (from the inlet to the
blade leading edge), the blade passage block (from the blade leading edge to the blade trailing edge and from the hub to the blade tip), two blade tip blocks between the blade tip and the casing, and the exit block from the blade trailing edge to the exit. Grid lines are continuous across block interfaces.
There are three types of boundary conditions associated with these grid structures: inlet and exit boundaries, periodic boundaries between adjacent blade passages, and non-slip wall boundaries including rotating and nonrotating blade surfaces and the stationary casing. For the present applications, Method of Characteristics (MOC) procedures are used to derive the number of inlet and exit boundary conditions [26]. This follows the hyperbolic equation concept that information that propagates into the flow field must be specified at the boundary while information that propagates across the boundary from the interior of the domain is dictated by the governing equations. These boundary conditions are then enforced by specifying the velocity components at inlet boundaries and extrapolating the static pressure from conditions on the inside. At outflow boundaries, the static pressure is calculated from local radial equilibrium and the velocity is extrapolated.
On solid surfaces, the non-slip condition supplemented by the normal momentum condition is used to determine the flow quantities. In the rotational frame, this leads to zero velocity on the blade and hub surfaces and a specified tangential velocity on the counter-rotating casing surface. Periodic boundary points are treated in a manner analogous to that used for field points.
NUMERICAL RESULTS
Description of Geometries Studied
As noted above, two geometries are used to study tip-leakage flow. The first is a stationary linear compressor cascade studied experimentally by Kang and Hirsch [2,3]. The second is a one-stage stator-rotor pump measured by Zierke et al. [13,14]. For the cascade case, the wall is stationary, and the tip-leakage flow is totally pressure driven. For the rotor case, the tip-leakage flow is also facilitated by the relative motion at the blade tip. The results show that the tip-leakage flow of the cascade case presents stronger mixing phenomena including tip leading edge separation, a larger tip-leakage vortex and more pronounced blade suction-side reloading.
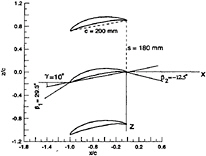
The blades used in the linear cascade tests of Kang and Hirsh [2,3] have a modified NACA 65– 1810 cross section with a rounded trailing edge. As shown in Fig 2, the blade has a chord of 200 mm and a solidity of 1.1. The stagger angle is 10 degrees and the blade aspect ratio is unity. At the design condition, the inflow angle is 29.3 degrees and the flow deflection angle is about 40 degrees. The inflow is turbulent and has a Reynolds number of 3×105 based on the average inlet velocity and the blade chord length. The cascade flow was measured at tip-gap clearances of 0%, 1% and 2% of the chord. Predictions of both the 0% and 2% cases are presented in this paper.
The axial-flow pump consists of a 13-blade inlet guide vane (IGV) followed by a 7-blade backward swept rotor. This stator-rotor configuration is referred to as the HIREP rotor [13,14]. The separation between the IGV blade row and the rotor blade row at the outer casing is approximately 1.3 IGV chord lengths. The pump has a constant hub diameter of 0.533 m and a constant casing diameter of 1.067 m. The IGV blades have a constant spanwise chord of 0.175 m. The chord length of the rotor blades decreases from 0.285 m at the hub to 0.266 m at the tip. The corresponding solidity values are 1.19 at the hub and 0.56 at the tip. The tip section of the rotor blade has a thickness-to-chord ratio of 10.1%. The nominal rotor tip clearance is 0.330 mm, which corresponds to 0.64% of the pump casing radius. The pump operates at an inlet velocity of 10.7 m/s and an inlet pressure of 3.04 kg/cm2. The rotational speed and tip speed are 260 RPM and 14.5 m/s, respectively, while the flow coefficient 1.36. The tested Reynolds number based on the chord of the IGV blade is 2.3× 106. The details of the measurement hardware and results are given in Zierke et al. [13, 14].
Tip-Gap Flow in the Cascade
Calculations of the cascade geometry were made for two blade tip clearances, zero and 2% chord (and span), at an inflow angle corresponding to the design condition. For the tip clearance calculation, the blade height was decreased by 2%, thereby reducing the blade aspect ratio to 0.98. In both cases, the embedded H-type grid described above was used. As shown in Fig.1a, the embedded grid provides a good representation of both the blade leading and trailing edge regions while also providing a smooth grid change from the blade tip to the tip-clearance region. The grid has 95 nodes in the axial direction, 51 nodes from blade to blade, and
41 nodes from hub to tip. For the case of 2% tip gap, the grid is heavily stretched near the blade tip and there are ten grid points in the spanwise direction between the blade tip and the endwall. Twelve grid points are placed inside the gap in the blade-to-blade direction. Such a grid resolution appears to satisfy the minimum accuracy requirement needed to capture most features of the tip-leakage flow [20].
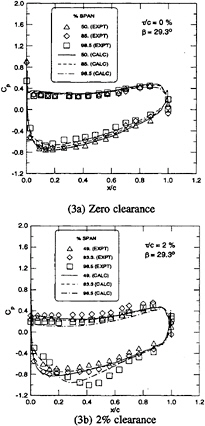
In Fig.3, the blade surface pressure distributions for both the zero and 2% tip gap cases are presented at three span locations, 50%, 85% and 98.5%. The predicted pressure distributions for the zero tip clearance case which are shown in Fig.3a agree well with the experimental data. The flow, which is approximately symmetric about the mid-span, separates near the mid-chord at the endwall. This separation region grows rapidly until it covers about 25% of the span at the trailing edge.
For the 2% tip gap case, the predicted pressures at mid-span (49%) and 83.3% span shown in Fig.3b again agree quite well with the measured values. At the 96.5% span, the experimental measurements show a local minimum in the suction side pressure distribution at about the 40% chord location. This minimum is evidence that a strong tip-leakage vortex exists. The impact of the reloading characteristics of this vortex are indicated by the fact that the minimum pressure peak at 96.5% span is even lower than that at 49% span. Similarly, the computational pressure distribution shows a minimum in the suction side pressure distribution at 96.5% span that is also lower than that at 49% span indicating that the prediction clearly captures the qualitative features of the leakage vortex. Quantitative comparison of the experimental and computational results, however, shows that both the location and the magnitude of the suction side reloading is somewhat different from the experimental measurements. Similar suction-side reloading is also seen by the experimental investigations of Graham [12] and Foley et al. [6] and suggests that the tip gap may not always lead to blade tip unloading, as has been widely assumed.
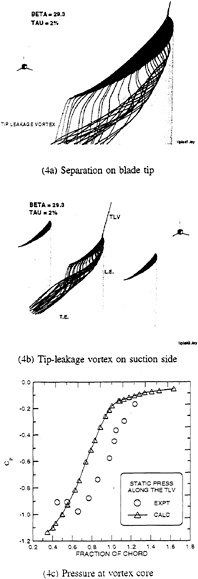
The tip reloading noted in Fig.3b is governed by the details of the transport of the tip-leakage vortex as is demonstrated in more detail in Fig.4. Because of the relatively high blade loading in the cascade, the tip vortex starts to separate relatively close to the blade leading edge as shown in Fig.4a. After separating from the tip at about 30% chord, the vortex core is washed away from the suction side of the blade in the lateral direction and is also pushed down towards the hub as it is converted downstream. The overall trajectory of the vortex is shown in Fig.4b.
An indication of the variation in the local strength of the vortex can be deduced from measurements of the static pressure at the vortex center. Representative results of this nature are shown in Fig.4c for both the experiment and the computations. The pressure measurements in Fig. 4c indicate that the vortex strength is a maximum where it first separates from the blade tip. As it is converted away from the blade and in the downstream (chord-wise) direction, it begins to weaken and disperse although it continues to grow in size. Figure 4c shows comparisons between the calculated pressure along the vortex core and the measurements [2,3]. The two vortex trajectories are similar in shape and magnitude, although the predictions are somewhat displaced from the experimental results.
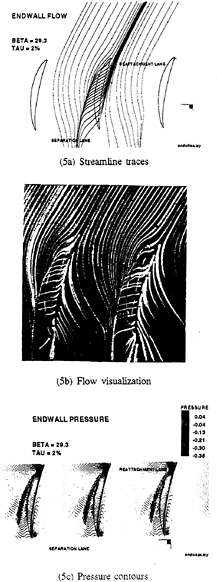
The tip-leakage flow can also be evaluated from the flow pattern on the endwall in the vicinity of the tip as shown in Fig.5. The comparison between the calculated endwall streamlines in Fig. 5a and the experimental paint traces in Fig.5b indicates that the experimental suction-side separation line in the blade wake region is closer to the suction side than in the computational prediction. The predicted pressure contours on the tip endwall are shown in Fig.5c. The high pressure-gradient region on the suction side of the blade matches with the suction-side separation line shown in Fig.5a. A comparison of these two figures also clearly shows that the tip-leakage vortex leaves the blade tip section at the minimum pressure location.
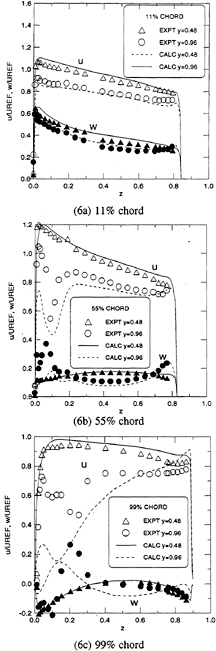
Figure 6 presents a more detailed comparison of the predicted and measured velocity components. This comparison shows two velocity components in the blade-to-blade plane at three axial sections, 11%, 55% and 99% chord. In particular, the axial velocity component, u, and the blade-to-blade velocity component, w, are compared. At each of the three sections results for two spanwise locations, mid-span (y=0.48) and near tip (y=0.96), are presented. The mid-span predictions agree well with the measurements at all three locations. For the near-tip section, the agreement is good at 11% chord (Fig.6a), where the tip-leakage vortex is not yet formed. At mid-chord ( Fig.6b), where the tip-leakage vortex is well established, its influence is clearly reflected in the two velocity components. The axial velocity dips strongly and the lateral velocity accelerates dramatically because of the presence of the tip-leakage vortex on the suction side. The computation slightly overpredicts the dip
while it underpredicts the tangential peak. This difference implies a small disagreement in the vortex location and/or the vortex core orientation between the computation and the experiment. This disagreement is augmented somewhat at the trailing-edge section further downstream (see Fig.6c). Here, the computational solutions predicts the magnitude of the tangential velocity peak reasonably well, but its location is too close to the suction side. Meanwhile, the peak in the axial velocity is much too large in the predictions.
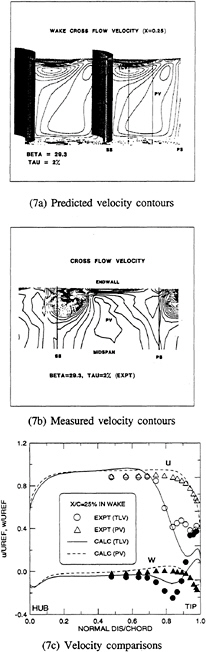
The downstream remnants of the gap flow on the cascade wake are shown Fig.7. Here we show the contours of the absolute cross sectional velocity in the blade-to-blade and hub-to-tip plane for both the predictions and the measurements. These results are presented at an axial section that is 25% chord downstream of the blade trailing edge. Figure 7a presents the predicted cross-sectional velocity contours, while Fig.7b shows the corresponding experimental results. It is important to note that Fig.7b presents only the upper half (mid-span to casing) of the flow passage, while Fig. 7a shows the full passage (hub to casing). The local concentration of velocity contours on the suction side of the blade near the tip in both figures represents the tip-leakage vortex. The passage vortex (PV) occupies the center region of the cross section and is labeled in both Fig.7a and 7b. The horseshoe vortex generated at the leading-edge of the blade exists only in the immediate vicinity of the leading edge and then quickly disperses and merges with the passage vortex. Consequently it can no longer be distinguished in the wake, and so is not visible in these contour plots.
As a last comparison in the wake, Fig.7c shows the axial and blade-to-blade velocity components on hub-to-tip lines passing through the center of the tip-leakage vortex and the center of the passage vortex as determined from Figs.7a and 7b. The axial velocity on the line passing through the passage vortex shows only the characteristics of a normal boundary layer: the velocity decreases monotonically from the mean passage to both the casing and the hub. The experimental and computational comparisons for both the u and w velocity components on this line are seen to be in quite good agreement. The velocity components on the line passing through the tip-leakage vortex, however, show considerably different behavior. The tip leakage vortex causes the axial velocity to dip to a minimum considerably before reaching the casing wall. The blade-to-blade velocity component, however, shows a very complicated shape with, particularly, a strong peak near the casing wall because of the residual strength of the tip leakage vortex. For these much more sensitive profiles, the comparisons between the measurements and the computations are again qualitatively similar, but quantitatively quite different. The computation clearly overpredicts the tip-leakage vortex velocity, but its general features are reasonably well captured.
In summary, the comparisons between the predictions and the measurements for the cascade case show that the pressure distributions with and without tip clearance effects agree quite well with the measured values. In general, however, pressure levels are less sensitive and easier to predict than the cross-plane velocities. The comparisons of the more sensitive flow quantities such as the tip-leakage vortex core velocity and pressure are qualitatively accurate, but there is some difficulty in predicting the exact location and strength of the tip-leakage vortex. Overall, the comparisons suggest that the flow features are captured reasonably although there remains room for improvement.
Tip-Gap Flow In the HIREP Rotor
As compared to a stationary blade, a rotating pump stage facilitates the gap flow because the blade rotates in the opposite direction to the gap flow, and hence, the casing tends to pump the flow in the tip region and to enhance the gap flow effects. Obviously, the degree of such rotational effects depends on the tip gap height, the RPM, the blade loading and the blade thickness. As noted above, the computations were carried out for the HIREP rotor for which detailed experimental measurements have been carried out by Zierke et al [ 13,14].
An H-type multi-block embedded grid structure similar to that shown in Fig.1b is used to describe the rotor blade geometry. Two grid sizes are used for the present investigation: a coarse grid of 79×53×47 nodes in the axial, blade-to-blade and spanwise directions respectively, and a fine grid of 105×108×87 nodes. Like the linear cascade, the coarse grid maintains 12×10 grid points inside the gap. The fine grid has 24×12 grid points inside the gap and approximately doubles the grid everywhere else on each axial, cross-sectional plane. Because the coarse grid is approximately similar in grid resolution to the cascade grid, we first present solutions on the coarse grid and compare them with experiment. After that, the fine grid solutions are used to ascertain the accuracy of the coarse grid solution. Unless specifically mentioned, the computational solutions were presented for the
coarse grid. Again the blade leading and trailing edges are adequately represented with both grids.
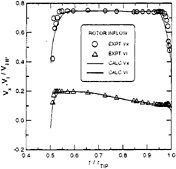
Three different tip clearance cases were computed. They are 0.64%, 1.17% and 3.22% of the outer casing radius respectively. For all three gap sizes, the number of grid nodes inside the tip gaps remained the same. For all computations presented in this paper, the rotor inflow was determined from the circumferentially averaged stator exit flow solution. The profiles of the velocity components obtained from this averaging process are shown in Fig.8. This simple mixed-out approach was proven to be adequate in handling the present stage flow in a steady manner [22, 24].
The design tip clearance for the HIREP rotor is 0.64% of the outer casing radius. The predicted tip-leakage flow for this design condition is shown in Fig.9. Because of the interaction of the tip-leakage vortex and the trailing-edge vortex, the tip vortex travels further tangentially as it is convected downstream as compared to the tip-leakage vortex in the cascade computations.
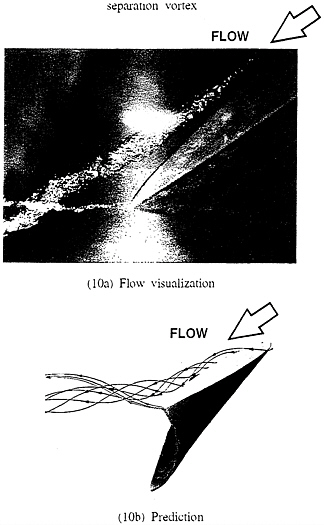
Figure 10 shows a comparison between an experimental visualization of the interaction between the tip vortex and the trailing-edge vortex and the corresponding predictions. This visualization photograph was obtained by reducing the tunnel pressure to the point that cavitation appeared at the core of both vortices. Based on the sizes of the cavitating vortices, the tip-leakage vortex seems to have a larger strength than the trailing-edge vortex. The two vortices pass one another at different radii and do not intersect. The present photo shows only the last 30% of the blade chord. Both Inoue and Kuroumaru [4] and Zierke et al. [13] located the onset of the tip-leakage vortex roll-up as the point of minimum pressure on the suction surface.
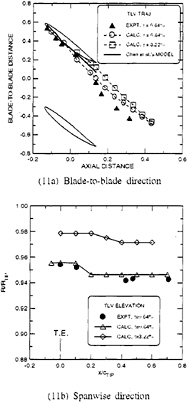
The predicted results indicate that the tip-leakage vortex passes over the tip section from the pressure side to the suction side at about 15% of the chord as shown in Fig.11a at the design clearance. This location is in good agreement with that observed by Zierke et al. [13] for the onset of vortex roll-up on the suction side. Also shown in Fig.11a is the predicted vortex path by Chen et al. [21]. Figure 11b shows the spanwise location of the tip-leakage vortex downstream of the trailing edge, In this figure, the origin of the abscissa, x/cTIP=0, corresponds to the trailing edge of the rotor. For both the predictions and the measurements, the path of the tip-leakage vortex moves radially inward by approximately 1% of the casing radius in the near wake and then levels off at an essentially constant radius from the near wake to the far wake. The sudden change in radial location may relate to the development of the blade passage boundary layer to the free-shear wake flow. Considering the difficulty in locating the exact location of the vortex core, the trajectory of the tip-leakage vortex in both the blade-to-blade and the spanwise directions compares favorably with the experimental data. The calculation also correctly predicts the relative size and the crossover location of both vortices.
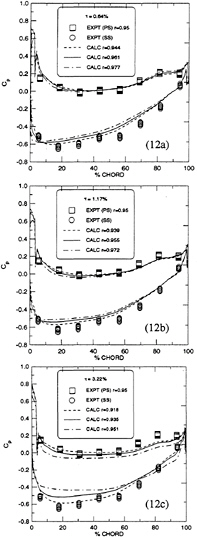
A comparison of the effect of tip gap height on the pressure distribution in the rotor is shown in Fig.12 for each of the three tip gap sizes mentioned above. The results on Fig.12 are presented for three radial blade locations: 1%, 3% and 5% of the casing radius away from the blade tip. The only available measurement is performed at a radial location of 95% of the casing radius at the design condition (0.64% tip gap). As can be seen in Fig.12a, when the tip gap is small (0.64%), the pressure distribution shows little gap unloading like that seen in the cascade even close to the tip gap, however, as the gap spacing increases, the unloading develops. At the largest gap (3.22%), the tip unloading toward the outer radius becomes significant as indicated by the reduction of the enclosed area between the pressure and suction side pressure distributions as can be seen on Fig.12c. Comparing against the cascade case, the reloading on the suction side appears to be weaker and does not appear until much further downstream, indicating a much weaker tip leakage vortex. However, the suction-side reloading starts around 1% tip gap as indicated in Fig.12b.
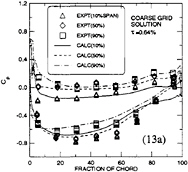
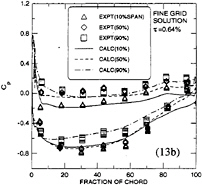
In Fig.13, the pressure distributions at three radii from hub to tip are presented together with corresponding experimental measurements at the design clearance, 0.64%. For brevity, the 1.17% case is omitted in this figure. The computations and the experiments are in excellent agreement, except near the blade trailing edge where a small difference exists. Also note that the unloading occurs at 90% span for the larger gap case.
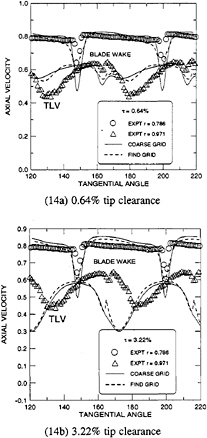
Figure 14 shows the comparison of the wake velocity at 16.1% casing radius (or 32.4% tip chord) downstream of the tip trailing edge. Although the test data is only for the small gap, the comparison between the experiment and the calculation is made for both gap sizes. Two radial sections are selected for comparisons, i.e. r=0.786 (mid-span) and 0.971 (near tip) respectively. Although the calculation overpredicts the thickness of the shear layer, the fine grid solution captures the blade wake more precisely as shown for the mid-span comparison. For the tip velocity comparison, the blade wake becomes much smaller in both size
and magnitude, and the TLV dominates the variation of the velocity distribution. The prediction at the design gap clearly captures the vortex activity but underpredicts the strength of the TLV. The difference is also related to the deviation in predicting the location of the TLV as shown in Fig. 11a where the axial distance for this wake comparing section is 0.324. For the larger gap, the blade wake at the tip shown in Fig.14 disappears and the TLV covers the whole passage from the suction side to the pressure side. Figure 11 indicates that this TLV leaves the suction side around 60% tip chord, and moves closer to the suction side and to the casing wall than the smaller gap TLV. However, the sharp drop-off seen for the small gap solution in Fig.11b exists also for the large gap solution, but with a milder slope.
CONCLUSIONS
Numerical solutions obtained by solving the Reynolds-averaged Navier Stokes equations, with a two-equation k-ε turbulence model and a wall-function model, were compared with the measured tip-leakage flows for a compressor cascade and a one-stage pump rotor. The grid topology used in the tip gap region is an embedded grid approach, which ensures the precise representation of the blade tip geometry and the smooth grid variation from the blade region to the tip clearance region. The tip-clearance sizes studied in this paper are 0% and 2% chord for the cascade, and 0.64%, 1.77% and 3.22% casing radius for the pump rotor. The tip-leakage flow for the pump rotor is not well-structured as the cascade, but many flow characteristics are similar. In addition, the radial-moving trailing-edge vortex further complicate the rotor tip-leakage flow near the tip trailing edge. Although the present cascade calculation was performed for a full turbulent flow simulation, the transition model should be examined in order to evaluate the Reynolds number effect on these calculations. The present calculation captures almost all the features of the tip-leakage flow and the transport of the tip-leakage vortex for both the cascade and the rotor. Some specific conclusions are as follows.
-
Both the cascade and the rotor show suction-side reloading and pressure-side unloading when the tip clearance size exceeds a certain size. For the pump rotor, this happens when the tip clearance is about 1% of the casing radius. This suction-side reloading is a by-product of the transport of the tip-leakage vortex.
-
The tip-leakage vortex leaves the suction side from 15% to 60% chord depending on the gap size and the rotor speed. This location matches with the location of the minimum pressure on the casing endwall. A sharp large drop in spanwise direction when the vortex leaves the suction side, another smaller drop happens when the vortex leaves the blade passage and into the wake.
-
The velocity distributions associated with the passage vortex and the tip-leakage vortex are quite different. The former is a regular boundary-layer type and the latter has several peaks due to stronger effect from the tip-leakage vortex.
-
The present coarse grid resolution is adequate for the passage flow calculation, particularly the blade loading prediction. Fine grid provides better prediction for the viscous blade wake. For the tip-clearance region, however, the 10 or 12 span wise grids and 12 or 24 blade-to-blade grids may not be enough in capturing the vortex generation and transportation precisely.
ACKNOWLEDGMENTS
The two experimental data sets were provided by Drs. S.Kang and C.Hirsch of the Vrije Universiteit Brussel and by Messrs. W.C.Zierke, P. D.Taylor and W.A.Straka of Pennsylvania State University. This work was funded under the Applied Hydrodynamics Program and the Block Program for Hydrodynamics and Hydroacoustics of Internal Flow. The program monitor at the Office of Naval Research is Dr. P.Purtell. The computing time was provided by the DOD High Performance Computational Program.
REFERENCES
1. Farrell, K.J., and Billet, M.L., “A Correlation of Leakage Vortex Cavitation in Axial-Flow Pumps,” ASME Journal of Fluid Engineering, Vol. 116, No. 3, 1994, pp. 551–557.
2. Kang, S., and Hirsch, C., “Experimental Study on the Three Dimensional Flow within a Compressor Cascade with Tip Clearance: Part II— The Tip Leakage Vortex,” ASME Journal of Turbomachinery, Vol. 115, 1989, pp. 444–452.
3. Kang, S., and Hirsch, C., “Tip Leakage Flow in a Linear Compressor Cascade,” ASME Paper GT-93–303, 1993.
4. Lakshminarayana, B., Sitaram, N., and Zhang, J., “End-Wall and Profile Losses in a Low-Speed Axial Flow Compressor Rotor,” ASME Journal of Engineering for Gas Turbines and Power, Vol. 108, 1986, pp. 22–31.
5. Inoue, M., Kuroumaru, M., and Fukuhara, M., “Behavior of Tip Leakage Flow Behind an Axial Compressor Rotor,” ASME Journal of Engineering for Gas Turbines and Power, Vol. 108, 1986, pp. 7–14.
6. Inoue, M. and Kuroumaru, M., “Structure of Tip Clearance Flow in an Isolated Axial Compressor Rotor, ” ASME Journal of Turbomachinery, Vol. 111, 1989, pp. 250–256.
7. Suder, K.L., and Celestina, M.L., “Experimental and Computational Investigation of the Tip Clearance Flow in a Transonic Axial Compressor Rotor,” ASME Paper 94-GT-365, 1994.
8. Foley, A.C., and Ivey, P.C., “Measurement of Tip-Clearance Flow in a Multistage, Axial Flow Compressor, ” ASME Paper 94-GT-431, 1994.
9. Chan, J.K.K., Yaras, M.I., and Sjolander, S.A., “Interaction Between Inlet Boundary Layer, Tip-Leakage and Secondary Flows in a Low-Speed Turbine Cascade,” ASME Paper 94-GT-250, 1994.
10. Yamamoto, A., Matsunuma, T., Ikeuchi, K., and Outa, E., “Unsteady Endwall/Tip-Clearance Flows and Losses due to Turbine Rotor-Stator Interaction,” ASME Paper 94-GT-461, 1994.
11. De Cecco, S., Yaras, M.I., and Sjolander, S.A., “Measurements of the Tip-Leakage Flow in A Turbine Cascade with Large Clearances,” ASME Paper 95-GT-77, 1995.
12. Graham, J.A.H., “Investigation of a Tip Clearance Cascade in a Water Analogy Rig,” ASME Journal of Engineering for Gas Turbines and Power, Vol. 108, 1986, pp. 38–46.
13. Zierke, W.C., Farrell, K.J., and Straka, W.A., “Measurement of the Tip Clearance Flow for a High Reynolds Number Axial-Flow Rotor: Part 1— Flow Visualization,” ASME Paper 94-GT-453, 1994.
14. Zierke, W.C., Farrell, K.J., and Straka, W.A., “Measurement of the Tip Clearance Flow for a High Reynolds Number Axial-Flow Rotor: Part 2— Detailed Flow Measurements,” ASME Paper 94-GT-454, 1994.
15. Hah, C., “A Numerical Modeling of Endwall and Tip-Clearance Flow of an Isolated Compressor Rotor,” ASME Journal of Engineering for Gas Turbine and Power, Vol. 108, 1986, pp. 17– 21.
16. Dawes, W.N., “A Numerical Analysis of the Three-Dimensional Viscous Flow in a Transonic Compressor Rotor and Comparison with Experiment,” ASME Journal of Turbomachinery, Vol. 109, 1987, pp. 83–90.
17. Crook, A.J., “Numerical Investigation of Endwall/Casing Treatment Flow Phenomena, ” M.S. Thesis, Department of Aeronautics and Astronautics, Massachusetts Institute of Technology, 1989.
18. Adamczyk, J.J., Celestina, M.L., Beach, T.A., and Bartnett, M., “Simulation of Three-Dimensional Viscous Flow Within a MultiStage Turbine,” ASME Journal of Turbomachinery, Vol. 112, 1990, pp. 370–376.
19. Copenhaver, W.W., Mayhew, E.R., and Hah, C., “The Effect of Tip Clearance on a Swept Transonic Compressor Rotor, ” ASME Paper 94-GT-363 , 1994.
20. Kang, S., and Hirsch, C., “Numerical Simulation of 3D Viscous Flow in a Linear Compressor Cascade with Tip Clearance,” ASME Paper 94-GT-364, 1994.
21. Chen, G.T., Greitzer, E.M., Tan, C.S., Marble, F.E., “Similarity Analysis of Compressor Tip Clearance Flow Structure,” ASME Journal of Turbomachinery, Vol. 113, 1991, pp. 260–271.
22. Yang, C.I., “A Simulation of Viscous Incompressible Flow Through a Multiple-Blade-Row Turbomachinery with a High-Resolution Upwind Finite Differencing Scheme,” ASME FED Vol. 227, Numerical Simulations in Turbomachinery, 1995.
23. Dreyer, J.J., and Zierke, W.C., “Solution of the Average-Passage Equation for the Incompressible Flow Through Multiple-Blade_row Turbomachinery,” Report No. TR 94–05, The Pennsylvania State University/Applied Research Laboratory, 1994.
24. Lee, Y.T., Hah, C., and Loellbach, J., “Flow Analyses in a Single-Stage Propulsion Pump,” ASME Journal of Turbomachinery, Vol. 118, 1996.
25. Chien, K.Y., “Predictions of Channel and Boundary-Layer Flows with a Low-Reynolds-Number Turbulence Model,” AIAA Journal, Vol. 20, No. 1, 1982, pp. 33–38.
26. Merkle, C.L. and Tsai, Y-L.P., “Application of Runge-Kutta Schemes to Incompressible Flows,” AIAA Paper 86–0553, AIAA 24th Aerospace Sciences Meeting, Reno, NV, Jan. 1986.