4
Contributions of Measurement and Statistical Modeling to Assessment
Over the past century, scientists have sought to bring objectivity, rigor, consistency, and efficiency to the process of assessment by developing a range of formal theories, models, practices, and statistical methods for deriving and interpreting test data. Considerable progress has been made in the field of measurement, traditionally referred to as “psychometrics.” The measurement models in use today include some very sophisticated options, but they have had surprisingly little impact on the everyday practice of educational assessment. The problem lies not so much with the range of measurement models available, but with the outdated conceptions of learning and observation that underlie most widely used assessments. Further, existing models and methods may appear to be more rigid than they actually are because they have long been associated with certain familiar kinds of test formats and with conceptions of student learning that emphasize general proficiency or ranking.
Findings from cognitive research suggest that new kinds of inferences are needed about students and how they acquire knowledge and skills if assessments are to be used to track and guide student learning. Advances in technology offer ways to capture, store, and communicate the multitude of things one can observe students say, do, and make. At issue is how to harness the relevant information to serve as evidence for the new kinds of inferences that cognitive research suggests are important for informing and improving learning. An important emphasis of this chapter is that currently available measurement methods could yield richer inferences about student knowledge if they were linked with contemporary theories of cognition and learning.1
FORMAL MEASUREMENT MODELS AS A FORM OF REASONING FROM EVIDENCE
As discussed in Chapter 2, assessment is a process of drawing reasonable inferences about what students know on the basis of evidence derived from observations of what they say, do, or make in selected situations. To this end, the three elements of the assessment triangle—cognition, observation, and interpretation—must be well coordinated. In this chapter, the three elements are defined more specifically, using terminology from the field of measurement: the aspects of cognition and learning that are the targets for the assessment are referred to as the construct or construct variables, observation is referred to as the observation model, and interpretation is discussed in terms of formal statistical methods referred to as measurement models.
The methods and practices of standard test theory constitute a special type of reasoning from evidence. The field of psychometrics has focused on how best to gather, synthesize, and communicate evidence of student understanding in an explicit and formal way. As explained below, psychometric models are based on a probabilistic approach to reasoning. From this perspective, a statistical model is developed to characterize the patterns believed most likely to emerge in the data for students at varying levels of competence. When there are large masses of evidence to be interpreted and/or when the interpretations are complex, the complexity of these models can increase accordingly.
Humans have remarkable abilities to evaluate and summarize information, but remarkable limitations as well. Formal probability-based models for assessment were developed to overcome some of these limitations, especially for assessment purposes that (1) involve high stakes; (2) are not limited to a specific context, such as one classroom; or (3) do not require immediate information. Formal measurement models allow one to draw meaning from quantities of data far more vast than a person can grasp at once and to express the degree of uncertainty associated with one’s conclusions. In other words, a measurement model is a framework for communicating with others how the evidence in observations can be used to inform the inferences one wants to draw about learner characteristics that are embodied in the construct variables. Further, measurement models allow people to avoid reasoning errors that appear to be hard-wired into the human mind, such as biases associated with preconceptions or with the representativeness or recency of information (Kahneman, Slovic, and Tversky, 1982).
|
|
be useful for cognitively informed assessment. Junker’s paper reviews some of the measurement models in more technical detail than is provided in this chapter and can be found at <http://www.sat.cmu.edu/~brian/nrc/cfa/>. [March 2, 2001]. |
Reasoning Principles and Formal Measurement Models
Those involved in educational and psychological measurement must deal with a number of issues that arise when one assumes a probabilistic relationship between the observations made of a learner and the learner’s underlying cognitive constructs. The essential idea is that statistical models can be developed to predict the probability that people will behave in certain ways in assessment situations, and that evidence derived from observing these behaviors can be used to draw inferences about students’ knowledge, skills, and strategies (which are not directly observable).2 In assessment, aspects of students’ knowledge, skills, and strategies that cannot be directly observed play the role of “that which is to be explained” —generally referred to as “cognition” in Chapter 2 and more specifically as the “construct” in this chapter. The constructs are called “latent” because they are not directly observable. The things students say and do constitute the evidence used in this explanation—the observation element of the assessment triangle.
In broad terms, the construct is seen as “causing” the observations, although generally this causation is probabilistic in nature (that is, the constructs determine the probability of a certain response, not the response itself). More technically there are two elements of probability-based measurement models: (1) unobservable latent constructs and (2) observations or observable variables, which are, for instance, students’ scores on a test intended to measure the given construct. The nature of the construct variables depends partly on the structure and psychology of the subject domain and partly on the purpose of assessment. The nature of the observations is determined by the kinds of things students might say or do in various situations to provide evidence about their values with respect to the construct. Figure 4– 1 shows how the construct is related to the observations. (In the figure, the latent construct is denoted θ [theta] and the observables x.) Note that although the latent construct causes the observations, one needs to go the other way when one draws inferences—back from the observations to their antecedents.
Other variables are also needed to specify the formal model of the observations; these are generally called item parameters. The central idea of probability models is that these unknown constructs and item parameters do not determine the specifics of what occurs, but they do determine the probability associated with various possible results. For example, a coin might be expected to land as heads and as tails an approximately equal number of
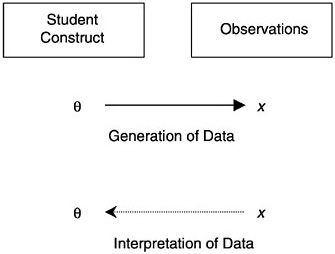
FIGURE 4–1 The student construct and the observations.
times. That is, the probability of heads is the same as the probability of tails. However, this does not mean that in ten actual coin tosses these exact probabilities will be observed.
The notion of “telling stories that match up with what we see” corresponds to the technical concept of conditional independence in formal probability-based reasoning. Conditional independence means that any systematic relationships among multiple observations are due entirely to the unobservable construct variables they tap. This is a property of mathematical probability models, not necessarily of any particular situation in the real world. Assessors choose where, in the real world, they wish to focus their attention. This includes what situation they want to explore and what properties of that situation are most important to manipulate. They then decide how to build a model or “approximation” that connects the construct variables to the specific observations. The level of unobservable constructs corresponds to “the story” people tell, and it is ultimately expressed in terms of important patterns and principles of knowledge in the cognitive domain under investigation. The level of observations represents the specifics from which evidence is derived about the unobservable level. Informally, conditional independence expresses the decision about what aspects of the situation are built into one’s story and what is ignored.
Psychometric models are particular instances of this kind of reasoning. The most familiar measurement models evolved to help in “constructing stories” that were useful in situations characterized by various psychological perspectives on learning, for particular educational purposes, with certain recurring forms of evidence. The following sections describe some of these
models, explaining how these stories have grown and adapted to handle the increasingly complex demands of assessment. Knowing the history of these adaptations may help in dealing with new demands from more complex models of learning and the types of stories we would now like to be able to tell in many educational contexts.
The BEAR Assessment System
An example of the relationships among the conception of learning, the observations, and the interpretation model is provided by the Berkeley Evaluation and Assessment Research (BEAR) Center (Wilson and Sloane, 2000). The BEAR assessment system was designed to correspond to a middle school science curriculum called Issues, Evidence and You (IEY) (Science Education for Public Understanding Program, 1995). We use this assessment as a running example to illustrate various points throughout this chapter.
The conception of cognition and learning underlying IEY is not based on a specific theory from cognitive research; rather it is based on pedagogic content knowledge, that is, teachers’ knowledge of how students learn specific types of content. Nevertheless, the BEAR example illustrates many of the principles that the committee is setting forth, including the need to pay attention to all three vertices of the assessment triangle and how they fit together.
The IEY curriculum developers have conceptualized the learner as progressing along five progress variables that organize what students are to learn into five topic areas and a progression of concepts and skills (see Box 4–1). The BEAR assessment system is based on the same set of progress variables. A progress variable focuses on progression or growth. Learning is conceptualized not simply as a matter of acquiring more knowledge and skills, but as progressing toward higher levels of competence as new knowledge is linked to existing knowledge, and deeper understandings are developed from and take the place of earlier understandings. The concepts of ordered levels of understanding and direction are fundamental: in any given area, it is assumed that learning can be described and mapped as progress in the direction of qualitatively richer knowledge, higher-order skills, and deeper understandings. Progress variables are derived in part from professional opinion about what constitutes higher and lower levels of performance or competence, but are also informed by empirical research on how students respond or perform in practice. They provide qualitatively interpreted frames of reference for particular areas of learning and permit students’ levels of achievement to be interpreted in terms of the kinds of knowledge, skills, and understandings typically associated with those levels. They also allow individual and group achievements to be interpreted with respect to the achievements of other learners. The order of the activities intended to take
|
BOX 4–1 Progress Variables from the Issues, Evidence and You (IEY) Curriculum Designing and Conducting Investigations—designing a scientific experiment, performing laboratory procedures to collect data, recording and organizing data, and analyzing and interpreting the results of an experiment. Evidence and Trade-offs—identifying objective scientific evidence, as well as evaluating the advantages and disadvantages of different possible solutions to a problem on the basis of the available evidence. Understanding Concepts—understanding scientific concepts (such as properties and interactions of materials, energy, or thresholds) in order to apply the relevant scientific concepts to the solution of problems. Communicating Scientific Information—effectively, and free of technical errors, organizing and presenting results of an experiment or explaining the process of gathering evidence and weighing trade-offs in selecting a solution to a problem. Group Interaction—developing skill in collaborating with teammates to complete a task (such as a laboratory experiment), sharing the work of the activity, and contributing ideas to generate solutions to a given problem. SOURCE: Roberts, Wilson, and Draney (1997, p. 8). Used with permission of the authors. |
students through the progress variables is specified in a blueprint—a table showing an overview of all course activities, indicating where assessment tasks are located and to which variables they relate.
During IEY instruction, students carry out laboratory exercises and investigations in structured quadruples, work on projects in pairs, and then create reports and respond to assessment questions on their own. Observations of student performance consist of assessment tasks (which are embedded in the instructional program, and each of which has direct links to the progress variables) and link tests (which are composed of short-answer items also linked to the progress variables). Recording of teacher judgments about students’ work is aided by scoring guides—criteria unique to each progress
variable that are used for assessing levels of student performance and interpreting student work (an example is provided in Table 4–1 for the Evidence and Trade-offs variable). These are augmented with exemplars—samples of actual student work illustrating performance at each score level for all assessment tasks.
The interpretation of these judgments is carried out using progress maps— graphic displays used to record the progress of each student on particular progress variables over the course of the year. The statistical underpinning for these maps is a multidimensional item response model (explained later); the learning underpinning is the set of progress variables. An example of a BEAR progress map is shown in Box 4–2. Teacher and student involvement in the assessment system is motivated and structured through assessment moderation—a process by which groups of teachers and students reach consensus on standards of student performance and discuss the implications of assessment results for subsequent learning and instruction (Roberts, Sloane, and Wilson, 1996).
To summarize, the BEAR assessment system as applied in the IEY curriculum embodies the assessment triangle as follows. The conception of learning consists of the five progress variables mentioned above. Students are helped in improving along these variables by the IEY instructional materials, including the assessments. The observations are the scores teachers assign to student work on the embedded assessment tasks and the link tests. The interpretation model is formally a multidimensional item response model (discussed later in this chapter) that underlies the progress maps; however, its meaning is elaborated through the exemplars and through the teacher’s knowledge about the specific responses a student gave on various items.
STANDARD PSYCHOMETRIC MODELS
Currently, standard measurement models focus on a situation in which the observations are in the form of a number of items with discrete, ordered response categories (such as the categories from an IEY scoring guide illustrated in Table 4–1) and in which the construct is a single continuous variable (such as one of the IEY progress variables described in Box 4–1). For example, a standardized achievement test is typically composed of many (usually dichotomous3) items that are often all linked substantively in some way to a common construct variable, such as mathematics achievement. The construct is thought of as a continuous unobservable (latent) characteristic
TABLE 4–1 Sample Scoring Guide for the BEAR Assessment
|
|
Evidence and Trade-offs (ET) Variable |
||
|
|
Using Evidence: |
Using Evidence to Make Trade-offs: |
|
|
Score |
Response uses objective reason(s) based on relevant evidence to support choice. |
Response recognizes multiple perspectives of issue and explains each perspective using objective reasons, supported by evidence, in order to make choice. |
|
|
4 |
Response accomplishes Level 3 AND goes beyond in some significant way, such as questioning or justifying the source, validity, and/or quantity of evidence. |
Response accomplishes Level 3 AND goes beyond in some significant way, such as suggesting additional evidence beyond the activity that would further influence choices in specific ways, OR questioning the source, validity, and/or quantity of evidence and explaining how it influences choice. |
|
|
3 |
Response provides major objective reasons AND supports each with relevant and accurate evidence. |
Response discusses at least two perspectives of issue AND provides objective reasons, supported by relevant and accurate evidence, for each perspective. |
|
|
2 |
Response provides some objective reasons AND some supporting evidence, BUT at least one reason is missing and/or part of the evidence is incomplete. |
Response states at least one perspective of issue AND provides some objective reasons using some relevant evidence, BUT reasons are incomplete and/or part of the evidence is missing; OR only one complete and accurate perspective has been provided. |
|
|
1 |
Response provides only subjective reasons (opinions) for choice and/or uses inaccurate or irrelevant evidence from the activity. |
Response states at least one perspective of issue BUT only provides subjective reasons and/or uses inaccurate or irrelevant evidence. |
|
|
0 |
No response; illegible response; response offers no reasons AND no evidence to support choice made. |
No response; illegible response; response lacks reasons AND offers no evidence to support decision made. |
|
|
X |
Student had no opportunity to respond. |
||
|
SOURCE: Roberts, Wilson, and Draney (1997, p. 9). Used with permission of the authors. |
|||
of the learner, representing relatively more or less of the competency that is common to the set of items and their responses. This can be summarized graphically as in Figure 4–2, where the latent construct variable θ (represented inside an oval shape in the figure to denote that it is unobservable) is thought of as potentially varying continuously from minus infinity to plus
|
BOX 4–2 Example of a BEAR Progress Map Below is an example of one of the types of progress maps produced by the BEAR assessment program. This particular example is called a “conference map” and is created by the GradeMap software (Wilson, Draney and Kennedy, 1999). This map shows the “current estimate” of where a student is on four of the IEY progress variables (the variable Group Interaction is not yet calibrated). The estimate is expressed in terms of a series of levels that are identified as segments of the continua (e.g., “Incorrect,” “Advanced”) and are specified in greater detail in the scoring guide for each progress variable. Additional examples of BEAR maps are provided later in this chapter. 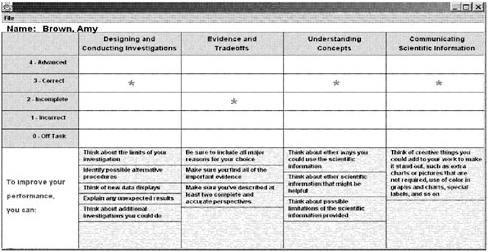 SOURCE: Wilson, Draney, and Kennedy (2001). Used with permission of the authors. |
infinity. The assessment items are shown in boxes (to denote that they are observed variables), and the arrows show that the construct “causes” the observations. Although not shown in the figure, each observed response consists of a component that statisticians generally call “error.” Note that error in this context means something quite different from its usual educational sense—it means merely that the component is not modeled (i.e., not attributable to the construct θ).
The representation in Figure 4–2 corresponds to a class of measurement models called item response models, which are discussed below. First, how-
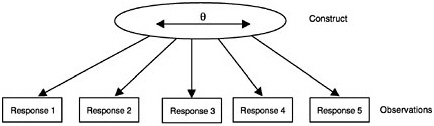
FIGURE 4–2 Unidimensional-continuous constructs. Boxes indicate observable variables; oval indicates a latent variable.
ever, some methods that emerged earlier in the evolution of measurement models are described.
Classical Test Theory
Early studies of student testing and retesting led to the conclusion that although no tests were perfectly consistent, some gave more consistent results than others. Classical test theory (CTT) was developed initially by Spearman (1904) as a way to explain certain of these variations in consistency (expressed most often in terms of the well-known reliability index). In CTT, the construct is represented as a single continuous variable, but certain simplifications were necessary to allow use of the statistical methods available at that time. The observation model is simplified to focus only on the sum of the responses with the individual item responses being omitted (see Figure 4–3). For example, if a CTT measurement model were used in the BEAR example, it would take the sum of the student scores on a set of assessment tasks as the observed score. The measurement model, sometimes referred to as a “true-score model,” simply expresses that the true score (θ) arises from an observed score (x) plus error (e). The reliability is then the ratio of the variance of the true score to the variance of the observed score. This type of model may be sufficient when one is interested only in a single aspect of student achievement (the total score) and when tests are considered only as a whole. Scores obtained using CTT modeling are usually translated into percentiles for norm-referenced interpretation and for comparison with other tests.
The simple assumptions of CTT have been used to develop a very large superstructure of concepts and measurement tools, including reliability indices, standard error estimation formulae, and test equating practices used to link scores on one test with those on another. CTT modeling does not allow
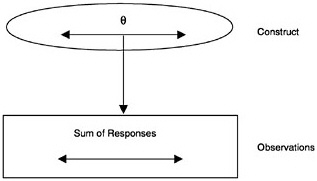
FIGURE 4–3 Classical test theory model.
the simultaneous assessment of multiple aspects of examinee competence and does not address problems that arise whenever separate parts of a test need to be studied or manipulated. Formally, CTT does not include components that allow interpretation of scores based on subsets of items in the test. Historically, CTT has been the principal tool of formal assessments, and in part because of its great simplicity, it has been applied to assessments of virtually every type. Because of serious practical limitations, however, other theories—such as generalizability theory, item response modeling, and factor analysis—were developed to enable study of aspects of items.
Generalizability Theory
The purpose of generalizability theory (often referred to as G-theory) is to make it possible to examine how different aspects of observations—such as using different raters, using different types of items, or testing on different occasions—can affect the dependability of scores (Brennan, 1983; Cronbach, Gleser, Nanda, and Rajaratnam, 1972). In G-theory, the construct is again characterized as a single continuous variable. However, the observation can include design choices, such as the number of types of tasks, the number of raters, and the uses of scores from different raters (see Figure 4–4). These are commonly called facets4 of measurement. Facets can be treated as fixed or random. When they are treated as random, the observed elements in the facet are considered to be a random sample from the universe of all possible elements in the facet. For instance, if the set of tasks included on a test were
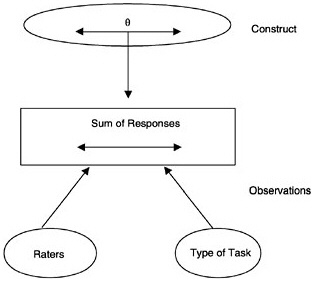
FIGURE 4–4 Generalizability theory model with two facets— raters and item type.
treated as a random facet, it would be considered a random sample of all possible tasks generated under the same rules to measure the construct, and the results of the g-study would be considered to generalize to that universe of tasks. When facets are treated as fixed, the results are considered to generalize only to the elements of the facet in the study. Using the same example, if the set of tasks were treated as fixed, the results would generalize only to the tasks at hand (see Kreft and De Leeuw, 1998, for a discussion of this and other usages of the terms “random” and “fixed”).
In practice, researchers carry out a g-study to ascertain how different facets affect the reliability (generalizability) of scores. This information can then guide decisions about how to design sound situations for making observations—for example, whether to average across raters, add more tasks, or test on more than one occasion. To illustrate, in the BEAR assessment, a g-study could be carried out to see which type of assessment—embedded tasks or link items—contributed more to reliability. Such a study could also be used to examine whether teachers were as consistent as external raters. Generalizability models offer two powerful practical advantages. First, they allow one to characterize how the conditions under which the observations were made affect the reliability of the evidence. Second, this information is expressed in terms that allow one to project from the current assessment design to other potential designs.
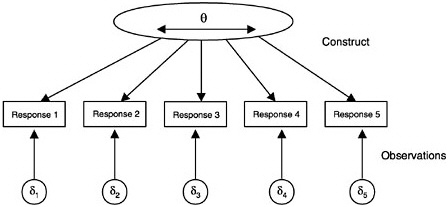
FIGURE 4–5 Item response model. (di= item parameters).
Item Response Modeling
Perhaps the most important shortcoming of both CTT and G-theory is that examinee characteristics and test characteristics cannot be separated; each can be interpreted only in the specific context of the other. An examinee’s achievement level is defined only in terms of a particular test. When the test is “difficult,” the examinee will appear to have low achievement; when the test is “easy,” the examinee will appear to have high achievement. Whether an item is difficult or easy depends on the ability of the examinees being measured, and the ability of the examinees depends on whether the test items are difficult or easy.
Item response modeling (IRM) was developed to enable comparisons among examinees who take different tests and among items whose parameters are estimated using different groups of examinees (Lord and Novick, 1968; Lord, 1980). Furthermore, with IRM it is possible to predict the properties of a test from the properties of the items of which it is composed. In IRM, the construct model is still represented as a single continuous variable, but the observation model is expressed in terms of the items (as in Figure 4– 5). The model is usually written as an equation relating the probability of a
certain response to an item in terms of student and item parameters. The student parameter (same as the latent construct θ) indicates level of proficiency, ability, achievement, or sometimes attitude. The student parameter is usually translated into a scaled score5 for interpretation. The item parameters express, in a mathematical equation, characteristics of the item that are believed to be important in determining the probabilities of observing different response categories. Examples include (1) how “difficult” it is to get an item correct; (2) the extent to which an item differentiates between students who are high and low on the latent construct (sometimes called an item “discrimination” parameter); and (3) other complications, such as how guessing or rater harshness might influence the result. (Note that IRMs that assume an a priori discrimination parameter have particular characteristics and are generally dubbed “Rasch” models in honor of George Rasch [Rasch, 1960)]. Most applications of IRM use unidimensional models, which assume that there is only one construct that determines student responses. Indeed, if one is interested primarily in measuring a single main characteristic of a student, this is a good place to start. However, IRMs can also be formulated for multidimensional contexts (discussed below).
Formal components of IRM have been developed to help diagnose test and item quality. For instance, person and item fit indices help identify items that do not appear to work well and persons for whom the items do not appear to work well.
As an example of how IRM can be used, consider the map of student progress for the variable Designing and Conducting Investigations displayed in Figure 4–6. Here, the successive scores on this variable (similar to the levels in Table 4–1) are indicated by the categories in the far right-hand column (the “criterion zones”) and by the corresponding bands across the map. As students move “up” the map, they progress to higher levels of performance. The ability to express the student construct and item parameters on the same scale is one of the most useful and intuitive features of IRM, allowing one to interpret the student’s rise in performance over time as an increased probability of receiving higher scores (corresponding to higher qualitative levels of performance) on the items and link items. Although hidden in this image of the results, the underlying foundation of this map (i.e., the unconfounding of item difficulty and student change) is based on a technical manipulation of the item parameters that would not be possible with a CTT approach.
As with CTT, with IRM one can still tell a story about a student’s proficiency with regard to the latent construct. One can now, additionally, talk about what tends to happen with specific items, as expressed by their item parameters. This formulation allows for observation situations in which different students can respond to different items, as in computerized adaptive testing and matrix-sampling designs of the type used in the National Assessment of Educational Progress (NAEP).
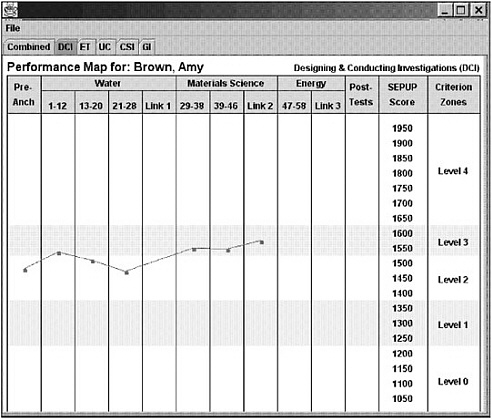
FIGURE 4–6 Example of a performance map for the Designing and Conducting Investigations variable.
SOURCE: Wilson, Draney, and Kennedy (2001). Used with permission of the authors.
Figure 4–5 can also be used to portray a one-dimensional factor analysis, although, in its traditional formulation, factor analysis differs somewhat from IRM. Like IRM, unidimensional factor analysis models the relationship between a latent construct or factor (e.g., mathematics computation skill) and observable manifestations of the construct (e.g., scores on tests of mathematics computation). With traditional factor analysis, the relationship between an observed variable and the factor is called a “factor loading.” Factor loadings correspond to item discrimination parameters in IRM. In factor analysis, the observable variables are strictly continuous rather than ordered categories as in IRM. This latter feature implies that the “items” in factor analysis might better be thought of as sums from subsets of more basic items. More recent formulations relax these limitations.
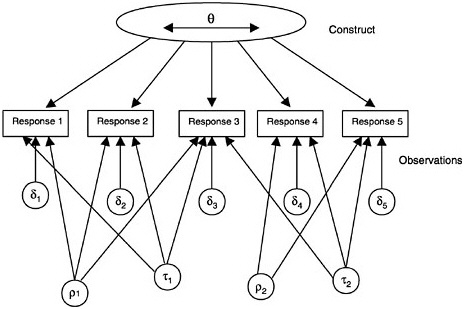
FIGURE 4–7 Item response model with two observation model facets—raters (ρ1and ρ2), and item type (τ1and τ2).
Similar to ways in which G-theory has extended CTT, elements of the observations, such as raters and item features, can be added to the basic item response framework (see Figure 4–7) in what might be called faceted IRMs. Examples of facets are (1) different raters, (2) different testing conditions, and (3) different ways to communicate the items. One foundational difference is that in IRMs the items are generally considered fixed, whereas in G-theory they are most often considered random. That is, in G-theory the items are considered random samples from the universe of all possible similarly generated items measuring the particular construct. In practice very few tests are constructed in a way that would allow the items to be truly considered a random sampling from an item population.
Latent Class Models
In the measurement approaches described thus far, the latent construct has been assumed to be a continuous variable. In contrast, some of the research on learning described in Chapter 3 suggests that achievement in certain domains of the curriculum might better be characterized in the form of discrete classes or types of understanding. That is, rather than assuming
that each student lies somewhere on a continuum, one could assume that the student belongs to one of a number of categories or classes. Models based on this approach are called latent class models. The classes themselves can be considered ordered or unordered. When the classes are ordered, there is an analogy with the continuum models: each latent class can be viewed as a point on the continuum (see Figure 4–8). When the classes are unordered, that analogy breaks down, and the situation can be represented by deleting the “>” signs in Figure 4–8.
An argument could be made for using latent classes in the BEAR example discussed earlier. If one assumed that a student’s responses are “caused” by being in ordered latent classes corresponding to the successive scores in the Designing and Conducting Investigations scoring guide, one could construct something like the progress map in Figure 4–6, although the vertical dimension would lose its metric and become a set of four categories. For interpretation purposes, this map would probably be just about as useful as the current one.
One might ask, which assumption is right—continuous or discrete? The determining factor should be how useful the measurement model is in reflecting the nature of achievement in the domain, not whether the continuous or the categorical assumption is “the right one.” In fact, there have been cases in which both the continuous and discrete models have been fit reasonably well to the same dataset (see, e.g., Haertel, 1990). The important question is, given the decisions one has to make and the nature of cognition and learning in the domain, which approach provides the most interpretable information? Investigating this question may indeed reveal that one approach is better than the other for that particular purpose, but this finding does not answer the more general question.
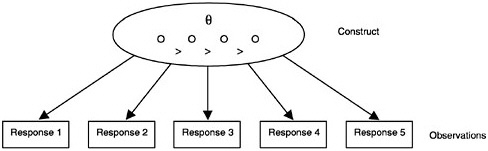
FIGURE 4–8 Ordered latent class model with four classes (indicated by “O”)
Multiattribute Models
Each of the four general classes of models described above—classical, generalizability, item response, and latent class—can be extended to incorporate more than one attribute of the student. Doing so allows for connections to a richer substantive theory and educationally more complex interpretations. In multidimensional IRM, observations are hypothesized to correspond to multiple constructs (Reckase, 1972; Sympson, 1978). For instance, performance on mathematics word problems might be attributable to proficiency in both mathematics and reading. In the IEY example above, the progress of students on four progress variables in the domain of science was mapped and monitored (see Box 4–2, above). Note that in this example, one might have analyzed the results separately for each of the progress variables and obtained four independent IRM estimations of the student and item parameters, sometimes referred to as a consecutive approach (Adams, Wilson, and Wang, 1997).
There are both measurement and educational reasons for using a multidimensional model. In measurement terms, if one is interested, for example, in finding the correlation among the latent constructs, a multidimensional model allows one to make an unbiased estimate of this correlation, whereas the consecutive approach produces smaller correlations than it should. Educationally dense longitudinal data such as those needed for the IEY maps can be difficult to obtain and manage: individual students may miss out on specific tasks, and teachers may not use tasks or entire activities in their instruction. In such a situation, multidimensional models can be used to bolster sparse results by using information from one dimension to estimate performance on another. This is a valuable use and one on which the BEAR assessment system designers decided to capitalize. This profile allows differential performance and interpretation on each of the single dimensions of IEY Science, at both the individual and group levels. A diagram illustrating a two-dimensional IRM is shown in Figure 4–9. The curved line indicates that the two dimensions may be correlated. Note that for clarity, extra facets have not been included in this diagram, but that can be routinely done. Multidimensional factor analysis can be represented by the same diagram. Among true-score models, multivariate G-theory allows multiple attributes. Latent class models may also be extended to include multiple attributes, both ordered and unordered. Figures analogous to Figure 4–9 could easily be generated to depict these extended models.
MODELS OF CHANGE AND GROWTH
The measurement models considered thus far have all been models of status, that is, methods for taking single snapshots of student achievement in
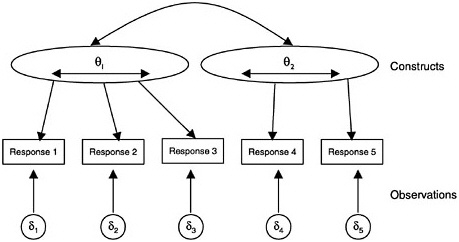
FIGURE 4–9 Multidimensional item response model.
time. Status measures are important in many assessment situations, but in an educational setting it is also important to track and monitor student change over time. One way to do this is to repeatedly record status measures at different times and to directly interpret patterns in those measures. This approach is not the same, however, as explicitly modeling changes in performance.
The account that follows should make clear that quite flexible and complex formal models of growth and change are available to complement the status models described in the previous section. Use of these models is currently limited by their relative newness and the statistical sophistication they demand of the user. More important, however, growth models require the existence of longitudinal data systems that can be used for measuring growth. In fact, as the following IEY example shows, monitoring of growth can take place without the use of any formal growth model.
The IEY maps are examples of repeated status measures; in particular see the map of student progress in Figure 4–6. Although a complex statistical model lies behind the measures of status recorded on that map, no overall model of growth was used to arrive at the map for each individual. Each map is simply a record of the different estimates for each student over time. For many assessment applications, especially when previous work has not established expectations for patterns of growth, this may be the most useful approach. The constraints on the use of a growth o`r change perspective tend to be due not to a lack of applicable models, but to the difficulties of
collecting, organizing, and maintaining data that would allow one to display these sorts of maps.
However, models of change or growth can be added to the status models described above. That is, when it is important to focus on modeling change or growth in the stories one builds, one can formally include a framework for doing so in the statistical models employed. The formal modeling of such change adds a hierarchical level to the construct. Specifically, one level of the construct is a theory for the status measurement of a student at a particular time, and a second level is the theory of how students tend to change over time. Higher levels of analysis can also be added, such as how classrooms or schools change over time. This can be done with each of the three types of models described above—true-score models (e.g., CTT), models with continuous latent variables (e.g., IRM), and models with discrete latent variables (e.g., latent class analysis).
True-Score Modeling of Change
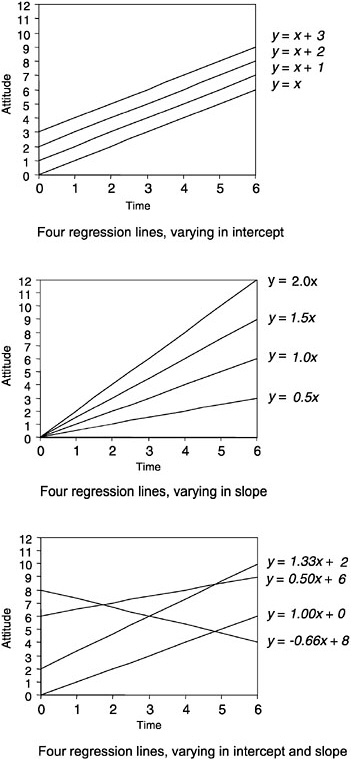
One can incorporate change into a true-score framework by modeling changes in performance over time. Often, simple polynomial models (e.g., linear, quadratic) are used, but other formulations may be preferable under certain circumstances. Effectively, data for each individual are grouped together, the point in time when each observation was made is recorded, and a linear or other model is fitted to each individual. This approach is termed “slopes as outcomes” (Burstein, 1980) or, more generally, “varying coefficients” (Kreft and De Leeuw, 1998), since it examines the relationship between performance on the outcome variable and the timing of the observation. Such an approach seeks to determine the change in the outcome variable associated with a given unit change in time.
For example, one might be interested in the variation in particular students’ scores on an attitude scale, administered several times over a year when a new curriculum was being tried. Figure 4–10 shows three different families of linear models, where x = time; y = attitude, and each line represents a different student’s trajectory. The first panel would model a situation in which students began with differing attitudes and changed in unison as the year progressed. The second panel would model a situation in which all students began with the same attitude, but their attitudes changed at different rates throughout the year, all in the same general direction. The third panel would model a situation in which both initial status and rates of change varied from student to student.
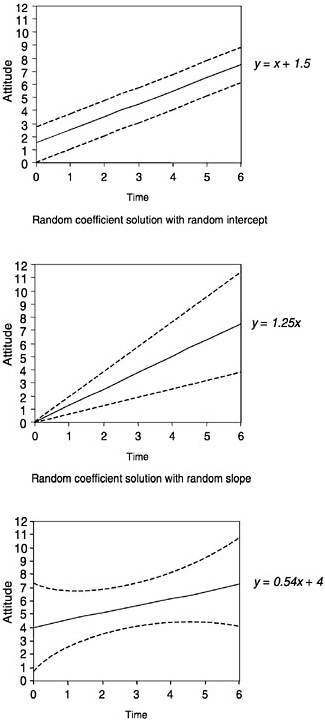
A different formulation would see these individual students as “random”; that is, they would be regarded as a sample that represents some population, and the model would then be termed a “random coefficients” model. Figure 4–11 shows a presentation equivalent to that in Figure 4–10
under the random coefficients model. In this case, only a single solid line is shown, expressing the general tendency inferred for the population; two dashed lines on either side express the variation observed around that general tendency. Here the interpretation of results would focus on (1) the general tendency and (2) the variation around that general tendency. For example, it might be found in the attitude example that students tended to improve their attitudes throughout the year (slope of general tendency is up), but that the variation was such that some students still had negative growth (see the third panel of Figure 4–11).
With random coefficients models, the next step is to investigate whether certain conditions—such as students’ scores on an entry test or different variants of the educational program—affect the slope or its variability. For example, students who score higher on the entry test (presumably those who are better prepared for the curriculum) might be found to improve their attitude more quickly than those who score lower, or it might be found that students who are given better feedback tend to have greater gains. With students clustered within classrooms, classrooms within schools, and schools within higher levels of organization, further hierarchical levels of the models can be added to investigate within- and across-level effects that correspond to a wide variety of instructional, organizational, and policy issues. Several software packages have been developed to implement these approaches, the most prominent probably being hierarchical linear modeling (HLM) (Bryk and Raudenbush, 1992) and MLn (Goldstein, Rasbash, Plewis, and Draper, 1998).
Modeling of Change in Continuous Latent Variables
There are a number of approaches that extend the above ideas into the continuous latent variables domain. One such approach is to modify the true-score approaches to incorporate measurement error; an example is the “V-known” option in the HLM software (Raudenbush, Bryk, and Congdon, 1999), which makes it possible to include the standard error of measurement of latent variable estimates as input to the analysis. Another approach is structural equation modeling (SEM) (Willet and Sayer, 1994; Muthen and Khoo, 1998). Here each time point is regarded as a separate factor, and thereafter, all the tools and techniques of SEM are available for modeling. Software packages with quite generalized modeling capabilities (e.g., LISREL, M-Plus) are available that can incorporate growth and change features into SEM. The limitation of this approach is that the assignment of time points as factors means that the data need to be structured with (not too many) fixed time points. This pattern, called time-structured data (Bock, 1979), is common in planned studies, but may be difficult to impose on many forms of educational data, especially those close to the classroom.
IRMs that address these issues have also been proposed. Fischer (1995) has developed models that focus on uniform group change (analogous to that in the first panel of Figure 4–10) by adding parameters to the observation model. Embretson (1996) has proposed more complex models of change that span both student and observation models. These models were built expressly for contexts for which there is an explicit cognitive theory involving conditional dependence among the responses. All of the approaches mentioned thus far have been unidimensional in the student model. IRMs that incorporate both a multidimensional and a hierarchical student model have been implemented in the ConQuest software (referred to as “multidimensional latent regression”) (Wu, Adams, and Wilson, 1998).
Modeling of Change in Discrete Latent Variables
When the latent construct(s) is best represented by classes rather than by a continuum, it makes sense to examine the probabilities of individuals moving from one latent class to another over time. One way to do this is with a latent Markov model, the application of which within psychological studies has been termed latent transition analysis. For example, Collins and Wugalter (1992) expressed the mathematics learning theory of Rock and Pollack-Ohls (1987) as in Figure 4–12. This is a five-attribute model with just two latent classes (“has ability” and “does not have ability”) for each attribute (note that only the “has ability” latent classes are represented here by the circles). The arrows indicate that under this model, the learning of mathematical skills takes place in a forward direction only. More complex relationships can also be modeled. Quite general software packages for implementing these models are available, such as LCAG (Hagenaars and Luijkx, 1990) and PANMARK (van de Pol, Langeheine, and de Jong, 1989).
INCORPORATION OF COGNITIVE ELEMENTS IN EXISTING MEASUREMENT MODELS
The array of models described in the previous section represents a formidable toolkit for current psychometrics. These models can be applied in many educational and psychological settings to disentangle systematic effects and errors and to aid in their interpretation. However, there is considerable dissatisfaction with this standard set of approaches, especially among cognitive psychologists, but also among educational reformers. This dissatisfaction is due in part to the dominance of the older, simpler, and more widely known parts of the toolkit—for example, models for dichotomous (right-wrong) responses over those for polytomous responses (e.g., constructed response items scored into several ordered categories), models for continuous attributes over those for discrete attributes, and single-attribute
FIGURE 4–12 A stage-sequential dynamic latent variable exhibiting cumulative monotonic development.
SOURCE: Collins and Wugalter (1992, p. 135). Reprinted by permission of Lawrence Erlbaum Associates.
over multiattribute models. If some of the less common models in the toolkit were more widely utilized, much of the dissatisfaction might well disappear. However, this is probably not a sufficient response to the criticisms. For example, Wolf, Bixby, Glenn, and Gardner (1991) present a strong argument for the following needs:
If we are able to design tasks and modes of data collection that permit us to change the data we collect about student performance, we will have still another task in front of us. This is the redesign or invention of educational psychometrics capable of answering the much-changed questions of educational achievement. In place of ranks, we will want to establish a developmentally ordered series of accomplishments. First…we are opening up the possibility of multiple paths to excellence…. Second, if we indeed value clinical judgment and a diversity of opinions among appraisers (such as certainly occurs in professional settings and post secondary education), we will have to revise our notions of high-agreement reliability as a cardinal symptom of a useful and viable approach to scoring student performance…. Third, we will have to break step with the drive to arrive
at a single, summary statistic for student performance…. After all, it is critical to know that a student can arrive at an idea but cannot organize her or his writing or cannot use the resources of language in any but the most conventional and boring ways…. Finally, we have to consider different units of analysis…because so much of learning occurs either in social situations or in conjunction with tools or resources, we need to consider what performance looks like in those more complex units, (pp. 63–64)
Although a single statement could not be expected to outline all possible needs, the list provided here is challenging and instructive. Much of this agenda could be accomplished now, with the measurement tools already available. For example, the second call—for the “valuing of diversity of opinions among appraisers” —could be incorporated through the use of rater facets in the observations model (see Figure 4–4, above). And the third call—for something beyond “a single, summary statistic for student performance” —could be addressed using multidimensional item response models or, more broadly, the range of multiattribute models (as in Figure 4–7, above). Other parts of this agenda are less easily satisfied. Below we discuss some ways in which statistical approaches have been augmented to address the types of issues raised in the Wolf et al. agenda.
Progress Maps: Making Numbers More Interpretable
Wolf et al. call for a “developmentally ordered series of accomplishments” which could be regarded as a prompt to apply an ordered latent class approach; indeed, some see this as the only possible interpretation. Yet while there have been explications of that approach, this has not been a common usage. What has been attempted more frequently is enhancement of the continuous approaches to incorporate a developmental perspective. This approach, dubbed developmental assessment by Masters, Adams, and Wilson (1990), is based on the seminal work of Wright using the Rasch model and its extensions (Wright and Masters, 1982). In this approach, an attempt is made to construct a framework for describing and monitoring progress that is larger and more important than any particular test or method of collecting evidence of student achievement. A simple analogy is the scale for measuring weight. This scale, marked out in ounces and pounds, is a framework that is more important and “true” than any particular measuring instrument. Different instruments (e.g., bathroom scales, kitchen scales) can be constructed and used to measure weight against this more general reporting framework. This is done by developing a “criterion-referenced” interpretation of the scale (Glaser, 1963).
Under the “norm-referenced” testing tradition, each test instrument has a special importance. Students’ performances are interpreted in terms of the
performances of other students on that same test.6 In developmental assessment, the theory of developing knowledge, skills, and understandings is of central importance. The particular instruments (approaches to assembling evidence) are of transient and secondary importance, and serve only to provide information relative to that psychological scale or theory. The frameworks for describing and monitoring progress are often referred to as progress maps (see the above example in Figure 4–6), and go by many other names including progress variables, developmental continua, progressions of developing competence, and profile strands. What these frameworks have in common is an attempt to capture in words and examples what it means to make progress or to improve in an area of learning.
An important feature of a developmental framework is that it provides a substantive basis for monitoring student progress over time. It also provides teachers, parents, and administrators with a shared understanding of the nature of development across the years of school and a basis for monitoring individual progress from year to year. A further advantage of a developmental framework or progress map is that it provides a frame of reference for setting standards of performance (i.e., desired or expected levels of achievement). An example of how results may be reported for an individual student at the classroom level, taken from the First Steps Developmental Continuum (West Australian Ministry of Education, 1991), is presented in Box 4–3.
Note that while the example in Box 4–3 illustrates change over time, no formal measurement model of growth was involved in the estimation, only a model of status repeated several times. These broad levels of development are based on the estimated locations of items on an item response scale. An example in the area of arithmetic, from the Keymath Diagnostic Arithmetic Test (Connolly, Nachtman, and Pritchett, 1972), is shown in Box 4–4. An example of the use of progress maps at the national level is given in Box 4– 5. This map is an example of using information available beyond the formal statistical model to make the results more useful and interpretable. In contexts where interpretation of results is relatively more important than formal statistical tests of parameters, this sort of approach may be very useful.
Enhancement Through Diagnostics
Another fairly common type of enhancement in educational applications is the incorporation of diagnostic indices into measurement models to add richer interpretations. For example, as noted above, the call for something beyond “a single, summary statistic for student performance” could be addressed using multidimensional IRMs; this assumes, however, that the
|
6 |
See Chapter 5 for discussion of norm-referenced vs. criterion-referenced testing. |
|
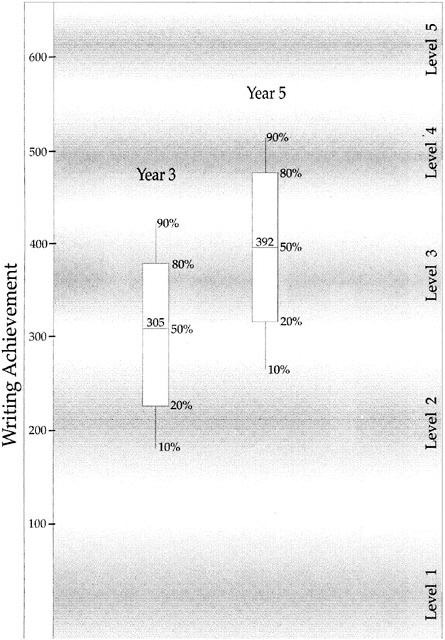
BOX 4–3 Reporting Individual Achievement in Spelling Pictured below is a developmental continuum that has been constructed as a map for monitoring children’s developing competence in spelling. Five broad levels of spelling development, labeled “Preliminary Spelling” to “Independent Spelling” are shown. On the left of the figure, one child’s estimated levels of spelling attainment on four occasions are shown. Each estimate has been dated to show the child’s progress as a speller over time. 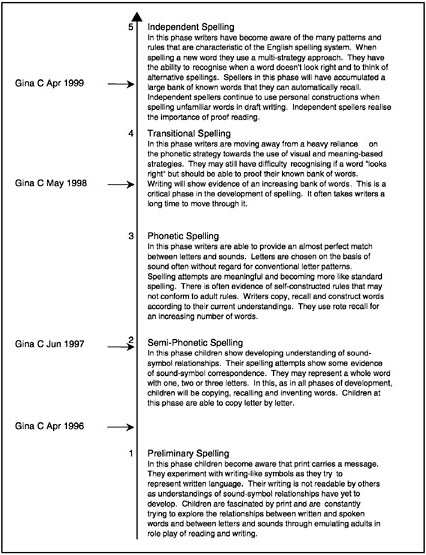 SOURCE: Masters and Forster (1996, p. 41). Used with permission of authors. |
|
BOX 4–4 Keymath Diagnostic Arithmetic Test Here the range for successive grades is shown on the left side of the figure. Shown on the right are arithmetic tasks that are typically learned during that year. That is, tasks in each band are examples of tasks that the average student in that grade probably could not complete correctly at the beginning of the year, but probably could do by the end of the year.  SOURCE: Masters and Forster (1996, p. 61). Used with permission of the authors. |
|
The line in the middle of the box is the mean; the top and bottom of the boxes show the 80th and 20th percentiles, respectively; and the ends of the “whiskers” show the 90th and 10th percentiles. The left panel alone allows the usual interpretations—e.g., grade 5 achievement is above that of grade 3, with the average grade 5 student being at about the same level as the 80th percentile of grade 3 students, but considerably below the level of the 80th percentile of grade 5 students. Looking at the right panel, one can interpret these results in a criterion-referenced way in the context of spelling. For example, one can see the difference between those in the 80th percentile of the grade 3 students and their equivalent among the grade 5 students. While these excellent grade 3 students are spelling many words correctly and their writing is quite readable (e.g., they are spelling many common words correctly), the excellent grade 5 students are spelling most words correctly (e.g., they are spelling correctly a number of words with two or more syllables and words containing silent letters). One can thus obtain a richer educational interpretation of the results of the national survey, an interpretation that can be consistent with an in-classroom one. SOURCE: Management Committee for the National School English Literacy Survey (1997, p. 84). Used with permission of the Commonwealth of Australia Department of Employment, Education, Training, and Youth Affairs. |
complexities are well modeled by an extra dimension, which may not be the case. A number of tools have been developed to examine the ways in which the models do not fit the data; these tools are generally used to relate these discrepancies to features of the test content. For example, within the Rasch approach to continuous IRM, a technique has been developed for interpreting discrepancies in the prediction of individual student responses to individual items. (These types of diagnostics can also be constructed for items with most IRM software packages.) This technique, called KIDMAP (Mead, 1976), presents a graphical display of a student’s actual responses, along with a graphical indication of what the expected responses would be under the estimated model. This is a kind of residual analysis, where the residual is the difference between expected and observed. The task is then to generate a substantive interpretation of the resulting patterns. Box 4–6 illustrates some results from a test of “number” items, using output from the Quest program
(Adams and Khoo, 1992). A different format for displaying these diagnostic data is shown in Box 4–7, which presents an example constructed by the GradeMap software (Wilson, Draney, and Kennedy, 2001) for the IEY curriculum.
These fit investigation techniques can be applied broadly across many contexts. When one has substantive theoretical underpinnings based on cognitive analysis, one can probe in greater detail. An example is the rule-space representation of Tatsuoka (1990, 1995). The first component of this representation is an analysis of correct and incorrect rules, or attributes, underlying student performance on a set of items. These rules arise from cognitive theory and an examination of the way people solve the problems presented in the items. The second is a measure of the fit of each student’s pattern of right and wrong answers to a unidimensional IRM, sometimes called a “caution index” in this literature; the closer to zero is the caution index, the better is the fit of the student’s response pattern to the IRM.
Each student is thus assigned an ability value and a caution index value. All student pairs of ability and caution indices are plotted as in the schematic. The ability-by-caution index plot is called a “rule-space plot”; it is a way of examining residuals for the IRM. Usually the students cluster in some way in rule space (in Figure 4–13, five clusters can be seen). Roughly speaking, one now examines the response patterns for the students in each cluster to see what combination of correct and incorrect rules accounts for most of the answer patterns in each cluster. In Figure 4–13, all the clusters are already distinguished by their ability values, except the clusters labeled A and B. The IRM assigns a subset of the cluster B proficiencies to cluster A; the two clusters are initially distinguished only by their caution indices. It is also likely that a different combination of correct and incorrect rules explains the response patterns of students in the two clusters. The rule-space plot shows how answer pattern residuals from a unidimensional IRM can be used to seek patterns in the data that are more complex than the model itself accounts for.
Regardless of whether one finds these enhancements satisfying in a formal statistical modeling sense, there are three important points to be made about the use of such strategies. First, they provide a bridge from familiar to new and from simpler to more complex formulations; thus they may be needed to aid the comprehension of those not immersed in the details of measurement modeling. Second, they may provide an easier stance from which to prepare reports for consumers and others for whom statistical testing is not the primary purpose of assessment. Third, strategies such as these may always be necessary, given that the complex models of today are probably going to be the simple models of tomorrow.
|
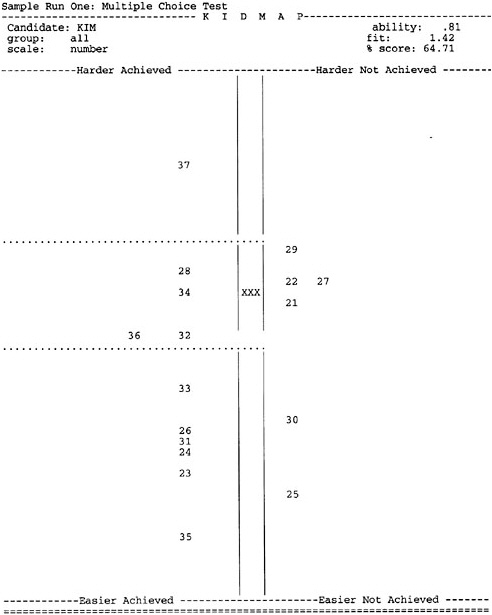
BOX 4–6 A KIDMAP Opposite is an example of a KIDMAP. The symbol “XXX” shows the location of a student named Kim on the item map. Items the student answered correctly are represented by the items in the left-hand panel (with the locations indicating their relative difficulty). Items the student answered incorrectly are indicated in the same way in the right-hand panel. Under the standard IRM convention for representing item and student location, the probability of success is 0.50 for items located at exactly the same point as the student; the probability increases as the item drops below the student and decreases as it rises above. Thus, we would expect items located below the student (i.e., near the “XXX”) to be ones the student would be more likely to get right; we would expect items located above the student to be ones the student would be more likely to get wrong; and we would not be surprised to see items located near the student to be gotten either right or wrong. The exact delineation of “near” is somewhat arbitrary, and the Quest authors have chosen a particular value that we will not question here. What they have done is divide the map into three regions: above, near, and below the student (indicated by the dotted lines in the figure). Items on the left-hand side below the dotted line should not be surprising (i.e., they are relatively easy for Kim), nor should items above the dotted line on the right-hand side (i.e., they are relatively difficult for Kim). But the items in the top left and bottom right quadrants are ones for which Kim has given surprising responses; she has responded to the relatively difficult item 37 correctly and the relatively easy items 30 and 25 incorrectly. With more information about these items and about student Kim, we could proceed to a tentative interpretation of these results. |
|
BOX 4–7 Diagnostic Results: An Example of a Target Performance Map for the IEY Curriculum The figure below shows a target performance map for the IEY curriculum. In this figure, the expected performance on each item is shown by the gray band through the middle of the figure. The actual responses for each item are shown by the height of the darker gray shading in each of the columns (representing individual items). In much the same way as discussed earlier (see Box 4–6), this graphical display can be used to examine patterns of expected and unexpected responses for individual diagnosis. 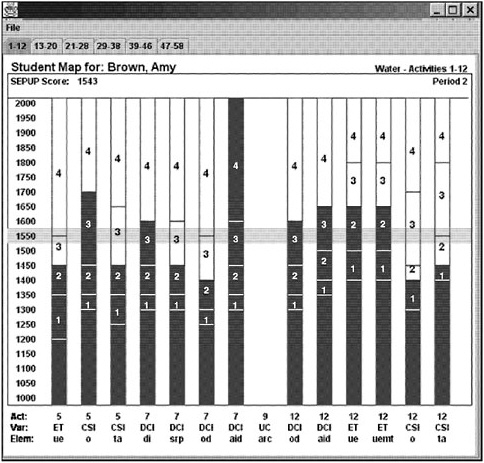 SOURCE: Wilson, Draney, and Kennedy (2001, p. 137). Used with permission of the author. |
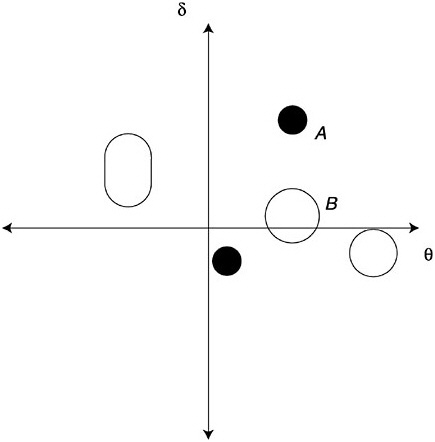
FIGURE 4–13 Clustering of examinees in Tatsuoka’s (1990, 1995) rule space.
SOURCE: Junker (1999, p. 29).
ADDING COGNITIVE STRUCTURE TO MEASUREMENT MODELS
The preferred statistical strategy for incorporating substantive structure into measurement models is to make the measurement model more complex by adding new parameters. An example was provided in the earlier discussion of generalizability theory (see Figure 4–4), where parameters representing raters and item types were used to explain some of the parameters in the existing model (in Figure 4–5, the item difficulties). This allows formal statistical testing of effects; thus the question of whether the raters are “fair” corresponds to testing whether the effect of raters is statistically significant.
The methods described below for incorporating cognitive structural elements as parameters in standard psychometric models are but a sampling of
what is at present a fairly small population of such studies. It may be hoped that further development of the current approaches and diversification of the available models will take place so that measurement models can better serve assessment.
Addition of New Parameters
A straightforward example of adding parameters to common psychometric models for substantive interpretations is the use of differential item functioning (DIF) methods. DIF methods have been used in examining differential response patterns for gender and ethnic groups for the last two decades and for language groups more recently. They are now being used for investigating whether different groups of examinees of approximately the same ability appear to be using differing cognitive processes to respond to test items. Such uses include examining whether differential difficulty levels are due to differential cognitive processes, language differences (Ercikan, 1998), solution strategies and instructional methods (Lane, Wang, and Magone, 1996), and skills required by the test that are not uniformly distributed across examinees (O’Neil and McPeek, 1993). Lane et al. (1996) used DIF analyses to detect differential response patterns and used analyses of differences in students’ solution strategies, mathematical explanations, and mathematical errors to determine reasons for those patterns. Ercikan (1998) used DIF methods for detecting differential response patterns among language groups. The statistical detection was followed up with linguistic comparison of the test versions to determine reasons for the differential response patterns observed. DIF methods, which include Mantel-Haenzsel (Holland and Thayer, 1988), item response theory-based methods (Lord, 1980), and logistic regression (Swaminathan and Rogers, 1990), can also be used to test the validity of a measurement model. A finding of significant DIF can imply that the observation framework needs to be modified, or if the DIF is common to many items, that the underlying theory of learning is oversimplified.
Hierarchization
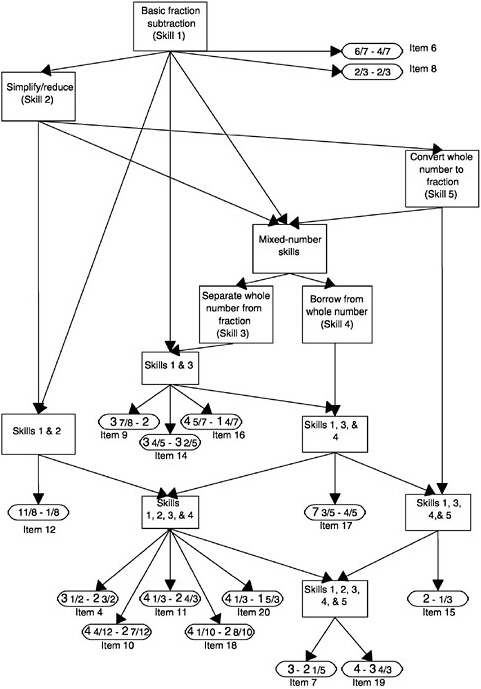
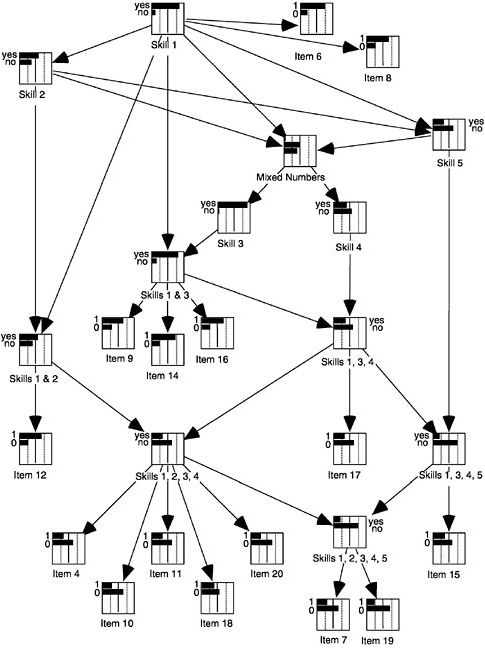
Returning to the Wolf et al. quotation given earlier, their initial call was for “a developmentally ordered series of accomplishments.” A statistical approach to this would be to posit a measurement model consisting of a series of latent classes, each representing a specific type of tasks. Item sets would be considered to be samples from their respective latent class. Formalization of this approach would allow one to make statements about students, such as “whether the student actually possesses the ‘compare fractions’ skill” (Junker, 1999), by including items and an item class that represent that skill. Such a model looks like that in Figure 4–14, where “compare fractions”
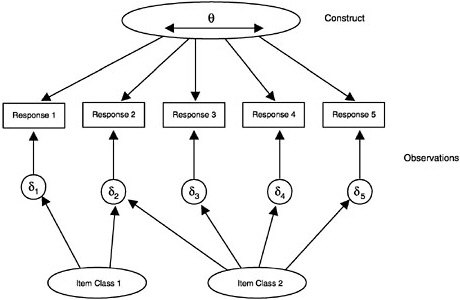
FIGURE 4–14 Item response model with a hierarchy on the observations model.
would be one of the item classes. Models of this sort, which one might term “hierarchical in the observations model,” have been implemented by Janssen, Tuerlinckx, Meulders, and De Boeck (2000) in the context of criterion-referenced classes of achievement items. Implementing the suggestion of Wolf and colleagues would involve developmentally ordering the item classes, but that is not a major step from the model of Janssen et al.
One can also consider models that would be hierarchical on the student construct model such that the development of certain competencies would be considered to precede the development of other competencies. There are a number of ways to develop measurement models suitable for hierarchical contexts, depending on which of the several approaches outlined above—true score models, IRM, and latent class modeling—one is using. For example, hierarchical factor analysis has been used to postulate hierarchies of dimensions (i.e., dimensions that “cause” subdimensions). One could also postulate hierarchies of latent classes.
Figure 4–15 illustrates one variation on a class of models that is useful for thinking about the situation in which students’ patterns of responses cannot be represented by a single dimension. The figure is labeled to suggest a progression of competencies into which a student population might be di-
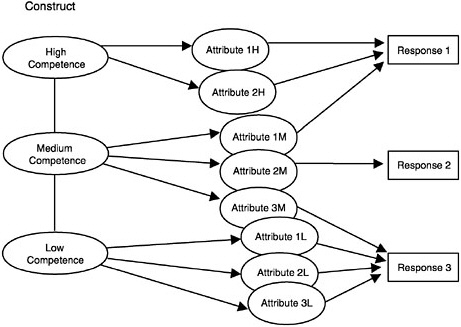
FIGURE 4–15 Latent class model with a hierarchy on the student construct model. Note: There is no observations model in this example.
vided or through which a single student might pass over time. In this model, a student can be in only one of three states of competence (low, medium, or high). Within a state of competence, the student has access only to the student attributes associated with that state and can apply only those attributes to each task. Thus a student in the “low competence” state would have only the tools to respond correctly to the third, easiest task; a student in the “medium competence” state would have the tools to respond correctly to all three tasks but would require a different attribute for each task; and a student in the “high competence” state could use a single attribute for all three tasks, but the first task has a twist that requires an extra attribute. Some states of competence might share attributes, but this would unnecessarily complicate the figure. The restricted latent class model of Haertel (1989) and Haertel and Wiley (1993) is similar in structure to this example. Clearly, the low/medium/high competence labels on the three knowledge states in Figure 4–15 could be replaced with labels that are merely descriptive and do not indicate ordering. Thus, the same figure could illustrate the modeling of multiple states of knowledge that simply represent different strategies for performing tasks in a particular domain.
Combining of Classes and Continua
The development of separate latent class and latent continuum approaches to psychometric modeling leads to distinct families of measurement models that can be given distinct substantive interpretations in assessment applications. Although this split in the psychometric families makes sense from a mathematical point of view, it does not fully reflect the more complex thinking of cognitive and developmental psychologists and educators. Consider, for example, the concept of Piagetian stages. Because the states are clearly intended to be ordered classes, it makes sense to model them with latent transition analysis. Yet it is easy to conceive of milestones within a given stage and to construct items of (meaningfully) varying difficulty that will identify differing levels of success within Piagetian stages of child development (Wilson, 1989). This sort of thinking leads one to seek ways of combining the continuum and class models we have been describing. There are a number of different possible ways to do this. One of these—the mixture model approach—is described by Mislevy and Verhelst (1990). In this approach, students are considered to be members of one of a set of latent classes, but each latent class may be characterized by a latent continuum or some other latent structure (for an alternative formulation, see Yamamoto and Gitomer, 1993).
For example, Wilson’s (1984, 1989) Saltus model was developed to address stage-like cognitive development. Each student is characterized by two variables, one quantitative and the other qualitative. The quantitative parameter indicates the degree of proficiency, while the qualitative parameter indicates the nature of proficiency and denotes group membership. The Saltus model uses a simple IRM (Rasch, 1960, 1980) technique for characterizing development within stages and posits a certain number of developmental stages among students. A student is assumed to be in exactly one group at the time of testing, though group membership cannot be directly observed. Problem situations are also classified into a certain number of classes that match the stages. The model estimates parameters that represent the amounts by which problem classes vary in terms of difficulty for different groups. These parameter estimates can capture how certain types of problem situations become much easier relative to others as people add to or reconceptualize their content knowledge. Or they can capture how some problem situations actually become more difficult as people progress from an earlier to a more advanced group because they previously answered correctly or incorrectly for the wrong reasons. Examples of this can be found in Siegler’s developmental analysis of performance on the balance scale as students’ strategy rules change (see Chapter 2).
Mislevy and Wilson (1996) demonstrated how to use a mixture model approach to estimate the parameters of this model. They used an example
dataset that had also been analyzed with Tatsuoka’s rule-space analysis (discussed earlier). Two skills involved in mixed-number subtraction are (1) finding a common denominator and (2) converting between mixed numbers and improper fractions. In this study, three types of items in mixed-number subtraction were identified: (1) those that required neither (item class 1) (e.g., 6/7–6/7); (2) those that required just finding a common denominator (item class 2) (e.g., 5/3–3/4); and (3) those that required converting to improper fractions and (maybe) finding a common denominator as well (item class 3) (e.g., 33/8–2 5/6). The qualitative aspect of student development is signaled by first acquiring the common-denominator skill (i.e., moving from student stage 1 to 2) and then the converting skill (i.e., moving from student stage 2 to 3). Mislevy and Wilson (1996) showed that in analyzing these data, the Saltus model does a better job of capturing the relationships among the item sets than does a Rasch model.
GENERALIZED APPROACHES TO PSYCHOMETRIC MODELING OF COGNITIVE STRUCTURES
Great effort may be required to develop and apply measurement models with features specific to particular substantive assessment contexts. The process may involve not only mastery of mathematical and statistical modeling, but also comprehension of and creative involvement in the theories of learning involved. The different assessment contexts far outnumber the existing psychometric models, and probably will continue to do so for a long time. Hence one is drawn to the possibility of establishing families of models that can be applied more broadly. Several such models have been developed and, in varying degrees, implemented. Two examples are reviewed in the next section—the unified model and M2RCML.7 A third example, referred to as Bayes nets, is then described.
Unified Model and M2RCML
The first instance to be described was developed specifically for the sort of case in which it can be assumed that students’ performance on tasks can be categorized into distinct and qualitative latent classes. DiBello, Stout, and Roussos (1995) cite four reasons why a measurement model may not adequately explain students’ performance if it is based on analyses that describe tasks in terms of their component attributes (e.g., skills, bits of knowl-
edge, beliefs). The first two reasons may be interpreted at least partially in terms of validity issues: first, students may choose a different strategy for performance in the task domain than that presumed by the task analysis; second, the task analysis may be incomplete in that it does not uncover all of the attributes required for task performance or does not incorporate all of them into the model. These are threats to construct validity to the extent that they indicate areas in which the measurement model may not map well to the underlying set of beliefs about cognition and learning in the domain.
The second two reasons may be interpreted at least partially in terms of reliability. DiBello et al. (1995) say a task has low “positivity” for a student attribute if there is either (1) a high probability that a student who possesses the attribute can fail to perform correctly when it is called for (we call this a “slip probability”) or (2) a high probability that a student who lacks the attribute can still perform correctly when it is called for (we call this a “guessing probability”). Of course, this latter scenario may not be a guess at all: it may result from the student’s applying an alternative strategy or a less general version of the attribute that works in the present case. Similarly, the first scenario may not be due to a “slip” but to poor question wording, transcription errors, and the like. Other deviations from the task analysis model that lead to incorrect task performance are grouped under a separate category of slips that includes such problems as transcription errors and lapses in student attention.
DiBello, Stout, and colleagues (DiBello, Stout, and Roussos, 1995; DiBello, Jiang, and Stout, 1999) have developed a multistrategy model they call the unified model, within which one can manipulate positivity, completeness, multiple strategies, and slips by turning on and shutting off various parts of the model. The components of the unified model can be adjusted to include a catchall strategy that is basically an IRM (for more detail, see Junker, 1999).
A second generalized scheme has been developed by Pirolli and Wilson (1998). This approach integrates the facets and multiattribute continuum models described earlier (e.g., as in Figures 4–4 and 4–6) with the Saltus model (also described above). Pirolli and Wilson developed an approach to measuring knowledge content, knowledge access, and knowledge learning. This approach has two elements. First it incorporates a theoretical view of cognition, called the Newell-Dennett framework, which the authors regard as being especially favorable to the development of a measurement approach. Second, it encompasses a class of measurement models, based on Rasch modeling, which the authors view as being particularly favorable to the development of cognitive theories. According to the model, in an observable situation, the knowledge a student has determines the actions he or she selects to achieve a desired goal. To the extent that models within the theory fit the data at hand, one considers measures of observed behavior to be manifestations of persons having specific classes of content knowledge
and varying degrees of access to that knowledge. Although persons, environment, and knowledge are defined in terms of one another, successful application of this approach makes it possible to separate the parameters associated with the person from those associated with the environment.
In specifying their model, dubbed M2RCML, Pirolli and Wilson assume that access to knowledge within a particular knowledge state varies continuously, but perhaps multidimensionally. That is, within a particular knowledge-content state (latent class), a student may be represented by a vector of student constructs. For instance, a group of people who know a particular problem-solving strategy or a specific set of instructions may be arrayed along a continuous scale to represent their proficiency in accessing and using that knowledge. Pirolli and Wilson also assume that people can belong to different knowledge-content states, and that each state can be characterized by the probability of people being in it. Also, they suppose that the environment in which these variables operate can be represented by a vector of environment parameters (traditionally termed “item parameters”). This approach makes an important distinction between knowledge-level and symbol-level learning (Dennett, 1988; Newell, 1982): the knowledge level is seen as being modeled by the knowledge states, and the symbol level by the IRM involving the proficiency continuum and the environment parameters. Pirolli and Wilson have illustrated their approach for data related to both learning on a LISP tutor and a rule assessment analysis of reasoning involving the balance scale as described in Chapter 2.
The generalized approaches of both the unified model and M2RCML have emerged from somewhat different branches of the psychometric tradition. Together they can be regarded as addressing almost all of the calls by Wolf and colleagues (1991, pp. 63–64) as cited earlier. The last call, however, poses a somewhat more demanding challenge: “…we have to consider different units of analysis…because so much of learning occurs either in social situations or in conjunction with tools or resources, we need to consider what performance looks like in those more complex units.” This call raises issues that are effectively outside the range of both general approaches discussed thus far: there are issues of the basic unit of analysis (individual or group), and of the interconnection between the different levels of analysis and the observations (whether the observations are at the individual or group level). For complications of this order (and this is certainly not the only such issue), greater flexibility is needed, and that is one of the possibilities offered by the approach described in the next section.
Bayes Nets
A more general modeling approach that has proven useful in a wide range of applications is Bayesian inference networks, also called Bayes nets
because of their gainful use of Bayes’ theorem.8 A probability model for an inferential problem consists of variables that characterize aspects of the problem and probability distributions that characterize the user’s knowledge about these aspects of the problem at any given point in time. The user builds a network of such variables, along with the interrelated probability distributions that capture their substantively important interrelationships. Conditional independence relationships introduced earlier in this chapter play a key role, both conceptually and computationally. The basic idea of conditional independence in Bayes nets is that the important interrelationships among even a large number of variables can be expressed mainly in terms of relationships within relatively small, overlapping, subgroups of these variables.
Bayes nets are systems of variables and probability distributions that allow one to draw inferences within complex networks of independent variables. Examples of their use include calculating the probabilities of disease states given symptoms and predicting characteristics of the offspring of animals in light of the characteristics of their ancestors. Spurred by applications in such diverse areas as pedigree analysis, troubleshooting, and medical diagnosis, these systems have become an active topic in statistical research (see, e.g., Almond, 1995; Andersen, Jensen, Olesen, and Jensen, 1989; Pearl, 1988).
Two kinds of variables appear in a Bayes net for educational assessment: those which concern aspects of students’ knowledge and skill (construct variables in the terminology of this chapter) and those which concern aspects of the things students say, do, or make (observations). The nature and grain size of the construct variables is determined jointly by a conception of knowledge in the domain and the purpose of the assessment (see Chapter 2). The nature of the observations is determined by an understanding of how students display the targeted knowledge, that is, what students say or do in various settings that provides clues about that knowledge. The interrelationships are determined partly by substantive theory (e.g., a student who does not deeply understand the control-of-variables strategy in science may apply it in a near-transfer setting but probably not in a far-transfer setting) and partly by empirical observation (e.g., near transfer is less likely to be observed for task 1 than task 2 at any level of understanding, simply because task 2 is more difficult to read).
All of the psychometric models discussed in this chapter reflect exactly this kind of reasoning, and all of them can in fact be expressed as particular implementations of Bayes nets. The models described above each evolved in their own special niches, with researchers in each gaining experience, writing computer programs, and developing a catalog of exemplars. Issues of substance and theory have accumulated in each case. As statistical methodology continues to advance (see, e.g., Gelman, Carlin, Stern, and Rubin, 1995), the common perspective and general tools of Bayesian modeling may become a dominant approach to the technical aspects of modeling in assessment. Yet researchers will continue to draw on the knowledge gained from both theoretical explorations and practical applications based on models such as those described above and will use those models as building blocks in Bayes nets for more complex assessments. The applications of Bayes nets to assessment described below have this character, reflecting their heritage in a psychometric history even as they attack problems that lie beyond the span of standard models. After presenting the rationale for Bayes nets in assessment, we provide an example and offer some speculations on the role of Bayes nets in assessment in the coming years.
Bayes nets bring together insights about the structuring of complex arguments (Wigmore, 1937) and the machinery of probability to synthesize the information contained by various nuggets of evidence. The three elements of the assessment triangle lend themselves to being expressed in this kind of framework.
Example: Mixed-Number Subtraction
The form of the data in this example is familiar—right/wrong responses to open-ended mixed-number subtraction problems—but inferences are to be drawn in terms of a more complex student model suggested by cognitive analyses. The model aims to provide short-term instructional guidance for students and teachers. It is designed to investigate which of two strategies students apply to problems and whether they can carry out the procedures necessary to solve the problems using those strategies. While competence in domains such as this can be modeled at a much finer grain size (see, e.g., VanLehn’s [1990] analysis of whole-number subtraction), the model in this example does incorporate how the difficulty of an item depends on the strategy a student employs. Rather than treating this interaction as error, as would be done under CTT or IRM, the model leverages this interaction as a source of evidence about a student’s strategy usage.
The example is based on studies of middle school students conducted by Tatsuoka (1987, 1990). The students she studied characteristically solved mixed-number subtraction problems using one of two strategies:
-
Method A—Convert mixed numbers to improper fractions; subtract; then reduce if necessary.
-
Method B—Separate mixed numbers into whole-number and fractional parts; subtract as two subproblems, borrowing one from minuend whole number if necessary; then reduce if necessary.
The responses of 530 students to 15 items were analyzed. As shown in Table 4–2, each item was characterized according to which of seven skills or subprocedures were required to solve it with Method A and which were required to solve it with Method B. The student model in the full network we build up to consists of one variable that indicates which of the two strategies a student uses and a variable for each of the subprocedures called upon by one or both strategies. If the values of these variables were known for a given pupil, one would know which strategy he or she had used on problems in this domain and which of the skills he or she had brought to bear on items when using that strategy. These unobservable constructs are connected to the observable responses through the following logic. Ideally, a student using either method would answer correctly only those items requiring the specific subprocedures the student had at his or her disposal; the student would answer incorrectly those items requiring subprocedures he or she did not know, even though the item might be solvable using the method being employed (Falmagne, 1989; Haertel and Wiley, 1993; and Tatsuoka, 1990). However, students sometimes miss items even when they do know the required subprocedures (situations called false negatives), and sometimes they answer items correctly even when they do not know the requisite subprocedures by using other, possibly faulty, strategies (false positives). The connection between observations and student-model variables is thus considered in a probabilistic sense. That is, even given the student’s knowledge, skills, and strategy preference and given the demands of an item under both of the strategies, we cannot say for sure whether the student will solve the problem correctly; the best we can do is model the probability that he or she will do so.
Bayes nets rely on conditional independence relationships. In this example, conditional independence means that students’ levels of skill in procedure knowledge and strategy usage explain all the relationships among the observed item responses; that is, no other constructs are needed to explain the relationships. As always, we know this is not strictly true; it is an approximation of the far more complex thinking in which students actually engage when they work through these problems. The cognitive analyses Tatsuoka and colleagues carried out to ground this application were already far more subtle than this model. Rather, the model has a more utilitarian purpose. Using the results of the cognitive analyses, the objective for the statistical model was merely to approximate students’ response patterns to
TABLE 4–2 Skill Requirements for Fraction Items
|
Skills Used* |
||||||||||
|
|
|
|
If Method A Used |
If Method B Used |
||||||
|
Item# |
Text |
1 |
2 |
5 |
6 |
7 |
2 |
3 |
4 |
5 |
|
4 |
|
x |
x |
x |
x |
x |
||||
|
6 |
|
x |
||||||||
|
7 |
|
x |
x |
x |
x |
x |
x |
x |
||
|
8 |
|
x |
||||||||
|
9 |
|
x |
x |
x |
x |
x |
x |
|||
|
10 |
|
x |
x |
x |
x |
x |
x |
|||
|
11 |
|
x |
x |
x |
x |
x |
x |
|||
|
12 |
|
x |
x |
x |
||||||
|
14 |
|
x |
x |
x |
||||||
|
15 |
|
x |
x |
x |
x |
x |
x |
|||
|
16 |
|
x |
x |
x |
|
x |
||||
|
17 |
|
x |
x |
x |
|
x |
x |
|||
|
18 |
|
x |
x |
x |
x |
x |
x |
x |
||
|
19 |
|
x |
x |
x |
x |
x |
x |
x |
x |
x |
|
20 |
|
x |
x |
x |
x |
x |
x |
x |
||
|
*Skills: 1. Basic fraction subtraction. 2. Simplify/reduce. 3. Separate whole number from fraction. 4. Borrow one from whole number to fraction. 5. Convert whole number to fraction. 6. Convert mixed number to fraction. 7. Column borrow in subtraction. SOURCE: Mislevy (1996, p. 399). Reprinted by permission of the National Council on Measurement in Education and by permission of the author. |
||||||||||
see which lessons in their curriculum on mixed-number subtraction would be useful for them to work on next.
Figure 4–16 depicts the structural relationships in an inference network for Method B only. That is, it is an appropriate network if we know with certainty that a student tackles items using Method B, but we do not yet know which of the required procedures he or she can carry out. Nodes represent variables—some student-model variables, the others item responses—and arrows represent dependence relationships. The probability distribution of all variables can be represented as the product distributions for the variables that are connected in the graph. The more one knows about the domain and the more thoughtfully one structures task situations, the more parsimonious these graphs become.9 Five nodes represent basic subprocedures a student using Method B needs to solve various kinds of items, such as basic fraction subtraction or mixed-number skills. Conjunctive nodes, such as “skills 1 and 2,” represent, for example, either having or not having both skill 1 and skill 2. Each subtraction item is the “child” of a node representing the minimal conjunction or combination of skills needed to solve that item with Method B. The relationship between such a node and an item incorporates false positive and false negative probabilities (that is, that some students will answer the question correctly without having the requisite skills, and some students will miss the question even though they do have the needed skills).
Cognitive theory inspired the structure of this network; the numerical values of conditional probability relationships were approximated using results from Tatsuoka’s (1983) “rule space” analysis of the data, based only on students classified as method B users. Ways of estimating these conditional probabilities from data or combining empirical and judgmental sources of information about them are discussed by Spiegelhalter, Dawid, Lauritzen, and Cowell (1993).
Figure 4–17 depicts base rate probabilities of students possessing a certain skill and getting a certain item correct, or the prior knowledge one would have about a student known to use method B before observing any of the student’s responses to the items. Figure 4–18 shows how one’s beliefs about a particular student change after seeing that student answer correctly
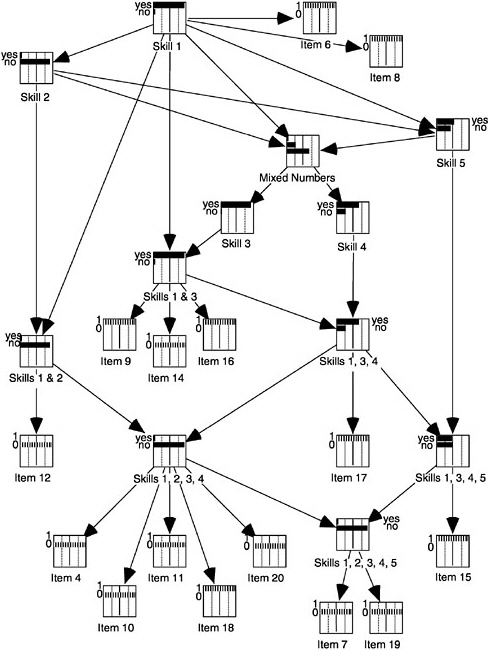
FIGURE 4–18 Updated probabilities for Method B following item responses. NOTE: Bars represent probabilities, summing to one for all the possible values of a variable. A shaded bar extendign the full width of a node represents certainty, due to having observed the value of that variable; i.e., a students actual responses to tasks.
SOURCE: Mislevy (1996, p. 403). Reprinted by permission of National Council on Measurement in Education and by permission of author.
TABLE 4–3 Base Rate and Updated Probabilities of Subprocedure Profile
|
Skill(s)* |
Prior Posterior |
Probability Probability |
|
1 |
.883 |
.999 |
|
2 |
.618 |
.056 |
|
3 |
.937 |
.995 |
|
4 |
.406 |
.702 |
|
5 |
.355 |
.561 |
|
1 & 2 |
.585 |
.056 |
|
1 & 3 |
.853 |
.994 |
|
1, 3, & 4 |
.392 |
.702 |
|
1, 2, 3, & 4 |
.335 |
.007 |
|
1, 3, 4, & 5 |
.223 |
.492 |
|
1, 2, 3, 4, & 5 |
.200 |
.003 |
|
*Skills: 1. Basic fraction subtraction. 2. Simplify/reduce. 3. Separate whole number from fraction. 4. Borrow one from whole number to fraction. 5. Convert whole number to fraction. 6. Convert mixed number to fraction. 7. Column borrow in subtraction. SOURCE: Mislevy (1996, p. 404). Reprinted by permission of the National Council on Measurement in Education and by permission of the author. |
||
most of the items that do not require skill 2 and answer incorrectly the items that do require skill 2. The updated probabilities for the five skills shown in Table 4–3 show substantial shifts away from the base rate toward the belief that the student commands skills 1, 3, 4, and possibly 5, but almost certainly not skill 2. This is shown graphically in the comparison between the initial base rate probabilities in Figure 4–17 and the probabilities updated in light of the student’s responses in Figure 4–18.
A similar network was built for Method A, and then a network was built incorporating both it and the Method B network into a single model that is appropriate when one does not know which strategy a student is using. Each item now has three parents: minimally sufficient sets of procedures under Method A and Method B, plus a new node, “Is the student using Method A or Method B?” An item with mixed fractions and large numbers but no borrowing from the first whole number, such as 72/3–51/3, is difficult under Method A but easy under Method B; an item with simple numbers that does require borrowing, such as 2 1/3–12/3, is easy under Method A but difficult under Method B. A student who responds correctly to most of the first kind of items and incorrectly to most of the second kind is probably
using Method B; a student who gets most of the first kind wrong but most of the second kind right is probably using Method A.
This example could be extended in many ways with regard to both the nature of the observations and the nature of the student model. With the present student model, one might explore additional sources of evidence about strategy use, such as monitoring response times, tracing solution steps, or simply asking the students to describe their solutions. Each such extension involves trade-offs in terms of cost and the value of the evidence, and each could be sensible in some applications but not others. An important extension of the student model would be to allow for strategy switching (Kyllonen, Lohman, and Snow, 1984). Although the students in Tatsuoka’s application were not yet operating at this level, adults often decide whether to use Method A or Method B for a given item only after gauging which strategy would be easier to apply. The variables in the more complex student model needed to account for this behavior would express the tendencies of a student to employ different strategies under different conditions. Students would then be mixed cases in and of themselves, with “always use Method A” and “always use Method B” as extremes. Situations involving such mixes pose notoriously difficult statistical problems, and carrying out inference in the context of this more ambitious student model would certainly require the richer information mentioned above.
Some intelligent tutoring systems of the type described in Chapter 3 make use of Bayes nets, explicitly in the case of VanLehn’s OLEA tutor (Martin and VanLehn, 1993, 1995) and implicitly in the case of John Anderson’s LISP and algebra tutors (Corbett and Anderson, 1992). These applications highlight again the interplay among cognitive theory, statistical modeling, and assessment purpose. Another example of this type, the HYDRIVE intelligent tutoring system for aircraft hydraulics, is provided in Annex 4–1 at the end of this chapter.
Potential Future Role of Bayes Nets in Assessment
Two implications are clear from this brief overview of the use of Bayes nets in educational assessment. First, this approach provides a framework for tackling one of the most challenging issues now faced: how to reason about complex student competencies from complex data when the standard models from educational measurement are not sufficient. It does so in a way that incorporates the accumulated wisdom residing within existing models and practices while providing a principled basis for its extension. One can expect further developments in this area in the coming years as computational methods improve, examples on which to build accumulate, and efforts to apply different kinds of models to different kinds of assessments succeed and fail.
Second, classroom teachers are not expected to build formal Bayes nets in their classrooms from scratch. This is so even though the intuitive, often subconscious, reasoning teachers carry out every day in their informal assessments and conversations with students share key principles with formal networks. Explicitly disentangling the complex evidentiary relationships that characterize the classroom simply is not necessary. Nevertheless, a greater understanding of how one would go about doing this should it be required would undoubtedly improve everyday reasoning about assessment by policy makers, the public at large, and teachers. One can predict with confidence that the most ambitious uses of Bayes nets in assessments would not require teachers to work with the nuts and bolts of statistical distributions, evidence models, and Lauritzen-Spiegelhalter updating. Aside from research uses, one way these technical elements come into play is by being built into instructional tools. The computer in a microwave oven is an analogy, and some existing intelligent tutoring systems are an example. Neither students learning to troubleshoot the F-15 hydraulics nor their trainers know or care that a Bayes net helps parse their actions and trigger suggestions (see the HYDRIVE example presented in Annex 4–1). The difficult work is embodied in the device. More open systems than these will allow teachers or instructional designers to build tasks around recurring relationships between students’ understandings and their problem solving in a domain, and to link these tasks to programs that handle the technical details of probability-based reasoning.
The most important lesson learned thus far, however, is the need for coordination across specialties in the design of complex assessments. An assessment that simultaneously pushes the frontiers of psychology, technology, statistics, and a substantive domain cannot succeed unless all of these areas are incorporated into a coherent design from the outset. If one tries to develop an ambitious student model, create a complex simulation environment, and write challenging task scenarios—all before working through the relationships among the elements of the assessment triangle needed to make sense of the data—one will surely fail. The familiar practice of writing test items and handing them off to psychometricians to model the results cannot be sustained in complex assessments.
MODELING OF STRATEGY CHANGES10
In the preceding account, measurement models were discussed in order of increasing complexity with regard to how aspects of learning are mod-
|
10 |
This section draws heavily on the commissioned paper by Brian Junker. For the paper, go to <http://www.stat.cmu.edu/~brian/nrc/cfa/>. [March 2, 2001]. |
eled. Alternatively, one could organize the discussion in accordance with specific ideas from cognitive psychology. For example, one highly salient concept for cognitive psychologists is strategy. This section examines how the models described above might be used to investigate this issue.
It is not difficult to believe that different students bring different problem-solving strategies to an assessment setting; sufficiently different curricular backgrounds provide a prima facie argument that this must happen. Moreover, comparative studies of experts and novices (e.g., Chi, Glaser, and Farr, 1988) and theories of expertise (e.g., Glaser, 1991) suggest that the strategies one uses to solve problems change as one’s expertise grows. Kyllonen et al. (1984) show that strategies used by the same person also change from task to task, and evidence from research on intelligent tutoring systems suggests it is not unusual for students to change strategy within a task as well. Thus one can distinguish at least four cases for modeling of differential strategy use, listed in increasing order of difficulty for statistical modeling and analysis:
-
Case 0—no modeling of strategies.
-
Case 1—strategy changes from person to person.
-
Case 2—strategy changes from task to task for individuals.
-
Case 3—strategy changes within a task for individuals.
Which case is selected for a given application depends, as with all assessment modeling decisions, on trade-offs between capturing what students are actually doing and serving the purpose of the assessment. Consider, for example, the science assessment study of Baxter, Elder, and Glaser (1996), which examined how middle school students’ attempts to learn what electrical components were inside “mystery boxes” revealed their understanding of electrical circuits. One might decide to conduct an assessment specifically to identify which attributes of high competence a particular student has, so that the missing attributes can be addressed without regard to what low-competence attributes the student possesses; this could be an instance of Case 0. On the other hand, if the goal were to identify the competency level of the student—low, medium, or high—and remediate accordingly, a more complete person-to-person model, as in Case 1, would be appropriate. In addition, if the difficulty of the task depended strongly on the strategy used, one might be forced to apply Case 1 or one of the other cases to obtain an assessment model that fit the data well, even if the only valuable target of inference were the high-competence state.
Many models for Case 1 (that is, modeling strategy changes among students, but assuming that strategy is constant across assessment tasks) are variations on the latent class model of Figure 4–8. For example, the Haertel/
Wiley latent class model, which defines latent classes in terms of the sets of attributes class members possess, maps directly onto Figure 4–8.
The Mislevy and Verhelst (1990) model used to account for strategy effects on item difficulty in IRM also models strategy use at the level of Case 1. This approach uses information about the difficulties of the tasks under different strategies to draw inferences about what strategy is being used. Wilson’s Saltus model (Wilson, 1989; Mislevy and Wilson, 1996) is quite similar, positing specific interactions on the θ scale between items of a certain type and developmental stages of examinees. The M2RCML model of Pirolli and Wilson (1998) allows not only for mixing of strategies that drive item difficulty (as in the Mislevy and Verhelst and the Saltus models), but also for mixing over combinations of student proficiency variables. All of these Case 1 approaches are likely to succeed if the theory for positing differences among task difficulties under different strategies produces some large differences in task difficulty across strategies.
Case 2, in which individual students change strategy from task to task, is more difficult. One example of a model intended to accommodate this case is the unified model of DiBello and colleagues (DiBello et al, 1995; DiBello, et al., 1999). In fact, one can build a version of the Mislevy and Verhelst model that does much the same thing; one simply builds the latent class model within task instead of among tasks. It is not difficult to build the full model or to formulate estimating equations for it. However, it is very difficult to fit, because wrong/right or even polytomously scored responses do not contain much information about the choice of strategy.
To make progress with Case 2, one must collect more data. Helpful additions include building response latency into computerized tests; requesting information about the performance of subtasks within a task (if informative about the strategy); asking students to answer strategy-related auxiliary questions, as did Baxter, Elder, and Glaser (1996); asking students to explain the reasoning behind their answers; or even asking them directly what strategy they are using. In the best case, gathering this kind of information reduces the assessment modeling problem to the case in which each student’s strategy is known with certainty.
Case 3, in which the student changes strategy within task, cannot be modeled successfully without rich within-task data. Some intelligent tutoring systems try to do this under the rubric of “model tracing” or “plan recognition.” The tutors of Anderson and colleagues (e.g., Anderson, Corbett, Koedinger, and Pelletier, 1995) generally do so by keeping students close to a modal solution path, but they have also experimented with asking students directly what strategy they are pursuing in ambiguous cases. Others keep track of other environmental variables to help reduce ambiguity about the choice of strategy within performance of a particular task (e.g., Hill and Johnson, 1995). Bayesian networks are commonly used for this purpose.
The Andes tutor of mechanics problems in physics (e.g., Gertner, Conati, and VanLehn, 1998) employs a Bayesian network to do model tracing. The student attributes are production rules, the observed responses are problem-solving actions, and strategy-use variables mediate the relationships between attributes and responses. Various approaches have been proposed for controlling the potentially very large number of states as the number of possible strategies grows. Charniak and Goldman (1993), for example, build a network sequentially, adding notes for new evidence with respect to plausible plans along the way.
CONCLUSIONS
Advances in methods of educational measurement include the development of formal measurement (psychometric) models, which represent a particular form of reasoning from evidence. These models provide explicit, formal rules for integrating the many pieces of information that may be relevant to specific inferences drawn from observation of assessment tasks. Certain kinds of assessment applications require the capabilities of formal statistical models for the interpretation element of the assessment triangle. These tend to be applications with one or more of the following features: high stakes, distant users (i.e., assessment interpreters without day-to-day interaction with the students), complex student models, and large volumes of data.
Measurement models currently available can support many of the kinds of inferences that cognitive science suggests are important to pursue. In particular, it is now possible to characterize students in terms of multiple aspects of proficiency, rather than a single score; chart students’ progress over time, instead of simply measuring performance at a particular point in time; deal with multiple paths or alternative methods of valued performance; model, monitor, and improve judgments on the basis of informed evaluations; and model performance not only at the level of students, but also at the levels of groups, classes, schools, and states.
Nonetheless, many of the newer models and methods are not widely used because they are not easily understood or packaged in accessible ways for those without a strong technical background. Technology offers the possibility of addressing this shortcoming. For instance, building statistical models into technology-based learning environments for use in their classrooms enables teachers to employ more complex tasks, capture and replay students’ performances, share exemplars of competent performance, and in the process gain critical information about student competence.
Much hard work remains to focus psychometric model building on the critical features of models of cognition and learning and on observations that reveal meaningful cognitive processes in a particular domain. If anything, the task has become more difficult because an additional step is now
required—determining in tandem the inferences that must be drawn, the observations needed, the tasks that will provide them, and the statistical models that will express the necessary patterns most efficiently. Therefore, having a broad array of models available does not mean that the measurement model problem has been solved. The long-standing tradition of leaving scientists, educators, task designers, and psychometricians each to their own realms represents perhaps the most serious barrier to progress.
ANNEX 4–1: AN APPLICATION OF BAYES NETS IN AN INTELLIGENT TUTORING SYSTEM
As described in Chapter 3, intelligent tutoring systems depend on some form of student modeling to guide tutor behavior. Inferences about what a student does and does not know affect the presentation and pacing of problems, the quality of feedback and instruction, and the determination of when a student has achieved tutorial objectives. The following example involves the HYDRIVE intelligent tutoring system, which, in the course of implementing principles of cognitive diagnosis, adapts concepts and tools of test theory to implement principles of probability-based reasoning (Mislevy and Gitomer, 1996).
HYDRIVE is an intelligent tutoring/assessment system designed to help trainees in aircraft mechanics develop troubleshooting skills for the F-15’s hydraulics systems. These systems are involved in the operation of the flight controls, landing gear, canopy, jet fuel starter, and aerial refueling. HYDRIVE simulates many of the important cognitive and contextual features of troubleshooting on the flightline. A problem begins with a video sequence in which a pilot who is about to take off or has just landed describes some aircraft malfunction to the hydraulics technician (for example, the rudders do not move during preflight checks). HYDRIVE’s interface allows the student to perform troubleshooting procedures by accessing video images of aircraft components and acting on those components; to review on-line technical support materials, including hierarchically organized schematic diagrams; and to make instructional selections at any time during troubleshooting, in addition to or in place of the instruction recommended by the system itself. HYDRIVE’s system model tracks the state of the aircraft system, including changes brought about by user actions.
Annex Figure 4–1 is a simplified version of portions of the Bayes net that supports inference in HYDRIVE. Four groups of variables can be distinguished (the last three of which comprise the student model). First, the rightmost nodes are the “observable variables” —actually the results of rule-driven analyses of a student’s actions in a given situation. Second, their immediate parents are knowledge and strategy requirements for two proto-
ANNEX FIGURE 4–1 Simplified version of portions of the inference network through which the HYDRIVE student model is operationalized and updated. NOTE: Bars represent probabilities, summing to one for all the possible values of a variable. A shaded bar extending the full width of a node represents certainty, due to having observed the value of that variable; i.e., a student’s actual responses to tasks.
SOURCE: Mislevy (1996, p. 407). Used with permission of the author.
typical situations addressed in this simplified diagram; the potential values of these variables are combinations of system knowledge and troubleshooting strategies that are relevant in these situations. Third, the long column of variables in the middle concerns aspects of subsystem and strategic knowledge, corresponding to instructional options. And fourth, to their left are summary characterizations of more generally construed proficiencies. The structure of the network, the variables that capture the progression from novice to expert hydraulics troubleshooter, and the conditional probabilities implemented in the network are based on two primary sources of information: in-depth analyses of how experts and novices verbalize their problem-solving actions and observations of trainees actually working through the problems in the HYDRIVE context.
Strictly speaking, the observation variables in the HYDRIVE Bayes net are not observable behaviors, but outcomes of analyses that characterize sequences of actions as “serial elimination,” “redundant action,” “irrelevant action,” “remove-and-replace,” or “space-splitting” —all interpreted in light of the current state of the system and results of the student’s previous actions. HYDRIVE employs a relatively small number of interpretation rules (about 25) to classify each troubleshooting action in these terms. The following is an example:
IF active path which includes failure has not been created and the student creates an active path which does not include failure and edges removed from the active problem area are of one power class, THEN the student strategy is power path splitting.
Potential observable variables cannot be predetermined and uniquely defined in the manner of usual assessment items since a student could follow countless paths through the problem. Rather than attempting to model all possible system states and specific possible actions within them, HYDRIVE posits equivalence classes of system-situation states, each of which could arise many times or not at all in a given student’s work. Members of these equivalence classes are treated as conditionally independent, given the status of the requisite skill and knowledge requirements. Two such classes are illustrated in Annex Figure 4–1: canopy situations, in which space-splitting11
is not possible, and landing gear situations, in which space-splitting is possible.
Annex Figure 4–1 depicts how one changes belief after observing the following actions in three separate situations from the canopy/no-split class: one redundant and one irrelevant action (both ineffectual troubleshooting moves) and one remove-and-replace action (serviceable but inefficient). Serial elimination would have been the best strategy in such cases, and is most likely to be applied when the student has strong knowledge of this strategy and all relevant subsystems. Remove-and-replace is more likely when a student possesses some subsystem knowledge but lacks familiarity with serial elimination. Weak subsystem knowledge increases chances of irrelevant and redundant actions. It is possible to get any of these classes of actions from a trainee with any combination of values of student-model variables; sometimes students with good understanding carry out redundant tests, for example, and sometimes students who lack understanding unwittingly take the same action an expert would. These possibilities must be reflected in the conditional probabilities of actions, given the values of student-model variables.
The grain size and the nature of a student model in an intelligent tutoring system should be compatible with the instructional options available (Kieras, 1988). The subsystem and strategy student-model variables in HYDRIVE summarize patterns in trouble shooting solutions at the level addressed by the intelligent tutoring system’s instruction. As a result of the three aforementioned inexpert canopy actions, Annex Figure 4–1 shows belief shifted toward lower values for serial elimination and for all subsystem variables directly involved in the situation—mechanical, hydraulic, and canopy knowledge. Any or all of these variables could be a problem, since all are required for a high likelihood of expert action. Values for subsystem variables not directly involved in the situation are also lower because, to varying degrees, students familiar with one subsystem tend to be familiar with others, and, to a lesser extent, students familiar with subsystems tend to be familiar with troubleshooting strategies. These relationships are expressed by means of the more generalized system and strategy knowledge variables at the left of the figure. These variables take advantage of the indirect information about aspects of knowledge that a given problem does not address directly, and they summarize more broadly construed aspects of proficiency that are useful in evaluation and problem selection.