LARS VALERIAN AHLFORS
April 18, 1907–October 11, 1996
BY FREDERICK GEHRING
PERSONAL AND PROFESSIONAL HISTORY
LARS AHLFORS WAS BORN in Helsinki, Finland, on April 18, 1907. His father, Axel Ahlfors, was a professor of mechanical engineering at the Institute of Technology in Helsinki. His mother, Sievä Helander, died at Lars’s birth. As a newborn Lars was sent to the Åland Islands to be taken care of by two aunts. He returned to his father’s home in Helsinki by the age of three.
At the time of Lars’s early childhood, Finland was under Russian sovereignty but with a certain degree of autonomy, and civil servants, including professors, were able to enjoy a fairly high standard of living. Unfortunately, all this changed radically during World War I, the Russian Revolution, and the Finnish civil war that followed. There was very little food in 1918, and Lars’s father was briefly imprisoned by the Red Guard.
For historical reasons the inhabitants of Finland are divided into those who have Finnish or Swedish as their mother tongue. The Ahlfors family was Swedish speaking, so Lars attended a private school where all classes were taught in Swedish. He commented that the teaching of mathematics was mediocre, but credited the school with helping
him become almost fluent in Finnish, German, and English, and less so in French. A sister of Lars was two years ahead of him in school. Hence Lars was able to learn high school mathematics by doing her homework and by means of clandestine visits to his father’s engineering library. Indeed, the teachers eventually relied on Lars to provide problems for the class.
Lars spent a summer vacation as a young student with a Finnish-speaking family to improve his knowledge of Finnish. He had hoped to pay for his keep that summer by teaching mathematics, but having found no takers, he earned his board by giving lessons to the children of the family in the German language and playing the cello.
In 1924 Lars Ahlfors entered the University of Helsinki, where his teachers were two internationally known mathematicians, Ernst Lindelöf and Rolf Nevanlinna. At that time the university was still run on the system of one professor for each subject. Lindelöf was the professor for mathematics. There were no graduate courses then, and all advanced reading was done under the supervision of Lindelöf. Lars remembered well the Saturday mornings when he had to visit Lindelöf in his home at 8 a.m. to be praised or scolded—as the case may have been.
In the spring of 1928 Lars completed all examinations for the master’s degree, and in the fall of the same year he accompanied Nevanlinna to Zürich. Nevanlinna had been invited to the Eidgenösische Technische Hochschule in Zürich for a year to fill Hermann Weyl’s chair while Weyl was on leave of absence. Lindelöf persuaded Lars’s father to let his son accompany Nevanlinna to Zürich. Later Lars emphasized the importance of this visit to Zürich: “I found myself suddenly transported from the periphery to the center of Europe.”
Nevanlinna’s course of lectures at Zürich was Lars’s first
exposure to contemporary function theory, and he became “addicted” to complex analysis. Among other things, Nevanlinna introduced the class to a 21-year-old conjecture made by the French mathematician Denjoy on the asymptotic values of an entire function, namely that an entire function of order k can have at most 2k finite asymptotic values. Lars created a sensation in the mathematical world when he found a different way to approach this problem and obtained a beautiful proof of this conjecture by means of conformal mapping (1929). His name became known to all those working in this area and, as he remarked later, “my future was made.” Lars returned to Finland and undertook his first teaching assignment as lecturer at Åbo Akademi, the Swedish-language university in Turku. At the same time he began work on his thesis, which he defended in the spring of 1930.
During 1930-1932 Lars made several trips to continental Europe, including a longer stay in Paris supported by a fellowship from the Rockefeller Foundation. In 1933 he returned to Helsinki as an adjunct professor at the University of Helsinki. That same year he married Erna Lehnert, an Austrian who with her parents had first settled in Sweden and then in Finland. Half a century later, in the preface to his Collected Papers, Lars wrote, “This was the happiest and most important event in my life.”
In 1935 Lars was first offered and then accepted a three-year appointment at Harvard University as a visiting lecturer. One year later, at the quadriennal International Congress of Mathematicians in Oslo, he was awarded a Fields Medal, the equivalent for mathematicians of a Nobel Prize.
During the 1924 International Congress of Mathematicians in Toronto, the president of the congress, Professor J. C. Fields of Canada, had proposed that two gold medals be awarded at each International Congress of Mathematicians
“for outstanding achievements in mathematics.” The winners were to be selected by an international jury. The 1932 Congress in Zürich had approved Fields’s proposal and named the medals after Fields, who had died just before the 1932 Congress. The first two Fields Medals were then awarded to Lars Ahlfors and Jesse Douglas of the United States in 1936. That he was to be awarded a Fields Medal came as a complete surprise for Lars. Indeed, he was told officially that he was to receive this honor only hours before the formal award ceremony.
Lars Ahlfors’s appointment at Harvard was for three years. He and his wife had found life in Cambridge very rewarding and they had to decide in 1938 whether to stay at Harvard or return to Finland, where he had been offered a professorship at the University of Helsinki. In the end, patriotic feelings and loyalty to his teachers drew them back to Helsinki, where they had a happy year.
Unfortunately, World War II broke out in 1939, and Lars’s wife and two children were evacuated and found refuge with relatives in Sweden. Helsinki was bombarded, the university was closed for lack of male students, but otherwise life went on. Lars was never called to military duty because of an earlier physical condition, and it is quite ironic that one of his best papers was written while he was in an air raid shelter.
Soon after the winter war the Ahlfors family was able to return to Helsinki and resume a seemingly normal life. However, politics in Finland took an unfortunate turn, and, when Hitler attacked the Soviet Union in 1941, Finland was his ally. When the Russians were able to repulse the Germans, they intensified the war in Finland with foreseeable results. The Finnish-Russian war ended with a separate armistice in September 1944, and Finland was forced to expel the German troops that had been stationed there.
The war continued off and on until 1944, and Lars felt he could not remain in Finland without sacrificing his research. He therefore accepted an invitation to the University of Zürich and, after a very difficult journey, joined their faculty in the spring of 1945. He and his wife found the postwar era a difficult time for strangers to take root in Switzerland. Hence in 1946 Lars was delighted to accept an invitation to return to Harvard, where he remained for the rest of his career.
We consider next excerpted descriptions of three aspects of Ahlfors’s research by Robert Osserman, Irwin Kra, and the present author, respectively, which appear in Volume 45 of the Notices of the American Mathematical Society.
CONFORMAL GEOMETRY
BY ROBERT OSSERMAN
There are two directions in which one can pursue the relations between Riemann surfaces and Riemannian manifolds. First, if a two-dimensional Riemannian manifold is given, then not only lengths but also angles are well defined, so that it inherits a conformal structure. Furthermore, there always exist local isothermal coordinates, which are local conformal maps from the plane into the surface. The set of all such local maps forms a complex structure for the manifolds, which can then be thought of as a Riemann surface. One then has all of complex function theory to bring to bear in studying the geometry of the surface. The most notable successes of this approach have been in the study of minimal surfaces, as exemplified in the contributions to that subject made by some of the leading function theorists of the nineteenth century: Riemann, Weierstrass, and Schwarz.
In the other direction, given a Riemann surface one can consider those metrics on the surface that induce the given
conformal structure. By the Koebe uniformization theorem, such metrics always exist. In fact, for “classical Riemann surfaces” of the sort originally considered by Riemann, which are branched covering surfaces of the plane, there is the natural Euclidean metric obtained by pulling back the standard metric on the plane under the projection map. One can also consider the Riemann surface to lie over the Riemann sphere and to lift the spherical metric to the surface. Both metrics prove very useful for obtaining information about the complex structure of the surface.
For simply connected Riemann surfaces the Koebe uniformization theorem tells us that they are all conformally equivalent to the sphere, the plane, or the unit disk. Since the first case is distinguished from the other two by the topological property of compactness, the interesting question concerning complex structure is deciding in the noncompact case whether a given surface is conformally the plane or the disk, which became known as the parabolic and hyperbolic cases, respectively. In 1932 Andreas Speiser formulated the “problem of type,” which was to find criteria that could be applied to various classes of Riemann surfaces to decide whether a given one was parabolic or hyperbolic. That problem and variants of it became a central focus of Ahlfors’s work for several decades. He started by obtaining conditions for a branched surface to be of parabolic type in terms of the number of branch points within a given distance of a fixed point on the surface, first using the Euclidean metric and later realizing that a much better result could be obtained from the spherical metric. But perhaps his main insight was that one could give a necessary and sufficient condition by looking at the totality of all conformal materics on the surface.
The problem of type may be viewed as a special case of the general problem of finding conformal invariants. There one has some class of topologically defined objects, such as
a simply or doubly connected domain or a simply connected domain with boundary and four distinguished points on the boundary, and one seeks to define quantities that determine when two topologically equivalent configurations are conformally equivalent. One example is the “extremal length” of a family of curves in a domain, which is defined by a minimax expression in terms of all conformal metrics on the domain and is thereby automatically a conformal invariant. Ahlfors and Beurling, first independently and then jointly, developed this idea into a very useful tool that has since found many further applications.
From the first, Ahlfors viewed classical results like Picard’s theorem and Bloch’s theorem as special cases of the problem of type, in which such conditions as the projection of a Riemann surface omitting a certain number of points would imply that the surface was hyperbolic and hence could not be the image of a function defined in the whole plane. He felt that the Nevanlinna theory should also fit into that framework. Finally, in 1935 he produced one of his most important papers, in which he used the idea of specially constructed conformal metrics (or “mass distributions” in the terminology of that paper) to give his own geometric version of Nevanlinna theory. When he received his Fields Medal the following year, Carathéodory remarked that it was hard to say which was more surprising: that Nevanlinna could develop his entire theory without the geometric picture to go with it or that Ahlfors could condense the whole theory into 14 pages.
Not satisfied that he had yet got to the heart of Nevanlinna theory from a geometric point of view, Ahlfors went on to present two further versions of the theory. The first, also from 1935, was one of his masterpieces: the theory of covering surfaces (1935). The guiding intuition of the paper is this: If a meromorphic function is given, then the funda-
mental quantities studied in Nevanlinna theory, such as the counting function, determined by the number of points inside a disk of given radius where the function assumes a given value, and the Nevanlinna characteristic function, measuring the growth of the function, can be reinterpreted as properties of the Riemann surface of the image of the function, viewed as a covering surface of the Riemann sphere. The counting function, for example, just tells how many points in the part of the image surface given by the image of the disk lie over the given point on the sphere. The exhaustion of the plane by disks of increasing radii is replaced by an exhaustion of the image surface. Ahlfors succeeded in showing that by using a combination of metric and topological arguments (the metric being that of the sphere and its lift to the covering surface), one can not only recover basically all of standard Nevanlinna theory but that—quite astonishingly—the essential parts of the theory all extend to a far wider class of functions than the very rigid special case of meromorphic functions, namely, to functions that Ahlfors calls “quasiconformal”; in this theory the smoothness requirements may be almost entirely dropped, and asymptotically, images of small circles—rather than having to be circles—can be arbitrary ellipses as long as the ratio of the radii remains uniformly bounded.
Of his three geometric versions of Nevanlinna theory, Ahlfors has described the one on covering surfaces as a “much more radical departure from Nevanlinna’s own methods” and as “the most original of the three papers,” which is certainly the case. (According to Carathéodory that paper was singled out in the decision of the selection committee to award the Fields Medal to Ahlfors.) Nevertheless, the last of the three, published two years later in 1937, was destined to be probably at least as influential (1937,1). Here the goal was to apply the methods of differential geometry
to the study of covering surfaces. The paper is basically a symphony on the theme of Gauss-Bonnet. The explicit relation between topology and total curvature of a surface, now called the “Gauss-Bonnet theorem,” had not been around all that long at that time, perhaps first appearing in Blaschke’s 1921 Vorlesungen über Differentialgeometrie.
It occurred to Ahlfors that if one hoped to develop a higher-dimensional version of Nevanlinna theory, it might be useful to have a higher dimensional Gauss-Bonnet formula, a fact that he mentioned to André Weil in 1939, as Weil recounts in his collected works. When Weil spent the year 1941-1942 at Haverford, where Allendoerfer was teaching, he heard of Allendoerfer’s proof of the higher-dimensional Gauss-Bonnet theorem; and remembering Ahlfors’s suggestion, he worked with Allendoerfer on their joint paper, proving the generalized Gauss-Bonnet theorem for a general class of manifolds that need not be embedded. That in turn led to Chern’s famous intrinsic proof of the general Gauss-Bonnet theorem. As for Ahlfors’s idea of adapting the method to obtain a higher-dimensional Nevanlinna theory, that had to wait until the paper by Bott and Chern in 1963.
The year following his Gauss-Bonnet Nevanlinna theory paper, Ahlfors published a deceptively short and unassuming paper called “An Extension of Schwarz’s Lemma” (1938). The main theorem and its proof take up less than a page. That is followed by two brief statements of more general versions of the theorem and then four pages of applications. Initially it was the applications that received the most attention and that Ahlfors was most pleased with, since they were anything but a straightforward consequence of the main theorem. That is particularly true of the second application, which gives a new proof of Bloch’s theorem in a remarkably precise form. Bloch’s theorem states that there is a uniform constant B such that every function analytic in
the unit disk, and normalized so that its derivative at the origin has modulus 1, must map some subdomain of the unit disk one-to-one conformally onto a disk of radius B. The largest such constant B is known as Bloch’s constant. In 1937 Ahlfors and Grunsky published a paper giving an upper bound for B that they conjectured to be the exact value for this constant (1937,2). The conjectured extremal function maps the unit disk onto a Riemann surface with simple branch points in every sheet over the lattice formed by the vertices obtained by repeated reflection over the sides of an equilateral triangle, where the center of the unit disk maps onto the center of one of the triangles. One obtains the map by taking three circles orthogonal to the boundary of the unit disk that form an equilateral triangle centered at the origin with 30° angles and mapping the interior of that triangle onto the interior of a Euclidean equilateral triangle. Under repeated reflections one gets a map of the entire unit disk onto the surface described. Ahlfors and Grunsky write down an explicit expression for the function of that description with the right normalization at the origin and thereby get the size of the largest circular disk in the image, which is just the circumscribed circle of one of the equilateral triangles whose vertices are the branch points of the image surface. The size of that circle turns out to be approximately .472.
The above mentioned extension for the Schwarz lemma yielded the lower bound ![]() for the Bloch constant, a bound that has been improved by only .0001 in the intervening 67 years.
for the Bloch constant, a bound that has been improved by only .0001 in the intervening 67 years.
When his collected papers were published in 1982, Ahlfors commented that this particular paper “has more substance than I was aware of.” He also said, “Without applications my lemma would have been too lightweight for publication.” It is a lucky thing for posterity that he found applications
that he considered up to his standard, since it would have been a major loss for us not to have the published version of the Ahlfors-Schwarz lemma. As elegant and important as his applications were, I believe that they have long ago been dwarfed by the impact of the lemma itself, which has proved its value in countless other applications and has served as the underlying insight and model for vast parts of modern complex manifold theory, including Kobayashi’s introduction of the metric that now bears his name and Griffith’s geometric approach to higher dimensional Nevanlinna theory. It demonstrates perhaps more strikingly than anywhere else the power that Ahlfors was able to derive from his unique skill in melding the complex analysis of Riemann surfaces with the metric approach of Riemannian geometry.
KLEINIAN GROUPS
BY IRWIN KRA
Of the many significant contributions of Lars Ahlfors to the modern theory of Kleinian groups, I will discuss only two, which are closely related: the Ahlfors finiteness theory and the use of Eichler cohomology as a tool for proving this and related results. Both originated in the seminal paper (1964).
For the purposes of this note, a Kleinian group G will always be finitely generated, nonelementary, and of the second kind. Thus, G consists of Möbius transformations, a subgroup of PSL(2,C), and it acts discontinuously on a nonempty maximal open set Ω ⊂ C ∪ ∞, the region of discontinuity of G, whose complement Λ in C ∪ ∞, is an uncountable perfect nowhere dense subset of the Riemann sphere.
In the early 1960s not much was known about Kleinian groups. Around the beginning of this century, Poincaré sug-
gested a program for studying discrete subgroups of PSL(2,C); Poincaré’s program was based on the fact that PSL(2,R) acts on the upper half plane H2, a model for hyperbolic 2-space. The quotient of H2 by a discrete subgroup (a Fuchsian group) of PSL(2,R) is a 2-dimensional orbifold (a Riemann surface with some “marked” points). By analogy PSL(2,C) acts on H3, hyperbolic 3-space, and the quotient of H3 by a torsion free discrete subgroup of PSL(2,C) is a 3-dimensional hyperbolic manifold. The study of subgroups of PSL(2,C) was successful because of its connection to classical function theory and to 2-dimensional topology and geometry, about which a lot was known, including the uniformization theorem classifying all simply connected Riemann surfaces. Poincaré’s program was to take advantage of the connection of PSL(2,C) to 3-dimensional topology and geometry to study groups of Möbius transformations. However, in 1965 very little was known about hyperbolic 3-manifolds. Research in the field seemed to be stuck and going nowhere. Ahlfors completely ignored Poincaré’s program and took a different route to prove the finiteness theorem. He used complex analytic methods and his result described the Riemann surfaces that can be represented by a Kleinian group. About 15 years later in the mid-1970s, as a result of the fundamental contributions of W. Thurston (1982), 3-dimensional topology came to the forefront in the study of Kleinian groups.
The history of Ahlfors’s work on Kleinian groups is also part of a remarkable collaboration between Lars Ahlfors and Lipman Bers. Although they coauthored only one paper (1960), their work and the work of many of their students was intertwined. See, for example, Kra (1996). Ahlfors’s finiteness theorem says that the ordinary set Ω of a finitely generated Kleinian group G factored by the action of the group is an orbifold of finite type, finitely many “marked”
points and compactifiable as an orbifold by adding a finite number of points.
Bers (1965) reproved an equivalent known result in the Fuchsian case, a much simpler case to handle. The finiteness theorem for PSL(2,R) had been known for a long time, and Bers reproved it using modern methods, Eichler cohomology. Bers constructs Eichler cohomology classes from analytic potentials by integrating cusp forms sufficiently many times, using methods developed by Eichler (1957) for number theory.
Ahlfors generalized Bers’s method to a much wider class of subgroups of PSL(2,C). This generalization was completely nontrivial. It required the passage from holomorphic potentials to smooth potentials. This involved a conceptual jump forward—a construction of Eichler cohomology classes via an integral operator, producing a conjugate linear map a that assigns an Eichler cohomology class a(![]() ) to a bounded holomorphic q-form
) to a bounded holomorphic q-form ![]() for the group G. In addition, there appeared a very difficult technical obstacle that Ahlfors had to surmount to prove the injectivity of α. To do so Ahlfors introduced a mollifier, a function used to construct an approximate identity. Ahlfors worked only with the case q = 2. Using a modified Cauchy kernel, he constructed a potential for
for the group G. In addition, there appeared a very difficult technical obstacle that Ahlfors had to surmount to prove the injectivity of α. To do so Ahlfors introduced a mollifier, a function used to construct an approximate identity. Ahlfors worked only with the case q = 2. Using a modified Cauchy kernel, he constructed a potential for ![]() a continuous function on C whose
a continuous function on C whose ![]() derivative is
derivative is ![]() , where is λ a weight function.
, where is λ a weight function.
In his proof of the finiteness theorem (1964), Ahlfors omitted the case of infinitely many thrice-punctured spheres appearing in Ω/G. Such surfaces admit no moduli deformations and alternatively carry no nontrivial integrable quadratic differentials. This case was covered in subsequent papers of Bers, Greenberg, and Ahlfors. Ahlfors also initially limited his work to quadratic differentials, in part because this case and the abelian case are the only ones with geometric significance. Perhaps more significantly, it was Ahlfors’s style
to make the pioneering contributions to a field and leave plenty of room for others to continue in the same area. In this particular case much remained to be done.
Bers saw that if he studied the more general case of q-differentials, he would be able to improve on the results of Ahlfors and get quantitative versions of the finiteness theorem that have become known as the Bers area theorems. The first of these (Bers, 1967) implies that if G is generated by N-motions, then
Since the minimal area of a hyperbolic orbifold is π/21, Bers’s area theorem gives an upper bound on the number of connected Riemann surfaces represented by a nonelementary Kleinian groups as 84(N – 1). Ahlfors lowered that bound to 18(N – 1) (1968). Even after some important work of Abikoff, there is still no satisfactory bound on the number of surfaces that a Kleinian group represents, especially if one insists on using only 2-dimensional methods. Bers’s paper (1967) also showed that the thrice-punctured spheres issue can be resolved “without new ideas.” It, together with Ahlfors’s discoveries on Kleinian groups, led 15 years later to work on the vanishing of Poincaré and relative Poincaré series.
The so-called measure zero problem first surfaced during a conference at Tulane in 1965, the first of a series of periodic meetings, roughly every four years, of researchers in fields related to the mathematical interests of Lars Ahlfors and Lipman Bers. In his 1964 paper Ahlfors remarked that perhaps of greater interest than the theorems he had been able to prove were the ones he was not able to prove. First of these was the assertion that the limit set of a finitely generated Kleinian group has two-dimensional Lebesgue
measure zero. This has become known as the Ahlfors measure zero conjecture. It is still unsolved, although important work on it has been done by Ahlfors, Maskit, Thurston, Sullivan, and Bonahan. In some sense the problem has been solved for analysts by Sullivan (1980), who showed that a nontrivial deformation of a finitely generated Kleinian group cannot be supported entirely on its limit set; topologists are still interested in the measure zero problem. Formulae in Ahlfors’s attempt (1982) to establish the measure zero conjecture led Sullivan to prove a finiteness theorem on the number of maximal conjugacy classes of purely parabolic subgroups of a Kleinian group.
The measure zero problem not only opened up a new industry in the Kleinian groups “industrial park,” it also revived the connection with 3-dimensional topology following the fundamental work of Marden and Thurston. It showed that Poincaré was not all wrong when he thought we could study Kleinian groups by 3-dimensional methods.
The second theorem that Ahlfors had wanted to establish in his 1964 paper can be rephrased in today’s language to say that a finitely generated Kleinian groups is geometrically finite. A counter-example was later produced by Greenberg.
QUASICONFORMAL MAPPINGS
BY FREDERICK GEHRING
In 1982 Birkhäuser Boston published two volumes of Lars Ahlfors’s collected papers and his fascinating commentaries on them. Volume 2 contains 43 articles. Twenty-one of these are directly concerned with quasiconformal mappings and Teichmüller spaces, 12 with Kleinian groups, and 10 with topics in geometric function theory. This distribution illustrates the dominant role that quasiconformal mappings played in this part of Ahlfors’s work. Moreover, quasiconformal
mappings played a key role in several other papers, for example, the important finiteness theory for Kleinian groups. For this reason I have chosen quasiconformal mappings as the subject of the final part of this survey. In particular, I will consider four papers on this subject that have had great impact on contemporary analysis.
ON QUASICONFORMAL MAPPINGS (1954)
In his commentary on this paper Ahlfors wrote, “It had become increasingly evident that Teichmüller’s ideas would profoundly influence analysis and especially the theory of functions of one complex variable…. The foundations of the theory were not commensurate with the loftiness of Teichmüller’s vision, and I thought it was time to reexamine the basic concepts.” The quasiconformal mappings considered by Grötzsch and Teichmüller were assumed to be continuously differentiable except for isolated points or small exceptional sets. Teichmüller’s theorem concerned the nature of the quasiconformal mappings between two Riemann surfaces S and S′ with minimum maximal dilatation. This and the fact that any useful theory that generalizes conformal mappings should have compactness and reflection properties led Ahlfors to formulate a geometric definition that was free of all a priori smoothness hypotheses.
A quadrilateral Q is a Jordan domain Q with four distinguished boundary points. The conformal modulus of Q, denoted by mod(Q), is defined as the side ratio of any conformally equivalent rectangle R. Grötzsch showed that if f : D → D′ is K-quasiconformal in the classical sense, then
(1)
for each quadrilateral Q ⊂ D. Ahlfors used this inequality to define his new class of quasiconformal mappings: a homeo-
morphism f : D → D′ is K-quasiconformal if (1) holds for each quadrilateral Q ⊂ D. Ahlfors then established all of the basic properties of conformal mappings for this general class of homeomorphisms, including a uniform Hölder estimate, a reflection principle, a compactness property, and an analogue of the Hurwitz theorem. He did all of this in nine pages. The major part of this article was, of course, concerned with a statement, several interpretations, and a proof of Teichmüller’s theorem.
In his commentary on this paper Ahlfors modestly wrote, “My paper has serious shortcomings, but it has nevertheless been very influential and has led to a resurgence of interest in quasiconformal mappings and Teichmüller theory.”
This is an understatement. Ahlfors’s exposition made Teichmüller’s ideas accessible to the mathematical world and resulted in a flurry of activity and research in the area by scientists from several different fields, including analysis, topology, algebraic geometry, and even physics.
Next Ahlfors’s geometric approach to quasiconformal mappings stimulated analysts to study this class of mappings in the plane, in higher-dimensional Euclidean spaces, and now in arbitrary metric spaces. His inspired idea to drop all analytic hypotheses eventually led to striking applications of these mappings in other parts of complex analysis such as discontinuous groups, classical function theory, complex iteration, as well as in other fields of mathematics, including harmonic analysis, partial differential equations, differential geometry, and topology.
THE BOUNDARY CORRESPONDENCE UNDER QUASICONFORMAL MAPPINGS (1956)
In the previous paper Ahlfors proved that a quasiconformal mapping f : D → D’ between Jordan domains has a homeomorphic extension to their closures. A classical
theorem due to F. and M. Riesz implies that the induced boundary correspondence ![]() is absolutely continuous with respect to linear measure whenever ∂D and ∂D′ are rectifiable and f is conformal. Mathematicians asked whether this conclusion holds when f is K – quasiconformal.
is absolutely continuous with respect to linear measure whenever ∂D and ∂D′ are rectifiable and f is conformal. Mathematicians asked whether this conclusion holds when f is K – quasiconformal.
By composing f with a pair of conformal mappings, one can reduce the problem to the case where D = D′ = H, where H is the upper half plane and ![]() (∞) = ∞. Next if x and t are real with t > 0 and if Q is the quadrilateral with vertices at x – t, x, x + t, ∞, then mod(Q) = 1 and inequality (1) implies that
(∞) = ∞. Next if x and t are real with t > 0 and if Q is the quadrilateral with vertices at x – t, x, x + t, ∞, then mod(Q) = 1 and inequality (1) implies that
(2)
where λ = λ(K). Inequality (2) is a quasisymmetry condition that many thought would imply that ![]() is absolutely continuous.
is absolutely continuous.
In 1956 Ahlfors and Beurling published the paper cited above in which they exhibit for each K > 1 a K – quasiconformal mapping f : H → H for which the boundary correspondence ![]() : ∂H → ∂H is completely singular. The importance of this example was, however, overshadowed by the authors’ main theorem, which showed that inequality (2) characterizes the boundary correspondences induced by quasiconformal self-mappings of H. The sufficiency part at the remarkable formula
: ∂H → ∂H is completely singular. The importance of this example was, however, overshadowed by the authors’ main theorem, which showed that inequality (2) characterizes the boundary correspondences induced by quasiconformal self-mappings of H. The sufficiency part at the remarkable formula
(3)
yields a K – quasiconformal self-mapping of H with K = K(λ) whenever ![]() satisfies (2). Moreover, f is a hyperbolic quasi-
satisfies (2). Moreover, f is a hyperbolic quasi-
isometry of H, a fact that turns out to have many important consequences.
In 1962 it was observed that a quasiconformal self-mapping of the n-dimensional upper half space Hn induces a quasiconformal self-mapping of the (n – 1)–dimensional boundary plane ∂Hn. This fact, for the case n = 3, was an important step in the original proof of Mostow’s important rigidity theorem. It was then natural to ask if every quasiconformal self-mapping f of ∂ Hn admits a quasiconformal extension to Hn. This question was eventually answered in the affirmative by Ahlfors in 1963 for the case when n = 3, by Carleson in 1972 when n = 4, and by Tukia-Väisälä in 1982 for all n ≥ 3.
RIEMANN’S MAPPING THEOREM FOR VARIABLE METRICS (1960)
If f : D → D is K – quasiconformal according to (1), then f is differentiable with fz ≠ 0 a.e in D and
(4)
is measurable with
(5)
a.e. in D. The complex dilatation µf determines f uniquely up to post composition with a conformal mapping. The main result of this article, joint with Lipman Bers, states that for any function µ that is measurable with |µ| ≤ k < 1 a.e. in D, there exists a K – quasiconformal mapping f of D that has µ as its complex dilatation. Moreover, if f is suitably normalized, then f depends holomorphically on µ.
The above result, known by many as the “measurable Riemann mapping theorem,” has proved to be an enormously effective tool in analysis. It is a cornerstone for the
study of Teichmüller space, it was the key for settling several outstanding questions of classical function theory including Sullivan’s solution of the Fatou-Julia problem on wandering domains, and it currently plays a major role in the study of iteration of rational functions.
Unfortunately, as we all know, important theorems in mathematics sometimes become definitions. This theorem may already have become a verb in complex dynamics. For at a plenary lecture at the International Congress of Mathematicians in 1986 a distinguished French mathematician Adrien Douady was heard to explain that “before mating two polynomials, one must first Ahlfors-Bers the structure.”
QUASICONFORMAL REFLECTIONS (1963)
A Jordan curve C is said to be a quasicircle if it is the image of a circle or line under a quasiconformal self-mapping of the extended complex plane. A domain D is a quasidisk if ∂D is a quasicircle. Quasicircles can be very wild curves. Indeed, for each constant 0 < a < 2 there exists a quasicircle C with Hausdorff dimension at least a.
Nevertheless, the first theorem of this elegant paper contains the following remarkable characterization for this class of curves. A Jordan curve C is a quasicircle if and only if there exists a constant b such that
(6)
for each ordered triple of points z1,z2,z3 ∈ C. The proof for the sufficiency of (6) depends on the fact that the function in (3) is a hyperbolic quasi-isometry.
The fact that quasicircles admit such a simple geometric description is one of the reasons why these curves play an important role in many different areas of analysis. Inequality (6) is universally known as the “Ahlfors condition” and many regard it as the best way to define the notion of a quasicircle.
The second main result of this paper asserts that the set S of Schwarzian derivatives
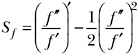
(7)
of conformal mappings f that map the upper half plane H onto a quasidisk D is an open subset of the Banach space of holomorphic functions ![]() with norm
with norm
(8)
This fact is the key step in proving that the Bers universal Teichmüller space T(1) is the interior of S with the topology induced by the norm (8). It also led to another surprising connection between quasiconformal mappings and classical function theory, namely, that a simply connected domain D is a quasidisk if and only if each function f, analytic with small Schwarzian derivative Sf in D, is injective. Here the size of Sf is measured by
(9)
where ρD is the hyperbolic metric in D.
Lars’s beautiful paper on quasiconformal reflections pointed out how these mappings occur naturally in many different areas of mathematics. Lars lectured on this material at the Forschungs Institute at Oberwolfach, Germany, in 1963. He, Professor Olli Lehto of the University of Helsinki, and I were to speak the same morning. After several hours of socializing and wine the evening before, Olli and I tried to excuse ourselves so that we could get some sleep before our talks. We were told by Lars that that “was a very silly
idea indeed” and that it would be far better to relax and drink with the pleasant company. The next day Lars’s talk went extremely well and he was asked if he believed that staying up late always improved his lectures. “I am not sure,” he replied, “but at least they always sound better to me!”
Quasiconformal mappings appear first under this name in Ahlfors’s 1935 paper on covering surfaces, the famous paper for which he received the Fields Medal in 1936. In discussing Lars’s work, Carathédory said that this article opened a completely new chapter in analysis, one that could be called “metric topology.” In a commentary on this article Lars wrote, “Little did I know at the time what an important role quasiconformal mappings would come to play in my own work.”
Lars’s geometric approach to quasiconformal mappings stimulated their development in higher dimensional Euclidean space and recently in general spaces, such as the Heisenberg and Carnot groups. The fact that this class is so natural and flexible has led to striking applications to Kleinian groups, classical function theory, complex dynamics, and to other parts of mathematics, including harmonic analysis, differential geometry, elasticity, and topology.
The class of quasiconformal mappings offers a stripped-down picture of the geometric essentials of complex function theory and, as such, admits applications of these ideas to many other parts of analysis and geometry. They constitute just one illustration of the profound and lasting effect that the deep, central, and seminal character of Lars’s research has had on the face of mathematics.
FINAL REMARKS
In addition to the Fields Medal he received in 1936, Lars was awarded an International Prize from the Wihuri
Foundation of Finland in 1968, an award also known as the Sibelius Prize when given to composers.
He was honored with the Wolf Prize in Jerusalem in 1981. In describing the mathematical achievements of the prizewinner, the jury ended its report with the following final comment: “Everyone working today in complex analysis is in some sense a student of Ahlfors.”
At each International Congress of Mathematicians it is customary for the host country to nominate its most prestigious mathematician as honorary president of the congress. This congress was held in the United States in 1986, 50 years after Lars had been awarded the Fields Medal in Oslo. At this time Lars was asked by his American colleagues to serve as the honorary president of this meeting in recognition of his achievements in research.
Lars was very generous with his time and always glad to talk with and advise young students and mathematicians. He has also had a powerful and lasting influence in his field through the aid and direction he gave to the 24 doctoral students who wrote theses under his direction as well as to at least an equal number of postdoctoral visitors and many close associates who benefited greatly from the opportunity to consult with him on problems of common interest. At a conference held in Storrs, Connecticut, to commemorate his seventy-fifth birthday, Lars remarked that “retirement is wonderful. I can’t perish any more, so I don’t have to publish!” The upshot of his remark was that he could now devote himself full time to understanding the new developments in his field without the pressure of having to write them up. At 75 Lars was devoting himself to learning the newest ideas in the subject!
Lars died in Pittsfield, Massachusetts, in October 1996. He was survived by his wife, Erna, and three daughters, Cynthia, Vanessa, and Caroline. A son, Christopher, died in infancy.
REFERENCES
Bers, L. 1965. Automorphic forms and Poincaré series for infinitely generated Fuchsian groups. Am. J. Math. 87:196-214.
Bers, L. 1967. Inequalities for finitely generated Kleinian groups. J. Anal. Math. 18:23-41,
Eichler, M. 1957. Eine Verallgemeinerung der Abelschen Integrale. Math. Z. 67:267-298.
Kra, I. 1996. Creating an American mathematical tradition: The extended Ahlfors-Bers family. In A Century of Mathematical Meetings, pp. 265-280. Providence, R.I.: American Mathematical Society.
Sullivan, D. 1980. On the ergodic theory at infinity of an arbitrary discrete group of hyperbolic motions, Riemann surfaces and related topics. Ann. Math. Study 97, pp. 465-496. Princeton, N.J.: Princeton University Press.
Thurston, W. P. 1982. Three dimensional manifolds, Kleinian groups and hyperbolic geometry. Bull. Am. Math. Soc. (N.S.) 6:357-381.
SELECTED BIBLIOGRAPHY
1929 Über die asymptotischen Werte der ganzen Funktionen endlicher Ordnung. Ann. Acad. Sci. Fenn. Ser. A 32(6):1-15.
1935 Zur Theorie der Überlagerungsflächen. Acta Math. 65:157-194.
1937 [1] Über die Anwendung differentialgeometrischer Methoden zur Untersuchung von Überlagerungsflächen. Acta Soc. Sci. Fenn. N. S. A. Tom II(6):1-17.
[2] With H. Grunsky. Über die Blochsche Konstante. Math. Z. 42:671-673.
1938 An extension of Schwarz’s Lemma. Trans. Am. Math. Soc. 43:359-364.
1954 On quasiconformal mappings. J. Anal. Math. 3:1-58 (correction loc. cit., pp. 207-208).
1956 With A. Beurling. The boundary correspondence under quasiconformal mappings. Acta Math. 96:125-142.
1960 With L. Bers. Riemann’s mapping theorem for variable metrics. Ann. Math. 72:385-404.
1963 Quasiconformal reflections. Acta Math. 109:291-301.
1964 Finitely generated Kleinian groups. Am. J. Math. 86:413-429: 87(1965):759.






























