BEHIND THE MYTHS
Undergraduate mathematics is the bridge between research and schools and holds the power of reform in mathematics education.
—Everybody Counts, 1989
No other collegiate discipline teaches as many students with such widely differing levels of preparation as does mathematics.
—A Challenge of Numbers, 1990
Undergraduate mathematics plays a pivotal role in our system of mathematics education. It is in college where our nation's engineers and technicians are educated, where future scientists are recruited, and where many of society's leaders acquire basic quantitative skills. In addition, the instructional traditions of undergraduate mathematics form the model for all future teachers of mathematics.
Undergraduate mathematics is also a source of much of the mythology about mathematics that pervades society. Adults' attitudes about mathematics are largely shaped by their own experiences as students in school or college and by images created by media leaders. School teachers, politicians, writers, editors—all those whose careers influence the
public's image of mathematics—view mathematics through a lens that was polished by their own education. Important clues to the widespread public misunderstanding of mathematics can be found in the traditions and habits of mathematics departments in colleges and universities across the nation.
|
"The immensity and richness of the methods and ideas developed by pure and applied mathematicians and statisticians over the last fifty years constitute a huge resource being tapped by the intellectual machine of science and engineering." —Renewing U.S. Mathematics, 1990 |
Departments Under Stress
In the last twenty years the demand for undergraduate mathematics courses has risen more than twice as fast as have faculty resources in departments of mathematical sciences. Increased demand is due both to demographic and
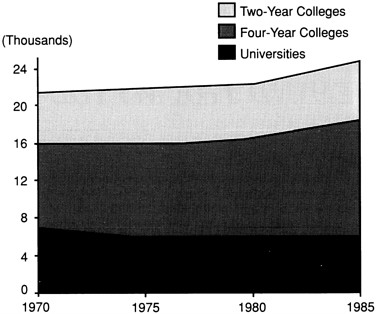
Figure 2
Number of full-time mathematical sciences faculty at colleges and universities.
social trends and to an increase in the use of mathematics in other disciplines. Consequently, today's students are much more diverse in mathematical preparation and needs. But since 1970, enrollments have increased by more than 70 percent while faculty size has increased by less than 30 percent. As a result, a faculty increase of more than 30 percent would be required today to recapture the student-faculty ratio of twenty years ago.
|
Quantitative Reasoning The demands of today's technological society require a work force that can understand complex processes, develop and test hypotheses, and draw logical conclusions. Innovative courses, set in the context of students' interests, have proven far more effective as a means of teaching this type of quantitative reasoning than have traditional requirements such as college algebra or elementary statistics. One successful course of this type was developed at Mount Holyoke College as part of the New Liberal Arts initiative supported by the Sloan Foundation. A collection of case studies allows students to develop an appreciation of graphical techniques, approximation methods, and statistical concepts. Using a combination of lectures, laboratory sessions, and small discussion groups, the students work on three case studies:
Computers are used as the primary tool in the analysis of these case studies, and for writing papers, manipulating data, and creating graphical images. Although not required, the course is now elected by more than one-third of the students at Mount Holyoke. |
Rather than articulating forcefully the need to keep student-faculty ratios within reasonable bounds, the mathematics community sought to handle the increased workload in inexpensive ways, such as larger classes and increased use of graduate teaching assistants and part-time faculty. As a consequence, the image of mathematics as a low-cost, high-enrollment discipline became institutionalized on many campuses. It remains so today.
The last thirty years have also been a period of extraordinary achievements in mathematical research, during which time federal agencies and research universities elevated their research mission over their educational mission. Intensified competition for research funding created a climate in mathematics departments in which research accomplishments received increasing prestige, while contributions to improving education received lower priority. As a consequence, innovations in undergraduate teaching lag far behind advances in research. Both in instructional methodology and in curricular content, undergraduate mathematics is far below what it should be to best serve today's students. What is required is a balanced commitment to scholarship and instruction.
For a variety of reasons, not least being the ambivalent atmosphere in many college and university mathematics departments, interest in teaching college mathematics has declined significantly at both undergraduate and graduate levels. This trend is compounded by projections of impending retirements that foretell a severe future shortage in the number of college mathematics teachers. This situation has serious implications for the quality of mathematics education at all levels and for the related human resource needs of our nation.
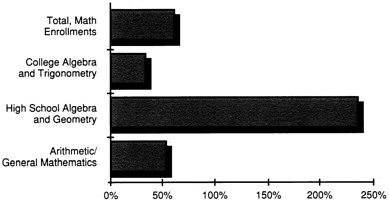
Figure 3
Percent increase in enrollments in selected mathematics courses in colleges and universities, 1965 to 1985.
|
''Mathematics may be the only discipline that bases its instruction on hundreds of exercises of five minutes or less." —Priming the Calculus Pump, 1990 |
Inadequacies and Deficiencies
For far too long, myth has substituted for reality in the U.S. approach to mathematics education. Mathematics departments find themselves trapped in institutional structures that assume that the instructional practices that have evolved over the past thirty years in mathematics are appropriate and acceptable. The result is a dysfunctional system of undergraduate mathematics beset on all sides by inadequacies and deficiencies:
|
"Computers have profoundly influenced the mathematical sciences themselves, not only in facilitating mathematical research, but also in unearthing challenging new mathematical questions." —Renewing U.S. Mathematics, 1990 |
-
In mathematical preparation of students: Most U.S. students do not acquire quantitative skills sufficient for future study or careers. The evidence is all around us: chronically high attrition rates in mathematics courses at all levels, increasing numbers of college students enrolled in remedial courses, and international comparisons that show U.S.
-
students lagging far behind students from other countries. Although many students enter college having completed a year or more of calculus, a sizable proportion of undergraduates have difficulty even with elementary arithmetic. Many college students find themselves unready to begin standard college mathematics courses.
|
"The losses of mathematical talent are not evenly distributed among racial and ethnic groups or the sexes. At each critical juncture in the pipeline more women and minority students drop out than do white males." —A Challenge of Numbers, 1990 |
-
In support and reward for teaching: Few universities offer much incentive for developing new approaches to teaching. Resources for instruction are meager and tend to reinforce reliance on large classes and packaged learning. The reward structure at most universities undervalues innovation in teaching or evidence of improved learning.
-
In teaching methods, course content, and instructional materials: The way mathematics is taught at most colleges—by lectures—has changed little over the past 300 years, despite mounting evidence that the lecture-recitation method works well only for a relatively small proportion of students. Moreover, the syllabi of many undergraduate mathematics courses and the template-style textbooks are detached from the life experiences of students and are seen by many students as irrelevant.
-
In the use of computers in undergraduate mathematics: Nothing in recent times has had as great an impact on mathematics as computers, yet in most college courses mathematics is still taught just as it was 30 years ago—as a cerebral, paper-and-pencil discipline for which computers either are irrelevant or can be ignored. Computers serve mathematics these days as indispensable aids in research and application. Yet only in isolated experimental courses has the impact of computing on the practice of mathematics penetrated the undergraduate curriculum.
-
In resources that support undergraduate mathematics: The typical college or university mathematics department has been viewed historically as a source of large enrollments with low costs of instruction—a "cash cow" for institutional budgets. In contrast, departments of science and engineering have large budgets to support their established
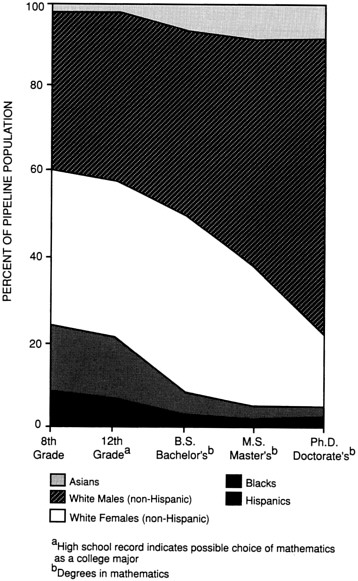
Figure 4
A representation of U.S. students in the mathematics pipeline.
|
Mathematics for the Masses At a large midwestern state university with over 50,000 students, the average enrollment in mathematics courses during the fall term is approximately 16,000. The mathematics department has about 125 full-time (FTE) faculty members, 225 graduate teaching assistants (more than half of whom are foreign nationals, and a quarter of whom come from other departments), and 25 undergraduate instructional aides. The circumstances of mathematics instruction in this institution are typical of many major research universities. Service and lower-level courses dominate the teaching load with enrollments of over 14,000, ninety percent of the total. One such course, taken by approximately 1400 students, is taught by 45 teaching assistants and 6 part-time lecturers, all working under the supervision of one faculty member as a half-time assignment. Over 55 percent of the total faculty teaching effort in the department is devoted to the 11 percent of students enrolled in upper-division and graduate courses; only 22 percent of faculty effort is assigned to the 67 percent of students enrolled in pre-calculus mathematics courses. |
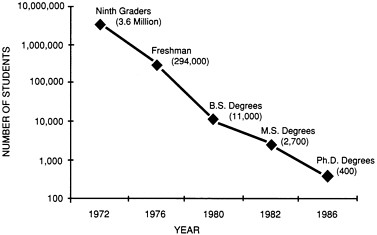
Figure 5
Students in the mathematical sciences pipeline—about half are lost each year.
|
"If present patterns persist, most socioeconomic and demographic trends indicate that fewer students will study mathematics and choose mathematics-based careers." —A Challenge of Numbers, 1990 |
-
needs for instructional and research laboratories. Even though the role of technology—hence of computer labs—in mathematics has grown in recent years, most mathematics departments still operate with budget allocations that, when compared with those for other departments, are among the smallest per credit hour of instruction. The resources available to most departments of mathematics are insufficient to meet their responsibilities.
-
In the number of minorities and women who study mathematics: College mathematics attracts far too few Black and Hispanic students, and their attrition rates between high school and the sophomore year of college are much too high. Although the number of women enrolled in un-
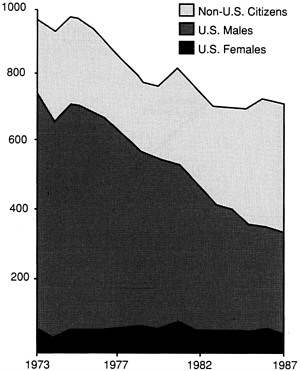
Figure 6
Ph.D. degrees in mathematics.
-
dergraduate mathematics courses is only slightly smaller than the number of men, the relative number of women drops dramatically in graduate enrollments. Only a small fraction of our population—consisting primarily of white males—complete a mathematics education that matches their potential and interests. The result is an appalling waste of human potential, denying to individuals opportunity for productive careers and to the nation the resources for economic strength.
-
In the number of students who study mathematics: The number of students electing to take mathematics courses declines precipitously from ninth grade to graduate school. Each year from high school through graduate school, on average, one of every two students stops taking mathematics courses.
-
In the number of new engineers and scientists: As students discontinue prematurely their study of mathematics, the quantitative skills of our work force fall behind the requirements of an international economy. Moreover, the number of individuals in their mid-twenties will decline until the end of this century, making it increasingly difficult to sustain present production of new engineers and scientists.
-
In the number of qualified school mathematics teachers: Although many teachers hold certificates, few school teachers meet the standards for curriculum and professional preparation set forth by the National Council of Teachers of Mathematics. In addition, half the nation's mathematics teachers will leave teaching by the year 2000.
-
In the number of U.S. mathematics graduate students: The number of U.S. students who pursue graduate studies in mathematics is now much smaller than it was twenty years ago. Today only one in every ten thousand students enrolled in ninth grade mathematics will pursue and eventually earn a doctorate in the mathematical sciences, far too few to replace retiring faculty in coming decades. Although shortfalls in U.S. mathematics students can be mitigated to some extent by immigration, current trends portend a serious future shortage of mathematical sciences faculty.










