The Basic Science of Inertial Fusion Energy
The aim of inertial confinement fusion (ICF) is to ignite a target containing compressed fusion fuel—deuterium (heavy hydrogen) and tritium (super-heavy hydrogen)—so that it will burn (react) significantly before the target blows itself apart. Clearly, if this is to be of use for energy production, the energy required to initiate the burn must be significantly less than the energy released by the fusion reactions. Furthermore the energy release of the target must also be sufficiently small that it can be contained and converted into useful power. This appendix outlines the basic physics of the process as it is currently envisaged.
The thermonuclear reaction between deuterium and tritium (DT) yields helium (an alpha particle) and a neutron. The neutron is used to “breed” tritium from lithium in a secondary reaction (see Figure A.1). The energy released is huge: burning only 12 mg of a 50-50 DT mixture yields 4.2 GJ of energy, equivalent to 1 ton of TNT.
In a DT plasma at temperatures over about 50 million degrees, random collisions of D and T produce more energy via the fusion reaction than is radiated away by photons. This is the expected initiation temperature for fusion burn—typically the plasma would then heat itself to above 200 million degrees while burning. The reaction rate per particle depends on temperature and density. At 200 million degrees the reaction rate per particle is 5.2 × 107 ρs–1, where r is the DT mixture’s mass density in grams per cubic centimeter. The disassembly time of an isothermal sphere is roughly R/(3Cs), where R is the radius and Cs is the speed of sound—at 200 million degrees, Cs is roughly 108 cm/s. Thus (very approximately) the areal density, ρR, must be >3-7 g/cm2 in order to get a significant proportion of the
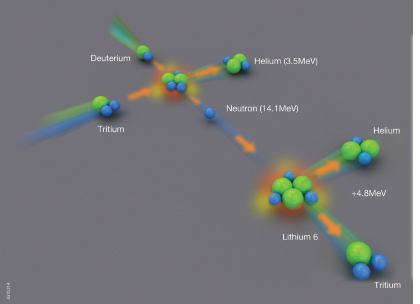
FIGURE A.1 The deuterium-tritium fusion reaction and the tritium breeding reaction from lithium 6. SOURCE: Steve Cowley, United Kingdom Atomic Energy Authority, and Imperial College London.
nuclei to react in the disassembly time. At DT liquid density this would require a sphere 10-30 cm in radius and a huge release of energy. To keep the energy to initiate fusion small and the energy released manageable, a small sphere (weighing a few milligrams) must be used. This requires compression. The areal density rises during compression (at fixed mass, ρR ∞ R–2) until it reaches a substantial fraction of fusion-relevant levels (of order 3-7 g/cm2). For 3 mg of solid/liquid DT an increase in the density of order one thousand is needed.
In most ICF schemes, a shell of cryogenic deuterium and tritium fuel is accelerated inward and compressed by the reaction force from an ablating outer shell. The ablating outer shell is heated either by direct laser irradiation (called “direct drive”) or by the X-rays produced by heating a high-Z enclosure (hohlraum) that surrounds the fuel target (called “indirect drive”). The hohlraum in indirect drive schemes may be driven (heated) by lasers, particle beams, or pulsed power systems. During compression the fuel is kept as cold as possible to minimize the work needed for compression. At stagnation, a central hot spot enclosing a few percent of the total mass is heated and ignited. Ignition occurs when the alpha-particle
heating of the hot spot exceeds all the energy losses. Ignition triggers a runaway process (the thermonuclear instability), resulting in a large amplification of the hot spot energy. If the inertia of the surrounding dense DT shell confines the ignited hot spot pressure long enough, the thermonuclear burn will propagate from the central hot spot to the dense shell and the entire fuel mass will burn. The burn is driven by the fusion alpha particles depositing their energy in the cold dense fuel. The burn lasts until the target disassembles, and the fuel burn-up fraction increases with the shell areal density.
Compressing a target to ignition conditions is very challenging and has yet to be fully realized in experiments, although major advances have been made. Drivers must deliver very uniform ablation; otherwise the target is compressed asymmetrically. Asymmetric compression excites strong Rayleigh-Taylor instabilities that spoil compression and mix dense cold plasma with the less dense hot spot. Preheating of the target can also spoil compression. For example, mistimed driver pulses can shock heat the target before compression. Also, interaction of the driver with the surrounding plasma can create fast electrons that penetrate and preheat the target.
A widely used parameter to assess the performance of an ICF target is the target gain, G, representing the ratio of the fusion energy output to the driver energy entering the target chamber. Clearly a high gain is desirable for fusion energy and must remain a central focus of any IFE program.
The fraction of driver energy that couples to the fusion fuel contained in the target is typically small—a few percent—but the fusion gain can still be substantial. In a National Ignition Facility (NIF) indirect-drive ignition target driven by ~1 MJ of UV laser light into the hohlraum, the shell of fuel implodes with an expected kinetic energy of about 15-20 kJ. Roughly half of that energy (7-10 kJ) is used to heat up the hot spot and the other half to compress the surrounding shell. If the fusion yield (alpha and neutron energy) is 1 MJ (i.e., G = 1), the hot spot energy is amplified 100× by the thermonuclear instability. At 1 MJ fusion yield, the alpha particles have deposited 200 kJ of energy into the hot spot and surrounding fuel, about 20 times the energy provided by the compression of the hot spot. The thermonuclear burn stays localized near the hot spot and propagates within about 5 times the initial hot spot mass (partial burn). If the burn propagates through the entire DT mass, the gain of a NIF target will exceed ~10 (full burn and 10 MJ yield). While a NIF implosion yielding G >> 1 would elucidate many aspects of the ignition and basic burn physics, a gain of G ≥ 10 is required for demonstrating full burn propagation over the inertial confinement time of the compressed shell (i.e., fuel burnup fraction compatible with the fuel inertia).
While the target gain can be used to validate the target physics, a new parameter is required for assessing the viability of a fusion energy system. The so-called “Engineering Q,” or “QE,” is often used as a figure of merit for a power plant. It represents the ratio of the total electrical power produced to the (recirculating) power required
to run the plant—i.e., the input to the driver and other auxiliary systems. Clearly QE = 1/f, where f is the recycling power fraction (see Figure A.2). Typically Q ≥ 10 is required for a viable electrical power plant. For a power plant with a driver wall-plug efficiency ηD, target gain G, thermal-to-electrical conversion efficiency ηth, and blanket amplification AB (the total energy released per 14.1 MeV neutron entering the blanket via nuclear reactions with the structural, coolant, and breeding material), the engineering Q is QE = ηth ηthABG (see Figure A.2). An achievable value of the blanket amplifications and thermal efficiency might be AB ~ 1.1 and ηth ~ 0.4 and should be largely independent of the driver. Therefore, the minimum required target gain is inversely proportional to the driver efficiency. For a power plant with a recirculating power f = 10 percent (QE = 10), the required target gain is G = 150 for a 15 percent efficient driver and G = 320 for a 7 percent efficient driver.
Energy gain does not, of course, guarantee commercial viability. Key challenges remain even after high gain is achieved. These are discussed in detail elsewhere in this report, but they include:
- Low-cost targets. For example, a target producing a fusion energy, ED, of 200 MJ could make net electricity, Egrid ~ 80 MJ ~ 22 kWh, or about $1 worth of electricity at current prices. The target cost should be some small fraction of this.
- Repetitive ignition of targets. To produce a gigawatt of electrical power, targets with ED = 200 MJ must be ignited roughly 12 times a second.
- Reliable target chamber and blanket to extract power and breed tritium. This is a challenge shared with magnetic fusion.
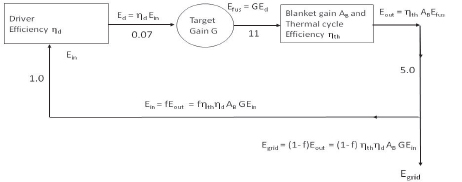
FIGURE A.2 Schematic energy flow in an inertial fusion power plant. Note the “Engineering Q” is defined as QE = 1/f. The numbers beside the arrows indicate the proportionality of the energy flows. Tritium breeding (discussed in Chapter 3) is excluded from this diagram for simplicity.




