3
Mitigating the Consequences of Nonresponse
Survey nonresponse has consequences, most notably the potential for nonresponse bias. The techniques and procedures for dealing with nonresponse bias depend on how one approaches the problem. Singer (2006) points out that statisticians have been concerned mainly with imputation and weighting as ways of adjusting for the bias introduced by nonresponse, while social scientists and survey methodologists have tended to focus on measuring, understanding, and reducing the nonresponse rates themselves.
Because of the negative effect that nonresponse can have on survey quality, in recent years survey researchers and managers have been responding very aggressively to the problem of growing nonresponse in surveys. However, as Couper (2011a) observed in the panel’s workshop, the approaches have become more selective, and survey researchers are rejecting the older approach that aimed simply to maximize the overall response rate. The newer approaches target interventions at subgroups, at domains of interest, and at maximizing the response from specific cases based on their perceived special contribution to the quality of key statistics. Survey researchers are focusing less attention on increasing overall rates and are increasingly focusing on understanding the causes and correlates of nonresponse and making adjustments based on that understanding.
In this chapter, we explore some of the ways in which survey methodologists and managers are responding to the growing problem of survey nonresponse. We outline the results of some very good work that has gone into the development of weighting adjustments and adjustment models, and we document the increased use of paradata in nonresponse adjustment.
Some of this work is in early stages, and other work is more advanced. We make several recommendations for research to solidify and further advance these lines of development.
NONRESPONSE WEIGHTING ADJUSTMENT METHODS1
The need for nonresponse adjustment arises because probability samples, in which all units have a known, positive probability of selection, require complete responses. Without other non-sampling errors, estimators for probability samples are approximately design-unbiased, consistent, and measurable. Base weights, or inverse probability selection weights, can be used to implement standard estimators.
One possible simple estimator is the ratio mean, which is approximately unbiased and consistent for the population mean:
![]()
with di equal to the inverse of the probability of selection. If some of the sample units do not respond (unit nonresponse), and the estimator is unchanged, then the estimator may be biased:
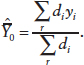
The bias can be expressed in two ways:
(1) A deterministic framework assumes the population contains a stratum of respondents and a stratum of nonrespondents. Let the population means in the two strata be ![]() and
and ![]() , respectively. The respondent stratum is R percent of N, and the bias of the unadjusted estimator is
, respectively. The respondent stratum is R percent of N, and the bias of the unadjusted estimator is
![]()
In the deterministic view, the bias arises when the means of the respondents and of the nonrespondents differ.
(2) A stochastic framework assumes every unit in the population has some non-zero probability of responding (its response propensity). The bias of the unadjusted estimator is
______________________________________
1The discussion of nonresponse weighting adjustment methods is abstracted from the presentation by Michael Brick at the panel’s workshop (Brick, 2011).
![]()
where ![]() is an individual response propensity and
is an individual response propensity and ![]() is the mean of the response propensities. Thus, in the stochastic view, the bias arises when the characteristic and response propensity covary.
is the mean of the response propensities. Thus, in the stochastic view, the bias arises when the characteristic and response propensity covary.
A natural adjusted estimator is then
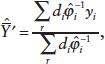
where ![]() is an estimate of the response propensity and
is an estimate of the response propensity and ![]() represents the adjusted weight
represents the adjusted weight ![]() .
.
The selection of the weighting framework—deterministic or stochastic—depends then on the theoretical model of the response mechanism. In other words, the underlying model is the rationale for the selection of the adjustment scheme.
Most adjustments now in use assume that the missing data are missing completely at random (MCAR) or missing at random (MAR). The MCAR assumption holds if all of the units in the population have the same probability of responding, that is, if the respondents are just a smaller random sample. MCAR means that the distribution of the missingness (an indicator for whether the unit responds or not) is independent of the y-variable and all auxiliary (or x) variables.
MAR is a more realistic assumption than MCAR. MAR implies that the probability of response does not depend on the y-variable once we control for a vector of known x-variables. Weighting class adjustment schemes that define subgroups using the auxiliary data, assuming that the sample units within the subgroups (h = 1,...,H) have the same response propensity, are consistent with the MAR assumption. These methods adjust the weights for respondents in the group with ![]()
This type of estimator is either a weighting-class estimator or a post-stratified estimator, depending on the type of data available for computing the adjustment. If the data are at the sample level (known for sampled units but not for the entire population), it is a weighting-class estimator; if the data are at the population level, then it is a post-stratified estimator. The adjustment requires that sample members can be divided into cells using the vector of observable characteristics.
In the weighting-class approach, the adjusted weight is calculated in four stages:
1. A base weight is calculated that is the reciprocal of the probability of selection of the case under the sample design.
2. When there is nonresponse and the eligibility of the nonrespondents cannot be determined, the base weights for these nonrespondents are distributed into the eligible nonresponse category based on the proportion of the weights that are eligible in the respondent set.
3. These weights are adjusted to compensate for eligible nonrespondents.
4. A final weight for the eligible respondent cases is computed as the product of the base weight, the eligibility adjustment factor, and the nonresponse adjustment factor (Yang and Wang, 2008).
In choosing weighting classes for the adjustment in stage 3, bias is eliminated when the variables and classes are such that either:
![]()
That is, the bias from nonresponse is eliminated if, within the weighting cells, all cases have the same response propensity or the same value for the survey variable. As noted in the stochastic model of nonresponse, nonresponse bias only exists when the response propensities and the outcomes are correlated. However, since most surveys have a multitude of survey outcomes, the idea of using classes that are related only to the response propensities is commonly adopted.
Models constructed to meet stage 1 are called response propensity stratification, and those designed to meet stage 2 are referred to as predicted mean stratification. The classes themselves are sometimes formed by subject matter experts, based on information on the key survey outcomes.
An empirical method that is used often with categorical data is to form weighting classes by using classification software such as CART, CHAID, or SEARCH. Often the dependent variable is the response (respondent or not), and sometimes the survey outcomes are used as dependent variables, depending on the criteria being used. In either case, this approach may result in a very large number of weighting classes. Eltinge and Yansaneh (1997) suggested methods to test whether appropriate classes are formed.
Many alternative methods of making these adjustments are sometimes used. We describe several of these alternatives below.
Propensity Model Approach
The propensity model approach uses multiple logistic regression analysis (or some similar approach) to examine the nonresponse mechanism and calculate a nonresponse adjustment. In this method a response indicator is regressed on a set of independent variables, such as those used to define weighting class cells. A predicted value derived from the regression equation is called the propensity score, which is simply an estimated response probability (Rosenbaum and Rubin, 1983). Survey population members with the same observable characteristics are assigned the same propensity score. The response propensity can be used to adjust directly by using the inverse of the estimated response propensity to adjust the weights for the respondents. This is the response propensity stratification, although in many cases the propensity scores are used to divide the sample into propensity classes based on quintiles of the distribution, and the average propensity within the class is the adjustment.
Advantages of propensity-weighting methods over the traditional weighting-class methods are that continuous variables can be used to define cells, the models can accommodate a large number of variables, and the technique is simple to apply (Hazelwood et al., 2007). If large adjustments are avoided by using classes rather than the inverse of the estimated response propensities, then the methods can be as stable as other weighting-class methods. Like other response probability adjustments, this approach also implicitly assumes that one weighting adjustment is sufficient to address nonresponse bias in all estimates.
Selection Models
Heckman (1979) first proposed the sample selection model for regressions. The model is based on the observation that respondents self-select to participate in a survey, either explicitly by refusing to participate or implicitly through inability to answer or be contacted.
Selection models are the conventional method among empirical economists for modeling samples with nonresponse (or other types of selectivity). Sampling statisticians have viewed this approach with skepticism, mainly because most selection models make strong assumptions about the nonresponse mechanism that may not hold in practice. Selection models are also typically variable-specific solutions, in the sense that the model is constructed for one particular estimate and cannot be used for a wide variety of statistics. While this feature can be of benefit because selection models may improve the quality of individual estimates, survey users are typically interested in producing many statistics. The goal is most often a
consistency among estimates (e.g., the sum of the estimates for males and females should equal the total) that the selection models do not confer.
The most popular form of selection model requires an explicit distributional assumption. In principle, different selectivity corrections could be made from a given set of data, depending on the model to be estimated.
Raking Ratio Adjustment Approach
Raking ratio adjustments are used to benchmark sampling weights to known control totals and can be considered a form of multidimensional post-stratification. This approach reduces sampling error through the use of auxiliary variables correlated to survey response and has been used to reduce nonresponse bias (Brick et al., 2008). The advantage of raking is that more variables that are correlated with response propensities and outcome variables can be included in the weighting process without creating large weight adjustments. Like post-stratification and weighting-class methods, careful review of the weights is required to make sure large weight adjustments are not introduced by the raking process.
Calibration
Post-stratification and raking are two specific methods of calibration, as described by Särndal (2007). Calibration is a method of computing weights in a manner that equates the sum of the calibrated totals to totals defined by auxiliary information. Calibrated weights can then be used to produce estimates of totals and other finite population parameters that are consistent internally, as discussed above in raking.
Calibration is used to correct for survey nonresponse (as well as for coverage error resulting from frame undercoverage or unit duplication). Kott and Chang (2010) showed that calibration weighting treats response as an additional phase of random sampling. This method is particularly valuable when many important auxiliary variables are related either to response propensity or to the key survey outcomes. As a result, it has been heavily studied for use in countries with population registers or when the sampling frame is rich in auxiliary data, such as in establishment surveys.
Mixture Models
Selection models can be thought of as expressing the joint distribution of the outcome and “missingness” as the product of the distribution of the missing data mechanism conditional on the outcome variable and on the marginal distribution of the outcome variable. An alternative approach is to write the joint distribution as the product of the distribution of the outcome
conditional on the missingness mechanism and on the marginal distribution of the missingness mechanism. The two approaches do not result in the same estimates in some situations. Little (1993) described the difference in the two approaches and discussed when pattern mixture models might be preferred.
Observations About Weighting Adjustment Approaches
All of these weighting adjustment schemes depend very heavily on the availability of auxiliary data that are highly correlated with either the response propensities or the key outcomes. Without these types of data, the adjustments are ineffective in reducing nonresponse bias. As response rates decline, these weighting adjustments may become even more important tools for producing high-quality survey estimates.
Recommendation 3-1: More research is needed on the use of auxiliary data for weighting adjustments, including whether weighting can make estimates worse (i.e., increase bias) and whether traditional weighting approaches inflate the variance of the estimates.
In his summary, Brick (2011) makes the case for the development and refinement of survey theory, suggesting that empirical adjustment methods may work in many cases, but pointing out that they are unsatisfying in several ways. Some possible paths to a solution would be to develop a more comprehensive theory relating response mechanisms to nonresponse bias, and a more comprehensive statistical theory of adjustment to deal with different types of statistics.
Recommendation 3-2: Research is needed to assist in understanding the impact of adjustment procedures on estimates other than means, proportions, and totals.
USE OF PARADATA IN REDUCING NONRESPONSE AND NONRESPONSE BIAS
There is a growing interest in paradata—that is, data about the process by which the survey data were collected that are obtained in the process of conducting the survey. Paradata encompass information about the interviews (times of day interviews were conducted and how long the interviews took); about the contacts (how many times contact was made with each sample person or how many attempts to contact the sample person were made, the apparent reluctance of the sample person); as well as survey modes (such as phone, Web, e-mail, or in person). These data have
many uses. They help in managing the survey operation (scheduling and evaluating interviewers) and assessing its costs. They are also important for understanding the findings of a survey and making inferences about nonrespondents. Indeed, there is a long history in the research literature of collecting additional data (what has become known as paradata) for nonresponse.
Hansen and Hurwitz (1946) suggested two-phase sampling, with the second phase of sampling looking at nonrespondents by using an intensive follow-up of units selected for the second phase. If data can be collected from all the sampled second-phase nonrespondents, then standard two-phase sampling weights can be developed to eliminate nonresponse bias. Even with an incomplete response at the second phase, the potential for bias can be reduced by using information from the additional second-phase sample.
Significant advances have been made in the state of the science for using paradata for reducing nonresponse bias (Olson, 2013). Today there are two main options for reducing such bias. One is to use paradata to introduce new design features to recruit uncontacted or uncooperative sample members—and, hopefully, respondents with different characteristics—into the respondent pool. The new design features rely on the use of paradata in a “responsive” design. The second option is to use paradata in adjusting base weights of the respondents. A third use of paradata is to use the data to better understand the survey participation phenomenon so that future surveys may reduce nonresponse, but this use does not result in reducing nonresponse bias for the survey at hand.
The initial focus of research on paradata was to explore nonresponse rates. The types of paradata that were considered as predictors of response were respondent-voiced concerns, the presence of a locked entrance or other safety measures, a multiunit building, and an urban setting (Campanelli et al., 1997; Groves and Couper, 1998).
More recently the work on paradata has taken a new direction and has focused more on the reduction of nonresponse bias by using paradata in responsive designs or in weighting adjustments. Adjustments that are effective in reducing nonresponse bias must be based on data that are predictive of the likelihood of participating in a survey or on the key survey outcomes or both (Little, 1986; Kalton and Flores-Cervantes, 2003; Little and Vartivarian, 2005; Groves, 2006; Kreuter et al., 2010).
The current challenges for paradata research are to enhance the underlying theory (e.g., what paradata are correlated with both response propensities and outcome measures); to better understand measurement error in the paradata and what effect these errors have on the utility of the paradata for reducing nonresponse bias; to operationally assign new tasks for interviewers that are feasible and do not detract from their ability to
conduct the interviews; and to better understand the environment for the interview—such as doorstep interactions, reasons for non-participation, and the quality of interviewer observations of the neighborhoods and the housing unit—so that better paradata measures can be developed.
Generally, the quality of paradata is relatively good if the data are automatically generated. When interviewers are asked to collect additional data that are not a byproduct of the data collection process, there is often a drop in quality. Additional data collection requirements often lead to substantial missing data rates. Likewise, when interviewer judgment is required, the data are of varying quality (see Casas-Cordero, 2010; Kreuter and Casas-Cordero, 2010; McCulloch et al., 2010; and West and Olson, 2010).
Kreuter holds that paradata carry a compelling theoretical potential for nonresponse adjustment. With paradata, the development of proxy variables is possible, and it is also possible to identify large variations in correlations across outcome variables. However, research has shown that although interviewers are good at making observations that are relevant for the primary act of data collection, they can have difficulty in collecting the additional proxy variables (Ys).
According to Kreuter, a case can be made for further collaboration with subject-matter experts, statisticians, psychologists, and fieldwork staff in the refinement of paradata, so these are examples of areas in which further investigation may be fruitful. Such collaboration would be useful, for instance, with substantive researchers to develop interviewer observation measures for labor force surveys (at-home pattern), health surveys (too ill to participate), housing surveys (condition of the dwelling), crime surveys (bars on windows), and educational surveys (literacy). Collaboration with statisticians could help improve statistical models, providing answers to such questions as how to balance multiple predictors of response and Ys, how to handle large and messy data, how to model and cluster sequences of unequal length, and how to address issues of discrete times and mixed processes. Psychologists, in collaboration with survey methodologists, could aid in understanding the factors that drive errors in interviewer observation, how training could improve ratings, how much error can be tolerated, and what the quality is relative to other sources. Finally, collaboration with fieldwork staff could help identify the costs associated with paradata collection as well as cheaper alternatives, the risks in interviewer multitasking, the appropriate level of observation, and ethical and legal matters issues that need to be resolved.
A focus on reducing nonresponse by using paradata in responsive designs, or through other means, should not lead to neglect of other sources of
error in survey estimates. In particular, measurement error (overreporting, underreporting, or misreporting) should be addressed, particularly in terms of the possible interaction with nonresponse.
Recommendation 3-3: Research is needed on the impact that reduction of survey nonresponse would have on other error sources, such as measurement error.










