JULIA BOWMAN ROBINSON
December 8, 1919–July 30, 1985

BY SOLOMON FEFERMAN
One of my earliest memories is of arranging pebbles in the shadow of a giant saguaro . . . I think I have always had a basic liking for the natural numbers. To me they are the one real thing. We can conceive of a chemistry which is different from ours, or a biology, but we cannot conceive of a different mathematics of numbers. What is proved about numbers will be a fact in any universe.
(From The Autobiography of Julia Robinson by Constance Reid)
AS A MATHEMATICIAN, Julia Bowman Robinson will long be remembered for her many important contributions to questions of algorithmic solvability and unsolvability of mathematical problems, in particular for her part in the negative solution of Hilbert's "Tenth Problem." And, despite her expressed wish, she will be remembered as the first woman to be elected to the mathematical section of the National Academy of Sciences, as well as the first woman to be president of the American Mathematical Society. By those who knew her personally she will be remembered for her rare qualities of idealism, integrity, modesty, openness, and generosity, and for her appreciation and encouragement of the work of others.
She was born Julia Bowman on December 8, 1919, in St. Louis, Missouri, the second of two daughters, to Helen Hall Bowman and Ralph Bowers Bowman. Her mother died when she was two years old, and her father retired not long after, having lost interest in his machine tool and equipment business. Ralph Bowman remarried a few years later to Edenia Kridelbaugh, and the family moved first to Arizona and then to San Diego; a third daughter, Billie, joined Constance and Julia a few years later. As a child, Julia was said to be stubborn and slow to talk, but she exhibited a precocious liking for the natural numbers, as evidenced by her earliest reported memories.
At the age of nine, Julia was stricken first with scarlet fever, and then with rheumatic fever, which, after several relapses, forced her to spend a year in bed. As a result, she lost more than two years of school, and there were more serious, lifelong consequences for her health.
Julia returned to school after a year of tutoring, during which she went through the state syllabuses for the fifth, sixth, seventh, and eighth grades. Shy and out of the swim socially, she took to her studies and found herself especially attracted to mathematics. Moving on in high school through the standard courses of algebra, trigonometry, and plane and solid geometry, she stood out as the only girl in the advanced mathematics and physics courses. She graduated from high school with awards in all the sciences (except chemistry, which she had not taken) and a special medal (the Bausch-Lomb) for all-round excellence in mathematics and science.
Following in the footsteps of her older sister Constance, Julia entered San Diego State College (now University) in 1936. It was common for students there to attend State for a couple of years and then transfer to UCLA or the Univer-
sity of California at Berkeley; those who remained generally obtained teaching credentials. Julia majored in mathematics because she liked it and was good at it, but she had no idea that there was such a thing as being a mathematician. When she came across the book Men of Mathematics by E. T. Bell, she became very excited at the intellectual vistas that opened up and she was determined to transfer to UCLA or Berkeley to learn some real mathematics. Finances were strained due to the suicide in 1937 of her father, whose retirement savings had been wiped out by the 1929 crash and the subsequent depression. However, with the assistance of an aunt and her older sister, in 1939 she managed finally to transfer to U.C.B. as a senior. It happened to be a particularly fortuitous time to enter the mathematics program at Berkeley, as the noted chairman, Griffith C. Evans, had been building up the department with outstanding researchers and teachers. In her first year at Berkeley, Julia took five mathematics courses, including one in number theory taught by Raphael M. Robinson. She was extremely happy at Berkeley, finding herself among so many students and faculty excited by and talking about mathematics.
Julia received her A.B. degree in 1940 and, at the urging of Raphael Robinson, continued on with graduate studies at Berkeley. She also managed to obtain a part-time position as an assistant to Professor Jerzy Neyman for his work on statistics. During this period, Julia and Raphael developed a personal friendship that blossomed into a courtship, and they married in December 1941. The relationship with Raphael was also to have major significance for Julia's development as a mathematician; he was an excellent teacher, both in class and in one-to-one discussions, and he had a deep knowledge of many parts of classical
and modern mathematics. Julia counted Raphael Robinson as one of her two most important scientific influences, the second one being the famous logician Alfred Tarski, who joined the Berkeley faculty in 1942.
Unfortunately, her marriage to a faculty member was to limit Julia's employment opportunities in Berkeley, since there was at that time (and for many years after) a nepotism rule in the U.C. system that prevented members of the same family from working in the same department. This did not affect her at first, since she had already received a teaching assistantship in mathematics for the second year of her graduate studies. Julia had wanted to teach calculus, but Jerzy Neyman pushed her to teach statistics, which she didn't like as much. The connection was useful, though, as Neyman was to employ her in his "Stat Lab" later during the war, and her work there would result in her first published paper.
From the beginning of their marriage, the Robinsons wanted and expected to have a family, and though Julia continued to audit mathematics courses, her preoccupations shifted more toward their home life. She became pregnant but, unfortunately, lost the baby a few months later; then, shortly afterward, on a visit home to San Diego, she contracted viral pneumonia. A doctor there was the first to recognize that there was substantial scar tissue in the mitral valve of the heart, a residue of her early bout with rheumatic fever, and he strongly advised her against becoming pregnant. He also told her mother in private that Julia would be lucky to live to age forty.
Julia was deeply depressed for a long time over not being able to have children, but, encouraged by Raphael, she returned eventually to the rewards of mathematics. She attended the first seminar that Tarski conducted at Berke-
ley and soon provided an ingenious solution to a definability problem in number theory that had been posed by Tarski's former student Andrzej Mostowski. The question was whether addition can be defined in terms of the successor operation and multiplication. Tarski was impressed by her positive solution to this problem and viewed it as suitable thesis material. It, and other similar work, was eventually to be incorporated as a relatively minor part of her thesis, the major part of which is to be described below.
During the immediate postwar period, Tarski was building a school in mathematical logic at Berkeley. One of the two most important logicians of the 20th century (the other being Kurt Gödel), he was a very systematic yet intense and charismatic lecturer with extensive research programs and a wealth of good problems to match. Tarski's main subjects of interest were metamathematics, set theory, model theory, universal (abstract) algebra, and algebraic theory. During a period of thirty-odd years following the war, he directed the doctoral work of a series of outstanding students, of whom Julia Robinson was one of the first.
Except for two papers, all of Robinson's work is concerned with the effective solvability and unsolvability of various mathematical problems, as well as with the characterization of various notions of effectiveness. The exceptions were her very first paper (1948), on a topic in sequential analysis, which came out of her work in the U.C.B. Stat Lab during World War II, and a paper (1951) on the theory of games. The latter resulted from her work during a year (1949–50) spent at the RAND Corporation in Santa Monica, where game theory was at the time a topic of intense investigation. Robinson succeeded there in solving in the affirmative a "prize" problem that had been posed by George W. Brown, whether a certain iterative method of play al-
ways leads to the value of a two-person zero-sum game; that result has been considered a very significant contribution to the subject.
To return to the main topic of Robinson's work: the informal idea of effective solvability (or decidability) of a class of mathematical problems of the form—Is P(a) true? (where a ranges over a given set S)—is that provided by an algorithm, i.e., a completely determined finitely described procedure which, given any element (or "input"), leads step-by-step to a definite conclusion as to the truth or falsity of the predicate P(a). Similarly an operation (function) f on elements of S to S is said to be effectively computable if there is an algorithm which, given any element a ε S as argument, leads to the value (or "output") b of f(a), for which f(a) = b. (We here use ∈ for the membership relation and read "a in S" for "a ∈ S".) The elements of the set S must themselves be presented in finite form as a finite sequence of symbols. Using any one of the standard systems of representation, these notions thus apply to predicates and operations on the set Z of integers and its subsets N+ of positive integers and N of non-negative integers (natural numbers), i.e., to Z = {. . . , -3, -2, -1, 0, 1, 2, 3, . . .}, N+ = {1, 2, 3, . . .} and N = {0, 1, 2, 3, . . .}. The notions extend directly to the set Q of all rational numbers, i.e., all fractions n/m with n, m ε Z and m ≠ 0. Furthermore, if A = {α1, . . . , αk} is any finite alphabet, we can apply the notions of effectiveness to predicates and functions on the set S = W(A) of all finite expressions (or "words") αi1 . . . αim with letters from A. Finally, if effectiveness is meaningful for predicates and operations on S, the same holds for the set Sn of all n-tuples (a1, . . . , an) where we deal with n-ary relations P(a1, . . . , an) and operations f(a1, . . . , an) = b.
It should be noted that the notion of effectiveness for
predicates and relations can be reduced to that for operations, using distinct elements t1, t0∈S (e.g., 1 and 0) to represent truth and falsity, respectively. By the characteristic function of P (an n-ary relation between elements of S), is meant the operation fP defined on Sn by fP(a1, . . . , an) = t1 if P(a1, . . . , an) is true and fP(a1, . . . , an) = t0 otherwise. Then, clearly, P is effectively decidable if and only if fP is effectively computable.
Since the beginning of abstract mathematics in antiquity, many algorithms have been presented for various specific mathematical problems and operations. In each case it was verified that the algorithm does the required work by following through its application to see that it gives the appropriate answer for an arbitrarily given argument as input. No general notion of effectiveness was required for such verifications, i.e., the informal conception of effectiveness sufficed. However, if one is to show that a problem of the form—Is P(a) true? (for a ∈ S)—is effectively undecidable, i.e., that no possible algorithm can serve to effectively determine the truth or falsity of P(a) for each a∈S, we must have a completely general and precise definition of effective decidability, so that its extent can be sharply delimited. The same applies to the task of showing that a given operations f is not effectively computable. By the remark above, once the general notion of effectively computable function is made precise, the same applies to that of effectively decidable predicate or relation.
Several independent proposals for a general, mathematically precise definition of effectively computable function on the natural numbers N (or N+) were made in the 1930s, and before long all were shown to be equivalent. Among the first was that made by Alonzo Church who advanced, for this, calculability in a certain restricted symbolism for
functions called the λ-calculus. Independently, and around the same time (using a suggestion of Jacques Herbrand), Kurt Gödel proposed the class of general recursive functions as a candidate for the algorithmically computable functions. Before this, in his famous 1931 paper on the incompleteness of Principia Mathematica and other formal axiomatic systems concerning the natural numbers, Gödel had made heavy use of a subclass of these, called the primitive recursive functions. In 1936, Church's student Stephen C. Kleene proved the equivalence of the λ-definable and general recursive functions; in the same year Church first proposed in print to identify the algorithmically computable functions with either one of these (coextensive) classes, and this proposal was subsequently dubbed Church's Thesis. Unaware of the preceding work, Alan Turing in 1937 proposed a notion of mechanically computable functions, where the calculations are carried out by an idealized machine (subsequently dubbed Turing machines) without limitation on storage or time. When Turing learned of Church's Thesis, he established the equivalence of the λ-calculable functions with his own mechanically computable functions. All these (and related) contributions bolstered the arguments for Church's Thesis, which has since gained practically universal acceptance; in particular, Turing's notion is considered to be one of the most faithful to the informal concept of a step-by-step finite mechanical procedure. His definition also extends directly to that of effective computability on any set of expressions generated from a finite alphabet.
The systematic development of the theory of effectively computable functions, assuming Church's Thesis, was initially due to Kleene; in particular, working with the Herbrand-Gödel definition, he showed how the general recursive functions can be obtained from the primitive recursive functions,
themselves generated by some relatively perspicuous schemata, by the adjunction of one new scheme embodying the construction "do . . . until . . . " It became convenient to work with Kleene's schemata as a means for verifying various properties of the effectively computable functions. As a result of this, the subject of effective computability (both for positive and negative results) came to be called recursive function theory. One mildly complicating feature, though, of Kleene's schemata is that they pass through functions of arbitrarily many arguments in order even to obtain the functions of one argument (the unary functions). The problem thus arose of finding a simple set of schemata for generating the unary general recursive functions. An important step in this direction had been made by Raphael Robinson, who obtained a simple set of schemata for the unary primitive recursive functions; he suggested to Julia the problem of extending this to a characterization of the unary general recursive functions. After several years' work, she succeeded in obtaining an elegant solution in 1948, which was published in a paper (1950). She returned to this problem in a later paper (1968, 1) with an even more elegant characterization of the class of unary general recursive functions as the least class containing the zero and successor functions and closed under composition and a new special scheme of general recursion. Related to these papers is her note (1955) on primitive recursive functions. Somewhat in the same spirit, but for other classes of functions or sets, are her papers (1967; 1969, 1; 1973, 2) (in the last, within an axiomatic setting). Of these, one (1967) is noteworthy for its beautifully simple and direct exposition of the theory of hyperarithmetical functions, a class originally obtained by a complicated transfinite iteration of the "jump" process associated with general recursion in
a relativized form. These papers comprise one of three main areas of Robinson's contributions to the theory of effective computability.
For an explanation of Julia Robinson's dissertation work with Tarski and her later work on the Diophantine problem, we consider two further notions from recursive function theory. Suppose S is a set to which the notion of effectively computable (alias general recursive) function is applicable, either directly or by an effective enumeration of S by N. A subset D of S is said to be decidable (or recursive) if its characteristic function fD on S is effectively decidable (or recurvsive) if its characteristic function fD on S is effectively computable; in other words, D is decidable if its membership problem is effectively decidable. A subset E of S is said to be effectively (or recursively) enumerable if it is the range of a recursive function f from N to S, i.e., if E is the set of values f(0), . . . , f(n), . . . for nεN; for simplicity, the empty set is also counted as being effectively enumerable. It is not hard to see that D is decidable if and only if both D and its complement S – D are effectively enumerable.
Of special interest in modern logic are the sets S = WFF (L) of well-formed formulas in a formal Language L, which are special kinds of expressions generated from a finite symbolism. In the first-order predicate calculus these are generated from one or more basic relations R(x1, . . . , xn) by closure under ∧ ("and"), ∨ ("or"), ¬ ("not"), → ("if . . . then . . . " ), ∀x ("for all x, . . . "), and ∃x ("there exists x, . . . "). In the following we consider the special case where the basic relations are x = y, x + y = z, and x · y = z. We define x ≠ y by ¬ (x = y), x = 0 by x + x = x, x = 1 by (x · x = x) ∧ (x ≠ 0), etc. In this language we can speak of firstorder properties of the structures of the natural numbers
N, the integers Z, as well as of the rational numbers Q, the real numbers R, and the complex numbers C.
A formula A of L, such as ∃x "y (xy = y), is said to be closed if it contains no free variables. For any mathematical structure (M, R1, . . . , Rm) in which the basic relations of S are interpreted in a definite way (with x = y interpreted as equality) each closed formula A of S has a definite truth value in M. By the theory of M, in symbols Th(M, R1, . . . , Rm), is meant the set T of closed well-formed formulas which are true in M under this interpretation. This theory is said to be decidable if T is a decidable subset of S, otherwise undecidable. One of the basic consequences of the work of Gödel and Church is that the theory of the natural number systems, Th(N, +, ·) is undecidable, and the same applies to Th(Z, +, ·) since N is definable in the latter theory by: x ε N if and only if ∃y ∃z ∃u ∃w (x = y2 + z2 + u2 + w2) (according to a famous theorem of Lagrange). On the other hand, it was known from earlier work of M. Presburger (1930) that Th(Z, +) and Th(N, +) are decidable; note that the product relation x y = z is not included in these structures.
One of Tarski's main long-term programs, beginning in the 1930s in Warsaw and continuing over into his Berkeley period, was the systematic investigation of the decision problem for first-order theories associated with mathematical structures met in practice. Tarski's most famous result in this direction, first announced in 1931 but not published in full until 1948, was his decision procedure for the elementary (first-order) theory of real numbers, i.e., Th(R, +, ·); moreover, this was shown to be the same as the theory of any real-closed field (M, +, ·), including the countable field of real algebraic numbers, i.e., the real number solutions of polynomial equations over Q. Tarski had also shown
(what was easier) that the elementary theory of the complex number field Th(C, +, ·) is decidable and that any algebraically closed field (M, +, ·) of characteristic zero has the same theory.
This is where things stood when Julia Robinson took up, at Tarski's suggestion (via Raphael Robinson), the question of definability of the set N in Th(Q, +, ·). The status of the decision problem for the theory of the field of rational numbers was at that point the big unknown between the undecidable theory of integers Th(Z, +, ·) and the decidable theory of real numbers Th(R, +, ·). Robinson's exceptional achievement in her thesis work was to show that the set Z (and hence N) is first-order definable in Th(Q, +, ·), and hence that the latter theory is also undecidable. It was far from obvious how to do this. Her first breakthrough came with the realization that if r is a rational number and r is expressed as a quotient of integers a/b in lowest terms, then b is odd if and only if (Ǝx1 Ǝx2 Ǝx3) (7r2+ 2 = x12 + x22 + x32) is true in Q. Thus one ternary quadratic form can be used to "eliminate" 2 as a factor from the denominator of a rational number. Robinson then found other ternary quadratic forms to eliminate in turn all the other prime numbers from denominators. The final problem that she overcame was to combine these infinitely many different quadratic forms into a finitely described class of forms which would succeed in eliminating all (and only) denominators of fractions in lowest terms and thus in characterizing the integers Z as exactly the rationals satisfying a first-order property in (Q, +, ·). Among the important consequences of this deep and difficult work were the result that the axiomatic theory of fields is undecidable; this is a corollary using some general results of Tarski on undecidable theo-
ries. Robinson received her Ph.D. in 1948, and the results of the thesis were published soon after in the paper (1949).
In a later paper (1959, 1), Robinson extended her thesis work to algebraic fields (F, +, ·) of finite degree over the rationals (subfields of the complex numbers C). Here she showed that N is definable in the ring (A, +, ·) of algebraic integers of F and that A is in turn definable in the field F, so that both Th(A, +, ·) and Th(F, +, ·) are undecidable. The papers (1962, 2) and (1965) contain further related results of interest.
We can now finally return to the third main area of Robinson's mathematical preoccupations, that of existential definability in arithmetic, also called Diophantine definability. The background to this problem is as follows.
In the third century A.D., the Greek mathematician Diophantus worked on solving equations with arbitrary integer coefficients, for integer values. The general linear Diophantine equation in two variables is ax + by = c where a, b, c are arbitrarily given integers. An algorithm to determine whether or not there are x, y ∈ A satisfying ax + by = c makes use of an algorithm, due to Euclid, for finding the greatest common divisor of two integers: provided a ≠ 0 or b ≠ 0, the equation has a solution x, y ∈ Z if and only if the greatest common divisor d of a and b is a divisor of c; then if there is a solution at all, we have a further algorithm for finding all possible solutions. Another classical algorithm, to find all possible x, y, z ∈ N+ satisfying x2 + y2 = z2, connects number theory with geometry; the solutions of this equations such as 3, 4, 5 and 5, 12, 13, provide all possible right triangles with each side of integer length. The famous Fermat problem concerns the existence of integer solutions, if any, of xm + ym = zm, with x, y, z ≠ 0 and m > 2.
The general Diophantine equation in n variables x1, . .
. ,xn is given by an equation P1(x1, . . . , xn) = P2(x1, . . . , xn) where P1, P2 are polynomials with integer coefficients. By subtraction this can always be brought to the form P(x1, . . . , xn) = 0, where P is again such a polynomial, i.e., P is a finite sum of terms of the form ![]() where a is in Z and the exponents ki are in N. The statement that (or question whether) there exist integer solutions at all to this equation is symbolized by (∃x1 . . . xn ∈ Z) [P(x1, . . . , xn) = 0]. Closely related questions are whether there exist natural number solutions (∃x1 . . . xn ∈ N) [P(x1, . . . , xn) = 0] or positive integer solutions (∃x1 . . . xn ∈ N+) [P(x1, . . . , xn) = 0].
where a is in Z and the exponents ki are in N. The statement that (or question whether) there exist integer solutions at all to this equation is symbolized by (∃x1 . . . xn ∈ Z) [P(x1, . . . , xn) = 0]. Closely related questions are whether there exist natural number solutions (∃x1 . . . xn ∈ N) [P(x1, . . . , xn) = 0] or positive integer solutions (∃x1 . . . xn ∈ N+) [P(x1, . . . , xn) = 0].
Interest in Diophantine problems lay mostly dormant until the 17th century, when they were taken up by the outstanding amateur mathematician Pierre de Fermat, who solved many individual Diophantine problems, often challenging others to do the same without revealing his methods. Subsequently the subject was pursued by such great mathematicians as Euler, Lagrange, Gauss, Dirichlet, Dedekind, and others through the 19th century. This work brought to bear many ingenious and difficult arguments, which were organized by various techniques; however, no general theory emerged.
Faced with this situation at the turn of the 20th century, David Hilbert proposed the following decision problem for arbitrary Diophantine equations: To devise a process according to which it can be determined by a finite number of operations whether the equation is solvable in integers.1 This problem was the tenth on his famous list of twenty-three problems in a wide variety of fields, which Hilbert dramatically presented as a challenge in his address to the International Congress of Mathematicians in 1900. Hilbert's optimism about finding a general algorithm for deciding all questions of the
form (∃x1, . . . , xn ε Z) [P(x1, . . . , xn) = 0] with P an integer polynomial was in line with his proclaimed optimism about the eventual solvability of all mathematical problems, but flew in the face of the fact that Diophantine equations were known to be exceptionally resistant to general methods of solution. Indeed, for classifications according to degree, an algorithm was subsequently provided by Carl Ludwig Siegel only for the general problem of Diophantine equations of degree 2 and arbitrarily many unknowns. (The degree of P(x1, . . . , xn) is the maximum of the sums of the exponents k1 + . . . + kn of its terms ![]() ; the general polynomial of degree 2 in two variables is thus of the form ax12 + bx1x2 + cx22 + dx1 + ex2 + f.) On the other hand, in classifications according to the number n of variables, some progress has been made in recent years only for n = 2 and here only for a wide class of equations of degree higher than 2.2 Even now, practically nothing systematic is known for nonquadratic equations in more than two variables.
; the general polynomial of degree 2 in two variables is thus of the form ax12 + bx1x2 + cx22 + dx1 + ex2 + f.) On the other hand, in classifications according to the number n of variables, some progress has been made in recent years only for n = 2 and here only for a wide class of equations of degree higher than 2.2 Even now, practically nothing systematic is known for nonquadratic equations in more than two variables.
With the emergence in the 1930s of the theory of recursive functions and the demonstrated effective unsolvability of some logical and mathematical problems, it became possible to consider giving a negative solution to Hilbert's Tenth Problem. In fact, there were already related negative results due to Gödel in his famous 1931 paper on incompleteness of formal systems of arithmetic. He there associated with each consistent axiom system T containing a sufficient amount of arithmetic, a true statement not provable in T, of the form "x( f(x) ≠ 0) where f is primitive recursive. Then he succeeded in showing that the relation f(x) = y is definable over N in the form:
where each Qi is either the universal quantifier "∀" or the existential quantifier "∃", and P is a polynomial with integer coefficients. Somewhat later (1950), Martin Davis succeeded in showing that one can choose in place of the right-hand side of (1), a definition in which all but one of the Qi are existential, and where the universal quantifier is "bounded," so that f is definable in the form:
for a suitable polynomial P. Hence elimination of the bounded universal quantifier would give a negative solution to Hilbert's Tenth Problem. For, by the work of Church, Turing, and Kleene:
(3) (a) Every non-empty recursively enumerable set A of natural numbers is definable in the form
with f primitive recursive; and
(b) one can construct a recursively enumerable set A which is not recursive and hence not effectively decidable.
Thus, elimination of the bounded universal quantifier in the form (2) for such A would eventually give
for a suitable integer polynomial P, and this would show that there is no general algorithm for deciding whether a Diophantine equation has any solutions at all in the natural numbers.
A set A of natural numbers is called Diophantine if it is definable in the form (4) with the variables "zi" ranging over N. This is equivalent to its being definable in purely
existential form in the structure (N, +, ·). Julia Robinson's work here started with the specific question, posed by Tarski, whether the set {2, 22, . . . , 2n, . . .} of powers of 2 is Diophantine. At first she tried to establish Tarski's conjecture that the answer would be negative, but failing in that, she began to consider the opposite conjecture, and before long was led to the general problem of the Diophantine definability of arbitrary recursively enumerable sets. In her paper (1952) Robinson reported her first results in this direction. She showed there if R is any binary relation in the natural numbers of roughly exponential growth in the sense of (5) next, then the relation x Pow y (x is some power of y) is existentially definable in the structure (N, +, ·, R), where:
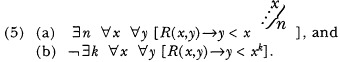
Furthermore, she showed that
(6) The relations xy = z, (x/y) = z and x! = y are all existentially definable in terms of Pow, hence in terms of any R of roughly exponential growth.
The full significance of Robinson's 1952 results was not to emerge for close to a decade. During that period she continued to work hard on the general problem of Diophantine definability without substantial progress, though, as described above, she was able to obtain very satisfying results in her other two main areas of interest.
Around 1960, Julia received the draft of a paper by Martin Davis and Hilary Putnam in which they showed that if the famous hypothesis that there exist arbitrarily long arithmetic progressions containing only prime numbers were true, then every recursively enumerable (r.e.) set would be exponen-
tial Diophantine, i.e., existentially definable in (N, +, ·, Exp), where Exp(x, y) = xy. She quickly succeeded in eliminating that hypothesis (still unproved) and also simplified their arguments in many other respects. This led to the joint publication (1961) with Davis and Putnam in which the main result is that every r.e. set A is the set of all x for which a Diophantine equation P(x, z1, . . . , zm) = 0 with variable exponents has solutions z1, . . . , zm in N. The Davis, Putnam, Robinson paper (1961) also featured the "J. R. Hypothesis," that some relation R of roughly exponential growth is Diophantine. By her 1952 results and this joint paper, the J. R. Hypothesis implies that every r.e. set is Diophantine. But, once more, matters would rest without essential progress for almost a decade.
Julia Robinson's doctor had told her mother in 1941 that she would be lucky to live to age forty. In 1961, when she was forty-one, her heart was functioning so poorly that the only alternative to a life of invalidism was an operation, by a technique then in its pioneering stage, to remove the built-up scar tissue. Her health improved dramatically, and one month after surgery, Julia took up bicycling as a new form of exercise. Over the following years, she bought a half dozen increasingly better bicycles and thereby enjoyed many outings and cycling trips in the U.S. and elsewhere, including The Netherlands. Raphael Robinson sometimes complained that "while other men's wives buy fur coats and diamond bracelets, [my] wife buys bicycles." (Autobiography, p. 18.)
Julia continued to work hard on Hilbert's 10th Problem throughout the 1960s. Then in 1970 the news came from the U.S.S.R. that a twenty-two-year old mathematician in Leningrad named Yuri Matijasevic had succeeded in establishing the J. R. Hypothesis. He showed that the sequence
of even Fibonacci numbers, known to be of exponential growth, formed a Diophantine relation. This work involved elementary properties of the so-called Pell (Diophantine) equation x2 + (a2 - 1) y2 = 1 for a > 0. As it happens, Robinson had used the same equation in her 1952 paper and was very familiar with its properties. In retrospect, she realized that she had herself been very close to the solution of Hilbert's 10th Problem. Nevertheless, she was very excited and pleased to see the long effort capped by Matijasevic's achievement, and she immediately sent her generous congratulation:" . . . now I know it is true, it is beautiful, it is wonderful. . . . If you really are 22, I am especially pleased to think that when I first made the conjecture you were a baby and I just had to wait for you to grow up." (Autobiography, p. 19.) In 1971, the Robinsons visited Leningrad and had the pleasure of meeting Matijasevic and his wife.
Capitalizing on the breakthrough, Julia Robinson and Yuri Matijasevic subsequently collaborated on three papers, (1974), (1975), and (1976), the last of these jointly with Martin Davis. In the 1975 paper Robinson and Matijasevic succeeded in reducing to 13 the number m of unknowns in the representation (4). In later work (by Matijasevic alone), this number was further reduced to 9. There is still a wide gap between the positive information on algorithmically solvable Diophantine equations in two unknowns mentioned above and the negative results for 9 and more unknowns. The most challenging open problem currently in this direction is whether there is a general algorithm for deciding the solvability of Diophantine equations in three unknowns.
The paper of Davis, Matijasevic, and Robinson (1976) provides a beautifully exposed yet concisely presented sur-
vey of these results on Hilbert's 10th Problem, together with a series of new "positive" applications, such as the Diophantine representation (i.e., as the range of positive values of a polynomial) of the set of prime numbers, and the equivalence of many famous problems—including the Riemann Hypothesis—with statements of the form (" z1 . . . zm) [P(z1, . . . , zm) ≠ 0]; the paper also presented a number of further interesting open problems. This work was solicited for the Proceedings of the 1974 Symposium on Mathematical Developments Arising from Hilbert Problems (ed. Browder, 1976). Other papers that Robinson wrote herself on the subject of Hilbert's 10th Problem, both before and after the 1970 breakthrough, are (1962, 1), (1969, 1, 3, 4), and (1973, 1).
In recognition of her various outstanding contributions and, in particular, of her central role in the work leading to the solution of Hilbert's 10th Problem, Julia Robinson was elected in 1975 to the mathematical section of the National Academy of Sciences, the first woman to be so honored. In the same year, the University of California at Berkeley offered her a full professorship in the Department of Mathematics with a special arrangement permitting her to serve quarter-time since, although her health had improved greatly as a result of the operation mentioned earlier, she still did not feel that she could take on a full teaching load. In the past she had on occasion taught classes in the Department of Mathematics, but this was her first appointment as a regular member of the faculty at Berkeley since her receipt of the Ph.D. there in 1949.
Other signal honors followed in the next decade. Robinson was chosen as the colloquium lecturer at the 84th Summer Meeting of the American Mathematical Society in 1980; her lectures covered the main areas of her interests between logic and number theory, and the notes for these
constitute her last writings, though they were not in final form for publication. In 1982, she was nominated for the presidency of the American Mathematical Society (for the years 1983–84), again the first woman to be so honored. Uncertain whether to take on the position because of her limited energies, she finally decided that, in the words from her Autobiography (pp. 20–21):" . . . as a woman and as a mathematician I had no alternative but to accept. I have always tried to do everything I could to encourage talented women to become research mathematicians. I found my service as President of the Society taxing but very, very satisfying." In 1983, Julia Robinson received a MacArthur Fellowship with its substantial award for a five-year period. And, in 1985, she was chosen as a member of the American Academy of Arts and Sciences.
While she was presiding over the summer A.M.S. meeting in Eugene, Oregon, in 1984, it was discovered that she was suffering from leukemia. After prolonged treatment and hospital stays, she enjoyed a remission of several months in the spring of 1985. But then the disease returned, and she died on July 30, 1985 at the age of sixty-five. She is survived by her husband, Raphael Robinson, and two sisters, Constance Reid and Billie Comstock.
One of Julia's last requests was that there be no funeral service and that those wishing to make a gift in her memory contribute to the Alfred Tarski Fund, which she had been instrumental in setting up in honor of her late teacher, friend, and colleague. Modest to the end, she let her character and achievements speak for themselves.
I AM INDEBTED to Constance Reid, as well as to John Addison, Leon Henkin, and Raphael Robinson of the University of California at Berkeley for materials on the life, work, and career of Julia Robinson. From published sources I have drawn most heavily on The Autobiog-
raphy of Julia Robinson by Constance Reid, and Julia Bowman Robinson (1919–1985) by Constance Reid with Raphael M. Robinson. Other valuable biographical material and personal impressions are listed in the references which follow.
NOTES
REFERENCES
Alan Baker, "Contributions to the Theory of Diophantine Equations: I. On the Representation of Integers by Binary Forms, II. The Diophantine Equation y2 = x3 + k," Philos. Trans. Roy. Soc. London, Ser. A. 263 (1968):173–208.
Felix E. Browder, ed. Mathematical Developments Arising from Hilbert Problems. Proc. Symp. Pure Math. XXVIII (Providence: American Mathematical Society, 1976).
Martin Davis, "Hilbert's Tenth Problem is Unsolvable," Am. Math. Mon. 80(1973):233–69.
Lisl Gaal, "Julia Robinson's Thesis," Assoc. Women Math. Newsl. 16(3) (1986):6–8.
Kurt Gödel, "Über formal unentscheidbare Sätze der Principia Mathematica und verwandter Systeme I," Monatsh. Math. Phys. 38 (1932):173–98; reprinted and translated in Gödel (1986), pp. 144–95.
Kurt Gödel, Collected Works, Vol. I. Publications 1929–1936, ed. by S. Feferman et al. (New York: Oxford University Press, 1986).
Stephen C. Kleene, "Origins of Recursive Function Theory," Ann. Hist. Computing 3(1981):52–67.
Constance Reid, Hilbert (New York: Springer-Verlag, 1970).
Constance Reid, "The Autobiography of Julia Robinson," Coll. Math. J. 17(1986):2–21.
Constance Reid with Raphael M. Robinson, "Julia Bowman Robinson (1919–1985)," Women of Mathematics, A Bibliographic Source Book,
ed. by Louise S. Grinstein and Paul J. Campbell (Westport, Conn.: Greenwood Press, 1987):182–89.
Carl Ludwig Siegel, "Zur Theorie der quadratischen Formen," Nach. Akad. Wiss. Göttingen Math. Phys. Kl. II (1972):21–46.
Craig Smorynski, "Julia Robinson, In Memoriam," Math. Intelligencer, 8(1986):77–79.
Alfred Tarski, A Decision Method for Elementary Algebra and Geometry, prepared for publication by J. C. C. McKinsey (RAND Report R–109, 1948; 2nd rev. ed. University of California Press, Berkeley and Los Angeles, 1951).
BIBLIOGRAPHY
1948 A note on exact sequential analysis. Univ. Calif. Pub. Math. New Ser. 1:241–46.
1949 Definability and decision problems in arithmetic. J. Symb. Logic 14:98–114.
1950 General recursive functions. Proc. Am. Math. Soc. 1:703–18. An iterative method of solving a game. Ann. Math. 54:296–301.
1952 Existential definability in arithmetic. Trans. Am. Math. Soc. 72:437–49.
1955 A note on primitive recursive functions. Proc. Am. Math. Soc. 6:667–70.
1959 The undecidability of algebraic rings and fields. Proc. Am. Math. Soc. 10:950–57.
Problems of number theory arising in metamathematics. Report of the Institute in the Theory of Numbers (Boulder):303–6.
1961 With Martin Davis and Hilary Putnam. The decision problem for exponential Diophantine equations. Ann. Math. 74:425–36.
1962 The undecidability of exponential Diophantine equations. In Logic, Methodology, and Philosophy of Science: Proceedings of the 1960 International Congress, ed. E. Nagel et al. (Stanford: Stanford University Press):12–13.
On the decision problem for algebraic rings. In Studies in Math-
ematical Analysis and Related Topics (essays in honor of George Pólya). (Stanford: Stanford University Press):297–304.
1965 The decision problem for fields. In The Theory of Models: Proceedings of the 1963 International Symposium at Berkeley, ed. by J. W. Addison et al. (Amsterdam: North-Holland):299–311.
1967 An introduction to hyperarithmetical functions. J. Symb. Logic 32:325–42.
1968 Recursive functions of one variable. Proc. Am. Math. Soc. 19:815–20.
Finite generation of recursively enumerable sets. Proc. Am. Math. Soc. 19:1480–86.
1969 Diophantine decision problems. Studies in Number Theory, ed. W. J. LeVeque. MAA Stud. Math. 6:76–116.
Finitely generated classes of sets of natural numbers. Proc. Am. Math. Soc. 21:608–14.
Unsolvable Diophantine problems. Proc. Am. Math. Soc. 22:534–38.
Hilbert's tenth problem. In Proceedings of the 1969 Summer Institute in Number Theory, ed. D. J. Lewis. Proc. Symp. Pure Math. 20, (Providence: AMS):191–94.
1973 Solving Diophantine equations. In Proceedings of the Fourth International Congress for Logic, Methodology and Philosophy of Science, ed. P. C. Suppes (Amsterdam: North-Holland):63–67.
Axioms for number-theoretic functions. In Selected Questions of Algebra and Logic, ed. A. I. Shirshov et al. (Novosibirsk: Siberian Academy of Sciences):253–63.
1974 With Y. Matijasevic. Two three-quantifier universal representations of recursively enumerable sets. (in Russian). In Theory of Algorithms and Mathematical Logic (Moscow):112–23.
1975 With Y. Matijasevic. Reduction of an arbitrary Diophantine equation to one in 13 unknowns. Acta Arith. 27:521–53.
1976 With Martin Davis and Y. Matijasevic. Hilbert's 10th problem. Diophantine equations: Positive aspects of a negative solution. Mathematical Developments Arising from Hilbert Problems, Proc. Symp. Pure Math. 28, ed. by F. A. Browder. (Providence: AMS):323–78.
1980 Between logic and arithmetic. Lecture notes distributed in conjunction with the Colloquium Lectures given at the Eighty-fourth Summer Meeting of the American Mathematical Society, University of Michigan, Ann Arbor, August 19–22, 1980.




























