7
Quantum Information with Light and Atoms
What lies beyond Moore’s law? Quantum mechanics and information theory are two of the scientific cornerstones of the 20th century. One describes physics at very small scales, from molecules and atoms to electrons and photons; the other provides a mathematical analysis of data communication and storage. As the last decades have witnessed the remarkable shrinking to near-atomic scales of the electronic components that carry and process information, these two disciplines are naturally beginning to merge. The exponential shrinking of computer chip components, as posited by Moore’s law, will soon slow as individual electronic transistors approach the atomic scale, where there is no room for packing more components. However, the revolutionary principles of quantum mechanics could offer a way out: Quantum information science may have profound and far-reaching relevance to economic growth, secure communication, and number-crunching into the 21st century. The quantum hardware now found in atomic, molecular, and optical (AMO) systems is a key to realizing future quantum devices.
THE QUANTUM INFORMATION REVOLUTION
Two of the great scientific, philosophical, and technological revolutions of the 20th century were quantum mechanics and information science. Each of these changed our lives in fundamental and lasting ways. Today we are witnessing the beginning of another revolution, that of quantum information, a revolution that promises similar changes in the 21st century. This new science has come from a merging of the two revolutionary disciplines of the 20th century (see Figure 7–1).
Quantum mechanics describes the world of the very small—the submicroscopic world of elementary particles, electrons, atoms, and molecules, as well as the properties of light at the level of single photons. A revolutionary aspect of quantum theory is its prediction of fundamental ambiguities, where physical properties of objects such as their positions or velocities may coexist in multiple states, a condi-
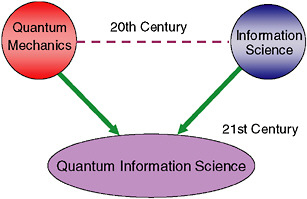
FIGURE 7–1 Two of the profound societal revolutions of the 20th century are combining in the 21st century to create a new science with incredible technological implications.
tion that is inconceivable in our macroscopic world. These ideas are not just arcane academic curiosities, however, but provide the physical basis for chemistry, semiconductor electronics, x rays, and other ubiquitous elements of modern living.
Classical information science describes the storage, transmission, and manipulation of information that is encoded as bits—the ones and zeros of the binary number system. Computers, the Internet, and video games are all products of bitbased information science, and one reason these modern marvels work so well is the nearly complete absence of errors or ambiguities. Bit-based information must be virtually error-free, or else the exponential growth in complexity and speed of computing devices would eventually lead to chaos. Thus, the fundamental ambiguity of quantum mechanics and the fundamental certainty of information science seem totally at odds.
Quantum information changes all of that. A new scientific and technological revolution is emerging in the 21st century out of the new and intimate connection between quantum mechanics and information science. The processing of quantum information requires a physical system that obeys the laws of quantum mechanics. Quantum physics is prevalent in very small, isolated systems such as individual atoms and photons. Thus, AMO physical systems and techniques have taken the major role in the development of quantum information science, just as in the 20th century they were in the vanguard of the development of quantum mechanics. The new quantum information science promises to be as radical in its effect on human society as quantum physics and information science were individually in the last century. In the next 10 years, it will be one of the major driving forces in AMO physics.
WHAT IS INFORMATION?
Information is physical. The storage and processing of information always requires some physical means, such as the orientation of a die, the physical position of a switch, or the amount of electrical charge on a capacitor. In conventional computers information is stored as bits that have two possible (binary) values. Bits are everywhere. Binary information is present in our homes, offices, and cars, contained in literally hundreds of information processors secreted in everyday appliances, in addition to laptop and desktop computers. Our telephone conversations, the music and video entertainment we enjoy, our bank transactions—all involve the storage, transmission, and manipulation of digital information in the form of zeros and ones, represented by billions upon billions of bits. Information is also fungible. These bits take many physical forms, from tiny charges on a transistor, to micron-sized patches of magnetic material, to microscopic burn marks on a CD or DVD. However, all conventional physical bits share one defining feature: A bit is in one state or the other—that is, it is always either zero or one but never both.
Quantum information is completely different. Quantum information is stored not in bits but in “qubits,” quantum bits whose value can be one or zero but can also be both zero and one at the same time. An ordinary transistor cannot be both on and off. But if it is small enough, so that the rules of quantum mechanics take over, such an oddity is not only possible but is also typical. Thus, a single atom can be in what is known as a “superposition” of two different states. For example, an atom’s outermost electron can be spinning with its axis pointing up or down, or it can be in a superposition of up and down. Figure 7–2 shows how this can be represented by a vector having arbitrary orientation in space, in contrast to only two possible orientations for a classical bit. An essential and nonintuitive (!) characteristic of this superposition is that in this state the spin axis is not someplace between up and down. If we observe the spin, it will always be seen to be either up or down (although we cannot predict which it will be beforehand), never someplace in between. But this is not because the spin is indeed up or down before being measured—it is truly in both states and does not appear in one or the other state until it is measured. This very fundamental aspect of the unknown nature of the quantum state until a measurement is made flies in the face of all classical experience and lies at the core of quantum mechanics as we know it today.
Why Quantum Information?
What makes quantum information so special? Superposition allows qubits to do things that ordinary bits cannot. To see why this is so, consider a register of three classical bits (see Figure 7–3). The three-bit register stores the binary number
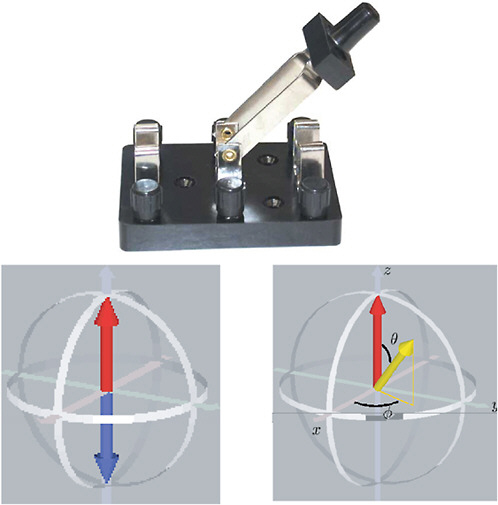
FIGURE 7–2 Top: A mechanical switch representing a bit of classical information is either on or off, representing a value of one or zero. SOURCE: L.P.Kelvin. Bottom left: A bit can be represented by either up (red arrow) or down (blue arrow) orientations of a classical spin. Bottom right: A quantum bit, or “qubit,” can be represented by both spin up and spin down at the same time—that is, it can exist in superposition, which is represented by the yellow vector oriented at some direction other than the up and down directions. An electron in an atom can thus provide a quantum switch whose value is indeterminate until measured. SOURCE: R.Laflamme Institute for Quantum Computing, University of Waterloo, Canada.

FIGURE 7–3 Three classical bits of binary values 101.
101, which is 5 in the usual decimal system. A three-bit classical register can store any one of eight different numbers from zero=000 to seven=111. In contrast, a quantum three-qubit register can store a superposition of all of the eight different numbers at the same time. More precisely, that three-qubit register can be in a coherent superposition of all eight numbers, which we write as follows:
This is a shorthand notation for saying that the quantum state of the qubit register ![]() is a superposition of each of the possible classical states. The variables a through h are related to the relative weights of each state in the superposition. These numbers can take any value, positive, negative, or complex, as long as the squares of their absolute values add up to one. The above superposition is “coherent,” because its weights have definite phase relationships between them. This allows interference to occur, much like the interference of any wavelike phenomena (Box 5–2).
is a superposition of each of the possible classical states. The variables a through h are related to the relative weights of each state in the superposition. These numbers can take any value, positive, negative, or complex, as long as the squares of their absolute values add up to one. The above superposition is “coherent,” because its weights have definite phase relationships between them. This allows interference to occur, much like the interference of any wavelike phenomena (Box 5–2).
The flexibility gained by allowing the qubit register to be in such a quantum superposition is enormous when the number of individual qubits becomes large. The number of states allowed in the superposition grows exponentially with the number of qubits in the register. For the three-qubit register shown, the number of possible states in the superposition is 23=8. For an N-qubit register, the number of states in superposition is 2N. Thus, while a classical N-bit register can represent a single N-bit number, a quantum N-qubit register can be in a superposition of all 2NN-bit numbers. For a modest 300-qubit register, the number of states in the superposition can be 2300, a number that is enormously larger than the number of atoms in the entire universe.
In addition to this ability to store exponentially many quantum states, the linear nature of quantum mechanics means that these states can all be manipulated at the same time—that is, massive “quantum parallelism” is possible. This is one of the keys to the power of quantum computation. It allows a quantum processor to
perform an exponentially large number of calculations all at the same time, since the quantum register contains that large number of different classical registers. This can make a quantum computer mind-bogglingly faster than even the fastest imaginable classical computer. A problem that could take more than a lifetime to solve on the best classical computer of the future might be solved in minutes or hours on a quantum computer. The best example of this today is the problem of factoring a large number into its primes, a computational problem that is extremely time-consuming on a classical computer. In fact, the factorization of large numbers is so hard that it forms the basis of most data encryption standards. In 1994, Peter Shor showed that a quantum computer would be capable of doing this task exponentially faster than any known classical algorithm, i.e., the solution time using the classical algorithm grows exponentially with the number of qubits required to represent the number, while the corresponding time for a quantum solution grows much more slowly. Consequently, quantum computers would compromise the security of many forms of encryption in use today.
QUANTUM INFORMATION AT THE FRONTIERS OF SCIENCE
Quantum information encompasses one of the grand challenges in science in the last century: the reconciliation between quantum physics and classical physics. Here we describe some aspects of this challenge and how quantum information technology from AMO physics may someday bridge this gap.
Despite the dramatic success of quantum mechanics, glaring difficulties remain in reconciling quantum rules of nature with our everyday notions of reality. If quantum mechanics is indeed a complete theory of nature, why does it appear to conflict with classical descriptions of everyday life? Richard Feynman, one of the iconic figures of 20th century physics, memorably stated that
we have always had a great deal of difficulty in understanding the world view that quantum mechanics represents. Okay, I still get nervous with it. It has not yet become obvious to me that there is no real problem. I cannot define the real problem, therefore I suspect there’s no real problem, but I’m not sure there’s no real problem.
This “problem” concerns the interpretation of quantum measurements. The superposition principle, telling us that quantum systems can exist in two or more states simultaneously, is by itself not so foreign. After all, any wave phenomenon, such as a sound or a water wave, can exist in many places at the same time and also admits superpositions. But quantum theory goes farther by claiming that the superposition principle for quantum states is only valid in the absence of measurements. When a measurement is made, the superposition randomly “collapses” into one of the definite states that make up the superposition, with a probability given
by the weighting of the state measured. For instance, in the three-qubit superposition ![]() above, the probability of measuring the definite state
above, the probability of measuring the definite state ![]() (decimal 4) is given by the squared magnitude of its weight, |g|2.
(decimal 4) is given by the squared magnitude of its weight, |g|2.
The mechanics of this wavefunction collapse, and the resort to probabilities in the measurement of quantum superpositions is perhaps the most revolutionary and bizarre feature of quantum mechanics. The measurement of a quantum superposition, completely different from the behavior of classical wave superpositions, highlights the special role of the observer in quantum phenomena. It recalls the question, Does a falling tree make a sound if no one is there to hear it? Most of us are more comfortable with a physical principle that is independent of whether one (or anything) observes it. Quantum mechanics is the only physical theory that has a special place for the observer, and it is the only physical theory that calls into question our definition of physical reality. Indeed, one interpretation stipulates that whenever a quantum measurement is performed, the universe divides into several universes, each experiencing its own measurement result.
Perhaps the most popular (and usable) melding of quantum mechanics and quantum measurement is the theory of decoherence. This describes how a coherent quantum superposition of states loses its ability to interfere and evolves instead to a classical mixture. In its most common form, decoherence theory applies the usual quantum mechanics to an isolated system and additionally stipulates that when a measurement occurs, the isolation ends and the measuring device (or even the observer) becomes entangled with the original quantum system (see Boxes 7–1 and 7–2). Entanglement with a large object like a measuring device (or a person) enormously increases the complexity of the quantum physics. This increase in complexity causes the nonclassical aspects of the quantum evolution to dissipate, or average out, extremely quickly—far too fast to ever be recaptured. Just as the fragrance that leaves a flower and escapes into the air can never be gathered in once it has dissipated, the quantum aspects of the system appear to become classical once they are measured by a large object. This is the essence of quantum “collapse.” Analysis of decoherence allows a practical reconciliation of quantum mechanics with classical physics.
A large-scale quantum information processor can be considered a complex quantum entangled state with many degrees of freedom, but with special architecture or controls that delay the onset of decoherence (see Box 7–2). While such a system could certainly be used for computational applications such as factoring numbers (see Box 7–3) and complex simulations of physical, chemical, and biological systems, the mere survival of coherence at such a large scale may also provide deep insight into the fundamentals of the quantum mechanical description of nature. Can entangled superpositions persist beyond a threshold number of qubits in a real physical system? And apart from the formidable technical prob-
|
BOX 7–1 Entanglement The exponential scaling of quantum information is related to one of the weirdest aspects of quantum theory, entanglement (see Figure 7–1–1). This feature is so strange that in 1935, when quantum mechanics was in its infancy, Einstein and two colleagues wrote a paper pointing out just how strange it is. They argued that nothing so strange could be true and instead there must be something wrong with quantum theory. In fact, this was a rare instance where Einstein was wrong—nature is indeed that weird, and we hope to use that weirdness to make useful quantum computers. Consider just two qubits, each of which can be in one of two states. We can think of these as two atoms, labelled a and b, whose spins could be either up The first of these states is said to be “separable” because it can be written as the product of the state of one atom and the state of the other. In this state, each atom is in a quantum superposition of being up and being down. If we measure the spin of one of the atoms, it will be either up or down (recall that we cannot predict which result will actually be found). We might measure atom a to be up and then also find b to be down. Or we might find that a is up and b is also up. The result of each measurement will be random and the result for one atom will not depend on the result for the other. This is a characteristic of separable states. In contrast, the second state cannot be written as the product of the state of one atom and the state of the other. This is an “entangled” state. If we measure the state of atom a (or of b), it may be up or down, and the result is random. But if we measure a to be up, then for this state b is bound with certainty to be measured as up. Conversely, if a is down, b will definitely be found to be down. Thus while the fate of each atom is random, these fates are inextricably linked or correlated. This is what we mean by entanglement. 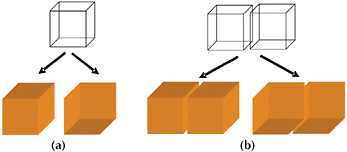 FIGURE 7–1–1 The “ambiguous cube” representations above give a visual sense of superposition, entanglement, and quantum measurement. In (a), the ambiguous perspective of the upper (mesh) cube represents a superposition of a single qubit, and a measurement is analogous to the mind randomly locking onto one of the definite perspectives drawn below. In (b), the ambiguous perspective of two cubes is analogous to an entangled superposition of two qubits. Here, a measurement of either qubit is again akin to locking onto either definite perspective. In this case, however, the other qubit usually appears in the same perspective, even though there is no physical connection between the cubes. SOURCE: Based on figures and descriptions taken from pp. 131, 179, and 180, F.A.Wolf, Taking the Quantum Leap: The New Physics for Nonscientists, New York: Harper & Row (1989). |
|
BOX 7–2 Entanglement, Coherence, Schrödinger’s Cat, and Decoherence The most general state of N qubits is an entangled superposition of all 2N binary numbers: The state is referred to as a “Schrödinger cat” state because the two constituents of the superposition are as far apart as possible, analogous to the dead and alive states of the famous feline discussed by Schrödinger in his 1935 analysis of conceptual problems in quantum mechanics: As Schrödinger himself noted, describing macroscopic concepts such as alive or dead with quantum terms is not necessarily justifiable or useful. However, for mesoscopic systems where N is not too large—for example, between 10 and 1,000—these cat states are useful in both visualizing and characterizing large-scale entanglement. For example, a Schrödinger cat state highlights the difficulty of maintaining complex entangled quantum superpositions, because if just one of the N qubits gets measured by the environment, every qubit will lose its coherence. Any source of decoherence thus makes it more difficult to engineer large entangled states. In fact the survival probability of such states declines exponentially with the number of qubits, posing severe challenges to physical implementation of quantum information processing with large numbers of qubits. |
lems that inhibit the construction of a large-scale quantum computer, are there fundamental reasons why such a device cannot be built? Quantum information science is directed at answering these questions. Among the many possible outcomes in this quest, two are earth-shattering. One is that the technical difficulties will be overcome and a useful quantum computer will be built. The second is that in our quest to build such a device, we may discover that the theory of quantum mechanics is incomplete.
QUANTUM INFORMATION TECHNOLOGY
In 1965, Intel cofounder Gordon Moore predicted that the number of electronic components on a computer chip would double every year or two. Moore’s law has been remarkably accurate even to this day, when the latest silicon processors now host some 10 million transistors (see Figure 7–4). This exponential growth in
|
BOX 7–3 Serendipity: Better Atomic Clocks and an Early Quantum Computer In the early 1990s, experimental AMO physicists in Boulder, Colorado, were investigating the quantum linking of individual trapped atomic ions in order to enhance the signal from atomic clocks based on very few atoms. They determined ways to create certain correlated atomic states that made the atomic clock effectively run faster (see Figure 2–6), resulting in a significantly higher precision. This work was performed at the Time and Frequency Division of NIST, also funded in large part by the Office of Naval Research. These states were precisely the entangled states that are now of central interest to quantum information processing, although that was not realized at the time. At the 1994 International Conference on Atomic Physics in Boulder, a lecture by an information theorist brought the topic of quantum computation and mathematician Peter Shor’s new factoring algorithm to the atomic physics community. AMO theorists at that meeting realized that quantum computers capable of making arbitrary (“universal”) computations such as Shor’s algorithm could be built with this very same technology of trapped atomic ions. This realization fed into renewed progress on the entangled atomic clock experiments at NIST, so that by early 1995 the experimentalists succeeded in demonstrating the basic step in correlating individual atomic ions in their quest for better atomic clocks by actually implementing the scheme for quantum computation outlined by AMO theorists in the previous year. The course of this quick turn of events is a case study on how interdisciplinary science happens, how seemingly unrelated areas of research become intertwined, and how funding of fundamental research can lead to very unexpected outcomes. A critical part of these developments involved the interplay between theorists and experimentalists, and between mathematicians, information theorists, and atomic physicists. Quantum information science is now a vigorous activity involving people from nearly all branches of science, mathematics, and engineering. |
chip density has been the driving force behind the modern electronic age and has played an instrumental economic role over the last several decades. Will Moore’s law continue indefinitely? No. The problem is that adding components by simply expanding the size of chips will slow their speed, so that the only way to sustain this kind of growth is to make transistors ever smaller (assuming that the heat can be dissipated). By the year 2010, Moore’s law predicts that a 1 cm2 chip will have perhaps 10 billion transistors, with each transistor not much larger than a single molecule. At this point, radical change is inevitable. Feynman himself saw far into the future in 1957, evidenced by his famous lecture “There’s Plenty of Room at the Bottom,” from which the following extract is taken:
When we get to the very, very small world—say circuits of seven atoms—we have a lot of new things that would happen that represent completely new opportunities for design. Atoms on a small scale behave like nothing on a large scale, for they satisfy the laws of quantum mechanics.
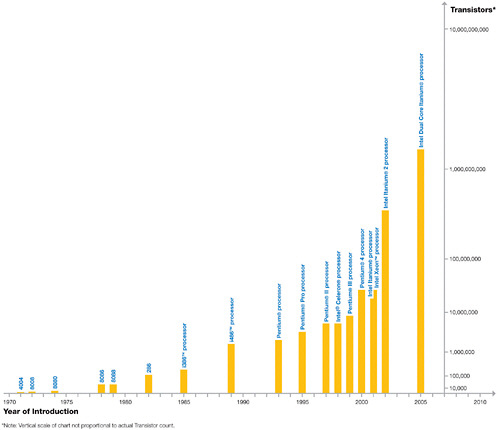
FIGURE 7–4 Processing power, measured in millions of instructions per second, has risen because of increased transistor counts. SOURCE: Copyright © 2005 Intel Corporation.
Quantum mechanics may hold a key to sustained growth in computing power in the coming decades, not by continuing along the path of Moore’s law of miniaturization but by changing the rules of the game. This was recognized by several mathematicians, computer scientists, and physicists in the early 1980s and led to the formulation of rules for a computing device operating with qubits that would be manipulated according to the laws of quantum mechanics. Quantum circuits can be drawn up for such a quantum computer. The notion of performing computations quantum mechanically received a major boost in 1994 with the discovery of how to construct a quantum algorithm for the strategic factorization problem (Shor’s algorithm, discovered at Bell Labs). The exponential increase in speed that this algorithm shows over the best known classical algorithm circumvents the
limitations imposed by Moore’s law in a very dramatic manner. For such quantum algorithms to achieve their potential, it is necessary to build a quantum information processor containing many thousands of qubits.
QUANTUM COMMUNICATION
The foundations of information theory were expressed at Bell Labs in 1954 by Claude Shannon, who quantified the concept of information transmitted over a channel (e.g., a series of photons propagating down an optical fiber). Shannon calculated the information content of the photon source, the physical resources needed to store the information, and how much information could be reliably transmitted through a noisy or imperfect channel. These results provide powerful bounds on the maximum possible rate of data compression and the maximum amount of information that can be faithfully transmitted. These results, all for classical information, have had a profound influence on the development of modern communications and information theory.
What benefits might be gained by communicating information with quantum sources and/or quantum channels? Quantum versions of Shannon’s results suggest that greater data compression is possible when information is coded into quantum states instead of classical states, and this has been demonstrated in systems of individual photons and atoms. Error correction, through clever coding of additional transmitted information, has also been extended to quantum states. Networks of quantum channels can be used for improved distributed information processing. However, much is still unknown about the capabilities of quantum information.
Quantum Cryptography: A Real-World Application
Coded messages are almost as old as language itself, and today, encryption is essential not only for military and diplomatic purposes but also for industry and commerce. In general, the sender and receiver of the coded message (Alice and Bob in modern parlance) must share some secret key that allows Alice to encrypt the message and Bob to decrypt it. The only completely secure method of encryption is the one-time pad, a random key that connects the plain text to the encoded text. This key must never be reused and is itself as long as the message. Traditionally, Alice and Bob might meet and agree upon the pad to be used, or a trusted agent could be sent from one to the other to distribute the key. The difficulty and inefficiency of such an operation for the transmission of frequent or voluminous coded information is obvious, so other more efficient, but less secure, methods are generally used.
Most key distribution systems in use today derive their security by requiring an eavesdropper to make very hard (and time-consuming) calculations to obtain the key. A simple example is number factoring: given two numbers a computer can very quickly multiply them together to find the product. However, given only the product, the computer must work much harder to find the original numbers. This is the factoring problem mentioned above. Key distribution systems based on this idea are very practical and efficient, but their security is based on the assumption that the eavesdropper has not made advances in computing that are unknown to the users—an assumption that does not always hold. For example, in the 1970s cryptosystems using the original Digital Encryption Standard were thought to be entirely secure but are now easily cracked with modern computers.
Quantum key distribution (QKD) is a new approach that offers unconditional security: The eavesdropper is assumed not to be limited by current technology but to be bound by the known laws of nature. One of the properties of quantum mechanics is that the act of observing, or measuring, a quantum state can cause changes in that state. QKD exploits this property by using quantum systems for key distribution; with the proper choice of quantum states, it is possible to create the situation where an eavesdropper cannot avoid causing changes that can be detected. In this way it is possible to create a natural “wax seal” on the key; as long as no measurment is made, the seal is intact and the key is known to be secure. Figure 7–5 illustrates one method for producing a quantum key.
QKD is most commonly realized with pulses of light containing single photons (the smallest possible amount of light). Single optical-frequency photons on demand are not so easy to make, transport, or detect, but progress toward this goal in the past decade has been very promising. Single-photon QKD systems have been demonstrated over free-space links longer than 20 km, and optical-fiber-based QKD systems now support fairly robust key distribution (10 kilobits per second) over lengths on the order of 10 km. This is already useful for metropolitan-area networks. This may seem slow—it’s about the speed of an old telephone modem circa 1980. Indeed, QKD is not likely to ever be as convenient and efficient as conventional key distribution systems. But QKD offers what conventional systems cannot: unconditionally secure key generation. One need not be concerned that advances in decryption technology will reveal one’s encrypted messages. This level of security is sufficiently appealing that there are already two commercial ventures selling off-the-shelf QKD systems. The best free-space QKD systems (now only in research labs) can currently support the encryption of streaming video and, as improvements are made in single-photon generation and detection technology, both the bandwidth and reach of QKD systems will increase. There is enough potential for improvement that researchers envision global-scale QKD that supports high-bandwidth, quantum-encrypted networks.
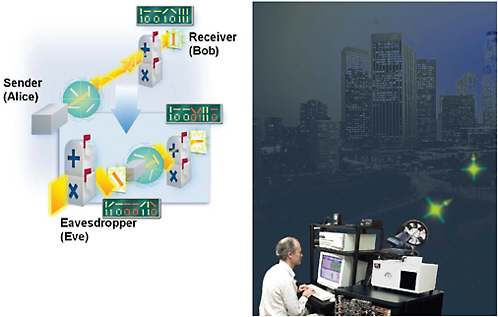
FIGURE 7–5 Left: To generate the key, the sender (Alice) randomly chooses one of four polarization orientations for a photon (vertical, horizontal, +45 degrees, or -45 degrees). The photon is sent to the receiver (Bob), who randomly chooses one of two modes (or mailboxes) in which to measure the orientation (vertical/horizontal or +/-45 degrees). After the photons are received, Alice and Bob compare modes, only saving data where their modes match and discarding or ignoring the rest. This guarantees that they will only keep results that are measured correctly. (See final key above Bob’s mailbox.) If someone (Eve) tries to measure and resend the photons, errors occur in the data that alert Alice and Bob to the eavesdropping. In the inset picture, Eve tries to receive a vertical photon in the wrong mode and measures it incorrectly as a -45 degree photon. Eve then sends a -45 degree photon to Bob. Bob receives the photon in the vertical/horizontal mode and records a horizontal photon. When Alice and Bob compare their sending and receiving modes they will end up with errors in the key (red data) and thus know that Eve has been listening. SOURCE: National Institute of Standards and Technology, copyright L.Barr. Right: Researcher at Los Alamos National Laboratory running a free-space QKD experiment over a 10-km distance between Los Alamos and Pajarito Mountain in New Mexico. SOURCE: R.Hughes, Los Alamos National Laboratory.
Quantum Teleportation Demystified
The notion of transferring an object from one location to another by “teleporting” it in a way that causes it to disappear at the first location and to simultaneously reappear at the second location is familiar to all readers of modern science fiction, and to Star Trek aficionados in particular. The mechanism for such a magical
transport of objects is explained as the transfer of all information about the object to an equivalent set of components in the remote location and is usually assumed to result in destruction of the original object. Teleportation of macroscopic or live objects remains science fiction today, not least because of the massive amount of information that would be required to be transferred (~1032 bits for a minimal description of the state of a human, which would require over 108 centuries to be transmitted by optical fibers). However, the addition of quantum mechanics to this scenario, together with recent experimental advances in AMO physics, has indeed allowed the quantum states of photons and atoms to be teleported, for atoms over very short distances and for photons over distances of several kilometers (see Figure 7–6). Photon teleportation over global distances via satellite links is now under consideration.
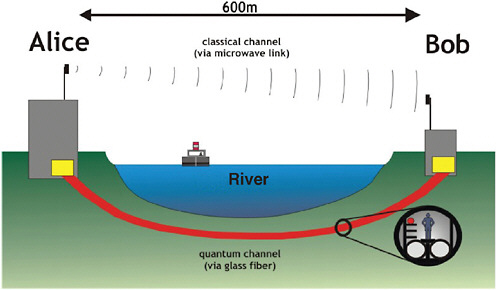
FIGURE 7–6 Quantum teleportation experiment demonstrated using an 800-m-long optical fiber fed through public sewer system tunnels under a river. Quantum teleportation is very different from the transporter described in Star Trek. In a quantum teleportation only the quantum state is transferred and not the qubit itself—that is, the atom or photon constituting the two-level quantum system is not transferred. This is very different from the image of a disappearing Captain Kirk when all of the information contained in his vast collection of constituent atoms is scanned by a mysterious transporter. Furthermore, quantum teleportation cannot occur instantaneously, unlike the commonly assumed science fictional mode of intergalactic personnel teleportation. The speed of quantum teleportation is limited by factors such as the speed at which the necessary entanglement can be generated and measurements made, as well as classical transmission of the result of the two-qubit measurement. Thus there is no violation of the laws of relativity. SOURCE: Copyright © Institut für Experimentalphysik, University of Vienna, Austria.
Quantum teleportation provides a route to perfect transfer of quantum states between spatially separated locations, without transfer of matter. Sometimes referred to as the “disembodied transfer of quantum information from one place to another,” it has already found numerous applications in quantum communication and computation. It could become the basis for a quantum internet and might be very useful in overcoming architectural constraints in construction of quantum computers. The origin and destination points need only be connected by a classical communication channel, and they must also share entanglement. This introduces the quantum nonlocality that allows the direct transfer of quantum information without sending it through the classical channel. Methods for producing entangled pairs of photons are becoming a standard tool of quantum optics.
What is the limit to quantum teleportation? All experiments to date have teleported states of single qubits. In principle, multiqubit states could also be teleported, although more complex measurements would be required. “Teleporting” the complete quantum state of a complex molecule with internal dynamics might constitute the next stage, perhaps ultimately approaching even transfer of the quantum information describing the complete state of a small biological molecule. The difficult synchronization requirements this would introduce are as yet unaddressed. In the meantime, the use of quantum teleportation for moving states of atoms and photons around with high fidelity promises significant advantages for any schemes manipulating quantum states for metrology and high-precision measurements, or for facilitating data transfer in quantum information processing.
VISION FOR LARGE-SCALE QUANTUM HARDWARE
Shannon’s definition of information in terms of bits led to the experimental representation of bits in nature, from unwieldy vacuum tubes in the mid-20th century to the modern semiconductor transistors of less than 0.1 micrometers in size. In the 21st century, we find the new theory of quantum information is stimulating the development of a very high level quantum control of physical systems, resonating with the goal of modern AMO—to control our quantum world. The main hardware requirements for a quantum information processor are these:
-
Requirement 1. The quantum system (i.e., a collection of qubits) must be initialized in a well-defined quantum state.
-
Requirement 2. Sufficient operations must be available and controlled to launch the initial state to an arbitrary entangled state.
-
Requirement 3. Measurements of the qubits must be performed with high quantum efficiency.
From Requirements 1 and 2, the qubits must be well isolated from the environment to ensure pure initial quantum states and to preserve their superposition character, but they must also interact strongly with one another in order to become entangled. On the other hand, Requirement 3 calls for the strongest possible interaction with the environment to be switched on at will.
These severe hardware requirements rule out most known physical systems. The most advanced candidates for quantum information processors in the next decade will likely come from atomic, molecular, and optical physics. Many solid-state architectures hold promise in the long run, and the quantum control of simple solid-state degrees of freedom is now beginning to take hold, but the environmental isolation afforded by individual atoms and photons is unsurpassed by that of other physical systems. Complex quantum entangled states of AMO systems can be generated by controlled quantum operations on small numbers of atoms with lasers. Such operations can be used to construct quantum circuits, the analog of Boolean circuits for classical computation, with classical gates replaced by corresponding reversible quantum logic gates. The complex global entangled states that can exist in strongly correlated materials such as Bose condensates and Fermi gases might also be useful for quantum computing, given that each atom in the collection can be independently measured, enabling an alternative paradigm for quantum computation.
The following subsections summarize several implementations of qubits and basic elements of future quantum information processors that are composed of individual atoms and photons. Typically, qubit memories will be formed from atoms or molecules, with links between qubits established by electromagnetic interactions between the atomic or molecular memories.
Trapped Atomic Ions
Individual atomic ions can be confined with electromagnetic fields to be nearly motionless, forming well-defined crystals of atoms separated from each other through their mutual Coulomb repulsion. The isolation of trapped ions, along with their strongly coupled motion, makes them a natural candidate for quantum hardware. Trapped ions can be entangled following a number of schemes, most involving laser beams that apply a force to the ion crystal depending on the internal state of one or more of the trapped-ion qubits. Moreover, the qubit states within trapped ions can routinely be measured with near-perfect efficiency.
Nearly all of the rudiments of quantum information processing have already been demonstrated at the few-atom level in ion traps, and the future will see the extension of these systems to hundreds and thousands of atomic qubits. With a growing number of trapped-ion qubits, it will become difficult to control the mo-
tion of such a complex crystal as the system approaches a solid-state system with large thermal vibrations in too many degrees of freedom. Instead, one idea for scaling the trapped-ion quantum computer is to entangle only a small number of ions at a time in very simple crystals, while shuttling ions between zones to connect with other ions. Figure 7–7 depicts visions of ion trap architectures that electromagnetically shuttle individual ions between various trap zones in a very complex “quantum computer chip” composed of semiconductor electrodes that are fabricated much like current silicon chips.
Optical Lattices
Neutral atoms can be confined similarly to atomic ions, but because they have no electric charge, they can only be held with laser beams or magnetic fields. In the context of quantum information processing, the optical lattices described
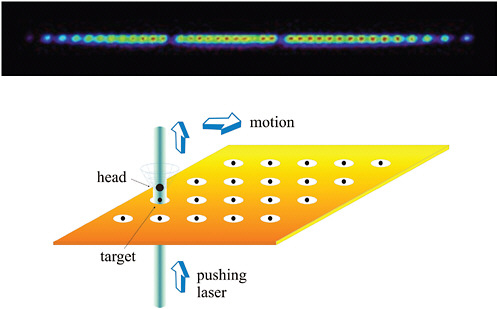
FIGURE 7–7 Top: Array of a few dozen trapped mercury ions. The ions fluoresce from applied laser radiation, and the apparent gaps are different isotopes that fluoresce at different wavelengths. The distance between the first and last ions is about 1 mm. SOURCE: J.Bergquist and D.Wineland, National Institute of Standards and Technology. Bottom: Array of stationary trapped-ion quantum memories, with a single roving head ion interacting with any memory ion in order to move quantum information between memories. SOURCE: J.I.Cirac and P.Zoller, University of Innsbruck, Austria.
in Chapter 3 present a promising avenue for large-scale applications. The use of quantum degenerate gases (Bose condensates or Fermi gases) may allow loading of the individual lattice sites with exactly one (or two, or three, or more) atoms per site. The separation between atoms in an optical lattice is thousands of times larger than a typical separation of atoms in a solid-state crystal and offers the possibility of doing controlled operations on qubits that are defined in terms of internal electronic states of the atoms. Figure 7–8 shows how atoms trapped in a two-dimensional optical lattice can be manipulated by controlling the laser fields. Knobs representing the laser strengths and phases are turned to change the shape of the lattice, bringing atoms into contact with their neighbors. Turning these knobs in different ways allows interactions with any of the four neighbors. Notice that massive parallelism is designed into this particular manipulation. In certain lattices it is also possible to address and manipulate individual atoms.
Optical lattices present a fascinating possible way to avoid the decoherence that limits the realization of a practical quantum computer, through creation of entangled states of atoms. Atoms produced in topologically protected quantum states—that is, quantum superpositions of states whose relative phase is embodied only in many-particle, nonlocal correlations—cannot have their states randomized by local interactions or interactions involving only a single particle, which is generally how the environment causes decoherence. Such entangled states can therefore be more robust against decoherence.
Solid-State Quantum Bits
There are now several solid-state systems that have successfully reproduced the quantum behavior typical of AMO systems. These have involved confined superconducting systems where either the magnetic flux or the electric charge is quantized (see Figure 7–9). This exciting development underscores the inherent interdisciplinary nature of the field of quantum information science. In particular, as was also discussed in Chapter 3, more and more links between AMO and condensed matter physics are materializing, providing fertile new ground for advances in both areas.
Photonic Qubits
Individual photons are notoriously difficult to produce in a controllable fashion. Even though a simple attenuated light source can be made to produce primarily single photons, it is impossible to know exactly when a photon appears. To produce single photons on demand, the photon is typically produced by some matter quantum system, such as a single atom or a single semiconductor quantum dot.
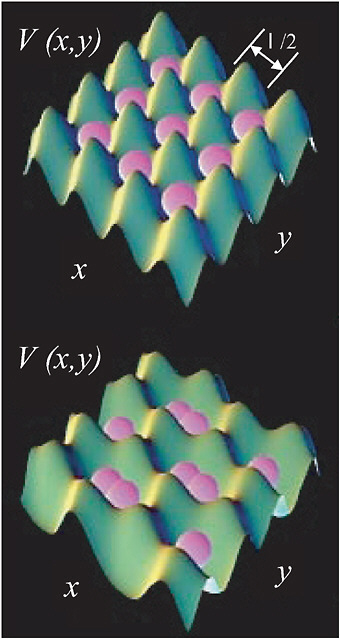
FIGURE 7–8 Controlling interactions of atomic qubits trapped in an optical lattice. Top: Individual atoms (purple) are confined in two-dimensional potential wells formed by crisscrossed laser beams, spaced by one half of the optical wavelength. Bottom: By controlling the parameters of the external lasers, atoms can be made to approach and interact with their neighbors. SOURCE: National Institute of Standards and Technology.

FIGURE 7–9 An example of a superconducting circuit which is used for quantum information processing. A quantum bit made from a Cooper-pair box, consisting of two pieces of superconductor (purple), coupled together by a pair of Josephson junctions (white squares) in a small loop. Manipulation of the quantum states of the qubit are made by transferring single Cooper pairs across the junctions, under the influence of electric fields applied to a gate lead (beige leads on above and below) and magnetic fields through the loop. Such qubits can also be integrated with microwave transmission line resonators (top) to realize a solid-state testbed for quantum optics, called circuit quantum electrodynamics, where single microwave photons can be coherently coupled to qubits. These and other solid-state technologies have great potential for the future of quantum information processing. SOURCE: R.Schoelkopf, Yale University.
Once this is accomplished, these single-photon sources can be used for a variety of applications, ranging from secure quantum cryptography to full-blown quantum computing. One source of entangled photons that has been used for many seminal demonstrations of quantum information applications is the nonlinear downconverter, where a single (blue) photon entering a nonlinear crystal produces twin (red) photons at the output, as depicted in the Figure 7–10.
Qubit Converters Between Atoms and Photons
In classical information processing, electrical current communicates information from place to place, and magnetic domains or electrical voltages act as
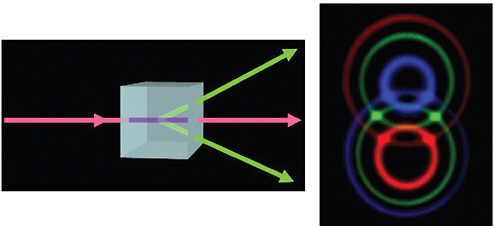
FIGURE 7–10 Left: When an ultraviolet laser beam (purple) passes through a nonlinear crystal, the photons in the beam can interact with the crystal to produce two daughter photons in the visible spectrum (each green, for example). Right (view looking into laser beam): When a laser beam sequentially traverses two specially oriented crystals, many colors are produced, with each crystal producing a series of concentric circular patterns of light. Considering only the directions where the green circles intersect, it is unknown which of the two green photons came from which crystal, and this can produce entanglement between the two photons. Such sources are the workhorse for optical implementations of quantum information protocols. SOURCE: A.Zeilinger, University of Vienna, Austria, Copyright © Institut für Experimentalphysik, University of Vienna, Austria. Photo: P.Kwiat and M.Reck.
memory elements where the information is stored. The fundamental device that links storage and communication is the transistor, depicted in Figure 7–11, a switch for electrical current that is controlled by the amount of charge stored in a memory. Throughout the second half of the 20th century, the development and refinement of the transistor catalyzed the information era, from the original unwieldy vacuum tubes in the 1940s and the first digital computers to the solid-state transistor developed in the 1950s and ultimately miniaturized to submicrometer (10–6 m) dimensions.
In quantum information processing, storage and communication of qubits will likely take far different forms. Good quantum memories should be localized in space and quite isolated from the environment, while good quantum communication resources must travel easily between locations with minimal environmental disturbance. AMO physics presents some nearly ideal candidates for quantum memories (atoms) and ideal quantum communication channels (photons) and is therefore at the forefront of the development of good quantum information hardware. A grand challenge in AMO science is the development of a “quantum transistor” that interconverts quantum memories of individual atoms to quantum

FIGURE 7–11 Left: Vacuum-tube transistor. SOURCE: Lucent Technologies. Center: First solid-state transistor, developed by Bardeen, Brattain, and Shockley in 1947. SOURCE: Lucent Technologies. Right: Modern microscale transisitors on an integrated circuit. SOURCE: IBM.
information channels of individual photons. Simple interconversion methods could lead to the development of quantum networks of qubits and distributed quantum computing, where small numbers of atomic qubit memories are linked within a single device or between remotely located devices with optical fibers. As photonic quantum information propagates through optical fibers over very long distances—say, across a continent or through space—the quantum signal will eventually degrade. However, while conventional (classical) signals can be boosted through amplification, quantum information cannot be amplified without adding significant noise to the system. This is a result of the quantum “no-cloning” theorem—that is, the fundamental impossibility of reproducing an unknown quantum state. A quantum amplifier is tantamount to a measurement that destroys the information itself. Nevertheless, quantum information can indeed be “purified” as it slowly degrades through a long communication channel by converting photonic qubits to atomic qubit memories and implementing small quantum computers at “quantum repeater” nodes that provide quantum error correction (see Figure 7–12).
One natural approach for linking atomic and photonic qubits is to trap single atoms and single photons simultaneously in the same space. Here, the photon is itself confined between two highly reflecting mirrors for long enough so that multiple atoms can interact with the same photon. The technical requirements for such cavity mirrors are extreme, sometimes requiring mirror losses and transmission on

FIGURE 7–12 Optical equipment at the Georgia Institute of Technology is used to transfer information from two different groups of atoms onto a single photon in a prototypical quantum network node or quantum repeater. A quantum repeater converts photons into atomic quantum memories at periodic intervals, whereby small quantum computers can purify the quantum information without destroying it, before it is sent out again. This is similar to the use of conventional repeater circuits, which can, for example, deliver power over large distances. Quantum repeater networks allow stored quantum information to propagate over long distances despite noise and losses en route. Single photons can typically travel no more than about 10 km before they are lost. SOURCE: A.Kuzmich, Georgia Institute of Technology.
the order of one part per million. Nevertheless, there is constant progress in the controlled interaction between atoms and photons within optical cavities.
In these cavities, qubit states stored within the atoms can be interconverted to photon states in the cavity with the use of external laser beams, as depicted in Figure 7–13. The photon can be made to leak out of the cavity within a preset time window, resulting in an ideal source of single photons for use in quantum communication. Moreover, after the photon leaks out of the cavity, it can be caught in a second cavity by the application of an appropriate laser pulse in the second cavity. Generalizations involving more than one atom in each cavity can distribute entanglement to many nodes.
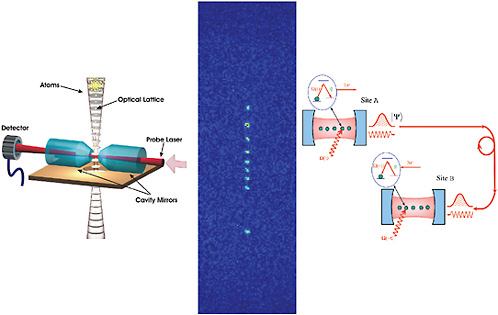
FIGURE 7–13 Left: Schematic of atoms confined in a laser beam “conveyor belt” being loaded into an optical cavity. Quantum information from each atom can be transferred to the state of photons in the cavity, which can subsequently be mapped onto other atoms. SOURCE: M.Chapman, Georgia Institute of Technology. Center: Image of individual neutral atoms confined in a one-dimensional lattice formed by counterpropagating laser beams. SOURCE: M.Chapman, Georgia Institute of Technology. Right: An alternative method for linking atoms through photons is to allow the photons’ quantum information to leak controllably through the mirrors and carry the quantum information to another cavity, possibly remote. SOURCE: H.J.Kimble, California Insitute of Technology.
WHAT WOULD WE WANT TO COMPUTE WITH A QUANTUM PROCESSOR?
Quantum computers derive their power through quantum parallelism, as discussed above. Not only can N quantum bits store a superposition of all 2N binary numbers, but also, when a quantum computation is performed on this superposition, each piece gets processed simultaneously. For example, quantum logic operations can shift all of the bits one position to the left, equivalent to multiplying the input by 2. When the input state is in superposition, all inputs are simultaneously doubled with one turn of the crank (see Figure 7–14).
After this quantum parallel processing, the state of the qubits must ultimately be measured. Herein lies the difficulty in designing useful quantum computing
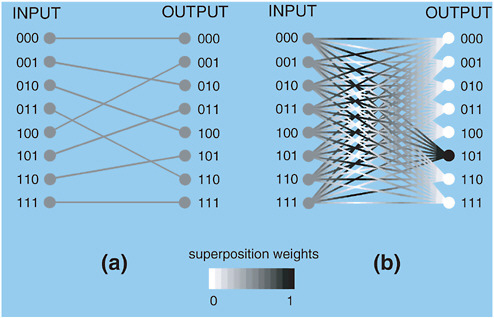
FIGURE 7–14 Simplified evolution during a quantum algorithm on N=3 quantum bits. The inputs are prepared in superposition states of all 2N=8 possible numbers (written in binary). The weights of the superposition are denoted on the gray scale, where black is a 100 percent weight and white is a 0 percent weight, (a) Quantum algorithm for simultaneously doubling all input numbers by shifting all qubits one position to the left and wrapping around the leftmost bit. The outputs are also in superposition, and a final measurement projects one answer at random, (b) Quantum algorithm involving wavelike interference of weights. Here, quantum logic gates cause the input superposition to interfere, ultimately canceling all of the weights except for one (101 in the figure), which can then be measured. For some algorithms, this lone answer (or the distribution of a few answers after repeated runs) can depend on the weights of all 2N input states, leading to an exponential speedup over classical computers.
algorithms: According to the laws of quantum mechanics, this measurement yields just one answer out of the 2N possibilities; worse still, there is no way of knowing which answer will appear. It seems that quantum computers offer no advantage in computing functions where each input results in a unique output, as in the doubling algorithm above. The trick behind a useful quantum computer algorithm involves the phenomenon of quantum interference and delaying the measurement. The weights in a coherent quantum superposition are wavelike, so they can be made to interfere with each other. Some weights interfere constructively, like the crests of an ocean wave, while others cancel, as when a valley meets a crest. In the end, the parallel inputs are processed with quantum logic gates so that almost all
of the weights cancel, leaving only a very small number of answers, or even a single answer, as depicted in Figure 7–14b. By measuring this answer (or repeating the computation a few times and recording the distribution of answers), information can be gained pertaining to all 2N inputs. This answer (or sparse distribution of answers) can, in some cases, carry global information pertaining to all inputs.
The best known algorithm that can be cast in this form is Shor’s quantum factoring algorithm, described in Box 7–4. Factoring is the reverse of multiplication: Given a number, M, we are interested in finding numbers p and q that produce M when multiplied (M=p×q). For instance,
But,
Determining the factors of a number is a difficult problem, and the difficulty scales exponentially with the size of M. Demonstrating this difficulty, it is noteworthy that in 2005, 80 supercomputers took more than a year to factor a 200-digit number. Given the same resources, factoring a 500-digit number would take over a trillion years.
The extreme difficulty in factoring large numbers is precisely the reason that commonly used encryption schemes remain safe. The most popular encryption scheme is RSA public key cryptography, named after its inventors, R. Rivest, A. Shamir, and L. Adleman. Unlike one-time keys, which are intrinsically secret, here the cryptographic key is made public. A very large number—possessing perhaps 300 decimal digits—is broadcast. The factors of this key are known only by the recipient (Bob) of a message. The sender (Alice) encodes her message in a special way using Bob’s publicly available key, and because Bob is the only person on Earth who knows the factors of his key, he is the only one who can decrypt Alice’s message (see Figure 7–15).
As mentioned above, Shor’s quantum algorithm for factoring would factor large numbers exponentially faster than any known classical algorithm.1 This quantum algorithm has not yet been implemented for anything approaching an interesting number. Indeed, factoring a number with 300 digits would require near-perfect control of at least 106 quantum bits and perhaps 109 near-perfect
|
BOX 7–4 Shor’s Quantum Factoring Algorithm The breakthrough discovery of the quantum factoring algorithm by Peter Shor in 1994 involves a juxtaposition of the disjoint disciplines of number theory and quantum physics. There is no known efficient method for factorizing a number N into a product of two smaller numbers, N=p×q. The fastest classical algorithms effectively amount to a brute-force elimination of prime numbers following repeated division tests (is N divisible by 2? By 3? By 5? By 7? and so on), resulting in an exponential scaling of computation time with the size of the number N (as measured in the number of bits). An alternative, but equally slow, method of factorization is to search for the periodicity of the function where a is an arbitrary constant (sharing no common divisors with N) and the “mod N" notation tells us to take the remainder of ax after dividing by N. The function f(x) is indeed periodic with x, but it is not at all obvious what the period is. In fact, it has been known for centuries that the period r of f(x) is closely related to the factors p and q of N. This is because by simple substitution of f(x+r)=f(x) into the preceding equation, we find or, equivalently, N divides (ar1) evenly, so the factor p (or q) divides (ar/2±1). Thus, we find that both N and (ar/2±1) share p (or q) as a common divisor, and Euclid’s algorithm for finding the greatest common divisor of two numbers can be used to efficiently deduce the factor p. Unfortunately, finding the period of f(x)=ax (mod N) in the first place is tantamount to performing on the order of N2 brute-force evaluations of f(x) and checking for when the function repeats, once more requiring a computing time that scales exponentially with the number of bits required to represent the number N. Finding the period of a function is exactly the type of application that quantum computers can do very efficiently. Quantum computers can evaluate an exponential number of inputs simultaneously through the superposition principle. Of course, if a measurement is performed at this stage, a useless random result will be recorded. But the period of a function is a global property, so that by calculating f(x) for all inputs (up to about N2) simultaneously, it would seem possible to shuffle things so that this joint property could be extracted. Indeed, by performing a Fourier transform on this periodic function, the spectrum of results is only sparsely populated, meaning that nearly all of the weights of the resulting quantum superposition are almost zero. Now, following a measurement of the system (actually a distribution of a relatively small number of measurements), the period can be determined with high probability. In the end, the required time (for both quantum and ancillary classical computations in the algorithm) scales only as a polynomial of the number of bits required to represent N. This represents an exponential reduction in the time compared with the time for the execution of a classical factoring algorithm. |
quantum logic gates, the analog of classical Boolean operations. In addition, if some overhead is included to ensure error correction during the factoring process, the factoring computer is estimated to require a whopping 109 quantum bits and 1014 quantum gates. These numbers are dauntingly large and will not likely be reached
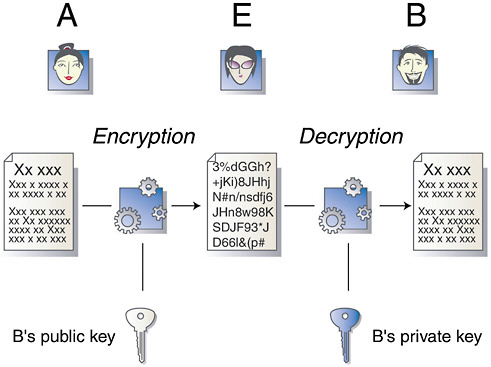
FIGURE 7–15 Public key cryptography. Alice (A) would like to send a secret message to Bob (B) without Eve (E) being able to read the message. Alice encrypts a document using Bob’s public key. The encrypted document is unreadable to Eve and to anyone else but Bob, who can decrypt the document using his private knowledge of the prime factors of the public key. SOURCE: Cryptomathic Ltd.
in the coming decades. However, the mere existence of Shor’s algorithm demands a long-term perspective on the future evolution of information processing. The possibility of having a full-blown quantum computer in 50 years should impact today’s encryption standards, especially when applied to information that must be kept secure for long periods of time.
Another quantum algorithm that has received considerable attention is the quantum algorithm for searching a database, Grover’s algorithm, named after its inventor, also from Bell Laboratories. Suppose you want to find the person in an alphabetized phone book who has a given phone number. Because the phone numbers are completely uncorrelated with the spelling of the name, you would have to look through half of the phone book on average—N/2—before finding the correct name. Grover’s algorithm uses quantum mechanics to succeed in the search after examining only ![]() items in the list, a quadratic speeding up. For
items in the list, a quadratic speeding up. For
example, using a classical computer to search for a single item in a database containing a million items would typically require 500,000 steps. This effort would require only 1,000 steps with the quantum search. This speeding up offered by a quantum search is again due to quantum parallelism, which permits us to search the entire database at once. Grover’s search algorithm has been implemented in very small quantum computers built from quantum components spanning all realms of AMO physics: electrons within individual atoms, trapped atomic ions, complex molecules, nuclear spins, and individual photons. Although these are all rudimentary implementations of quantum search, they exemplify the flexibility of AMO systems for quantum information applications and also indicate how to scale up to more complex versions of this and other quantum algorithms in any physical system.
The quantum search algorithm has broad applicability to many problems in computer science and our information-oriented society beyond searching of large databases. For example, Grover’s algorithm can be adapted to the task of quickly finding two equal items among N given items. More generally, the quantum search algorithm can offer a significant speeding up of any application involving exhaustive trial-and-error or brute-force solution techniques. This may have the most notable impact in exhaustive searches for the solution to so-called “NP" problems, whose solutions can be efficiently verified but not easily found and which have long confounded computer scientists. To quote mathematician and Fields medalist Michael Freedman of Microsoft Corporation,
Setting aside the constraints of any particular computational model, the creation of a physical device capable of brutally solving NP problems would have the broadest consequences. Among its minor applications it would supersede intelligent, even artificially intelligent, proof finding with an omniscience not possessing or needing understanding. Whether such a device is possible or even in principle consistent with physical law, is a great problem for the next century.
Many common problems in daily life such as the famous traveling-salesman problem and other resource optimization problems can be reduced to an NP-complete problem. This class of problems possesses the tantalizing property that if an efficient solution to one example can be found, then all such problems possess an efficient solution. Quantum search methodology provides a new perspective with some potential for this notoriously hard but important class of computational problems.
The immense significance of Shor’s quantum algorithm for factoring has led to extensive work toward the development of new quantum algorithms for other problems. More generally, characterizing the limitations of efficient problems for quantum computers is just as important as finding new quantum algorithms, because it would allow us to implement classical cryptosystems today that would be
impervious to quantum cryptoanalysis should quantum computers ever become practical.
USING A QUANTUM PROCESSOR TO PREDICT THE BEHAVIOR OF COMPLEX QUANTUM SYSTEMS
Richard Feynman pointed out that since everything we experience in our physical world is made from the microscopic building blocks of electrons, nuclei, photons, and so forth, a quantum mechanical description will be essential to understand all of its details. But, he contended, our computers calculate in the classical world and will never be up to the task of such complex quantum calculations. Predicting the behavior of a single qubit can be done with reasonable accuracy by using a classical computer to simulate its dynamics according to the rules of quantum mechanics. However, when many qubits interact, the number of possible states or configurations of the system increases exponentially with the number of qubits, and prediction becomes an impossible task. For example, 30 qubits can be in any of 230 (about a billion) states. Two decades ago a typical desktop computer could solve for the energies and configurations of 10 interacting electrons. Today’s conventional computers are more than 100 times as powerful, yet this only allows us to solve a system with two more electrons.
Feynman recognized in 1982 that one quantum system is like any other when measured by its capacity to store and process information, just as information processing with the classical bit is independent of the form of the bit. This means that an atom with two energy levels can be made to act like a photon with two polarization directions, which can be made to act like an electron with two spin orientations, and so on. These quite different physical systems can all be represented as qubits. A quantum simulation is a computation using many qubits of one system type that can be initialized and controlled in the laboratory to simulate an equal number of qubits of another type that cannot be easily controlled. Quantum simulations are special cases of quantum computations and hence may be much easier to implement. For instance, a model-sized device of 30 qubits would be able to perform calculations on quantum systems that would require an array of 1 billion billion values to be represented in a conventional classical computer, far beyond the memory capacity of any of today’s computers.
It is increasingly being realized that such quantum simulations can have practical utility. For example, a long-term problem in statistical physics and engineering is finding solutions to lattice spin models. Spin lattices are regular arrays of quantummechanical spins whose interactions are limited to short distances. An example is the common permanent magnet (ferromagnet). More complex systems can display “frustration” (see Figure 7–16). Because spin lattice models capture the essential

FIGURE 7–16 Frustration in magnetic spin systems, (a) In an antiferromagnetic material, magnetic interactions between atoms cause adjacent spins to have alternate orientations, (b) In the simplest example of spin frustration, given two antialigned spins in an antiferromagnetic system, the state of the third spin is confused, (c) With four spins, there is even more ambiguity. Calculating the ground states of frustrated spin systems and quantum phase transitions in the spin orientations is very difficult using conventional computers. SOURCE: P.Lemmens, Institute for Condensed Matter Physics, Technische Universtät Carolo-Wilhelmina zu Braunschweig, Germany.
physics of more complicated systems, their relevance ranges from commercial materials fabrication to basic problems in condensed matter physics. Another exciting prospect for quantum simulations is to gain insight into the mechanism of high-temperature superconductivity, for which the correct microscopic physics is still unknown. Various models have been proposed, but even simplified versions of these involve solving a highly correlated many-body system. Classical algorithms are not adequate to predict the correct macroscopic behavior of these models. Quantum simulations using trapped ultracold fermionic gases for which a high-temperature superfluid phase has recently been discovered (Chapter 3) may provide critical insight into the mechanism for this high-temperature superconductivity.
There may be a less practical but equally exciting use for quantum simulators—namely, to strengthen our understanding of nature at the subatomic level. For instance, a variety of spin lattice models have been proposed that create lowenergy states with a special kind of global property termed topological order. Such theories predict that some physical entities assumed to be fundamental in the Standard Model of particle physics, such as electrons and light, are actually low-energy excitations of a network of spins. If this were actually the way the universe worked then the underlying spin network would be operating at the incredibly small Planck scale, far beyond our level of observation. But the models themselves can be simulated and their predictions tested in a tabletop experiment. Quantum simulators open the door to testing this and other modern theories of quantum cosmology.
LOOKING FORWARD
One of the most tantalizing aspects of quantum information science is that a quantum computer may eventually arise from technology that is completely unknown at present. Whatever the evolution of such devices, experiments that control individual atoms and photons will continue to lead exploration of the bizarre features of quantum mechanical foundations and their application to information processing. After all, the systems currently under study are precisely the “thought experiments” envisioned by Einstein, Bohr, Heisenberg, and the other founding figures of quantum theory over 80 years ago. With the new language of quantum information, we hope to gain more insight into the underlying quantum physical principles, just as the classical theory of information ushered in the advances in physics responsible for our current digital age.
The interdisciplinary nature of this field and the important role played by theory are characteristic trademarks of quantum information. Theory continues to play a key role, even as experimental progress is made toward the quantum processing of information for communication and computational tasks. This exciting and rapidly moving area promises to be a major driver of AMO physics in the next few decades, demanding advances in control of our quantum world that will continue to surprise and amaze.

































