5
Principles and Methods of Sensitivity Analyses
This chapter concerns principles and methods for sensitivity analyses that quantify the robustness of inferences to departures from underlying assumptions. Unlike the well-developed literature on drawing inferences from incomplete data, the literature on the assessment of sensitivity to various assumptions is relatively new. Because it is an active area of research, it is more difficult to identify a clear consensus about how sensitivity analyses should be conducted. However, in this chapter we articulate a consensus set of principles and describe methods that respect those principles.
We begin by describing in some detail the difficulties posed by reliance on untestable assumptions. We then demonstrate how sensitivity to these assumptions can be represented and investigated in the context of two popular models, selection and pattern mixture models. We also provide case study illustrations to suggest a format for conducting sensitivity analyses, recognizing that these case studies cannot cover the broad range of types and designs of clinical trials. Because the literature on sensitivity analysis is evolving, the primary objective of this chapter is to assert the importance of conducting some form of sensitivity analysis and to illustrate principles in some simple cases. We close the chapter with recommendations for further research on specific aspects of sensitivity analysis methodology.
BACKGROUND
There are fundamental issues involved with selecting a model and assessing its fit to incomplete data that do not apply to inference from complete data. Such issues occur even in the missing at random (MAR)
case, but they are compounded under missing not at random (MNAR). We believe that, especially when the primary analysis assumes MAR, the fit of an MAR model can often be addressed by standard model-checking diagnostics, leaving the sensitivity analysis to MNAR models that deviate from MAR. This approach is suggested in order not to overburden the primary analysis. The discussion in Chapter 4 provides some references for model-checking of MAR models. In addition, with MAR missingness mechanisms that deviate markedly from missing completely at random (MCAR), as in the hypertension example in Chapter 4, analyses with incomplete data are potentially less robust to violations of parametric assumptions than analyses with complete data, so checking them is even more critical.
The data can never rule out an MNAR mechanism, and when the data are potentially MNAR, issues of sensitivity to modeling asumptions are even more serious than under MAR. One approach could be to estimate from the available data the parameters of a model representing an MNAR mechanism. However, the data typically do not contain information on the parameters of the particular model chosen (Jansen et al., 2006).
In fact, different MNAR models may fit the observed data equally well but have quite different implications for the unobserved measurements and hence for the conclusions to be drawn from the respective analyses. Without additional information, one cannot usefully distinguish between such MNAR models based solely on their fit to the observed data, and so goodness-of-fit tools alone do not provide a relevant means of choosing between such models.
These considerations point to the necessity of sensitivity analysis. In a broad sense, one can define a sensitivity analysis as one in which several statistical models are considered simultaneously or in which a statistical model is further scrutinized using specialized tools, such as diagnostic measures. This rather loose and very general definition encompasses a wide variety of useful approaches.
A simple procedure is to fit a selected number of (MNAR) models, all of which are deemed plausible and have equivalent or nearly equivalent fit to the observed data; alternatively, a preferred (primary) analysis can be supplemented with a number of modifications. The degree to which conclusions (inferences) are stable across such analyses provides an indication of the confidence that can be placed in them.
Modifications to a basic model can be constructed in different ways. One obvious strategy is to consider various dependencies of the missing data process on the outcomes or the covariates. One can choose to supplement an analysis within the selection modeling framework, say, with one or several in the pattern mixture modeling framework, which explicitly models the missing responses at any given time given the previously observed responses. Alternatively, the distributional assumptions of the models can be altered.
The vast range of models and methods for handling missing data highlights the need for sensitivity analysis. Indeed, research on methodology has shifted from formulation of ever more complex models to methods for assessing sensitivity of specific models and their underlying assumptions. The paradigm shift to sensitivity analysis is, therefore, welcome. Prior to focused research on sensitivity, many methods used in practice were potentially useful but ad hoc (e.g., comparing several incompatible MNAR models to each other). Although informal sensitivity analyses are an indispensable step in the analysis of incomplete longitudinal data, it is desirable to have more formal frameworks within which to develop such analyses.
It is possible to assess model sensitivities of several different types, including sensitivity to: (a) distributional assumptions for the full data, (b) outlying or influential observations, and (c) assumptions about the missing data mechanism. Assessment of (a) can be partially carried out to the extent that one can compare observed and fitted values for the observables under the model specified for the full data. However, distributional assumptions for the missing data cannot be checked. Assessment of (b) can be used to identify observations that are outliers in the observed-data distribution or that may be driving weakly identified parts of an MNAR model (Molenberghs and Kenward, 2007). This chapter focuses on (c), sensitivity to assumptions about the missing data mechanism.
FRAMEWORK
To focus ideas, we restrict consideration to follow-up randomized study designs with repeated measures. We consider the case in which interest is focused on treatment comparisons of visit-specific means of the repeated measures. With incomplete data, inference about the treatment arm means requires two types of assumptions: (i) untestable assumptions about the distribution of missing outcomes data, and (ii) testable assumptions about the distribution of observed outcomes. Recall that the full-data distribution, described in Chapter 4, can be factored as
(1)
Type (i) assumptions are needed to estimate the distribution [Ymis | Yobs,M,X], while type (ii) assumptions are used, if necessary, to model the observables [Yobs,M | X] in a parsimonious way.
Type (i) assumptions are necessary to identify the treatment-specific means. Informally, a parameter is identified if one can write its estimator as a function that depends only on the observed data. When a parameter is not identified, it would not be possible to obtain a point estimate even if the sample size were infinite. It is therefore essential to conduct a sensitivity
analysis, whereby the data analysis is repeated under different type (i) assumptions, in order to clarify the extent to which the conclusions of the trial are dependent on unverifiable assumptions. The usefulness of a sensitivity analysis ultimately depends on the transparency and plausibility of the unverifiable assumptions. It is key that any sensitivity analysis methodology allow the formulation of these assumptions in a transparent and easy-to-communicate manner.
Ultimately, type (i) assumptions describe how missing outcomes are being “imputed” under a given model. A reasonable way to formulate these assumptions is in terms of the connection (or link) between the distributions of those having missing and those having observed outcomes but similar covariate profiles. Making this difference explicit is a feature of pattern mixture models. Examples discussed in this chapter illustrate both pattern mixture and selection modeling approaches.
In general, it is also necessary to impose type (ii) assumptions. An important consideration is that modeling assumptions of type (ii), which apply to the distribution of observed data, can be supported and scrutinized with standard model-checking techniques.
Broadly speaking, there are two approaches for combining type (i) and (ii) assumptions to draw inferences about the treatment-specific means: pattern mixture and selection modeling. To illustrate these approaches, the next four sections present four example designs of increasing complexity. The first two examples involve a single outcome, without and then with auxiliary data. These examples are meant to illustrate when and why the assumptions of type (i) and (ii) are needed. The third and fourth examples extend the designs to those with repeated measures, with monotone and non-monotone missing data, respectively, with and without auxiliary data.
Our examples are not meant to be prescriptive as to how every sensitivity analysis should be conducted, but rather to illustrate principles that can guide practice. Type (i) assumptions can only be justified on substantive grounds. As the clinical contexts vary between studies, so too will the specific form of the sensitivity analysis.
EXAMPLE: SINGLE OUTCOME, NO AUXILIARY DATA
We start with the simple case in which the trial records no baseline covariate data, and the only measurement to be obtained in the study is that of the outcome Y, taken at a specified time after randomization. We assume that the treatment-arm-specific means of Y form the basis for treatment comparisons and that in each arm there are some study participants on whom Y is missing. We let R = 1 if Y is observed and R = 0 otherwise.
Because estimation of each treatment arm mean relies solely on data from subjects assigned to that arm, the problem reduces to estimation of a mean E(Y) based on a random sample with Y missing in some units. Thus, formally, the problem is to estimate µ = E(Y) from the observed data, which comprises the list of indicators R, and the value of Y for those having R = 1.
The MAR assumption described in Chapter 4 is a type (i) assumption. In this setting, MAR means that, within each treatment arm, the distribution of Y among respondents (i.e., those with R = 1) is the same as that for nonrespondents (i.e., with R = 0).
This example illustrates several key ideas. First, it vividly illustrates the meaning of an untestable assumption. Let µ1 = E(Y | R = 1) denote the mean among respondents, µ0 = E(Y | R = 0) the mean among nonrespondents, and π = P(R=1) the proportion of those responding. The full-data mean µ is a weighted average
(2)
but there is no information in the data about the value of µ0. Hence, any assumption one makes about the distribution for the nonrespondents will be untestable from the data available. In particular, the MAR assumption—that µ1 = µ0 —is untestable.
Second, this example also illustrates the identifiability (or lack thereof) of a parameter. Without making assumptions about µ0, the full-data mean µ cannot be identified (estimated) from the observed data. However, if one is prepared to adopt an untestable assumption, µ will be identified. For example, one can assume MAR is equivalent to setting µ1 = µ0. From (2), MAR implies that µ = µ1, or that the full-data mean is equal to the mean among those with observed Y. Hence, under MAR, a valid estimate of µ1 is also valid for µ. A natural choice is the sample mean among those with observed data, namely, ![]() .
.
Third, this example is the simplest version of a pattern mixture model: the full-data distribution is written as a mixture—or weighted average—of the observed and missing data distributions. Under MAR, their means are equal. However, it is more typical to use pattern mixture models when the means are not assumed to be equal (MNAR).
By contrast, in the selection model approach, type (ii) assumptions are made in terms of how the probability of nonresponse relates to the possibly unobserved outcome. The full-data mean can be estimated using a weighted average of the observed outcomes, where the weights are individual-specific and correspond to the conditional probability of being observed given the observed outcome value. The reweighting serves to create a “pseudo
population” of individuals who are representative of the intended full-data sample of outcomes.
Importantly, there is a one-to-one relationship between the specification of a selection model and specification of a pattern-mixture model. The key distinction ultimately arises in how type (ii) assumptions are imposed. As it turns out, the two approaches generate equivalent estimators in this simple example, but for more complex models that rely on type (i) assumptions to model the observed data, that is not the case.
Pattern Mixture Model Approach
Because we are only interested in the mean of Y, it suffices to make assumptions about how the mean of Y among nonresponders links to the mean of Y among respondents. A simple way to accomplish this is by introducing a sensitivity parameter ∆ that satisfies µ0 = µ1 + ∆, or
(3)
It is easy to see that ∆ = µo – µ1, the difference in means between respondents and nonrespondents. To accommodate general measurement scales, the model should be parameterized so that the sensitivity parameter satisfies an identity such as
(4)
where g( ) is a function, specified by the data analyst, that is strictly increasing and maps values from the range of Y to the real line. The function g determines the investigator’s choice of scale for comparisons between the respondents’ and nonrespondents’ means and is often guided by the nature of the outcome.
For a continuous outcome, one might choose g(u) = u, which reduces to the simple contrast in means given by (3), where ∆ represents the difference in mean between nonrespondents and respondents.
For binary outcomes, a convenient choice is g(u) = log(u/(1–u)), which ensures that the µ0 lies between 0 and 1. Here, ∆ is the log odds ratio comparing the odds of Y = 1 between respondents and nonrespondents.
Each value of ∆ corresponds to a different unverifiable assumption about the mean of Y in the nonrespondents. Any specific value of ∆ corresponds to an estimate of µ because µ can be written as the weighted average
(5)
After fixing ∆, one can estimate µ by replacing µ1 and π with their sample estimators ![]() and
and ![]() . Formulas for standard error estimators can be derived from standard Taylor expansions (delta method), or one can use the bootstrap.
. Formulas for standard error estimators can be derived from standard Taylor expansions (delta method), or one can use the bootstrap.
To examine how inferences concerning µ depend on unverifiable assumptions about the missing data distribution, notice that µ is actually a function of ∆ in (5). Hence, one can proceed by generating an estimate of µ for each value of ∆ that is thought to be plausible. In this model, ∆ = 0 corresponds to MAR; hence, examining inferences about µ over a set or range for ∆ that includes ∆ = 0 will summarize the effects of departures from MAR on inferences about µ.
For fixed ∆, assumption (4) is of type (i). In this simple setting, type (ii) assumptions are not needed because µ1 and π can be estimated with sample means, and no modeling is needed.
Finally, to test for treatment effects between two arms, one adopts a value ∆0 for the first arm and a value ∆1 for the second arm. One then estimates each mean separately under the adopted values of ∆ and conducts a Wald test that their difference is zero. To investigate how the conclusions depend on the adopted values of ∆, one repeats the testing over a range of plausible values for the pair (∆0, ∆1).
Selection Model Approach
A second option for conducting sensitivity analysis is to assume that one knows how the odds of nonresponse change with the values of the outcome Y. For example, one can assume that the log odds of nonresponse differs by α for those who differ by one unit on Y. This is equivalent to assuming that one knows the value of α (but not h) in the logistic regression model
(6)
Models like (6) are called selection models because they model the probability of nonresponse (or selection) as a function of the outcome. Each unique value of α corresponds to a different unverifiable assumption about how the probability of nonresponse changes with the outcome.
The model in (6) is also equivalent to assuming that
(7)
Adopting a value of α is equivalent to adopting a known link between the distribution of the respondents and that of the nonrespondents, because one
cannot use the data to learn anything about the nonrespondent distribution or to check the value of α. Moreover, one cannot check two other important assumptions: that the log odds of nonresponse is linear in y and that the support of the distribution of Y among nonrespondents is the same as that among respondents (as implied by (7)).
Although not immediately apparent, once a value of α is adopted, one can estimate µ = E[Y] consistently. A sensitivity analysis consists of repeating the estimation of µ at different plausible values of α so as to assess the sensitivity of inferences about µ to assumptions about the missing data mechanism as encoded by α and model (6).
Estimation of µ relies on the identity
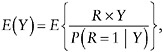
(8)
which suggests estimation of µ through inverse probability weighting (see below); in this case, the weights can depend on missing values of Y. The inverse probability weighting estimator is
(9)
where expit(u) = logit–1(u) = exp(u) / {1 + exp(u)}. To compute ĥ, one solves the unbiased estimating equation
(10)
for h.1 Analytic formulas for consistent standard error estimators are available (e.g., Rotnitzky et al., 1998), but bootstrap resampling can be used. Sensitivity analysis for tests of treatment effects proceeds by repeating the test over a set of plausible values for α, where different values of α can be chosen for each arm.
With the selection model approach described here we can conduct sensitivity analysis, not just about the mean but about any other component of the distribution of Y, for example, the median of Y. Just as in the preceding pattern mixture approach, the data structure in this setting is so simple that we need not worry about postulating type (ii) assumptions.
EXAMPLE: SINGLE OUTCOME WITH AUXILIARY DATA
We next consider a setting in which individuals are scheduled to have a measurement Y0 at baseline, which we assume is never missing (this constitutes the auxiliary data), and a second measurement Y1 at some specified follow-up time, which is missing in some subjects. We let R1 = 1 if Y1 is observed and R1 = 0 otherwise. As in the preceding example, we limit our discussion to estimation of the arm-specific mean of Y1, denoted now by µ = E(Y1 ).
In this example, the type (i) MAR assumption states that, within each treatment group and within levels of Y0, the distribution of Y1 among nonrespondents is the same as the distribution of Y1 among respondents. That is,
(11)
Pattern Mixture Model Approach
In this and the next section, we demonstrate sensitivity analysis under MNAR. Under the pattern mixture approach one specifies a link between the distribution of Y1 in the nonrespondents and respondents who share the same value of Y0. One can specify, for example, that
(12)
where η(Y0) = E(Y1 | R1 = 1, Y0) and g is defined as in the example above.
Example: Continuous Values of Y Suppose Y1 is continuous. One needs a specification of both the sensitivity analysis function g and the relationship between Y1 and Y0 , represented by η(Y0). A simple version of η is a regression of Y1 on Y0,
(13)
(14)
Now let g(u) = u as in the first example above. In this case, using (12), the mean of the missing Y1 are imputed as regression predictions of Y1 plus a shift ∆,
(15)
Hence, at a fixed value of ∆, an estimator of E∆ (Y1 | R1 = 0) can be derived as the sample mean of the regression predictions ![]() among those with R1 = 0. The estimators
among those with R1 = 0. The estimators ![]() and
and ![]() come from a regression of Y1 on Y0 among those with R1 = 1.
come from a regression of Y1 on Y0 among those with R1 = 1.
In this case, ∆ represents the baseline adjusted difference in the mean of Y1 between nonrespondents and respondents. If ∆ > 0 (< 0), then for any fixed value of Y0 , the mean of Y1 among nonrespondents is ∆ units higher (lower) than the mean of Y1 among respondents.
A few comments are in order for this example:
-
Model (12) assumes that mean differences do not depend on Y0. If one believes that they do, then one may choose a more complex version of the g function, such as
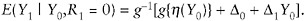
(16)
If this version is coupled with a linear regression for η(Y0), then both the slope and the intercept of that regression will differ for respondents and nonrespondents.
-
In general, any user-specified sensitivity function d(Y0,∆) can be posited, including the simple versions d(Y0,∆) = ∆ and d(Y0,∆) = ∆0 + ∆1Y0. Importantly, no version of d(Y0,∆) can be checked using the observed data. The choice of d function is a type (i) assumption.
-
Likewise, more general choices can be made for the form of η(Y0), including versions that are nonlinear in Y0. The choice of η is a type (ii) assumption; it can be critiqued by standard goodness-of-fit procedures using the observed data.
Example: Binary Outcome Y If Y is binary, the functional form of g and η will need to be different than in the continuous case. Choosing g(u) = log(u/(1 + u) implies that ∆ is the log odds ratio comparing the odds of Y1 = 1 between respondents and nonrespondents, conditional on Y0. As with the continuous case, ∆ > 0 (∆ < 0) implies that, for every level of Y0, nonrespondents are more (less) likely to have Y1 = 1 than respondents.
The function η(Y0), which describes E(Y1 | Y0,R = 1), should be specified in terms of a model that is appropriate for binary outcomes. For example, a simple logistic specification is
(17)
which is equivalent to writing
(18)
When Y0 is binary, this model is saturated. But when Y0 is continuous, or includes other auxiliary covariates, model choice for η will take on added importance.
Inference A sensitivity analysis to examine how inferences are impacted by the choice of ∆ consists of repeating the inference over a set or range of values of ∆ deemed to be plausible. It can proceed in the following manner:
Step 1. Specify models for η(Y0) and d(Y0,∆).
Step 2. Fit the model η(Y0) to those with R1 = 0, and obtain the estimated function ![]() .
.
Step 3. The full-data mean µ = E(Y1) is
(19)
where expectations are taken over the distribution of Y0 | R. Although the general formula looks complex, it is easily computed for a fixed value of ∆ once the model for η has been fit to data. Specifically,
Step 3a. The estimate of E {η (Y0) | R = 1} is the sample mean ![]() .
.
Step 3b. The estimate of ![]() also is computed as a sample mean,
also is computed as a sample mean,
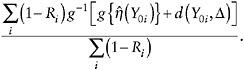
(20)
Step 3c. The estimate of ![]() .
.
Step 3d. The estimate ![]() of µ is computed by replacing parameters in (19) by their estimators described in the previous steps.
of µ is computed by replacing parameters in (19) by their estimators described in the previous steps.
Step 4. Standard errors are computed using bootstrap resampling.
Step 5. Inferences about µ are carried out for a plausible set or range of values of ∆. Because each unique value of ∆ yields an estimator ![]() , it is possible to construct a contour plot of Z-scores, p-values, or confidence
, it is possible to construct a contour plot of Z-scores, p-values, or confidence
intervals for treatment effect as a function of ∆. An illustration, computed using data from a diabetic neuropathy trial, appears in Figure 5-1.
Selection Model Approach
In parallel to the first example, with no auxiliary data, another way to postulate type (i) assumptions about the nature of selection bias is by postulating a model for the dependence of the probability of nonresponse on the (possibly missing) outcome Y1, within levels of Y0. For example, one can assume that, conditionally on Y0, each unit increase in Y1 is associated with an increase of α in the log odds of nonresponse. That is,
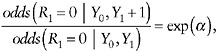
(21)
or, equivalently,
(22)
where h(Y0) is an unknown function of Y0. This can also be written as
(23)
In this latter form,2 one can see that the observed data have no information about α. The choice of α = 0 specifies that within levels of Y0, R1 and Y1 are independent (i.e., MAR). Values of α ≠ 0 reflect residual association between missingness and nonresponse after adjusting for Y0.3
Analogous to the example with no auxiliary data, estimation of µ = E(Y1) relies on the identity
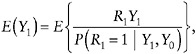
(24)
which suggests the inverse probability weighted (IPW) estimator
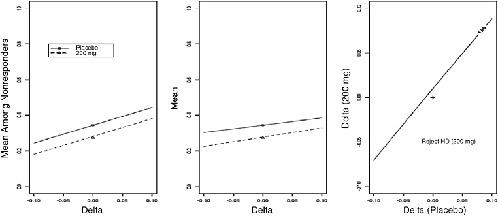
FIGURE 5-1 Pattern mixture sensitivity analysis. Left panel: plot of mean outcome among nonrespondents as a function of sensitivity parameter Δ, where Δ = 0 corresponds to MAR. Center panel: plot of full-data mean as function Δ. Right panel: contour of Z statistic for comparing placebo to active treatment, where Δ is varied separately by treatment.
(25)
where ĥ(Y0) is an estimator of h(Y0).
Unless Y0 is discrete with a few levels, estimation of h(Y0) requires the assumption that h(Y0) takes a known form, such as h(Y0;γ) = γ0 + γ1Y0. (Note that if one adopts this model, one is assuming that the probability of response follows a logistic regression model on Y0 and Y1 with a given specified value for the coefficient α of Y1.) Specifying h(Y0) is a type (ii) assumption that is technically not needed to identify µ but is needed in practical situations involving finite samples.
One can compute an estimator ![]() of γ by solving a set of estimating equations4 for γ,
of γ by solving a set of estimating equations4 for γ,
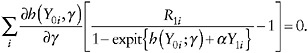
(26)
Formulas for sandwich-type standard error estimators are available, but the bootstrap can also be used to compute standard error estimates. Hypothesis-testing sensitivity analysis is conducted in a manner similar to the one described in the example above with no auxiliary data.
As with the pattern mixture models, by repeating the estimation of µ at a set or interval of known α values, one can examine how different degrees of residual association between nonresponse and the outcome Y1 affect inferences concerning E(Y1). A plot similar to the one constructed for the pattern mixture model is given in Figure 5-2.
EXAMPLE: GENERAL REPEATED MEASURES SETTING
As the number of planned measurement occasions increases, the complexity of the sensitivity analysis grows because the number of missing data patterns grows. As a result, there can be limitless ways of specifying models.
Consider a study with K scheduled postbaseline visits. In the special case of monotone missing data, there are (K + 1) patterns representing each of the visits at which a subject might last be seen, that is, 0,…,K. The
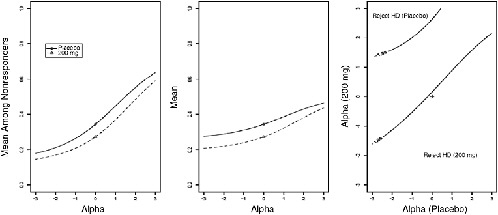
FIGURE 5-2 Selection model sensitivity analysis. Left panel: plot of mean outcome among nonrespondents as a function of sensitivity parameter α, where α = 0 corresponds to MAR. Center panel: plot of full-data mean as function of α. Right panel: contour of Z statistic for comparing placebo to active treatment where α is varied separately by treatment.
(K + 1)st pattern represent subjects with complete data, while the other K patterns represent those with varying degrees of missing data. In the general setting, there are many ways to specify pattern models—the models that link the distribution of missing outcomes to the distribution of observed outcomes within specified strata—and it is generally necessary to look for simplifications of the model structure.
For example, one could link the conditional (on a shared history of observed outcomes through visit k – 1) distribution of missing outcomes at visit k among those who were last seen at visit k – 1 to (a) the distribution of outcomes at visit k among those who complete the study, (b) the distribution of outcomes at visit k among those who are in the study through visit k, or (c) the distribution of outcomes at visit k among those who are last seen at visit k.
Let Yk denote the outcome scheduled to be measured at visit k, with visit 0 denoting the baseline measure. We use the notation ![]() to denote the history of the outcomes through visit k and
to denote the history of the outcomes through visit k and ![]() to denote the future outcomes after visit k. We let Rk denote the indicator that Yk is observed, so that Rk = 1 if Yk is observed and Rk = 0 otherwise. We assume that Y0 is observed on all individuals so that R0 = 1. As above, we focus on inference about the mean µ = E(YK) of the intended outcome at the last visit K.
to denote the future outcomes after visit k. We let Rk denote the indicator that Yk is observed, so that Rk = 1 if Yk is observed and Rk = 0 otherwise. We assume that Y0 is observed on all individuals so that R0 = 1. As above, we focus on inference about the mean µ = E(YK) of the intended outcome at the last visit K.
Monotone Missing Data
Under monotone missingness, if the outcome at visit k is missing, then the outcome at visit k + 1 is missing. If we let L be the last visit that a subject has a measurement observed, then the observed data for a subject is ![]() , where L ≤ K.
, where L ≤ K.
A Pattern Mixture Model Approach
As noted above, there are many pattern models that can be specified. Here, we discuss inference in one such model. Recall that both type (i) and type (ii) assumptions are needed. We first address type (i) specification, illustrating a way to link distributions with those having missing observations to those with observed data.
The general strategy is illustrated for the case K = 3, which relies on an assumption known as “nonfuture dependence” (Kenward et al., 2003). In simple terms, the nonfuture dependence assumption states that the probability of drop out at time L can only depend on observed data up to L and the possibly missing value of YL, but not future values of L.
In the model used here, we assume there is a link between ![]() and
and ![]() , which are, respectively, the distributions of Yk among those who do and do not drop out at time k – 1. The idea is to use the distribution of those still in the study at time k – 1 to identify the distribution of those who drop out at k – 1.
, which are, respectively, the distributions of Yk among those who do and do not drop out at time k – 1. The idea is to use the distribution of those still in the study at time k – 1 to identify the distribution of those who drop out at k – 1.
It can be shown that µ = E(YK) can be estimated by a recursion algorithm, provided the following observed-data distributions are estimated:
(27)
and the following dropout probabilities
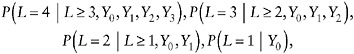
(28)
can also be estimated. Each is identified from observed data when missingness is monotone.
What is needed to implement the estimation of µ= E(YK) is a model that links the distributions with observed data (27) to the distributions having missing observations. One simple way to do this is to assume the distribution of Yk among recent dropouts, ![]() , follows the same parametric model as the distribution of Yk among respondents,
, follows the same parametric model as the distribution of Yk among respondents, ![]() , but with a different—or shifted—parameter value. This assumption cannot be verified and may not be realistic in all studies; we use it here simply as an illustration.
, but with a different—or shifted—parameter value. This assumption cannot be verified and may not be realistic in all studies; we use it here simply as an illustration.
To be more concrete, suppose that the outcomes Y0,…,Y3 are continuous. One can assume regression models for each of (27) as follows,
(29)
(30)
(31)
(32)
This modeling of the observed data distribution comprises our type (i) assumptions. These can (and must) be checked using the observables.
Using type (ii) assumptions, the distributions of missing Y can be linked in a way similar to those for the first example above. For example,
those with L = 1 are missing Y1. One can link the observed-data regression E(Y1 | Y0 , L ≥ 2) to the missing-data regression E(Y1 | Y0,L = 1) through
(33)
where, say, ![]() and
and ![]() . Models for missing Y2 and Y3 can be specified similarly.
. Models for missing Y2 and Y3 can be specified similarly.
As with the previous cases, (33) is a type (ii) assumption and cannot be checked with data. Moreover, even using a simple structure like (33), the number of sensitivity parameters grows large very quickly with the number of repeated measures. Hence, it is important to consider simplifications, such as setting ∆β = 0, assuming ∆µ is equivalent across patterns, or some combination of the two.
Note that under our assumptions, ![]() is the difference between the mean of Yk among those who drop out at k – 1 and those who remain beyond k – 1, conditional on observed data history up to k – 1. In this example, the assumption of linearity in the regression models, combined with an assumption that
is the difference between the mean of Yk among those who drop out at k – 1 and those who remain beyond k – 1, conditional on observed data history up to k – 1. In this example, the assumption of linearity in the regression models, combined with an assumption that ![]() for all k, means that one does not need a model for
for all k, means that one does not need a model for ![]() to implement the estimation via recursion algorithm.
to implement the estimation via recursion algorithm.
A sensitivity analysis consists of estimating µ and its standard error repeatedly over a range of plausible values of specified ∆ parameters. For this illustration, setting ∆ = 0 implies MAR.5
Selection Model
Another way to posit type (i) assumptions in this setting is to postulate a model for how the odds of dropping out between visits k and k + 1, depends on the (possibly missing) future outcomes, ![]() , given the recorded history
, given the recorded history ![]() . That is,
. That is,
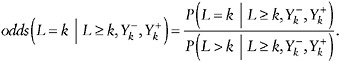
The MAR assumption states that the odds do not depend on the future outcomes ![]() . The nonfuture dependence assumption above states that it depends only on the future through Yk+1. That is,
. The nonfuture dependence assumption above states that it depends only on the future through Yk+1. That is,
(34)
and is equivalent to assuming that after adjusting for the recorded history, the outcome to be measured at visit k + 1 is the only predictor of all future missing outcomes that is associated with the odds of dropping out between visits k and k + 1.
This last assumption, coupled with an assumption that quantifies the dependence of the odds in the right hand side on Yk+1, suffices to identify µ = E(YK): in fact, it suffices to identify E(Yk) for any k = 1,…,K. For example, one might assume
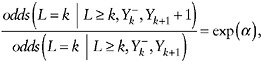
(35)
that is, that each unit increase in Yk+1 is associated with a constant increase in the log odds of nonresponse of α, the same for all values of ![]() and all visits k.
and all visits k.
Under (34), α = 0 implies MAR. One would make this choice if it is believed that the recorded history ![]() encodes all the predictors of Yk+1 that are associated with missingness. Values of α ≠ 0 reflect residual association of dropping out between visits k and k + 1 and the possibly unobserved outcome Yk+1, after adjusting for previous outcomes, and hence the belief that dropping out cannot be entirely explained by the observed recorded history
encodes all the predictors of Yk+1 that are associated with missingness. Values of α ≠ 0 reflect residual association of dropping out between visits k and k + 1 and the possibly unobserved outcome Yk+1, after adjusting for previous outcomes, and hence the belief that dropping out cannot be entirely explained by the observed recorded history ![]() . By repeating estimation of the vector µ for each fixed α, one can examine how different degrees of residual association between dropping out and outcome at each occasion after adjusting for the influence of recorded history affects inferences concerning µ.
. By repeating estimation of the vector µ for each fixed α, one can examine how different degrees of residual association between dropping out and outcome at each occasion after adjusting for the influence of recorded history affects inferences concerning µ.
Assumptions (34) and (35) together are equivalent to specifying that
(36)
where ![]() is an unknown function of Y. This, in turn, is equivalent to the pattern mixture model
is an unknown function of Y. This, in turn, is equivalent to the pattern mixture model
(37)
In this latter form, one can see that there is no evidence in the data regarding α since it serves as the link between the conditional (on ![]() ) distribution of Yk+1 among those who drop out between visits k and k + 1 and those who remain through visit k + 1. If one believes that the association between dropping out and future outcomes depends solely on the current outcome but varies according to the recorded history, one can replace α with a known function of
) distribution of Yk+1 among those who drop out between visits k and k + 1 and those who remain through visit k + 1. If one believes that the association between dropping out and future outcomes depends solely on the current outcome but varies according to the recorded history, one can replace α with a known function of ![]() .
.
For instance, replacing in equation (36) the constant α with the function α0 + α1Yk with α0 and α1 specified, encodes the belief that the residual association between dropping out between k and k + 1 and the outcome Yk+1 may be stronger for individuals with, say, higher (if α1 > 0) values of the outcome at visit k. As an example, if Yk is a strong predictor of Yk+1 and that lower values of Yk+1 are preferable (e.g., HIV-RNA viral load), then it is reasonable to postulate that subjects with low values of Yk drop out for reasons unrelated to the drug efficacy (and, in particular, then to their outcome Y k+1) while subjects with higher values of Yk drop out for reasons related to drug efficacy and hence to their outcome Yk+1.
Regardless of how the residual dependence is specified, µ can be expressed in terms of the distribution of the observed data, that is, it is identified. Estimation of µ = E[YK] relies on the identity
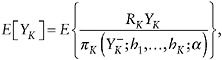
(38)
where
This formula suggests that one can estimate µ with the IPW estimator
(39)
This estimator relies on estimators ![]() . In order to estimate these functions, one needs to impose type (ii) modeling assumptions on
. In order to estimate these functions, one needs to impose type (ii) modeling assumptions on ![]() , that is,
, that is, ![]() . For example, one can assume that
. For example, one can assume that ![]() (adopting such a model would be tantamount to assuming that the probability of dropping out at each time follows a logistic regression model on just the immediately preceding recorded data and on the current outcome).
(adopting such a model would be tantamount to assuming that the probability of dropping out at each time follows a logistic regression model on just the immediately preceding recorded data and on the current outcome).
As with the selection approach of the two preceding examples, to estimate γk, one cannot fit a logistic regression model because YK+1 is missing when L = k. However, one can estimate it instead by solving the estimating equations
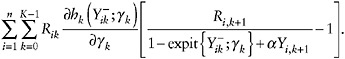
(40)
for γ, justified on similar grounds as the estimators of h functions in the previous examples.
Formula for sandwich-type standard error estimators are available (see Rotnitzky et al., 1997), but the bootstrap can also be used to compute standard error estimates. Sensitivity analysis with regard to hypothesis testing is conducted in a manner similar to the one described in the first example above.
Nonmonotone Missing Data
A typical way to analyze nonmonotone missing data is to treat the time of dropout as the key missing data variable and then to assume MAR within dropout pattern (or conditional on dropout time). The advantage of this approach is purely practical: It interpolates missing data under a specified model. That said, however, the current literature suggests that MAR within pattern does not easily correspond to realistic mechanisms for generating the data. This raises concern among members of the panel that nonmonotone dropouts may require more specialized methods for modeling the missing data mechanism, and accounting for departures from MAR.
This topic has not been deeply studied in the extant statistical literature, and in particular numerical studies are lacking. We recommend this as a key area of investigation that will: (a) examine the appropriateness of existing models and in particular the potential pitfalls of assuming MAR within missing data pattern; and (b) develop and apply novel, appropriate methods of model specification and sensitivity analysis to handle nonmonotone missing data patterns.
COMPARING PATTERN MIXTURE AND SELECTION APPROACHES
The main appeal of the selection model approach is that, since it models the probability of nonresponse rather than the distribution of outcomes, it can easily accommodate vectors of auxiliary factors with components that can be of all types, discrete, categorical, and continuous.
Two disadvantages of the selection approach as they relate to drawing inferences are (a) the inverse weighting estimation procedure, which can yield relatively inefficient inferences (i.e., large standard errors), and (b) that model checking of the type (ii) assumptions must be conducted for each unique value of the sensitivity analysis parameters. Formal model checking procedures have yet to be formally developed for this setting. The inefficiencies associated with the inverse weighting procedure are mitigated in settings with a sizable fraction of missing data, as the sampling variability is often of less concern than the range of type (i) assumptions that are entertained. To address (b), one should fit a highly flexible model for the h function in the selection model.
Another potential disadvantage of selection models relates to interpretation of the sensitivity parameter. Particularly for continuous measures, it may be difficult to interpret nonresponse rates on the odds scale and to specify reasonable ranges for the sensitivity parameter. Plots such as those shown in Figure 5-2 (above) can be helpful in understanding how values of the sensitivity parameter correspond to imputed means for the missing outcomes.
Advantages of the pattern mixture model include transparent interpretation of sensitivity parameters and straightforward model checking for the observed-data distribution. The sensitivity parameters are typically specified in terms of differences in mean between respondents and nonrespondents, which appeal directly to intuition and contributes to formulating plausible ranges for the parameter. Pattern mixture models also can be specified so that the fit to the observed data is identical across all values of the sensitivity parameters; hence, model checking will be straightforward and does not depend on the assumed missing data assumption.
Disadvantages of pattern mixture modeling include difficulties in including auxiliary information, which will generally require additional modeling. Computation of the weighted averages across patterns for models of large numbers of repeated measures also can become complex without significant simplifying assumptions.
TIME-TO-EVENT DATA
A major challenge in the analysis of time-to-event outcomes in randomized trials is to properly account for censoring that may be informative. Different approaches have been proposed in the research literature to address this issue. When no auxiliary prognostic factors are available, the general strategy has been to impose nonidentifiable assumptions concerning the dependence between failure and censoring times and then vary these assumptions in order to assess the sensitivity of inferences on the estimated survivor function. When prognostic factors are recorded, Robins and colleagues in a series of papers (Robins and Rotnitzky, 1992; Robins, 1993;
Robins and Finkelstein, 2000) proposed a general estimation strategy under the assumption that all measured prognostic factors that predict censoring are recorded in the database. Scharfstein and Robins (2002) proposed a method for conducting sensitivity analysis under the assumption that some but not all joint prognostic factors for censoring and survival are available. Their approach is to repeat inference under different values of a nonidentifiable censoring bias parameter that encodes the magnitude of the residual association between survival and censoring after adjusting for measured prognostic factors.
In randomized studies, censoring typically occurs for several reasons, some noninformative, others informative. For instance, in studies with staggered entry, the administrative end of the follow-up period typically induces noninformative censoring. However, loss to follow-up due to dropouts induces a competing censoring mechanism that is likely to be informative. Treatment discontinuation might induce yet another informative censoring process.
Under the Scharfstein and Robins methodology, the analyst specifies a range for the parameter encoding the residual dependence of the hazard of the minimum of competing censoring times on the censored outcome. However, this range might be rather difficult to specify if the reasons that each censoring might occur are quite different, more so if some censoring processes are informative and some are not. To ameliorate this problem in studies with staggered entry, one can eliminate the censoring by the administrative end of the follow-up period (typically a source of noninformative censoring) by restricting the follow-up period to a shorter interval in which (with probability) no subject is administratively censored. However, in doing so, one would lose valuable information on the survival experience of the study patients who remain at risk at the end of the reduced analysis interval. Rotnitzky et al. (2007) provide estimators of the survival function under separate models for the competing censoring mechanisms, including both informative and noninformative censoring. The methods can be used to exploit the data recorded throughout the entire follow-up period and, in particular, beyond the end of the reduced analysis interval discussed above.
DECISION MAKING
Even after model fitting and sensitivity analysis, investigators have to decide about how important the treatment effect is. Unfortunately, there is no scientific consensus on how to synthesize information from a sensitivity analysis into a single decision about treatment effect. At least three possibilities can be considered.
One possibility is to specify a plausible region for the sensitivity parameters and report estimates of the lower and upper bounds from this range. These
endpoints form bounds on the estimated treatment effect and would be used in place of point estimates. Accompanying these bounds would be a 95 percent confidence region. This procedure can be viewed as accounting for both sampling variability and variability due to model uncertainty (i.e., uncertainty about the sensitivity parameter value): see Molenberghs and Kenward (2007) for more detailed discussion and recommendations for computing a 95 percent confidence region.
A second possibility is to carry out inference under MAR and determine the set of sensitivity parameter values that would lead to overturning the conclusion from MAR. Results can be viewed as equivocal if the inference about treatment effects could be overturned for values of the sensitivity parameter that are plausible.
The third possibility is to derive a summary inference that averages over values of the sensitivity parameters in some principled fashion. This approach could be viewed as appropriate in settings in which reliable prior information about the sensitivity parameter value is known in advance.
Regardless of the specific approach taken to decision making, the key issue is weighting the results, either formally or informally, from both the primary analysis and each alternative analysis by assessing the reasonableness of the assumptions made in conjunction with each analysis. The analyses should be given little weight when the associated assumptions are viewed as being extreme and should be given substantial weight when the associated assumptions are viewed as being comparably plausible to those for the primary analysis. Therefore, in situations in which there are alternative analyses as part of the sensitivity analysis that support contrary inferences to that of the primary analysis, if the associated assumptions are viewed as being fairly extreme, it would be reasonable to continue to support the inference from the primary analysis.
RECOMMENDATION
Recommendation 15: Sensitivity analyses should be part of the primary reporting of findings from clinical trials. Examining sensitivity to the assumptions about the missing data mechanism should be a mandatory component of reporting.
We note that there are some often-used models for the analysis of missing data in clinical trials for which the form of a sensitivity analysis has not been fully developed in the literature. Although we have provided principles for the broad development of sensitivity analyses, we have not been prescriptive for many individual models. It is important that additional research be carried out so that methods to carry out sensitivity analyses for all of the standard models are available.

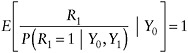 .
.






















