Past efforts to meet COSPAR’s planetary protection requirements for the outer planets relied on the Coleman-Sagan formula to calculate the probability that a mission would introduce a single viable microorganism capable of growth on or within a mission destination. The formula typically multiplies together estimates for the number of organisms on the spacecraft, the probability of growth on the target body, and a series of bioload reduction factors to determine whether or not estimates of the probability of contamination fall below 10–4. COSPAR guidelines require that less than 1 in 10,000 missions will deliver a single viable microbe that is able to grow on a target destination in the solar system, i.e., a 10–4 probability of contamination per mission flown. Failure to meet the standard developed to achieve this mandated objective could impose requirements for more stringent cleaning or terminal bioload-reduction procedures comparable to those employed by the Viking missions. In extreme cases, satisfying planetary protection requirements might require spacecraft redesign or cancellation of an entire mission.
PROBLEMS WITH COLEMAN-SAGAN CALCULATIONS
The lack of independence for many bioload reduction factors and the minimal precision obtained when assigning values for the initial number of microbes within or on a spacecraft compromise the utility of the Coleman-Sagan formulation as a framework for incorporating planetary protection requirements into mission design. The National Research Council’s (NRC’s) 2000 report Preventing the Forward Contamination of Europa1 illustrates the application of the Coleman-Sagan formulation, while at the same time recognizing its shortcomings, when estimating the risk of forward contamination. To accommodate new knowledge about extremophiles on Earth, the Europa report study committee increased the model complexity by using different bioload reduction factors for physiologically distinct classes of microbes, including non-specialized microbes, bacterial spores, radiation-resistant spores, and highly radiation resistant non-spore-forming microorganisms. The 2000 Europa report acknowledged that its improved methodology continued to rely on the uncertain nature of values for nearly every factor in a chain of “uncorrelated” factors: “The values assigned to individual parameters are not definitive.… All parameters are assumed to be independent and uncorrelated.”2 As described in Appendix A of the 2000 Europa report, an example of the Coleman-Sagan formula calculates the probability of contamination by each of four different classes of organisms, each of which represent four different sensitivities to ionizing radiation. Using the formula
NXs = NX0 F1F2F3F4F5F6F7
the authors of the 2000 Europa report calculated NXs, or the number of organisms estimated to survive and grow in the target environment, summed across each physiological class, where
NX0 = Number of viable cells on the spacecraft before launch,
F1 = Total number of cells relative to cultured cells,
F2 = Bioburden reduction treatment fraction,
F3 = Cruise survival fraction,
F4 = Radiation survival fraction,
F5 = Probability of landing at an active site,
F6 = Burial fraction,
F7 = Probability that an organism survives and proliferates,
F7a = Survivability in exposure environments,
F7b = Availability of nutrients,
F7c = Suitability of energy sources, and
F7d = Suitability of environment for active growth.
Figure 2.1 shows how the Coleman-Sagan factors are mapped to the different phases of a planetary mission.
The example calculation in the 2000 Europa report shows that the value of NX (summed across all four physiological classes) had a combined probability of 3.8 × 10–5, i.e., below COSPAR requirements of 10–4. This approach, which seeks to identify conditions that constrain the sum of NXs below 10–4, identifies multiple factors that could influence contamination of solar system objects, but only if each factor represents an independent process and their values and variances are known.
The committee departs from the conclusions of the 2000 Europa report by claiming that not all bioload reduction factors are independent, and with the possible exception of F5 (probability of landing at an active site) current knowledge makes it impossible to confidently assign values for these factors within orders of magnitude of their true value. Multiplication of uncertain overestimates of bioload reduction factors can lead to unsubstantiated, low estimates of likely contamination. Alternatively, underestimates of bioload reduction coupled with overestimates of bioload on the spacecraft and the flawed assumption that any organism delivered to the target body will grow (Pg = 1), would impose unnecessary and possibly unachievable planetary protection demands. The vast majority of different terrestrial microbes have specific requirements for growth that rarely occur in nature or in manipulated laboratory environments. The assumption that Pg = 1 in any environment inclusive of icy bodies is conservative. However, the expectation that all microbes can grow anywhere is not supported by available scientific data.
In the example calculation for the NRC’s 2000 Europa report, the bio-reduction factors F3 (cruise survival fraction) and F4 (radiation survival fraction) have a combined bio-load reduction of 10–6 to 10–11 for the different physiological classes. Yet F3 and F4 represent highly correlated, non-independent mechanisms of sensitivity to radiation and vacuum. A significant fraction of the organisms lost due to the combination of ultrahigh vacuum

FIGURE 2.1 Mapping the Coleman-Sagan factors to the different phases of a planetary mission. The initial cell counts and cleaning are performed during spacecraft assembly. The survival fraction to irradiation and deep-space conditions corresponds to interplanetary cruise; and the characteristics of the planetary destination, either in orbit or within the planetary environment, dictate the remaining factors.
and radiation during the cruise phase will correspond to a subset of those that will succumb during orbit in a high-radiation flux around Europa or other icy moons. The factor F4 (radiation survival fraction) is part of F3 (cruise survival fraction), and F3, F4, and F6 (burial fraction) reflect non-independent measures of bio-reduction factor due to radiation flux. In this example, burial fraction dictates the radiation dose profile as a function of depth. The level of protection offered by burial over unit time correlates with estimates of radiation sensitivity as reflected by F4.
The environmental factors F7a through F7d constrain the survivability of organisms on or in the spacecraft and their ability to proliferate for a combined bio-load reduction of 10–6, but these factors either lack independence or use “survivability” as a substitute for the probability of growth, Pg, which is impossible to estimate. With respect to the independence of these factors, F7a will include radiation sensitivity as measured by F4. The factors F7b through F7d reflect non-independent environmental resources required for growth. The combination of the factors F7a through F7d substitutes for Pg, which most planetary protection studies assume to be unitary because of the complexity of predicting whether a microbe can or cannot grow under a given set of environmental conditions. By assigning probabilities less than 1 for the non-independent bio-reduction factors and the Pg-like estimates for “organism survivability and proliferation,” the Coleman-Sagan calculation can reduce the value of NXs by several orders of magnitude. Yet, with the exception of the geologically influenced parameter F5, all of these factors have dependencies on other factors.
Because the overall uncertainty factor in the final result from the Coleman-Sagan equation is greater than the uncertainty factor for the least-constrained variable, a three or four order-of-magnitude uncertainty in estimates of the number of organisms on spacecraft would lead to approximately a three or four order-of-magnitude uncertainty in the overall probability of contamination.
Even greater uncertainty arises from the inability to confidently assign values to many of these factors, including estimates of the number of viable microbes NX0, on the spacecraft prior to launch. As described in Chapter 1 of this report, the standard NASA assay of heat-resistant microbes serves as an indicator of the number of spores on the sampled spacecraft surfaces. These measurements provide no information about the number of heat-sensitive but radiation- and vacuum-resistant microbes on a spacecraft, nor do these surveys provide accurate estimates of heat-resistant spores that are refractory to cultivation. Over the past two decades culture-independent microbial diversity investigations based on comparisons of highly conserved sequences (ribosomal RNA genes) in Bacteria and Archaea demonstrate that microbiologists have successfully cultivated only a small fraction (<1 percent) of the different kinds of single-cell organisms that occur in nature.3 Deep-sequencing surveys suggest that microbial diversity may be 1,000 to 10,000 times greater than estimates from cultivation-based studies and that most of this novelty corresponds to low-abundance taxa described as the “rare biosphere.”4,5 Similar analyses of simple mock communities containing one or a few taxa suggested that sequencing errors can lead to inflated estimates of microbial diversity.6 More recent studies show that a 2 percent single-linkage preclustering methodology followed by an average-linkage clustering based on pair-wise sequence alignments more accurately predicts expected complexity of mock communities of known taxonomic composition. However, this analytical paradigm does not reduce the fraction of novel taxa in the long-tailed rank abundance curves that define the rare biosphere for complex, naturally occurring microbial communities. This implies that the standard spore assay likely underdetermines the number of heat-resistant organisms on a spacecraft. If many spore-forming organisms cannot grow under laboratory conditions, then growth-based assays of survival will not accurately report the size of the surviving populations.
Given current technology, non-rigorous estimates of NX0 can lead to significant underestimates of the number of organisms delivered to the target body. Estimates for other bioload reduction factors suffer similar uncertainties. The current inability to cultivate most of the different microbes that comprised by a community makes it impossible to estimate what fraction of a community succumbs to radiation and ultralow vacuum during cruise or orbit in a high-radiation environment. Because the overall uncertainty factor in the final result from the Coleman-Sagan equation is greater than the uncertainty factor for the least-constrained variable, a three or four order-of-magnitude
uncertainty in estimates of the number of organisms on spacecraft would lead to approximately a three or four order-of-magnitude uncertainty in the overall probability of contamination.
The most robust estimate for independent factors in the 2000 Europa report describe the likelihood that a spacecraft will impact an active area. For example, as described in Chapter 4, calculating the fraction of the surface area that might theoretically communicate with a subsurface ocean over a given period of time yields a first-order approximation of the likelihood that microbes on the spacecraft might contaminate the ocean. Under this scenario, the probability of contamination would be estimated according to where and how the spacecraft impacts a surface, rather than being derived from uncertain estimates from a series of difficult-to-determine bio-reduction factors. Multiplying the number of surviving organisms on the spacecraft by the chance that the spacecraft will encounter an area of active surface-subsurface transport implicitly assumes that each organism or class of organisms has an independent chance of encountering the active area. Yet the probability that two different organisms on the same spacecraft will be transported to the subsurface is tightly correlated; either the spacecraft will land in an active area, in which case most of the spacecraft’s surviving bioload can contaminate the subsurface environment, or the spacecraft will land in an inactive area, in which case even a highly contaminated spacecraft cannot affect the subsurface.
COSPAR’S SIMPLIFIED VERSION OF THE COLEMAN-SAGAN APPROACH
As mentioned in Chapter 1, following on the discussions and deliberations at two workshops held in 2009, COSPAR’s Panel on Planetary Protection (PPP) ultimately recommended the adoption of a simplified version of the Coleman-Sagan approach presented in the NRC’s 2000 Europa report. Similarly, the simplified recommendations in the formulation described in the COSPAR Planetary Protection Policy of October 20, 2002, as amended, and the COSPAR Workshop on Planetary Protection for Outer Planet Satellites and Small Solar System Bodies (Vienna, Austria, 2009) and the COSPAR Workshop on Planetary Protection for Titan and Ganymede (2009) include, in its most simplified form, the following factors:7
• Bioburden at launch;
• Cruise survival for contaminating organisms;
• Organism survival in the radiation environment adjacent to Europa;
• Probability of landing on Europa;
• The mechanisms and timescales of transport to the europan subsurface; and
• Organism survival and proliferation before, during, and after subsurface transfer.
However, the same arguments the present committee has leveled against the more complex approach presented in the NRC’s 2000 Europa report (see above) apply to the simplified formulation adopted as official COSPAR policy. For example, current technology, including the NASA standard spore assay and culture-independent molecular technologies, displays a wide variance over many orders of magnitude when estimating bioburden at launch (factor 1 above). Cruise survival and organism survival (factors 2 and 3) are not independent processes. The timescales of transport to the europan subsurface (factor 5) are also not independent of irradiation survival during cruise or in environments adjacent to Europa—in effect they reflect use of the same biological information to estimate parameters that affect an organism’s ability to survive exposure to radiation. Moreover, the COSPAR policy’s open-ended nature—i.e., the possibility of adding additional numerical factors to the calculation (as was done for the Juno mission)—potentially compounds issues relating to statistical uncertainty and non-independence.
Based on these observations and conclusions, the committee saw no scientifically or logically defensible path for improving estimates of factors for the Coleman Sagan formulation as called for in its charge (see Appendix A). In order to make progress, the committee explored the utility of a binary decision matrix similar to that previously employed in the NRC report Evaluating the Biological Potential in Samples Returned from Planetary Satellites and Small Solar System Bodies: Framework for Decision Making.8 Such an approach has already been adopted by COSPAR for determining whether or not sample-return missions from small solar system bodies are classified as restricted or unrestricted Earth-return missions.9
AN ALTERNATIVE TO THE COLEMAN-SAGAN FORMULATION
A binary decision-making framework (Figure 2.2) provides an alternative to Coleman-Sagan estimates of contamination that are constrained by uncertain and possibly unknowable factors. The decision framework should consider the habitability of different solar system objects, including environmental conditions necessary for propagation of terrestrial life (see Chapter 3 for details), the probability of transport to a subsurface, habitable environment (see Chapter 4 for details), and the ability of terrestrial organisms to survive nominal bioload reduction treatments and adapt to non-terrestrial environments (see Chapter 5 for details). When the decision framework indicates that contamination would occur if the spacecraft impacted the surface, stricter planetary protection efforts would be required. It should be noted that the binary decision framework presented in Figure 2.2 can be presented in alternative formats, such as an event sequence diagram (Appendix C), which indeed may be preferred in the engineering community.
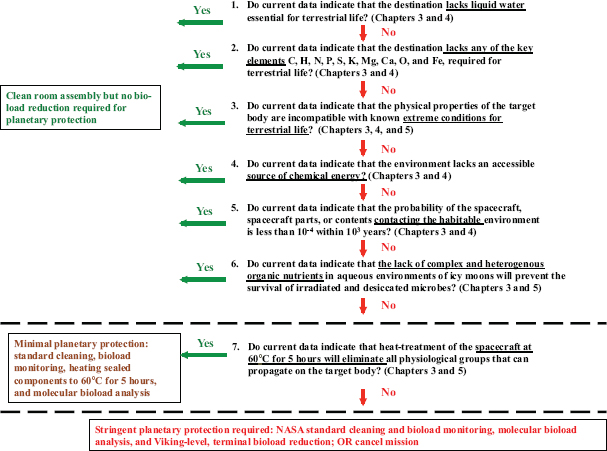
FIGURE 2.2 Binary decision-making framework for planetary protection of icy solar system bodies. “Yes” answers to Decision Points 1-6 release the mission from rigorous planetary protection procedures, whereas a “Yes” to Decision Point 7 requires moderate heating of sealed components. “No” answers to Decision Points 1-7 will require the use of stringent planetary protection procedures, e.g., terminal bioload reduction or mission cancellation. The phrase “do current data indicate” conveys a scientific consensus about the reliability of available information at the time of assessing planetary protection risk.
CONCLUSIONS AND RECOMMENDATIONS
The committee expresses caution about the use of the Coleman-Sagan approach for assessing the risk of forward contamination. The uncertainty in assigned values for initial bioloads and bioload reduction factors, and the multiplication of factors that are not mutually independent, cannot provide robust estimates of the probability of forward contamination.
In contrast, a binary decision-making framework would provide a more robust basis for determining the appropriate level of planetary protection for a given mission, because such a procedure would not compound inaccurate and non-independent estimates of probability factors. Separate and independent decision points in the framework should consider different parameters that define the habitability of the target solar system object(s), the probability of transporting terrestrial organisms to a habitable environment on a given target body, and the ability of terrestrial organisms to endure bioload reduction treatments and subsist in non-terrestrial environments.
Recommendation: Approaches to achieving planetary protection should not rely on the multiplication of bioload estimates and probabilities to calculate the likelihood of contaminating solar system bodies with terrestrial organisms unless scientific data unequivocally define the values, statistical variation, and mutual independence of every factor used in the equation.
Recommendation: Approaches to achieving planetary protection for missions to icy solar system bodies should employ a series of binary decisions that consider one factor at a time to determine the appropriate level of planetary protection procedures to use.
1. National Research Council, Preventing the Forward Contamination of Europa, National Academy Press, Washington, D.C., 2000.
2. National Research Council, Preventing the Forward Contamination of Europa, National Academy Press, Washington, D.C., 2000, p. 29.
3. N.R. Pace, A molecular view of microbial diversity and the biosphere, Science 276(5313):734-740, 1997.
4. M.L. Sogin, H.G. Morrison, J.A. Huber, D.M. Welch, S.M. Huse, P.R. Neal, J.M. Arrieta, and G.J. Herndl, Microbial diversity in the deep sea and the under-explored “rare” biosphere, Proceedings of the National Academy of Sciences USA 103(32):12115-12120, 2006.
5. J.A. Huber, D.M. Welch, H.G. Morrison, S.M. Huse, P.R. Neal, D.A. Butterfield, and M.L. Sogin, Microbial population structures in the deep marine biosphere, Science 318:97-100, 2007.
6. V. Kunin, A. Engelbrektson, H. Ochman, and P. Hugenholtz, Wrinkles in the rare biosphere: Pyrosequencing errors lead to artificial inflation of diversity estimates, Environmental Microbiology 12: 118-123, 2009.
7. COSPAR, “COSPAR Planetary Protection Policy (20 October 2002; As Amended to 24 March 2011),” COSPAR, Paris, p. A-6, available at http://cosparhq.cnes.fr/Scistr/PPPolicy%20(24Mar2011).pdf.
8. National Research Council, Evaluating the Biological Potential in Samples Returned from Planetary Satellites and Small Solar System Bodies: Framework for Decision Making, National Academy Press, Washington, D.C., 1998.
9. COSPAR, “COSPAR Planetary Protection Policy (20 October 2002; As Amended to 24 March 2011),” COSPAR, Paris, pp. A-7 and A-8, available at http://cosparhq.cnes.fr/Scistr/PPPolicy%20(24Mar2011).pdf.






