2
Refinements to the SMART Vaccines Model
SMART Vaccines is based on a multi-attribute utility model. The rationale, the structure, and the mechanistic basis of the computational and value submodels were detailed in Ranking Vaccines: A Prioritization Framework (IOM, 2012). A brief review is presented here.
A Brief Review of the Modeling Framework
The multi-attribute utility model underpinning SMART Vaccines is able to blend quantitative and user-based qualitative attributes. Priorities for vaccine candidates are then set according to a weighted average of the attributes chosen by the user (Keeney and Raiffa, 1976).
Some attributes are computed quantities, such as the estimated number of deaths averted due to the presence of the new vaccine under consideration. This particular attribute relies on data and expert estimates concerning known or partly known aspects of the epidemiology of the disease and anticipated characteristics of the hypothetical vaccine (e.g., effectiveness, duration of immunity, and coverage or uptake in the population).
Attributes can also be qualitative, involving a “yes” or “no” indication to, for example, represent whether the vaccine benefits infants and children (e.g., perinatal group B streptococcus infection) or adolescent girls (e.g., human papillomavirus infection). Attributes can also be represented by categorical rating scales to capture, for example, the user’s best estimate of the likelihood that a targeted vaccine might be financially profitable for
a manufacturer, with a 5 representing highest likelihood and 1 representing least likelihood.
Using each attribute’s measure (Xi for the ith attribute), a utility scale, Ui(xi), is formed so that the least desired (worst) level (Xi=xi0) is scaled as Ui(xi0)=0 and the most desired (best) level for that attribute (Xi=xi1) is scaled as Ui(xi1)=100. In SMART Vaccines the intermediate levels of Xi are scaled linearly relative to these two endpoints.
Each vaccine to be prioritized, V, may be considered as a vector of attributes, V=(x1, x2, …, xn), where each component of the vector indicates the expected performance of that vaccine on the measure for the particular attribute. This is rescaled into a vector of single attribute utility scales, Vj=(U1(x1j), …, Un(xnj)), to represent the vaccine as input to the multi-attribute utility scoring algorithm.
Finally a set of weights, wi, i=1…n, is specified to represent the relative value from 0 to 100 for each attribute in relation to the others. The weights are then normalized so that their sum is equal to 100, which allows each weight to be interpreted as a percentage of the total weight. The final scoring function is the weighted sum represented as
![]()
where U(Vj) is the utility score for the vaccine Vj. By scaling the worst and the best levels of each attribute between 0 and 100 and by normalizing the sum of the wi’s to be 1, this score will also range between 0 and 100. In SMART Vaccines this resulting score is labeled the “SMART Score.” Vaccines are ranked in priority according to the rank order of their SMART Scores. Figure 2-1 shows a diagram of the SMART Vaccines framework, slightly revised from the 2012 IOM report. Appendix A details the computational model supporting SMART Vaccines.
In the 2012 report, the committee organized 29 stakeholder-informed attributes into eight categories. Following the Phase II deliberations, the committee slightly revised this listing (see Table S-1). In SMART Vaccines 1.0, a choice of 28 attributes spread across eight categories is available to users, with an option of adding up to seven user-defined attributes in a ninth category.
One attribute, the likelihood of successful licensure within the next 10 years, was removed from the original list and instead incorporated as a vaccine characteristic because this attribute works as a multiplier on the overall SMART Score. In the extreme, if there is no chance of licensure, then it does not matter how good the vaccine scores on other attributes—
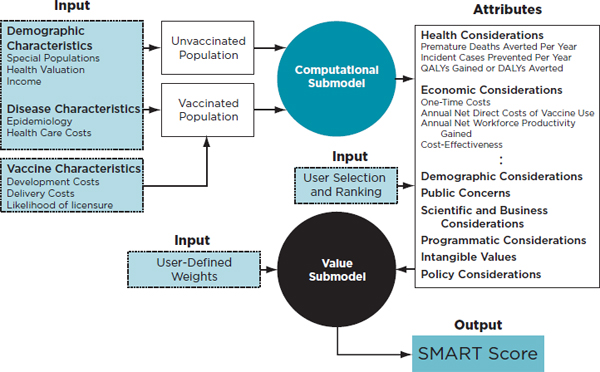
FIGURE 2-1
SMART Vaccines framework showing the computational and value submodels that help produce the SMART Score for various vaccine candidates under consideration.
NOTE: DALYs = disability-adjusted life years; QALYs = quality-adjusted life years.
the overall value should be zero. If there is a 50 percent chance of licensure, then the expected score should be 0.50 times the overall SMART Score. To reflect this multiplicative impact of the licensure attribute, this value is now elicited from the user after the SMART Scores are produced for the vaccines being compared. Thus, if the resulting SMART Score for a specific vaccine candidate is calculated as 70, but the user-defined likelihood of successful licensure of that vaccine over a 10-year period is 50 percent, then the SMART Score is set to 35 to reflect the product of the original score and the probability of licensure. Using this multiplier is optional for the user, but it is helpful for comparative assessment when the probabilities of licensure success differ significantly across vaccine candidates.
SMART Vaccines 1.0 uses the rank-order centroid method (Barron and Barrett, 1996) (detailed in the 2012 report, Chapter 2) to obtain quick initial weights, but the redesigned software interface allows dynamic adjustment of these weights (using slider bars) to obtain a final weighting leading up to the SMART Score. This adjustment process uses the so-called “swing weighting” method, in which the relative effect of an attribute is determined by the effect of changing the attribute level from the worst one to the best one.
Setting Ranges for Attributes: A Heuristic Process
SMART Vaccines is designed for prioritizing a wide but realistic range of vaccine candidates. This led the committee to provide specific design choices of scales for the attributes.
A useful analogy in this context is the task of designing an instrument to measure the weights of a class of objects. To design a useful instrument one needs to know the range of weights that will be measured. A bathroom scale is not useful to weigh the quantities of ingredients normally used for meal recipes in the kitchen, nor is a roadside vehicle scale useful to weigh either these kitchen ingredients or to weigh people. The point is that weight scales are built to accommodate a suitable range of objects.
Similarly, SMART Vaccines has been devised to accommodate the variation expected across a range of different vaccine candidates. For some attributes, two levels—a minimum value at 0 and a maximum value at 100—appear to be sufficient. For others it is difficult to find appropriate reference points. For example, the committee found it challenging to scale the attributes related to health and economic considerations. The reference points described next are a first attempt, which was based on an appraisal of the relevant literature but not on an actual application of SMART Vaccines to the six test vaccine candidates used to assure its current functionality. Future users of SMART Vaccines may wish to revisit the setting of these reference points following cumulative experiences with the software.
Weights and Ranks: Attention to the Ranges of the Attributes
Once the attributes are selected by the user to inform the calculation of SMART Score, they must be weighted. In the 2012 report the committee suggested that the attributes be ranked in order of importance, from most to least important. Then the weights were computed from the user’s ordering using the rank order centroid method to approximate ratio scale weights. The process of ranking and weighting has been substantially upgraded in SMART Vaccines 1.0, and it is briefly reviewed in this section.
In the previous section a utility function for the ith attribute was scaled between Ui(xi0)=0 and Ui(xi1)=100, where xi0 and xi1 were the worst and best level of attribute i, respectively. But the size of the units of these U(x) scales still needs to be set so that the units of one scale, Ui, may be added to those of another scale, Uj. That is, the 100 point on one scale may indicate a much larger distance in units of value from the 0 point on that scale than does the 100 point on another scale.
For example, the English scale of distance uses inches as its unit of distance, while the metric scale uses centimeters. The distance between 0 and 100 inches is not the same as the distance between 0 and 100 centimeters even though they are numerically labeled the same. One inch is approximately 2.54 centimeters, and a scaling factor of 2.54, therefore, must be applied to translate the units from one format to another. In the context of SMART Vaccines, the “distance” measured is not objective, but rather a subjective judgment that reflects the values of the decision maker.
Let us assume, for example, that a user has selected four attributes from among the 28 attributes relating to a U.S. population in SMART Vaccines:
Health Considerations:
Premature deaths averted per year (x0=0 deaths averted; x1=14,000 deaths averted)
Economic Considerations:
Cost-effectiveness, $/QALY gained (x0=$203,000/QALY gained; x1=$0/QALY gained)
Demographic Considerations:
Benefits infants and children (x0=No; x1=Yes)
Programmatic Considerations:
Reduces challenges relating to cold-chain requirements (x0=No—requires refrigeration; x1=Yes—thermostable)
If all four of these attributes score at level x0, the vaccine candidate will receive a SMART Score of zero (on a scale of 0 to 100), irrespective of the weights, because all four Ui(xi) components of the score would be zero. This low-achieving vaccine defines zero on the SMART Score scale. Its opposite, with all four attributes at level x1—that is, a vaccine that has the potential to avert 14,000 premature deaths per year, has net incremental costs of $0 per QALY gained, is targeted to the primary benefit of infants and children, and is thermostable—would achieve a SMART score of 100 and defines the highest value possible on the SMART Score.
At this stage the user is asked, in essence, “If you currently had a vaccine candidate which had all attributes at the x0 level, and you could change one and only one attribute to the x1 level, which attribute would you choose?” This question identifies that attribute for which the most value is achieved by this change, and this attribute is ranked as most important. Suppose the user chooses “Deaths averted per year.” This implies that the change from x0=0 deaths to x1=14,000 deaths per year is valued most highly by the user among all such changes among the attributes. This attribute is
TABLE 2-1
Attribute Ranking and Weights for a Hypothetical User Scenario
| Attribute | Rank | Preliminary Weight from the Rank Order Centroid Method |
| Premature deaths averted per year | 1 | 52.1% |
| Benefits infants and children | 2 | 27.1% |
| Cost-effectiveness ($/QALY) | 3 | 14.6% |
| Reduces challenges relating to cold-chain requirements | 4 | 6.3% |
NOTE: QALY = quality-adjusted life year.
thus ranked as the most important. Correspondingly, when asked for the least important attribute to be changed from x0 to x1 level, if the user picks, “Reduces challenges relating to cold-chain requirements,” and then this attribute is valued least by the user.
Finally, after having decided on the most important and least important attributes, the user ranks the remaining attributes. If the user ranks “Benefits infants and children” at 2 and “Cost-effectiveness” at 3, then SMART Vaccines assigns preliminary weights to the four attributes using the rank order centroid method as shown in Table 2-1.
The rank order centroid method calculates the geometric average of all possible combinations of weights that are consistent with the rank ordering chosen by the user and normalizing the weights so that they sum to 100 percent (Barron and Barrett, 1996; Edwards and Barron, 1994).
In the Phase I work that produced SMART Vaccines Beta, the rank order centroid approximation resulted in the final weights. In Phase II, however, the user is allowed to use the ranked weights as a starting point and then to adjust the relative weights for the four attributes using slider bars and see the changes reflected in the SMART Score of the vaccine. These adjustments should be done so that the magnitude of the weights reflects the relative importance of changing an attribute from its worst to its best level. In parallel, the graphical changes resulting from slider bar adjustments are a visual representation of the relative distance in value from the x0 to x1 levels on the attributes. This feature also permits real-time sensitivity analysis in SMART Vaccines 1.0.
Now suppose that having obtained the rank order centroid outputs, the user chooses to alter the weights using slider bars for the specific attributes under consideration to 60 percent (premature deaths averted per year), 18 percent (benefits infants and children), 18 percent (cost-effectiveness), and 4 percent (reduces challenges relating to cold-chain requirements). Let V be a candidate vaccine whose levels are now x1 = 3,000
deaths averted per year, x2 = primary benefit to infants and children; x3 = –$30,000/QALY gained; and x4 = requires refrigeration. The final SMART Score is then numerically calculated as follows:
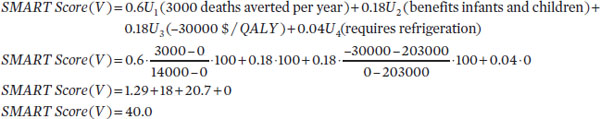
The output indicates that the candidate vaccine is approximately 40 percent of the distance “up” from a vaccine that is scored 0 toward a vaccine that is scored 100.
Given the intrinsic variability in SMART Scores from user to user, how can the ranks then be compared in a user group? While some comparisons can be made, nothing guarantees the ability to map user A’s scores to those of users B, C, and D. The committee has used the analogy of Fahrenheit and Celsius thermometers to assist users in understanding what the SMART Scores mean (and what they do not mean), but the choices of parameter settings in the software may create further complexity in multi-user group settings.
All multi-attribute utility models—including SMART Vaccines—have the characteristic that a difference of, say, 10 points for user A has the same meaning all along user A’s scale, so it is correct to say that the difference between 20 and 10 has the same meaning as the difference between 80 and 70. But one cannot say that “20 is twice as good as 10” any more than one can say that “20°F is twice as warm as 10°F.” It is also correct to say that a 10-point difference on user A’s scale is not the same as a difference of 10 points on user B’s scale, just as with the thermometer analogy: A difference of 10 degrees is not the same in Fahrenheit and Celsius scales.
Unfortunately, the analogy becomes less useful when users A and B have employed a different set of attributes for their valuation. To the extent that they have commonly chosen attributes (e.g., premature deaths averted per year, cost-effectiveness, or potential to improve delivery methods), then the weights they have placed on these attributes lead to predictable changes in each user’s SMART Scores. If they have no common attributes in their respective value models, then it is not possible to compare one user’s SMART Scores (and hence rankings) to those of another user.
This issue is closely related to Arrow’s impossibility theorem—after economist Kenneth Arrow—in the realm of social choice theory (Arrow, 1950, 1963). Arrow sought to understand the conditions under which voting rules could be devised that would translate individual voter’s rankings of various alternatives into a global “community” ranking. He famously demonstrated that, subject to certain “fairness conditions,” no voting system can transform the ranked preferences of individuals into a society-wide ranking
Similarly, in the context of SMART Vaccines, individual SMART Scores cannot be lumped into a society-wide SMART Score by any voting system. This is not a defect of the SMART Vaccines system per se, but rather it is intrinsic to all ranking systems when people (voters) have different preference structures.
Arrow’s impossibility theorem and the mechanism to interpret SMART Scores come from the same basic source: different people value different things differently. The priorities that drive user A to prefer different vaccine attributes may be similar to those of users B, C, and D, or they may be completely different. This does not mean that SMART Vaccines is not effective in establishing ranking lists for new preventive vaccines. Quite to the contrary, SMART Vaccines makes clear what assumptions users have made about vaccine attributes and how they value each candidate vaccine’s attributes.
In the following chapter, the approaches taken to expand the test vaccine candidates and evaluate them using SMART Vaccines 1.0 are discussed.








