People in the Mathematical Sciences Enterprise
The growth and broadening of research opportunities described in Chapters 3 and 4 necessitate changes in the way students are prepared, along with planning about how to attract a sufficient number of talented young people into the discipline. From its discussions with representatives from industry and government who hire mathematically trained individuals, plus other information cited in Chapters 3-4, the committee concludes that demand for people with strong mathematical science skills is already growing and will probably grow even more. The range of positions that require mathematical skills is also expanding, as more and more fields are presented with the challenges and opportunities of large-scale data analysis and mathematical modeling. While these positions can be filled by individuals with a variety of postsecondary degrees, all of them will need strong skills in the mathematical sciences. This has implications for the mathematical sciences community in its role as educators with a responsibility to prepare students from many disciplines to be ready for a broad range of science, technology, engineering, and mathematics (STEM) careers. Indeed, producing an adequate number of people with expertise in the mathematical sciences at the bachelor’s, master’s, and Ph.D. levels and an adequate pipeline of well-trained students emerging from grades K-12 is necessary if the STEM fields are to thrive.
CHANGING DEMAND FOR THE MATHEMATICAL SCIENCES
At its meeting in December 2010, the committee heard from four people in sectors of industry that are becoming increasingly reliant on the mathematical sciences:
• Nafees Bin Zafar, who heads the research division at DreamWorks Animation,
• Brenda Dietrich, vice president for Business Analytics and Mathematical Sciences at IBM’s T.J. Watson Research Center,
• Harry (Heung-Yeung) Shum, head of Core Search Development at Microsoft Research, and
• James Simons, head of Renaissance Technologies.
The goal of this discussion was to gain insight about some of the topical areas in which the mathematical sciences are critical. Speakers brought knowledge of the demand for the mathematical sciences in the financial sector and the growing demands in business analytics, the entertainment sector, and the information industry. Because Dr. Shum had been a founder of Microsoft Research–Asia, in Beijing, he was also able to comment on the growing mathematical science capabilities in China. The focus of these interactions was to learn about current and emerging uses of mathematical sciences skills, whether or not carried out by people who consider themselves to be mathematical scientists. The financial sector, for example, employs thousands of financial engineers, only a fraction of whom have a terminal degree in mathematics or statistics. (Many are trained in physics or economics, and many have M.B.A. training.) Understanding the demand for mathematical science skills per se is critical for two reasons: (1) the demand for those skills, especially where it is increasing or moving in new directions, requires college and university education that in part relies on academic mathematical scientists and (2) the demand for those skills implies at least the possibility that the nation would benefit from a larger number of master’s or Ph.D.-level mathematical scientists, especially if their training were designed with consideration of the emerging career options.
Dr. Simons noted that Renaissance Technologies has carried out all of its trading through quantitative models since 1998; it now works with several terabytes of data per day from markets around the world. The company has about 90 Ph.D.s, most in the research group but some in the programming group. Some of these people have backgrounds in mathematics, but others have degrees in astronomy, computer science, physics, or other disciplines that provide strong mathematical science skills. He listed a number of financial functions that rely on mathematical science skills: prediction, valuation, portfolio construction, volatility modeling, and so
on. Even though the financial sector hires a large number of people with strong mathematical science expertise, he thinks the level of mathematical knowledge in the finance world is still lower than it should be. As an example, he said that many people do not know the distinction between beta (the difference between an instrument’s performance and that of a relevant market) and volatility; they are related but different. He thinks finance will continue to be permeated by quantitative methods. Some of the skills that are necessary, in Dr. Simons’s view, include statistics (though not normally at the level of new research) and optimization, and good programming skill is essential.
Dr. Simons is concerned about the pool of U.S.-born people with strong skills in the mathematical sciences. The majority of people hired by Renaissance are non-Americans. Most are from Europe, China, and India, though most have gone through a U.S. graduate program, and the fraction of U.S.-born people hired is declining. He thinks he probably could have found an adequate number of U.S.-born people if pressed, but it would have required a lot of work. He worries that high school teaching in the United States is simply not good enough, even though our economy is increasingly dependent on mathematical models and data analysis.
Dr. Dietrich described the kinds of mathematical science opportunities she sees and the kind of people IBM-Watson would like to hire. She said that much of IBM’s business has become data-intensive, and numerical literacy is needed throughout the corporation. The mathematical sciences are increasingly central to economics, finance, business, and marketing, including areas such as risk assessment, game theory, and machine learning for marketing. But she noted that it is difficult to find enough people who have the ability to deal with large numerical data sets plus the ability to understand simple concepts such as range and variability. Many mathematical scientists at IBM must also operate as software developers, and they must be flexible enough to move from topic to topic.
She listed some qualifications that are especially valuable in her division, which employs over 300 people worldwide. It needs people with statistical expertise who are also are very computational. They should not rely on existing models and toolkits and should be comfortable working with messy data. The division needs people who are strong in discrete mathematics and able to extract understanding from big data sets. In her experience, most employees do not need to know calculus, and she would like to see more emphasis in the undergraduate curriculum on stochastic processes and large data. Programming ability is essential.
Mr. Bin Zafar presented impressions about the mathematical science skills that are important to the movie industry. (Similar skills are presumably important for the creation of computer games and computer-based training and simulation systems.) He showed the committee an example of
a lengthy computer-generated sequence, from a major film release, that simulates the destruction of Los Angeles by a tsunami. Mathematical modeling was behind realistic images of wave motion and of building collapses, down to details such as the way windows would shatter and dust would rise and swirl. A great deal of effort is expended in creating tools for animation and computer-generated effects, both generic capabilities and particular instantiations.
Mr. Bin Zafar reported that of the several hundred people working in R&D at DreamWorks, about 13 percent have Ph.D.s and 34 percent have master’s degrees. Just over half of the R&D staff have backgrounds in computer science, 19 percent in engineering, and 6 percent in a mathematical science. He mentioned that he does not receive many applications from mathematical scientists, and he speculated that perhaps they are not aware of the mathematical nature of work in the entertainment sector. He observed that creating robust and maintainable software is essential in his business—most software must be reliable enough to last perhaps 5 years— and that very few of their applicants develop that skill through education. Their schooling seems to assume that actual code creation is just an “implementation detail,” but Mr. Bin Zafar observed that the implementation step often exposes very deep details that, if caught earlier, would have led the developer to take a different course.
Dr. Shum spoke first of his experience in helping Microsoft Research to establish a research laboratory in Beijing, beginning in 1999. He reported that there is plenty of raw talent in China, “every bit as good as MIT,” so in setting up the research center in Beijing, a conscious effort was made to include some training opportunities that would enable the laboratory to develop that raw talent. By the time Dr. Shum left Beijing in 2006, Microsoft Research–Asia employed about 200 researchers, a few dozen postdoctoral researchers, and 250 junior workers.
Speaking more generally about Microsoft Research’s needs, Shum mentioned three mathematical science areas that are of current importance to his search technology division of over 1,000 people:
• Auction theory, including mechanism design. The problem of mechanism design (see Chapter 2) is critical, and people with backgrounds in the mathematical theory are necessary. He has a few dozen people working on this topic.
• Graphs, including research that helps us manage enormous graphs such as Internet traffic patterns and research to understand social graphs, entity graphs, and click graphs (which show where users clicked on a hyperlink). His team at Microsoft Research includes many people with theoretical and mathematical backgrounds.
• Machine learning, which is a core foundation for advancing search technologies. His division includes perhaps 50 people working on aspects of machine learning.
More than half the people in Dr. Shum’s division have backgrounds in computer science, and he has also hired engineers who have strong programming skills. Perhaps 5-10 percent of the people in his division received their final degrees in mathematics or statistics. Not too many of these people have Ph.D.s, though he has recently hired some Ph.D. statisticians.
This anecdotal information gathered by the committee is echoed in a more thorough examination by the McKinsey Global Institute.1 That report estimated that U.S. businesses will need an additional 140,000-190,000 employees with “deep analytical talent” and a high level of quantitative skills by 2018. On p. 10, the report points out that “a significant constraint on realizing value from big data will be a shortage of talent, particularly of people with deep expertise in statistics and machine learning,” to carry out analyses in support of corporate decision making. Preparing enough professionals to address this need constitutes both an opportunity and a challenge for the mathematical sciences. The careers examined by that report are those that deal with business analytics, especially as driven by large-scale data. Most of the people who fill those slots will need very strong mathematical science backgrounds, whether or not they actually receive a graduate degree in mathematics or statistics. And academic mathematical scientists must prepare to educate these additional people, regardless of what degrees they actually pursue. The McKinsey report goes on to say (p. 105) that “although we conducted this analysis in the United States, we believe that the shortage of deep analytical talent will be a global phenomenon. . . . Countries with a higher per capita production of deep analytical talent could potentially be attractive sources of these skills for other geographies either through immigration or through companies off-shoring to meet their needs.”
This McKinsey result supplements a well-known observation from Google’s chief economist, Hal Varian, who was quoted in the New York Times as saying “the sexy job in the next 10 years will be statisticians . . . and I’m not kidding.”2 In addition to new careers spawned by the availability of large amounts of data and the information industry, many other fields—e.g., medicine—are also experiencing a growing need for professionals with sophisticated skills in the mathematical sciences.
______________________
1 James Manyika, Michael Chui, Jacques Bughin, Brad Brown, Richard Dobbs, Charles Roxburgh, and Angela Hung Byers, 2011, Big Data: The Next Frontier for Innovation, Competition, and Productivity. McKinsey Global Institute, San Francisco.
2 “For Today’s Graduate, Just One Word: Statistics,” New York Times, August 5, 2009.
Throughout its study, the committee heard many expressions of concern about the supply of home-grown talent in the mathematical sciences. That is, of course, a concern shared across all STEM disciplines. For a long time, the U.S. STEM workforce has been dependent on the flow of talented young people from other countries and on the fact that many of them are interested in building careers in the United States. Our country cannot depend on that situation continuing.
In recent years, there has been a great advance in our ability to quantify. But even top undergraduates too often have little or no experience and intuition about probability or concepts such as the central limit theorem, the law of large numbers, or indeterminacy. In order to prepare students for today’s opportunities in the mathematical sciences, we need to push earlier on these skills. Our high schools focus on getting people prepared for calculus, and that influences even the elementary school curriculum. But we do little to teach statistics, probability, and uncertainty, instead acting as though students can just pick this up in the course of other learning. This is one of the biggest issues facing U.S. mathematical sciences; it is also a big problem in terms of national competitiveness.
The statistics profession might learn from the physics profession’s attitude with regard to training. Physicists who have been trained as theoreticians may often then gain postdoctoral experience in experimental work (often in a different field). But statisticians are more rigid in their attitudes. For example, it is rare that statistics departments embrace a broad range of theoreticians, applied statisticians, and experimentalists. The latter category is important: When statisticians collect their own data, as some do, they are less likely to be relegated to supporting roles in scientific investigations, as can sometimes happen. Students educated in such an environment would have innate understanding of how to work in an interdisciplinary setting. However, statisticians may have difficulty obtaining funding to support data collection, and so the field cannot change in this direction unless funding programs evolve as well.
The mathematical sciences community plays a critical role in educating a broad range of students. Some will exhibit a special talent in mathematics from a young age and may remind successful researchers of their youthful selves. But there are many more whose interest in the mathematical sciences arises later and perhaps through nontraditional pathways, and these latter students constitute a valuable pool of potential majors and graduate students. A third cadre consists of students from other disciplines who need strong mathematical sciences education. All three pools of students need expert guidance and mentoring from successful mathematical scientists, and their needs are not identical. The mathematical sciences must successfully attract and serve all three of these cadres of students.
The challenge of producing an adequate number of people for STEM careers is of interest far beyond the mathematical sciences, of course. For example, a recent report3 from the President’s Council of Advisors on Science and Technology (PCAST) “provides a strategy for improving STEM education during the first two years of college that [it believes] is responsive to both the challenges and the opportunities that this crucial stage in the STEM education pathway presents,” according to the cover letter to the President that accompanies the report.4 That cover letter goes on to recount the reason why STEM fields receive this attention:
Economic forecasts point to a need for producing, over the next decade, approximately 1 million more college graduates in STEM fields than expected under current assumptions. Fewer than 40% of students who enter college intending to major in a STEM field complete a STEM degree. Merely increasing the retention of STEM majors from 40% to 50% would generate three-quarters of the targeted 1 million additional STEM degrees over the next decade.5
That PCAST report goes on to recommend, among other steps, a “multi-campus 5-year initiative aimed at developing new approaches to remove or reduce the mathematics bottleneck that is currently keeping many students from pursuing STEM majors.” This proposed initiative might involve approximately 200 “experiments” exploring a variety of approaches, including the following:
(1) Summer and other bridge programs for high school students entering college;
(2) remedial courses for students in college, including approaches that rely on computer technology;
(3) college mathematics teaching and curricula developed and taught by faculty from mathematics-intensive disciplines other than mathematics, including physics, engineering, and computer science; and
(4) a new pipeline for producing K-12 mathematics teachers from undergraduate and graduate programs in mathematics-intensive fields other than mathematics.
It is critical that the mathematical sciences community actively engage with STEM discussions going on outside the mathematical sciences community
______________________
3 PCAST, 2012, Engage to Excel: Producing One Million Additional College Graduates with Degrees in Science, Technology, Engineering, and Mathematics. The White House, Washington, D.C.
4 Available at http://www.whitehouse.gov/sites/default/files/microsites/ostp/pcast-engage-to-excel-final_2-25-12.pdf.
5 bid.
and not be marginalized in efforts to improve STEM education, especially since those plans would greatly affect the responsibilities of mathematics and statistics faculty members. This committee knows of no evidence that teaching lower-division college mathematics and statistics or providing a mathematical background for K-12 mathematics teachers can be done better by faculty from other subjects but it is clear that the mathematics-intensive disciplines are full of creative people who constitute a valuable resource for innovative teaching ideas. The need to create a truly compelling menu of creatively taught lower-division courses in the mathematical sciences tailored to the needs of twenty-first century students is pressing, and partnerships with mathematics-intensive disciplines in designing such courses are eminently worth pursuing.
The traditional lecture-homework-exam format that often prevails in lower-division mathematics courses would benefit from a reexamination. One aspect of the changes PCAST would like to see is explained in its report:
Better teaching methods are needed by university faculty to make courses more inspiring, provide more help to students facing mathematical challenges, and to create an atmosphere of a community of STEM learners. Traditional teaching methods have trained many STEM professionals, including most of the current STEM workforce. But a large and growing body of research indicates that STEM education can be substantially improved through a diversification of teaching methods. These data show that evidence-based teaching methods are more effective in reaching all students—especially the ‘underrepresented majority’—the women and members of minority groups who now constitute approximately 70% of college students while being underrepresented among students who receive undergraduate STEM degrees (approximately 45%).
In an appendix to the report, some of the methods the PCAST working group would like to see explored are (1) active learning techniques; (2) motivating learning by explaining how mathematics is used and making courses more relevant for students’ fields of specialization; (3) creating a community of high expectations among students; and (4) expanding opportunities for undergraduate research.
The PCAST report should be viewed as a wake-up call for the mathematical sciences community. While there have been numerous promising experiments within the community for addressing the issues it raises—especially noteworthy has been the tremendous expansion in opportunities for undergraduate research in the mathematical sciences—at this point a community-wide effort is called for. The professional societies should work cooperatively to spark this. Change is unquestionably coming to lower-division undergraduate mathematics, and it is incumbent upon the
mathematical sciences community to ensure that it is at the center of these changes and not at the periphery.
THE TYPICAL EDUCATIONAL PATH IN THE MATHEMATICAL SCIENCES NEEDS ADJUSTMENTS
Chapter 3 showed exciting emerging opportunities for anyone with expertise in the mathematical sciences. The precise thinking and conceptual abilities that are hallmarks of mathematical science training continue to be an excellent preparation for many career paths. However, it is apparent that an ability to work with data and computers is a common need. An understanding of statistics, probability, randomness, algorithms, and discrete mathematics are probably of greater importance than calculus for many students who will follow such careers, and indeed students with this training will be much more employable in those areas. The educational offerings of typical departments in the mathematical sciences have not kept pace with the changes in how the mathematical sciences are used. A redesigned offering of courses and majors is needed. Although there are promising experiments, a community-wide effort is needed in the mathematical sciences to make its undergraduate courses more compelling to students and better aligned with needs of user departments.
The 2012 report of the Society for Industrial and Applied Mathematics (SIAM) on mathematical sciences in industry6 adds support for this, with regard to those students who would like to work in industry. The SIAM report makes the following statement about useful background for such people:
Useful mathematical skills include a broad training in the core of mathematics, statistics, mathematical modeling, and numerical simulation, as well as depth in an appropriate specialty. Computational skills include, at a minimum, experience in programming in one or more languages. Specific requirements, such as C++, a fourth-generation language such as MATLAB, or a scripting language such as Python, vary a great deal from company to company and industry to industry. Familiarity with high-performance computing (e.g., parallel computing, large-scale data mining, and visualization) is becoming more and more of an asset, and in some jobs is a requirement. . . . In general, the student’s level of knowledge [of an application domain] has to be sufficient to understand the language of that domain and bridge the gap between theory and practical implementation.7
______________________
6 SIAM, 2012, Mathematics in Industry. Society for Industrial and Applied Mathematics, Philadelphia, Pa. Available at http://www.siam.org/reports/mii/2012/index.php.
7 Ibid., p. 2 of Summary.
TABLE 5-1 Enrollment (in 1000s) in Undergraduate Courses Taught in the Mathematics or Statistics Departments of Four-Year Colleges and Universities, and in Mathematics Programs of Two-Year Colleges, for Fall 1990, 1995, 2000, 2005, and 2010
| Discipline | Fall 1990 | Fall 1995 | Fall 2000 | Fall 2005 | Fall 2010 |
| Mathematics | 1,621 | 1,471 | 1,614 | 1,607 | 1,971 |
| Statistics | 169 | 208 | 245 | 260 | 371 |
SOURCES: CBMS, 2007, 2012.
It may be that students are already “voting with their feet.” According to data from the Conference Board of the Mathematical Sciences (CBMS), the number of enrollments in mathematics courses in 1990-2010 remained generally flat, while the number of enrollments in statistics courses increased by 120 percent.8,9 The raw numbers are shown in Table 5-1.
The four industry leaders who spoke with the committee, and whose observations were recounted earlier in this chapter, raised the need for more people who focus on real problems—rather than on models that omit too much of the messiness of reality—and who are able to work with computers, statistics, and data so as to test and validate their modeling. Theory alone is not the best preparation for, say, careers at IBM, Technologies, or DreamWorks Animation. But an optimistic lesson to draw from these discussions is that industry has an increasing need for students with mathematical science skills, whether or not the skills are explicitly labeled that way.
The role of the mathematical sciences in science, engineering, medicine, finance, social science, and society at large has changed enormously, at a pace that challenges the university mathematical sciences curriculum. This change necessitates new courses, new majors, new programs, and new educational partnerships with those in other disciplines, both inside and outside universities. New educational pathways for training in the mathematical sciences need to be created—for students in mathematical sciences departments, for those pursuing degrees in science, medicine, engineering, business, and social science, and for those already in the workforce needing additional quantitative skills. New credentials may be needed, such as professional master’s degrees for those about to enter the workforce or
______________________
8 CBMS, 2007, Statistical Abstract of Undergraduate Programs in the Mathematical Sciences in the United States; Fall 2005 CBMS Survey, Table S.1. Available at http://www.ams.org/profession/data/cbms-survey/full-report.pdf.
9 CBMS, 2012, Draft of the Statistical Abstract of Undergraduate Programs in the Mathematical Sciences in the United States; Fall 2010 CBMS Survey. Table S.1. Available at http://www.ams.org/profession/data/cbms-survey/cbms2010-work.
already in it. The trend toward periodic acquisition of new job skills by those already in the workforce provides an opportunity for the mathematical sciences to serve new needs.
Most mathematics departments still tend to use calculus as the gateway to higher-level coursework, and that is not appropriate for many students. Although there is a very long history of discussions about this issue, the need for a serious reexamination is real, driven by changes in how the mathematical sciences are being used. For example, someone who wants to study bioinformatics ought to have a pathway whereby he or she can learn probability and statistics; learn enough calculus to find maxima and minima and understand ordinary differential equations, get a solid dose of discrete mathematics; learn linear algebra; and get an introduction to algorithms. Space could be made in their curriculum by deemphasizing such topics as line integrals and Stokes’s theorem, epsilons and deltas, abstract vector spaces, and so on. Different pathways are needed for students who may go on to work in bioinformatics, ecology, medicine, computing, and so on. It is not enough to rearrange existing courses to create alternative curricula. As one step in this direction, colleges and universities might encourage AP statistics courses as much as they do AP calculus. Such a move would also help those in secondary education who believe that teaching of probability, statistics, and uncertainty should be more common.
The dramatic increase over the past 20 years in the number of NSF Research Experience for Undergraduate (REU) programs has, in the experience of members of the study committee, been a noticeable force for attracting talented undergraduates to major in a mathematical science while also providing a stronger foundation for graduate study.10 Another striking trend over the past decade or two is the increase in double majors. This increase means that undergraduates who might otherwise pursue a nonmathematical sciences major gain exposure to a broader array of mathematics and statistics courses and, in essence, keep more career options open. Double or flexible majors have also enabled some departments in mathematics and statistics to increase the number of undergraduates in their programs and keep them strongly involved at least through their bachelor’s degrees.
Many graduate students will end up not with traditional academic jobs but with jobs where they are expected to deal with problems much less well formulated than those in the academic setting. They must bring their mathematical
______________________
10 PCAST, 2012, Engage to Excel: Producing One Million Additional College Graduates with Degrees in Science, Technology, Engineering, and Mathematics. The White House, Washington, D.C. Appendix G of this report recounts some anecdotal evidence of the value of undergraduate research experiences for building student commitment to STEM fields and retaining it.
sciences talent and sophistication to bear on ill-posed problems so as to make a contribution to the solution of these problems. This requires different skills from the ones that they trained for during their graduate student days, and it suggests that the training of graduate students in the mathematical sciences needs to be rethought given the changing landscape in which students may now work. At the least, mathematics and statistics departments should take steps to ensure that their graduate students have a broad and up-to-date understanding of the expansive reach of the mathematical sciences.
Recommendation 5-1: Mathematics and statistics departments, in concert with their university administrations, should engage in a deep rethinking of the different types of students they are attracting and wish to attract and must identify the top priorities for educating these students. This should be done for bachelor’s, master’s, and Ph.D.-level curricula. In some cases, this rethinking should be carried out in consultation with faculty from other relevant disciplines.
Recommendation 5-2: In order to motivate students and show the full value of the material, it is essential that educators explain to their K-12 and undergraduate students how the mathematical science topics they are teaching are used and the careers that make use of them. Modest steps in this direction could lead to greater success in attracting and retaining students in mathematical sciences courses. Graduate students should be taught about the uses of the mathematical sciences so that they can pass this information along to students when they become faculty members. Mathematical science professional societies and funding agencies should play a role in developing programs to give faculty members the tools to teach in this way.
The mathematical science community collectively does not do a good job in its interface with the general public or even with the broader scientific community, and improving this would contribute to the goal of enlarging the STEM pipeline. Internet tools such as blogs and video lectures offer new pathways for this outreach, which may be appealing to both practicing and retired mathematical scientists. There is a special need to improve the general level of understanding about uncertainty, which relies on an understanding of probability and statistics.
Recommendation 5-3: More professional mathematical scientists should become involved in explaining the nature of the mathematical sciences enterprise and its extraordinary impact on society. Academic departments should find ways to reward such work. Professional societies
should expand existing efforts and work with funding entities to create an organizational structure whose goal is to publicize advances in the mathematical sciences.
Finally, the committee notes that the boom-and-bust cycles of the academic job market, especially for new Ph.D.s, result in a substantial loss of talent because they both discourage entry to research in the mathematical sciences and increase the likelihood of exit from it. The impact on core mathematical sciences, where the academic job market is central, is especially severe. Important workforce programs, such as NSF’s former VIGRE program, are often dwarfed by these macroeconomic trends. Stabilizing these swings by expanding the availability of postdoctoral fellowships during downturns in the job market should be an important component of the nation’s overall strategy to strengthen the mathematical sciences workforce and ensure continuity over long time horizons. NSF/DMS did just that during the recession of 2008-2009, and it would be ideal if a mechanism were in place to respond similarly during the next downturn in hiring.
It is because of the importance and centrality of the mathematical sciences, as detailed elsewhere in this report, that these educational issues are as important as they are. As a community, mathematical scientists have been handed an extraordinary opportunity to play a central role in educating researchers and professionals in many of the most exciting career and research areas of the twenty-first century. Taking advantage of this opportunity requires a certain amount of cultural flexibility and the development of educational partnerships with those in other disciplines. The benefits to the country and to the mathematical sciences profession would be enormous.
Appendix C provides additional basic data about employment and Ph.D. production in the mathematical sciences.
ATTRACTING MORE WOMEN AND UNDERREPRESENTED MINORITIES TO THE MATHEMATICAL SCIENCES
Concerns About the Current Demographics
The underrepresentation of women and ethnic minorities in mathematics has been a persistent problem for the field. Fifty years ago, the mathematical sciences community consisted almost exclusively of white males, and that segment of the population remains the dominant one from which the community attracts new members. This implies that talent in other sectors of the population is being underutilized, and as white males become a smaller fraction of the population, it is even more essential that the mathematical sciences attract and retain students from across the totality of the population. While there has been significant progress in the last
10-20 years, the fraction of women and minorities in the mathematical sciences drops with each step along the pipeline and up the career ladder. This very leaky pipeline, which was identified as a problem in the 1990 “David II” report11 and earlier, is now the key problem in achieving further diversity and undermines the ability of the mathematical sciences to make full use of its potential talent pool. This section briefly examines the current state of minority and female representation at various levels (K-12, undergraduate, master’s, Ph.D., and the professoriate) along with recent trends, and it profiles some efforts that are under way to encourage greater representation.
In elementary school, girls perform much like boys on mathematics standardized testing. Standardized testing scores indicate that young girls (age 9) are performing at the same level—if not a higher one—than boys of the same age. However, a score gap between girls and boys appears in middle school (age 13) and grows in high school (age 17). A contrasting and rather revealing study of this issue appeared in a 2008 article that studied the effects of culture on the participation of girls at the International Mathematical Olympiad (IMO) teams among children from different countries.12 The authors found that, based on IMO participation, some East European and Asian countries produce girls with profound ability in mathematical problem solving; most other countries, including the United States, do not. Further, they found that girls on the U.S. team often are recent immigrants from countries that typically produce such talented girls. While they do not identify the environmental factors that make these countries more supportive of girls, the study shows the strong effect of the environment on bringing out mathematical talent in girls, and it suggests that the United States can do a lot more to avoid wasting this talent, as discussed below.
In the United States, approximately 40 percent of the bachelor’s degrees awarded in the mathematical sciences are awarded to women. Because more women than men now attend college, there is definitely room for improvement. Although this rate of female participation is enviable compared to rates found in many other technical fields, there is still a lost opportunity, because more women than men drop out of the mathematical sciences pipeline after high school. Then in college, while mathematics initially attracts as many women as men, women seem to move away from the field at a higher rate before graduation. In particular, graduate training in mathematics clearly does not attract as many women as men. Of the total doctorates granted in 2009-2010 (1,632), 31 percent of recipients were female. Figure 5-1 shows the trends in the percentage of females receiving bachelor’s, master’s, and Ph.D. degrees in mathematics and statistics from 1969 to 2009.13
______________________
11 NRC, 1990, Renewing U.S. Mathematics: A Plan for the 1990s. National Academy Press, Washington, D.C.
12 Titu Andreescu, Joseph A. Gallian, Jonathan M. Kane, and Janet E. Mertz, 2008, Cross-cultural analysis of students with exceptional talent in mathematical problem solving. Notices of the AMS 55(10):1248-1260.
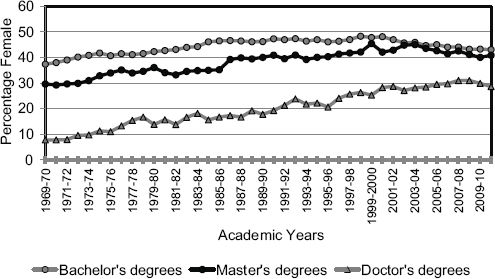
FIGURE 5-1 Degrees in mathematics and statistics conferred by degree-granting institutions, by level of degree and sex of student, 1969-1970 through 2010-2011. SOURCE: National Center for Education Statistics, 2012, Digest for Education Statistics. Table 327. Available at http://nces.ed.gov/programs/digest/d12/tables/dt12_327.asp.
It is interesting to note that, while the fraction of mathematics Ph.D.s awarded to women is about 30 percent, in recent years women have been awarded more than half the statistics Ph.D.s in the United States. The fact that statistics attracts a higher percentage of women than mathematics is worth understanding better.
Within the professoriate, the data get more complicated. As shown in Table 5-2, the percentage of women among full-time faculty at 4-year institutions rose to 26 percent in mathematics departments and 22 percent in statistics departments in 2005, when the most recent CBMS data were collected. However, this “full-time” status can be used to describe different positions, and women tended to be disproportionately represented in positions that were not tenured or tenure-track in 2005.14
______________________
13 From Digest of Education Statistics, 2010, Table 323. Available at http://nces.ed.gov/programs/digest/d10/tables/dt10_323.asp.
14 More recent data are in being assembled by CBMS but have not yet been published.
TABLE 5-2 Gender of Full-Time Faculty Members in Departments of Mathematics and Statistics at 4-Year Colleges and Universities and in Departments of Statistics at Universities
| Department | Number of | 1975 | 1980 | 1985 | 1990 | 1995 | 2000 | 2005 | 2010 |
| Mathematics | Full-time faculty | 16,863 | 16,022 | 17,849 | 19,411 | 18,248 | 19,779 | 21,885 | 22,294 |
| Women | 1,686 (10%) |
2,243 (14%) |
2,677 (15%) |
3,843 (20%) |
3,880 (21%) |
4,346 (22%) |
5,641 (26%) |
6,417 (29%) |
|
| Statistics | Full-time faculty | NA | NA | 740 | 735 | 988 | 1,022 | 946 | 1,265 |
| Women | NA | NA | 74 (10%) |
105 (14%) |
107 (11%) |
179 (18%) |
211 (22%) |
327 (26%) |
|
NOTE: 1975, 1980, 1985, 1990, and 1995 data from CBMS, 1997, Statistical Abstract of Undergraduate Programs in the Mathematical Sciences in the United States, Fall 1995 CBMS Survey, Table SF8, available at http://www.ams.org/profession/data/cbms-survey/cbms1995; 2000 and 2005 data from CBMS, 2007, Table F.1; 2010 data from CBMS, 2012, Table F.1.
Another consideration is what type of 4-year institution employed these women. Data in Appendix C show that women are much less represented in Ph.D.-granting universities than in other types of 4-year institutions. However, there are some indications that in the last 5 years or so all kinds of universities made good progress in increasing the percentage of women who were hired.15 Still, the mathematical sciences are not retaining as many women in the pipeline as would be desired, and, in particular, not enough women are being hired into academic careers.16
Several racial and ethnic groups (most notably black, Hispanic, and Native American/Alaska Native) are even more seriously underrepresented in the mathematical sciences. Standardized mathematics tests in K-12 show a performance gap between whites and both blacks and Hispanics, with a notable score gap existing between whites and blacks through elementary, middle, and high school. Data show that there is also a notable and persistent score gap between whites and Hispanics. However, the score gap has been decreasing at the elementary school level for Hispanics over the past decade. It is important to note that these populations do have an interest in STEM subjects. A recent report from the National Academies points out as follows:
Recent data from the Higher Education Research Institute (HERI) at UCLA show that underrepresented minorities aspire to major in STEM in college at the same rates as their white and Asian American peers, and have done so since the late 1980s.17
At the college and university level, only 5.7 percent and 6.4 percent of bachelor’s degrees in mathematics and statistics are awarded to blacks and Hispanics, respectively. This underrepresentation continues in graduate school, where blacks make up only 2.9 percent of master’s degree recipients and 2.0 percent of Ph.D. recipients. Hispanics make up 3.1 percent of master’s degree recipients and 2.5 percent of the Ph.D. recipients. American Indians/Alaska natives make up, respectively, 0.5, 0.2, and 0.2 percent of bachelor’s, master’s, and Ph.D. recipients.18
______________________
15 A recent report from MIT, Report on the Status of Women Faculty in the Schools of Science and Engineering at MIT, 2011, recounts that university’s progress on this issue over the last 10 years and the important remaining issues it faces. Available at http://web.mit.edu/newsoffice/images/documents/women-report-2011.pdf.
16 A recent article—Corinne A. Moss-Racusin, John F. Dovidio, Victoria L. Brescoll, Mark J. Graham, and Jo Handelsman, 2012, Science faculty’s subtle gender biases favor male students, Proceedings of the National Academy of Sciences 109 (September 17)—suggests that some subtle and pervasive cultural biases may be at play and need to be countered.
17 Institute of Medicine, National Academy of Sciences, and National Academy of Engineering, 2011, Expanding Underrepresented Minority Participation: America’s Science and Technology Talent at the Crossroads. The National Academies Press, Washington, D.C., p. 4, based on UCLA Higher Education Research Institute, 2010, Degrees of Success: Bachelor’s Degree Completion Rates Among Initial STEM Majors. HERI Report Brief, January 2010.
TABLE 5-3 Proportion of Full-Time Faculty Belonging to Various Ethnic Groups, by Gender and Type of Department, in Fall 2005
| Department | Asian | Black, Not Hispanic | Mexican American/Puerto Rican/Other Hispanic | White, Not Hispanic | Other/Unknowna |
| Mathematics | |||||
| Ph.D.-awarding | |||||
| Men | 13 | 1 | 2 | 59 | 3 |
| Women | 4 | 0 | 1 | 16 | 1 |
| Master’s-awarding | |||||
| Men | 12 | 4 | 2 | 47 | 2 |
| Women | 5 | 2 | 1 | 26 | 1 |
| Bachelor’s-awarding | |||||
| Men | 4 | 2 | 2 | 57 | 2 |
| Women | 2 | 1 | 1 | 28 | 1 |
| Statistics | |||||
| Men | 20 | 1 | 1 | 49 | 3 |
| Women | 8 | 0 | 1 | 15 | 2 |
NOTE: Zero means less than 0.5 percent. Except for round-off, the percentages within each departmental type sum to 100.0. SOURCE: CBMS, 2012, Table F.5.
aThe column “Other/Unknown” includes the federal categories Native American/Alaskan Native and Native Hawaiian/Other Pacific Islander.
Table 5-3 gives a high-level view of the participation of traditionally underrepresented minorities among full-time faculty in all mathematics departments and in Ph.D.-awarding statistics departments.
According to AMS data,19 the number of U.S.-citizen Ph.D.s from all under-represented minority groups was 12 in 1992, 27 in 2000, and 45 in 2011. (The total number of U.S. citizens receiving Ph.D.s from or statistics departments in 2011 was 802.) It is perhaps gratifying to see an approximate doubling each decade, but the total numbers are still strikingly small. Moreover, only 11 of the Ph.D.s in 2011 were awarded from Group I departments. For comparison, in 2011 Group I departments awarded a total of 272 Ph.D.s to U.S. citizens and 560 Ph.D.s overall.
In order for the nation to have a workforce that can exploit the kinds of opportunities described in Chapters 3 and 4, the mathematical sciences
______________________
18 See Figures C-4, C-5, and C-6 in Appendix C.
19 Available at http://www.ams.org/profession/data/annual-survey/2011Survey-SREC.pdf.
enterprise must improve its ability to attract and retain a greater fraction of talented young people. As indicated in the introduction to this chapter, this is a high-priority national issue.
What Can Be Done?
There have been some notable successes in attracting and retaining more under-represented minorities in the mathematical sciences. For example, William Vélez of the University of Arizona at Tucson has successfully increased minority enrollment. He offered the following advice for recruiting all types of students:
• Provide timely information to students. Help them to understand the system and future opportunities. Even good students need attention and advice.
• Examine ways to ease the transition from high school to college or university.
• Encourage students who are interested in science and engineering to have a second major in mathematics.
• Pay more individual attention to talented students by having faculty reach out to them directly.
• Communicate the necessity of studying mathematics.20
While these suggestions are not unique, the practices are often not implemented. They can be broadly applied to all students, regardless of race or gender, to increase the population of undergraduate majors in the mathematical sciences.
Despite the small numbers of underrepresented minorities entering the mathematical sciences, there are a number of programs across the country that are quite successful at achieving greater participation. They have established practices that work and which could be replicated elsewhere. A recent report from the National Academies21 presents a thorough examination of approaches for tapping this talent.
The NSF-supported mathematical science institutes have also been active in efforts to reach out to underrepresented groups. For example, the Institute for Mathematics and its Applications (IMA) and the Institute for Pure and Applied Mathematics (IPAM) offer workshops in professional development
______________________
20 William Yslas Vélez, 2006, “Increasing the number of mathematics majors,” FOCUS Newsletter, Mathematical Association of America, March.
21 Institute of Medicine, National Academy of Sciences, and National Academy of Engineering, 2011, Expanding Underrepresented Minority Participation: America’s Science and Technology Talent at the Crossroads. The National Academies Press, Washington, D.C.
aimed at mathematical scientists from under-represented groups. At the K-12 level, IPAM, IMA, and other institutes have offered week-long programs for middle and high school girls. In rotation, the institutes offer the Blackwell-Tapia conferences, which aim to increase the exposure of underrepresented groups to mathematics. Some efforts of the Mathematical Sciences Research Institute (MSRI) aim at increasing the participation of women and minorities:
• Connections for Women workshops, 2-day workshops that aim to showcase women’s talent in the field and that sometimes offer an intensive minicourse on fundamental ideas and techniques;
• MSRI-UP, a program for undergraduates aimed at increasing the participation of underrepresented groups in mathematics graduate programs; and
• The Network Tree, a project to compile names and contact information for mathematicians from underrepresented groups.
Colette Patt from the Science Diversity Office of the University of California, Berkeley, and Deborah Nolan and Bin Yu from the Statistics Department at that university shared with the committee the following lists of issues (adapted by the committee) they compiled that academic departments should consider when determining how to improve their recruitment and retention of women and other underrepresented groups.
Issues That Affect Recruitment and Retention at the Undergraduate Level
• Affordability of undergraduate education and awareness of assistance programs, such as Research Experiences for Undergraduates and support for travel to conferences;
• Awareness of and motivation to enter the mathematical sciences, such as information about career options made possible by mathematical science coursework or majors and comparison of those options to some more common career paths;
• Adequacy of mentoring, including encouragement, coaching, and strategic advising;
• Access to, and encouragement to participate in, a variety of research opportunities;
• The possibility of boosting confidence by departmental approaches to structuring the curriculum and course pedagogies, such as confidence, study habits, sense of community, and so on;
• Academic requirements, structure of courses and majors, academic support, choice of gateway courses, teaching effectiveness, and classroom practices;
• Campus climate and department culture.
Issues That Affect Recruitment and Retention at the Graduate Level
• Availability of role models;
• Need for a sense of belonging and community to avoid possible isolation;
• Possible harassment, peer interactions, and climate issues;
• Availability and skill of mentoring;
• Opportunities for professional development and socialization;
• Psychological factors that possibly can be boosted by departments’ approaches to structuring the graduate curriculum, courses, and tests to influence factors such as confidence, self-concept, science identity, and the threats of being stereotyped.
• Monitoring and possible intervention to assist at the critical transition from the graduate to postdoctoral positions;
• Assistance in goal-setting and evaluation.
Issues That Affect Recruitment and Retention of Underrepresented Faculty
• Understanding and countering the drop-off of women and minorities at the critical transition from postdoctoral years to faculty careers;
• Understanding and countering the difficulties of achieving a life-work balance, which tends to affect women more than men;
• Identifying perceptions that are gender differentiated and can affect seemingly objective measures—for example, gender bias in letters of recommendation, teaching evaluations, perceptions of leaders;
• Opportunities for leadership;
• Differential recognition, awards, and the accumulation of cultural capital in the field.
Many of these issues have been the subject of published studies that document their impact on the recruitment and retention of women and other underrepresented groups, and most should be familiar to anyone who has spent time in academic departments.
Statistics departments have been quite successful in recent years in attracting and retaining women, and it would be very helpful to understand better how the broader mathematical sciences community can learn from this success. A similar observation has been made with regard to attracting women to application-oriented computer science (CS) programs.22
Overall, there has been progress in attracting women and minorities to the mathematical sciences. Unfortunately, the accumulation of small disadvantages women and minorities face throughout their career can add up to a significant disadvantage and can cause the leaking of the pipeline that
______________________
22 See Christine Alvarado and Zachary Dodds, 2010, Women in CS: An evaluation of three promising practices. Proceedings of SIGCSE 2010 March 10-13. Association for Computing Machinery, Milwaukee, Wisc.
is documented above. Beyond this, one or more egregious incidents can tip the balance for an individual. This is an important issue for the mathematical sciences to address.
Recommendation 5-4: Every academic department in the mathematical sciences should explicitly incorporate recruitment and retention of women and underrepresented groups into the responsibilities of the faculty members in charge of the undergraduate program, graduate program, and faculty hiring and promotion. Resources need to be provided to enable departments to monitor and adapt successful recruiting and mentoring programs that have been pioneered at many schools and to find and correct any disincentives that may exist in the department.
Appendix E lists some of the organizations and programs that are committed to improving participation by women and minorities in the mathematical sciences at all levels of education.
THE CRITICAL ROLE OF K-12 MATHEMATICS AND STATISTICS EDUCATION
The extent to which size of the pipeline of students preparing for mathematical science-based careers can be enlarged is fundamentally limited by the quality of K-12 mathematics and statistics education. The nation’s well-being is dependent on a strong flow of talented students into careers in STEM fields, but college students cannot even contemplate those careers unless they have strong K-12 preparation in the mathematical sciences. Absent such preparation, most are unlikely to be interested. Those statements are even more apt with respect to young people who could become mathematical scientists per se. The K-12 pipeline is an Achilles heel for U.S. innovation. Fortunately, a lot of innovation is taking place in K-12 mathematics and statistics education, and the mathematical sciences community has a role to play in strengthening and implementing the best of these efforts. This section gives a brief overview of the issues and pointers to the relevant literature. It is beyond the mandate of the current study to recommend actions in response to this general national challenge.
There are a large number of K-12 schools, both public and private, that perform at a high level year after year across the United States. Annual rankings of the best U.S. high schools document the top few on the basis of student performance parameters and other criteria.23 Most states employ
______________________
23 For example, US News and World Report, America’s Best High Schools, November 29, 2007; Newsweek, Best High Schools in the U.S., June 19, 2011; Bloomberg Business Week, America’s Best High Schools 2009, January 15, 2009.
information systems that keep detailed public school records for students, teachers, and school administrators on the basis of parameters established for mandatory statewide use. Public schools are subject to state-enforced sanctions when a school fails to meet the mandated performance criteria. But overall, particularly in the sciences and mathematics, U.S. K-12 students continue to perform substantially below average in international comparisons.
Education Secretary Arne Duncan’s report on December 7, 2010, presented on the occasion of the release of the 2009 results of the Program for International Student Assessment (PISA) of the Organisation for Economic Co-operation and Development (OECD), did not contain encouraging news about the performance of U.S. 15-year-olds in mathematics.24 U.S. students ranked 25th among the 34 participating OECD nations, the same level of performance as 6 years earlier in 2003. The results were not encouraging in reading literacy either, with U.S. students placing 14th, effectively no change since 2000. The only improvement noted was a 17th place ranking in science, marginally better than the 2006 ranking. Secretary Duncan added that the OECD analysis suggests the 15-year-olds in South Korea and Finland are, on average, 1 or 2 years ahead of their American peers in math and science.
The picture is not improving. In September 2011, the College Board reported that the SAT scores for the U.S. high school graduating classes of 2011 fell in all three subject areas tested: reading, writing, and mathematics. The writing scores were the lowest ever recorded.25 A report from Harvard’s Program on Education Policy and Governance in August of 2011 revealed that U.S. high school students in the Class of 2011 ranked 32nd in mathematics among OECD nations that participated in PISA for students at age 15. The report noted that 22 countries significantly outperform the United States in the share of students who reach the “proficient” level in math (a considerably lower standard of performance than “advanced”).26
In September 2007 McKinsey & Co. produced what it called a first-of-its-kind approach that links quantitative results with qualitative insights on what high-performing and rapidly improving school systems have in common.27 McKinsey studied 25 of the world’s school systems, including 10 of the top performers. They examined what high-performing school systems have in common and what tools they use to improve student outcomes. They concluded that, overall, the following matter most:
______________________
24 Available at http://www.ED.gov, December 7, 2010.
25 Wall Street Journal, “SAT Reading, Writing Scores Hit New Low,” September 15, 2011.
26 Paul E. Peterson, Ludgar Woessmann, Eric A. Hanushek, and Carlos X. Lastra-Anadon, 2011, Globally Challenged: Are U.S. Students Ready to Compete. Harvard Kennedy School of Government, August.
27 McKinsey & Co., 2007, How the World’s Best Performing School Systems Came Out on Top.
• Getting the right people to become teachers (the quality of an education system cannot exceed the quality of its teachers);
• Developing them into effective instructors (the only way to improve outcomes is to improve instruction); and
• Ensuring that the system is able to provide the best possible instruction for every child (high performance requires every child to succeed).
The McKinsey report concludes: “The available evidence suggests that the main driver of the variation in student learning at school is the quality of the teachers.” Three illustrations are provided to support this conclusion:
• Ten years ago, seminal research based on data from the Tennessee Comprehensive Assessment Program tests showed that if two average 8-year-old students were given different teachers—one of them a high performer, the other a low performer—the students’ performance diverged by more than 50 percentile points within 3 years.28
• A study from Dallas showed that the performance gap between students assigned three effective teachers in a row and those assigned three ineffective teachers in a row was 49 percentile points.29
• In Boston, students placed with top-performing math teachers made substantial gains, while students placed with the worst teachers regressed—their math actually got worse.
The McKinsey report further concluded as follows:
Studies that take into account all of the available evidence on teacher effectiveness suggest that students placed with high-performing teachers will progress three times as fast as those placed with low-performing teachers.
The second McKinsey report (2010) addresses the teacher talent gap by examining the details of teacher preparation and performance in three top-performing countries: Singapore, Finland, and South Korea.30 These
______________________
28 W. Sanders and J. Rivers, 1996, Cumulative and Residual Effects of Teachers on Future Student Academic Achievement. University of Tennessee, Value-Added Research and Assessment Center, Knoxville, Tenn.
29 Heather R. Jordan, Robert L. Mendro, and Dash Weerasinghe, 1997, “Teacher Effects on Longitudinal Student Achievement: A Report on Research in Progress,” Presented at the CREATE Annual Meeting Indianapolis, Ind. Available at http://dallasisd.schoolwires.net/cms/lib/TX01001475/Centricity/Shared/evalacct/research/articles/Jordan-Teacher-Effects-on-Longitudinal-Student-Achievement-1997.pdf.
30 Byron Auguste, Paul Kihn, and Matt Miller, 2010, “Closing the talent gap: Attracting and retaining top-third graduates to careers in teaching.” McKinsey & Company, September.
three countries recruit 100 percent of their teacher corps from the top third of their college graduate academic cohort, then screen for other important qualities as well. By contrast, in the United States only 23 percent of new K-12 teachers come from the top third, and in high poverty schools, the fraction is only 14 percent. The report concludes that Finland, Singapore, and South Korea “use a rigorous selection process and teacher training more akin to medical school and residency than a typical American school of education.” It goes on to examine what an American version of a “top third” strategy might entail and concludes that “if the U.S. is to close its achievement gap with the world’s best education systems—and ease its own socio-economic disparities—a top-third strategy for the teaching profession must be a part of the debate.” Undoubtedly, a part of closing this gap must address the situation that most teachers of mathematics and science in U.S. public middle and high schools do not have degrees or other certification in mathematics or science.31
ENRICHMENT FOR PRECOLLEGE STUDENTS WITH CLEAR TALENT IN MATHEMATICS AND STATISTICS
While, as noted above, the current study does not have a mandate to examine the broad question of K-12 mathematics education, the mathematical sciences community does have a clear interest in those precollege students with special talent for and interest in mathematics and statistics. Such students may very well go on to become future leaders of the research community, and in many cases they are ready to learn from active researchers while still in high school, or even earlier.
A 2010 paper32 reported on two studies into the relationship between precollegiate advanced/enriched educational experiences and adult accomplishments in STEM fields. In the first of these studies, 1,467 13-year-olds were identified as mathematically talented on the basis of scores of at least 500 on the mathematics section of the Scholastic Assessment Test, which puts them in the top 0.5 percentile. Their developmental trajectories were studied over 25 years, with particular attention being paid to accomplishments in STEM fields, such as scholarly publications, Ph.D. attainment, tenure, patents, and types of occupation(s) over the period. The second study profiled, retrospectively, the adolescent advanced/enriched educational
______________________
31 NRC, 2010, Rising Above the Gathering Storm, Revisited: Rapidly Approaching Category 5. The National Academies Press, Washington, D.C.
32 Jonathan Wai, David Lubenski, Camilla Benbow, and James Steiger, 2010, Accomplishment in science, technology, engineering, and mathematics (STEM) and its relation to STEM educational dose: A 25-year longitudinal study. Journal of Educational Psychology 102 (4).
experiences of 714 top STEM graduate students and related their experiences to their STEM accomplishments up to age 35.
In both longitudinal studies, those with notable STEM accomplishments had been involved in a richer and more robust collection of advanced precollegiate educational opportunities in STEM (“STEM doses”) than the members of their cohorts with lower levels of STEM-related professional achievement. This finding holds for students of both sexes. The types of “STEM doses” noted in these studies include advanced placement (AP) and early college math and science courses, science or math project competitions, independent research projects, and writing articles within the disciplines. Of these mathematically inclined students, those who participated in more than the median number of science and math courses and activities during their K-12 school years were about twice as likely, by age 33, to have earned a doctorate, become tenured, or published in a STEM field than were students who participated in a lower-than-average number of such activities. The differences in achieving a STEM professional occupation or securing a STEM patent between the “low dose” and “high dose” students were evident but not as pronounced. Note, however, that these results are merely an association and do not imply a cause-and-effect relationship. For example, those with the most interest and abilities in STEM fields might self-select for the enrichment programs. Nevertheless, it does fit with the individual experiences of many members of this committee that early exposure to highly challenging material in the mathematical sciences had an impact on their career trajectories.
One means by which the mathematical sciences professional community contributes to efforts to attract and encourage precollege students is through Math Circles. Box 5-1 gives an overview of this mechanism, which has proved to be of real value in attracting and encouraging young people with strong talent in the mathematical sciences.
From 1988 to 1996, the National Science Foundation (NSF) sponsored a Young Scholars Program that supported summer enrichment activities for high school students who exhibited special talent in mathematics and science.33 It was begun at a time when the United States was worried about the pipeline for scientists and engineers just as it worries now. By 1996, the NSF was “funding 114 summer programs that reached around 5,000 students annually [and about] 15% of the Young Scholars programs were in mathematics.”34 Some of the successful funding of mathematics programs through this mechanism included programs at Ohio State University, Boston University, and Hampshire College. The committee believes
______________________
33 This description is drawn from Allyn Jackson, 1998, The demise of the Young Scholars Program. Notices of the AMS, March.
34 Ibid.
BOX 5-1 Mathematical Circles: Teaching Students to Explorea
In 2006, an eighth-grade home-schooled student named Evan O’Dorney came to an evening meeting of the Berkeley Mathematics Circle with his mother. For an hour he listened to the director, Zvezdelina Stankova, talk about how to solve geometry problems with a technique called circle inversion. Then, during a 5-minute break, he went back to his mother and told her, “Mom, there are problems here I can’t do!”
It’s not something that O’Dorney has said very often in his life. By the time he graduated from high school, he had become as famous for academic excellence as any student can be. In 2007, he won the National Spelling Bee. From 2008 to 2010 he participated in the International Mathematics Olympiad (IMO) for the U.S. team three times, winning two silver medals and a gold. And in 2011 he won the Intel Science Talent Search with a mathematics project on continued fractions. President Barack Obama called O’Dorney personally to congratulate him after his IMO triumph, and the two met in person during the Intel finals.
It would be easy to say that a student as talented as O’Dorney probably would have achieved great things even without the Berkeley Math Circle. But that would miss the point. For 5 years, the mathematics circle gave him direction, inspiration, and advice. It put him in contact with university professors who could pose problems difficult enough to challenge him. (As a ninth-grader, he took a university course on linear algebra and found a solution to a previously unsolved problem.) By the time he was a high-school senior, he was experienced enough and confident enough to teach sessions of the Berkeley Mathematics Circle himself. The experience helped him develop the communication skills he needed to win the Intel Science Talent Search.
Not all students can be O’Dorneys, of course. But the math circle concept, imported from Eastern Europe, has begun to find fertile ground in the United States. The National Association of Math Circles now counts 97 active circles in 31 states, most of them based at universities and led by university professors. As is the case in Eastern Europe, math circles have become one of the most effective ways for professional mathematicians to make direct contact with precollege students. In math circles, students learn that there is mathematics beyond the school curriculum. And yes, they discover problems that might be too hard for them to solve. But that is exactly the kind of problem that a student like O’Dorney wants to work on. Gifted students are often completely turned off by the problems they see in their high-school classes, which for them are as about as challenging as a game of tic-tac-toe.
Dr. Stankova, who was then a postdoctoral fellow at the Mathematical Sciences Research Institute at Berkeley (she now teaches at Mills College in began the Berkeley Math Circle in 1998, hoping to replicate the experience she had as a grade-school student in Bulgaria. In Bulgaria and throughout Eastern Europe, math circles are found in most grade schools and many high schools. Just as students with a talent for soccer might play on a school soccer team, students with a talent for mathematics go to a math circle. This does not mean that the
school’s regular math curriculum is insufficient or inadequate; it simply recognizes that some students want more.
Dr. Stankova was surprised that a similar system did not exist in the United States. (The first math circle in the United States was founded at Harvard by Robert and Ellen Kaplan in 1994; Stankova’s was the second.) Originally the Berkeley Math Circle was intended as a demonstration for a program that would move into secondary schools.
But the United States turned out to be different from Eastern Europe in important ways. Here, very few secondary school teachers had the knowledge, the confidence, or the incentive to start a math circle and keep it going. This was different from the situation in Bulgaria, where schoolteachers were compensated for their work with math circles. Although some U.S. math circles have flourished without a university nearby (for example, the math circle in Payton, Illinois), most have depended on leadership from one or more university mathematicians. For example, the Los Angeles Math Circle has very close ties to the math department at UCLA.
Other differences showed up over time. With circles based at universities, logistics—getting kids to the meeting, and finding rooms for them to meet in— became more difficult. At present the Berkeley Math Circle, with more than 200 students, literally uses every seminar room available within the UC Berkeley math department on Tuesday nights. Most universities offer little or no support to the faculty who participate. Administrators do not always realize that the high-school students who attend the math circles are potential future star students at their universities. In fact, some of them are already taking courses at the university. Stankova has often had to alert UC Berkeley faculty members to expect a tenth-grader in their classes who will outshine the much older college students.
One part of the math circles philosophy has, fortunately, survived its transplantation from Eastern Europe to America. Math circles encourage open-ended exploration, a style of learning that is seldom possible in high-school curricula that are packed to the brim with mandatory topics. Problems in a math circle are defined as interesting questions that one does not know at the outset how to answer—the exact opposite of “exercises.” They introduce students to topics that are almost never taught in high school: for example, circle inversion, complex numbers, continued fractions (the subject of O’Dorney’s Intel project), cryptology, topology, and mathematical games like Nim and Chomp.
Many participants in math circles have gone on to success in scholastic math competitions, such as the USA Mathematical Olympiad (USAMO) and the IMO. For example, Gabriel Carroll, from the Berkeley Math Circle, earned a silver medal and two golds in the IMO, including a perfect score in 2001. He participated in the Intel Science Talent Search and finished third. As a graduate student in economics at MIT, Carroll proposed problems that were selected for both the 2009 and 2010 IMO events. Ironically, the latter problem was the only one that stumped O’Dorney.
But not all students are interested in competitions. Victoria Wood participated in the local Bay Area Math Olympiad but did not like having to solve problems in a limited time. She liked problems that required longer reflection (as real research
problems almost always do). She started attending the Berkeley Math Circle at age 11, matriculated at UC Berkeley at age 13, and is now a graduate student with several patents to her name. Some math circles, such as the Kaplans’ original math circle in Boston, deliberately avoid preparing students for math competitions. Others do provide preparation for competition, but it is far from being their main emphasis.
In 2006, the American Institute of Mathematics (AIM) began organizing math teachers’ circles, designed specifically for middle-school teachers. After all, why should students have all the fun? By exposing teachers to open-ended learning, and encouraging them to view themselves as mathematicians, the organizers hope to have a trickle-down effect on thousands of students. At present, AIM lists 30 active teachers’ circles in 19 states.
Despite their very promising start, it remains to be seen whether math circles will become a formal part of the American educational system or remain a poorly funded adjunct that depends on the passion and unpaid labor of volunteers. Clearly they have already provided an invaluable service to some of America’s brightest youngsters. Conceivably, if teachers’ circles take root, or if enough teachers come to observe math circles with their students, they could begin transforming American schools in a broader way, so that mathematical competence is expected and mathematical virtuosity is rewarded.
______________________
a The committee thanks Dana Mackenzie for drafting the text in this box.
that reviving this sort of program would contribute in exciting ways to the mathematical sciences (or STEM) pipeline.
Recommendation 5-5: The federal government should establish a national program to provide extended enrichment opportunities for students with unusual talent in the mathematical sciences. The program would fund activities to help those students develop their talents and enhance the likelihood of their pursuing careers in the mathematical sciences.
In making this recommendation, the committee does not intend in any way to detract from the important goal of ensuring that every student has access to excellent teachers and training in the mathematical sciences. The goal of growing the mathematical sciences talent pool broadly is synergistic with the goal of attracting and preparing those with exceptional talent for high-impact careers in the mathematical sciences.





























