Appendix Models, Uncertainty, and Confidence Intervals
This appendix examines technical issues pertaining to models, model validation or measuring the uncertainty of model projections, and representing the uncertainty in some sort of summary form.1 As in the body of the report, we make use of definitions for terms such as model, model validation, and variance of a model's output that may differ somewhat from the definitions used elsewhere. This is unavoidable because there is currently no standard terminology for these concepts and because the situation in which we use them is somewhat special.
MODELS
Models often can be expressed as the sequential application of components or modules. The precise algorithm or data set used for certain components is often only one among several possibilities, the choice being arbitrary because of the lack of precise information about the effectiveness of the different choices. If a component is a regression model, the precise form of the regression model, the covariates to use, and the data set on which to estimate the regression coefficients may be arbitrary, at least to some extent. Examples of this appear in population projections and macroeconomic models, in which the selection of projected fertility and mortality rates in the former, or the selection of projected inflation rates and productivity indices in the latter, is somewhat arbitrary.
The correspondence of two models can range from being near replicates to essential independence. Two models can differ from one another due to use of
different regression coefficients, due to use of different covariates, due to use of a different regression specification (e.g., log-linear or linear), through use of an approach other than regression for a particular component, or by having such different structures that identifying a parallel component is impossible. It is important for the discussion that follows to point out that some of the possible choices have classes of alternatives that can more easily be considered part of a sample space with subjectively assigned probabilities than others. For example, the usual theory underlying regression analysis provides the sample space of alternate vectors of regression coefficients, due to sampling variability, along with their associated densities. In that case, the sample space and the associated probabilities are easily supported. However, the class of approaches other than regression, including time-series analysis, models from linear programming, etc., is difficult to consider as part of a well-defined sample space and is also difficult to attribute probabilities of being "right." There is currently some disagreement about the extent to which subjective probabilities can be assigned to alternative model specifications. We point out that Rubin, in a series of papers on multiple imputation (see Little and Rubin, 1987), has provided a rigorous formulation for the variability due to alternative imputation models, which is closely related to the issue discussed here.
As we stress in Chapter 3, all sources of uncertainty in a model's output need to be communicated to policy analysts and the modeling community. The question is whether uncertainty arising from choices about model structure should be incorporated in a confidence interval, which specifies a precise coverage probability, or whether this uncertainty is more justifiably represented and communicated as part of a sensitivity analysis (in addition to the confidence interval representing the variation due only to sampling error). To many analysts, this is the same question as whether the difference between two models is too extreme to consider the two models to be versions of one another.
UNCERTAINTY OF AN ESTIMATE
The uncertainty of an estimate is an umbrella term for the quantification of the differences between a model's estimates and the truth. As noted in Chapter 3, estimates generated by models will differ from the truth for a variety of reasons, which can be summarized in four broad categories: (1) sampling variability in the input database, which is only one of a family of possible data sets that could have been obtained; (2) sampling variability in other inputs, such as imputations, regression coefficients, and control totals; (3) errors in the database and other inputs; and (4) errors due to model misspecification.
The first two categories of uncertainty listed above—sampling variability and errors from imprecise estimation of other model inputs—are most easily estimated and summarized. These estimates are frequently labeled mean square error. (As discussed further below, the concept of mean square error properly
includes the third and fourth sources of uncertainty—input data errors and model misspecification—as well. However, in practice, measures of mean square error almost always ignore the fourth source and often ignore the third source as well.)
For simple models, mean square error is measured with standard techniques for variance estimation.2 For relatively complicated models, it has recently become possible to use nonparametric sample reuse techniques for this purpose. Available sample reuse techniques include the jackknife, bootstrap, balanced half-sample replication, and cross-validation; in particular, the bootstrap has shown good flexibility and utility (see Efron, 1979). Simply put, the bootstrap measures variability by using the observed sample distribution in place of the unobserved population distribution. The strength of this approach is that variance estimation becomes a function of computing power rather than an exercise in solving multidimensional integrations for complex estimators and distributions.
For complex models, sample reuse techniques can generally be used to measure the uncertainty in a model's estimates due to category 1. They can also be used to measure the uncertainty due to category 2, as can related parametric resampling techniques. The typical measurement of uncertainty due to categories 1 and 2 is the standard deviation, with the associated confidence interval for estimates that follow an approximately normal distribution.
Uncertainty due to category 3 is often measured by using a sensitivity analysis, because the error in the inputs may not be understood well enough to be approximated with a probabilistic model. This is accomplished by identifying a small number of methods for reweighting or "correcting" the data. One can then rerun the model with these alternate data sets and measure the impact on model projections. Sometimes, discrepancies due to category 3 can be given a probabilistic structure: in the case of forecasts of the inflation rate, for example, the sample space is well defined.
For discrepancies due to category 4, a well-defined sample space can usually not be defined, or, if defined, elements of that sample space cannot be given probabilities (even subjective) of being "correct," because it is difficult to collect all of the various methods that might be used to model a quantity of interest and to determine their associated uncertainties. Therefore, it is very difficult to impose a probabilistic structure on alternative model specifications. Certainly, sensitivity analyses can be performed for components of interest when alternative specifications for these components are suggested, and such analyses
should be performed on a regular basis for components that are suspected to be suboptimal. However, many analysts believe that it is not possible to provide a confidence interval, with even approximate coverage probability, for uncertainty due to model misspecification.
Some members of the panel believe that the last statement can be relaxed in situations in which a number of versions of a model can be created by making use of equally likely a priori alternatives for a small number of modules. In this situation, the distinction between using alternative econometric forecasts and using alternative modules is not always clear, and it is possible that higher and lower limits defined by the values an estimate takes for these different model versions would provide a reasonable assessment of uncertainty due to model misspecification. Certainly, these ranges need to be communicated as part of an error profile of a model, but it is not completely clear how they could be incorporated into a confidence interval with known coverage probability, because the multivariate density corresponding to certain joint selections of alternatives of model components may not be known.
To frame this discussion in another way, the variability of an estimator about the "truth" can often be decomposed into two terms, variance and bias: variance is a measure of the variability of an estimator about its mean; bias is a measure of the difference between an estimator's mean and the truth. The variance plus the square of the bias is the formal definition of mean square error, which is also the average squared difference between an estimator and the truth. The square root of the mean square error, or the root mean square error, is often used the same way as is the standard deviation: to create confidence intervals, by adding and subtracting, say, two times the root mean square error from the estimate to form a 95 percent confidence interval.
By using the above taxonomy, model outputs can be biased as a result of errors in an input data set or as a result of model misspecification,3 and therefore the root mean square error is often a better summary of the performance of a model's estimates than the standard deviation. 4 External validation directly measures root mean square error (if there is a well-defined experiment) and is therefore directly useful in assessing an estimator's uncertainty. In contrast, a sensitivity analysis provides information about the size of the bias, but only indirectly, because there is no knowledge of the truth, and therefore a sensitivity analysis does not directly measure root mean square error.
CONDITIONAL VERSUS UNCONDITIONAL CONFIDENCE INTERVALS
The issue of how best to communicate the uncertainty in a model's estimates to decision makers raises a number of difficult questions. Through application of sample reuse techniques and sensitivity analysis, policy analysts will have some quantitative and some qualitative information about the uncertainty in a model's estimates. Often, they will have quantitative information about the variability in the estimates due to sampling error (in the primary database and other sources) and qualitative information about variability due to errors in the data and model component misspecification. But if the quantitative measure of uncertainty is presented alone in the form of a confidence interval that assumes that other aspects of the model are correct, unsophisticated users may interpret the confidence interval in an unconditional rather than a conditional sense and hence ignore many potential sources of error.
An example of the tendency to misinterpret conditional confidence intervals is the communication of sampling error in public opinion and political preference polls. Although providing this kind of information is an important step forward, readers are all too apt to assume that the confidence interval expresses the total error in the poll, instead of just the sampling variability, and hence to overlook the effects of nonresponse, order of the questions, form of the questions, interviewer methods, and other nonsampling errors on the quality of the results.
Another problem in the use of conditional confidence intervals is that the contribution to uncertainty from components other than sampling error, although generally difficult to quantify, very often (once quantified) turns out to be much larger than the contribution from sampling error. Therefore, there is a very real danger that decision makers will form an overly optimistic picture of the quality of the estimates. In addition, even when information about the nonsampling error components can be qualified roughly through the use of sensitivity analysis, it is often impossible to incorporate this information into an unconditional confidence interval with a known coverage probability. Therefore, the problem for unsophisticated users is how to present them with information combining different levels of probabilistic rigor.
To make clearer what we mean by conditional confidence intervals, consider the case of a multiple regression model that is being used to estimate some quantity of interest. There is a well-defined theory that provides a confidence interval of specified coverage probability due to sampling variability for the fitted values. The theory is based on various assumptions, including that the expectation of the quantity of interest is a specific function of the covariates used. This assumption is often difficult to verify. For example, assume that another individual models the same quantity with a different set of covariates. There is an associated confidence interval for the second model, and if some of the underlying assumptions for either of the models do not obtain, there
is no reason that these confidence intervals need to overlap. That is, two reasonable models can produce confidence intervals for the same quantity that have no values in common. Two such confidence intervals do not necessarily overlap because they are both conditional on the assumptions underlying the two models. At least one model's assumptions are wrong, possibly both. There is no problem in using confidence intervals that are conditional as long as analysts are aware of the assumptions being made.
The use of sensitivity analysis is an attempt to begin the process of developing unconditional confidence intervals, or at least less conditional ones, to develop a better understanding of the possible modeling approaches and their effectiveness. The ultimate objective is to narrow the alternatives to a single best method, with no contribution to uncertainty from model misspecification. A model is developed by an individual or individuals with a perspective on how certain steps of the modeling process can be accomplished optimally. If experts are truly divided about which way a step should be modeled, a research program should be carried out so that the uncertainty due to model misspecification is reduced.
Returning to the regression example, one way in which to develop an unconditional confidence interval is to include the contribution of variability from the model development process in the confidence interval; this has been done when modelers work from the same data set through use of the bootstrap (see Brieman, 1988).
Many of the problems in communicating uncertainty to decision makers are overcome when an analyst has information from several external validation studies of the same type of policy analysis. It is then straightforward to construct a measure of overall error—specifically, the root mean square error—by taking the square root of the average of the squared differences between each estimate and the applicable measure of what actually occurred. This statistic then provides the basis to form, at least approximately, unconditional confidence intervals for the current set of estimates. However, this approach is easily misused. First, the external validation studies will necessarily pertain to different time periods and policy initiatives, so it is not clear to what extent the information applies to the current analysis. Similarly, it is not clear to what extent the various studies are themselves replications of any defined experiment, and thus it is difficult to interpret the root mean square error. Also, the confidence interval formed from the root mean square error does not communicate the uncertainty in the estimated root mean square error itself. That is, was it based on a single external validation study or 10 or 20? 5 Thus, even in the uncommon situation in which policy analysts can make use of external
validation studies to generate confidence intervals for current estimates, there are serious problems that need to be researched.
AN ILLUSTRATIVE DIAGRAM
To assist in understanding some of these ideas, Figure A-1 describes a simple situation, with five models. The estimated ranges for models 1, 2, and 3—none of which includes the true value (x)—are 95 percent confidence intervals for three different model versions that incorporate only sampling variability. (We have represented the densities of the estimates above the confidence intervals as approximate normal distributions, in which case 95 percent confidence intervals are formed by multiplying an estimated standard deviation by 1.96.)
The differences among the ranges for models 1, 2, and 3 are due to, say, different macroeconomic forecasts. Therefore, range 6 is a range of uncertainty due to sampling variability in the input data set and of uncertainty due to the macroeconomic forecast. It is generally impossible to provide range 6 with a rigorous estimate of coverage probability, but it might admit to a probabilistic interpretation if a probabilistic model for the various macroeconomic forecasts can be developed. (Range 6 also might be considered by some to represent root mean square error, with contributions of variance from sampling variability and bias from use of incorrect macroeconomic forecasts.)
Similarly, the ranges for models 4 and 5 are 95 percent confidence intervals for two versions of a completely different model, with the variability represented due to sampling variability. (Neither of these ranges includes the true value.) The difference between the model 4 and model 5 ranges is due to, say, the use of different imputation routines. Range 7, therefore, is another uncertainty range incorporating sampling variability and uncertainty due to imputation method. Some might consider range 7 more difficult to treat as a confidence interval with a known coverage probability than range 6, because the probabilistic structure of potential imputation routines might be more difficult to specify than that of macroeconomic forecasts.
Finally, range 8 is what one might hope to communicate as an estimate of total uncertainty. It is, in this diagram, the only interval that actually contains
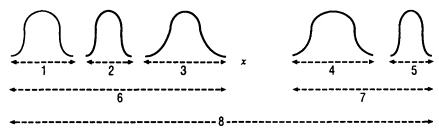
FIGURE A-1 Ranges of estimates of x (truth) from five models.
the truth. However, this range is difficult to interpret because there may be yet another modeling approach that would further broaden the range of uncertainty. In addition, range 8 cannot be given an associated coverage probability, which greatly weakens its utility. However, it does provide an indication of the amount of uncertainty due to sampling variability, macroeconomic forecasts, imputation routines, and modeling approaches.








