3
Relationship Between Language and STEM Learning for English Learners
English learners (ELs) develop science, technology, engineering, and mathematics (STEM) knowledge and language proficiency when they are engaged in meaningful interaction in the classroom and participate in the kinds of activities in which STEM experts and professionals regularly engage. This chapter provides the committee’s consensus views of the inextricable relationship between language and content. It begins with the committee’s stance on language in the STEM subjects and articulates the ways in which ELs can be afforded opportunities in the STEM classroom to draw on language and other meaning-making resources while engaging in disciplinary content. The committee then describes the current view of the STEM subjects in PreK–12 and concludes with a vision of STEM education for ELs.
THE ROLE OF LANGUAGE AND CULTURE IN STEM LEARNING
All children grow up in communities that use language to engage in cultural practices that have developed historically and are shaped in ongoing ways to achieve the goals and values of the communities (Nasir et al., 2014). Each community has particular ways of conceptualizing, representing, evaluating, and engaging with the world, and initially children are socialized into the language and ways of being in their families and local communities (Gutiérrez and Rogoff, 2003). Over time, however, each person becomes a member of a larger set of communities and engages in new cultural practices that are sometimes complementary but may sometimes
conflict with the practices of their home communities (Moje, 2000). For most children, these new communities include both in-school and out-of-school affiliations through which they engage in new cultural practices (Nasir et al., 2014).
Any particular student coming from a home community into a school context may present herself or himself in a variety of ways, including ways that may or may not be consistent with stereotypes of the home communities or different cultural groups. Expecting individuals to act or think in particular ways because of their group memberships limits those individuals’ opportunities to learn and constrains their opportunity to thrive in educational settings. Schools are enriched through the diverse experiences and perspectives of children and families from different cultural communities, and ELs simultaneously bring unique experiences as individuals and as knowledgeable members of the communities to which they belong (Gutiérrez and Rogoff, 2003; Moll et al., 1991; see Chapter 5 for a deeper discussion of the role of families, communities, and cultural contexts). All of these experiences, individual and collective, can provide resources for learning STEM (Ishimaru, Barajas-López, and Bang, 2015; Nasir et al., 2014).
Once they enter preschool, children encounter communities of academic disciplines, and they leverage their existing linguistic and cultural resources as they begin to engage in this context. The STEM disciplines constitute communities in which language and other ways of making sense of the world have evolved to enable participants to accomplish their functional goals. STEM subjects offer the potential for membership in the communities of mathematicians, scientists, engineers, and other technical experts—communities with their own ways of conceptualizing, representing, evaluating, and engaging with the world. In turn, STEM students from a wide range of backgrounds bring the potential to contribute to shaping STEM fields in critical ways that transform and remake focal topics, practices, and contributions (Vossoughi, Hooper, and Escudé, 2016).
Language is simultaneously a cognitive ability and a cultural resource that children first learn to draw on in their homes and communities. As they interact with caregivers in the early years, the language they develop enables them to participate in the community’s cultural practices and learn its ways of being, as well as to organize and make sense of their complex worlds. For example, children begin to learn about cause and effect in everyday contexts as they experience and talk about conditions, purposes, and reasons (e.g., Painter, 1999). Their understanding of cause and effect develops along with the language through which causal relationships are expressed (e.g., through language such as if you see a snake, don’t touch it because it may be dangerous). Through many such interactions, they learn both the language and values of their culture and are introduced to con-
cepts relevant for later STEM learning. For some children, this development occurs in more than one language.
When children enter school, they begin to use language in new ways and encounter new cultural practices through talk, text, and other systems for sharing meaning (e.g., gesture, visual display) and making sense of the world (Schleppegrell, 2004). These new ways of using language can build upon and enhance children’s experiences, as well as encourage new ideas and knowledge. Across school subjects, as children learn new concepts, they also learn new discourse patterns, new ways of using language to interact with all of their meaning-making resources to share their perspectives as they engage with the concepts. In other words, language development and concept development occur simultaneously; in humans, language development and concept development are inextricable (National Research Council, 2000). As learners add concepts and language, adding new concepts through language becomes progressively easier as the linguistic skills and abilities of the learner increase. The learner possesses a broader and deeper foundation upon which to layer new concepts and language. Concept development is made more challenging for ELs to the extent that educators rely exclusively on the English language to develop concepts and may not recognize the added challenge of learning new concepts in a language that one is also learning (Coady, Harper, and de Jong, 2016; de Araujo, 2017).
To learn STEM subjects, students will learn the requisite new patterns of language and expression only through opportunity for and engagement in STEM disciplinary practices. The developmental pathways available to individual learners in STEM classrooms are influenced by the opportunities they are offered to participate in the practices and discourses of STEM fields. As described throughout Chapter 4, participation in these practices and discourses increases learners’ capacities to generalize and express abstract ideas, develop disciplinary habits of mind and dispositions, and achieve success in STEM learning. Learning STEM subjects requires support for learning to use the discourse patterns through which the knowledge in each subject area is presented and engaged with. All children require such support, including those learning in their mother tongues or first language (also referred to as L1). For ELs, success often hinges on engaging in classroom and out-of-school experiences that encourage them to draw on the languages and multicompetences they already control and to connect new concepts with the knowledge they bring from their homes and communities (Moll et al., 1991). When allowed to interact in varied ways to build from what they already know and to develop new technical knowledge at school, ELs can learn STEM content and practices while simultaneously building their proficiency in English beyond STEM.
LANGUAGE AS MEANING-MAKING
Language is experienced as sounds and wordings (words/phrases), but the primary function of language is to make sense of the world and share meanings with others. The use of language is to “make meanings” that fulfill goals in the social contexts where people interact (Schleppegrell, 2004). The meanings vary not only according to what is being done (the “content”), but also according to with whom the interactions take place (e.g., how many people are present, the status of the relationships, the roles taken on in the discourse, etc.) And it is not just in language that people interact. Along with language, nonlinguistic modalities—including gesture, visual displays (e.g., symbols, diagrams, graphs, tables), and other multimodal representations (e.g., in everyday life, maps, emojis, pictures, etc.; in STEM subjects, artifacts of engineering design, computational modeling, etc.)—offer different affordances and limitations, potentials, and constraints for meaning-making (Bezemer and Kress, 2008).
It is important to recognize that the content taught in STEM subjects is not separable from the language through which the content is presented (Schleppegrell, 2007). There is no language-free content; language use always presents some content, and most representations of content require some language use, even with multimodal resources for meaning-making. This understanding of language means that to learn the language of STEM subjects, students must participate in STEM contexts and activities. For ELs, this means that they must be encouraged to draw on all of their multicompetencies, which include all of their languages and their different varieties, as well as gesture, drawing, and other modalities for meaning-making.
Language is used in different ways depending on what is being done—making different language choices in doing mathematics than in doing science, for example—and who is being spoken to (e.g., a friend or family member versus a stranger) and the mode of communication (e.g., talking on the phone or writing a letter) (Schleppegrell, 2004, 2007). Linguists use the term register to refer to this kind of variation in the ways that meaning-making resources are drawn upon. Register refers to the different ways people draw on linguistic and nonlinguistic resources as they engage in different kinds of activities, with different kinds of people, through different modes of communication. It is a concept articulated by linguist Michael Halliday1 in describing features of the language of mathematics (1978) and science
___________________
1 Halliday (1978, 2014) and Halliday and Martin (1993) developed systemic functional linguistics (SFL), a theory of language that relates language choices to features of social contexts. SFL offers a functional grammar that can be used to describe and analyze the meanings that are expressed in different registers, helping show how linguistic choices vary across fields of study and in different tasks and contexts within the same field of study. There have been others who have conceptualized and studied registers (see Ferguson, 1994).
(1993) and has been a key linguistic construct for exploring variation in meaning in context in all subjects. Students use multiple registers as they engage in classroom activities in the same ways they use multiple registers as they engage in activities outside of school. Figure 3-1 shows how three aspects of a context, the content being engaged with, the relationships being enacted, and the modalities available to draw on, shape the actual language and meanings being presented.
It is perhaps most obvious that language varies according to content. Different words are used in mathematics than in science. But consider how different modalities present and enact meaning; for example, by writing rather than speaking, and how different wordings depending on the relationship of the speakers, for example, whether speaking one-on-one or with a small group. The registers used respond to the contexts participated in, so shaping contexts to enable students to expand their linguistic repertoires is an important goal of instruction in all subjects; adding new registers and developing existing registers is a main goal of schooling. The notion of register helps point out how teachers can engage learners in activities that build from everyday ways of interacting toward more formal ways of presenting disciplinary meanings, as well as how learners can unpack disciplinary meanings into language that connects with the language and meanings they bring to the classroom. The notion of register also helps teachers recognize students’ subject-matter understandings even as their proficiency
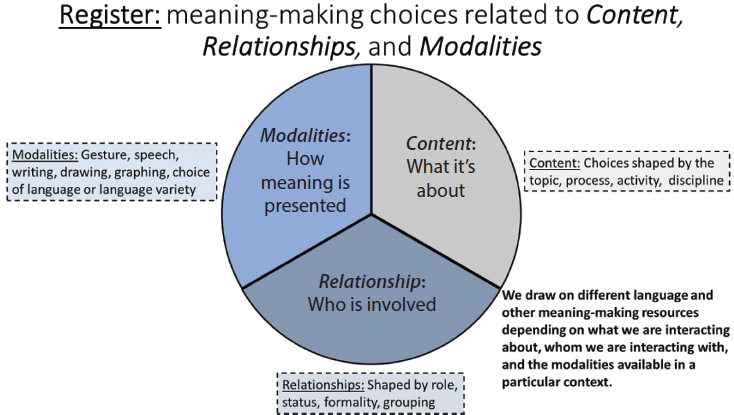
SOURCE: Based on concepts proposed by Halliday (1978).
in English is still developing. Within the same classroom, different activities offer learners different affordances for drawing on language and the multicompetencies they already are comfortable with and for learning new ways of making meaning that are subject-specific.
“Content” can be held constant as students who are learning English engage with the same concept in different ways across a set of activities designed to involve them in sense-making as they learn STEM subjects. ELs who are less proficient in English may be most confident in participating when encouraged to use a range of modalities and work in a small group setting with peers, while those with greater proficiency may participate in imperfect but comprehensible English and interact in whole class settings. While different participation structures present different challenges and affordances to particular students, language will develop as students have multiple opportunities to engage with the same content and concepts over a unit of study (Haynes and Zacarian, 2010). The particular ways to talk and write (discourse patterns) about the content will not be the same across the unit. Introducing and working with a concept initially, students may use everyday language and informal vocabulary and sentence structure. As they become more familiar with the technical aspects of the STEM concepts they are learning and the STEM practices they are engaging in, they move toward more disciplinary ways of talking about what they are learning, using technical language, sentence structure, and arguments more typical of written or formal discourse. This is how students develop new academic registers at the same time they learn new concepts, and teachers’ awareness of the affordances of this register development over time can enable them to challenge ELs (Gibbons, 2015).
For example, in a unit of instruction about division with fractions, the activities that 5th-grade students can engage in move from hands-on interaction to reporting on the interaction and then writing about what was learned. In moving across these different activities, students work in different participation structures and use different modalities, even while the underlying “content,” understanding and using the concept of division by a fraction in a word problem involving the measurement meaning of division (not the partitive meaning used in “fair share” problems), remains the same.Table 3-1 illustrates the variation in register that results as the children work to make sense of, represent, and discuss multiple solutions to a problem. It presents hypothetical responses that could occur with any group of children as they engage in different participation structures across an activity sequence:
Sophia wants to make peach tarts for her friends. She needs two-thirds of a peach for each tart and she has 10 peaches. What is the greatest number of tarts that she can make with 10 peaches?
TABLE 3-1 Shifting Registers in Mathematics Activities While Holding Content Constant
| Context | Context 1 | Context 2 | Context 3 | Context 4 |
|---|---|---|---|---|
| Modalities | Spoken by a small group of students with accompanying action or gesture | Spoken by a student about the action, after the event | Written by a student | Written using equations in the textbook |
| S1: Mark it like this S2: No, try this way S1: Ok, count those . . . 30 S2: the tarts all need 2; 30 divided by 2 S1: 15 |
S1: We drew the 10 peaches and then cut each 1 into 3 parts. Then we counted all the parts. So it was 30 parts, and each tart had to have 2 parts, so we divided 30 by 2 and got 15. |
When you want to find how many thirds there are, you can divide each peach into 3. When you count how many thirds, you get 30. Since each tart needs two thirds, you can divide 30 by 2 and get 15. That means that Sophia can make 15 tarts. |
To divide a whole number by a fraction, multiply the whole number by the reciprocal of the fraction. 10 ÷ (2/3) = 10 * (3/2) = (10*3) /2) = 15 |
|
| Relationship | Peer-to-peer, face-to-face interaction | Reporting on behalf of a small group | Individual written production for the teacher | Author writing for a remote audience of learners |
| Content | Solving a fractions division problem | Solving a fractions division problem | Solving a fractions division problem | Solving a fractions division problem |
In Context 1, the children first interact in a small group using manipulatives that represent the peaches to explore this problem. In this context, while the “content” is about the problem, their relationship is that of small group interaction, and the modalities they use to make meaning involve talk, gestures, and perhaps drawings. Their language includes commands to each other to act, sentence fragments, and words like this and those that are meaningful only because of the shared context and the objects or manipulatives. This language and interaction is functional for finding and discussing solutions in a small group.
In Context 2, when a student has to tell the class what the group did,
although the “content” is still about the word problem and the meaning of division by a fraction, the relationship is now one student talking to the whole class about something that the others have not experienced. This change in context leads to different language choices. Instead of those, the student says the 10 peaches, as the shift in context requires the speaker to make explicit referents that could be pointed at when the group was interacting with the manipulatives. Instead of commands to act, the student uses past tense to say what the group did, and sequencing terms (then) to order the procedures they engaged in, and conjunctions (so) to draw conclusions.
In Context 3, the students work individually to write about their solutions, discuss which solution may be general, and finally settle on a general statement. The language choices are different as the students discuss multiple solutions and write a general statement about how to find the answer. The audience is now distant, so everything that could be left implicit, known from the context, in Context 1, has to be made explicit. When the goal is to share a generalized description of the experience, instead of what we did, the writer would describe what a generalized you can do to make sense of and solve the problem, using simple present tense to present timeless generalizations. Words like since and phrases such as that means help the writers construct a cohesive description of what they did to solve the problem and words like because would be part of an explanation or justification for why they did what they did and why it works.
These students are shifting registers, drawing on language and other meaning-making resources in different ways as they engage with the same content and present it to audiences with which they have different relationships. A textbook, as in Context 4, represents yet another register with which students must engage; this register presents a mathematical generalization about the meaning of division by fractions in a sentence that distills several concepts into technical language accompanied by an equation in mathematical symbolic language. To understand this technical language, teacher and students are likely to engage in further talk and interaction that “unpacks” the technicality and uses more everyday register features to help learners see meaning in what is represented through mathematical symbols. Through opportunities to engage with language in all these different forms of interactions, none of which is inherently “better” or “more appropriate” than any others in the abstract, learners are enabled to move between the language(s) and registers they bring to the classroom and the new registers they are learning to engage with as they participate in STEM learning. With textbooks, through which students are exposed to the written language of the disciplines, stylistic differences in language are also well-documented (e.g., Bailey et al., 2007).
This understanding of language suggests important implications for providing instruction and supports that will engage and challenge ELs and
enable their success in learning STEM content, concepts, and practices. In Chapter 4, the committee reports on what is known about how best to support high-quality instruction for ELs; with more evidence in science and mathematics than in technology and engineering. This understanding of language is also fundamental to preparing teachers to create learning environments and design STEM instruction that is effective with diverse learners, including ELs. Chapter 6 reports on research that shows how teachers’ knowledge about language and STEM can be developed in preservice and in-service contexts. It is the committee’s stance that through participation in such STEM learning contexts that engage all learners in using all of their meaning-making capacities, ELs will develop English language proficiency along with subject area knowledge, understanding, and practices.
CURRENT CONTEXT OF STEM PREK–12 EDUCATION FOR ENGLISH LEARNERS
In this section, the committee describes contemporary views of STEM education with ELs that provide important background for understanding the current literature; specific instructional strategies and the research associated with these views are discussed in Chapter 4. Due to the imbalance of research in these disciplinary content areas, we acknowledge that science and mathematics are necessarily overrepresented.
Science and Science Education
Based on extensive research on how children learn science in school (National Research Council, 2006, 2007) and in informal settings (National Research Council, 2009), the National Research Council (2012) report A Framework for K–12 Science Education: Practices, Crosscutting Concepts, and Core Ideas (hereafter referred to as the Framework) captures contemporary knowledge of what counts as science and engineering and provides a broad set of expectations for K–12 students (see Box 3-1).
Science and Language Instructional Shifts with English Learners
Recent years have witnessed parallel shifts toward promoting the social and sense-making nature of both science learning and second language development. In science education, whereas traditional views focused on individual learners’ mastery of discrete elements of science content, contemporary views emphasize that students engage in science and engineering practices (e.g., developing models, arguing from evidence, constructing explanations) to make sense of the world around them (National Research Council, 2012). Because this approach to science learning involves using
and applying knowledge for a particular purpose, it has been referred to as knowledge-in-use (e.g., Harris et al., 2016). In second-language development, whereas earlier theories saw it as the accumulation of discrete elements of vocabulary (lexicon) and grammar (syntax) to be internalized by learners, more recent thinking has taken a sociocultural turn, viewing language as a set of dynamic meaning-making practices learned through participation in social contexts (Beckner et al., 2009; Larsen-Freeman, 1997, 2007; Valdés, 2015; Zuengler and Miller, 2006). Because this approach to language learning involves using language for a particular purpose, it has been referred to as language-in-use (e.g., Lee, Quinn, and Valdés, 2013). Knowledge-in-use in science education and language-in-use in second-language development complement each other, such that science instructional shifts promote language learning with ELs, while language instructional shifts promote science learning with ELs. Recognizing science and language instructional shifts as mutually supportive can lead to better and more coherent instructional approaches that promote both science and language learning with all students, especially ELs (see the example in Box 3-1 and more details in Chapter 4).
Language, Discourse, and Practices in Science
The importance of discourse processes in science education builds from longstanding research examining the multiple ways language supports the creation of knowledge. In particular, sociocultural approaches brought more focused attention to the role of cultural tools such as language in mediating the processes of individual learning and cultural production and change (Nasir et al., 2014). This perspective offers an important opportunity to see how scientific knowledge accrues and changes over time as well as how knowledge is created and negotiated through social engagement and discussion in classroom settings. As will be further articulated in the Mathematical Practices section below, classroom activities should be constructed to be developmentally appropriate approximations of scientific practices, as described in Box 3-1.
Research on science practices often focuses on the establishment and evaluation of knowledge claims. These epistemic practices are central to learning the disciplinary knowledge and ways of being for various science fields. Kelly (2008) defined epistemic practices as “specific ways members of a community propose, justify, evaluate, and legitimize knowledge claims” (p. 99). Such practices vary across disciplinary communities, ways of knowing, and power dynamics that also operate in the presentation of cultures (Knorr-Cetina, 1999; Watson-Verran and Turnbull, 1995). Those epistemic practices leading to generalized knowledge claims about nature tend to be legitimized in disciplinary communities in science and engineering (Kelly,
2016). Chinn, Buckland, and Samarapungavan (2011), drawing on work in the philosophy of science, suggested five focal areas: (1) epistemic aims and values, (2) structure of knowledge and other epistemic achievements, (3) sources of justification of knowledge, (4) epistemic virtues and vices, and (5) reliable and unreliable processes for achieving epistemic aims. These epistemic practices of science have been examined in a number of studies. For example, Manz (2012) examined how uses of epistemic practices supported students’ use of modeling of a local ecosystem adjacent to their school.
Studies of student uses of knowledge in problem solving also entail engagement in scientific practices. This focus on everyday knowledge construction practices forms students’ practical epistemology2 that can serve to help make sense of phenomena, to develop conceptual knowledge, and to learn about the nature of science (Sandoval, 2005; Wickman, 2004; see Chapter 4 for a deeper discussion on phenomena and place-based learning). In each of these cases, examining student engagement in epistemic or scientific practices relies on a methodological focus on discourse processes because the ways that communities affiliate, build knowledge, and construct social practices are constructed in and through discourse (Berland et al., 2016; Jiménez-Aleixandre, 2014; Kelly and Licona, 2018; Östman and Wickman, 2014; Pluta, Chinn, and Duncan, 2011; Sandoval, 2014).
Working in groups engages students in discourse through which they both construct knowledge and enact relationships, highlighting the social nature of science learning. By focusing on the ways that knowledge was constructed, negotiated, and valued, a number of studies identified key aspects of discourse for productive educational aims (Duschl, 2008; Herrenkohl and Cornelius, 2013). For example, the interaction of the interpersonal and cognitive was made evident in Bianchini’s (1999) study of student groupwork. This study showed how students’ perceived status influenced participation and science learning. A number of studies illustrated how access to scientific knowledge was negotiated through discourse processes and tied to the ongoing social practices and norms of the classrooms (Alozie, Moje, and Krajcik, 2010; Barton and Tan, 2009; Oliveira, 2010).
An important development in the study of classroom discourse emerged from a focus on teachers’ and students’ uses of evidence. The alignment of evidence in disciplinary-specific and genre-specific forms of language has entered studies of science education as argumentation (Duschl and Osborne, 2002). Studies of argumentation have explored different contexts, have drawn from multiple argumentation analytics for analysis, and
___________________
2 Epistemology deals with questions about what knowledge is and how knowledge is developed. Practical epistemology is “the epistemological ideas that students apply to their own scientific knowledge building through inquiry” (Sandoval, 2005).
have focused on different dimensions of science from conceptual learning to socioscientific issue (Berland and Reiser, 2011; Bricker and Bell, 2008; Cavagnetto, 2010; Evagorou, Jiménez-Aleixandre, and Osborne, 2012; Sadler, 2009; Sampson and Clark, 2008). Argumentation has been applied across multiple science subject areas (Herrenkohl and Cornelius, 2013) and entered into teacher education to prepare teachers to orchestrate uses of evidence among students (Elby and Hammer, 2010; Sadler, 2006; Zembal-Saul, 2009).
Technology and Technology Education
Education related to technology—the T in STEM—is interpreted in a variety of ways (National Academy of Engineering and National Research Council, 2014, pp. 17–18). One interpretation focuses on technological literacy, which is defined as the “ability to use, manage, assess, and understand technology” (International Technology Education Association, 2000, p. 242), and traditionally, career and technical education (CTE) programs of study have emphasized technological literacy as a goal (Asunda, 2012). A second interpretation focuses on educational, or instructional, technology as a central tool for teaching and learning (language and content) both in and out of the classroom. Some influential educational technologies to date are personal computers (as well as laptops, tablet computers, and smart-phones), the Internet (including online resources and educational software), and cloud computing. A third interpretation focuses on the tools used by practitioners of science, mathematics, engineering, and beyond. These tools include computers, software, sensors, and other data collection instruments. For all interpretations, there is limited research on technology and technology education with respect to ELs; nevertheless, we highlight what is known from the existing literature.
Within K–12, the goal of technology education is to prepare students to make well-informed decisions about matters that influence technology or are influenced by technology (National Academy of Engineering and National Research Council, 2002). Typically, aspects of technology education are incorporated into multiple disciplines (e.g., mathematics aligned to the Common Core State Standards, science and engineering aligned to the Next Generation Science Standards [NGSS], and computer science aligned to the Computer Science Teachers Association [CSTA] standards), but many states have also developed separate technology education standards. Yet, no explicit recommendations for supporting linguistically diverse students in meeting these standards have been outlined.
Research describing teachers’ conceptualization of the role of technology in teaching and learning highlights that the primary goal is for students to become skillful communicators of the language learned rather than
simply learners of the language, maximizing student autonomy and empowerment in the classroom (Garrett, 2009; Warschauer and Meskill, 2000). For example, students were found to write more via computer compared to when given pen and paper, and computer-based collaborative activities encouraged more attentiveness to listening, speaking, reading, and writing (Warschauer and Meskill, 2000). Moreover, these activities help students integrate language and culture, which led students to converse in English in more meaningful ways (Garrett, 2009; Warschauer and Meskill, 2000). These findings have implications for how technology could support ELs in engaging in meaningful discourse beyond learning a language.
Likewise, educational technologies have also been shown to benefit ELs in learning science content (Ryoo and Bedell, 2017; Zheng et al., 2014). In a year-long, quasi-experimental study involving linguistically diverse 5th-grade students, laptop use was found to be correlated with higher science scores for ELs on the California Standards Test compared to their counterparts in the control group (Zheng et al., 2014). In a mixed-methods study approach, Ryoo and Bedell (2017) investigated the impact of interactive visualizations on 7th-grade students’ coherent understanding of complex life science core ideas. These visualization technologies were embedded in Web-based inquiry instruction in science, and EL and non-EL students were randomly assigned to either a static or dynamic visualization condition. Compared to the students in the static group, ELs and non-ELs within the dynamic visualization group engaged in more discourse and used both text and visual representations to make sense of the scientific phenomena. Additionally, these students more successfully evaluated the range of ideas presented in order to develop coherent scientific explanations based on evidence from the visualizations. These findings suggest that dynamic visualization technology can support the development of coherent scientific understanding for all students, including ELs (Ryoo and Bedell, 2017).
Related to the third interpretation, computational thinking is becoming increasingly essential for all students to become STEM professionals or participants in an information society. The STEM Education Act of 2015 that was recently signed into law states that “the term ‘STEM education’ means education in the subjects of science, technology, engineering, and mathematics, including computer science.”3 Thus, the definition of STEM education has been formally expanded to include computer science.
There has been an emergence of the importance of adding computational thinking to “every child’s analytical ability as a vital ingredient of science, technology, engineering, and mathematics (STEM) learning” (Grover and Pea, 2013, p. 38). Computational thinking, according to Wing (2006), “involves solving problems, designing systems, and understanding human
___________________
3 See https://www.congress.gov/bill/114th-congress/house-bill/1020/text [June 2018].
behavior, by drawing on the concepts fundamental to computer science” (p. 33) and involves key aspects, such as abstraction, pattern generalization, representational competence, modularization, algorithmic notions of flow of control, and conditional logic (Grover and Pea, 2013).
Despite the growing emphasis on computational thinking in STEM education, incorporating computational thinking in the school curriculum faces challenges. One major challenge involves lack of an agreement on what constitutes computational thinking (National Research Council, 2010, pp. vii–viii). One approach emphasizes computer literacy, which generally involves using tools to create newsletters, Web pages, or multimedia presentations. A second approach emphasizes computer science by teaching students about programming in particular languages as a way to process, analyze, and interpret information with an emphasis on key computer science concepts such as abstraction, modularization, loops, and conditionals. A third approach emphasizes programming applications, such as games, robots, and simulations, often with an emphasis on students’ participation and identity in authentic communities and practices. A fourth approach emphasizes learning to think computationally4 as a fundamental analytical skill that everyone, not just computer scientists, can use to help solve problems, design systems, and understand human behavior. This approach mirrors the growing recognition that computational thinking (and not just computation) has begun to influence and shape thinking in STEM disciplines and beyond (Weintrop et al., 2016). Few studies have examined instructional materials that enable teachers of STEM subjects to support ELs in developing computational thinking.
Engineering and Engineering Education
Engineering is a relatively recent addition to K–12 education (Carr, Bennett, and Strobel, 2012). It traces some of its beginnings to CTE programs and technology education programs at the middle and high school levels, which traditionally involved a trade or job skills program, but over the past decade, have adopted a more academic program of study (Park, Pearson, and Richardson, 2017). Over time, individual states introduced engineering in their CTE or science standards and some, such as Massachusetts, expanded to include engineering at the elementary level as well (Massachusetts Department of Education, 2001). Such state-level efforts, coupled with a series of influential reports produced by the National Academy of Engineering (National Academy of Engineering, 2010; National Academy of Engineering and National Research Council, 2002, 2009,
___________________
4 To formulate a problem and express its solution(s) in a way that a computer can effectively carry out.
2014) propelled the idea that engineering should be included in K–12 education. In 2012, the Framework (National Research Council, 2012) and the resulting NGSS articulated a new vision for three-dimensional learning by blending disciplinary core ideas, crosscutting concepts, and science and engineering practices that encompass both engineering and science.
The inclusion of engineering in these documents was pivotal for efforts to integrate engineering into K–12 settings. Many more schools and teachers across the country have begun to consider how to implement engineering in their classrooms. The introduction of a new discipline in classrooms offers a number of exciting opportunities with respect to ELs.
Engineering design and analysis offer unique opportunities for ELs. Most age-appropriate engineering for elementary and middle school students focuses on producing a material product. As they do so, students explore different materials and their properties and consider which ones are important to the functioning of their design. For example, creating a materials table, such as the one shown in Figure 3-2, not only stores such information, but also introduces students to a variety of descriptive properties to consider as they communicate. As students construct and manipulate materials and design solutions, they can show their understandings with concrete models. Designs are tangible, possibilities and ideas demonstrated, and the performance of a design against a set of evaluative criteria observed. This materiality can invite participation of students with varying degrees of English proficiency—they can show what they know.
Authentic engineering tasks are open-ended, permitting multiple solutions. Thus, students can draw upon their own funds of knowledge (see Positioning of ELs in the Classroom in Chapter 4) and creativity as they generate possible designs. As they engage in such meaningful, relevant, purposeful activity, they naturally use different registers to describe their unique ideas and convince others to consider their approaches. The use of language is tied to and often follows from experiences with concrete materials, models, and designs—there is an interplay of concepts, words, language, and experiences (Yocom de Romero, Slater, and DeCristofano, 2006).
As students engage with a real problem, they build identity with the discipline and begin to consider it as a possible future (Kelly, Cunningham, and Ricketts, 2017). Thus, engaging in the language-rich tasks of engineering design and analysis provides opportunities to use language in science, mathematics, and engineering, while building students’ confidence through the development of their academic identities.
Because the discipline is new at the precollege level, research studies of K–12 engineering education are nascent. Although some studies of classroom engineering include students from culturally, linguistically, racially, ethnically, and economically diverse backgrounds (Cunningham

SOURCE: Reprinted by permission of the publisher. From C.M. Cunningham and the Museum of Science, Boston, Engineering in Elementary STEM Education: Curriculum Design, Instruction, Learning, and Assessment. New York: Teachers College Press. Copyright © 2018 by Christine M. Cunningham and the Museum of Science, Boston. All rights reserved.
and Kelly, 2017; Hertel, Cunningham, and Kelly, 2017; Kelly et al., 2017; Silk, Schunn, and Cary, 2009; Wendell, Wright, and Paugh, 2017), to date no studies of K–12 classroom engineering specifically focus on ELs.
Mathematics and Mathematics Education
The mathematics education community presents a contemporary view of mathematics instruction based on decades of research on mathematical proficiency and beliefs, and more recent research on mathematical practices, mathematical discourse, and the role of language in learning and teaching mathematics. Research focusing on language and mathematical discussions blossomed in the past 30 years (i.e., since Pimm, 1987), and research
specifically on ELs has started to appear in the past 20 years (i.e., since Khisty, 1995). A view of academic literacy in mathematics (Moschkovich, 2015a) that balances the three components—mathematics proficiency, practices, and discourse—is especially crucial for supporting ELs (Moschkovich, 2015a). These three aspects of mathematics instruction are based on mathematics education research and are evident in reforms initiated by the National Council of Teachers of Mathematics (NCTM) in the 1990s. They are also evident in the report Adding It Up (National Research Council, 2001) and are reflected in the Common Core State Standards (CCSS) for Mathematics:
- Make sense of problems and persevere in solving them
- Construct viable arguments and critique the reasoning of others
- Reason abstractly and quantitatively
- Model with mathematics
- Attend to precision
- Use appropriate tools strategically
- Look for ad make sure of structure
- Look for and express regularity in repeated reasoning5
Mathematical Proficiency
A current description of mathematical proficiency (National Research Council, 2001) shows five intertwined strands, meant to portray the successful mathematics learner:
- conceptual understanding, or comprehension of mathematical concepts, operations, and relations;
- procedural fluency, or skill in carrying out procedures flexibly, accurately, efficiently, and appropriately;
- strategic competence, or competence in formulating, representing, and solving mathematical problems (novel problems, not routine exercises);
- adaptive reasoning, or logical thought, reflection, explanation, and justification; and
- productive disposition, a habitual inclination to see mathematics as sensible, useful, and worthwhile, coupled with a belief in diligence and one’s own efficacy.
Procedural fluency refers to computational fluency, strategic competence to problem-solving skills, and adaptive reasoning to justification
___________________
5 See http://www.corestandards.org/Math/Practice [September 2018].
and proof. Moreover, the second part of productive disposition (belief in diligence and one’s own efficacy) anticipates current ideas around growth mindset.6 This view of mathematical proficiency has important implications for instruction. In particular, all strands of proficiency, not just procedural fluency, are developed through access to effective instruction, materials, and interactions. If students are excluded from instructional interactions designed to foster conceptual understanding, strategic competence, adaptive reasoning, and productive disposition, their opportunity to develop proficiency will be limited to procedural fluency.
For example, if teachers want their ELs to learn whole number multiplication, either as grade-level instruction in the early grades or as remediation in later grades, this does not mean their instruction should be focused principally or primarily on memorizing multiplication facts. Such a narrow focus includes only procedural fluency while disregarding the other four components of mathematical proficiency. In particular, this narrow focus leaves out conceptual understanding, which supports accurate recall. Based on research on how to best teach multiplication for student understanding, as ELs learn whole number multiplication, instruction balances a focus on procedural fluency or drill with support for conceptual understanding by asking students to represent, apply, and connect the meaning of multiplication to other important mathematical ideas. This balance can be accomplished, for example, by representing multiplication using arrays and area models, solving multidigit multiplication exercises by grouping and regrouping and making a connection to the distributive property, or solving multiplication word problems.
It is crucial that teachers who work with ELs develop a contemporary view of what conceptual understanding is and how to teach mathematics for understanding. Conceptual understanding is fundamentally about the meanings that learners construct for mathematical solutions: knowing the meaning of a result (i.e., what the number, solution, or result represents), knowing why a procedure works, or explaining why a particular result is the right answer. Another central aspect of conceptual understanding involves connecting representations (e.g., words, drawings, symbols, diagrams, tables, graphs, equation, etc.), procedures, and concepts (Hiebert and Carpenter, 1992).
Reasoning, logical thought, explanation, and justification are closely related to conceptual understanding. Student reasoning is evidence of conceptual understanding when a student explains why a particular result is the right answer or justifies a conclusion. For example, multiplication involves many subtle issues: If multiplication of whole numbers is repeated addition,
___________________
6 Research by Carol Dweck defines growth mindset as the understanding that abilities and intelligence can be developed (Blackwell, Trzesniewski, and Dweck, 2007).
why is it commutative? If multiplying by 10 puts a 0 on the right, why doesn’t this work for decimal numbers? Why doesn’t multiplying always make a number larger? Why is a negative times a negative positive? Why do we invert and multiply when dividing by a fraction? Using multiple representations, explaining the meaning of what they are doing when they perform a calculation, and justifying why they chose a particular operation to solve a word problem are all evidence of students’ conceptual understanding. Typically, making sense of a problem (a mathematical practice discussed below) includes creating meaning by connecting representations, one procedure to other procedures, and/or a procedure to a concept.
Teachers who develop a contemporary view of mathematics instruction that does not rigidly prescribe the sequence of mathematical topics are better positioned to provide challenging grade-level instruction to ELs. An important result from research on mathematical proficiency is that students profit from exposure to advanced competencies as they build proficiency in less advanced competencies. For example, students who are still developing proficiency with whole number multiplication are not precluded from participating in instruction that supports algebraic thinking; proficiency with the first is not a rigid prerequisite for exposure to and progress toward proficiency in the second. Instruction that supports early algebraic thinking can be provided in the early grades or in parallel with instruction focusing on whole number operations (Carpenter et al., 1999).
Lastly, teachers who develop a broader view of the role of communication are better positioned to work with ELs in mathematics; for these teachers, English proficiency is not seen as a prerequisite for doing more complex mathematics, because conceptual understanding and communication are closely related. Communicating about mathematics is important because it supports conceptual understanding. The more opportunities a learner has to make connections among multiple representations, the more opportunities that learner has to develop conceptual understanding (Grapin, 2018; Lemke, 1990). However, not all kinds of communication will support conceptual understanding in mathematics. Classroom communication that engages students in evidence-based arguments by focusing on explanations, arguments, and justifications builds conceptual understanding (Moschkovich, 2010) whereas communication limited to just procedures or calculation may be inadequate. Communication that includes multiple modes (e.g., talking, listening, writing, drawing, etc.) is also essential, because making connections among multiple ways of representing mathematical concepts is central to developing conceptual understanding in mathematics (Dominguez, 2005; Sorto and Bower, 2017).
In summary, this view of mathematical proficiency has important implications for instruction for ELs. If, for example, ELs are building proficiency in procedural skills for whole number multiplication, instruction that bal-
ances a focus on procedural fluency or drill approaches to multiplication facts with the other four strands of mathematical proficiency will help students understand, represent, apply, and connect multiplication to other important mathematical ideas.
Mathematical Practices
The five strands of mathematical proficiency, described above, provide a cognitive account of mathematical activity focused on knowledge and beliefs. From a contemporary sociocultural perspective, mathematics students are not only acquiring mathematical knowledge, but also learning to participate in valued mathematical practices (Moschkovich, 2004, 2007, 2013). In 1992, Schoenfeld described mathematical practices as being acquired through enculturation and socialization, entry into the mathematical community, legitimate peripheral participation (Lave and Wenger, 1991), and interaction with others: “If we are to understand how people develop their mathematical perspectives, we must look at the issue in terms of the mathematical communities in which the students live and the practices that underlie those communities. The role of interaction with others will be central in understanding learning. . . (p. 363).”7
Work in mathematics education in the past 20 years has assumed that mathematics instruction in schools should parallel, at least in some ways, the practices of mathematicians (e.g., Cobb, Wood, and Yackel, 1993; Lampert, 1990; Schoenfeld, 1992). These proposals emphasize classroom activities that are developmentally appropriate approximations of academic mathematical practices. This view of students as mathematicians expects student activities to approximate at least some aspects of a mathematician’s practices, such as making generalizations or conjectures and subjecting them to review and refutation by a (classroom) community. Students are expected to explore the nature of mathematical objects, make and test conjectures, and construct arguments, and instruction is expected to emphasize abstracting and generalizing as central mathematical practices. Bringing the practices of mathematicians into the classroom creates a common set of practices that parallel academic mathematical practices. Students are expected to make conjectures, agree or disagree with the conjectures made by their peers or the teacher, and engage in public discussion and evaluation of claims and arguments made by others. This approach is intended to give students access to academic mathematical practices, such as the construction and presentation of mathematical proofs or arguments.
From a contemporary research perspective, mathematical practices
___________________
7 A new series of books published by the National Council of Teachers of Mathematics focuses on access and equity. See https://www.nctm.org/Publications/Books [August 2018].
are cognitive, in that they involve mathematical thinking and reasoning as described in the five strands of mathematical proficiency. They are social, cultural, and discursive, because they arise from communities, mark membership in communities, and involve discourse. They are also semiotic, because they involve such semiotic systems as signs, tools, and their meanings.
Academic mathematical practices can be understood in general as using language and other symbols systems to think, talk, and participate in the practices that are the objective of school learning. There is no single set of mathematical practices or one mathematical community (see Moschkovich, 2002). Mathematical activity can involve different communities (e.g., mathematicians, teachers, or students) and different genres (e.g., explanations, proofs, or presentations). Practices vary across communities of research mathematicians, traditional classrooms, and reformed classrooms. However, across these various communities and genres, there are common practices that can be labeled as academic mathematical practices (see CCSS mathematical practices listed above).
Mathematical Discourse
The sociocultural framing of mathematical practices described above has implications for connecting practices to discourse. Discourse is central to participation in many mathematical practices, as meanings are situated and constructed while participating in mathematical practices.
Work on the language of disciplines (e.g., Bailey et al., 2007; Pimm, 1987; Schleppegrell, 2007) provides a complex view of mathematical language not only as specialized vocabulary—new words and new meanings for familiar words—but also as extended discourse that includes other symbolic systems as well as artifacts (Moschkovich, 2002), syntax and organization (Crowhurst, 1994), the mathematics register (Halliday, 1978), and discourse practices (Moschkovich, 2002, 2007). Mathematical discourse refers to the communicative competence necessary and sufficient for competent participation in mathematical practices (Moschkovich, 2007).
Mathematical discourse is not principally about formal or technical vocabulary (Moschkovich, 2002, 2007). Textbook definitions and formal ways of talking are only one aspect of school mathematical discourse. In classrooms, students use multiple resources, including everyday registers and experiences, to make sense of mathematics. It is not always possible or constructive to tell whether a student’s competence in communicating mathematically originates in their everyday or school experiences. It is thus important to avoid construing everyday and academic registers as opposites (Moschkovich, 2010). Box 3-2 provides a discussion of recent research with ELs on language practices during mathematical activity.
Mathematical discourse as described here is complex. As a contrast,
a simplified view would be that it lies primarily in individual word meaning, an assumption that could have dire consequences for ELs, as they are likely to use imperfect language to describe their mathematical thinking. For example, one interpretation of CCSS Mathematical Practice Standard 6 “attending to precision” is that precision lies in using two different words for the set of symbols “x + 3” and “x + 3 = 10.” By focusing on precision at the individual word meaning level, the first is an “expression” while the second is an “equation.” However, the mathematical practice of attending to precision should not be interpreted as using the perfect word. Attending to precision can also refer to deciding when and what kind of precision is necessary during a computation, including when an exact answer is or is not necessary, a mathematical practice that does not require a precise word. Attending to precision is also involved in making precise claims, a practice that is not at the word level but at the discourse level. For example, contrast the claim “Multiplication makes bigger,” which is not precise, with the claim “Multiplication makes the result bigger than the original number when the original number is positive and you multiply by a positive number greater than 1.” When contrasting the two claims, precision does not lie in the individual words nor are the words used in the second claim more precise or formal mathematical words. Rather, the precision lies in specifying when the claim is true. In a classroom, a teacher’s response to the first claim focusing on precision at the word level might be to ask a student to use a more formal word for “bigger.” In contrast, a teacher focusing on precision at a discourse level would ask, “When does multiplication make a result bigger?”
NEW OPPORTUNITIES FOR EL STEM LEARNING
Educational standards shape the educational system, students’ experience within education, and the research that is conducted in education. New standards such as those put forth in the states’ College and Career Readiness Standards set new high standards, while new instructional frameworks in science (National Research Council, 2012) and mathematics (National Governors Association Center for Best Practices and Council of Chief State School Officers, 2010) promote linguistically rich teaching and a focus on disciplinary practices. This report references these and other sets of standards and frameworks, but such reference does not constrain or limit the report’s relevance to other sets of standards or instructional frameworks. This report is agnostic with respect to specific sets of standards except to say that expectations for what all students should know and be able to do are delineated in states’ educational standards, and that high standards are the foundation for high achievement expectations for all students. We will have occasion to point out specific aspects of standards that have the
potential to promote academic success for ELs; such is the case with recent developments in mathematics and science to which the research community quickly responded (Lee, Quinn, and Valdés, 2013; Moschkovich, 2012).
In fact, the most recent standards and frameworks have articulated language demands that comprise considerable potential for literacy development (Kibler, Walqui, and Bunch, 2015) if ELs are granted full curricular access. To fully realize this potential, and for the new standards and frameworks to ensure equity, considerable efforts must be made to improve upon teachers’ professional development for EL students (National Research Council, 2012; Quinn, Lee, and Valdés, 2012). In addition, if ELs are to truly access rich academic content, assessments must be developed alongside the new frameworks and standards (Bunch, Walqui, and Pearson, 2014).
SUMMARY
Learning STEM subjects involves extending students’ meaning-making potential through language. To engage effectively with disciplinary learning, students expand their repertoires of language skills developed during the early years of schooling and learn to recognize how language is used to make meaning, discuss ideas, present knowledge, construe value, and create specialized texts across disciplines. This expansion of students’ language repertoires is observed in the science, mathematics, and engineering classroom as ELs use language purposefully in the service of “doing” and communicating ideas about science, engineering, and mathematics. Just as each discipline requires that students engage with a specialized body of knowledge and practices, each also requires that students engage with the specialized language through which the knowledge and practices are presented. And because practices vary across disciplines, these practices are best learned and taught within each discipline.
STEM subjects are best learned with the help of teachers who can support ELs in engaging in the disciplinary practices through which both disciplinary concepts and disciplinary language are developed simultaneously. Supporting language development across STEM disciplines requires that teachers develop both disciplinary concepts and practices, as well as knowledge about language and registers relevant to the discipline. This knowledge has been characterized in various ways: as literacy pedagogical content knowledge (Love, 2010), pedagogical language knowledge (Bunch, 2013; Galguera, 2011), or disciplinary linguistic knowledge (Turkan et al., 2014). Bunch (2013), for example, argued that teachers need “knowledge of language directly related to disciplinary teaching and learning and situated in the particular (and multiple) contexts in which teaching and learning take place” (p. 307). Teachers also need to effectively use their own
language during content instruction. That is, they can be intentional in their linguistic pedagogies such as crafting STEM explanations in ways that make content most accessible to ELs without reducing the level of complexity of the content (Bailey and Heritage, 2017).
REFERENCES
Alozie, N.M., Moje, E.B., and Krajcik, J.S. (2010). An analysis of the supports and constraints for scientific discussion in high school project-based science. Science Education, 94(3), 395–427.
Asunda, P. (2012). Standards for technological literacy and STEM education delivery through career and technical education programs. Journal of Technology Education, 23(2), 44–60.
Bailey, A.L., Butler, F.A., Stevens, R., and Lord, C. (2007). Further specifying the language demands of school. In A.L. Bailey (Ed.), The Language Demands of School: Putting Academic English to the Test (pp. 103–156). New Haven, CT: Yale University Press.
Bailey, A.L., and Heritage, M. (2017). Imperatives for teacher education: Findings from studies of effective teaching for English language learners. In M. Peters, B. Cowie, and I. Menter (Eds.), A Companion to Research in Teacher Education. (pp. 697–712). Berlin, Germany: Springer.
Barton, A.C., and Tan, E. (2009). Funds of knowledge and discourses and hybrid space. Journal of Research in Science Teaching, 46(1), 50–73.
Beckner, C., Blythe, R., Bybee, J., Christiansen, M., Croft, W., Ellis, N.C., Holland, J., Ke, J., Larsen-Freeman, D., and Schoenemann, T. (2009). Language is a complex adaptive system: Position paper. Language Learning, 59(1), 1–26. doi:10.1111/j.1467-9922.2009.00533.x.
Berland, L.K., and Reiser, B.J. (2011). Classroom communities’ adaptations of the practice of scientific argumentation. Science Education, 95(2), 191–216.
Berland, L.K., Schwarz, C.V., Krist, C., Kenyon, L., Lo, A.S., and Reiser, B.J. (2016). Epistemologies in practice: Making scientific practices meaningful for students. Journal of Research in Science Teaching, 53(7), 1082–1112.
Bezemer, J., and Kress, G. (2008). Writing in multimodal texts: A social semiotic account of designs for learning. Written Communication, 25(2), 166–195.
Bianchini, J.A. (1999). From here to equity: The influence of status on student access to and understanding of science. Science Education, 83(5), 577–601.
Blackwell, L.S., Trzesniewski, K.H., and Dweck, C.S. (2007). Implicit theories of intelligence predict achievement across an adolescent transition: A longitudinal study and an intervention. Child Development, 78(1), 246–263.
Bricker, L.A., and Bell, P. (2008). Conceptualizations of argumentation from science studies and the learning sciences and their implications for the practices of science education. Science Education, 92(3), 473–493.
Bunch, G.C. (2013). Pedagogical language knowledge: Preparing mainstream teachers for English learners in the new standards era. Review of Research in Education, 37(1), 298–341.
Bunch, G.C., Walqui, A., and Pearson, P.D. (2014). Complex text and new common standards in the United States: Pedagogical implications for English learners. TESOL Quarterly, 48(3), 533–559.
Carpenter, T.P., Fennema, E., Franke, M.L., Levi, L., and Empson, S.B. (1999). Children’s Mathematics: Cognitively Guided Instruction. Portsmouth, NH: Heinemann.
Carr, R.L., Bennett, L.D., and Strobel, J. (2012). Engineering in the K–12 STEM standards of the 50 U.S. states: An analysis of presence and extent. Journal of Engineering Education, 101(3), 539–564.
Cavagnetto, A.R. (2010). Argument to foster scientific literacy: A review of argument interventions in K–12 science contexts. Review of Educational Research, 80(3), 336–371.
Chinn, C.A., Buckland, L.A., and Samarapungavan, A. (2011). Expanding the dimensions of epistemic cognition: Arguments from philosophy and psychology. Educational Psychologist, 46(3), 141–167.
Coady, M.R., Harper, C., and de Jong, E. J. (2016). Aiming for equity: Preparing mainstream teachers for inclusion or inclusive classrooms? TESOL Quarterly, 50(2), 340–356. doi:10.1002/tesq.223.
Cobb, P., Wood, T., and Yackel, E. (1993). Discourse, mathematical thinking, and classroom practice. In E.A. Forman, N. Minick, and C.A. Stone (Eds.), Context for Learning: Sociocultural Dynamics in Children’s Development (pp. 91–119). New York: Oxford University Press.
Crowhurst, M. (1994). Language and Learning Across the Curriculum. Scarborough, Ontario: Allyn and Bacon.
Cunningham, C.M., and Kelly, G.K. (2017). Framing engineering practices in elementary school classrooms. International Journal of Engineering Education, 33(1B), 295–307.
de Araujo, Z. (2017). Connections between secondary mathematics teachers’ beliefs and their selection of tasks for English language learners. Curriculum Inquiry, 47(4), 363–389. doi:10.1080/03626784.2017.1368351.
Dominguez, H. (2005). Articulation and gesticulation of mathematical knowledge during problem solving. Bilingual Research Journal, 29(2), 269–293.
Duschl, R.A. (2008). Science education in three-part harmony: Balancing conceptual, epistemic, and social learning goals. Review of Research in Education, 32, 268–291.
Duschl, R.A., and Osborne, J. (2002). Supporting and promoting argumentation discourse in science education. Studies in Science Education, 38(1), 39–72.
Elby, A., and Hammer, D. (2010). Epistemological resources and framing: A cognitive framework for helping teachers interpret and respond to their students’ epistemologies. In L.D. Bendixen and F.C. Feucht (Eds.), Personal Epistemology in the Classroom: Theory, Research, and Implications for Practice (pp. 409–434). Cambridge: Cambridge University Press.
Evagorou, M., Jiménez-Aleixandre, M.P., and Osborne, J. (2012). ‘Should we kill the grey squirrels?’ A study exploring students’ justifications and decision-making. International Journal of Science Education, 34(3), 401–428.
Ferguson, C.A. (1994). Dialect, register, and genre: Working assumptions about conventionalization. In D. Biber and E. Finegan (Eds.), Sociolinguistic Perspectives on Register (pp. 15–30). New York: Oxford University Press.
Galguera, T. (2011). Participant structures as professional learning tasks and the development of pedagogical language knowledge among preservice teachers. Teacher Education Quarterly, 38(1), 85–106.
Garrett, N. (2009). Technology in the service of language learning: Trends and issues. The Modern Language Journal, 23, 697–718.
Gibbons, P. (2015). Scaffolding Language, Scaffolding Learning: Teaching English Language Learners in the Mainstream Classroom (2nd ed.). Portsmouth, NH: Heinemann.
Grapin, S.E. (2018). Multimodality in the new content standards era: Implications for English learners. TESOL Quarterly. Available: https://onlinelibrary.wiley.com/doi/abs/10.1002/tesq.443?af=R [June 2018].
Grover, S., and Pea, R. (2013). Computational thinking in K–12: A review of the state of the field. Educational Researcher, 42(1), 38–43.
Gutiérrez, K.D., and Rogoff, B. (2003). Cultural ways of learning: Individual traits or repertoires of practice. Educational Researcher, 32(5), 19–25.
Halliday, M.A.K. (1978). Sociolinguistic aspects of mathematical education. In The Social Interpretation of Language and Meaning (pp. 194–204). London, UK: University Park Press.
Halliday, M.A.K. (2014). Halliday’s Introduction to Functional Grammar (4th ed.). New York: Routledge.
Halliday, M.A.K., and Martin, J.R. (1993). Writing Science: Literacy and Discursive Power. Pittsburgh, PA: University of Pittsburgh Press.
Harris, C.J., Krajcik, J.S., Pellegrino, J.W., and McElhaney, K.W. (2016). Constructing Assessment Tasks That Blend Disciplinary Core Ideas, Crosscutting Concepts, and Science Practice for Classroom Formative Applications. Menlo Park, CA: SRI International.
Hawkins, M.R., and Mori, J. (2018). Special issue on ‘trans’ perspectives. Applied Linguistics, 39(1).
Haynes, J., and Zacarian, D. (2010). Teaching English Language Learners Across the Content Areas. Alexandria, VA: ACSD.
Healy, L., and Fernandes, S.H.A.A. (2014). Blind students, special needs, and mathematics learning. In S. Lerman (Ed.), Encyclopedia of Mathematics Education (pp. 61–63). Dordrecht: Springer.
Herrenkohl, L.R., and Cornelius, L. (2013). Investigating elementary students’ scientific and historical argumentation. Journal of the Learning Sciences, 22(3), 413–461.
Hertel, J.D., Cunningham, C.M., and Kelly, G.K. (2017). The roles of engineering notebooks in shaping elementary engineering student discourse and practice. International Journal of Science Education, 39(9), 1194–1217. doi:10.1080/09500693.2017.1317864.
Hiebert, J., and Carpenter, T.P. (1992). Learning and teaching with understanding. In D.A. Grouws (Ed.), Handbook of Research on Mathematics Teaching and Learning: A Project of the National Council of Teachers of Mathematics (pp. 65–97). New York: Macmillan.
International Technology Education Association. (2000). Standards for Technological Literacy: Content for the Study of Technology. Reston, VA: Author. Available: https://www.iteea.org/42511.aspx [August 2018].
Ishimaru, A., Barajas-López, F., and Bang, M. (2015). Centering family knowledge to develop children’s empowered mathematics identifies. Journal of Family Diversity in Education, 1(4), 1–22.
Jiménez-Aleixandre, M.P. (2014). Determinism and underdetermination in genetics: Implications for students’ engagement in argumentation and epistemic practices. Science & Education, 23(2), 465–484.
Kelly, G.J. (2008). Inquiry, activity, and epistemic practice. In R. Duschl and R. Grandy (Eds.), Teaching Scientific Inquiry: Recommendations for Research and Implementation (pp. 99–117, 288–291). Rotterdam, The Netherlands: Sense.
Kelly, G.J. (2016). Methodological considerations for the study of epistemic cognition in practice. In J.A. Greene, W.A. Sandoval, and I. Braten (Eds.), Handbook of Epistemic Cognition (pp. 393–408). New York: Routledge.
Kelly, G.J., and Licona, P. (2018). Epistemic practices and science education. In M.R. Matthews (Ed.), History, Philosophy, and Science Teaching: New Perspectives (pp. 139–165). Springer International.
Kelly, G.J., Cunningham, C.M., and Ricketts, A. (2017). Engaging in identity work through engineering practices in elementary classrooms. Linguistics & Education, 39, 48–59. doi:10.1016/j.linged.2017.05.003.
Khisty, L.L. (1995). Making inequality: Issues of language and meanings in mathematics teaching with Hispanic students. In W.G. Secada, E. Fennema, and L.B. Adajian (Eds.), New Directions for Equity in Mathematics Education (pp. 279–297). New York: Cambridge University Press.
Kibler, A.K., Walqui, A., and Bunch, G.C. (2015). Transformational opportunities: Language and literacy instruction for English language learners in the common core era in the United States. TESOL Journal, 6(1), 9–35.
Knorr-Cetina, K. (1999). Epistemic Cultures: How the Sciences Make Knowledge. Cambridge, MA: Harvard University Press.
Lampert, M. (1990). When the problem is not the question and the solution is not the answer: Mathematical knowing and teaching. American Educational Research Journal, 27(1), 29–63.
Larsen-Freeman, D. (1997). Chaos/complexity science and second language acquisition. Applied Linguistics, 18(2), 141–165. doi:10.1093/applin/18.2.141.
Larsen-Freeman, D. (2007). Reflecting on the cognitive-social debate in second language acquisition. The Modern Language Journal, 7(S1), 773–787.
Lave, J., and Wenger, E. (1991). Situated Learning: Legitimate Peripheral Participation. Cambridge, UK: Cambridge University Press.
Lee, O., Quinn, H., and Valdés, G. (2013). Science and language for English language learners in relation to Next Generation Science Standards and with implications for Common Core State Standards for English language arts and mathematics. Educational Researcher, 42(4), 223–233.
Lee, O., Valdés, G., and Llosa, L. (2015–2019). Development of Language-Focused Three-Dimensional Science Instructional Materials to Support English Language Learners in Fifth Grade. Alexandria, VA: National Science Foundation, Discovery Research K–12.
Lee, O., Grapin, S., and Haas, A. (2018). How science instructional shifts and language instructional shifts support each other for English learners: Talk in the science classroom. In A. Bailey, C. Maher, and L. Wilkinson (Eds.), Language, Literacy and Learning in the STEM Disciplines: How Language Counts for English Learners (pp. 35–52). New York: Routledge.
Lemke, J.L. (1990). Talking Science: Language, Learning and Values. Norwood, NJ: Ablex.
Love, K. (2010). Literacy pedagogical content knowledge in the secondary curriculum. Pedagogies: An International Journal, 5(4), 338–355.
Manz, E. (2012). Understanding the co-development of modeling practice and ecological knowledge. Science Education, 96(6), 1071–1105.
Massachusetts Department of Education. (2001, May). Massachusetts Science and Technology/Engineering Framework. Available: http://www.doe.mass.edu/frameworks/scitech/2001/ [July 2018].
Moje, E.B. (2000). “To be part of the story”: The literacy practices of “gangsta” adolescents. Teachers College Record, 102(3), 652–690.
Moll, L.C., Amani, C., Neff, D., and Gonzalez, N. (1991). Funds of knowledge for teaching: Using a quantitative approach to connect homes and classrooms. Theory into Practice, XXXI(2), 132–141.
Moschkovich, J.N. (1999). Supporting the participation of English language learners in mathematical discussions. For the Learning of Mathematics, 19(1), 11–19.
Moschkovich, J.N. (2002). A situated and sociocultural perspective on bilingual mathematics learners. Mathematical Thinking and Learning, 4(2–3), 189–212.
Moschkovich, J.N. (2004). Appropriating mathematical practices: A case study of learning to use and explore functions through interaction with a tutor. Educational Studies in Mathematics, 5(1/3), 49–80.
Moschkovich, J.N. (2007). Examining mathematical discourse practices. For the Learning of Mathematics, 27(1), 24–30.
Moschkovich, J.N. (2010). Language(s) and learning mathematics: Resources, challenges, and issues for research. In J.N. Moschkovich (Ed.), Language and Mathematics Education: Multiple Perspectives and Directions for Research (pp. 1–28). Charlotte, NC: Information Age.
Moschkovich, J.N. (2012). How equity concerns lead to attention to mathematical discourse. In B. Herbel-Eisenmann, J. Choppin, D. Wagner, and D. Pimm (Eds.), Equity in Discourse for Mathematics Education: Theories, Practices, and Policies. New York: Springer.
Moschkovich, J.N. (2013). Issues regarding the concept of mathematical practices. In Y. Li and J.N. Moschkovich, (Eds.), Proficiency and Beliefs in Learning and Teaching Mathematics: Learning from Alan Schoenfeld and Günter Toerner (pp. 257–275). Rotterdam, The Netherlands: Sense.
Moschkovich, J.N. (2015a). Academic literacy in mathematics for English Learners. Journal of Mathematical Behavior, 40(Pt. A), 43–62.
Moschkovich, J.N. (2015b). Scaffolding mathematical practices. ZDM, The International Journal on Mathematics Education, 47(7), 1067–1078.
Nasir, N.S., Rosebery, A.S., Warren, B., and Lee, C.D. (2014). Learning as a cultural process: Achieving equity through diversity. In The Cambridge Handbook of the Learning Sciences (2nd ed., pp. 686–706). New York: Cambridge University Press.
National Academy of Engineering. (2010). Standards for K–12 Engineering Education? Washington, DC: The National Academies Press.
National Academy of Engineering and National Research Council. (2002). Technically Speaking: Why All Americans Need to Know More About Technology. Washington, DC: National Academy Press.
National Academy of Engineering and National Research Council. (2009). Engineering in K–12 Education. Washington, DC: The National Academies Press.
National Academy of Engineering and National Research Council. (2014). STEM Integration in K–12 Education: Status, Prospects, and an Agenda for Research. Washington, DC: The National Academies Press.
National Governors Association, Center for Best Practices, and Council of Chief State School Officers. (2010). Reaching Higher: The Common Core State Standards Validation Committee. Available: http://www.corestandards.org/assets/CommonCoreReport_6.10.pdf [September 2018].
National Research Council. (2000). How People Learn: Brain, Mind, Experience, and School: Expanded Edition. Washington, DC: National Academy Press.
National Research Council. (2001). Adding It Up: Helping Children Learn Mathematics. Washington, DC: National Academy Press.
National Research Council. (2006). America’s Lab Report: Investigations in High School Science. Washington, DC: The National Academies Press.
National Research Council. (2007). Taking Science to School: Learning and Teaching Science in Grades K–8. Washington, DC: The National Academies Press.
National Research Council. (2009). Learning Science in Informal Environments: People, Places, and Pursuits. Washington, DC: The National Academies Press.
National Research Council. (2010). Report of a Workshop on the Scope and Nature of Computational Thinking. Washington, DC: The National Academies Press.
National Research Council. (2012). A Framework for K–12 Science Education: Practices, Crosscutting Concepts, and Core Ideas. Washington, DC: The National Academies Press.
Oliveira, A.W. (2010). Improving teacher questioning in science inquiry discussion through professional development. Journal of Research in Science Teaching, 47(4), 422–453.
Östman, L., and Wickman, P.-O. (2014). A pragmatic approach on epistemology, teaching, and learning. Science Education, 98(3), 375–382.
Painter, C. (1999). Learning through Language in Early Childhood. London, UK: Cassell.
Park, T., Pearson, D., and Richardson, G.B. (2017). Curriculum integration: Helping career and technical education students truly develop college and career readiness. Peabody Journal of Education, 92(2), 192–208.
Pimm, D. (1987). Speaking Mathematically: Communication in Mathematics Classrooms. London, UK: Routledge.
Pluta, W.J., Chinn, C.A., and Duncan, R.G. (2011). Learners’ epistemic criteria for good scientific models. Journal of Research in Science Teaching, 48(5), 486–511.
Poza, L.E. (2018). The language of ciencia: Translanguaging and learning in a bilingual science classroom. International Journal of Bilingual Education and Bilingualism, 21(1), 1–19.
Quinn, H., Lee, O., and Valdés, G. (2012). Language Demands and Opportunities in Relation to Next Generation Science Standards for English Language Learners: What Teachers Need to Know. Stanford, CA: Stanford University, Understanding Language. Available: http://ell.stanford.edu/sites/default/files/pdf/academic-papers/03-Quinn%20Lee%20Valdes%20Language%20and%20Opportunities%20in%20Science%20FINAL.pdf [June 2018].
Ryoo, K., and Bedell, K. (2017). The effects of visualizations on linguistically diverse students’ understanding of energy and matter in life science. Journal of Research in Science Teaching, 54(10), 1274–1301.
Sadler, T.D. (2006). Promoting discourse and argumentation in science teacher education. Journal of Science Teacher Education, 17(4), 323–346.
Sadler, T.D. (2009). Situated learning in science education: socio-scientific issues as contexts for practice. Studies in Science Education, 45(1), 1–42.
Sampson, V., and Clark, D. (2008). Assessment of the ways students generate arguments in science education: Current perspectives and recommendations for future directions. Science Education, 92(3), 447–472.
Sandoval, W. (2005). Understanding students’ practical epistemologies and their influence. Science Education, 89, 634–656.
Sandoval, W. (2014). Conjecture mapping: An approach to systematic educational design research. Journal of the Learning Sciences, 23(1), 18–36.
Schleppegrell, M.J. (2004). The Language of Schooling: A Functional Linguistics Perspective. Mahwah, NJ: Lawrence Erlbaum Associates.
Schleppegrell, M.J. (2007). The linguistic challenges of mathematics teaching and learning: A research review. Reading & Writing Quarterly, 23(2), 139–159.
Schoenfeld, A.H. (1992). Learning to think mathematically: Problem solving, metacognition, and sense making in mathematics. In D.A. Grouws (Ed.), NCTM Handbook of Research on Mathematics Teaching and Learning (pp. 334–370). New York: Macmillan. Available: http://hplengr.engr.wisc.edu/Math_Schoenfeld.pdf [June 2018].
Silk, E.M., Schunn, C.D., and Cary, M.S. (2009). The impact of an engineering design curriculum on science reasoning in an urban setting. Journal of Science Education and Technology, 18(3), 209–223.
Sorto, M.A., and Bower, R.S.G. (2017). Quality of instruction in linguistically diverse classrooms: It matters! In A. Fernandes, S. Crespo, and M. Civil (Eds.), Access and Equity: Promoting High Quality Mathematics in Grades 6–8 (pp. 27–40). Reston, VA: National Council of Teachers of Mathematics.
Turkan, C., de Oliveira, C., Lee, O., and Phelps, G. (2014). Proposing a knowledge base for teaching academic content to English language learners: Disciplinary linguistic knowledge. Teachers College Record, 116(3).
Valdés, G. (2015). Latin@s and the intergenerational continuity of Spanish: The challenges of curricularizing language. International Multilingual Research Journal, 9(4), 253–273.
Valdés-Fallis, G. (1978). Code switching and the classroom teacher. Language in Education: Theory and Practice (vol. 4). Wellington, VA: Center for Applied Linguistics.
Vossoughi, S., Hooper, P., and Escudé, M. (2016). Making through the lens of culture and power: Towards transformative visions for educational equity. Harvard Educational Review, 86(2), 206–232.
Warschauer, M., and Meskill, C. (2000). Technology and second language learning. In J. Rosenthal (Ed.), Handbook of Undergraduate Second Language Education (pp. 303–318). Mahwah, NJ: Lawrence Erlbaum Associates.
Watson-Verran, H., and Turnbull, D. (1995). Science and other indigenous knowledge systems. In S. Jasanoff, G.E. Markle, J.C. Peterson, and T. Pinch (Eds.), Handbook of Science and Technology Studies (pp. 115–139). Thousand Oaks, CA: SAGE.
Weintrop, D., Beheshti, E., Horn, M., Orton, K., Jona, K., Trouille, L., and Wilensky, U. (2016). Defining computational thinking for mathematics and science classrooms. Journal of Science Education and Technology, 25(1), 127–147.
Wendell, K.B., Wright, C.G., and Paugh, P. (2017). Reflective decision-making in elementary students’ engineering design. Journal of Engineering Education, 106(3), 356–397.
Wickman, P.-O. (2004). The practical epistemologies of the classroom: A study of laboratory work. Science Education, 88(3), 325–344.
Wing, J.M. (2006). Computational thinking. Communications of the ACM, 49(3), 33–35.
Yocom de Romero, N., Slater, P., and DeCristofano, C. (2006). Design challenges are “ELLementary.” Science & Children, 34–37.
Zahner, W., and Moschkovich, J.N. (2011). Bilingual students using two languages during peer mathematics discussions: What does it mean? In K. Tellez, J. Moschkovich, and M. Civil (Eds.), Latinos/as and Mathematics Education: Research on Learning and Teaching in Classrooms and Communities (pp. 37–62). Charlotte, NC: Information Age.
Zembal-Saul, C. (2009). Learning to teach elementary school science as argument. Science Education, 93(4), 687–719.
Zentella, A.C. (1981). Tá bien, You could answer me en cualquier idioma: Puerto Rican code switching in bilingual classrooms. In R. Durán (Ed.), Latino Language and Communicative Behavior (pp. 109–130), Norwood, NJ: Ablex.
Zheng, B., Warschauer, M., Hwang, J.K., and Collins, P. (2014). Laptop use, interactive science software, and science learning among at-risk students. Journal of Science Education and Technology, 23(4), 591–603.
Zuengler, J., and Miller, E. (2006). Cognitive and sociocultural perspectives: Two parallel SLA worlds? TESOL Quarterly, 40(1), 35–58.
This page intentionally left blank.


































