Appendix A
Risk Modeling and Uncertainty Analysis
INTRODUCTION
Epidemiologic studies of underground miners exposed to radon have convincingly established that radon-decay products are carcinogenic and that exposure to these products at levels previously found in mines increases lung-cancer risk (NCRP 1984a,b; NRC 1988; Samet 1989; Lubin and others 1994a). Lubin and others (1994a) conducted a pooled analysis of data from 11 major studies of underground miners (identified as the studies from Colorado, Czechoslovakia, China, Ontario, Newfoundland, Sweden, New Mexico, Beaverlodge, Port Radium, Radium Hill, and France). That analysis included over 2,700 lung-cancer cases among 68,000 miners representing nearly 1.2 million person-years of observation. Lubin and others (1994) found that the relationship between the relative risk (RR) of lung-cancer and cumulative exposure to radon progeny was generally consistent with linearity within each cohort. However, estimates of the excess relative risk (ERR) due to exposure to radon progeny varied substantially among the cohorts. For example, the ERR following exposure to 100 working level months (WLM) varied from 0.16 in China to 5.06 in Radium Hill. The precision of these estimates was highly variable from cohort to cohort.
The combined effect of radon exposure and tobacco smoke on lung-cancer risk has been discussed in the literature (Lundin and others 1971; Whittemore and McMillan 1983; Moolgavkar and others 1993; Lubin 1994) (See also appendix C.) Although the Colorado Plateau uranium miners study has revealed a synergistic effect between exposure to radon and cigarette smoking, this interaction is not well characterized (NRC 1988; Lubin 1994). Data from two large studies, the
China tin miners study and the Colorado Plateau uranium miners study, indicated that the lung-cancer risk associated with the combined exposure is greater than the sum of the risks associated with each factor individually, evidence of a synergistic effect between radon and tobacco smoke in the induction of lung-cancer. Data on tobacco use, available for 6 of 11 cohorts, are summarized in Table A-1. In the Colorado, Newfoundland and New Mexico studies, detailed data on tobacco use including duration, intensity, and cessation are available, whereas studies in China and Radium Hill identify individuals only as ever-smokers or never-smokers.
Since publication of the report by Lubin and others (1994a), studies of the Chinese tin miners, and of the Czech, Colorado, and French uranium miners have been updated or modified (Lubin and others 1997). Modifications of these four data sets are described in Table A-2. In addition, there has also been a reassessment of exposure for a nested case-control series within the Beaverlodge cohort of uranium miners, including all lung-cancer cases and matched control subjects (Howe and Stager 1996). For the Beaverlodge miners, exposure estimates were about 60% higher than the original values. Because of the computational and conceptual difficulties of merging case-control data with cohort data, only the data from the Beaverlodge cohort study with the original exposure estimates were used in the BEIR VI analysis.
In the first part of this appendix, we consider models for describing the relationship between exposure to radon and lung-cancer risk. We begin with a review of risk models developed by other investigators. In order to lay the foundation for the committee's risk model, we then discuss methods for combining data from different sources, including random-effects and two-stage methods. Those methods are then used in a combined reanalysis of the updated data from the 11 miner cohorts considered previously by Lubin and others (1994a).
By using a random-effects model, the overall effect of radon on lung-cancer risk can be described by fixed regression coefficients, and variation across cohorts characterized by random regression coefficients (Wang and others 1995). Two-stage regression analysis represents an alternative to random-effects methods, which benefits from an element of numerical simplicity. Although both methods are considered, the emphasis in the report is on the computationally simpler two-stage method.
In the second part of the appendix we focus on uncertainties in predictions of risk. There are many sources of uncertainty in health-risk assessments. Epidemiologic data on exposed human populations can be subject to considerable uncertainty. Retrospective exposure profiles are difficult to construct, particularly with chronic diseases such as cancer for which exposure data many years prior to disease ascertainment are needed. For example, radon measurements in homes taken today may not reflect past exposures because people change residences, make building renovations, or change their lifestyle such as sleeping with the bedroom window open or closed, and because of inherent variability in radon
TABLE A-1 Characteristics of 11 underground miner studiesa
TABLE A-2 Summary of new information on 5 miner cohorts
|
Cohort |
Updated information |
Related reference |
|
Chinese tin miners |
New information indicated miners worked 313 days/yr before 1953, 285 days/yr from 1953–84, and 259 days/yr from 1985. |
Unpublished information |
|
Czech uranium miners |
Exposure histories re-evaluated and follow-up improved. There were 705 lung-cancer cases, compared to 661 in the previous analysis. Cohort was enlarged from 4,284 to 4,320 miners, including all miners who entered 1948–59. |
Tomásek and others 1994 |
|
Colorado uranium miners |
Follow-up extended from December 31, 1987 to December 31, 1990. In updated data, there were 336 lung-cancer deaths < 3,200 WLM used in the pooled analysis (and 377 total cases), compared to 294 lung-cancer deaths < 3,200 WLM (and 329 total cases). |
Hornung and others 1995 |
|
Beaverlodge uranium minersa |
Re-calculation of WLM exposures, but limited to a nested case-control sample. |
Howe and Stager 1996 |
|
French uranium miners |
Corrections of some (non-lung-cancer) outcomes and exposure data. Changes were not extensive. |
Unpublished information |
|
a The most recent update of the Beaverlodge data was not included in the BEIR VI analysis. |
||
measurements. Exposures in prospective studies may also be uncertain. In addition to errors in exposure ascertainment, errors in disease diagnosis are also possible. In epidemiologic studies using computerized record linkage to link exposure data from one database with health status in another database, even vital status can be in error (Bartlett and others 1993).
In addition to identifying sources of uncertainty, the committee attempted a quantitative analysis of uncertainty in radon risk estimates. This analysis is conducted within the general framework developed by Rai and others (1996) for quantitative uncertainty analysis in health risk assessment. Since not all sources of uncertainty and variability could be fully characterized, the committee acknowledges that this analysis is necessarily incomplete. Nonetheless, the committee felt that this analysis is informative, and provides a basis for further research in this area.
PREVIOUS RISK MODELS
A number of different exposure-response models may be used to describe the relationship between lung-cancer risk and exposure to radon (Krewski and others 1992). Analyses of miner cohorts have been largely based on empirical models that describe risk as a linear or linear-quadratic function of exposure. Those analyses have formed the basis for estimates of risks of exposure to radon prepared by the National Research Council (NRC), the National Commission on Radiological Protection and Measurements (NCRP), and the International Commission on Radiological Protection (ICRP). Previous estimates of risk prepared by those organizations are reviewed here.
Empirical Models
Numerous studies of lung-cancer in radon-exposed underground miners have been published, although until recently the number of distinct populations had been small and the total follow-up time and numbers of lung-cancer cases limited (NRC 1988). Those analyses are described in detail in appendix D. The relatively small numbers of lung-cancer cases in individual studies have hindered the evaluation of temporal patterns and other determinants of risk. Early efforts at risk modeling were limited by the lack of data and, as a result, investigators relied on summaries of the miner studies. A complete review of the earlier risk estimates was provided in the BEIR IV Report (NRC 1988). In the current report, we review the most relevant efforts.
National Research Council (1980)
The NRC BEIR III committee based their modeling efforts on results of miner studies (NRC 1980). The model assumed a linear relationship between
exposure and the absolute excess risk of lung-cancer. The absolute or excess risk (ER) model represents lung-cancer mortality as r(x,z,w) = ro(x) + g(z,w), where ro(x) is the background lung-cancer rate, and g(z,w) is the effect of exposure. Here, w denotes cumulative exposure, x is a vector of covariates which affect the background lung-cancer rate, and z is a vector of covariates that may modify the exposure-response relationship. The excess risk varied by categories of attained age, <35, 35–49, 50–65, >65 yrs, with 0, 10, 20, 30 excess cases per 106 person-years per unit of exposure in WLM. In addition, the model specified a minimum latent period of 15–20 yr for those exposed at ages 15–34 or 10 yr for those exposed above age 34. The derivation of this model and the method of combining the available miner data were not described. The model did not directly account for the effects of smoking.
National Council on Radiation Protection and Measurements (1984)
The National Council on Radiation Protection and Measurements (NCRP) committee's Report 77 (NCRP 1984a) and its Report 78 (NCRP 1984b) adopted the excess-risk model of Harley and Pasternak (1981). That model was based on the following assumptions.
-
The latent interval is 5 yr for persons first exposed at ages 35 yr and older, and (40-u) yr for persons exposed under age 35 yr, where u is the age at first exposure.
-
Following a latent interval, disease rate declines exponentially with time since exposure.
-
lung-cancer is rare before age 40 yrs.
-
The median age at lung-cancer occurrence for miners is age 60 yr for never-smokers and
-
50 yr for ever-smokers.
-
The minimum time from initial cell transformation to clinical detection is 5 yr.
For an annual exposure at age u, the excess lung-cancer risk at age t > u (and t > 40 years of age) is taken to be
A(t,u) = Re-m(t-u)S(t) / S(u), (1)
where R is the excess-risk coefficient per WLM, S(u) is the probability of survival to a specified age, and m is the rate of removal of transformed stem cells due to repair or cell death. The NCRP committee fixed m = ln(2)/20 yr-1, corresponding to a 20-yr half-life for exposure effects. The exponential term reduces the exposure effect with time after exposure, while the survival probability adjusts for competing causes of mortality. Lifetime risk for exposure at age u is obtained by integrating over age (t) from age 40 yr to some specified life-span. For chronic
exposures in years u1, ... ,un, lifetime risks are obtained by summing risks for each of the annual exposures.
Parameters for the NCRP model were values assumed to be ''reasonable" from published data, but not based on a direct evaluation of the miner data. Although the choices of R and m are critical in applying the model, the NCRP provides little guidance on their selection. The 20-yr half-life was selected as being "representative for extrapolation." S was taken from 1978 World Health Organization tables for the U.S. population. NCRP 78 had the first model to incorporate a reduction of risk with time-since-exposure.
In the NCRP model, the joint effects of radon-progeny exposure and smoking were considered additive. That is, radon exposure had the same effect on the excess risk, regardless of smoking status. The increased absolute excess risk with radon-progeny exposure was added to the background lung-cancer risk in ever-smokers or in never-smokers.
International Commission on Radiological Protection (1987)
Report 50 of the International Commission on Radiological Protection presented a risk model for indoor radon exposure (ICRP 1987). The ICRP model was based on a simple constant excess relative risk model of the form
RR(w) = 1 + ßw, (2)
where w is total cumulative exposure allowing for a lag interval of 10 years. No accommodation for variation in the exposure-response parameter ß with other factors was included. The value ß was taken as 0.7% per WLM, a representative value for the excess relative risk of the available miner studies after adjustment for exposure-dose differences between mines and homes. Based on the study of atomic-bomb survivors and on dosimetric considerations, the model assumed a greater effect for radon-progeny exposure at young ages; ß was set at 2.1% per VVLM for exposures occurring under the age of 20 years.
In the ICRP model, the joint effects of radon-progeny exposure and smoking were assumed multiplicative. Thus, for smoking status-specific risk estimation, the radon relative-risk model was applied separately to ever-smokers and to never-smokers. Similarly, the same model was applied to the background rates for males and for females.
Thomas and Others (1985)
In recent years, the number of data sets on radon-exposed miners has increased and follow-up has lengthened for the cohorts developed initially. Thus, direct synthesis of multiple miner studies has become increasingly important and informative for defining the form of the risk model and estimating the values of its parameters. The first joint analysis of results of epidemiologic studies using
modern statistical methodology was carried out by Thomas and others (1985). (See also Thomas and McNeill 1982, an earlier and more detailed report on which the more recent work was based.) They carried out a meta-analysis of 5 miner studies. They fit relative risk and excess (or attributable) risk models, including various "cell killing" and "non-linear" models to summary data from cohort studies from Czechoslovakia (now the Czech Republic), Colorado, Ontario, Newfoundland, and Sweden. Original data from these cohorts with more extensive follow-up are included in the analysis conducted by Lubin and others (1994a) and by this BEIR VI committee. Thomas and others found no significant deviation from a linear exposure-response relationship, although inferences on curvilinearity were somewhat dependent on the choice of referent population. Fitting a linear excess relative-risk (ERR) model, Thomas and others (1985) estimated the ERR to increase by 2.28% per WLM, implying a doubling of risk at 44 WLM. The ERR per WLM was found to vary with attained age. The risk with combined exposure to smoking and to radon progeny, while consistent with a multiplicative model, was most consistent with a relationship intermediate between additive and multiplicative. The analyses were necessarily limited by the extent of the data and not having access to original data. However, many of these results presaged subsequent work.
National Research Council (1988)
A comprehensive assessment of risk from underground exposure to radon progeny was carried out by the National Research Council's Biological Effects of Ionizing Radiation IV committee (BEIR IV). That committee conducted a pooled analysis of data from four cohort studies of underground miners including the studies of Colorado, Ontario, Beaverlodge, and Sweden (NRC 1988). The Beaverlodge and Swedish data sets were the same as in the current analysis, while less extensive data were available from the other 2 studies. The BEIR IV committee used regression methods similar to those used in this report. The committee found that excess risk did not increase in a simple fashion with exposure, either in direct proportion to background (a constant ERR model) or at a constant level above background (that is, a constant attributable or excess risk [ER] model). Rather, the risk varied with two time-dependent factors: time since exposure and attained age. The analysis showed that lung-cancer risk increased linearly with cumulative exposure to radon progeny, and that the exposure-response trend declined with attained age and with time since exposure. The committee evaluated other potentially important covariates, such as age at first exposure and exposure duration, but risk patterns were not consistent across studies. Although the constant ERR model was not compatible with the data, the ERR per WLM was estimated to be 1.34% (corresponding to a doubling of risk at 75 WLM) under this model.
Analyses of the combined effects of radon-progeny exposure and smoking in
the Colorado and New Mexico (a case-control subset of data included in the current analysis) miners were also presented in the BEIR IV Report. Results indicated that while a multiplicative risk relationship between the two factors could not be excluded, an intermediate relationship between additive and multiplicative was most consistent with the data.
International Commission on Radiological Protection (1993)
In a 1993 report on risks from radon-progeny exposure in homes and at work (ICRP 1993), ICRP did not provide its own risk model, but used the so-called "GSF model" developed by Jacobi and others (1992). That model was related to a "smoothed" version of the BEIR IV model (NRC 1988). Compared to the BEIR IV model, the GSF model provided a monotonic variation of the excess relative risk with age. The GSF model had the same general structure as the BEIR IV model, with the effect of exposure adjusted by time since the exposure occurred, but with the exposure-response relationship determined by age at exposure, as opposed to attained age. For attained age a, exposure we, occurring at age ae, and time since exposure f, the ERR at age a was defined as:
Exposures within 4 years f = a - ae = 4) were assumed to have no impact on the RR of lung-cancer. The function s was not explicitly defined in the ICRP Report, but was described as a decreasing function of age at exposure, taking values of 0.036 per WLM for age at exposure of 20 years and 0.017 per WLM for age at exposure of 60 years. The effect of time since exposure on risk was modeled through the function ![]() defined as
defined as
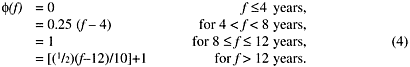
According to the ICRP report, risk projections based on the GSF model were similar to those of the BEIR IV model (ICRP 1993).
The ICRP approach was notable in two respects. First, in contrast to the earlier ICRP risk model, which was based on a constant relative risk in cumulative exposure (ICRP 1987), no modification to the exposure-response relationship was included for exposures received at ages 20 years and under. The previous ICRP model postulated a 3-fold greater exposure-response for young ages. Second, the ICRP model assumed an equal (absolute) excess risk in males and females. Thus, the model assumed that the radon-related excess risk in males should be directly added to the background lung-cancer rate in females. This additive feature of the model results in a markedly greater relative risk in females than in males.
National Cancer Institute (1994)
The analysis and risk model published by Lubin and others (1994a, 1995b), which served as the starting point for the current report, utilized methods similar to those of the BEIR IV committee (NRC 1988). This approach assumes that the time to death from lung-cancer is distributed in a fashion so that follow-up time to a key event was piece-wise exponential, that is, death rates are constant within fixed time intervals and exposure categories. Note that death times can be censored due to loss to follow-up or study termination. This assumption was considered appropriate for two reasons: 1) variability in lung-cancer mortality rates within each time interval and exposure category was small relative to the variability between intervals; and 2) disease rates within time intervals and exposure categories were well-characterized by the average rate. The method allowed for use of external referent rates (although they were not used in Lubin and others 1994a, 1995b or in the current analysis) and for the modeling of excess disease rates. A full discussion of these models, including regression of the standardized mortality ratio, is given in Breslow and others (1983) and Breslow and Day (1987).
Relative-risk regression procedures were applied to data summarized in a multi-way table, consisting of events, person-years, and summary variables for each cell of the cross-tabulation. Analyses were conducted using the EPICURE package of computer programs (Preston and others 1991). Data were cross-classified by various factors, depending on the cohort and on the variables being analyzed. For a typical cohort, data were cross-classified by attained age (<40, 40–44, ..., 65–69, = 75 years), calendar period (< 1950, 1950–54, ..., 1980–84, = 1985), estimated exposure (0, 1–49, 50–99, 100–199, 200–399, 400–799, = 800 WLM), duration of radon-progeny exposure (<5, 5–9, 10–14, =15 years), age at first radon progeny exposure (< 10, 10–19, 20–29, = 30 years) and other mining experience (no, yes). For each cell of the table, the number of observed lung-cancer deaths, the number of person-years, and the mean (weighted by person-years) for the cross-classification variables, such as cumulative exposure, exposure duration, attained age, and age at first exposure, were computed. For pooling purposes, data were further cross-classified by cohort. A 5-year lag period was assumed.
Whenever possible, similar categories for variables that specified dimensions of the person-year tables were established across the cohorts; however, because of intrinsic differences among the cohorts, this was not always possible. For example, some exposures in the Newfoundland cohort were as high as 21 Jhm-3 (6,000 WLM), while all exposures in the Radium Hill cohort were under 0.35 Jhm-3 (100 WLM).
The risk model was developed with the following approach. Suppose the lung-cancer mortality rate is given by r(x,z,w), and depends on cumulative exposure, w, a vector of covariates, x, which described the background lung-cancer
rate, and a vector of covariates, z, which may modify the exposure-response relationship. The relative risk, r, was expressed as a product of the background disease rate among nonexposed, denoted ro(x), and an exposure-response function, RR(z,w). The background rate ro depends on x while the exposure-response function RR depends on z, which may include one or more components of x, as well as w. This general relative risk model can be written as
r(x,z,w) = r0(x)RR(z,w). (5)
The background lung-cancer rate was modeled as r0(x) = exp(ax), with x being the vector of controlling variables and a the corresponding parameter vector. Components of x typically included indicator variables for age group, calendar period, and cohort, as well as variables describing other mine exposures. Main effects and all higher order interactions were included.
Specific models were fit for RR. A linear RR model in w was fitted, namely,
RR = 1 + βw. (6)
Here, β is a parameter which describes increase in ERR per unit increase in w (ERR/exposure). More generally, a model for the assessment of a broad range of exposure-response relationships was defined as
RR = (1 + βwk)eθw. (7)
Again, β reflects the overall ERR/exposure, the parameter, θ measures the exponential deviation from linearity (sometimes referred to in the radiation effects literature as a "cell killing" parameter), and k is a parameter to describe departure from linearity. This general model includes the linear ERR model (k = 1, θ = 0), the linear-exponential model (k = 1) and the "non-linear" model considered by Thomas and others (1995) (θ ![]() 0). Tests for improvement in model fit in relation to θ and k were carried out using likelihood ratio procedures.
0). Tests for improvement in model fit in relation to θ and k were carried out using likelihood ratio procedures.
An important goal of the analysis was to examine variations of the exposure-response trend with other variables, that is, to test whether β varied within categories of other factors, such as attained age, age at first exposure, duration and rate of exposure, and time since last exposure. In epidemiologic terms, they evaluated the components of the covariates vector z as an effect modifier. Suppose a particular covariate z had J categories with values z1, ... , z J. Variation in the exposure-response relationship within levels of z was assessed by fitting model (6) and comparing its deviance with model (8) below which included J exposure-response parameters, namely,
RR = 1 + βjw, (8)
where βj was the ERR/exposure within category zj. Under the null hypothesis of no effect modification, the difference in the model deviances was approximately
χ2 with J-1 degrees of freedom. A significant p-value indicated that the effect of exposure on lung-cancer mortality was not homogeneous across levels of z.
As in the BEIR IV Report (NRC 1988), cumulative exposure to radon progeny was divided into time-since-exposure windows, although the analysis in the National Cancer Institute report (Lubin and others 1994a) included additional categories. For each year of age, cumulative exposure (minus the 5-year lag interval) w*, was expressed as a weighted combination of three exposures:
w* = θ5–14w5–14 + θ15–24w15–24 + θ25+w25+, (9)
where w5–14 was the cumulative exposure received 5–14 years prior to the specific age, w15–24 was the cumulative exposure received 15–24 years prior, and w25+ was exposure 25 or more years ago. Model (6) was extended as
RR = 1 + βw* (10)
For identifiability, θ5–14 = 1, and the quantity w* is interpretable as the "effective exposure" to radon progeny, with θ15–24 and θ25+ defining the relative contributions to the total exposure from the corresponding time periods.
Biologic-Based Models
Moolgavkar and others (1993) have applied a biologic-based exposure-response model to the Colorado uranium miners' data. Specifically, the 2-stage clonal expansion model discussed by Moolgavkar and Luebeck (1990) was used in a first attempt to describe cancer mortality rates among the Colorado miners in terms of a mechanistic stochastic model of carcinogenesis.
Biologic-based models of carcinogenesis are useful for several reasons (Goddard and Krewski 1995). First, they provide a convenient framework within which to describe the process of carcinogenesis. Carcinogenesis is formulated as a multistage process in which the kinetics of cell division and cell death play important roles. The currently available biologic-based models incorporate these features of carcinogenesis. Second, the parameters of a biologic-based model have biologic meaning. With the two-stage clonal expansion model, separate parameters are used to describe the first and second stage mutation rates as well as the birth and death rates of initiated cells. Third, a validated biologic-based model is likely to enjoy greater acceptance when used for the quantitative estimation and prediction of cancer risks. And fourth, description of the temporal aspects of cancer risk is facilitated by the use of biologic-based models of carcinogenesis. In fact, these models provide a flexible family of hazard functions for analyses of time-to-tumor data that allow for incorporation of age and time dependent covariates in a natural way without increasing the number of parameters to be estimated. Empirical models offer less flexibility in this regard, using crude temporal indictors of risk such as age at first exposure, duration of expo-
sure, and cumulative lifetime exposure. Biologic-based models integrate important biologic aspects of carcinogenesis with rigorous statistical methods for data analyses (Moolgavkar and Luebeck 1990).
Although multi-stage biologic models are available, the 2-stage model represents a useful starting point. The 2-stage clonal expansion model is based on the following assumptions. First, there is a pool of stem cells within the tissue of interest susceptible to malignant transformation. Second, malignant tumors are clonal in origin, arising from a single transformed progenitor cell. Third, malignant transformation is the result of 2 specific rate-limiting mutations. Once a malignant cell is generated, it will give rise to a histologically detectable cancerous lesion following a certain lag time. This model has been found to satisfactorily describe a variety of toxicologic and epidemiologic data (Krewski and others 1992).
In chemical carcinogenesis, the occurrence of the first mutation is identified with initiation, whereas the second mutation is associated with malignant conversion of an initiated cell or completion. Carcinogenic chemicals and radionuclides may act by increasing the first or second stage mutation rates, or the rate of expansion of the initiated cell population. Clonal expansion of the initiated cell population is referred to as promotion.
Application to Colorado Uranium Miners' Data
Moolgavkar and others (1993) have re-analyzed data on lung-cancer mortality from the Colorado Plateau miners' cohort and British doctors' cohort within the framework of the two-stage clonal expansion model. The Colorado uranium miners' data used in this analysis were described by Hornung and Meinhard (1987), and included the information on the age at which exposure to radon progeny and cigarette smoke began, the ages at which these exposures stopped, the cumulative exposure to radon progeny, the number of cigarettes smoked per day, the age at last observation or death, and information on whether or not the individual had died of lung-cancer by that time. A lag period of 3.5 years between malignant transformation of lung tissue and death from lung-cancer was assumed. Consequently, exposures occurring within 3.5 years of disease diagnosis were not included in the analysis.
Lung-cancer mortality among a large cohort of British doctors was used to obtain information on the baseline lung-cancer risks in men not exposed occupationally to radon or to tobacco. (Since there were only eight miners who were not exposed to radon and who did not smoke, the background parameters cannot be precisely estimated from the Colorado data alone.) This cohort is of particular significance because data on tobacco consumption were obtained prospectively over the course of follow-up. Following Doll and Peto (1978), analysis was restricted to lung-cancer mortality among men aged 40–79 years who either were never-smokers or regularly smoked no more than 40 cigarettes per day. Former smokers were not considered.
In fitting the two-stage model to the data, it was assumed that X(t) is the number of susceptible cells at age t and that μ(dr,ds) is the rate of the first mutation as a function of the exposure rate of radon progeny, dr, measured in WLM/month (WLM/m), and the exposure rate of cigarette smoke, ds, measured in cigarettes per day. Specifically, intermediate or initiated cells are generated from normal ones as a nonhomogeneous Poisson process with intensity μX. The intermediate cells divide with rate α, die or differentiate with rate β, and divide into one intermediate and one malignant cell with rate ν. All of these transition rates may be influenced by exposure to radon or cigarette smoke. The manner in which rates of mutation and cell proliferation depend on exposure to these two agents is discussed below.
The Colorado miners' data and the British doctors' data were first analyzed separately. An analysis in which certain model parameters were assumed to be the same in both data sets was then conducted. It was found that assuming equal effects of tobacco on the mutation rates in the two data sets produced a likelihood that was virtually identical to the likelihood resulting from the separate analyses. Thus the data were consistent with the hypothesis that the spontaneous-and tobacco-related mutation rates are identical in the two cohorts.
The following exposure-response functions were used for each of the parameters:
μ(dr,ds) = a0 + asds + ardr, (11)
ν(dr,ds) = b0 + bsds + brdr (12)
where ν is the second-mutation rate and
(α - β)(dr,ds) = c0 + cs1(1 - exp(-cs2ds) + cr1(1 - exp(-cr2dr) (13)
in the Colorado miners' data, and
(α - β)(dr,ds) = e0 + es1(1 - exp(-es2ds) + er1(1- exp(-er2dr) (14)
in the British doctors' data.
In both data sets β/α = constant, independent of the level of exposure to radon or tobacco. In this model, referred to as model A, 15 parameters were estimated from the data. Estimates of the spontaneous mutation rates a0 and b0 were almost equal, and the second mutation rate v appears to be unaffected by either radon progeny or cigarette smoke. Since the likelihood is little changed by setting a0 = b0 and bs= br = 0, a reduced form of model A with only 12 parameters was therefore considered.
A second model B in which all model parameters common to the Colorado miners and British doctors' cohorts were assumed to be equal was also fit. This model eliminates the three parameters in Model A having to do with cell proliferation in the British doctors' data by taking c0 = e0, cs1 = es1, and cs2 = es2, leaving only 9 parameters to be estimated. Comparisons of the numbers of
observed and expected lung-cancer deaths within specified exposure categories suggested that both models fit the data reasonably well.
The qualitative conclusions based on the separate and joint analyses (models A and B) were similar. Both radon progeny and cigarette-smoking appear to affect the first mutation rate and the kinetics of intermediate cell division. The second mutation rate was found to be independent of radon progeny and cigarette-smoke exposures. With both models, the age-specific relative risks associated with joint exposure were supra-additive but submultiplicative, confirming previous findings by Whittemore and McMillan (1983) based on an empirical analysis of the Colorado miners' data. However, since addition of interaction terms to the exposure-response functions for any of the model parameters was not significant, there was no suggestion of any interaction between radon progeny and cigarette smoke at the cellular level. The analysis also confirmed the inverse exposure-rate effect in the Colorado miners' cohort.
The National Research Council (1988) examined risk assessment methods for the analysis of complex mixtures, including simple binary mixtures of the type of interest here. The NRC concluded that interactive effects between two carcinogens are likely to be negligible when the level of exposure to both agents is low. Further theoretical support for this finding was provided by Kodell and others (1991) within the context of the two-stage clonal expansion model of carcinogenesis. Application of the two-stage model to the Colorado uranium miners data provided empirical confirmation of these latter theoretical results.
The two-stage model has also been applied to data on the incidence of lung tumors in experiments conducted at Battelle Pacific Northwest Laboratories (Moolgavkar and Luebeck 1993; Luebeck and others 1996). Those experiments involved 3,750 rats subjected to cumulative radon-progeny exposures ranging from 0.07 to 35 Jhm-3 (20 to 10,000 WLM) at different exposure rates. The analysis of the data evaluated the dependence of the mutation and cell proliferation rates on the radon-progeny exposure rate, as well as exposure to uranium ore dust, which was a component (at a constant concentration) in all exposures. The two-stage model was found to provide an adequate fit to these data.
The analyses yielded results that were similar to those obtained from the application of the two-stage model to the Colorado miners' data discussed previously. Specifically, exposure to radon progeny was found to affect the first-stage mutation rate, but not the second-stage mutation rate. The estimated rate of the first mutation was consistent with rates measured experimentally in vitro. The authors found evidence of an inverse exposure-rate effect, which they attributed primarily to promotion of intermediate lesions.
METHODS FOR COMBINING DATA FROM SEVERAL COHORTS
In this section, we describe the models and methods used in the committee's combined re-analysis of the 11 miner cohorts. In developing the BEIR VI model,
modified Poisson regression methods were used to analyze data from the 11 miner studies. Following Lubin and others (1994a), the death rates are assumed to be constant within fixed time intervals and exposure categories. Data entering into regression analyses are in the form of a multi-way person-years table consisting of lung-cancer deaths, person-years, covariates of interest, and potential confounders. Under the Poisson regression model, the observed number of cases is assumed to follow a Poisson distribution for which the variance is equal to the mean (Breslow and Day 1987). Specifically, the expected number of deaths is Njkrjk(x,z,w). Here, Njk denotes the number of person-years at risk in the jth category (j = 1, ... ,Jk) in the kth cohort (k = 1, ... ,K) and rjk(x,z,w) denotes the corresponding mortality rate depending on the cumulative exposure w to radon progeny, a vector of covariates z, which can modify exposure-response relationship, and a vector of potential confounders x.
Although Poisson regression is widely used in the analysis of cohort mortality data, the existence of extra-Poisson variation cannot be ruled out. Although not affecting point estimates of the model parameters, such overdispersion, should it exist, can lead to overstatement of precision.
Under a general relative-risk model, the mortality rate can be expressed as the product
rjk(x,z,w) = r0jk(x)RRjk(z,w), (15)
where r0jk(x) and RRjk(z,w) denote the background mortality rate and relative risk for the jth state in the kth cohort, respectively. Covariates considered include attained age (years), rate of radon progeny exposure (WL), and duration of radon-progeny exposure (years). Age and other mining experience involving exposure to arsenic and gold are considered to be potential confounders. Six of the eleven cohorts include information on tobacco-smoking by the study subjects.
Relative Risk Model
The relative risk (RR) of lung-cancer associated with tobacco-smoking and exposure to radon progeny can be described quite generally in terms of a mixture of multiplicative and additive relationships (Breslow and Clayton 1993). Following Lubin and others (1994a), we consider a multiplicative model to describe the joint effects of radon and tobacco. The relative risk of lung-cancer associated with radon-progeny exposure in the jth category of the kth cohort is modeled as
where βk is the excess relative risk of lung-cancer associated with exposure to radon progeny for the kth cohort, Wjk denotes the cumulative radon exposure within the jth stratum of the kth cohort, ![]() a denotes the modifying effect of attained age, and γz denotes the effect of either exposure duration or exposure
a denotes the modifying effect of attained age, and γz denotes the effect of either exposure duration or exposure
concentration. The joint effects of radon and cigarette-smoking on lung-cancer risk are as described:
where θk = 1 for never-smokers and θk > 1 for ever-smokers. Although we do not fit this multiplicative model directly to the miner data (due to limited information on tobacco consumption patterns among the miners), it forms the basis for an indirect adjustment for tobacco due to Lubin and Steindorf (1995) described later.
Random-Effects Model
Heterogeneity across cohorts can be described by a random-effects model (Rutter and Elashoff 1994), in which the overall effects and variation among individual cohorts are characterized by fixed and random regression coefficients respectively. Specifically, to describe heterogeneity across cohorts, the parameter βk is decomposed into two parts:
βk = β + b β,k, (18)
where β is the fixed effect for all cohorts and bβ,k is the random effect specific to the kth cohort. More generally, the parameters ![]() in model (16) can be written as
in model (16) can be written as
αk = α + αk, (19)
where ![]() denotes the vector of fixed effects, and a vector of random-effects ak = (aβ,k,aθ,k,αg,k), specifies the deviation from the overall effect associ ated with the kth cohort. This generalization allows for inter-cohort variability in the parameters
denotes the vector of fixed effects, and a vector of random-effects ak = (aβ,k,aθ,k,αg,k), specifies the deviation from the overall effect associ ated with the kth cohort. This generalization allows for inter-cohort variability in the parameters ![]() a and γz, although this was not necessary for the miner data used in the present analysis.
a and γz, although this was not necessary for the miner data used in the present analysis.
Different statistical methods can be used to fit nonlinear random-effects regression models. Because exact methods for model fitting can be computationally intensive, Burnett and others (1995) proposed the use of a locally linear first order approximation to simplify the calculation. Wang and others (1995) provide a detailed discussion of how this approximation random effects model may be fit to data from the 11 miner cohorts using generalized estimating equations (GEEs). GEEs are robust in the sense that only the first two moments of the distribution of random effects need be specified (Zeger and others 1988) rather than the complete distribution needed to apply likelihood-based methods.
Even with these simplifications, fitting nonlinear random-effects models proved to be computationally difficult with the large number of categories in the multi-way person-years table. Consequently, two-stage regression methods were also used to fit the nonlinear models of interest here.
Two-Stage Regression Analysis
The two-stage regression method represents a simplification of and an approximation to the random-effects models. With the two-stage method, the model of interest is first fit separately within each cohort. An overall estimate of ß is then obtained as a simple linear combination of the cohort-specific estimates.
Details of the two-stage regression method have been given by Laird and Mosteller (1990) and Whitehead and Whitehead (1991). Without loss of generality, we will use the linear model
RRk(z,w,ak) = 1 + ßkw (20)
to illustrate how the two-stage analysis is conducted.
Stage 1. In the first stage, model (20) is fitted to each cohort. Let ![]() k be the estimate of model parameter ßk and sk be the estimated variance of
k be the estimate of model parameter ßk and sk be the estimated variance of ![]() k.
k.
Stage 2. Define

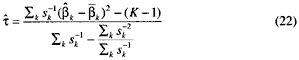
and
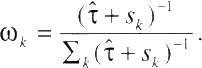
The pooled estimate ![]() of the overall effect is then given by
of the overall effect is then given by

The variance in the estimate of the overall effect is estimated by
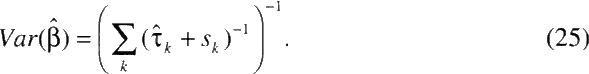
Heterogeneity among cohorts is reflected in positive values of t, which increase the estimated variance of the overall effect ![]() .
.
A statistical test for homogeneity of the ![]() k among cohorts is given by
k among cohorts is given by
which has a chi-square distribution with K - 1 degree of freedom.
Provided ![]() > 0, the shrinkage estimator of the cohort-specific effect
> 0, the shrinkage estimator of the cohort-specific effect ![]() is
is

with the deviation from the overall estimate given by
An estimate of the variance of this deviation is given by

Heterogeneity between different studies is taken into account in estimating overall risks with both the random-effects and two-stage analyses. This is particularly important when there are significant differences among the cohorts, that is, when the fixed-effects model fits the data poorly (Greenland 1994). Fitting nonlinear regression models is considerably easier with the two-stage method than with the random-effects method, particularly with large datasets and many parameters. The two stage regression method is applied by using well-established computer software to analyze each cohort separately; combining information across cohorts is then done by means of a simple linear combination of the parameter of interest. With random-effects methods, on the other hand, the data from all cohorts are analyzed simultaneously. Because of the computational complexity in fitting the random effects model, a first-order approximation simplifies the calculations. Even with this approximation, however, convergence was difficult to obtain in some situations. Consequently, the committee focused primarily on two-stage regression methods for model fitting.
Combined Analysis of Miner Cohorts
The updated data on the 11 miner cohorts were summarized in the form of a multi-way table prior to analysis. The categorizations were essentially the same as those used by Lubin and others (1994a). All models considered by the committee were fitted by Poisson regression using EPICURE (Preston and others 1991). The most recent release of EPICURE allows for extra-Poisson variation, but was not available to the committee during the course of its analysis. Cohort effects were included in the single model by stratifying the background disease risk by cohort, as well as age group, and other occupational exposures and ethnicity. Cohort-specific estimates of the ERR/WLM (ßi) were obtained from the single model fit to all the data. Since preliminary analyses indicated that the effect of time since exposure, attained age and exposure duration or radon con-
centration were similar in most cohorts, these parameters were considered to be the same in all cohorts. However, the parameter ß did vary considerably across the cohorts. Consequently, the overall estimate of ß was obtained using the two-stage method with associated standard errors reflecting variation within and between cohorts. We also used the random-effects method to obtain the overall estimate of ß. With the random-effects method, we used the background parameters obtained previously from the EPICURE (Preston and others 1991) fit of the corresponding model to all the data. The methods used to fit the random-effects model are identical to those of Wang and others (1996), with the exception that the parameter ß was obtained from the transformation ß = exp {ß*} after first estimating ß*. This same transformation was used with the two-stage method in order that the sampling distribution of the estimator ![]() be closer to normal. The standard error of
be closer to normal. The standard error of ![]() shown here for the two-stage method assumes that the
shown here for the two-stage method assumes that the ![]() k are independent; taking the covariance forms into account leads to a slight reduction in the standard error of
k are independent; taking the covariance forms into account leads to a slight reduction in the standard error of ![]() . These covariance forms are included in the more comprehensive uncertainty analysis discussed later in this appendix.
. These covariance forms are included in the more comprehensive uncertainty analysis discussed later in this appendix.
The results of fitting the simple linear model
to the miner data are shown in Table A-3. In addition to results for both the random-effects and two-stage methods, the results obtained by analyzing each cohort separately are also shown. The ERR per unit exposure is given by the
TABLE A-3 Estimated ERR/WLM(%)a based on two-stage and cohort-specific analyses
|
Cohort |
Two-stage analysis |
Cohort-specific analysis |
|
Combined |
0.76 (1.86)b |
|
|
|
|
|
|
China |
0.17 |
0.17 |
|
Czechoslovakia |
0.67 |
0.67 |
|
Colorado |
0.44 |
0.42 |
|
Ontario |
0.82 |
0.89 |
|
Newfoundland |
0.82 |
0.82 |
|
Sweden |
1.04 |
1.25 |
|
New Mexico |
1.58 |
2.84 |
|
Beaverlodge |
2.33 |
2.95 |
|
Port Radium |
0.24 |
0.19 |
|
Radium Hill |
2.75 |
4.76 |
|
France |
0.51 |
0.09 |
|
a ERR/WLM is the parameter ß in the model RR = 1 + ßw, where w denotes cumulative radon progeny exposure. b Multiplicative standard error; exp c Based on random-effects model. |
||
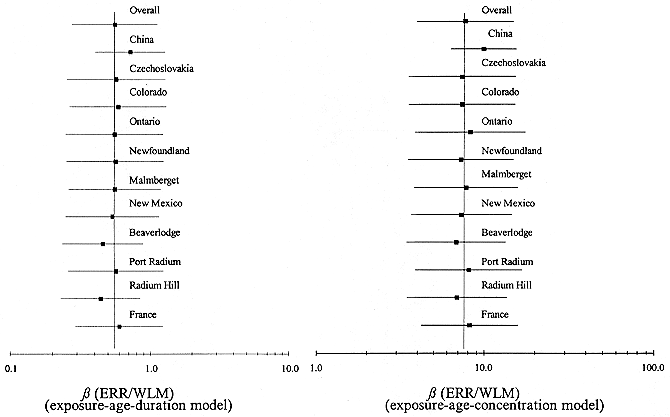
parameter ß. All methods provide estimates of this parameter separately for each cohort; the random-effects and two-stage methods also provide overall estimates of ß. Note that the estimates of ß for individual cohorts based on the two stage-method differ from the cohort-specific estimates. In general, the adjusted estimates of ß obtained using the two-stage method tend to ''shrink" towards the overall estimate of ß. The overall estimate of the ERR/WLM based on the random-effects analysis is 0.59% with a multiplicative standard error of 1.32. The two-stage analysis leads to an estimate of 0.76% with a multiplicative standard error of 1.86. (The difference in standard errors for the two-stage and random-effects methods is due to the different approaches used to estimate the standard error, and the small number of cohorts involved in the analysis.) The cohort-specific estimates of the excess relative risk per unit exposure are shown graphically in Figure A-1.
To evaluate overall patterns of risk, the committee investigated a number of other models of the form (16) with covariates including attained age, rate of exposure to radon progeny, time since exposure, and duration of exposure. This limited model selection process led the committee to the same two risk models favored by Lubin and others (1994a). These two models represent the committee's preferred risk models, and will be referred to as the exposure-age-duration model and exposure-age-concentration model, respectively.
Estimates of the parameters in the committee's two preferred models are shown in Table A-4. These estimates were obtained by fitting each of these two models to the data for all eleven cohorts simultaneously, constraining the covariates to be the same in all cohorts, but allowing ß to vary among cohorts. Again, an overall estimate of ß was obtained using the two-stage method. An overall estimate of ß was also obtained using the random-effects method. However, since convergence could not be obtained when attempting to estimate the covariate values using the random-effects method, the covariate values were fixed at their previously estimated values, leaving only the ERR per unit exposure to be determined in this simplified random-effects analysis.
The pattern of modifying effects of the covariates on the exposure-response relationship was similar to that observed in the original analysis of the 11 miner cohorts by Lubin and others 1994. Specifically, the exposure-response relationship decreased with time since exposure, attained age, and exposure rate, but increased with exposure duration.
In order to determine whether the overall estimate of the ERR per unit exposure was unduly affected by the data from any one cohort, the committee conducted an influence analysis in which the parameter ß was estimated after omitting, in turn, data from each individual cohort (Table A-5, Figure A-2). This influence analysis showed that the omission of any one cohort did not have a strong impact on the overall estimate of ß. Some caution is required in the interpretation of these results, since differences in age, exposure rate, exposure
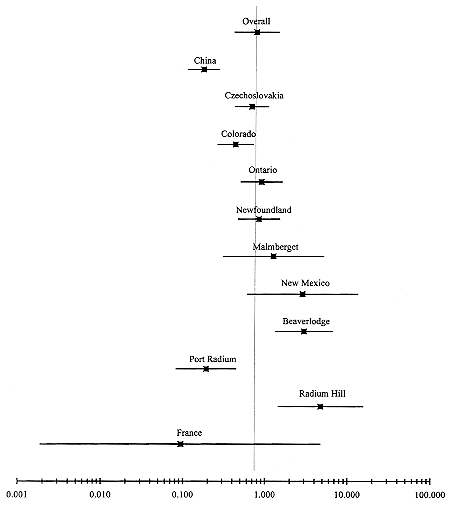
FIGURE A-1 Estimate of the ERR per unit exposure ERR/WLM (%) obtained by fitting a constant excess relative risk model to each cohort separately (overall estimate based on the 2-stage method) and 95% confidence intervals.
duration, time since exposure, and smoking habits among cohorts could explain some of the inter-cohort variation in the ß's observed in this analysis.
Smoking and Radon Progeny Exposure
Data on tobacco-smoking in the various cohorts were limited: either lacking entirely; not readily comparable among cohorts because of the method or the
amount of information collected; or incomplete for workers within particular cohorts. Six of the eleven cohorts included some data on smoking (China, Colorado, Newfoundland, Sweden, New Mexico and Radium Hill) although among these six cohorts, a substantial number of workers lacked smoking information. Moreover, surveys of smoking practices were not usually undertaken on a regular prospective basis, necessitating assumptions about the stability of smoking practices over time. The impact of incomplete information on tobacco is not clear, including the misclassification of ex-smokers as current smokers.
Smoking rates in Western countries have generally declined, although it is uncertain if smoking rates among miners have declined and, if so, to what extent. Among Chinese workers, smoking rates have been relatively stable, although tobacco use practices (cigarettes and bamboo water pipes) have changed, especially among younger workers. Company policies regarding smoking, such as prohibiting smoking while underground, are also evolving. In recent years, smoking, in some cohorts, may have been under-reported by workers concerned about health compensation issues.
TABLE A-4 Estimates of the parameters in the committee's two preferred risk models
|
Exposure-age-duration modela |
Exposure-age-concentration modela |
||
|
β × 100 |
β × 100 |
||
|
|
|
||
|
Time since exposure windows |
|||
|
θ5–14 |
1.00 |
θ5–14 |
1.00 |
|
θ15–24 |
0.72 |
θ15–24 |
0.78 |
|
θ25+ |
0.44 |
θ25+ |
0.51 |
|
Attained age |
|||
|
|
1.00 |
|
1.00 |
|
|
0.52 |
|
0.57 |
|
|
0.28 |
|
0.29 |
|
|
0.13 |
|
0.09 |
|
Duration of exposure |
|
Exposure rate (WL) |
|
|
γ<5 |
1.00 |
γ<0.5 |
1.00 |
|
γ5–14 |
2.78 |
γ0.5–1.0 |
0.49 |
|
γ15–24 |
4.42 |
γ1.0–3.0 |
0.37 |
|
γ25–34 |
6.62 |
γ3.0–5.0 |
0.32 |
|
γ35+ |
10.20 |
γ5.0–15.0 |
0.17 |
|
|
|
γ15+ |
0.11 |
|
a Parameters estimated based on the fitted model: b Two-stage method. c Random-effects method. d Multiplicative standard error: exp |
|||
TABLE A-5 Estimates of ß (ERR/WLM) based on the data from all cohorts except one
|
|
Exposure-age-duration model |
Exposure-age-concentration model |
||||
|
Omitted Cohort |
ßa |
95%C.I. |
|
ßa |
95%C.I. |
|
|
None |
0.553 |
0.271 |
1.125 |
7.681 |
3.969 |
14.864 |
|
China |
0.714 |
0.398 |
1.280 |
9.884 |
6.322 |
15.455 |
|
Czechoslovakia |
0.565 |
0.249 |
1.278 |
7.374 |
3.553 |
15.304 |
|
Colorado |
0.586 |
0.263 |
1.305 |
7.359 |
3.553 |
15.243 |
|
Ontario |
0.551 |
0.246 |
1.235 |
8.248 |
3.883 |
17.519 |
|
Newfoundland |
0.560 |
0.251 |
1.252 |
7.240 |
3.520 |
14.890 |
|
Malmberget |
0.555 |
0.259 |
1.188 |
7.773 |
3.821 |
15.810 |
|
New Mexico |
0.535 |
0.248 |
1.153 |
7.280 |
3.663 |
14.468 |
|
Beaverlodge |
0.456 |
0.234 |
0.888 |
6.785 |
3.451 |
13.339 |
|
Port Radium |
0.566 |
0.257 |
1.246 |
8.057 |
3.878 |
16.741 |
|
Radium Hill |
0.440 |
0.228 |
0.850 |
6.855 |
3.462 |
13.571 |
|
France |
0.598 |
0.289 |
1.237 |
8.169 |
4.207 |
15.862 |
|
a Combined estimate based on two-stage procedure. |
||||||
Adjustments for Smoking Status
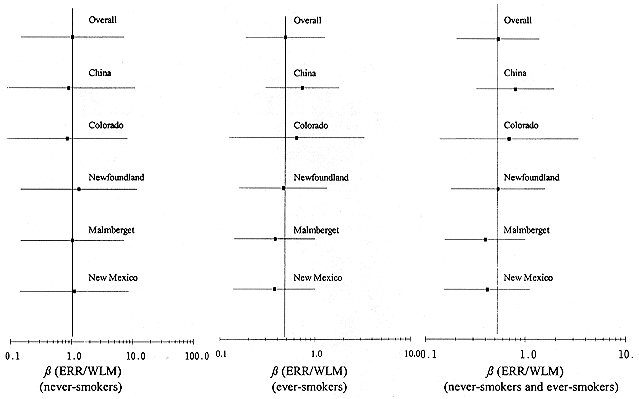
The data on smoking are generally too sparse to model the joint effects of smoking and radon exposure. However, using the results of analyses of the effect of radon-progeny exposure among never-smokers and among ever-smokers, it is possible to adjust the committee's preferred models to account for smoking status. In this regard, the committee adopted the approach introduced by Lubin and Steindorf (1995), based on the relative difference in the exposure-response relationship for ever-smokers and never-smokers. Restricting data to miners for whom some smoking information was available (China, Colorado, Newfoundland, New Mexico, and Radium Hill), the overall ERR/WLM was estimated to be 1.02% (95% CI: 0.15–7.18%) among never-smokers and 0.48% (95% CI: 0.18–1.27%) among ever-smokers. Among these same miners, the overall ERR/WLM, ignoring smoking status, was 0.53% (95% CI: 0.20–1.38%). The effects of sequentially omitting a single cohort from this analysis are shown in Table A-6 and Figure A-3.
Estimates of the ERR/WLM for ever-smokers and never-smokers are comparable only to the extent that the mean age, time since exposure, and exposure rate (factors known to modify the ERR/WLM) are similar for ever-smokers and never-smokers. Analysis revealed that these modifiers differed only slightly between the two groups: never-smokers were one year older, six months further from time of last exposure, and exposed at a rate 0.9 WL less than ever-smokers. We therefore assumed that the observed ERR/WLM estimates approximate the relative effects of radon-progeny exposure in ever-smokers and never-smokers.
TABLE A-6 Influence analysis of smoking correction factorsa
|
Omitted cohortb |
ß ever-smokers/ß overall |
ß never-smokers/ß overall |
|
None |
0.916 |
1.937 |
|
China |
0.921 |
1.121 |
|
Colorado |
0.929 |
1.220 |
|
Newfoundland |
0.864 |
2.448 |
|
Malmberget |
0.952 |
2.584 |
|
New Mexico |
0.897 |
2.651 |
|
a Based on cohorts for which smoking data were available (see Table A-1). b The data for Radium Hill were too sparse to obtain a meaningful estimate. |
||
Based on this analysis, the effect of exposure among ever-smokers, relative to the overall effect, ignoring smoking status, was 0.9 (0.48/0.53), whereas among never-smokers the relative effect, was approximately 2-fold (1.02/0.53). The influence analysis summarized in Table A-6 indicates that no one cohort has an inordinate effect on these two ratios. These crude correction factors were applied to the committee's preferred models to obtain estimates of risk for ever-smokers and never-smokers separately. Specifically, we adjusted the estimate of the baseline ERR/WLM ß in the exposure-age-duration and exposure-age-concentration models, while leaving the parameter estimates for the modifying factors unchanged. In the exposure-age-concentration model, the estimate of 0.0768 was reduced to 0.069 for ever-smokers and increased to 0.153 for never-smokers, while in the exposure-age-duration model the estimate of 0.0055 was reduced to 0.0050 for ever-smokers and increased to 0.011 for never-smokers. The present adjustment differs somewhat from that obtained by Lubin and Steindorf (1995) due to use of updated information, particularly for the China and Colorado cohorts.
The estimates of ß based on the data for all 11 cohorts (Table A-3) differed slightly from the estimates based on the six cohorts with data on tobacco consumption (Table A-7). However, within the six cohorts for which smoking information is available, the ERR/WLM was nearly twice as large in never-smokers as compared with ever-smokers. This analysis indicates that the effects of ever-smoking and radon progeny exposure are not incorporated multiplicatively, but as a submultiplicative mixture.
QUALITATIVE UNCERTAINTY ANALYSIS
In the remainder of this appendix, we focus on sources of uncertainty and variability in radon risk estimates. Clearly, lack of accurate information on a number of variables that affect radon risk, including critical variables such as radon exposure and tobacco consumption, confers uncertainty on committee projections of risk. Individual risks probably also vary within the population, de-
TABLE A-7 Influence analysis of ß for six cohorts with information on smokinga
|
Omitted Cohort |
ßb(%) |
95% Confidence Interval (%)c |
|
|
Never-smokers |
|||
|
None |
1.021 |
0.145 |
7.180 |
|
China |
0.880 |
0.069 |
10.889 |
|
Colorado |
0.831 |
0.085 |
8.113 |
|
Newfoundland |
1.298 |
0.144 |
11.701 |
|
Malmberget |
1.019 |
0.145 |
7.164 |
|
New Mexico |
1.097 |
0.138 |
8.685 |
|
Ever-smokers |
|||
|
None |
0.483 |
0.183 |
1.272 |
|
China |
0.724 |
0.296 |
1.769 |
|
Colorado |
0.633 |
0.122 |
3.286 |
|
Newfoundland |
0.458 |
0.157 |
1.335 |
|
Malmberget |
0.375 |
0.141 |
1.001 |
|
New Mexico |
0.371 |
0.137 |
1.007 |
|
Never-smokers and ever-smokers |
|||
|
None |
0.527 |
0.202 |
1.375 |
|
China |
0.785 |
0.320 |
1.927 |
|
Colorado |
0.681 |
0.137 |
3.386 |
|
Newfoundland |
0.530 |
0.178 |
1.575 |
|
Malmberget |
0.394 |
0.154 |
1.006 |
|
New Mexico |
0.414 |
0.153 |
1.122 |
|
a The data for Radium Hill was too sparse to obtain useful estimate of ß for never-smokers. b Based on the constant relative risk model RR = 1+ßw fit using the 2-stage method. c Confidence limits based on multiplicative standard error. |
|||
pending on radon-exposure patterns, tobacco consumption, and other (possibly unknown) factors.
It is important to distinguish clearly between uncertainty and variability. Uncertainty represents the degree of ignorance about the precise value of a particular parameter, such as the body weight of a given individual (Morgan and others 1990; NRC 1994b; Hattis and Burmaster 1994). On the other hand, variability represents inherent variation in the value of a particular parameter within the population of interest. In addition to being uncertain, body weight also varies among individuals. A parameter such as body weight, which can be determined with a high degree of accuracy and precision, may be subject to little uncertainty, but can be highly variable. Other parameters may be subject to little variability but substantial uncertainty. Yet others may be both highly uncertain and highly variable.
The committee attempted to identify the main sources of uncertainty in assessing the lung-cancer risk from radon exposure. The committee also conducted a limited quantitative analysis of the uncertainty in estimates of both relative risk and attributable risk. The committee did not find it feasible to
evaluate the combined effects of all sources of uncertainty affecting radon-risk estimates, but a discussion follows of sources that were included and those that were not. This discussion focuses on sources of uncertainties in estimates of risk resulting from radon exposure in somewhat general terms, and gives an indication of the likely magnitude of the uncertainty for many of the sources.
Measures of Risk
In this report, radon risks have been characterized in two ways. First estimates of relative risk (RR) were obtained using the committee's preferred risk models (chapter 3, Table 3-6). These estimates reflect the lifetime relative risk (LRR) of lung-cancer mortality at specified (constant) levels of exposure, for ever-smokers and never-smokers. Such estimates are subject to a number of uncertainties, which vary among individuals depending on the level of exposure to radon, smoking status, and other factors.
In order to gauge the public health impact of residential radon exposure, the population attributable risk (AR) is also considered (chapter 3, Table 3-7). It is important to note that such population-based measures of risk are subject to uncertainty, but not variability. Factors, such as the level of exposure to radon, or the dosimetric K-factor which vary among individuals within the population, are effectively integrated out when calculating the AR.
The type of risk estimate and purposes for which it is to be used affect the uncertainties in the risk. Estimates that are intended to reflect current U.S. exposure conditions are subject to uncertainty in estimating these conditions, whereas estimates intended to apply to hypothetical exposure scenarios are not.
The population to which the risk estimate is to be applied is also relevant; for example, because the underground miner studies included only males, estimates for females are less certain than those for males. In addition, because all factors that modify risks may not have been identified and included in risk models, estimates of individual risks are more uncertain than estimates of total (or average) population risks.
Categorization of Uncertainties
Sources of uncertainty may be categorized in different ways. One approach is to consider uncertainties arising at each step in the risk assessment process. This report focuses largely on the development of an exposure-response model that expresses the dependence of lifetime lung-cancer risks on radon exposure and demographic variables. This model was based on analyses of data from 11 underground miner cohorts. Risk estimates for persons exposed in residences also require a model for estimating differences in radon dosimetry in mines and in homes, referred to here as the "exposure/dose conversion model". In addition, risk estimates intended to reflect current U.S. exposure conditions require esti-
mates of these conditions. Demographic information, including baseline lung-cancer risks, is also needed. Thus, uncertainties are first categorized as indicated by the Roman numerals in chapter 3, Table 3-13. The material here primarily addresses uncertainties arising from the exposure-response model relating lung-cancer risk to radon exposure. The exposure/dose conversion model is discussed in appendix B, while estimation of the exposure distribution is discussed in appendix G. Uncertainties in the exposure/dose model and in the demographic data are briefly discussed later in this section.
Uncertainties in the model relating lung-cancer risk to exposure are further categorized by distinguishing uncertainties in the parameter estimates from uncertainties in specification of the model, and in its application to residential exposure of the U.S. population. This categorization is similar to that used by Morgan and others (1990), by the NRC committee on Risk Assessment of Hazardous Air Pollutants (NRC 1994b), and by the BEIR V committee (1990). As Morgan and others note, the distinction between parameter and model uncertainties is somewhat blurred, since the selected model can be viewed as a special case of a much richer model with many of the risk factors omitted. For example, the linear model used in this report is a special case of more general non-linear models, and was chosen because more general models did not provide significantly better fits to the underground miner data (Lubin and others 1994a) and because of the radiobiological considerations discussed in chapter 2. Morgan and others point out that every model is necessarily an oversimplification of reality, and, in this sense, all models are approximations. The distinction between parameter and model uncertainties is nevertheless a useful one, since the latter are especially important for extrapolating from exposure in mines to exposure in U.S. homes.
Because the risk model was developed from analyses of underground miner data, it provides a reasonably good description of the average risk for these miners. The U.S. population includes groups (for example, females) and conditions (for example, very low exposures) that are not represented in the underground studies, and, even for groups that are represented, the relative contributions of these groups differ (for example, the underground miner cohorts include a larger proportion of ever-smokers than the general U.S. population). A fully adequate model needs to take account of all modifying factors that differ between miners and the general population. To the extent that such factors are omitted from models, bias in risk estimates may result.
Rai and others (1996) distinguish between uncertainty and variability in risk assessment. Uncertainty represents ignorance about the values of model parameters, while variability represents the inherent variation in the values of parameters among individuals in the population of interest. Whereas population-based measures of risk such as the AR are not subject to variability, individual measures of risk such as the LRR do vary among individuals in the population. Models that take account of factors that modify risk and allow risk estimates for subgroups of
the population can reduce variability within these subgroups. For example, there may be less variability in separate estimates of risk for ever-smokers and never-smokers than in a combined estimate; however, there might still be considerable variability among ever-smokers if the model did not account for the amount of smoking or distinguish between current and former smokers. For many factors, there is little basis for estimating variability. For example, both the shape of the exposure-response function and the pattern of risks over time probably vary from person to person, but data for quantifying this variation are scarce. Past efforts to quantify uncertainties in estimates of risk from radon or from low-LET radiation have addressed only uncertainty, and have not attempted to quantify variability (NRC 1988, 1990; Puskin 1992).
Uncertainties in Parameter Estimates in the Lung Cancer Exposure-Response Model Derived from Underground Miner Data
Sampling Variation in Underground Miner Data
Uncertainty resulting from sampling variation differs from most other uncertainty sources in that it can be quantified using rigorous statistical approaches. Sampling uncertainty in the fitted coefficients of models based on analyses of data from the 11 miner cohorts can be described in terms of the variance-covariance matrix of these coefficients, which takes account of both random error and heterogeneity among cohorts. The assumption of multivariate normality is widely used and generally valid in large samples. However, because the population attributable risk is a complex function of the estimated parameters, and because the distributions of the statistics involved may not be adequately approximated by multivariate normal distributions, the committee conducted Monte Carlo simulations to obtain uncertainty distributions and confidence intervals for attributable risks as described later in this appendix.
Errors in the Underground Miner Data
In the three sections that follow, errors in the data from the 11 miner cohorts used to determine the committee's risk model are discussed. Ecological and case-control studies of people exposed to residential radon are also subject to biases from their data, but these are not discussed here because these data were not used directly in developing the risk model. These uncertainties are however discussed in appendix G.
Errors in the Underground Miner Data on Health Effects
Vital status and information on cause of death were determined from a variety of information sources in the 11 miner cohorts, including local and na-
tional cancer and vital statistics registries, company records, electoral rolls, driving license records, telephone directories, and death certificates. In most cohorts, follow-up methods were thorough, but undoubtedly some misclassification of vital status occurred because of identifier inaccuracies and subject mobility. Failure to determine that a subject had died would lead to incorrectly including person-years after death had occurred, and might also lead to omitting some deaths due to lung-cancer.
Errors in assignment of cause of death may also have occurred. Lung-cancer deaths that were incorrectly diagnosed as other diseases may have been missed, some deaths counted as lung-cancers may have in fact been due to other causes, and secondary and primary lung-cancers may sometimes have been confused. Several of the studies relied on death certificate diagnoses, and these were not always verified. Percy and others (1981) assessed the validity of death certificates for cancer in the United States in the 1970s by comparing the cause of death listed on death certificates with hospital records. For lung-cancer, death certificates were both sensitive (95% of lung-cancers were detected) and specific (93.9% of death certificates coded with lung-cancer as the cause of death were confirmed by hospital records). These results would not necessarily apply to data from other countries, but most of the countries contributing data have high standards of medical care and should have high confirmation rates. It is worth noting that China and Czechoslovakia, the two cohorts with the largest numbers of lung-cancer deaths, used special methods to ascertain cases, and did not rely on death certificate information.
Because analyses of miner cohorts were based on internal comparisons within each of the cohorts, bias from errors in health endpoint data would be largest if these errors depended on the level of exposure; dependencies of this type do not seem likely. Because non-lung-cancer deaths that were incorrectly classified as lung-cancers would not be related to exposure, such deaths could lead to slight underestimation of risk even if the misclassification were non-differential. Non-differential errors that resulted in missing some lung-cancer deaths would reduce power, but should not lead to bias. Relative to other sources of error, bias from errors in health outcome data is not thought to be large, and no attempt has been made to quantify it.
Errors in the Underground Miner Data on Exposure to Radon and Radon Progeny
The exposure estimates used in the committee's analyses of the 11 miner cohorts are subject to many sources of error, as discussed in detail in appendix F. These errors occur because measurements of radon and radon progeny were limited for many of the mines, especially during the early period of mine operations. When measurements were not available, it was necessary to estimate exposures on the basis of data from earlier or later years, from measurements in
proximal mines, or based on mine conditions. Even when measurements were available, they may not always have been entirely representative of the typical conditions to which workers were exposed, especially if the measurements were made for regulatory purposes. In some cases, especially in earlier years, measurements were made of radon rather than radon progeny, and these could not be used to estimate radon-progeny exposure accurately unless information on equilibrium was available.
In addition, the number of hours spent in the mine and in various locations were not fully documented. These limitations could have led to both systematic and random errors in estimates of radon-progeny exposure for individual miners. As indicated in appendix F, there are many factors that could lead to bias in exposure estimates. Data were not sufficient to determine the overall magnitude or even the overall direction of bias, and there is no assurance that various systematic biases ''cancel" each other. Thus, these potential biases increase the uncertainty in risk estimates. Random exposure-measurement error can be expected to lead to underestimation of risk, and can also distort exposure-response relationships. Statistical methods are available for adjusting for such errors, but require that the nature and magnitude of the errors be specified (see appendix E and Thomas and others 1993). These methods are often difficult to implement, especially when the error structure is complex. The result of a limited simulation study in which the impact of exposure assessment error is illustrated in given in appendix G. This study also illustrates how these effects can be mitigated using adjustments for measurement error, provided the measurement error model is known.
Errors may also vary by calendar-year period and by the specific method used to estimate each worker's exposure. Some sources of error are independent for estimates for different workers while others may be correlated. Even if the details of these errors were fully understood, accounting for them would not be a simple task.
It is likely that some unknown portion of the variation in risk estimates among the 11 cohorts results from variation in the direction and magnitude of systematic biases and random errors in exposure measurements. A portion of the uncertainty resulting from exposure-measurement error may thus be included in the heterogeneity component of the variance for the risk coefficient based on the combined analyses. However, it is unlikely that this takes account of all uncertainty from this source, and no account has been taken of the tendency for random error to bias risk estimates downward. For most of the cohorts, exposure measurement errors are likely to be greatest in the earliest periods of operation when exposures were largest and fewer measurements were made. For this reason, measurement errors not only affect the estimates of the overall risk coefficient, but may also bias estimates of parameters that describe the relationship of risk with other variables such as exposure rate, time since exposure, and age at risk. For example, the underestimation of risk due to random exposure errors may be
more severe at high exposure rates than at low exposure rates, leading to exaggeration of the effects of factors that modify the dependence of risk on exposure rate.
At this time, it is difficult to quantify bias and uncertainty resulting from exposure-measurement error. For the Czechoslovakian cohort, improvements in both exposure measurements and follow-up data increased the ERR/WLM from 0.37% to 0.61% with most of the increase attributed to the exposure-measurement changes (Tomásek and others 1994a). This does not reflect the full effect of measurement error in the earlier data since the revised data were still subject to error. Because exposure-measurement methods were not the same for all cohorts, the impact of exposure-measurement errors undoubtedly varies considerably among the eleven cohorts. Some efforts have been made to evaluate the impact of exposure measurement errors in individual miner cohorts, as described in appendix E.
In chapter 3, analyses with a focus on miner data below 0.175 Jhm-3 (50 WLM), are described. These restricted analyses did not involve estimation of an exposure-rate parameter. Furthermore, miners exposed at these low levels were predominantly miners who were employed in more recent periods when exposure-assessment methods had improved substantially over those employed earlier. More than a third of the lung-cancer deaths in the exposure restricted analyses came from the Ontario cohort, where exposure assessment methods were among the best of the 11 cohorts. Lifetime risk estimates based on models developed from these analyses were very similar to those obtained using the committee's recommended models.
Limitations in the Underground Miner Data on Other Exposures
In addition to the radon-progeny exposure, underground miners were also exposed to arsenic, silica, and diesel fumes. Because these exposures may be positively correlated with radon-progeny exposures, there is potential for confounding if no adjustment for such exposures is made. Even in the absence of such a correlation, these other exposures may have enhanced the risk due to radon progeny, leading to larger risks in miners than would result from exposure to radon progeny alone. Quantitative data on arsenic exposure were available only for China and Ontario, although Colorado, New Mexico, and France had data on whether subjects had previously worked in underground mines other than uranium mines. Adjustment for arsenic exposure reduced the estimated ERR/WLM for China from 0.61 % to 0. 16%, but had little effect on risk estimates for the other cohorts. Limitations in the available data make it very difficult to evaluate the potential bias in the overall risk estimate resulting from inadequate adjustment for arsenic exposure. Data on individual miner exposures to silica or to diesel fumes were not available. The possible effects of all three exposures are discussed in appendix F.
Smoking is another exposure that is of concern both as a confounder and as a risk modifier. The high prevalence of smoking in underground miners represents a source of uncertainty in extending the risk estimates from mines to the general population. Although tobacco-smoking is a very strong risk factor for lung-cancer, data on smoking are rarely sufficiently detailed to allow adequate adjustments for smoking in epidemiological studies of lung-cancer. Of the 11 cohorts used to develop the risk model, only 6 of the cohorts had data on smoking. These data were not always quantitative, and detailed data on changes in smoking status over time were not available for any of the cohorts except for some limited data on changes in smoking rates and dates of occurrence for miners in the Colorado cohort. Because there is no compelling reason to expect a correlation between smoking and radon progeny exposure, inadequacies in smoking data are of greater concern in evaluating the modifying effects of smoking on radon risks than in evaluating smoking as a confounder. This issue is discussed further below and in appendix C.
Uncertainties in the Specification of the Lung Cancer Exposure-Response Model and in Its Application to the General U.S. Population
As noted above, these uncertainties are most important for extrapolating risks from underground mines to persons exposed in homes.
Shape of the Exposure/Exposure-Rate Response Function
Cumulative exposures and exposure rates were generally much higher in underground mines than those encountered in homes. Perhaps the most fundamental aspect of the committee's model is the choice of method for extrapolating risks from occupational to residential exposure levels. Estimates of the ERR per unit exposure obtained using the committee's preferred models are based on data on miners with average exposure rates below 0.5 WL. In addition, both analyses restricted to miners with low cumulative exposures < 0. 175 Jhm-3 or 0.35 Jhm-3 (< 50 or <100 WLM) and a meta-analysis of studies of persons exposed in residences gave risk estimates that were similar to those obtained with the committee's recommended models. Nevertheless, the possibility of nonlinearity, even in this low exposure range, cannot be entirely excluded. This issue is discussed further in chapters 2 and 3.
Temporal Expression of Risks
The committee's risk models provide for a decline in risk with time since exposure and with age at risk. Although these patterns were consistently identified in nearly all of the underground miner cohorts, it is possible that the estimates of these effects could have been biased by time-dependent errors in both
exposure measurements and health-endpoint data, and also by possible changes in smoking habits over time. To estimate these effects, it was necessary to include the high exposure miner data; unfortunately, data were inadequate to effectively investigate whether such effects might vary by level of exposure. The statistical uncertainty in estimating the parameters quantifying age at risk effects was included in the Monte Carlo simulations that were conducted, but the uncertainty in estimating the parameters quantifying the time since exposure parameters was not included.
Dependence of Risks on Sex
The cohorts used to develop the committee's risk models included only male miners. Case-control studies of residential radon exposure include both males and females, but data are not yet sufficient to investigate the possible modifying effects of sex. Lung-cancer death rates in the United States are about three or four times higher for males than for females, which could affect risks resulting from radon exposure. It is not known with certainty whether risks for the two sexes follow the pattern of baseline risks, and are thus comparable on a multiplicative scale, or if they are independent of baseline risks, and thus are more comparable on an absolute scale. The committee has chosen to assume that risks are comparable on a multiplicative scale. However, the calculations were also made under the alternative assumption that risks for males and females were comparable on an absolute scale. This latter assumption increased the estimated excess lifetime risk for females by a factor of about 2.5.
A large portion of the difference in lung-cancer rates for males and females is undoubtedly due to differences in smoking habits. A multiplicative interaction between radon and smoking would thus support the use of a multiplicative treatment of sex, whereas an additive interaction would not. Analyses of the underground miner data indicated an interaction intermediate between multiplicative and additive, and this might suggest such an intermediate approach for addressing the modifying effects of sex. Also, lung-cancer risks in male and female A-bomb survivors were more comparable on a absolute scale than on a multiplicative one. See chapter 3 and Puskin (1992) for further discussion.
Dependence of Risks on Age at Exposure
Lubin and others (1994a) did not find evidence that age at exposure modified lung-cancer risks in underground miners. Consequently, the committee's preferred models are based on the assumption that the excess relative risk did not depend on age at exposure. Studies of cancer risk in A-bomb survivors and other populations (UNSCEAR 1994) have also failed to provide evidence of modification of lung-cancer risk by age at exposure, although a decline in the excess relative risk with increasing age at exposure has been observed for other cancer
categories including all solid tumors, digestive cancers, and cancers of the breast and thyroid. In most cases, the strongest evidence for a dependence of risk on age at exposure was based on a comparison of risks in those exposed as children (under age 20 years) and those exposed later in life.
Data from the miner cohorts on exposures in childhood are limited primarily to the China cohort. Of 813 lung-cancer deaths occurring in miners initially exposed under age 20 years, 735 occurred in this cohort, and all 54 of the lung-cancers occurring in miners exposed under age 10 yrs were from the China cohort. In fact, a large percentage of miners in the China cohort were first exposed at very young ages, with only 25% (245) of the lung-cancers occurring in those with first exposure at age 20 yrs and older. Analyses by Lubin and others (1994a) show statistically significant variations in ERR per unit exposure with age at first exposure in the China cohort, although the pattern was not consistent. Clearly the uncertainty in the lung-cancer risks in adults resulting from exposure in childhood is much greater than for risks resulting from exposure in adulthood Not only is there the possibility that the ERR per unit exposure for childhood exposures might differ from that predicted by the committee's models, it is also possible that the pattern of decline in risks differs from that observed for adult exposures. It is noted, for example, that the committee's preferred models are based on the assumption that risks persist for a lifetime, but there are no data to validate this assumption for exposure in childhood.
Dependence of Risks on Smoking Status
Limitations in the available data on smoking make it difficult to evaluate the modifying effect of smoking on radon risks. Because of the need to extrapolate from miners with a high proportion of ever-smokers to the general population with a lower proportion of ever-smokers, uncertainties in adjustments for smoking may even affect estimates of average population risks. Such uncertainties have a particularly strong effect on estimates that specifically address risks in ever-smokers and never-smokers. Because of limitations in available data, it was not possible to develop a model that took account of the amount smoked, degree of inhaling, and changes in smoking habits over time.
Uncertainties in the Model for Estimating Differences in Radon-Progeny Dosimetry in the Mines and in Homes
Several factors that affect the lung dosimetry of radon progeny differ between mines and homes. These differences must be accounted for in using risk estimates based on underground miners to estimate risks for persons exposed in homes. The parameter summarizing these differences is often referred to as the K-factor. This factor can be expected to vary among individuals, and its average value may also be subject to uncertainty. Uncertainty in the K-factor is discussed
in more detail in appendix B (dosimetry). Variability in the K-factor was included in the committee's Monte Carlo simulations.
Uncertainty in the K-factor values arises from several sources. These include the measurement error in the size-dependent concentrations of airborne radioactivity collected in the sampling devices, the error in deconvoluting a size distribution for the measured activity fractions, and the uncertainty in the relative fractions of time assigned to the various locations in the mine. The error in determining the collected activity concentration depends on the statistics of the counts used to estimate the amounts of the 3 decay products, and the variation in the pump flow. Thus, there is variation in the in-home measurements since the 222Rn concentrations ranged from about 30 Bqm-3 up to 800 Bqm-3, depending on the home being studied. For typical airborne activity concentrations, the uncertainties in the individual concentrations are of the order of 5 to 10% and for PAEC, the errors are 3 to 5%.
These errors then propagate in a non-linear manner since they are input values to the algorithms used to estimate the activity-weighted size distributions. In general, this inversion process is ill-posed since it is an undetermined problem for which a unique solution is not possible. It is known from simulation exercises (Ramamurthi and others 1990) that these algorithms can find acceptable solutions although not necessarily the "true" solution. Thus, it is not possible to definitively determine the overall uncertainties in the size distributions. Similarly, it is also extremely difficult to precisely determine the uncertainty in the times for various mining activities. Although an exact uncertainty cannot be assigned to each K-factor value, it is estimated that the values in the central portion of the distribution should not have errors in excess of 25%. Thus, the variability in K is larger than its uncertainty.
Uncertainties Relating to Background Exposures
The risk models developed by the committee based on its analysis of data from the 11 miner cohorts are based on occupational radon exposures. However, miners were also exposed to radon in their homes and outdoors. Although these additional exposures contribute to their lung-cancer risk, the residential and ambient exposures experienced by miners are much lower than their occupational exposures. Consequently, the impact of these non-occupational exposures on the coefficients in the committee's risk model is expected to be negligible.
Ambient exposures also need to be considered when evaluating residential radon risks, since people are exposed to radon in outdoor air as well as in their homes. Again, since ambient exposures are not widely available, it is not possible to adjust for the effects of outdoor exposures on residential radon risks. However, since ambient exposures are much lower than typical indoor exposures, any adjustment for outdoor exposures when evaluating residential radon risks is likely to be small.
Uncertainties in the Demographic Data Used to Calculate Lifetime Risks
An additional source of uncertainty in lifetime risks involves the application of the committee's risk model to obtain estimates of risks for the U.S. population. These calculations require assumptions about the age distribution of the population, life expectancy, and baseline age and sex-specific lung-cancer mortality rates. As described in chapter 3, current U.S. life table and vital statistics data were used for this purpose. It was assumed that these data were appropriate both now and in the future. Rather than evaluate uncertainty from this source, it seems preferable simply to state that the lifetime risk estimates presented in this report are appropriate only for a population with these demographic characteristics. If changes occur in the future, or risk projection for other populations are desired, these estimates will need to be recalculated to reflect these modifications.
QUANTITATIVE UNCERTAINTY ANALYSIS
Currently, there is a trend in risk assessment towards a more complete characterization of risk using quantitative techniques for uncertainty analysis (Bartlett and others 1996; Morgan and others 1990; NRC 1994b). The results of these analyses can be summarized in the form of a distribution of possible risks within the exposed population, taking into account as many sources of uncertainty and variability as possible. This distribution gives an indication of maximal and minimal risks that might be experienced by different individuals, and the relative likelihood of intermediate risks between these two extremes.
Finley and Paustenbach (1994) discuss the benefits and disadvantages of probabilistic exposure assessment compared to using point estimates. Point estimates are simple to interpret, but provide no indication of level of confidence. Probability distributions provide risk analysts with a more complete picture of the possible range of exposure, but are more complex to determine and to use in decision making. Edelmann and Burmaster (1996) show that distributions with the same 95th percentiles could have dramatically different shapes, and that risk-management decisions based on these distributions may be different. Recently, considerable effort has been extended in estimating distributions of risk for use in health-risk assessment (Finley and others 1994; Ruffle and others 1994).
Uncertainty exists in all stages of the risk-assessment process (Small 1994; Dakins and others 1994). An integrated environmental health-risk assessment model includes source characterization, fate and transport of the substance, exposure media, biological modeling, and estimation of risk using dose-response modeling. Each component of the integrated risk assessment is subject to uncertainty. Often what is known about input parameters may be admissible ranges, shape of the distribution, or the type of data. To estimate uncertainty in the output, uncertainty distributions are associated with the input parameters. Distributions characterizing the uncertainty associated with each adjustment factor are developed
using scientific knowledge to the extent possible These distributions can then be sampled using Monte Carlo methods to provide estimates of the output distributions. Monte Carlo methods have been used for estimating the impact of uncertainty in adjustment factors on estimation of human population thresholds for non-carcinogens (Baird and others 1996). Though convenient and easy to use with modern computing technology, Monte Carlo methods should be carefully monitored to ensure the integrity of the results (Burmaster and Anderson 1994).
Distinguishing between uncertainty and variability is necessary but sometimes difficult (Hoffman and Hammonds 1994; Bogen 1995). One approach for describing uncertainty and variability in lognormal random variables is to plot a range of probability distributions in two dimensions, representing uncertainty and variability, thereby permitting the impact of uncertainty to be visualized (Burmaster and Korsan 1996). Uncertainty can sometimes be reduced by collecting more information, but variability cannot. Information on metabolic activation, detoxification, and DNA repair was recently considered in evaluating interindividual variability (Hattis and Barlow 1996; Hattis and Silver 1994). It was shown that empirical studies of biological parameters are useful in establishing uncertainty factors for heterogeneity in individual risk. It was also noted that the interindividual variability tends to be overstated due to the presence of measurement error; adjustments can be made using empirical Bayes shrinkage estimators (Goddard and others 1994) and other statistical techniques.
Quantitative Analysis of Uncertainty and Variability
Rai and others (1996) have developed a general framework for the analysis of uncertainty and variability in risk. In the most general case, the risk R is defined as function
R = H(X1, X2, ... , Xp) (31)
of p risk factors X1, ... , Xp. Each risk factor X1 may vary within the population of interest according to some distribution with probability density function fi(Xi ¦ ![]() i), conditional upon the parameter
i), conditional upon the parameter![]() i. Uncertainty in Xi is characterized by a distribution
i. Uncertainty in Xi is characterized by a distribution ![]() for
for ![]() i, where
i, where ![]() is the true value of the parameter. If
is the true value of the parameter. If ![]() i is a vector valued, gi is a multivariate distribution. Here, it is assumed that the forms of the distributions f and g are known. The case in which the form of f or g is unknown introduces another level of complexity which remains to be addressed.
i is a vector valued, gi is a multivariate distribution. Here, it is assumed that the forms of the distributions f and g are known. The case in which the form of f or g is unknown introduces another level of complexity which remains to be addressed.
If ![]() i is a known constant and the distribution fi is not concentrated at a single point, Xi exhibits variability only. On the other hand, Xi is subject to both uncertainty and variability if both
i is a known constant and the distribution fi is not concentrated at a single point, Xi exhibits variability only. On the other hand, Xi is subject to both uncertainty and variability if both ![]() i and fi are stochastic. When fi is concentrated at a single point
i and fi are stochastic. When fi is concentrated at a single point ![]() i, and
i, and![]() i is stochastic, Xi is subject to uncertainty but not variability. Consequently, the variables X1, ... Xp can be partitioned into three groups: variables subject to uncertainty only, variables subject to variability only, and variables subject to both uncertainty and variability.
i is stochastic, Xi is subject to uncertainty but not variability. Consequently, the variables X1, ... Xp can be partitioned into three groups: variables subject to uncertainty only, variables subject to variability only, and variables subject to both uncertainty and variability.
Rai and Krewski (1998) consider the special case of a multiplicative risk model
R = X1X2 ... Xp. (32)
The multiplicative model is applicable in many situations encountered in practice, and affords a number of simplifications in the analysis. In particular, the multiplicative risk model in (32) is simplified by applying the logarithmic transformation. Xi = log Xi (i = 1, ...p). After transformation, the multiplicative model can be re-expressed as an additive model

where R* = log R. Assume that each Xi has mean mi and variance Var(Xi), where
and
The expected risk on logarithmic scale in  , with variance
, with variance 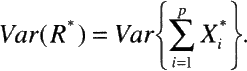
UNCERTAINTY IN POPULATION ATTRIBUTABLE RISK
In the present application, uncertainty in estimates of the population attributable risk of lung-cancer due to residential radon exposure is of primary interest. The general approach to uncertainty analysis proposed by Rai and others (1996) is used for this purpose. As discussed previously, the attributable risk (AR) is not subject to variability, since it is a measure of population rather than individual risk.
Following Levin (1953) and Lubin and Boice (1989), the attributable risk of lung-cancer due to radon exposure is defined as the proportion of lung-cancer deaths attributable to radon progeny. For continuous risk factors, the AR can be written as
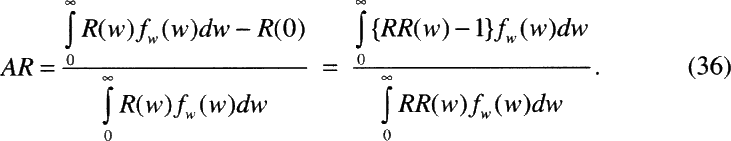
Here, fw is the marginal probability density function of the exposure distribution, reflecting variability in residential radon concentrations. R(w) is the lifetime risk of lung-cancer for a lifetime exposure to radon progeny at a yearly level w in the presence of competing risks, and

is the lifetime relative risk. Note that lifetime excess relative risk, ERR(w) = RR(w)-1, appears in the integrand (36).
The K-factor also influences the lifetime risk of lung-cancer. To accommodate the effect of the K-factor, equation (36) can be modified as
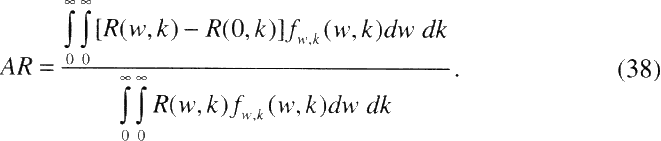
Here the joint marginal distribution of w and K, fw,k(w,k), is the product of the distributions of w and K, since we assume that these two variables are statistically independent.
Let hi and ![]() be the lung-cancer and overall mortality rates for age group i, respectively, in a referent population. Furthermore, let ei be the excess relative risk due to exposure w to radon progeny for age group i. Here, we consider two types of models for ei:
be the lung-cancer and overall mortality rates for age group i, respectively, in a referent population. Furthermore, let ei be the excess relative risk due to exposure w to radon progeny for age group i. Here, we consider two types of models for ei:
and
where
The factors w5–14,w15–24 and w25+ represent cumulative radon-progeny exposures received 5–14, 15–24 and more than 25 years prior to disease diagnosis, respectively. Note both (39) and (40) are multiplicative models of the type (32).
The remaining risk factors in (39) and (40) are redefined as
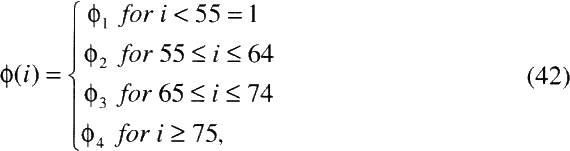
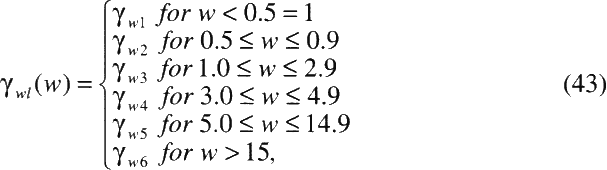
and
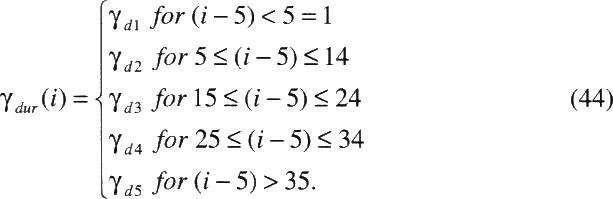
Models (39) and (40) express the age-specific excess relative risk using a risk factor γwl for exposure concentration and an alternative risk factor γdur for exposure duration, respectively. These correspond to the committee's exposure-age-concentration and exposure-age-duration models.
The lifetime risk of lung-cancer is given by the sum of the risk of lung-cancer death each year:
Here

and
is the probability of surviving year i for an individual with exposure w given that the individual survived up to year i-1.
The model for the AR in (38) depends on the uncertainty and variability distributions of w and K. We assume that w has lognormal distribution with geometric mean 24.8 Bqm-3 and geometric standard deviation 3.11, and has uncertainty only in the geometric standard deviation. We also assume that K has a lognormal distribution with geometric mean 1.0 and geometric standard deviation 1.5, and has no uncertainty. Since there is no closed form expression for the integrand in model (38), we approximate the integral by summing over the ranges of values for w and K.
This approximate version of the attributable risk model depends on the risk factors in either (39) or (40). The uncertainty in these factors is characterized by lognormal or log-uniform distributions as summarized in Table A-8. These uncertainty distributions were based on the committee's judgment as to the likely range of values for each of these factors. By postulating an uncertainty distribution for each of the factors in the model, the committee acknowledges that all factors are subject to some degree of uncertainty. Although statistical uncertainty in the estimates of the parameters in the committee's performed models is included, distributions also reflect other sources of uncertainty as discussed previously in this appendix.
Uncertainty distributions of the AR were obtained with Monte Carlo sampling (Rai and others 1996). Although computationally intensive, the analysis is straightforward. First, a set of model parameter values was obtained by sampling from a multivariate normal distribution with mean equal to the estimated parameter values and the values in the covariance matrix given in Table A-9 and based on the standard statistical software package S-Plus. (The Monte Carlo simulation was done on a log scale, with each risk factor Xi in (39) and (40) replaced by exp[Ef(X*i)].) Second, the attributable risk was calculated as described previously in this appendix. Repeating this procedure 10,000 times in case I and 1,000
TABLE A-8a Uncertainty and variability distributions for risk factors in the exposure-age-concentration model for excess relative risk
|
Risk factor |
Variability |
Uncertainty |
|
Model parameters |
Constant |
a ~ N (µ, S)a |
|
Exposure to radon w |
|
|
|
K-factor |
LN (gm = 1, gsd = 1.5) |
gm = 1.00, gsd~LUe (1.2, 2.2) |
TABLE A-8b Uncertainty and variability distributions for risk factors in the exposure-age-duration model for excess relative risk
|
Risk Factor |
Variability |
Uncertainty |
|
Model parameters |
Constant |
a ~ N (µ, S)f |
|
Exposure to radon w |
LN (gm = 24.8, gsd = 3.11) |
|
|
K-factor |
LN (gm = 1, gsd = 1.5) |
gm = 1. 00; gsd ~ LU(1.2, 2.2) |
|
a Multivariate normal distribution with µ and S specified in Table A-9a. bLN: Log-Normal. cgm: geometric mean. dgsd:geometric standard deviation = defined as exps, where s denotes the standard deviation of logeX. eLU(a,b): Log-uniform distribution, with, with logeX uniformly distributed between logea and logeb. f Multivariate normal distribution with µ and S specified in Table A-9b. |
||
TABLE A-9a Parameters for uncertainty distributions for risk factors in exposure-age-concentration modela
|
I. Estimated Values of Parametersb |
|||||||||||
|
Parameter |
β |
θ15–24 |
θ25+ |
|
|
|
γ0.5–1.0 |
γ1.0–3.0 |
γ3.0–5.0 |
γ5.0–15 |
γ15.0+ |
|
Value |
-2.57 |
0.77 |
0.51 |
-0.56 |
-1.23 |
-2.38 |
-0.72 |
-0.98 |
-1.13 |
-1.80 |
-2.21 |
|
II. Covariance Matrixc |
|||||||||||
|
|
β |
θ15–24 |
θ25+ |
|
|
|
γ0.5–1.0 |
γ1.0–3.0 |
γ3.0–5.0 |
γ5.0–15. |
γ15.0+ |
|
β |
9.47 |
|
|
|
|
|
|
|
|
|
|
|
θ15–24 |
-0.36 |
0.77 |
|
|
|
|
|
|
|
|
|
|
θ25+ |
-0.04 |
0.24 |
0.42 |
|
|
|
|
|
|
|
|
|
|
-2.87 |
-0.10 |
-0.15 |
5.71 |
|
|
|
|
|
|
|
|
|
-3.18 |
-0.17 |
-0.33 |
2.85 |
10.87 |
|
|
|
|
|
|
|
|
-3.44 |
-0.19 |
-0.54 |
2.90 |
3.20 |
87.65 |
|
|
|
|
|
|
γ0.5–1.0 |
-5.57 |
-0.10 |
-0.02 |
0.14 |
0.42 |
0.83 |
8.24 |
|
|
|
|
|
γ1.0–3.0 |
-6.36 |
-0.12 |
-0.11 |
0.15 |
0.53 |
0.97 |
5.88 |
6.93 |
|
|
|
|
γ3.0–5.0 |
-6.58 |
-0.16 |
-0.10 |
0.18 |
0.59 |
1.08 |
5.83 |
6.69 |
7.30 |
|
|
|
γ5.0–15.0 |
-6.90 |
-0.05 |
-0.09 |
0.26 |
0.61 |
0.81 |
5.69 |
6.51 |
6.67 |
7.84 |
|
|
γ15.0+ |
-7.04 |
-0.02 |
-0.08 |
0.27 |
0.54 |
0.50 |
5.63 |
6.44 |
6.64 |
7.33 |
8.59 |
|
a Interindividual variability in both the level of exposure to radon and the K-factor is also characterized by lognormal distributions. The parameters of the two distributions were determined from national data on the distribution of radon in U.S. homes and from data on a sample of homes used to estimate the K-factor. b Except for θ15–24 and θ25+ values are on log scale. c Except for θ15–24 and θ25+ values are on log scale. All values were multiplied by 100. |
|||||||||||
TABLE A-9b Parameters for uncertainty distributions for risk factors in exposure-age-duration model
|
I. Estimated Values of Parametersa |
||||||||||
|
Parameter |
β |
θ15–24 |
θ25+ |
|
|
|
γ5–14 |
γ15–24 |
γ25–34 |
γ35+ |
|
Value |
-5.20 |
0.72 |
0.44 |
-0.65 |
-1.29 |
-2.07 |
1.02 |
1.49 |
1.89 |
2.32 |
|
II. Covariance Matrixb |
||||||||||
|
|
β |
θ15–24 |
θ25+ |
|
|
|
γ5–14 |
γ15–24 |
γ25–34 |
γ35+ |
|
β |
7.98 |
|
|
|
|
|
|
|
|
|
|
θ15–24 |
-0.30 |
0.98 |
|
|
|
|
|
|
|
|
|
θ25+ |
-0.01 |
0.25 |
0.44 |
|
|
|
|
|
|
|
|
|
-2.07 |
-0.11 |
-0.21 |
4.32 |
|
|
|
|
|
|
|
|
-2.16 |
-0.20 |
-0.39 |
2.10 |
9.60 |
|
|
|
|
|
|
|
-2.43 |
-0.24 |
-0.59 |
2.15 |
2.43 |
95.37 |
|
|
|
|
|
γ5–14 |
-5.06 |
-0.21 |
-0.14 |
0.31 |
0.37 |
0.54 |
4.60 |
|
|
|
|
γ15–24 |
-5.56 |
-0.39 |
-0.23 |
0.31 |
0.54 |
0.93 |
4.67 |
5.94 |
|
|
|
γ25–34 |
-5.66 |
-0.40 |
-0.15 |
0.20 |
0.45 |
0.83 |
4.73 |
5.60 |
6.75 |
|
|
γ35+ |
-5.65 |
-0.37 |
-0.12 |
-0.15 |
0.18 |
0.65 |
4.76 |
5.61 |
6.03 |
7.26 |
|
a Except for θ15–24 and θ25+, values are on log scale. b Except for θ15–24 and θ25+, values are on log scale. All values were multiplied by 100. |
||||||||||
times in cases II and III (which require considerably more computational effort) produced uncertainty distributions for the AR.
The median of the uncertainty distribution for the AR is shown in Table A-10 along with 95% uncertainty limits covering the central mass of distribution. These limits range from 9.1–28.2% for the exposure-age-concentration model and from 6.8–21.0% for the exposure-age-duration model.
TABLE A-10a Impact of uncertainty and variability on uncertainty intervals for population attributable risk for males
|
|
Exposure-age-concentration model |
Exposure-age-duration model |
||
|
Source |
AR |
95%U.I. |
AR |
95%U.I. |
|
Uncertainty when K = 1 |
0.148 |
(0.091, 0.238) |
0.103 |
(0.068, 0.158) |
|
Uncertainty incorporating variability in K |
0.150 |
(0.097, 0.224) |
0.106 |
(0.077, 0.178) |
|
Uncertainty incorporating variability and uncertainty in K |
0.159 |
(0.095, 0.259) |
0.111 |
(0.081, 0.194) |
TABLE A-10b Impact of uncertainty and variability on uncertainty intervals for population attributable risk for females
|
|
Exposure-age-concentration model |
Exposure-age-duration model |
||
|
Source |
ARa |
95%U.I. |
ARa |
95%U.I. |
|
Uncertainty when K = 1 |
0.160 |
(0.099, 0.256) |
0.111 |
(0.079, 0.179) |
|
Uncertainty incorporating variability in Kb |
0.169 |
(0.104, 0.278) |
0.119 |
(0.084, 0.192) |
|
Uncertainty incorporating variability and uncertainty in Kc |
0.173 |
(0.104, 0.282) |
0.125 |
(0.088, 0.210) |
|
a Median of uncertainty distribution b K ~ LN(gm = 1, gsd = 1.5) c K ~ LN(gm = 1, gsd ~ LU(1.2, 2.2)) |
||||