| This page in the original is blank. |
Overview
Mathematics is the key to opportunity. No longer just the language of science, mathematics now contributes in direct and fundamental ways to business, finance, health, and defense. For students, it opens doors to careers. For citizens, it enables informed decisions. For nations, it provides knowledge to compete in a technological community. To participate fully in the world of the future, America must tap the power of mathematics. (NRC, 1989, p. 1)
The above statement remains true today, although it was written almost ten years ago in the Mathematical Sciences Education Board's (MSEB) report Everybody Counts (NRC, 1989). In envisioning a future in which all students will be afforded such opportunities, the MSEB acknowledges the crucial role played by formulae and algorithms, and suggests that algorithmic skills are more flexible, powerful, and enduring when they come from a place of meaning and understanding. This volume takes as a premise that all students can develop mathematical understanding by working with mathematical tasks from workplace and everyday contexts. The essays in this report provide some rationale for this premise and discuss some of the issues and questions that follow. The tasks in this report illuminate some of the possibilities provided by the workplace and everyday life.
Contexts from within mathematics also can be powerful sites for the development of mathematical understanding, as professional and amateur mathematicians will attest. There are many good sources of compelling problems from within mathematics, and a broad mathematics education will include experience with problems from contexts both within and outside mathematics. The inclusion of tasks in this volume is intended to highlight particularly compelling problems whose context lies outside of mathematics, not to suggest a curriculum.
The operative word in the above premise is "can." The understandings that students develop from any encounter with mathematics depend not only on the context, but also on the students' prior experience and skills, their ways of thinking, their engagement with the task, the environment in which they explore the task—including the teacher, the students, and the tools—the kinds of interactions that occur in that environment, and the system of internal and external incentives that might be associated with the activity. Teaching and learning are complex activities that depend upon evolving and rarely articulated interrelationships among teachers, students, materials, and ideas. No prescription for their improvement can be simple.
This volume may be beneficially seen as a rearticulation and elaboration of a principle put forward in Reshaping School Mathematics:
Principle 3: Relevant Applications Should be an Integral Part of the Curriculum.
Students need to experience mathematical ideas in the context in which they naturally arise—from simple counting and measurement to applications in business and science. Calculators and computers make it possible now to introduce realistic applications throughout the curriculum.
The significant criterion for the suitability of an application is whether it has the potential to engage students' interests and stimulate their mathematical thinking. (NRC, 1990, p. 38)
Mathematical problems can serve as a source of motivation for students if the problems engage students' interests and aspirations. Mathematical problems also can serve as sources of meaning and understanding if the problems stimulate students' thinking. Of course, a mathematical task that is meaningful to a student will provide more motivation than a task that does not make sense. The rationale behind the criterion above is that both meaning and motivation are required. The motivational benefits that can be provided by workplace and everyday problems are worth mentioning, for although some students are aware that certain mathematics courses are necessary in order to gain entry into particular career paths, many students are unaware of how particular topics or problem-solving approaches will have relevance in any workplace. The power of using workplace and everyday problems to teach mathematics lies not so much in motivation, however, for no con-
text by itself will motivate all students. The real power is in connecting to students' thinking.
There is growing evidence in the literature that problem-centered approaches—including mathematical contexts, "real world" contexts, or both—can promote learning of both skills and concepts. In one comparative study, for example, with a high school curriculum that included rich applied problem situations, students scored somewhat better than comparison students on algebraic procedures and significantly better on conceptual and problem-solving tasks (Schoen & Ziebarth, 1998). This finding was further verified through task-based interviews. Studies that show superior performance of students in problem-centered classrooms are not limited to high schools. Wood and Sellers (1996), for example, found similar results with second and third graders.
Research with adult learners seems to indicate that "variation of contexts (as well as the whole task approach) tends to encourage the development of general understanding in a way which concentrating on repeated routine applications of algorithms does not and cannot" (Strässer, Barr, Evans, & Wolf, 1991, p. 163). This conclusion is consistent with the notion that using a variety of contexts can increase the chance that students can show what they know. By increasing the number of potential links to the diverse knowledge and experience of the students, more students have opportunities to excel, which is to say that the above premise can promote equity in mathematics education.
There is also evidence that learning mathematics through applications can lead to exceptional achievement. For example, with a curriculum that emphasizes modeling and applications, high school students at the North Carolina School of Science and Mathematics have repeatedly submitted winning papers in the annual college competition, Mathematical Contest in Modeling (Cronin, 1988; Miller, 1995).
The relationships among teachers, students, curricular materials, and pedagogical approaches are complex. Nonetheless, the literature does supports the premise that workplace and everyday problems can enhance mathematical learning, and suggests that if students engage in mathematical thinking, they will be afforded opportunities for building connections, and therefore meaning and understanding.
In the opening essay, Dale Parnell argues that traditional teaching has been missing opportunities for connections: between subject-matter and context, between academic and vocational education, between school and life, between knowledge and application, and between subject-matter disciplines. He suggests that teaching must change if more students are to learn mathematics. The question, then, is how to exploit opportunities for connections between high school mathematics and the workplace and everyday life.
Rol Fessenden shows by example the importance of mathematics in business, specifically in making marketing decisions. His essay opens with a dialogue among employees of a company that intends to expand its business into
Japan, and then goes on to point out many of the uses of mathematics, data collection, analysis, and non-mathematical judgment that are required in making such business decisions.
In his essay, Thomas Bailey suggests that vocational and academic education both might benefit from integration, and cites several trends to support this suggestion: change and uncertainty in the workplace, an increased need for workers to understand the conceptual foundations of key academic subjects, and a trend in pedagogy toward collaborative, open-ended projects. Further-more, he observes that School-to-Work experiences, first intended for students who were not planning to attend a four-year college, are increasingly being seen as useful in preparing students for such colleges. He discusses several such programs that use work-related applications to teach academic skills and to prepare students for college. Integration of academic and vocational education, he argues, can serve the dual goals of "grounding academic standards in the realistic context of workplace requirements and introducing a broader view of the potential usefulness of academic skills even for entry level workers."
Noting the importance and utility of mathematics for jobs in science, health, and business, Jean Taylor argues for continued emphasis in high school of topics such as algebra, estimation, and trigonometry. She suggests that workplace and everyday problems can be useful ways of teaching these ideas for all students.
There are too many different kinds of workplaces to represent even most of them in the classrooms. Furthermore, solving mathematics problems from some workplace contexts requires more contextual knowledge than is reasonable when the goal is to learn mathematics. (Solving some other workplace problems requires more mathematical knowledge than is reasonable in high school.) Thus, contexts must be chosen carefully for their opportunities for sense making. But for students who have knowledge of a workplace, there are opportunities for mathematical connections as well. In their essay, Daniel Chazan and Sandra Callis Bethell describe an approach that creates such opportunities for students in an algebra course for 10th through 12th graders, many of whom carried with them a "heavy burden of negative experiences" about mathematics. Because the traditional Algebra I curriculum had been extremely unsuccessful with these students, Chazan and Bethell chose to do something different. One goal was to help students see mathematics in the world around them. With the help of community sponsors, Chazen and Bethell asked students to look for mathematics in the workplace and then describe that mathematics and its applications to their classmates.
The tasks in Part One complement the points made in the essays by making direct connections to the workplace and everyday life. Emergency Calls (p. 42) illustrates some possibilities for data analysis and representation by discussing the response times of two ambulance companies. Back-of-the-Envelope Estimates (p. 45) shows how quick, rough estimates and calculations
are useful for making business decisions. Scheduling Elevators (p. 49) shows how a few simplifying assumptions and some careful reasoning can be brought together to understand the difficult problem of optimally scheduling elevators in a large office building. Finally, in the context of a discussion with a client of an energy consulting firm, Heating-Degree-Days (p. 54) illuminates the mathematics behind a common model of energy consumption in home heating.
References
Cronin, T. P. (1988). High school students win "college" competition. Consortium: The Newsletter of the Consortium for Mathematics and Its Applications, 26, 3, 12.
Miller, D. E. (1995). North Carolina sweeps MCM '94.SIAM News, 28 (2).
National Research Council. (1989). Everybody counts: A report to the nation on the future of mathematics education. Washington, DC: National Academy Press.
National Research Council. (1990). Reshaping school mathematics: A philosophy and framework for curriculum. Washington, DC: National Academy Press.
Schoen, H. L. & Ziebarth, S. W. (1998). Assessment of students' mathematical performance (A Core-Plus Mathematics Project Field Test Progress Report). Iowa City: Core Plus Mathematics Project Evaluation Site, University of Iowa.
Strässer, R., Barr, G. Evans, J. & Wolf, A. (1991). Skills versus understanding. In M. Harris (Ed.), Schools, mathematics, and work (pp. 158-168). London: The Falmer Press.
Wood, T. & Sellers, P. (1996). Assessment of a problem-centered mathematics program: Third grade. Journal for Research in Mathematics Education, 27(3), 337-353.
1—
Mathematics as a Gateway to Student Success
DALE PARNELL
Oregon State University
The study of mathematics stands, in many ways, as a gateway to student success in education. This is becoming particularly true as our society moves inexorably into the technological age. Therefore, it is vital that more students develop higher levels of competency in mathematics.1
The standards and expectations for students must be high, but that is only half of the equation. The more important half is the development of teaching techniques and methods that will help all students (rather than just some students) reach those higher expectations and standards. This will require some changes in how mathematics is taught.
Effective education must give clear focus to connecting real life context with subject-matter content for the student, and this requires a more ''connected" mathematics program. In many of today's classrooms, especially in secondary school and college, teaching is a matter of putting students in classrooms marked "English," "history," or "mathematics," and then attempting to fill their heads with facts through lectures, textbooks, and the like. Aside from an occasional lab, workbook, or "story problem," the element of contextual teaching and learning is absent, and little attempt is made to connect what students are learning with the world in which they will be expected to work and spend their lives. Often the frag-
mented information offered to students is of little use or application except to pass a test.
What we do in most traditional classrooms is require students to commit bits of knowledge to memory in isolation from any practical application—to simply take our word that they "might need it later." For many students, "later" never arrives. This might well be called the freezer approach to teaching and learning. In effect, we are handing out information to our students and saying, "Just put this in your mental freezer; you can thaw it out later should you need it." With the exception of a minority of students who do well in mastering abstractions with little contextual experience, students aren't buying that offer. The neglected majority of students see little personal meaning in what they are asked to learn, and they just don't learn it.
I recently had occasion to interview 75 students representing seven different high schools in the Northwest. In nearly all cases, the students were juniors identified as vocational or general education students. The comment of one student stands out as representative of what most of these students told me in one way or another: "I know it's up to me to get an education, but a lot of times school is just so dull and boring. … You go to this class, go to that class, study a little of this and a little of that, and nothing connects. … I would like to really understand and know the application for what I am learning." Time and again, students were asking, "Why do I have to learn this?" with few sensible answers coming from the teachers.
My own long experience as a community college president confirms the thoughts of these students. In most community colleges today, one-third to one-half of the entering students are enrolled in developmental (remedial) education, trying to make up for what they did not learn in earlier education experiences. A large majority of these students come to the community college with limited mathematical skills and abilities that hardly go beyond adding, subtracting, and multiplying with whole numbers. In addition, the need for remediation is also experienced, in varying degrees, at four-year colleges and universities.
What is the greatest sin committed in the teaching of mathematics today? It is the failure to help students use the magnificent power of the brain to make connections between the following:
- subject-matter content and the context of use;
- academic and vocational education;
- school and other life experiences;
- knowledge and application of knowledge; and
- one subject-matter discipline and another.
Why is such failure so critical? Because understanding the idea of making the connection between subject-matter content and the context of application
is what students, at all levels of education, desperately require to survive and succeed in our high-speed, high-challenge, rapidly changing world.
Educational policy makers and leaders can issue reams of position papers on longer school days and years, site-based management, more achievement tests and better assessment practices, and other "hot" topics of the moment, but such papers alone will not make the crucial difference in what students know and can do. The difference will be made when classroom teachers begin to connect learning with real-life experiences in new, applied ways, and when education reformers begin to focus upon learning for meaning.
A student may memorize formulas for determining surface area and measuring angles and use those formulas correctly on a test, thereby achieving the behavioral objectives set by the teacher. But when confronted with the need to construct a building or repair a car, the same student may well be left at sea because he or she hasn't made the connection between the formulas and their real-life application. When students are asked to consider the Pythagorean Theorem, why not make the lesson active, where students actually lay out the foundation for a small building like a storage shed?
What a difference mathematics instruction could make for students if it were to stress the context of application—as well as the content of knowledge—using the problem-solving model over the freezer model. Teaching conducted upon the connected model would help more students learn with their thinking brain, as well as with their memory brain, developing the competencies and tools they need to survive and succeed in our complex, interconnected society.
One step toward this goal is to develop mathematical tasks that integrate subject-matter content with the context of application and that are aimed at preparing individuals for the world of work as well as for post-secondary education. Since many mathematics teachers have had limited workplace experience, they need many good examples of how knowledge of mathematics can be applied to real life situations. The trick in developing mathematical tasks for use in classrooms will be to keep the tasks connected to real life situations that the student will recognize. The tasks should not be just a contrived exercise but should stay as close to solving common problems as possible.
As an example, why not ask students to compute the cost of 12 years of schooling in a public school? It is a sad irony that after 12 years of schooling most students who attend the public schools have no idea of the cost of their schooling or how their education was financed. No wonder that some public schools have difficulty gaining financial support! The individuals being served by the schools have never been exposed to the real life context of who pays for the schools and why. Somewhere along the line in the teaching of mathematics, this real life learning opportunity has been missed, along with many other similar contextual examples.
The mathematical tasks in High School Mathematics at Work provide students (and teachers) with a plethora of real life mathematics problems and
challenges to be faced in everyday life and work. The challenge for teachers will be to develop these tasks so they relate as close as possible to where students live and work every day.
References
Parnell, D. (1985). The neglected majority. Washington, DC: Community College Press.
Parnell, D. (1995). Why do I have to learn this? Waco, TX: CORD Communications.
Note
DALE PARNELL is Professor Emeritus of the School of Education at Oregon State University. He has served as a University Professor, College President, and for ten years as the President and Chief Executive Officer of the American Association of Community Colleges. He has served as a consultant to the National Science Foundation and has served on many national commissions, such as the Secretary of Labor's Commission on Achieving Necessary Skills (SCANS). He is the author of the book The Neglected Majority which provided the foundation for the federally-funded Tech Prep Associate Degree Program.
2—
Market Launch
ROL FESSENDEN
L. L. Bean, Inc.
"OK, the agenda of the meeting is to review the status of our launch into Japan. You can see the topics and presenters on the list in front of you. Gregg, can you kick it off with a strategy review?"
"Happy to, Bob. We have assessed the possibilities, costs, and return on investment of opening up both store and catalog businesses in other countries. Early research has shown that both Japan and Germany are good candidates. Specifically, data show high preference for good quality merchandise, and a higher-than-average propensity for an active outdoor lifestyle in both countries. Education, age, and income data are quite different from our target market in the U.S., but we do not believe that will be relevant because the cultures are so different. In addition, the Japanese data show that they have a high preference for things American, and, as you know, we are a classic American company. Name recognition for our company is 14%, far higher than any of our American competition in Japan. European competitors are virtually unrecognized, and other Far Eastern competitors are perceived to be of lower quality than us. The data on these issues are quite clear.
"Nevertheless, you must understand that there is a lot of judgment involved in the decision to focus on Japan. The analyses are limited because the cultures are different and we expect different behavioral drivers. Also,
much of the data we need in Japan are simply not available because the Japanese marketplace is less well developed than in the U.S. Drivers' license data, income data, lifestyle data, are all commonplace here and unavailable there. There is little prior penetration in either country by American retailers, so there is no experience we can draw upon. We have all heard how difficult it will be to open up sales operations in Japan, but recent sales trends among computer sellers and auto parts sales hint at an easing of the difficulties.
"The plan is to open three stores a year, 5,000 square feet each. We expect to do $700/square foot, which is more than double the experience of American retailers in the U.S. but 45% less than our stores. In addition, pricing will be 20% higher to offset the cost of land and buildings. Asset costs are approximately twice their rate in the U.S., but labor is slightly less. Benefits are more thoroughly covered by the government. Of course, there is a lot of uncertainty in the sales volumes we are planning. The pricing will cover some of the uncertainty but is still less than comparable quality goods already being offered in Japan.
"Let me shift over to the competition and tell you what we have learned. We have established long-term relationships with 500 to 1000 families in each country. This is comparable to our practice in the U.S. These families do not know they are working specifically with our company, as this would skew their reporting. They keep us appraised of their catalog and shopping experiences, regardless of the company they purchase from. The sample size is large enough to be significant, but, of course, you have to be careful about small differences.
"All the families receive our catalog and catalogs from several of our competitors. They match the lifestyle, income, and education demographic profiles of the people we want to have as customers. They are experienced catalog shoppers, and this will skew their feedback as compared to new catalog shoppers.
"One competitor is sending one 100-page catalog per quarter. The product line is quite narrow—200 products out of a domestic line of 3,000. They have selected items that are not likely to pose fit problems: primarily outerwear and knit shirts, not many pants, mostly men's goods, not women's. Their catalog copy is in Kanji, but the style is a bit stilted we are told, probably because it was written in English and translated, but we need to test this hypothesis. By contrast, we have simply mailed them the same catalog we use in the U.S., even written in English.
"Customer feedback has been quite clear. They prefer our broader assortment by a ratio of 3:1, even though they don't buy most of the products. As the competitors figured, sales are focused on outerwear and knits, but we are getting more sales, apparently because they like looking at the catalog and spend more time with it. Again, we need further testing. Another hypothesis is that our brand name is simply better known.
"Interestingly, they prefer our English-language version because they find it more of an adventure to read the catalog in another language. This is probably
a built-in bias of our sampling technique because we specifically selected people who speak English. We do not expect this trend to hold in a general mailing.
"The English language causes an 8% error rate in orders, but orders are 25% larger, and 4% more frequent. If we can get them to order by phone, we can correct the errors immediately during the call.
"The broader assortment, as I mentioned, is resulting in a significantly higher propensity to order, more units per order, and the same average unit cost. Of course, paper and postage costs increase as a consequence of the larger format catalog. On the other hand, there are production efficiencies from using the same version as the domestic catalog. Net impact, even factoring in the error rate, is a significant sales increase. On the other hand, most of the time, the errors cause us to ship the wrong item which then needs to be mailed back at our expense, creating an impression in the customers that we are not well organized even though the original error was theirs.
"Final point: The larger catalog is being kept by the customer an average of 70 days, while the smaller format is only kept on average for 40 days. Assuming—we need to test this—that the length of time they keep the catalog is proportional to sales volumes, this is good news. We need to assess the overall impact carefully, but it appears that there is a significant population for which an English-language version would be very profitable."
"Thanks, Gregg, good update. Jennifer, what do you have on customer research?"
"Bob, there's far more that we need to know than we have been able to find out. We have learned that Japan is very fad-driven in apparel tastes and fascinated by American goods. We expect sales initially to sky-rocket, then drop like a stone. Later on, demand will level out at a profitable level. The graphs on page 3 [Figure 2-1] show demand by week for 104 weeks, and we have assessed several scenarios. They all show a good underlying business, but the uncertainty is in the initial take-off. The best data are based on the Italian fashion boom which Japan experienced in the late 80s. It is not strictly analogous because it revolved around dress apparel instead of our casual and weekend wear. It is, however, the best information available.
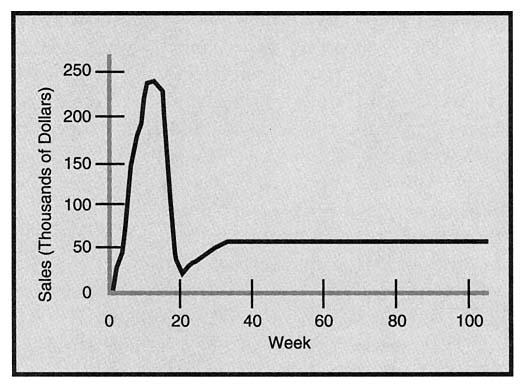
FIGURE 2-1: Sales projections by week, Scenario A
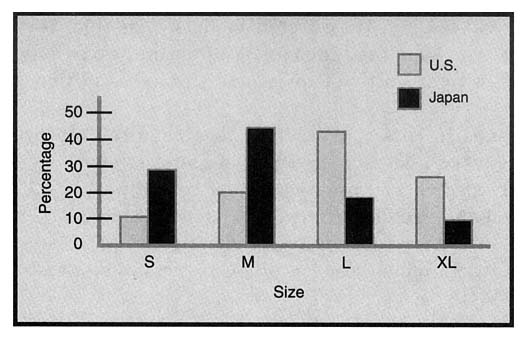
FIGURE 2-2: Size distributions, U.S. vs. Japan
"Our effectiveness in positioning inventory for that initial surge will be critical to our long-term success. There are excellent data—supplied by MITI, I might add—that show that Japanese customers can be intensely loyal to companies that meet their high service expectations. That is why we prepared several scenarios. Of course, if we position inventory for the high scenario, and we experience the low one, we will experience a significant loss due to liquidations. We are still analyzing the long-term impact, however. It may still be worthwhile to take the risk if the 2-year ROI1 is sufficient.
"We have solid information on their size scales [Figure 2-2]. Seventy percent are small and medium. By comparison, 70% of Americans are large and extra large. This will be a challenge to manage but will save a few bucks on fabric.
"We also know their color preferences, and they are very different than Americans. Our domestic customers are very diverse in their tastes, but 80% of Japanese customers will buy one or two colors out of an offering of 15. We are still researching color choices, but it varies greatly for pants versus shirts, and for men versus women. We are confident we can find patterns, but we also know that it is easy to guess wrong in that market. If we guess wrong, the liquidation costs will be very high.
"Bad news on the order-taking front, however. They don't like to order by phone. …"
Analysis
In this very brief exchange among decision-makers we observe the use of many critically important skills that were originally learned in public schools. Perhaps the most important is one not often mentioned, and that is the ability to convert an important business question into an appropriate mathematical one, to solve the mathematical problem, and then to explain the implications of the solution for the original business problem. This ability to inhabit simultaneously the business world and the mathematical world, to translate between the two, and, as a consequence, to bring clarity to complex, real-world issues is of extraordinary importance.
In addition, the participants in this conversation understood and interpreted graphs and tables, computed, approximated, estimated, interpolated, extrapolated, used probabilistic concepts to draw conclusions, generalized from
small samples to large populations, identified the limits of their analyses, discovered relationships, recognized and used variables and functions, analyzed and compared data sets, and created and interpreted models. Another very important aspect of their work was that they identified additional questions, and they suggested ways to shed light on those questions through additional analysis.
There were two broad issues in this conversation that required mathematical perspectives. The first was to develop as rigorous and cost effective a data collection and analysis process as was practical. It involved perhaps 10 different analysts who attacked the problem from different viewpoints. The process also required integration of the mathematical learnings of all 10 analysts and translation of the results into business language that could be understood by non-mathematicians.
The second broad issue was to understand from the perspective of the decision-makers who were listening to the presentation which results were most reliable, which were subject to reinterpretation, which were actually judgments not supported by appropriate analysis, and which were hypotheses that truly required more research. In addition, these business people would likely identify synergies in the research that were not contemplated by the analysts. These synergies need to be analyzed to determine if—mathematically—they were real. The most obvious one was where the inventory analysts said that the customers don't like to use the phone to place orders. This is bad news for the sales analysts who are counting on phone data collection to correct errors caused by language problems. Of course, we need more information to know the magnitude—or even the existance—of the problem.
In brief, the analyses that preceded the dialogue might each be considered a mathematical task in the business world:
- A cost analysis of store operations and catalogs was conducted using data from existing American and possibly other operations.
- Customer preferences research was analyzed to determine preferences in quality and life-style. The data collection itself could not be carried out by a high school graduate without guidance, but 80% of the analysis could.
- Cultural differences were recognized as a causes of analytical error. Careful analysis required judgment. In addition, sources of data were identified in the U.S., and comparable sources were found lacking in Japan. A search was conducted for other comparable retail experience, but none was found. On the other hand, sales data from car parts and computers were assessed for relevance.
- Rates of change are important in understanding how Japanese and American stores differ. Sales per square foot, price increases,
- asset costs, labor costs and so forth were compared to American standards to determine whether a store based in Japan would be a viable business.
- "Nielsen" style ratings of 1000 families were used to collect data. Sample size and error estimates were mentioned. Key drivers of behavior (lifestyle, income, education) were mentioned, but this list may not be complete. What needs to be known about these families to predict their buying behavior? What does "lifestyle" include? How would we quantify some of these variables?
- A hypothesis was presented that catalog size and product diversity drive higher sales. What do we need to know to assess the validity of this hypothesis? Another hypothesis was presented about the quality of the translation. What was the evidence for this hypothesis? Is this a mathematical question? Sales may also be proportional to the amount of time a potential customer retains the catalog. How could one ascertain this?
- Despite the abundance of data, much uncertainty remains about what to expect from sales over the first two years. Analysis could be conducted with the data about the possible inventory consequences of choosing the wrong scenario.
- One might wonder about the uncertainty in size scales. What is so difficult about identifying the colors that Japanese people prefer? Can these preferences be predicted? Will this increase the complexity of the inventory management task?
- Can we predict how many people will not use phones? What do they use instead?
As seen through a mathematical lens, the business world can be a rich, complex, and essentially limitless source of fascinating questions.
Note
ROL FESSENDEN is Vice-President of Inventory Planning and Control at L. L. Bean, Inc. He is also Co-Principal Investigator and Vice-Chair of Maine's State Systemic Initiative and Chair of the Strategic Planning Committee. He has previously served on the Mathematical Science Education Board, and on the National Alliance for State Science and Mathematics Coalitions (NASSMC).
3—
Integrating Vocational and Academic Education
THOMAS BAILEY
Columbia University
In high school education, preparation for work immediately after high school and preparation for post-secondary education have traditionally been viewed as incompatible. Work-bound high-school students end up in vocational education tracks, where courses usually emphasize specific skills with little attention to underlying theoretical and conceptual foundations.1 College-bound students proceed through traditional academic discipline-based courses, where they learn English, history, science, mathematics, and foreign languages, with only weak and often contrived references to applications of these skills in the workplace or in the community outside the school. To be sure, many vocational teachers do teach underlying concepts, and many academic teachers motivate their lessons with examples and references to the world outside the classroom. But these enrichments are mostly frills, not central to either the content or pedagogy of secondary school education.
Rethinking Vocational and Academic Education
Educational thinking in the United States has traditionally placed priority on college preparation. Thus the distinct track of vocational education has been seen as an option for those students who are deemed not capable of success in the more desirable academic track. As vocational programs acquired a reputation
as a ''dumping ground," a strong background in vocational courses (especially if they reduced credits in the core academic courses) has been viewed as a threat to the college aspirations of secondary school students.
This notion was further reinforced by the very influential 1983 report entitled A Nation at Risk (National Commission on Excellence in Education, 1983), which excoriated the U.S. educational system for moving away from an emphasis on core academic subjects that, according to the report, had been the basis of a previously successful American education system. Vocational courses were seen as diverting high school students from core academic activities. Despite the dubious empirical foundation of the report's conclusions, subsequent reforms in most states increased the number of academic courses required for graduation and reduced opportunities for students to take vocational courses.
The distinction between vocational students and college-bound students has always had a conceptual flaw. The large majority of students who go to four-year colleges are motivated, at least to a significant extent, by vocational objectives. In 1994, almost 247,000 bachelors degrees were conferred in business administration. That was only 30,000 less than the total number (277,500) of 1994 bachelor degree conferred in English, mathematics, philosophy, religion, physical sciences and science technologies, biological and life sciences, social sciences, and history combined. Furthermore, these "academic" fields are also vocational since many students who graduate with these degrees intend to make their living working in those fields.
Several recent economic, technological, and educational trends challenge this sharp distinction between preparation for college and for immediate post-high-school work, or, more specifically, challenge the notion that students planning to work after high school have little need for academic skills while college-bound students are best served by an abstract education with only tenuous contact with the world of work:
- First, many employers and analysts are arguing that, due to changes in the nature of work, traditional approaches to teaching vocational skills may not be effective in the future. Given the increasing pace of change and uncertainty in the workplace, young people will be better prepared, even for entry level positions and certainly for subsequent positions, if they have an underlying understanding of the scientific, mathematical, social, and even cultural aspects of the work that they will do. This has led to a growing emphasis on integrating academic and vocational education.2
- Views about teaching and pedagogy have increasingly moved toward a more open and collaborative "student-centered" or "constructivist" teaching style that puts a great deal of emphasis on having students work together on complex, open-ended projects. This reform strategy is now widely implemented through the efforts of organizations such as the Coalition of Essential Schools, the National Center for Restructuring Education, Schools, and Teaching at
- Teachers College, and the Center for Education Research at the University of Wisconsin at Madison. Advocates of this approach have not had much interaction with vocational educators and have certainly not advocated any emphasis on directly preparing high school students for work. Nevertheless, the approach fits well with a reformed education that integrates vocational and academic skills through authentic applications. Such applications offer opportunities to explore and combine mathematical, scientific, historical, literary, sociological, economic, and cultural issues.
- In a related trend, the federal School-to-Work Opportunities Act of 1994 defines an educational strategy that combines constructivist pedagogical reforms with guided experiences in the workplace or other non-work settings. At its best, school-to-work could further integrate academic and vocational learning through appropriately designed experiences at work.
- The integration of vocational and academic education and the initiatives funded by the School-to-Work Opportunities Act were originally seen as strategies for preparing students for work after high school or community college. Some educators and policy makers are becoming convinced that these approaches can also be effective for teaching academic skills and preparing students for four-year college. Teaching academic skills in the context of realistic and complex applications from the workplace and community can provide motivational benefits and may impart a deeper understanding of the material by showing students how the academic skills are actually used. Retention may also be enhanced by giving students a chance to apply the knowledge that they often learn only in the abstract.3
- During the last twenty years, the real wages of high school graduates have fallen and the gap between the wages earned by high school and college graduates has grown significantly. Adults with no education beyond high school have very little chance of earning enough money to support a family with a moderate lifestyle.4 Given these wage trends, it seems appropriate and just that every high school student at least be prepared for college, even if some choose to work immediately after high school.
Innovative Examples
There are many examples of programs that use work-related applications both to teach academic skills and to prepare students for college. One approach is to organize high school programs around broad industrial or occupational areas, such as health, agriculture, hospitality, manufacturing, transportation, or the arts. These broad areas offer many opportunities for wide-ranging curricula in all academic disciplines. They also offer opportunities for collaborative work among teachers from different disciplines. Specific skills can still be taught in this format but in such a way as to motivate broader academic and theoretical themes. Innovative programs can now be found in many vocational
high schools in large cities, such as Aviation High School in New York City and the High School of Agricultural Science and Technology in Chicago. Other schools have organized schools-within-schools based on broad industry areas.
Agriculturally based activities, such as 4H and Future Farmers of America, have for many years used the farm setting and students' interest in farming to teach a variety of skills. It takes only a little imagination to think of how to use the social, economic, and scientific bases of agriculture to motivate and illustrate skills and knowledge from all of the academic disciplines. Many schools are now using internships and projects based on local business activities as teaching tools. One example among many is the integrated program offered by the Thomas Jefferson High School for Science and Technology in Virginia, linking biology, English, and technology through an environmental issues forum. Students work as partners with resource managers at the Mason Neck National Wildlife Refuge and the Mason Neck State Park to collect data and monitor the daily activities of various species that inhabit the region. They search current literature to establish a hypothesis related to a real world problem, design an experiment to test their hypothesis, run the experiment, collect and analyze data, draw conclusions, and produce a written document that communicates the results of the experiment. The students are even responsible for determining what information and resources are needed and how to access them. Student projects have included making plans for public education programs dealing with environmental matters, finding solutions to problems caused by encroaching land development, and making suggestions for how to handle the overabundance of deer in the region.
These examples suggest the potential that a more integrated education could have for all students. Thus continuing to maintain a sharp distinction between vocational and academic instruction in high school does not serve the interests of many of those students headed for four-year or two-year college or of those who expect to work after high school. Work-bound students will be better prepared for work if they have stronger academic skills, and a high-quality curriculum that integrates school-based learning into work and community applications is an effective way to teach academic skills for many students.
Despite the many examples of innovative initiatives that suggest the potential for an integrated view, the legacy of the duality between vocational and academic education and the low status of work-related studies in high school continue to influence education and education reform. In general, programs that deviate from traditional college-prep organization and format are still viewed with suspicion by parents and teachers focused on four-year college. Indeed, college admissions practices still very much favor the traditional approaches. Interdisciplinary courses, "applied" courses, internships, and other types of work experience that characterize the school-to-work strategy or programs that integrate academic and vocational education often do not fit well into college admissions requirements.
Joining Work and Learning
What implications does this have for the mathematics standards developed by the National Council of Teachers of Mathematics (NCTM)? The general principle should be to try to design standards that challenge rather than reinforce the distinction between vocational and academic instruction. Academic teachers of mathematics and those working to set academic standards need to continue to try to understand the use of mathematics in the workplace and in everyday life. Such understandings would offer insights that could suggest reform of the traditional curriculum, but they would also provide a better foundation for teaching mathematics using realistic applications. The examples in this volume are particularly instructive because they suggest the importance of problem solving, logic, and imagination and show that these are all important parts of mathematical applications in realistic work settings. But these are only a beginning.
In order to develop this approach, it would be helpful if the NCTM standards writers worked closely with groups that are setting industry standards.5 This would allow both groups to develop a deeper understanding of the mathematics content of work.
The NCTM's Curriculum Standards for Grades 9-12 include both core standards for all students and additional standards for "college-intending" students. The argument presented in this essay suggests that the NCTM should dispense with the distinction between college intending and non-college intending students. Most of the additional standards, those intended only for the "college intending" students, provide background that is necessary or beneficial for the calculus sequence. A re-evaluation of the role of calculus in the high school curriculum may be appropriate, but calculus should not serve as a wedge to separate college-bound from non-college-bound students. Clearly, some high school students will take calculus, although many college-bound students will not take calculus either in high school or in college. Thus in practice, calculus is not a characteristic that distinguishes between those who are or are not headed for college. Perhaps standards for a variety of options beyond the core might be offered. Mathematics standards should be set to encourage stronger skills for all students and to illustrate the power and usefulness of mathematics in many settings. They should not be used to institutionalize dubious distinctions between groups of students.
References
Bailey, T. & Merritt, D. (1997).School-to-work for the collegebound. Berkeley, CA: National Center for Research in Vocational Education.
Hoachlander, G. (1997). Organizing mathematics education around work. In L.A. Steen (Ed.), Why numbers count: Quantitative literacy for tomorrow's America, (pp. 122-136). New York: College Entrance Examination Board.
Levy, F. & Murnane, R. (1992). U.S. earnings levels and earnings inequality: A review of recent trends and proposed explanations. Journal of Economic Literature, 30, 1333-1381.
National Commission on Excellence in Education. (1983). A nation at risk: The imperative for educational reform. Washington, DC: Author.
Notes
THOMAS BAILEY is an Associate Professor of Economics Education at Teachers College, Columbia University. He is also Director of the Institute on Education and the Economy and Director of the Community College Research Center, both at Teachers College. He is also on the board of the National Center for Research in Vocational Education.
4—
The Importance of Workplace and Everyday Mathematics
JEAN E. TAYLOR
Rutgers University
For decades our industrial society has been based on fossil fuels. In today's knowledge-based society, mathematics is the energy that drives the system. In the words of the new WQED television series, Life by the Numbers, to create knowledge we "burn mathematics." Mathematics is more than a fixed tool applied in known ways. New mathematical techniques and analyses and even conceptual frameworks are continually required in economics, in finance, in materials science, in physics, in biology, in medicine.
Just as all scientific and health-service careers are mathematically based, so are many others. Interaction with computers has become a part of more and more jobs, and good analytical skills enhance computer use and troubleshooting. In addition, virtually all levels of management and many support positions in business and industry require some mathematical understanding, including an ability to read graphs and interpret other information presented visually, to use estimation effectively, and to apply mathematical reasoning.
What Should Students Learn for Today's World?
Education in mathematics and the ability to communicate its predictions is more important than ever for moving from low-paying jobs into better-paying ones. For example, my local paper, The Times of Trenton, had a section "Focus
on Careers" on October 5, 1997 in which the majority of the ads were for high technology careers (many more than for sales and marketing, for example).
But precisely what mathematics should students learn in school? Mathematicians and mathematics educators have been discussing this question for decades. This essay presents some thoughts about three areas of mathematics—estimation, trigonometry, and algebra—and then some thoughts about teaching and learning.
Estimation is one of the harder skills for students to learn, even if they experience relatively little difficulty with other aspects of mathematics. Many students think of mathematics as a set of precise rules yielding exact answers and are uncomfortable with the idea of imprecise answers, especially when the degree of precision in the estimate depends on the context and is not itself given by a rule. Yet it is very important to be able to get an approximate sense of the size an answer should be, as a way to get a rough check on the accuracy of a calculation (I've personally used it in stores to detect that I've been charged twice for the same item, as well as often in my own mathematical work), a feasibility estimate, or as an estimation for tips.
Trigonometry plays a significant role in the sciences and can help us understand phenomena in everyday life. Often introduced as a study of triangle measurement, trigonometry may be used for surveying and for determining heights of trees, but its utility extends vastly beyond these triangular applications. Students can experience the power of mathematics by using sine and cosine to model periodic phenomena such as going around and around a circle, going in and out with tides, monitoring temperature or smog components changing on a 24-hour cycle, or the cycling of predator-prey populations.
No educator argues the importance of algebra for students aiming for mathematically-based careers because of the foundation it provides for the more specialized education they will need later. Yet, algebra is also important for those students who do not currently aspire to mathematics-based careers, in part because a lack of algebraic skills puts an upper bound on the types of careers to which a student can aspire. Former civil rights leader Robert Moses makes a good case for every student learning algebra, as a means of empowering students and providing goals, skills, and opportunities. The same idea was applied to learning calculus in the movie Stand and Deliver. How, then, can we help all students learn algebra?
For me personally, the impetus to learn algebra was at least in part to learn methods of solution for puzzles. Suppose you have 39 jars on three shelves. There are twice as many jars on the second shelf as the first, and four more jars on the third shelf than on the second shelf. How many jars are there on each shelf? Such problems are not important by themselves, but if they show the students the power of an idea by enabling them to solve puzzles that they'd like to solve, then they have value. We can't expect such problems to interest all students. How then can we reach more students?
Workplace and Everyday Settings as a Way of Making Sense
One of the common tools in business and industry for investigating mathematical issues is the spreadsheet, which is closely related to algebra. Writing a rule to combine the elements of certain cells to produce the quantity that goes into another cell is doing algebra, although the variables names are cell names rather than x or y. Therefore, setting up spreadsheet analyses requires some of the thinking that algebra requires.
By exploring mathematics via tasks which come from workplace and everyday settings, and with the aid of common tools like spreadsheets, students are more likely to see the relevance of the mathematics and are more likely to learn it in ways that are personally meaningful than when it is presented abstractly and applied later only if time permits. Thus, this essay argues that workplace and everyday tasks should be used for teaching mathematics and, in particular, for teaching algebra. It would be a mistake, however, to rely exclusively on such tasks, just as it would be a mistake to teach only spreadsheets in place of algebra.
Communicating the results of an analysis is a fundamental part of any use of mathematics on a job. There is a growing emphasis in the workplace on group work and on the skills of communicating ideas to colleagues and clients. But communicating mathematical ideas is also a powerful tool for learning, for it requires the student to sharpen often fuzzy ideas.
Some of the tasks in this volume can provide the kinds of opportunities I am talking about. Another problem, with clear connections to the real world, is the following, taken from the book entitled Consider a Spherical Cow: A Course in Environmental Problem Solving, by John Harte (1988). The question posed is: How does biomagnification of a trace substance occur? For example, how do pesticides accumulate in the food chain, becoming concentrated in predators such as condors? Specifically, identify the critical ecological and chemical parameters determining bioconcentrations in a food chain, and in terms of these parameters, derive a formula for the concentration of a trace substance in each link of a food chain. This task can be undertaken at several different levels. The analysis in Harte's book is at a fairly high level, although it still involves only algebra as a mathematical tool. The task could be undertaken at a more simple level or, on the other hand, it could be elaborated upon as suggested by further exercises given in that book. And the students could then present the results of their analyses to each other as well as the teacher, in oral or written form.
Concepts or Procedures?
When teaching mathematics, it is easy to spend so much time and energy focusing on the procedures that the concepts receive little if any attention. When teaching algebra, students often learn the procedures for using the quadratic formula or for solving simultaneous equations without thinking of intersections of curves and lines and without being able to apply the procedures in unfamiliar settings. Even
when concentrating on word problems, students often learn the procedures for solving "coin problems" and "train problems" but don't see the larger algebraic context. The formulas and procedures are important, but are not enough.
When using workplace and everyday tasks for teaching mathematics, we must avoid falling into the same trap of focusing on the procedures at the expense of the concepts. Avoiding the trap is not easy, however, because just like many tasks in school algebra, mathematically based workplace tasks often have standard procedures that can be used without an understanding of the underlying mathematics. To change a procedure to accommodate a changing business climate, to respond to changes in the tax laws, or to apply or modify a procedure to accommodate a similar situation, however, requires an understanding of the mathematical ideas behind the procedures. In particular, a student should be able to modify the procedures for assessing energy usage for heating (as in Heating-Degree-Days, p. 54) in order to assess energy usage for cooling in the summer.
To prepare our students to make such modifications on their own, it is important to focus on the concepts as well as the procedures. Workplace and everyday tasks can provide opportunities for students to attach meaning to the mathematical calculations and procedures. If a student initially solves a problem without algebra, then the thinking that went into his or her solution can help him or her make sense out of algebraic approaches that are later presented by the teacher or by other students. Such an approach is especially appropriate for teaching algebra, because our teaching of algebra needs to reach more students (too often it is seen by students as meaningless symbol manipulation) and because algebraic thinking is increasingly important in the workplace.
An Example: The Student/Professor Problem
To illustrate the complexity of learning algebra meaningfully, consider the following problem from a study by Clement, Lockhead, & Monk (1981):
Write an equation for the following statement: "There are six times as many students as professors at this university." Use S for the number of students and P for the number of professors. (p. 288)
The authors found that of 47 nonscience majors taking college algebra, 57% got it wrong. What is more surprising, however, is that of 150 calculus-level students, 37% missed the problem.
A first reaction to the most common wrong answer, 6S = P, is that the students simply translated the words of the problems into mathematical symbols without thinking more deeply about the situation or the variables. (The authors note that some textbooks instruct students to use such translation.)
By analyzing transcripts of interviews with students, the authors found this approach and another (faulty) approach, as well. These students often drew a diagram showing six students and one professor. (Note that we often instruct students to draw diagrams when solving word problems.) Reasoning
from the diagram, and regarding S and P as units, the student may write 6S = P, just as we would correctly write 12 in. = 1 ft. Such reasoning is quite sensible, though it misses the fundamental intent in the problem statement that S is to represent the number of students, not a student.
Thus, two common suggestions for students—word-for-word translation and drawing a diagram—can lead to an incorrect answer to this apparently simple problem, if the students do not more deeply contemplate what the variables are intended to represent. The authors found that students who wrote and could explain the correct answer, S = 6P, drew upon a richer understanding of what the equation and the variables represent.
Clearly, then, we must encourage students to contemplate the meanings of variables. Yet, part of the power and efficiency of algebra is precisely that one can manipulate symbols independently of what they mean and then draw meaning out of the conclusions to which the symbolic manipulations lead. Thus, stable, long-term learning of algebraic thinking requires both mastery of procedures and also deeper analytical thinking.
Conclusion
Paradoxically, the need for sharper analytical thinking occurs alongside a decreased need for routine arithmetic calculation. Calculators and computers make routine calculation easier to do quickly and accurately; cash registers used in fast food restaurants sometimes return change; checkout counters have bar code readers and payment takes place by credit cards or money-access cards.
So it is education in mathematical thinking, in applying mathematical computation, in assessing whether an answer is reasonable, and in communicating the results that is essential. Teaching mathematics via workplace and everyday problems is an approach that can make mathematics more meaningful for all students. It is important, however, to go beyond the specific details of a task in order to teach mathematical ideas. While this approach is particularly crucial for those students intending to pursue careers in the mathematical sciences, it will also lead to deeper mathematical understanding for all students.
References
Clement, J., Lockhead, J., & Monk, G. (1981). Translation difficulties in learning mathematics. American Mathematical Monthly, 88, 286-290.
Harte, J. (1988). Consider a spherical cow: A course in environmental problem solving. York, PA: University Science Books.
JEAN E. TAYLOR is Professor of Mathematics at Rutgers, the State University of New Jersey. She is currently a member of the Board of Directors of the American Association for the Advancement of Science and formerly chaired its Section A Nominating Committee. She has served as Vice President and as a Member-at-Large of the Council of the American Mathematical Society, and served on its Executive Committee and its Nominating Committee. She has also been a member of the Joint Policy Board for Mathematics, and a member of the Board of Advisors to The Geometry Forum (now The Mathematics Forum) and to the WQED television series, Life by the Numbers.
5—
Working with Algebra
DANIEL CHAZAN
Michigan State University
SANDRA CALLIS BETHELL
Holt High School
Teaching a mathematics class in which few of the students have demonstrated success is a difficult assignment. Many teachers avoid such assignments, when possible. On the one hand, high school mathematics teachers, like Bertrand Russell, might love mathematics and believe something like the following:
Mathematics, rightly viewed, possesses not only truth, but supreme beauty—a beauty cold and austere, like that of sculpture, without appeal to any part of our weaker nature, without the gorgeous trappings of painting or music, yet sublimely pure, and capable of a stern perfection such as only the greatest art can show. … Remote from human passions, remote even from the pitiful facts of nature, the generations have gradually created an ordered cosmos, where pure thought can dwell as in its nature home, and where one, at least, of our nobler impulses can escape from the dreary exile of the natural world. (Russell, 1910, p. 73)
But, on the other hand, students may not have the luxury, in their circumstances, of appreciating this beauty. Many of them may not see themselves as thinkers because contemplation would take them away from their primary
focus: how to get by in a world that was not created for them. Instead, like Jamaica Kincaid, they may be asking:
What makes the world turn against me and all who look like me? I won nothing, I survey nothing, when I ask this question, the luxury of an answer that will fill volumes does not stretch out before me. When I ask this question, my voice is filled with despair. (Kincaid, 1996, pp. 131-132)
Our Teaching and Issues it Raised
During the 1991-92 and 1992-93 school years, we (a high school teacher and a university teacher educator) team taught a lower track Algebra I class for 10th through 12th grade students.1 Most of our students had failed mathematics before, and many needed to pass Algebra I in order to complete their high school mathematics requirement for graduation. For our students, mathematics had become a charged subject; it carried a heavy burden of negative experiences. Many of our students were convinced that neither they nor their peers could be successful in mathematics.
Few of our students did well in other academic subjects, and few were headed on to two- or four-year colleges. But the students differed in their affiliation with the high school. Some, called ''preppies" or "jocks" by others, were active participants in the school's activities. Others, "smokers" or "stoners," were rebelling to differing degrees against school and more broadly against society. There were strong tensions between members of these groups.2
Teaching in this setting gives added importance and urgency to the typical questions of curriculum and motivation common to most algebra classes. In our teaching, we explored questions such as the following:
- What is it that we really want high school students, especially those who are not college-intending, to study in algebra and why?
- What is the role of algebra's manipulative skills in a world with graphing calculators and computers? How do the manipulative skills taught in the traditional curriculum give students a new perspective on, and insight into, our world?
- If our teaching efforts depend on students' investment in learning, on what grounds can we appeal to them, implicitly or explicitly, for energy and effort? In a tracked, compulsory setting, how can we help students, with broad interests and talents and many of whom are not college-intending, see value in a shared exploration of algebra?
An Approach to School Algebra
As a result of thinking about these questions, in our teaching we wanted to avoid being in the position of exhorting students to appreciate the beauty or utility of algebra. Our students were frankly skeptical of arguments based on
utility. They saw few people in their community using algebra. We had also lost faith in the power of extrinsic rewards and punishments, like failing grades. Many of our students were skeptical of the power of the high school diploma to alter fundamentally their life circumstances. We wanted students to find the mathematical objects we were discussing in the world around them and thus learn to value the perspective that this mathematics might give them on their world.
To help us in this task, we found it useful to take what we call a "relationships between quantities" approach to school algebra. In this approach, the fundamental mathematical objects of study in school algebra are functions that can be represented by inputs and outputs listed in tables or sketched or plotted on graphs, as well as calculation procedures that can be written with algebraic symbols.3 Stimulated, in part, by the following quote from August Comte, we viewed these functions as mathematical representations of theories people have developed for explaining relationships between quantities.
In the light of previous experience, we must acknowledge the impossibility of determining, by direct measurement, most of the heights and distances we should like to know. It is this general fact which makes the science of mathematics necessary. For in renouncing the hope, in almost every case, of measuring great heights or distances directly, the human mind has had to attempt to determine them indirectly, and it is thus that philosophers were led to invent mathematics. (Quoted in Serres, 1982, p. 85)
The "Sponsor" Project
Using this approach to the concept of function, during the 1992-93 school year, we designed a year-long project for our students. The project asked pairs of students to find the mathematical objects we were studying in the workplace of a community sponsor. Students visited the sponsor's workplace four times during the year—three after-school visits and one day-long excused absence from school. In these visits, the students came to know the workplace and learned about the sponsor's work. We then asked students to write a report describing the sponsor's workplace and answering questions about the nature of the mathematical activity embedded in the workplace. The questions are organized in Table 5-1.
Using These Questions
In order to determine how the interviews could be structured and to provide students with a model, we chose to interview Sandra's husband, John Bethell, who is a coatings inspector for an engineering firm. When asked about his job, John responded, "I argue for a living." He went on to describe his daily work inspecting contractors painting water towers. Since most municipalities contract with the lowest bidder when a water tower needs to be painted, they will often hire an engineering firm to make sure that the contractor works according to specification. Since the contractor has made a low bid, there are strong
TABLE 5-1: Questions to ask in the workplace
|
QUANTITIES: MEASURED OR COUNTED VERSUS COMPUTED |
|
|
|
COMPUTING QUANTITIES |
|
|
|
REPRESENTING QUANTITIES AND RELATIONSHIPS BETWEEN QUANTITIES |
|
|
|
COMPARISONS |
|
|
financial incentives for the contractor to compromise on quality in order to make a profit.
In his work John does different kinds of inspections. For example, he has a magnetic instrument to check the thickness of the paint once it has been applied to the tower. When it gives a "thin" reading, contractors often question the technology. To argue for the reading, John uses the surface area of the tank, the number of paint cans used, the volume of paint in the can, and an understanding of the percentage of this volume that evaporates to calculate the average thickness of the dry coating. Other examples from his workplace involve the use of tables and measuring instruments of different kinds.
Some Examples of Students' Work
When school started, students began working on their projects. Although many of the sponsors initially indicated that there were no mathematical dimensions to their work, students often were able to show sponsors places where the mathematics we were studying was to be found. For example, Jackie worked with a crop and soil scientist. She was intrigued by the way in which measurement of weight is used to count seeds. First, her sponsor would weigh a test batch of 100 seeds to generate a benchmark weight. Then, instead of counting a large number of seeds, the scientist would weigh an amount of seeds and compute the number of seeds such a weight would contain.
Rebecca worked with a carpeting contractor who, in estimating costs, read the dimensions of rectangular rooms off an architect's blueprint, multiplied to find the area of the room in square feet (doing conversions where necessary), then multiplied by a cost per square foot (which depended on the type of carpet) to compute the cost of the carpet. The purpose of these estimates was to prepare a bid for the architect where the bid had to be as low as possible without making the job unprofitable. Rebecca used a chart (Table 5-2) to explain this procedure to the class.
Joe and Mick, also working in construction, found out that in laying pipes, there is a "one by one" rule of thumb. When digging a trench for the placement of the pipe, the non-parallel sides of the trapezoidal cross section must have a slope of 1 foot down for every one foot across. This ratio guarantees that the dirt in the hole will not slide down on itself. Thus, if at the bottom of the hole, the trapezoid must have a certain width in order to fit the pipe, then on ground level the hole must be this width plus twice the depth of the hole. Knowing in advance how wide the hole must be avoids lengthy and costly trial and error.
Other students found that functions were often embedded in cultural artifacts found in the workplace. For example, a student who visited a doctor's office brought in an instrument for predicting the due dates of pregnant women, as well as providing information about average fetal weight and length (Figure 5-1).
TABLE 5-2: Cost of carpet worksheet
|
INPUTS |
|
OUTPUT |
|
|
LENGTH |
WIDTH |
AREA OF THE ROOM |
COST FOR CARPETING ROOM |
|
10 |
35 |
|
|
|
20 |
25 |
|
|
|
15 |
30 |
|
|
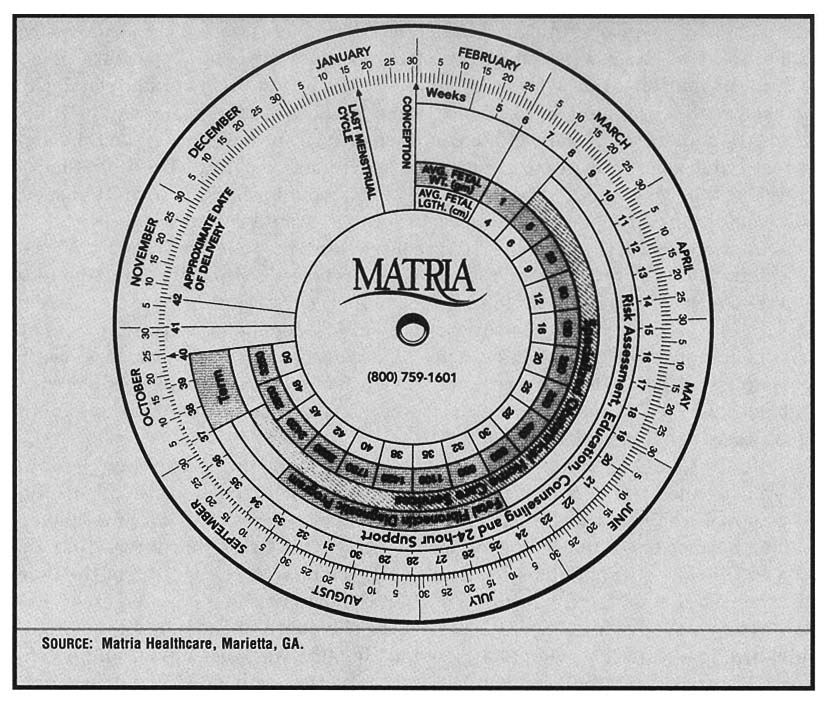
FIGURE 5-1: Pregnancy wheel
Conclusion
While the complexities of organizing this sort of project should not be minimized—arranging sponsors, securing parental permission, and meeting administrators and parent concerns about the requirement of off-campus, after-school work—we remain intrigued by the potential of such projects for helping students see mathematics in the world around them. The notions of identifying central mathematical objects for a course and then developing ways of identifying those objects in students' experience seems like an important alternative to the use of application-based materials written by developers whose lives and social worlds may be quite different from those of students.
References
Chazen, D. (1996). Algebra for all students? Journal of Mathematical Behavior, 15(4), 455-477.
Eckert, P. (1989). Jocks and burnouts: Social categories and identity in the high school. New York: Teachers College Press.
Fey, J. T., Heid, M. K., et al. (1995). Concepts in algebra: A technological approach. Dedham, MA: Janson Publications.
Kieran, C., Boileau, A., & Garancon, M. (1996). Introducing algebra by mean of a technology-supported, functional approach. In N. Bednarz et al. (Eds.), Approaches to algebra, (pp. 257-293). Kluwer Academic Publishers: Dordrecht, The Netherlands.
Kincaid, J. (1996). The autobiography of my mother. New York: Farrar, Straus, Giroux.
Nemirovsky, R. (1996). Mathematical narratives, modeling and algebra. In N. Bednarz et al. (Eds.) Approaches to algebra, (pp. 197-220). Kluwer Academic Publishers: Dordrecht, The Netherlands.
Russell, B. (1910). Philosophical Essays. London: Longmans, Green.
Schwartz, J. & Yerushalmy, M. (1992). Getting students to function in and with algebra. In G. Harel & E. Dubinsky (Eds.), The concept of function: Aspects of epistemology and pedagogy, (MAA Notes, Vol. 25, pp. 261-289). Washington, DC: Mathematical Association of America.
Serres, M. (1982). Mathematics and philosophy: What Thales saw … In J. Harari & D. Bell (Eds.), Hermes: Literature, science, philosophy , (pp. 84-97). Baltimore, MD: Johns Hopkins.
Thompson, P. (1993). Quantitative reasoning, complexity, and additive structures. Educational Studies in Mathematics, 25, 165-208.
Yerushalmy, M. & Schwartz, J. L. (1993). Seizing the opportunity to make algebra mathematically and pedagogically interesting. In T. A. Romberg, E. Fennema, & T. P. Carpenter (Eds.), Integrating research on the graphical representation of functions, (pp. 41-68). Hillsdale, NJ: Lawrence Erlbaum Associates.
Notes
|
DANIEL CHAZAN is an Associate Professor of Teacher Education at Michigan State University. To assist his research in mathematics teaching and learning, he has taught algebra at the high school level. His interests include teaching mathematics by examining student ideas, using computers to support student exploration, and the potential for the history and philosophy of mathematics to inform teaching.
SANDRA CALLIS BETHELL has taught mathematics and Spanish at Holt High School for 10 years. She has also completed graduate work at Michigan State University and Western Michigan University. She has interest in mathematics reform, particularly in meeting the needs of diverse learners in algebra courses.
Emergency Calls
Task
A city is served by two different ambulance companies. City logs record the date, the time of the call, the ambulance company, and the response time for each 911 call (Table 1). Analyze these data and write a report to the City Council (with supporting charts and graphs) advising it on which ambulance company the 911 operators should choose to dispatch for calls from this region.
TABLE 1: Ambulance dispatch log sheet, May 1–30
|
DATE OF CALL |
TIME OF CALL |
COMPANY NAME |
RESPONSE TIME IN MINUTES |
DATE OF CALL |
TIME OF CALL |
COMPANY NAME |
RESPONSE TIME IN MINUTES |
|
1 |
7:12 AM |
Metro |
11 |
12 |
8:30 PM |
Arrow |
8 |
|
1 |
7:43 PM |
Metro |
11 |
15 |
1:03 AM |
Metro |
12 |
|
2 |
10:02 PM |
Arrow |
7 |
15 |
6:40 AM |
Arrow |
17 |
|
2 |
12:22 PM |
Metro |
12 |
15 |
3:25 PM |
Metro |
15 |
|
3 |
5:30 AM |
Arrow |
17 |
16 |
4:15 AM |
Metro |
7 |
|
3 |
6:18 PM |
Arrow |
6 |
16 |
8:41 AM |
Arrow |
19 |
|
4 |
6:25 AM |
Arrow |
16 |
18 |
2:39 PM |
Arrow |
10 |
|
5 |
8:56 PM |
Metro |
10 |
18 |
3:44 PM |
Metro |
14 |
|
6 |
4:59 PM |
Metro |
14 |
19 |
6:33 AM |
Metro |
6 |
|
7 |
2:20 AM |
Arrow |
11 |
22 |
7:25 AM |
Arrow |
17 |
|
7 |
12:41 PM |
Arrow |
8 |
22 |
4:20 PM |
Metro |
19 |
|
7 |
2:29 PM |
Metro |
11 |
24 |
4:21 PM |
Arrow |
9 |
|
8 |
8:14 AM |
Metro |
8 |
25 |
8:07 AM |
Arrow |
15 |
|
8 |
6:23 PM |
Metro |
16 |
25 |
5:02 PM |
Arrow |
7 |
|
9 |
6:47 AM |
Metro |
9 |
26 |
10:51 AM |
Metro |
9 |
|
9 |
7:15 AM |
Arrow |
16 |
26 |
5:11 PM |
Metro |
18 |
|
9 |
6:10 PM |
Arrow |
8 |
27 |
4:16 AM |
Arrow |
10 |
|
10 |
5:37 PM |
Metro |
16 |
29 |
8:59 AM |
Metro |
11 |
|
10 |
9:37 PM |
Metro |
11 |
30 |
11:09 AM |
Arrow |
7 |
|
11 |
10:11 AM |
Metro |
8 |
30 |
9:15 PM |
Arrow |
8 |
|
11 |
11:45 AM |
Metro |
10 |
30 |
11:15 PM |
Metro |
8 |
Commentary
This problem confronts the student with a realistic situation and a body of data regarding two ambulance companies' response times to emergency calls. The data the student is provided are typically "messy"—just a log of calls and response times, ordered chronologically. The question is how to make sense of them. Finding patterns in data such as these requires a productive mixture of mathematics common sense, and intellectual detective work. It's the kind of reasoning that students should be able to do—the kind of reasoning that will pay off in the real world.
Mathematical Analysis
In this case, a numerical analysis is not especially informative. On average, the companies are about the same: Arrow has a mean response time of 11.4 minutes compared to 11.6 minutes for Metro. The spread of the data is also not very helpful. The ranges of their distributions are exactly the same: from 6 minutes to 19 minutes. The standard deviation of Arrow's response time is a little longer—4.3 minutes versus 3.4 minutes for Metro—indicating that Arrow's response times fluctuate a bit more.
Graphs of the response times (Figures 1 and 2) reveal interesting features. Both companies, especially Arrow, seem to have bimodal distributions, which is to say that there are two clusters of data without much data in between.
FIGURE 1: Distribution of Arrow's response times
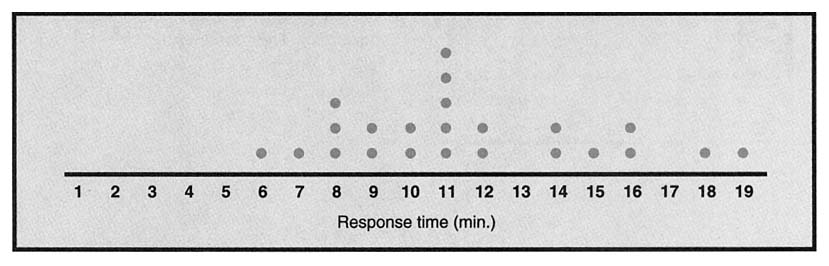
FIGURE 2: Distribution of Metro's response times
The distributions for both companies suggest that there are some other factors at work. Might a particular driver be the problem? Might the slow response times for either company be on particular days of the week or at particular times of day? Graphs of the response time versus the time of day (Figures 3 and 4) shed some light on these questions.
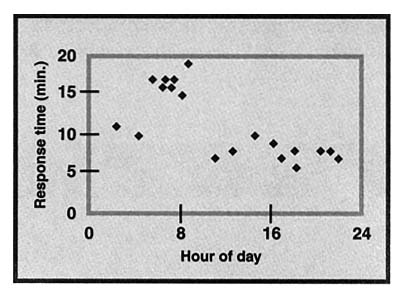
FIGURE 3: Arrow response times by time of day
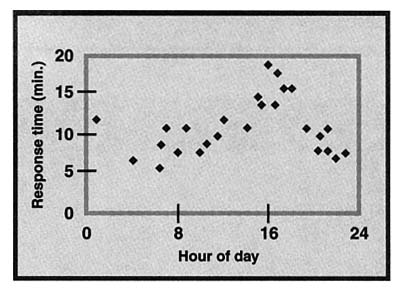
FIGURE 4: Metro response times by time of day
These graphs show that Arrow's response times were fast except between 5:30 AM and 9:00 AM, when they were about 9 minutes slower on average. Similarly, Metro's response times were fast except between about 3:30 PM and 6:30 PM, when they were about 5 minutes slower. Perhaps the locations of the companies make Arrow more susceptible to the morning rush hour and Metro more susceptible to the afternoon rush hour. On the other hand, the employees on Arrow's morning shift or Metro's afternoon shift may not be efficient. To avoid slow responses, one could recommend to the City Council that Metro be called during the morning and that Arrow be called during the afternoon. A little detective work into the sources of the differences between the companies may yield a better recommendation.
Extensions
Comparisons may be drawn between two samples in various contexts—response times for various services (taxis, computer-help desks, 24-hour hot lines at automobile manufacturers) being one class among many. Depending upon the circumstances, the data may tell very different stories. Even in the situation above, if the second pair of graphs hadn't offered such clear explanations, one might have argued that although the response times for Arrow were better on average the spread was larger, thus making their "extremes" more risky. The fundamental idea is using various analysis and representation techniques to make sense of data when the important factors are not necessarily known ahead of time.
Back-of-the-Envelope Estimates
Task
Practice "back-of-the-envelope" estimates based on rough approximations that can be derived from common sense or everyday observations. Examples:
- Consider a public high school mathematics teacher who feels that students should work five nights a week, averaging about 35 minutes a night, doing focused on-task work and who intends to grade all homework with comments and corrections. What is a reasonable number of hours per week that such a teacher should allocate for grading homework?
- How much paper does The New York Times use in a week? A paper company that wishes to make a bid to become their sole supplier needs to know whether they have enough current capacity. If the company were to store a two-week supply of newspaper, will their empty 14,000 square foot warehouse be big enough?
Commentary
Some 50 years ago, physicist Enrico Fermi asked his students at the University of Chicago, "How many piano tuners are there in Chicago?" By asking such questions, Fermi wanted his students to make estimates that involved rough approximations so that their goal would be not precision but the order of magnitude of their result. Thus, many people today call these kinds of questions "Fermi questions." These generally rough calculations often require little more than common sense, everyday observations, and a scrap of paper, such as the back of a used envelope.
Scientists and mathematicians use the idea of order of magnitude, usually expressed as the closest power of ten, to give a rough sense of the size of a quantity. In everyday conversation, people use a similar idea when they talk about "being in the right ballpark." For example, a full-time job at minimum wage yields an annual income on the order of magnitude of $10,000 or 104 dollars. Some corporate executives and professional athletes make annual salaries on the order of magnitude of $10,000,000 or 107 dollars. To say that these salaries differ by a factor of 1000 or 103, one can say that they differ by three orders of magnitude. Such a lack of precision might seem unscientific or unmathematical, but such approximations are quite useful in determining whether a more precise measurement is feasible or necessary, what sort of action might be required, or whether the result of a calculation is "in the right ballpark." In choosing a strategy to protect an endangered species, for example, scientists plan differently if there are 500 animals remaining than if there are 5,000. On the other hand, determining whether 5,200 or 6,300 is a better estimate is not necessary, as the strategies will probably be the same.
Careful reasoning with everyday observations can usually produce Fermi estimates that are within an order of magnitude of the exact answer (if there is one). Fermi estimates encourage students to reason creatively with approximate quantities and uncertain information. Experiences with such a process can help an individual function in daily life to determine the reasonableness of numerical calculations, of situations or ideas in the workplace, or of a proposed tax cut. A quick estimate of some revenue- or profit-enhancing scheme may show that the idea is comparable to suggesting that General Motors enter the summer sidewalk lemonade market in your neighborhood. A quick estimate could encourage further investigation or provide the rationale to dismiss the idea.
Almost any numerical claim may be treated as a Fermi question when the problem solver does not have access to all necessary background information. In such a situation, one may make rough guesses about relevant numbers, do a few calculations, and then produce estimates.
Mathematical Analysis
The examples are solved separately below.
Grading Homework
Although many component factors vary greatly from teacher to teacher or even from week to week, rough calculations are not hard to make. Some important factors to consider for the teacher are: how many classes he or she teaches, how many students are in each of the classes, how much experience has the teacher had in general and has the teacher previously taught the classes, and certainly, as part of teaching style, the kind of homework the teacher assigns, not to mention the teacher's efficiency in grading.
Suppose the teacher has 5 classes averaging 25 students per class. Because the teacher plans to write corrections and comments, assume that the students' papers contain more than a list of answers—they show some student work and, perhaps, explain some of the solutions. Grading such papers might take as long as 10 minutes each, or perhaps even longer. Assuming that the teacher can grade them as quickly as 3 minutes each, on average, the teacher's grading time is:

This is an impressively large number, especially for a teacher who already spends almost 25 hours/week in class, some additional time in preparation, and some time meeting with individual students. Is it reasonable to expect teachers to put in that kind of time? What compromises or other changes might the teacher make to reduce the amount of time? The calculation above offers four possibilities: Reduce the time spent on each homework paper, reduce the number of students per class, reduce the number of classes taught each day, or reduce the number of days per week that homework will be collected. If the teacher decides to spend at most 2 hours grading each night, what is the total number of students for which the teacher should have responsibility? This calculation is a partial reverse of the one above:
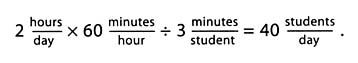
If the teacher still has 5 classes, that would mean 8 students per class!
The New York Times
Answering this question requires two preliminary estimates: the circulation of The New York Times and the size of the newspaper. The answers will probably be different on Sundays. Though The New York Times is a national newspaper, the number of subscribers outside the New York metropolitan area is probably small compared to the number inside. The population of the New York metropolitan area is roughly ten million people. Since most families buy at most one copy, and not all families buy The New York Times, the circulation might be about 1 million newspapers each day. (A circulation of 500,000 seems too small and 2 million seems too big.) The Sunday and weekday editions probably have different
circulations, but assume that they are the same since they probably differ by less than a factor of two—much less than an order of magnitude. When folded, a weekday edition of the paper measures about 1/2 inch thick, a little more than 1 foot long, and about 1 foot wide. A Sunday edition of the paper is the same width and length, but perhaps 2 inches thick. For a week, then, the papers would stack 6 × 1/2 + 2 = 5 inches thick, for a total volume of about 1 ft × 1 ft × 5/12 ft = 0.5 ft3.
The whole circulation, then, would require about 1/2 million cubic feet of paper per week, or about 1 million cubic feet for a two-week supply.
Is the company's warehouse big enough? The paper will come on rolls, but to make the estimates easy, assume it is stacked. If it were stacked 10 feet high, the supply would require 100,000 square feet of floor space. The company's 14,000 square foot storage facility will probably not be big enough as its size differs by almost an order of magnitude from the estimate. The circulation estimate and the size of the newspaper estimate should each be within a factor of 2, implying that the 100,000 square foot estimate is off by at most a factor of 4—less than an order of magnitude.
How big a warehouse is needed? An acre is 43,560 square feet so about two acres of land is needed. Alternatively, a warehouse measuring 300 ft × 300 ft (the length of a football field in both directions) would contain 90,000 square feet of floor space, giving a rough idea of the size.
Extensions
After gaining some experience with these types of problems, students can be encouraged to pay close attention to the units and to be ready to make and support claims about the accuracy of their estimates. Paying attention to units and including units as algebraic quantities in calculations is a common technique in engineering and the sciences. Reasoning about a formula by paying attention only to the units is called dimensional analysis.
Sometimes, rather than a single estimate, it is helpful to make estimates of upper and lower bounds. Such an approach reinforces the idea that an exact answer is not the goal. In many situations, students could first estimate upper and lower bounds, and then collect some real data to determine whether the answer lies between those bounds. In the traditional game of guessing the number of jelly beans in a jar, for example, all students should be able to estimate within an order of magnitude, or perhaps within a factor of two. Making the closest guess, however, involves some chance.
Fermi questions are useful outside the workplace. Some Fermi questions have political ramifications:
- How many miles of streets are in your city or town? The police chief is considering increasing police presence so that every street is patrolled by car at least once every 4 hours.
- When will your town fill up its landfill? Is this a very urgent matter for the town's waste management personnel to assess in depth?
- In his 1997 State of the Union address, President Clinton renewed his call for a tax deduction of up to $10,000 for the cost of college tuition. He estimates that 16.5 million students stand to benefit. Is this a reasonable estimate of the number who might take advantage of the tax deduction? How much will the deduction cost in lost federal revenue?
Creating Fermi problems is easy. Simply ask quantitative questions for which there is no practical way to determine exact values. Students could be encouraged to make up their own. Examples are: ''How many oak trees are there in Illinois?" or "How many people in the U.S. ate chicken for dinner last night?" "If all the people in the world were to jump in the ocean, how much would it raise the water level?" Give students the opportunity to develop their own Fermi problems and to share them with each other. It can stimulate some real mathematical thinking.
Scheduling Elevators
Task
In some buildings, all of the elevators can travel to all of the floors, while in others the elevators are restricted to stopping only on certain floors. What is the advantage of having elevators that travel only to certain floors? When is this worth instituting?
Commentary
Scheduling elevators is a common example of an optimization problem that has applications in all aspects of business and industry. Optimal scheduling in general not only can save time and money, but it can contribute to safety (e.g., in the airline industry). The elevator problem further illustrates an important feature of many economic and political arguments—the dilemma of trying simultaneously to optimize several different needs.
Politicians often promise policies that will be the least expensive, save the most lives, and be best for the environment. Think of flood control or occupational safety rules, for example. When we are lucky, we can perhaps find a strategy of least cost, a strategy that saves the most lives, or a strategy that damages the environment least. But these might not be the same strategies: generally one cannot simultaneously satisfy two or more independent optimization conditions. This is an important message for students to learn, in order to become better educated and more critical consumers and citizens.
In the elevator problem, customer satisfaction can be emphasized by minimizing the average elevator time (waiting plus riding) for employees in an office building. Minimizing wait-time during rush hours means delivering many people quickly, which might be accomplished by filling the elevators and making few stops. During off-peak hours, however, minimizing wait-time means maximizing the availability of the elevators. There is no reason to believe that these two goals will yield the same strategy. Finding the best strategy for each is a mathematical problem; choosing one of the two strategies or a compromise strategy is a management decision, not a mathematical deduction.
This example serves to introduce a complex topic whose analysis is well within the range of high school students. Though the calculations require little more than arithmetic, the task puts a premium on the creation of reasonable alternative strategies. Students should recognize that some configurations (e.g., all but one elevator going to the top floor and the one going to all the others) do not merit consideration, while others are plausible. A systematic evaluation of all possible configurations is usually required to find the optimal solution. Such a systematic search of the possible solution space is important in many modeling situations where a formal optimal strategy is not known. Creating and evaluating reasonable strategies for the elevators is quite appropriate for high school student mathematics and lends itself well to thoughtful group effort. How do you invent new strategies? How do you know that you have considered all plausible strategies? These are mathematical questions, and they are especially amenable to group discussion.
Students should be able to use the techniques first developed in solving a simple case with only a few stories and a few elevators to address more realistic situations (e.g., 50 stories, five elevators). Using the results of a similar but simpler problem to model a more complicated problem is an important way to reason in mathematics. Students
need to determine what data and variables are relevant. Start by establishing the kind of building—a hotel, an office building, an apartment building? How many people are on the different floors? What are their normal destinations (e.g., primarily the ground floor or, perhaps, a roof-top restaurant). What happens during rush hours?
To be successful at the elevator task, students must first develop a mathematical model of the problem. The model might be a graphical representation for each elevator, with time on the horizontal axis and the floors represented on the vertical axis, or a tabular representation indicating the time spent on each floor. Students must identify the pertinent variables and make simplifying assumptions about which of the possible floors an elevator will visit.
Mathematical Analysis
This section works through some of the details in a particularly simple case. Consider an office building with six occupied floors, employing 240 people, and a ground floor that is not used for business. Suppose there are three elevators, each of which can hold 10 people. Further suppose that each elevator takes approximately 25 seconds to fill on the ground floor, then takes 5 seconds to move between floors and 15 seconds to open and close at each floor on which it stops.
Scenario One
What happens in the morning when everyone arrives for work? Assume that everyone arrives at approximately the same time and enters the elevators on the ground floor. If all elevators go to all floors and if the 240 people are evenly divided among all three elevators, each elevator will have to make 8 trips of 10 people each.
When considering a single trip of one elevator, assume for simplicity that 10 people get on the elevator at the ground floor and that it stops at each floor on the way up, because there may be an occupant heading to each floor. Adding 5 seconds to move to each floor and 15 seconds to stop yields 20 seconds for each of the six floors. On the way down, since no one is being picked up or let off, the elevator does not stop, taking 5 seconds for each of six floors for a total of 30 seconds. This round-trip is represented in Table 1.
TABLE 1: Elevator round-trip time, Scenario one
|
|
TIME (SEC) |
|
Ground Floor |
25 |
|
Floor 1 |
20 |
|
Floor 2 |
20 |
|
Floor 3 |
20 |
|
Floor 4 |
20 |
|
Floor 5 |
20 |
|
Floor 6 |
20 |
|
Return |
30 |
|
ROUND-TRIP |
175 |
Since each elevator makes 8 trips, the total time will be 1,400 seconds or 23 minutes, 20 seconds.
Scenario Two
Now suppose that one elevator serves floors 1–3 and, because of the longer trip, two elevators are assigned to floors 4–6. The elevators serving the top
TABLE 2: Elevator round-trip times, Scenario two
|
|
ELEVATOR A |
ELEVATORS B & C |
||
|
|
Stop Time |
STOP TIME |
||
|
Ground Floor |
|
25 |
|
25 |
|
Floor 1 |
1 |
20 |
|
5 |
|
Floor 2 |
2 |
20 |
|
5 |
|
Floor 3 |
3 |
20 |
|
5 |
|
Floor 4 |
|
0 |
4 |
20 |
|
Floor 5 |
|
0 |
5 |
20 |
|
Floor 6 |
|
0 |
6 |
20 |
|
Return |
|
15 |
|
30 |
|
ROUND-TRIP |
|
100 |
|
130 |
floors will save 15 seconds for each of floors 1–3 by not stopping. The elevator serving the bottom floors will save 20 seconds for each of the top floors and will save time on the return trip as well. The times for these trips are shown in Table 2.
Assuming the employees are evenly distributed among the floors (40 people per floor), elevator A will transport 120 people, requiring 12 trips, and elevators B and C will transport 120 people, requiring 6 trips each. These trips will take 1200 seconds (20 minutes) for elevator A and 780 seconds (13 minutes) for elevators B and C, resulting in a small time savings (about 3 minutes) over the first scenario. Because elevators B and C are finished so much sooner than elevator A, there is likely a more efficient solution.
Scenario Three
The two round-trip times in Table 2 do not differ by much because the elevators move quickly between floors but stop at floors relatively slowly. This observation suggests that a more efficient arrangement might be to assign each elevator to a pair of floors. The times for such a scenario are listed in Table 3.
Again assuming 40 employees per floor, each elevator will deliver 80 people, requiring 8 trips, taking at most a total of 920 seconds. Thus this assignment of elevators results in a time savings of almost 35% when compared with the 1400 seconds it would take to deliver all employees via unassigned elevators.
TABLE 3: Elevator round-trip times, Scenario three
|
|
ELEVATOR A |
ELEVATOR B |
ELEVATOR C |
|||
|
|
STOP TIME |
STOP TIME |
STOP TIME |
|||
|
Ground Floor |
|
25 |
|
25 |
|
25 |
|
Floor 1 |
1 |
20 |
|
5 |
|
5 |
|
Floor 2 |
2 |
20 |
|
5 |
|
5 |
|
Floor 3 |
|
0 |
3 |
20 |
|
5 |
|
Floor 4 |
|
0 |
4 |
20 |
|
5 |
|
Floor 5 |
|
0 |
|
0 |
5 |
20 |
|
Floor 6 |
|
0 |
|
0 |
6 |
20 |
|
Return |
|
10 |
|
20 |
|
30 |
|
ROUND-TRIP |
|
75 |
|
95 |
|
115 |
Perhaps this is the optimal solution. If so, then the above analysis of this simple case suggests two hypotheses:
- The optimal solution assigns each floor to a single elevator.
- If the time for stopping is sufficiently larger than the time for moving between floors, each elevator should serve the same number of floors.
-
Mathematically, one could try to show that this solution is optimal by trying all possible elevator assignments or by carefully reasoning, perhaps by showing that the above hypotheses are correct. Practically, however, it doesn't matter because this solution considers only the morning rush hour and ignores periods of low use.
The assignment is clearly not optimal during periods of low use, and much of the inefficiency is related to the first hypothesis for rush hour optimization: that each floor is served by a single elevator. With this condition, if an employee on floor 6 arrives at the ground floor just after elevator C has departed, for example, she or he will have to wait nearly two minutes for elevator C to return, even if elevators A and B are idle. There are other inefficiencies that are not considered by focusing on the rush hour. Because each floor is served by a single elevator, an employee who wishes to travel from floor 3 to floor 6, for example, must go via the ground floor and switch elevators. Most employees would prefer more flexibility than a single elevator serving each floor.
At times when the elevators are not all busy, unassigned elevators will provide the quickest response and the greatest flexibility.
Because this optimal solution conflicts with the optimal rush hour solution, some compromise is necessary. In this simple case, perhaps elevator A could serve all floors, elevator B could serve floors 1-3, and elevator C could serve floors 4-6.
The second hypothesis, above, deserves some further thought. The efficiency of the rush hour solution Table 3 is due in part to the even division of employees among the floors. If employees were unevenly distributed with, say, 120 of the 240 people working on the top two floors, then elevator C would need to make 12 trips, taking a total of 1380 seconds, resulting in almost no benefit over unassigned elevators. Thus, an efficient solution in an actual building must take into account the distribution of the employees among the floors.
Because the stopping time on each floor is three times as large as the traveling time between floors (15 seconds versus 5 seconds), this solution effectively ignores the traveling time by assigning the same number of employees to each elevator. For taller buildings, the traveling time will become more significant. In those cases fewer employees should be assigned to the elevators that serve the upper floors than are assigned to the elevators that serve the lower floors.
Extensions
The problem can be made more challenging by altering the number of elevators, the number of floors, and the number of individuals working on each floor. The rate of movement of elevators can be determined by observing buildings in the local area. Some elevators move more quickly than others. Entrance and exit times could also be measured by students collecting
data on local elevators. In a similar manner, the number of workers, elevators, and floors could be taken from local contexts.
A related question is, where should the elevators go when not in use? Is it best for them to return to the ground floor? Should they remain where they were last sent? Should they distribute themselves evenly among the floors? Or should they go to floors of anticipated heavy traffic? The answers will depend on the nature of the building and the time of day. Without analysis, it will not be at all clear which strategy is best under specific conditions. In some buildings, the elevators are controlled by computer programs that "learn" and then anticipate the traffic patterns in the building.
A different example that students can easily explore in detail is the problem of situating a fire station or an emergency room in a city. Here the key issue concerns travel times to the region being served, with conflicting optimization goals: average time vs. maximum time. A location that minimizes the maximum time of response may not produce the least average time of response. Commuters often face similar choices in selecting routes to work. They may want to minimize the average time, the maximum time, or perhaps the variance, so that their departure and arrival times are more predictable.
Most of the optimization conditions discussed so far have been expressed in units of time. Sometimes, however, two optimization conditions yield strategies whose outcomes are expressed in different (and sometimes incompatible) units of measurement. In many public policy issues (e.g., health insurance) the units are lives and money. For environmental issues, sometimes the units themselves are difficult to identify (e.g., quality of life).
When one of the units is money, it is easy to find expensive strategies but impossible to find ones that have virtually no cost. In some situations, such as airline safety, which balances lives versus dollars, there is no strategy that minimize lives lost (since additional dollars always produce slight increases in safety), and the strategy that minimizes dollars will be at $0. Clearly some compromise is necessary. Working with models of different solutions can help students understand the consequences of some of the compromises.
Heating-Degree-Days
Task
An energy consulting firm that recommends and installs insulation and similar energy saving devices has received a complaint from a customer. Last summer she paid $540 to insulate her attic on the prediction that it would save 10% on her natural gas bills. Her gas bills have been higher than the previous winter, however, and now she wants a refund on the cost of the insulation. She admits that this winter has been colder than the last, but she had expected still to see some savings.
The facts: This winter the customer has used 1,102 therms, whereas last winter she used only 1,054 therms. This winter has been colder: 5,101 heating-degree-days this winter compared to 4,201 heating-degree-days last winter. (See explanation below.) How does a representative of the energy consulting firm explain to this customer that the accumulated heating-degree-days measure how much colder this winter has been, and then explain how to calculate her anticipated versus her actual savings.
Commentary
Explaining the mathematics behind a situation can be challenging and requires a real knowledge of the context, the procedures, and the underlying mathematical concepts. Such communication of mathematical ideas is a powerful learning device for students of mathematics as well as an important skill for the workplace. Though the procedure for this problem involves only proportions, a thorough explanation of the mathematics behind the procedure requires understanding of linear modeling and related algebraic reasoning, accumulation and other precursors of calculus, as well as an understanding of energy usage in home heating.
Mathematical Analysis
The customer seems to understand that a straight comparison of gas usage does not take into account the added costs of colder weather, which can be significant. But before calculating any anticipated or actual savings, the customer needs some understanding of heating-degree-days. For many years, weather services and oil and gas companies have been using heating-degree-days to explain and predict energy usage and to measure energy savings of insulation and other devices. Similar degree-day units are also used in studying insect populations and crop growth. The concept provides a simple measure of the accumulated amount of cold or warm weather over time. In the discussion that follows, all temperatures are given in degrees Fahrenheit, although the process is equally workable using degrees Celsius.
Suppose, for example, that the minimum temperature in a city on a given day is 52 degrees and the maximum temperature is 64 degrees. The average temperature for the day is then taken to be 58 degrees. Subtracting that result from 65 degrees (the cutoff point for heating), yields 7 heating-degree-days for the day. By recording high and low temperatures and computing their average each day, heating-degree-days can be accumulated over the course of a month, a winter, or any period of time as a measure of the coldness of that period.
Over five consecutive days, for example, if the average temperatures were 58, 50, 60, 67, and 56 degrees Fahrenheit, the calculation yields 7, 15, 5, 0, and 9 heating-degree-days respectively, for a total accumulation of 36 heating-degree-days for the five days. Note that the fourth day contributes 0 heating-degree-days to the total because the temperature was above 65 degrees.
The relationship between average temperatures and heating-degree-days is represented graphically in Figure 1. The average temperatures are shown along the solid line graph. The area of each shaded rectangle represents the number of heating-degree-days for that day, because the width of each rectangle is one day and the height of each rectangle is the number of degrees below 65 degrees. Over time, the sum of the areas of the rectangles represents the number of heating-degree-days accumulated during the period. (Teachers of calculus will recognize connections between these ideas and integral calculus.)
The statement that accumulated heating-degree-days should be proportional to gas or heating oil usage is based primarily on two assumptions: first, on a day for which the average temperature is above 65 degrees, no heating should be required, and therefore there should be no gas or heating oil usage; second, a day for which the average temperature is 25 degrees (40 heating-degree-days) should require twice as much heating as a day for which the average temperature is 45

FIGURE 1: Daily heating-degree-days
degrees (20 heating-degree-days) because there is twice the temperature difference from the 65 degree cutoff.
The first assumption is reasonable because most people would not turn on their heat if the temperature outside is above 65 degrees. The second assumption is consistent with Newton's law of cooling, which states that the rate at which an object cools is proportional to the difference in temperature between the object and its environment. That is, a house which is 40 degrees warmer than its environment will cool at twice the rate (and therefore consume energy at twice the rate to keep warm) of a house which is 20 degrees warmer than its environment.
The customer who accepts the heating-degree-day model as a measure of energy usage can compare this winter's usage with that of last winter. Because 5,101/4,201 = 1.21, this winter has been 21% colder than last winter, and therefore each house should require 21% more heat than last winter. If this customer hadn't installed the insulation, she would have required 21% more heat than last year, or about 1,275 therms. Instead, she has required only 5% more heat (1,102/1,054 = 1.05), yielding a savings of 14% off what would have been required (1,102/1,275 = .86).
Another approach to this would be to note that last year the customer used 1,054 therms/4,201 heating-degree-days = .251 therms/heating-degree-day, whereas this year she has used 1,102 therms/5,101 heating-degree-days = .216 therms/heating-degree-day, a savings of 14%, as before.
Extensions
How good is the heating-degree-day model in predicting energy usage? In a home that has a thermometer and a gas meter or a gauge on a tank, students could record daily data for gas usage and high and low temperature to test the accuracy of the model. Data collection would require only a few minutes per day for students using an electronic indoor/outdoor thermometer that tracks high and low temperatures. Of course, gas used for cooking and heating water needs to be taken into account. For homes in which the gas tank has no gauge or doesn't provide accurate enough data, a similar experiment could be performed relating accumulated heating-degree-days to gas or oil usage between fill-ups.
It turns out that in well-sealed modern houses, the cutoff temperature for heating can be lower than 65 degrees (sometimes as low as 55 degrees) because of heat generated by light bulbs, appliances, cooking, people, and pets. At temperatures sufficiently below the cutoff, linearity turns out to be a good assumption. Linear regression on the daily usage data (collected as suggested above) ought to find an equation something like U = -.251(T - 65), where T is the average temperature and U is the gas usage. Note that the slope, -.251, is the gas usage per heating-degree-day, and 65 is the cutoff. Note also that the accumulation of heating-degree-days takes a linear equation and turns it into a proportion. There are some important data analysis issues that could be addressed by such an investigation. It is sometimes dangerous, for example, to assume linearity with only a few data points, yet this widely used model essentially assumes linearity from only one data point, the other point having coordinates of 65 degrees, 0 gas usage.
Over what range of temperatures, if any, is this a reasonable assumption? Is the standard method of computing average temperature a good method? If, for example, a day is mostly near 20 degrees but warms up to 50 degrees for a short time in the afternoon, is 35 heating-degree-days a good measure of the heating required that day? Computing averages of functions over time is a standard problem that can be solved with integral calculus. With knowledge of typical and extreme rates of temperature change, this could become a calculus problem or a problem for approximate solution by graphical methods without calculus, providing background experience for some of the important ideas in calculus.
Students could also investigate actual savings after insulating a home in their school district. A customer might typically see 8-10% savings for insulating roofs, although if the house is framed so that the walls act like chimneys, ducting air from the house and the basement into the attic, there might be very little savings. Eliminating significant leaks, on the other hand, can yield savings of as much as 25%.
Some U.S. Department of Energy studies discuss the relationship between heating-degree-days and performance and find the cutoff temperature to be lower in some modern houses. State energy offices also have useful documents.
What is the relationship between heating-degree-days computed using degrees Fahrenheit, as above, and heating-degree-days computed using degrees Celsius? Showing that the proper conversion is a direct proportion and not the standard Fahrenheit-Celsius conversion formula requires some careful and sophisticated mathematical thinking.


















































