| This page in the original is blank. |
Overview
With President Clinton's call for voluntary national tests of reading in fourth grade and of mathematics in eighth grade, the debate about the role of the government in establishing standards and assessments has reached new heights on the political and educational landscapes. At the state level, debates about standards have been particularly heated in California, especially during the process of adopting state content and performance standards for all students. Throughout the country, much of the debate about standards has taken the form of dichotomies growing from language that positions opponents at extreme ends of the spectrum, arising particularly from opposing views about how people learn mathematics. For example, must automaticity with procedural skills precede any problem solving, or should thinking and reasoning permeate all aspects of the discipline, even before focusing on skill development? Although resolving these issues is beyond the scope of this document, finding common ground that transcends these dichotomies is a challenging but necessary part of the process of developing standards.
From any perspective in the standards debate, and from any political position, the call for standards is born, in part, out of parents' concerns for their children's futures: What should my child be learning? What should my child know in order to be admitted to a good college or university? What should my child
know in order to get a good job? One of the main themes of this document—that problems from the workplace and everyday life can enhance the mathematical education of all students—implies the fortunate conclusion that the answers to these questions need not conflict.
Discussion of national standards has a long history. The release of A Nation at Risk (National Commission on Excellence in Education, 1983) had an effect like that of national standards, for many high schools responded by increasing their course requirements for graduation. Since then, many organizations concerned with different aspects of education have released documents delineating standards. In 1989, the National Council of Teachers of Mathematics (NCTM) published Curriculum and Evaluation Standards for School Mathematics. More recently, many states have produced or are producing frameworks describing new goals for K-12 performance and instruction in mathematics as well as other disciplines. Some of those states have also produced state-wide assessments that are explicitly aligned with those frameworks. At the national level, the Secretary's Commission on Achieving Necessary Skills (SCANS) described competencies needed for careers in its 1991 report, What Work Requires of Schools. The Goals 2000: Educate America Act established the National Skill Standards Board in 1994 to serve as a catalyst in the development of a voluntary national system of skills standards, assessments, and certifications for business and industry. In science, the American Association for the Advancement of Science (AAAS) developed Benchmarks for Science Literacy (AAAS, 1993). After four years of development, consensus-building, and extensive formal review, the National Research Council (NRC) contributed the National Science Education Standards (NRC, 1996). Also in 1995, the American Mathematical Association of Two-Year Colleges published Crossroads in Mathematics: Standards for Introductory Mathematics Before Calculus.
With so many voices contributing standards and recommendations, teachers are faced with difficult challenges. Despite the fact that the meaning of the word ''standard" varies greatly among and even within the above documents—from statements about values to visions of the future; from statements about goals or expectations to criteria for evaluation—neverthless, some common themes emerge. The standards for mathematics and those for science, for example, have many commonalities, as Jane Butler Kahle discusses in her essay, including ideas such as problem solving and communication.
The SCANS requirements for the workplace, described in Arnold Packer's essay, also emphasize problem solving and communication, but these skills are embedded in a framework that is hard to reconcile with the traditional division of schooling into subject areas. In particular, the SCANS requirements for Planning Skills, Interpersonal Skills, and Personal Qualities, do not fall under any of the traditional grades 9-12 subject headings and are rarely explicitly discussed as part of the curriculum, especially in mathematics. How might such skills might be developed in a mathematics class? Part of an answer lies in the
SCANS Commission's belief that the requirements should be taught in context. Throughout the nation, calls for new standards, new pedagogy, or new curricula often meet with a challenge: But how will students do on standardized tests? Discussions of student achievement as measured by standardized tests often misses two important questions: For what purpose was the test designed? And what is the relationship between this test and the educational goals that I value? The NCTM Assessment Standards (NCTM, 1995) describe four purposes of assessment: monitoring students' progress, making instructional decisions, evaluating students' achievement, and evaluating programs. Though the relationship between standards and assessments often goes unarticulated in public discussions, a constructive discussion of changes in mathematics education must carefully consider the roles of the assessment tools in place, some of which function as implicit standards because they influence expectations about what counts mathematically. Because the SAT and the ACT have come to serve gatekeeping functions in college admissions and in scholarship decisions, they influence the ideas of parents and policy makers alike about what constitutes desirable mathematical performance. The ACT purports to measure the academic skills that students will need to perform college-level work. Based upon what is taught in the high school curriculum, and requiring integration of knowledge from a variety of courses, the ACT Assessment tests are designed to determine how well students solve problems, grasp implied meanings, draw inferences, evaluate ideas, and make judgments. The SAT aims to measure verbal and mathematical reasoning abilities. Both tests are intended as predictors of success in college (in particular, in the first year of college); they attempt to fulfill a necessary function: providing colleges with a metric that allows for comparison of students from different schools when grades might not be comparable.
But how do SAT and ACT scores compare with other measurements of mathematical performance? Can a test like the SAT adequately assess learning when the curriculum emphasizes extended, open-ended, or collaborative tasks? William Linder-Scholer poses these questions in his essay and suggests a data-analysis task for parents: assessing the SAT as a measurement of student achievement and school quality, and as a basis for comparing education in different states.
Though Linder-Scholer's essay provides some understanding of the difficulties in comparing average test scores for schools or states, many important questions are left unaddressed. Serious consideration of the role of college entrance exams depends upon answers to two perennial questions: What do colleges, parents, and scholarship organizations do with the individual scores from these tests? And does the SAT measure what colleges value? Both the ACT and the SAT have evolved over the years to better serve the needs of parents, colleges, and schools. Nonetheless, these questions require ongoing research in response to changing curricula in high schools and colleges, and in response to the changing needs of colleges and the workplace. Constructive
evolution of the role of college entrance exams requires collective deliberations among parents, teachers, college representatives, and testing experts around what these tests should be and how they may be used most effectively.
In his essay, John Dossey provides an international perspective on the character of the examinations given to students between high school and college. Looking at such examinations in the United States, England, Wales, and four European countries, he finds that contextualized, extended-response tasks are not routinely included. Such tasks are included, however, on the National Assessment of Educational Progress (NAEP), which provides national and state indicators about mathematics education but no individual scores (see, e.g., Reese et al., 1997). The NAEP results indicate that if such tasks are to assess individual student learning, "students will need a great deal of support in formulating, solving, and communicating their results."
The tasks that accompany these essays serve as examples and illustrations of tasks that might help provide that support. Well-chosen tasks are in no way to be construed as standards, but instead provide opportunities for building understanding of the mathematical ideas that are embodied in standards.
Mental Mathematics (p. 83) suggests ways that mental arithmetic and algebra might each contribute to the other. Though Buying on Credit (p. 87) is about finance and Drug Dosage (p. 80) is about pharmacology, the mathematics behind the tasks is quite similar, involving rates, series, and recursion. Despite the similar mathematical content of the two tasks, both are included to suggest an opportunity for students to engage in mathematical thinking: to describe and understand whole classes of tasks by noticing commonalities among their procedures or representations. The similarity, after all, can be clear only with sufficient mathematical understanding of multiple contexts.
References
American Association for the Advancement of Science. (1993). Benchmarks for science literacy. Washington, DC: Author.
American Mathematical Association of Two-Year Colleges (1995). Crossroads in mathematics: Standards for introductory college mathematics before calculus. Memphis, TN: Author.
National Commission on Excellence in Education. (1983). A nation at risk: The imperative for educational reform. Washington, DC: Author.
National Council of Teachers of Mathematics. (1989). Curriculum and evaluation standards for school mathematics. Reston, VA: Author.
National Council of Teachers of Mathematics. (1995). Assessment standards for school mathematics. Reston, VA: Author.
National Research Council. (1996). National science education standards. Washington, DC: National Academy Press.
Reese, C. M., Miller, K. E., Mazzeo, J., & Dossey, J. A. (1997). NAEP 1996 mathematics report card for the nation and the states. Washington, DC: National Center for Education Statistics.
United States Department of Labor. Secretary's Commission on Achieving Necessary Skills. (1991). What work requires of schools: A SCANS report for America 2000. Washington, DC: Author.
6—
Science and Mathematics Education: Finding Common Ground
JANE BUTLER KAHLE
Miami University
The current reforms in both science and mathematics education have many commonalities; in fact, for the first time, the two disciplines are advancing with common goals and objectives, as evidenced in the mathematics standards published by the National Council of Teachers of Mathematics (NCTM, 1989, 1991, 1995), and the science standards published by the National Research Council (NRC, 1996). Both sets of standards are based on the premises that all children can learn challenging mathematics and science, that literacy in both disciplines is necessary for productive work in the future, that learners construct their own knowledge, and that there are many effective ways to promote knowledge construction.
One way to elaborate such standards is to provide tasks that illustrate some of the ideas promoted by those standards. Tasks that fit with these standards have common characteristics: they require time, they allow multiple solution paths, they are open-ended, they may be revisited and extended, and they develop basic skills. Individually, each characteristic is applicable to both
science and mathematics; and collectively, these characteristics delineate a practical route from the rhetoric of standards to the reality of student achievement. Many of the skills involved in doing these tasks are critical to success in the sciences, as well as in mathematics.
Useful and compelling mathematics tasks illustrate both the logical and algorithmic nature of mathematics as well as its whimsy and beauty. These dual goals again make a connection with science. A national study of mine (Kahle, 1983) indicated that both ninth- and tenth-grade girls and boys were motivated to continue to study advanced science when their science teachers stressed both the basic skills of science (many of which may be learned in mathematics) and its more creative elements. I believe that problems that illustrate the whimsy and beauty of mathematics will encourage and excite many students who heretofore have been turned off to mathematics.
Mathematics instruction that fits with the NCTM Standards includes tasks that actively engage students in making meaning of mathematics and in proposing several possible solution processes. Such activities provide sites in which the NCTM process standards—mathematics as problem solving, mathematics as communication, mathematics as reasoning, and mathematical connections—can be emphasized and developed.
Science instruction consistent with the National Science Education Standards (NSES) (NRC, 1996) is characterized by similar parameters: students identify a problem from their observations of nature; they propose several solutions (hypotheses); in any one class, their investigations take multiple approaches; and they discuss and consider all reasonable solutions. The science as inquiry standards in particular promote the following processes:
… asking questions, planning and conducting investigations, using appropriate tools and techniques to gather data, thinking critically and logically about relationships between evidence and explanations, constructing and analyzing alternative explanations, and communicating scientific arguments. (NRC, 1996, p. 105)
Practically speaking, it is possible to write tasks that are directly applicable to both mathematics and science lessons. In this volume, Drug Dosage (p. 80) is a task in which students may either use a mathematical model to understand a scientific context or use a scientific context to understand mathematical ideas in the model. Because of their availability and low cost, paper towels are a common context for tasks that integrate mathematics and science.1 In order to compare brands for absorbency, strength when wet, or cost per sheet, or to investigate concepts such as the relationship between the number of water drops absorbed by the towel and the area of the wet spot, students design experiments and collect and interpret data.
The NSES includes an excellent example of an activity, "The Solar System," for an integrated mathematics and science program (NRC, 1996, pp. 215-217). The goal of the activity is to have students construct a scale model of the
sun, moon, and earth using techniques developed by early astronomers. Students observe the stars, discuss the patterns they observe, and use a particular pattern (the North Star, Polaris, doesn't appear to move) to suggest methods for estimating the circumference of the earth. In particular, if they know angle of the North Star at two locations on the same longitude and a known distance apart, they may estimate the circumference of the earth by using a two-dimensional diagram of the three-dimensional situation (see Figure 6-1), and by using geometric knowledge about circles, tangents, and angles. Through activities such as this, students can see not only that geometric understanding is necessary to understand the science problem, but also that science provides contexts for geometric and mathematical ideas.
These possibilities arise because of common skills that are needed to study both mathematics and science. For example, in both disciplines, students need to be able to estimate, to use mathematical models, to interpolate and extrapolate, to identify false negatives, to detect bias, to convert two-dimensional drawings to three-dimensional models and vice versa, to make and interpret graphs and other diagrams, and so on. Furthermore, when students use data gathered in science investigations in their mathematics courses, they encounter many of the anomalies of authentic data: inconsistencies, outliers, and errors. Indeed, tasks that build these kinds of skills are good examples of activities through which it should be possible to develop aspects of the scientific literacy stressed in the NSES (NRC, 1996), as well as the mathematical understandings promoted in the NCTM's Curriculum and Evaluation Standards for School Mathematics (NCTM, 1989).
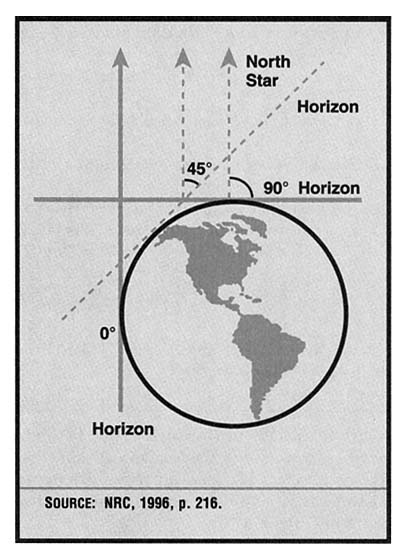
FIGURE 6-1: A diagram from the activity "The Solar System"
Because of these connections between mathematics and science, the NSES calls for coordinating the science and mathematics programs in schools. Such coordination results in opportunities to advance instruction in science beyond purely descriptive studies and to provide mathematics classes with authentic problems. The NCTM Standards documents (NCTM, 1989, 1991, 1995) also clearly encourage making connections between mathematics and the sciences, particularly in the sections on mathematical connections. The documents note the pervasiveness of the connections between mathematics and other disciplines and encourage such
connections in the classroom as a means of enabling students to see the utility of mathematics and to find motivation for mathematics.
We have been singularly unsuccessful in developing a long-term relationship, let alone a successful marriage, between science and mathematics as they are usually taught in schools. An often-promoted solution is simply using science examples in mathematical problems. This solution is too simple, obviously, and has not been successful in the past. However, both the NSES and this volume provide glimpses of what will work. First, students need to be able to integrate the scientific skills of observing, classifying, inferring, collecting, and interpreting data, using mathematical skills such as reasoning, computing, communicating, and making connections. For all students, the process of doing both good science and good mathematics holds the most promise of successful integration, an integration constructed by each learner as her or his skills and understandings develop. Mathematics at Work may help inspire a future in which value is placed upon the processes, not products, of learning, where science and mathematics are integrated through common skills, where relevant activities that integrate mathematics and science are readily available for each student, and where the common ground that is shared by those interested in high-quality mathematics and science education is explicit.
References
Kahle, J. B. (Ed.). (1983). Girls in school: Women in science. Washington, DC: National Science Board, Commission on Precollege Education in Mathematics. (ERIC Document Reproduction Service No. ED 258 812).
National Council of Teachers of Mathematics. (1989). Curriculum and evaluation standards for school mathematics. Reston, VA: Author.
National Council of Teachers of Mathematics. (1991). Professional standards for teaching mathematics. Reston, VA: Author.
National Council of Teachers of Mathematics. (1995). Assessment standards for school mathematics. Reston, VA: Author.
National Research Council. (1996). National science education standards. Washington, DC: National Academy Press.
Sneider, C. I. & Barber, J. (1987). Paper towel testing. Great Explorations in Math and Science (GEMS) Project. Berkeley, CA: Lawrence Hall of Science, University of California, Berkeley.
Teaching Integrated Mathematics and Science (TIMS) Project, Inc. (1992). Spreading Out II. Chicago: University of Illinois at Chicago.
Note
|
1. |
See, for example, Spreading Out II (Teaching Integrated Mathematics and Science (TIMS) Project, Inc. 1992) and Paper Towel Testing (Sneider & Barber, 1987). |
JANE BUTLER KAHLE is Conduit Professor of Science Education at Miami University. She is Chair of the Committee on Science Education, K-12. She has been President of the National Association of Biology Teachers and the National Association for Research in Science Teaching as well as Chair of National Science Foundation's Committee on Equal Opportunities in Science and Engineering and Biological Sciences Curriculum Studies' (BSCS) Board of Directors.
7—
Scans and Mathematics—Supporting the Transition from Schools to Careers
ARNOLD PACKER
Johns Hopkins University
This essay addresses two related questions: What kinds of tasks will support the learning of "SCANS" skills described by the report entitled What Work Requires of Schools (United States Department of Labor, 1991)? And will use of such tasks facilitate student success in making the transition from school to career?
The charge of the Secretary's Commission on Achieving Necessary Skills (SCANS) was to examine the demands of the workplace and whether students were being prepared to meet those demands. SCANS commissioned a variety of studies. Six special panels examined jobs ranging from manufacturing to government employment. Researchers interviewed a wide range of workers. The commission itself met with business owners, employers, union representatives, and workers. In summarizing the findings of these studies, the SCANS report describes five sets of competencies and a three-part foundation of skills
and attributes essential for all students, both those going directly to work and those planning further education. The commission believes that, in line with current research in cognitive science, the eight requirements should be taught in context rather than as abstract concepts and skills to be applied later.
The five competencies are
- Planning Skills, such as allocating time, money, space, and staff;
- Interpersonal Skills, such as negotiating and teaching;
- Information Skills, such as acquiring, evaluating, interpreting, and communicating information;
- Technology Skills, such as selecting, using, and fixing technology; and
- Systems Skills, such as understanding, improving, and designing systems.
For example, an entry-level restaurant worker should be able to estimate costs of replacing equipment and justify necessary expenses in writing. In order to plan where the equipment should be placed, the worker should be capable of reading blueprints and manufacturers' installation requirements. Such a worker might need interpersonal skills to explain technology or scheduling to a new employee, for example. A necessary information skill might include being able to use a spreadsheet program to estimate the costs of food required for different menus. And the worker should be able to analyze and modify the system, determining the average and maximum amount of time a customer waits between ordering and receiving an appetizer, and between receiving an appetizer and the entree.
In this example, aspects of the three-part foundation of attributes and skills are intertwined with the five competencies. The three-part foundation consists of
- Basic Skills, such as reading, writing, and computing;
- Thinking Skills, such as visualization, reasoning, and the ability to solve problems; and
- Personal Qualities, such as perseverance, politeness, self-esteem, and empathy.
In the restaurant scenario above, the worker needs to read blueprints, write a justification, and compute costs. Planning where to place equipment requires processing the information from the blueprints as well as the information given about the dimensions of the equipment. Throughout this scenario, politeness is necessary, in directing workers where to place equipment, in explaining matters to a new worker, and, of course, in dealing with customers.
What Work Requires of Schools describes these attributes and skills as both extensive and enduring. They are extensive because they are needed at all stages of careers of all kinds, including careers that require post-graduate education, and they are enduring because these skills have been needed for
centuries and will be needed for centuries to come. Furthermore, the report claims that any authentic workplace task requiring a high level of effort and perseverance will necessarily involve one or more of the five competencies.
When designing tasks to serve the SCANS goals, one needs to consider tasks likely to be encountered in the workplace. From the SCANS perspective, a good task is one that a million or more workers in the U.S. economy pare being paid to solve. (This is not to disparage tasks that students will need to solve in roles outside the workplace, such as citizenship or parenting. But in SCANS, workplace issues predominate.)
The most important worker in the educational system is the student. Recent surveys of jobs by the SCANS Commission, by American College Testing, and by the American Institute for Research (for O*NET) indicate that students need a firm grasp of applied algebra—not a vague understanding of calculus (Packer, 1997). They can always look up algorithms and formulas in order to solve a quadratic equation or complete a square. Even if students can recall them to pass their final exams, they are likely to forget many algorithms and formulas two weeks later. What they need to demonstrate on exams is that they know how to bring mathematics to bear on SCANS-like problems such as budgeting and scheduling.
The issue has become more important because President Clinton has called for a national 8th grade mathematics assessment. Should the test pose mathematical "puzzles" that are interesting to the mathematically inclined? Or should test items have a clear relationship to problems that students are likely to encounter outside the schoolroom walls?
The SCANS goals require more variety in the circumstances under which tasks are done. The traditional problem archetypes, such as canoe problems and train problems, also have a traditional format—they are done individually in 10 minutes or less. In contrast, the SCANS competencies of teaching, negotiating, interpreting, and communicating require tasks that can only be solved collectively by groups. All of these changes will help schools reflect the needs of the workplace with greater accuracy and ease the transition from schools to careers.
References
United States Department of Labor. Secretary's Commission on Achieving Necessary Skills. (1991). What work requires of schools: A SCANS report for America 2000. Washington, DC: Author.
Packer, A. (1997). Mathematical Competencies That Employers Expect. In L.A. Steen (Ed.), Why numbers count: Quantitative literacy for tomorrow's America, (pp. 137-154). New York: College Entrance Examination Board.
ARNOLD PACKER is a Senior Fellow at the Institute for Policy Studies of Johns Hopkins University. He was Executive Director of the Secretary's Commission on Achieving Necessary Skills (SCANS) and coauthor of Workforce 2000. He has served as Assistant Secretary at the U.S. Department of Labor, and as first Chief Economist at the U.S. Senate Budget Committee. He is a licensed (and practicing) engineer in New York and California. His Ph.D. in Economics is from University of North Carolina at Chapel Hill.
8—
Thinking About the SAT
WILLIAM LINDER-SCHOLER
Scimath Minnesota
For many parents, standardized test scores seem to answer the basic questions about education that everyone asks: How good is the school my child attends? How do the schools in our state or region compare with schools elsewhere? What chance does my son or daughter have of being admitted to a good college or university?
Schools commonly use achievement test results to determine whether students are making progress and to ensure that programs in basic subjects, such as mathematics and reading, are effective. The referendum-voting and home-buying public use test scores to judge the quality of their schools and the desirability of living in one community over another. Colleges often combine students' high school grade point averages and scores on standardized tests to make crucial in-or-out decisions about admissions.
But how reliable are standardized test results? Can we really use achievement test rankings or college-admissions test scores to make fair and meaningful comparisons of students, schools, and states?
Workplace and everyday tasks like those in this volume bring these questions into sharp relief in two very different ways. First, such tasks differ considerably from the tasks used in standardized tests, most notably in the time a student is expected to spend on the task and in what constitutes a solution.
This point raises questions about whether any standardized test can adequately assess a type of education in which extended tasks are used for instruction. Second, the kind of reasoning that parents need to gauge properly the significance of test score data is precisely the kind of reasoning that we might encourage. Interpreting test score data is itself a mathematical task!
Interpreting the SAT
For better or worse, we know that Americans have been making the comparisons outlined above for generations. This fact is perhaps best illustrated by the power and popularity of the SAT1—the single most-used standardized test of its type in the country and an important ingredient in college admissions since the 1940s. The SAT I: Reasoning Test, a multiple-choice exam2 with verbal and mathematics components, is used in combination with high school grades to predict a student's readiness for college. Fluctuations in average SAT scores are tracked as indicators, albeit indirect, of the quality of education in this country (Bracey, 1996; Powell & Steelman, 1996).
Beginning in 1964, average scores on the SAT dropped slowly but steadily for about 15 years. This led to much speculation and considerable hand-wringing about possible causes of the apparent decline in education quality in the U.S. By the early 1990s, average scores on the mathematics portion of the SAT had rebounded significantly, but scores on the verbal section had not.
Scores on other national standardized exams also declined during this same time period, but none attracted as much attention as the SAT. Further significance was attributed to this alarming drop in SAT scores by the many reports of poor mathematics and science performance by U.S. students relative to that of students in other countries. In the U.S., state-by-state comparisons of SAT results became a standard feature of the economic "warfare" among the states to lure businesses and their employees based on relative measures of "quality of life" as reflected in part by test-score rankings.
Missing Information
The trouble with all of this is that test scores, particularly average scores on nationally-normed standardized tests such as the SAT, don't mean as much as we typically think they do. Understanding who takes the test—and who doesn't—is the first and perhaps single most important factor to consider when trying to understand what raw SAT scores or state-to-state comparisons really mean.
For starters, we need to know what percentage of students actually take the test. Students who take the SAT (or equivalent admissions exams such as the ACT, used more extensively in the Midwestern states) are obviously prospective college students and thus not representative of the total school population. Thirty years ago, average national scores on the SAT exam were highly unrepresentative of the achievement of the "average" student in the U.S. because the pool of candidates taking the test was much smaller than it is
now. In fact, in 1975 SAT-takers included only one-third of the nation's graduating seniors, but by 1994, they included 42% of the nation's graduates (College Entrance Examination Board, 1994). Although experts disagree about specifics, the decline in SAT scores during the 1960s and 1970s seems due at least in part to the fact that the test-taking pool is formed of a larger percentage of high school graduates, and, thus, in the '60s and '70s, an average SAT-taker was more like an average high school graduate than was the case in the 1950s.
Today, with an even larger portion of total school population taking the SAT, we can more fairly make comparisons, yet in making state-to-state contrasts we must still account for differential rates of overall student participation. In 1993 for example, the average SAT score for students in Iowa was 1103. Students in Massachusetts averaged 903 (Powell & Steelman, 1996). But in Iowa only 5% of high school seniors took the SAT. In Massachusetts, participation was far greater—81% of high school seniors took the exam. Generally speaking, in states where SAT participation rates are relatively high, the likelihood is that average scores will be lower than in the low-participation states. (See Figure 8-1.)
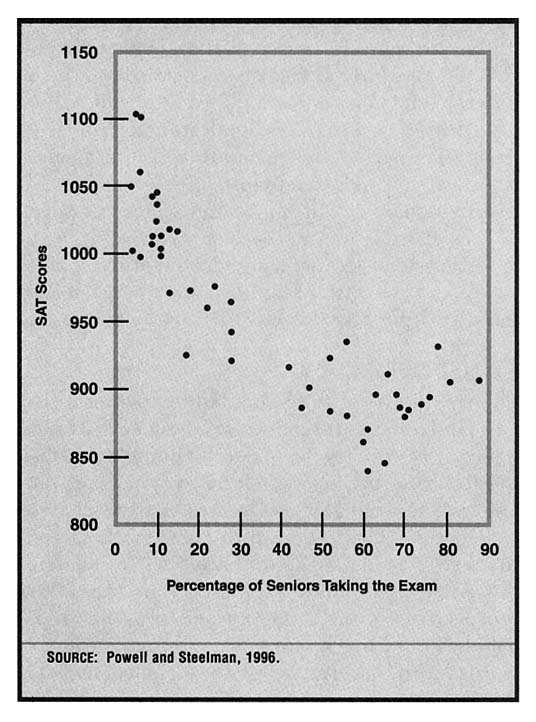
FIGURE 8-1 Average SAT scores or states vs. percentage of seniors taking exam
However, who takes the test, as well as how many take it, also makes a difference in scores. To some extent, the diversification of the SAT-taking pool during the 1960s and 1970s was due to the overdue "democratization" of the test-taking group, with the addition to the SAT pool of significant numbers of female students and students of color, groups who previously had been underrepresented among the college-bound. Students in these groups often do not experience the "same" education
as those from groups who are traditionally expected to be college-bound (Oakes, 1990; Wellesley College Center for Research on Women, 1992).
But the effect of this democratization is not simple. Changes and rates of change in SAT scores are linked in complex ways to both how many students take the test and the composition of the test-taking pool. Consider the following facts that run counter to the common expectation that such democratization causes average scores to fall:
- During the 1970s, at the very time that SAT scores fell fastest, high school graduation rates were stable, the percentage of students taking the test changed very little, and the percentage of students going to college also changed only minimally. Clearly, other factors were at work in causing the test score declines.
- The most dramatic compositional changes in the SAT test-taking pool (particularly the increase in numbers of ethnic minority students) occurred after 1980, at a time when SAT scores were leveling off and beginning to head back up, especially in mathematics (College Entrance Examination Board, 1994).
Comparing states gets even more complicated when we consider the fact that SAT scores can also be influenced by differences in school environments. Low expectations for student performance, tracking of students into unchallenging academic programs, high student-teacher ratios, and differences in curricula and instructional practices account for significant differences in school performance and can also influence a state's SAT average. And, conversely, some changes in curriculum and instruction may not influence SAT averages. For example, the Interactive Mathematics Program (IMP) is a nontraditional high-school curriculum based on complex extended problems. The average SAT score for IMP students was only 1 point higher than that of a matched sample of students enrolled in a traditional mathematics curriculum. But 87 percent of IMP students took the SAT and only 58% of their counter-parts did (Interactive Mathematics Program, 1995).
For reasons like these, the U.S. government long ago instituted the National Assessment of Educational Progress (NAEP), which tests a representative sampling of all high school students in the country, not just the college-bound. Although the NAEP does not adjust for state-to-state variation in expectations, curricula, and other environmental differences, it does test a representative sample of students on a range of tasks, which include SAT-like items as well as extended-response tasks. In this sense, it provides a more reliable way than the SAT of comparing one state's educational performance with another. In fact, a cross-check of the state-by-state NAEP results for grade 4 and grade 8 (White, 1993) is one way to put some "context" around SAT-score comparisons.
So here we have a mathematical task for parents and guardians. The calculations necessary for comparing one state's SAT scores with another's must include the percentage of total students taking the examination in each state as well as the composition of each pool and, secondarily, information regarding the relative strengths and weaknesses of the states based on existing measures of academic performance. Unlocking the mystery of test-score statistics means understanding raw numbers in the context of a host of student population and school environment factors. It means getting beyond the simplistic messages of test-score headlines in order to understand relative measures of student achievement and quality of the educational system.
References
Bracey, G. W. (1996). Money improves test scores—even state-level SATs . Phi Delta Kappan, 78(1), 91-92.
Burton, N. (1996). Have changes in the SAT affected women's mathematics performance? Educational Measurement: Issues and Practice, 15(4), 5-9.
College Entrance Examination Board. (1994). College-bound seniors: 1994 profile of SAT and achievement test takers. Princeton, NJ: Educational Testing Service.
Interactive Mathematics Program. (1995). Evaluation update. Issue 1, 1995. (Available from 2420 Van Leyden Way, Modesto, CA 95356.)
Oakes, J. (1990). Multiplying inequalities: The effects of race, social class, and tracking on opportunities to learn mathematics and science. Santa Monica, CA: Rand Corporation.
Powell, B. & Steelman, L. C. (1996). Bewitched, bothered, and bewildering: The use and misuse of state SAT and ACT scores. Harvard Educational Review, 66 (27-59).
Wellesley College Center for Research on Women. (1992). How schools shortchange girls. Washington, DC: American Association of University Women.
White, S. E. (1993). NAEP 1992 mathematics report card for the nation and the states. Washington, DC: National Center for Education Statistics.
Notes
WILLIAM LINDER-SCHOLER is Executive Director of SciMathMN, a statewide public/private partnership that advocates standards-based reform for K-12 mathematics and science education in Minnesota. He is a member of the National Research Council's Committee on Science Education, K-12, and served on the committee which guided development of the National Research Council's National Science Education Standards. He is a member of the Executive Council of the National Association for State Science and Mathematics Coalitions. Linder-Scholer previously served as Director of Community Affairs at Cray Research, Inc., the Fortune-500 supercomputer company, and as Director of the Cray Research Philanthropic Foundation, where he directed a national grant-making program focused on mathematics and engineering education.
9—
Extended Response Tasks in International Contexts
JOHN DOSSEY
Illinois State University
Mathematical tasks with a strong connection to today's workplace call for students to use procedures drawing on knowledge of recursion, numerical approximations, exploratory data analysis, and statistical hypothesis testing. Such problems are realistic, authentic, and representative of the real world. They can involve a great deal of good mathematics. However, they can also be quite different from what one sees in the examinations given to high school students of other countries (Britton & Raizen, 1996; Dossey, 1996).
An International View
School-leaving examinations (given to all students at the end of high school) in England and Wales, France, Germany, Japan, Sweden, and even the United States, tend to focus much more on the narrow "taught curriculum" of traditionally conceived concepts and procedures related to the road to calculus—and to the university. This canon of work is generally limited to various forms of algebra, geometry, elementary functions (including trigonometry), and introductory calculus. An analysis of representative examinations from these countries for 1991 and 1992 (Dossey, 1996) indicates that the heaviest concentration of test items falls in the areas of calculus (applications of the definite integral, applications of the derivative, and the use of the derivative in finding maxima
and minima), functions (interpreting the graphs of functions, trigonometric equations, and trigonometric identities), and probability distributions—notably, the normal distribution (also known as the bell curve) and its properties.
Little evidence was seen in the study of these school-leaving (or college-entrance) examinations of items that reflect rich ties to contemporary real-world problems. For example, when recursion appeared, it did so in a relationship between trigonometric functions or in the context of a radioactive substance which decayed exponentially, both rather theoretical settings. There were no tasks involving recursion as rich in contemporary connections as you will see in Lottery Winnings (p. 111), Drug Dosage (p. 80), or Buying on Credit (p. 87). In a like manner, no international evidence was seen of tasks concerning back-of-the-envelope calculations, estimation, rounding, or general number, operation, and symbol sense—all of which occur in various tasks in this volume.
The school-leaving and college-entrance examinations at the international level showed a strong predisposition to focus applications in one area: classical applications of mathematics to motion and mechanics problems from physics. Consider the following item taken from the 1991 University of Tokyo examination for students applying to enter the university in science. It presents a non-routine but classically oriented problem dealing with kinematics (Wu, 1993):
Let a, b, and c be positive real numbers. In the xyz-space, consider the truncated plane R consisting of points (x, y, z) satisfying the conditions
Let P be a source of light moving once around the ellipse
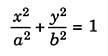
in the z = c + 1 plane. Sketch and calculate the area of the shadow projected by R on the xy-plane.
Only the examinations from Germany reflected applications to business. These applications tended to deal with quality control and applications of probability to production problems. For example, the 1992 abitur (an examination given college-bound students) in the state of Bavaria contained the following item (Dossey, 1996):
It is given that 8% of the golf balls made by a particular manufacturer are considered unusable by golf players. From past experience, it has been shown that 5% of the golf balls delivered by the manufacturer are returned because of defects. For every returned ball, the manufacturer takes a loss of 0.80 DM (Deutsche Marks), and for every ball not returned the manufacturer will make a net profit of 1.20 DM. What is the probability that the manufacturer will make a net profit of at least 210 DM on a 200-ball delivery?
One should be careful about criticizing the focus of most school-leaving examinations on applications of mathematics to classical problems in physics.
These problems remain valuable for many students who need the ability to translate and formulate problems drawing on the common languages of mathematics and science. These skills are inherently important for students continuing with the study of physics, engineering, and advanced mathematics.
Through a much broader and potentially richer set of mathematical activities for motivating a more diverse set of students, we can show all students the power of mathematics to effect change through decision-making in settings close to their lives. The ability to balance such traditional and contemporary forces in both curriculum and assessment will remain a challenge for years to come.
A U.S. View for all Students
The 1992 National Assessment of Educational Progress (NAEP) mathematics assessment evaluated the performance of a random sample of U.S. twelfth graders on a mixed set of tasks (Dossey, Mullis, & Jones, 1993). One task was somewhat similar to, but much simpler than, the motion problem given in the University of Tokyo examination:
The darkened segments in the figure on the left below [Figure 9-1] show the path of an object that starts at point A and moves to point C at a constant rate of 1 unit per second. The object's distance from point A (or from point C) is the shortest distance between the object and the point. In the graph paper on the right, complete the following steps:
|
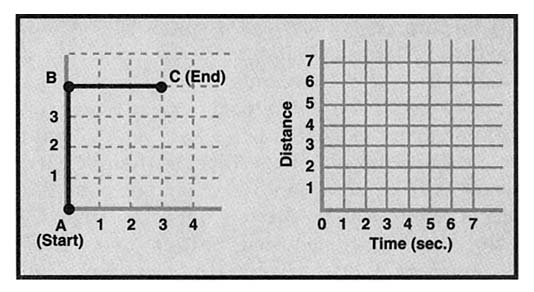
FIGURE 9-1: Diagrams from a NAEP problem
A second NAEP problem, set in perhaps a more real-world setting, asked students to consider the following situation involving a proposed income tax:
One plan for a state income tax requires those persons with income of $10,000 or less to pay no tax and those persons with income greater than $10,000 to pay a tax of 6 percent only on the part of their income that exceeds $10,000.
A person's effective tax rate is defined as the percent of total income that is paid in tax. Based on this definition, could any person's effective tax rate be 5 percent? Could it be 6 percent? Explain your answer. Include examples if necessary to justify your conclusion.
Students' performances on these two tasks were evaluated using a 6-point partial-credit rubric according to the categories of no response, totally incorrect work, minimal work, partial work, satisfactory work, and extended correct work. Only 1% of U.S. twelfth graders achieved one of the top two scoring categories (satisfactory or extended credit) for the particle-motion task. The performance was not much better for the tax item, where only 3% rated a satisfactory or extended score. These data are based on the performances of a random sample of U.S. students still attending school at the twelfth-grade level. The performance percentages would undoubtedly be lower if all youth of that age cohort were sampled.
Summary
Contextualized extended-response items like those shown from NAEP are very demanding for U.S. students. However, they in no way reach the level of complexity expected of students of similar ages in the terminal year of secondary school mathematics in countries that are our economic peers. The tasks in this volume push the envelope further for U.S. students by requiring that our students be able to draw on information from outside the traditional mathematics/science connection. However, additional focus must be given to communicating the expectation that U.S. students be able to deal with non-routine problems in contextualized settings. The ability of mathematics educators, curriculum specialists, and assessment directors to coordinate this forward movement will require a great deal of effort.
Comparisons with school-leaving examinations in other countries are always difficult to interpret (Gandal & Dossey, 1997). The NAEP examinations are designed to collect information on a random sample of American 12th graders, regardless of the secondary school mathematics they have taken. The University of Tokyo examination is an exceedingly challenging entrance examination given to select the best of the excellent students applying for entrance to that university. Regardless of that difference in purpose—status of the system versus selection of individuals—the data and analysis from comparisons of examinations (Britton & Raizen, 1996; Gandal & Dossey, 1997) suggest that contextualized, non-routine tasks are not commonly included even on the mathematics examinations in other countries, although
a great deal has been written concerning the need for such tasks. The U.S. experience with NAEP tasks requiring such work shows that students will need a great deal of support in formulating, solving, and communicating their results.
These cautions notwithstanding, the broad applications of mathematics in daily life, the need to motivate and retain students in mathematics, and the importance of reporting the ability levels of students in mathematics relative to the demands of the world all require that we begin to move both instruction and assessment to include tasks such as those illustrated in this volume. To do less is to abandon significant opportunities to relate the real world to the classroom while strengthening student problem-solving and modeling skills. The trick will be to balance this instruction and assessment with the concepts and skills that define the traditional core of mathematics. This is the real-life problem confronting the classroom teacher and the curriculum specialist.
References
Britton, E. D. & Raizen, S. A. (Eds.). (1996). Examining the examinations . Boston, MA: Kluwer Academic Publishers.
Dossey, J. A. (1996). Mathematics examinations. In E. D. Britton & S. A. Raizen (Eds.), Examining the examinations, (pp. 165-195). Boston, MA: Kluwer Academic Publishers.
Dossey, J. A., Mullis, I. V. S., & Jones, C. (1993). Can students do mathematical problem solving. Washington, DC: National Center for Education Statistics.
Gandal, M. & Dossey, J. (1997). What students abroad are expected to know about mathematics: Exams from France, Germany and Japan. Washington, DC: American Federation of Teachers.
Wu, L. E. (1993). Japanese university entrance examination problems in mathematics. Washington, DC: Mathematical Association of America.
JOHN DOSSEY is the Distinguished University Professor of Mathematics at Illinois State University. He is Chair of the Conference Board of the Mathematical Sciences and has served as President of the National Council of Teachers of Mathematics, and as Chair of the U.S. National Commission on Mathematics Instruction at the National Research Council.
Drug Dosage
Task
A student strained her knee in an intramural volleyball game, and her doctor has prescribed an anti-inflammatory drug to reduce the swelling. She is to take two 220-milligram tablets every 8 hours for 10 days. Her kidneys filter 60% of this drug from her body every 8 hours. How much of the drug is in her system after 24 hours?
Commentary
This task can be approached in many different ways using numeric or algebraic methods, by hand, with calculators or with computers. Regardless of their approach, mathematically literate students will need to be familiar with the mathematical structure in this task. Whether the situation involves understanding effective drug dosages, population growth, bank accounts or loans, amortization, heating or cooling, filtering pollution from lakes and streams, models of learning and forgetting, or models of the economy, students should be familiar with some of the many situations which give rise to iterative processes—repeated processes in which future levels are determined by present levels. The importance of technology in dealing with tasks of this type is worth noting. Students should be able to think and work with iterative processes, and also should be sufficiently comfortable with technology to expect, as a matter of course, to consider long-term behavior and trends. All high school graduates need to be comfortable with both the structure of such tasks and the technological tools for their investigation.
Iterative models illustrate a mathematical tool that has become increasingly important in recent years: difference equations, the discrete-time analogs of differential equations. In the past, students did not study difference equations until well into their undergraduate or graduate courses. But with the aid of a spreadsheet or graphing calculator, students can handle such iterative problems with relative ease, provided that they can make the translation from a problem statement to an equation describing the iterative process, also called a recursion equation.
Mathematical Analysis
One approach is to create a table of values relating the number of 8-hour periods to the amount of the drug remaining in the student's system. To do this, some assumptions must be made about how quickly the drug gets into her system after it is taken. The simplest model assumes that the drug is active immediately after the medication is taken.
In this task, the information given is the rate at which the drug is eliminated by the kidney, whereas the focus of the tasks is on how much remains. The fundamental unit of time is an 8-hour period.
If the student takes 440 mg of the anti-inflammatory drug, after 8 hours her kidneys have removed 60% of the 440 mg, leaving 40% of the dose in her system. After she has taken her second 440-mg dose, the total amount of drug in her system in mg is then: (.4)(440) + 440 = 616. After 16 hours, she has 40% of the total for 8 hours, plus another 440. After 24 hours, she has 40% of the total for 16 hours, plus another 440. These calculations are summarized in Table 1.
One way to generalize this method is to use Table 1 to see patterns. First, let An denote the amount of drug in the system after dose n. Then the "drug remaining" column may be represented as in Table 2. The relationship in Table 2 between the "drug remaining"
column and the ''total in system" column may then be represented as shown in Table 3, which can easily be converted into a spreadsheet. Table 3 also suggests the recursion equation: .4An - 1 + 440 = An, where An is the amount of drug present at the beginning of the nth 8-hour period (or nth dose).
TABLE 1: Calculation of amount of drug in system
|
DAY |
TIME IN HOURS |
DRUG REMAINING |
+ AMOUNT TAKEN |
= TOTAL IN SYSTEM |
|
1 |
0 |
0 |
+ 440 |
= 440 |
|
1 |
8 |
176 |
+ 440 |
= 616 |
|
1 |
16 |
246.40 |
+ 440 |
= 686.4 |
|
2 |
24 |
274.56 |
+ 440 |
= 714.56 |
TABLE 2: Calculation of amount of drug in system, first generalization
|
DOSE n |
DRUG REMAINING |
+ AMOUNT TAKEN |
= TOTAL IN SYSTEM, |
An |
|
1 |
0 |
+ 440 |
= 440 |
A1 |
|
2 |
(.4)(440) |
+ 440 |
= 616 |
A2 |
|
3 |
(.4)(616) |
+ 440 |
= 686.4 |
A3 |
|
4 |
(.4)(686.4) |
+ 440 |
=7 14.56 |
A4 |
TABLE 3: Calculation of amount of drug in system, second generalization
|
DOSE n |
DRUG REMAINING |
+ AMOUNT TAKEN |
= TOTAL IN SYSTEM, |
An |
|
1 |
0 |
+ 440 |
= A1 |
|
|
2 |
(.4)A1 |
+ 440 |
= A2 |
|
|
3 |
(.4)A2 |
+ 440 |
= A3 |
|
|
4 |
(.4)A3 |
+ 440 |
= A4 |
|
More advanced students might begin their solutions by modeling the process with this recursion equation, expressing the relationship between An - 1 and An. Such an equation is well suited for use in a programmable calculator or a spreadsheet, especially in investigating the long-term behavior of the model.
Students who have studied iterative models may also solve this equation analytically to find an explicit formula for An.
Extensions
How much of the drug is in the student's system after 10 days? The recursion equation above can be translated into a spreadsheet to answer this. Students will notice that the peak levels, An, don't get bigger indefinitely and can investigate ways of determining the limiting value.
Suppose she doesn't like taking medicine, so she decides to take only one pill every 8 hours for 20 days. Does this strategy of taking half the amount of the drug for twice as long a period result in the same level of drug in her system? Many drugs have what is known as a therapeutic level. Unless the amount of drug in one's system reaches the therapeutic level, the drug is not effective. If the therapeutic level for the drug she is taking is 650 mg, how effective is her strategy of taking half the drug for twice as long?
Sometimes doctors suggest that the patient take a double dose initially, called a loading dose. A simple variation in the standard model can illustrate the effect of the loading dose on the effectiveness of the drug.
In addition to a therapeutic level, drugs also have a toxic level. If too much of the drug is in your system, you can become ill as a result. As you age, the ability of your kidneys and liver to remove the drug is reduced. Suppose that, for older patients, only 40% of the drug is removed in an 8-hour period. What dangers does this pose for older patients? How would such a patient fare using a strategy of taking only one tablet for twice as long?
Once these situations have been examined, students could explore different dosages (e.g., two 200-milligram pills); dosage intervals, (e.g., taking one 220-milligram pill every 4 hours); and clearing rates (for example, the kidneys of most healthy individuals will filter 45% to 65% of the drug from their system within 8 hours). Though it requires more sophisticated methods for solution, students could also explore different models in which the drug does not get into the bloodstream immediately.
Some medications, particularly cold capsules, contain several different drugs. The liver and kidneys remove nearly 70% of a typical decongestant in an 8-hour period but only approximately 20% of a typical antihistamine during the same period. If a student takes one decongestant and one antihistamine every 8 hours for 5 days, how does the level of decongestant compare to the level of antihistamine? Once the initial spreadsheet or calculator formulas are created, this very sophisticated question is within reach.
Often the information on the rate of filtering by the liver and kidneys is given in terms of the half-life of the drug. For example, theophylline, a common asthma drug, has a half-life of approximately 4 hours. Local pharmacists can identify the half-life of drugs that people typically take during cold and flu season. Students can rewrite the half-life of the drugs in terms of the decay rate for the interval of time between doses of the medication. Since half-life is such a commonly given measure, it is important that students be able to use this terminology as well to compare residual levels over specific time periods.
Mental Mathematics
Tasks
- In a 6th grade mathematics class, one of the problems requires the following calculation:
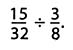
One student claims, without using pencil or paper, that the answer is 5/4 because 15 ÷ 3 = 5 and 32 ÷ 8 = 4. Is the student's answer correct? How can the student's reasoning be explained?
- The owners of a manufacturing company would like to be able to promise one-week delivery of special orders. The company is not ready, however, to make this promise to customers. Of the 56 orders filled so far this month, 49 were filled in one week or less and 7 took more than one week to fill, a success rate of 87.5%. During the weekly team meeting, the supervisor wants to know how many subsequent orders must be filled within one week to increase this month's success rate to 90%. Several employees know that this problem can be solved with algebra and scrounge around for paper and pencils. One employee, however, announces that the answer is 14. She describes her reasoning as follows: We want the 7 late orders so far to be only 10% of the total number of orders, which therefore must be 70. Subtracting the 49 on-time and 7 late orders so far yields 14 orders. Is she correct? How can her reasoning be explained?
-
Commentary
Mental arithmetic can save time, money, and even embarrassment—such as being caught short of cash at the check-out counter. In everyday life, people use mental arithmetic to estimate budgets, shopping bills, tips in restaurants, and taxes. On the job, an employee might be asked to give a quick estimate while talking to a boss or a colleague. Mental arithmetic depends not only upon number facts and estimating skills but also problem solving skills and algebraic reasoning skills because the standard paper-and-pencil algorithms are sometimes hard to do in one's head. As people become more familiar with number facts and gain number sense and symbol sense, their mental arithmetic can become more precise and more flexible. A study of 44 mathematicians' numerical estimation strategies found considerable variation in the strategies used (Dowker, 1992). As many as 23 different strategies were used for the same task!
The value in discussing mental arithmetic in high school is that number sense and symbol sense can build on each other, leading to greater facility with and understanding of both algebra and mental arithmetic. The examples above have been chosen to illustrate this possibility. In beginning algebra classes, students often arrive at answers without using symbolic techniques. Furthermore, as these examples illustrate, informal or non-standard methods can reveal sophisticated algebraic reasoning, even though it might not be expressed symbolically. Rather than disregarding such informal methods as distractions from the goal of teaching standard algebraic methods, teachers can exploit informal methods as sources of meaning for students by establishing connections between informal and formal methods. Such connections can go in two directions. First, an informal method may be expressed symbolically, thereby promoting algebra as a way of expressing ideas about numbers. In this way, symbol sense may build upon number sense. Second, after some manipulation, symbolic expressions may be reinterpreted informally, thereby promoting algebra as a way of thinking about numbers. In this way, number sense may build upon symbol sense.
For experienced users of algebra, some of its power of comes from the fact that symbols may be manipulated without concern for their meaning. Nevertheless, for students and experienced users alike, periodic re-interpretation of symbolic expressions can shed new light on the context, its mathematical representations, or its mathematical structure, potentially leading toward an understanding of algebra that is more flexible for solving familiar and unfamiliar problems.
Mathematical Analysis
Each task is solved separately below.
1. It is easy to verify that the student's answer is indeed correct:
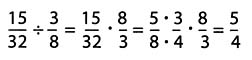
But the calculation does not shed much light on whether the approach makes sense. One way of explaining the approach is to note that if the calculation were 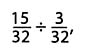 the answer would be 5, because 15 of anything divided by 3 of the same things is 5. But because we are dividing by 3/8, which is 4 times bigger than 3/32, the answer should be ¼ or 5, or 5/4.
the answer would be 5, because 15 of anything divided by 3 of the same things is 5. But because we are dividing by 3/8, which is 4 times bigger than 3/32, the answer should be ¼ or 5, or 5/4.
Another way to justify the approach is algebraic. The standard method is as follows:
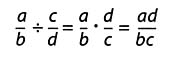
The student proposes that the answer is 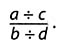
Simplifying this expression according to standard algebraic rules shows that the answer is indeed correct:
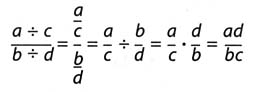
The awkwardness of the calculation, however, suggests that this approach, although correct, might not be efficient if, for example, c is not a factor of a.
2. Other employees might check the employee's answer. With 49 successes and 7 failures so far, and 14 future successes, the success rate will be:
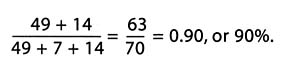
So her answer is correct. The deeper question is how to explain the employee's reasoning. Her reasoning is clear and understandable, too, indicating that there is probably a general procedure at work. What, then, is the relationship between her reasoning and the standard algebraic approach?
A typical way to solve the problem that the supervisor poses would be to let x represent the unknown number of subsequent (consecutive) orders to be delivered successfully within one week. Then,
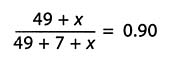
But this equation is hard to solve mentally. To generalize this approach, let x be as above, let r represent the desired success rate, let s represent the number of successes so far, and let f represent the number failures so far. Then, as before,
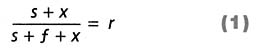
Solving this for x yields (after some manipulation):
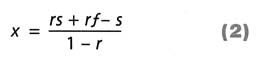
Though it is not immediately clear how to interpret this formula, the denominator, 1 - r, gives a clue about the employee's reasoning: if r is the desired success rate, then 1 - r is the desired failure rate, and the employee's reasoning began with the failure rate—10% in this case. Equation 1, which is based on successes, has an analog that is based on failures. Table 1 gives the analogous equation and several others that follow algebraically from it, along with explanations of how the equation might be interpreted.
TABLE 1: Equations relating successes and failures, with interpretations
|
 |
TABLE 2: More equations relating successes and failures, with interpretations
|
 |
The last equation in Table 1 is close to the reasoning that the employee described, and is a general procedure that may be done mentally. Thus, algebraic manipulation has provided justification for the employee's mental procedure.
Algebra can also provide suggestions for other mental procedures. Further algebraic manipulation of Equation 2, for example, gives additional possibilities, shown in Table 2.
The last equation in Table 2 gives another way to think about the original problem. Because the ratio of the desired success rate and failure rate is 90:10 or 9:1, there must be 9 times as many successes as failures. With 7 failures so far, there must be 63 successes, or 14 more than the 49 we already have.
Extensions
Traditional algebra problems can present similar opportunities for students to generate informal solutions. For example,

A student might say, "Well, I know from the second equation that Box is one more than Triangle. So I imagined that the Triangle in the first equation was a Box. Then the first equation would be Box + Box + Box + Box = 48. So, Box is 12 and Triangle is 11."
References
Dowker, A. (1992). Computational estimation strategies of professional mathematicians. Journal for Research in Mathematics Education, 23(1), 45–55.
Buying On Credit
Task
A credit card company, whose motto is "see the world on credit," charges 1.387% interest on the unpaid balance in an account each month, and requires a minimum payment of 2% of the outstanding balance each month. Suppose you charge $100 each month and make only the minimum payment each month. How much will you owe at the time of your 24th bill? Assuming you pay the whole bill at the end of that period, how much will be interest?
Commentary
Consumer debt is a big issue in this country. Thanks to the widespread availability of calculators and computers, consumers can easily do the calculations themselves to better understand the cost of maintaining credit card balances.
Powerful tools for this job are spreadsheets and programmable and graphing calculators. Mathematical analysis is still necessary, of course, but technology provides an avenue for mathematical modeling that gives students straightforward access to some mathematics that once required much more background. Once the spreadsheet is set up, students can explore different payment options and see the consequences. Spreadsheets can help demystify mathematics and provide an exploratory medium for doing calculations that are both relevant and meaningful for students.
Mathematical Analysis
The general mathematical structure of this task is the same as that of Drug Dosage (p. 80), and solutions can be obtained in similar ways. To analyze what happens when making only the minimum monthly payment, one might start with a table in order to obtain a recursion equation. That equation can be solved or used in a calculator or a spreadsheet.
In addition to charging interest on the previous month's unpaid balance, most credit card companies charge interest on new purchases, too, when the customer is carrying a balance. (The typical 25-day, interest-free grace period applies only if the entire balance is paid off each month.) The interest is usually computed based on an "average daily balance," so the actual amount of interest depends upon when the payment arrives and when the new charge is made. To simplify the calculations, assume that both the new charge and the payment come in at the end of the billing cycle and do not affect the interest that month.
To obtain a recursion equation, let xn be the amount of the nth statement. Because the minimum payment is 2% of xn, then, each month,
- the amount of the payment is .02xn,
- the interest charge is .01387xn, and
- there is an additional $100 of purchases.
So to find xn+1 (the amount of the (n + 1)st statement), the payment is subtracted from and the other amounts are added to xn, the amount of the nth statement:
or
To find out how much will be owed at the time of the 24th bill, start with x1 = 100, and repeat the calculation 23 times. Or, with a programmable calculator, define x1 = 100 and xn+1 by the formula given above and tell the program to calculate x24.
To calculate using a spreadsheet, begin with the first row which probably has cells named as shown in Table 1. In a spreadsheet, these cells might be used to contain the information shown in Table 2.
In the first month, there is no previous bill, no minimum payment, no unpaid balance, and no interest. Enter 100 in cell D1 representing the new charges and 100 in E1 to represent the balance at the end of month.1
In the second row, enter the numbers and formulas shown in Table 3. Then formulas for the next 22 rows are the same, except that the row numbers will change. Most spreadsheet programs will change the row numbers automatically if these cells are copied and then pasted into the next 22 rows. The spreadsheet will create a table similar to Table 4.
TABLE 1: Names of cells in a spreadsheet
|
A1 |
B1 |
C1 |
D1 |
E1 |
TABLE 2: How data might be organized in a spreadsheet
|
The previous bill |
The minimum payment |
The interest |
The new charges |
The new balance |
TABLE 3: Formulas for one row of the spreadsheet1
|
E1 |
.02*A2 |
.01387*A2 |
$100 |
A2-B2+C2+D2 |
The spreadsheet can total the columns, too, as illustrated. Table 4 shows that if you pay in the way suggested, you will have made $527.97 in payments on your $2,400 in purchases and still owe $2,238.18 because of $366.14 in interest.
If the calculations in Table 4 are correct, the purchases plus the interest minus the payments should give the outstanding balance.
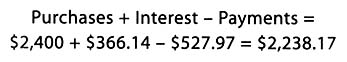
so the calculations are off by a penny somewhere. By asking the spreadsheet to display its results more accurately, it becomes clear that there is not a mistake, just "round-off" error.
TABLE 4: The completed spreadsheet2
|
MONTH |
PREVIOUS BALANCE |
PAYMENT |
INTEREST |
PURCHASES |
NEW BALANCE |
|
|
A |
B |
C |
D |
E |
|
1 |
|
|
|
$100.00 |
$100.00 |
|
2 |
$100.00 |
$2.00 |
$1.39 |
$100.00 |
$199.39 |
|
3 |
$199.39 |
$3.99 |
$2.77 |
$100.00 |
$298.16 |
|
4 |
$298.16 |
$5.96 |
$4.14 |
$100.00 |
$396.34 |
|
5 |
$396.34 |
$7.93 |
$5.50 |
$100.00 |
$493.91 |
|
6 |
$493.91 |
$9.88 |
$6.85 |
$100.00 |
$59.88 |
|
7 |
$590.88 |
$11.82 |
$8.20 |
$100.00 |
$687.26 |
|
8 |
$687.26 |
$13.75 |
$9.53 |
$100.00 |
$783.04 |
|
9 |
$783.04 |
$15.66 |
$10.86 |
$100.00 |
$878.24 |
|
10 |
$878.24 |
$17.56 |
$12.18 |
$100.00 |
$972.86 |
|
11 |
$972.86 |
$19.46 |
$13.49 |
$100.00 |
$1,066.90 |
|
12 |
$1,066.90 |
$21.34 |
$14.80 |
$100.00 |
$1,160.36 |
|
13 |
$1,160.36 |
$23.21 |
$16.09 |
$100.00 |
$1,253.24 |
|
14 |
$1,253.24 |
$25.06 |
$17.38 |
$100.00 |
$1,345.56 |
|
15 |
$1,345.56 |
$26.91 |
$18.66 |
$100.00 |
$1,437.31 |
|
16 |
$1,437.31 |
$28.75 |
$19.94 |
$100.00 |
$1,528.50 |
|
17 |
$1,528.50 |
$30.57 |
$21.20 |
$100.00 |
$1,619.13 |
|
18 |
$1,619.13 |
$32.38 |
$22.46 |
$100.00 |
$1,709.21 |
|
19 |
$1,709.21 |
$34.18 |
$23.71 |
$100.00 |
$1,798.73 |
|
20 |
$1,798.73 |
$35.97 |
$24.95 |
$100.00 |
$1,887.70 |
|
21 |
$1,887.70 |
$37.75 |
$26.18 |
$100.00 |
$1,976.13 |
|
22 |
$1,976.13 |
$39.52 |
$27.41 |
$100.00 |
$2,064.02 |
|
23 |
$2,064.02 |
$41.28 |
$28.63 |
$100.00 |
$2,151.37 |
|
24 |
$2,151.37 |
$43.03 |
$29.84 |
$100.00 |
$2,238.18 |
|
TOTAL |
|
$527.97 |
$366.14 |
$2,400.00 |
|

See Rounding Off (p. 119) for further discussion of this issue.
Extensions
The solution above made several assumptions to simplify the calculations. Some extensions can bring the solution closer to the way the credit card companies actually do their computations:
- For which of the above calculations is rounding necessary? Fix the table in the spreadsheet to properly account for rounding.
- For many credit card companies, the minimum payment is always a whole-dollar amount. Incorporate this idea into the solution.
- Expand on the solution above so that the dates of payments and new charges could be varied and so that the interest would be calculated according to an average daily balance. Investigate how the dates of payments and new charges affect the interest charges.
Other extensions could investigate alternative scenarios. Suppose, for example, you spent $2,400 up front and then made the minimum payment for each of 24 months. What would the accrued interest be?
The commentary mentioned that the mathematical structure of this task is the same as that of Drug Dosage (p. 80). Lottery Winnings (p. 111) also shares the same basic structure. Once students have sufficient experience with tasks like these, they might explore the difference and similarities among the procedures, formulas, and solutions of these tasks.
Notes
|


































