Nonlinear Ship Wave Calculations Using the RAPID Method
H.C.Raven (MARIN, The Netherlands)
ABSTRACT
The RAPID (RAised-Panel Iterative Dawson) approach for solving the fully nonlinear wave-resistance problem is described. This method, developed at MARIN, uses an iterative procedure based on a Rankine panel method similar to that of Dawson. No convergence problems are usually met in the speed and fullness range of practical ships, and even for cases showing extensive wave breaking in reality. The validity of the method regarding the occurrence of wave breaking and steep wave slopes is discussed. The modeling of the flow off a transom stern and its implementation in RAPID and in the corresponding linearized problem is studied. The nonlinear solution is found to be realistic and very accurate numerically. A number of validation studies shows that the RAPID results are very good in most respects, and often mean a surprisingly large improvement compared to linearized solutions. The principal remaining problems are resolution of short wave components, certain geometric complications, and the absence of a 3D model for wave breaking.
1. INTRODUCTION
Wave resistance is one of the most important resistance components of a ship, generally contributing 20 to 80 % of the total resistance of a ship sailing in still water. Experience has shown that this resistance component is quite sensitive to modifications in the design, and large reductions of the wave resistance can often be obtained without any important sacrifice in deadweight or cargo capacity. The effect of a bulbous bow is a well-known example. A capability to predict and minimize wave resistance in the design stage of a ship is, therefore, very desirable. Theoretical studies of the wave resistance problem have been carried out already for a century. Since Michell's paper of 1898, many studies of the linearized free-surface potential flow problem have been made, and several alternative solution methods and linearizations have been proposed; some of them very useful for a certain range of applications. Particularly in the early seventies much work has been done on this problem. In 1977, Dawson [1] proposed his well-known method, which in a number of comparative studies turned out to give realistic predictions, and to be more practical than most other proposals.
Much work has been done since on validation and improvement of Dawson 's method. There is a large body of literature on this method, and the mathematical background of the “engineering approach” has been more and more clarified. A code for Dawson's method is available at many institutes all over the world. Still, the actual use in commercial ship design work is quite limited. While at MARIN the code DAWSON [2] is being applied to 70 to 100 hull forms per year in commercial work and important successes have been obtained, most other versions of the method seem to be rarely applied.
As a matter of fact, the routine use at MARIN has made us aware of several shortcomings that make application more difficult. In particular, the resistance predicted by the code is not very reliable; for slender ships the estimate is usually fair, but for full hull forms the wave resistance is underestimated or even negative (a phenomenon explained in [3]). It is, therefore, not safe to optimize a hull form on the basis of the predicted wave resistance alone, as this sometimes even incorrectly indicates the order of merit of design variations. But at the same time the wave pattern and profile, the hull pressure distribution and flow direction have turned out to be realistic enough to be used for improving the design. Hull
form optimization using DAWSON is thus an art that requires insight in the assumptions made in the theory, knowledge of fluid dynamics and wave making, and much experience. Only few have collected enough experience to fruitfully use Dawson's method.
Although, therefore, the shortcomings of Dawson's method do not prohibit its very effective use, a next step has to be made. Not only a greater accuracy of the predictions is desired, but also we should like to include several aspects of the flow that cannot be taken into account in DAWSON. Specifically:
-
the neglect of nonlinear terms and transfer terms in the free surface boundary condition introduces inaccuracies;
-
the hull form above the undisturbed waterline cannot be taken into account in a linearized method; this eliminates the effects of bow flare, flat sterns, surface-piercing bulbous bows and so on;
-
doubts exist on the modeling of the flow off an immersed transom stern.
All these inaccuracies and limitations can in principle be removed by solving the fully nonlinear problem, rather than applying the slow-ship linearization underlying Dawson's method. At several institutes the development of a method for solving the fully nonlinear free surface flow problem is now in progress. Both panel or boundary integral methods, and field equation methods are used. The latter usually deal with viscous flows and almost invariably unsteady problems (or, at least, transient solution methods), and will not be discussed here.
The majority of methods for free surface flows around ships assumes a potential flow. Using Green's identity the problem is conventionally recast in a boundary integral form. There are many boundary integral methods addressing unsteady problems, e.g. [4,5]. Although in most cases the main purpose of the developments is to solve seakeeping or other actually unsteady problems, they may be applied to steady problems as well. One particular method to be mentioned here is that of Cao, Beck and Schultz [6] with its unconventional but very successful use of point sources at a distance above the free surface.
The most direct way to address the wave resistance problem is the solution of the steady free surface potential flow problem, which has been given much less attention. Most methods in this class are based on an approach similar to the linearized method of Dawson. This means that a distribution of Rankine sources or other simple singularities is used both on the hull and on a part of the free surface around it. For solving the nonlinear problem an iterative procedure is needed. Among the first to study such a method was Ni [7]. His method was Dawson-like, with panels on the free surface that were moved in every iteration. Although convergence was problematic, he succeeded to get converged solutions for a range of cases, subject to several restrictions on the use of particular difference schemes and so on. His method was later extended and improved in Larssons group [8]. Later Kim and Lucas [9] came up with a very similar approach, but found it necessary to apply artificial numerical damping in order to obtain convergence. In [10] they proposed a modified double iteration scheme which was claimed to improve the convergence. Another method was proposed by Delhommeau [11], also using panels on the free surface. Convergence again turned out to be problematic.
At the same time, some other developments were based on the use of singularity distributions not on but above the free surface. This choice was inspired by obvious practical advantages for the problem considered. One of the first efforts was due to Xia [12], who describes some initial attempts to solve the nonlinear problem. However, a too large sensitivity to the distance from the panels to the water surface made him give up. Much more successful were Jensen et al [13,14] with their method using point sources above the wave surface, analytical second derivatives and a special way of satisfying the radiation condition. In several further publications the method has been extended to shallow water, channel flows, unsteady cases in the frequency domain etc. At the same time, convergence of the method still can provide severe problems as soon as e.g. different panel distributions are used.
In [15,16], the present author proposed the so-called RAPID approach (RAised Panel Iterative Dawson). The use of free surface source panels raised above the free surface is largely similar to Jensen's method; but most details are different. The iterative procedure, selected on the basis of previous numerical estimates of the different nonlinear contributions [3], has appeared to be unusually stable and robust: Contrary to almost all previous methods for the same problem, no convergence problems are generally met. It thus seems to be one of the most practical methods, and, together with Jensen's method, it seems to be the only code for the nonlinear problem that is already actually applied in ship design work.
This paper describes recent progress in the further development and validation of the RAPID code. In [16], the essence of the method was explained and the results of several numerical experi-
ments were discussed. This will briefly be summarized in the next section, paying some more attention to the convergence properties and to the importance of nonlinear effects. Section 3 is devoted to a discussion of the flow off an immersed transom stern. The various flow regimes are studied, and the implementation of the transom flow model in both the linearized (DAWSON) and the nonlinear (RAPID) code are described and compared. Section 4 then discusses a number of detailed validation studies.
2. RAPID
2.1 The mathematical model
We consider the flow around a ship hull in a uniform flow from ahead. The origin of our coordinate system is located amidships at the level of the undisturbed free surface. The x-coordinate is positive astern, and y is positive in upward direction. The coordinate system does not move with the dynamic trim and sinkage of the ship. All quantities are nondimensionalized with the ship speed and length.
The potential flow assumption is made, and a velocity potential ![]() is introduced such that:
is introduced such that:
(1)
The field equation to be satisfied is the Laplace equation. The flow is undisturbed far ahead and at large lateral distances, while a wave pattern with a known rate of decay is present downstream.
On the wetted part of the hull the flow must be tangential to the hull, as represented by a Neumann boundary condition for the potential:
φn=0 (2)
On the free surface a kinematic boundary condition is to be satisfied, requiring that the flow is tangential to the wave surface:
φxηx+φyηy−φy=0 on y=η (3)
and a dynamic boundary condition that the pressure in the flow at the free surface must equal the atmospheric pressure (4):
![]() on y=η (4)
on y=η (4)
2.2 Iterative solution
Contrary to what is done in linearized methods, these boundary conditions will be applied on the correct surfaces; i.e. the hull condition on the part of the hull that is actually wetted, and the free surface conditions on the actual wave surface. No simplifications are thus made. Solving this fully nonlinear free surface problem requires iteration. The iteration procedure is set up as follows.
While in a linearized method such as DAWSON the flow field and free surface are decomposed into a known base flow and a small perturbation, and linearization in terms of this perturbation is performed, we now make a similar assumption that the solution of a certain iteration differs only by a small amount from the flow field and free surface shape found in the previous iteration. Again we linearize in terms of this perturbation and impose the boundary condition at the previous free surface. Thus we obtain a linear fixed-domain problem to be solved in the current iteration. Having found the solution we update the base flow field and free surface, and start the next iteration.
Specifically, defining
η=H+η′ (5)

(6)
and substituting this into the dynamic and kinematic boundary conditions, we obtain linearized kinematic and dynamic conditions:
(7)
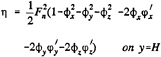 (8)
(8)
These two conditions are combined in exactly the same way as in Dawson 's method by eliminating the wave height perturbation, and we obtain the linearized free surface condition (FSC) to be imposed on the wave surface found in the previous iteration:
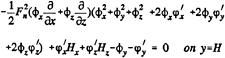 (9)
(9)
It is noted in passing that actually a consistent linearization would add certain terms representing the transfer of the boundary condition from the free surface to be calculated, towards the free surface found in the previous iteration. These terms are intentionally disregarded here, as they have been found to be rather irregular for the source distribution employed here and might lead to divergence of the iteration. To the converged solution these terms
make no contribution of course, since η' then vanishes and the FSC is imposed on the actual free surface.
Once the linear problem of the current iteration has been solved, the velocities found are substituted in the original dynamic condition (4), and a new free surface is found. This, together with the new velocity field, is the basis for the linearization of the next iteration.
This iterative process is started from any initial guess. As no assumptions have been made on the relation between the base flow field and the base free surface, this initial guess can be selected on the basis of convenience only. In most cases we start simply from a uniform flow and flat free surface; the first iteration thus becomes the Neumann-Kelvin problem. The iteration is repeated until the residual errors in both the dynamic and the kinematic boundary conditions are below a predefined tolerance in all free surface points (i.e. a maximum norm is used). In most cases, we impose tolerances of 0.1 % of the ship speed for the kinematic condition, and 0.2 % of the stagnation pressure for the dynamic condition. It is important to note that checking these residuals is the only safe procedure; visual inspection of the changes in a hull wave profile, as is often done, does not guarantee that the solution has converged !
2.3 Implementation
To implement the mathematical model outlined above, singularity distributions are specified for all boundaries where non-trivial boundary conditions are to be imposed, i.e. the wetted part of the hull and the surrounding part of the wave surface. On the hull the familiar distribution of quadrilateral constant-strength source panels is used, with collocation points in the panel centroids. For the free surface however, a less conventional choice has been made: quadrilateral constant-strength source panels are located at a certain distance above the wave surface, while the collocation points are on the wave surface itself. Within certain limits for the distance of the panel to the free surface this is permitted theoretically, and it has several practical advantages:
-
as there is freedom in the distance from a panel to the corresponding collocation point, the panels need not be repositioned in each iteration; only the collocation points are moved towards the new free surface position. This saves some work and avoids potentially destabilizing geometric manipulations;
-
the velocity field in the fluid domain is smoother than with constant-strength source panels on the boundary itself;
-
the numerical dispersion (i.e. the error in the wave length due to the discretization of the continuous velocity field and boundary condition) is far smaller than with the usual implementation;
-
the outer boundaries of the free surface domain are less reflective.
-
the implementation is simplified on several points.
There are, however, some disadvantages as well:
-
the conditioning of the system of equations is slightly worse; by a proper selection of the panel elevation this can, however, be minimized.
-
if the section shape has a large slope above the waterline, the collocation points right under the centers of the free surface panels adjacent to the hull are at a rather large distance from the waterline, with resulting inaccuracy. If the collocation points are kept at a constant distance from the actual waterline, the free-surface boundary condition is better resolved, but the conditioning is worse. This trade-off can present some problems, in particular for flat sterns, fter all, the use of raised panels has turned out to be extremely effective for this class of problems.
The limits of the distance from the panels to the free surface are, as shown in [16], roughly between 0.5 and 1.5 panel dimension. Here the panel length is more important than the transverse size. It will be obvious that the distance cannot be kept inside these limits if the panels are not adjusted to the free surface shape. E.g. the stagnation height at a ship speed U is U2/2g, and for a usual panel density of 20 panels per transverse wave length this is 1.6 times the panel length. Therefore, as described in [16], the free surface panel distribution must be adapted to the wave surface such as to stay at a more or less constant distance. But there is no need to do this very accurately, as the distance only has to be kept inside the limits mentioned before. Therefore, the calculation is made in separate jobs of 2 to 6 iterations, each time followed by an automatic adaptation of the free surface paneling to the last calculated wave shape, and of the hull paneling to the modified intersection with the free surface panels. If desired, the position of the hull is adapted to the new estimate of the trim and sinkage. Then the process is restarted from the results of the previous iteration. In this way, the efficiency and stability of the process is kept while a good conditioning and accuracy can be guaranteed.
Another detail of the implementation to be mentioned is the use of an upstream difference scheme for the derivatives of velocities in the free surface condition. This is exactly similar to the use in Dawson's method, and helps the satisfaction of the radiation condition at the expense of a small
numerical damping. The detrimental effect of this damping can be minimized by choosing a sufficient panel density. On the other hand, in order to increase the numerical accuracy at a given panel number, the use of a difference scheme might be dispensed with in the future.
The complete iterative procedure can be summarized as follows:
-
Define the initial hull and free surface panel distribution; choose the distance of the panels above the free surface.
-
Choose an initial free surface velocity distribution and wave elevation.
-
Impose the combined FSC, linearized with respect to the last free surface shape and velocity field, in the free surface collocation points; and the hull boundary condition in the hull points;
-
Solve the linear problem. Calculate the new free surface and velocity field;
-
Move the free surface collocation points to the new wave elevation, applying underrelaxation if desired;
-
If needed, adapt the free surface paneling to the new wave surface; adjust the hull paneling; adjust trim and sinkage of the hull.
-
Calculate the residual errors in all points, and decide to stop or to return to step 3.
2.4 Convergence and calculation time
As described in [16], the method displays
-
a good convergence with respect to increasing panel density;
-
only very little effect of the distance of the panels to the free surface;
-
a robust and easy convergence of the iterative procedure, without any tuning, smoothing or filtering.
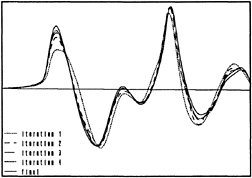
Figure 1. Convergence of hull wave profile
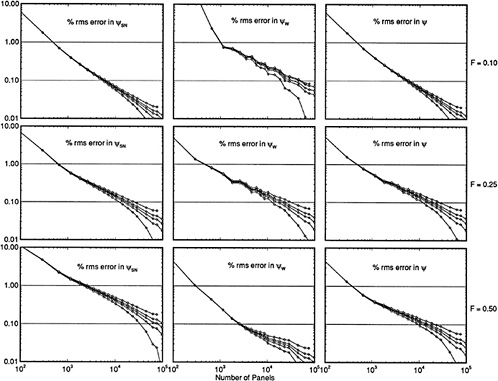
Fig. 1 illustrates the convergence of the hull wave profile for a Series 60 Cb=0.60 hull at Fn=0.316, with a very dense paneling. 12 iterations were required to reduce the residuals to the desired level, but already after 4 iterations the hull wave profile is very close to the final solution.
An example of the convergence history is shown in Fig. 2, in which the logarithms of the maximum residual errors in the kinematic and dynamic boundary conditions are plotted against the iteration level.
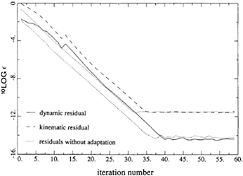
Figure 2. Convergence history with and without free surface panel adaption
The convergence rate is constant after the initial iterations, and the residuals are reduced until a minimum level determined by the machine accuracy is reached. For the kinematic residual this level is higher than for the dynamic residual as can be understood from its more complicated expression.
The same case was run with the method without any free surface panel adaptation. From Fig. 2 the convergence appears to be slightly faster; the free surface panel adaptations in the original method at iterations 4, 8 and 13 slightly delay the error decrease as a result of e.g. the geometric changes. On the other hand, adaptation from time to time is unavoidable if one wants to use a fine paneling for steep waves and still have convergence. It is noted that methods using panels on the free surface itself are forced to apply such panel adaptations in every iteration. That a raised-panel method makes it unnecessary to do so may be one of the explanations for its robustness.
The code currently runs on a CRAY-YMP supercomputer. Calculation times vary widely according to the number of panels. To give some examples:
|
# hull panels |
# FS panels |
CP sec/iteration |
|
340 |
540 |
2.7 |
|
680 |
1056 |
17 |
|
624 |
2312 |
100 |
These calculation times can probably be reduced substantially, but this has not been given priority up to now.
The number of iterations to reach the prescribed level of residual errors usually varies between 5 and 15, dependent on the difficulty of the case. On the basis of a visual inspection of the results, the calculations would probably be terminated after 5 iterations in most cases.
2.5 Nonlinearities and wave breaking
At the 1992 Symposium on Naval Hydrodynamics, discussers of [16] indicated some restrictions of this class of nonlinear solution methods. In the first place, methods that describe the free surface as a single-valued function of the two horizontal coordinates cannot cope with extreme wave slopes, which was stated to be an important drawback in practice. Thus such methods could impossibly converge in cases in which wave breaking occurs in reality, according to these discussers. And even, because of the above, this class of solution methods would be limited to so-called “weak singularities”. Similar statements can be found in [17].
As not all of these statements seem equally true, it may be useful to pay some more attention to the validity of the present method. Let us consider the physical phenomena that occur for steep waves. Most steady breakers are similar to spilling breakers: a region of turbulent flow with air entrainment, riding steadily on top of the wave pattern that otherwise remains relatively smooth. There are several experimental indications that this steady breaking occurs already at a smaller wave steepness than the Stokes limiting wave; but even the latter is described as a single-valued function of the horizontal coordinate. According to Duncan [18], wave breaking induced by a submerged hydrofoil occurs for wave slopes exceeding 16 to 24 degrees. That perhaps the spilling breaker itself has a very large local surface slope is a different issue, as the breaking will require another modeling anyway. But we can conclude that the potential flows giving rise to this kind of wave breaking and underlying the breaking zone can be easily described using a single-valued free surface; and that excessive wave slopes that cannot be described will rarely occur in reality because wave breaking eliminates them.
The next question is then: is it possible to compute waves so steep that breaking occurs? As mentioned above, some discussers expected that divergence would prohibit such calculations. In principle, I see three possibilities:
-
the iteration does not converge;
-
it converges, but a grid-independent solution cannot be obtained;
-
it converges, but to a non-breaking solution that is not physically realizable.
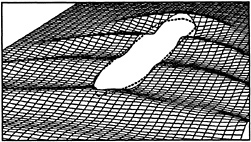
Figure 3 Calculated wave pattern for a tanker at Fn=0.25
Based on results obtained up to now the third option seems most likely, and we can at least reject the first possibility. As an example, Fig. 3 shows the wave pattern found for a tanker with a block coefficient of 0.83, at the unrealistic Froude number of 0.25. A converged solution was fairly easily obtained, although there is no doubt that extensive wave breaking will be present, e.g. in the wave trough behind the bow wave: The calculated local wave slope is almost 30 degrees, and the ratio of peak-to-trough wave height to wave length is 0.16. Both exceed known threshold values for inception of breaking. The panel length was 0.04 transverse wave length here, but grid independence has not been checked thoroughly for this case.
Similarly, in [10] a converged solution was obtained for a Series 60 CB=0.80 model at Fn=0.30, although on a rather coarse free surface grid.
Therefore wave breaking does not necessarily lead to divergence of the iteration process, and nonlinear methods like the one presented here can be a useful tool also in cases with wave breaking. But for completing the flow picture a separate criterion is required to determine whether a potential flow solution in practice will give rise to wave breaking, and some model of the breaking should eventually be incorporated. A proposal for such a model in 2D is [19].
The above example also illustrates that RAPID is stable enough to solve the nonlinear potential flow problem for all realistic speeds. At the same time it refutes the statement that these methods can only deal with “weak nonlinearities”. I am not aware of the existence of a clear definition of the latter, but I would not call the nonlinearities in this example
weak. The calculated peak-to-trough wave height is as large as the draft of the vessel and vertical velocities exceed 45 % of the ship speed.
Of course, other types of wave breaking occur. A sharp ship bow may act as a sort of ploughshare and induce a flow similar to a plunging breaker. This behaviour is definitely outside the reach of RAPID and all similar methods. Other methods, usually time-dependent, with a more general free surface description, have been applied to plunging breakers and do give a picture of the flow up to the moment of impact of the jet on the free surface. But then they stop ! Consequently also those methods have to be supplemented by some kind of local model for the plunging-type wave breaking and its effect on the flow field. In that respect they may have only a small advantage compared to the present approach.
An interesting related point of discussion is the question what happens if the discretization is further and further refined towards the bow. Again the same three pitfalls seem possible: divergence, unresolvable grid-dependence or an unphysical solution. The problem can be studied a little bit further by invoking the similarity between the steady flow at a sharp ship bow and a time-dependent 2D flow in cross planes. For a bow with a finite entrance angle the corresponding 2D case is that of an impulsively started wavemaker. From small-time expansions a logarithmic singularity in the wave elevation has been shown to exist in that case, representing a jet shooting up along the wavemaker. Numerical studies using time-dependent fully nonlinear boundary integral methods, e.g. [20,21] actually reproduced this behaviour. The finer the paneling, the higher the jet, and no grid-independence could be reached. But this is extremely localized, and the result at very small distances away from the wavemaker and everywhere else is totally unaffected by the grid dependence at the intersection. Analogously, and keeping in mind that in 3D steady flows singularities are likely to be weaker than in 2D time-dependent flows, I expect that for sharp bows in fact eventually no convergence will be obtained in RAPID if the discretization is refined towards the waterline; that locally no grid-independent solution or even no physically correct solution may thus be reached; but that the resulting error will be extremely localized and unimportant from the point of view of the global flow field. For almost all practical applications this theoretical drawback is then of no interest. Although there is some speculation in these statements, current experience with the method actually points in this direction. Further study is desired.
All this does not mean that the method proposed here is the final answer; but, subject to certain improvements in resolution and in numerical details, it may be the answer to most of the practical questions that can be dealt with using potential flow assumptions.
3. THE FLOW OFF A TRANSOM STERN
3.1 Physical Phenomena
As most current ship forms have a transom stern, the capability of a method to handle transom flows is of primary importance. In linearized methods the hull form above the undisturbed waterline has no effect, and transom sterns above the design waterline are usually not treated as transom sterns. But in a nonlinear method transom flow modeling is also required for all those cases in which a transom becomes immersed only at speed.
For ships having a transom stern, three flow regimes may be distinguished:
-
the “regular” type of flow, which is similar to the flow past a cruiser stern. This type of flow will occur if the transom is at a sufficient distance above the undisturbed free surface. Dependent on the hull form the last part of the actual waterline in potential flow may be either a streamline or an envelope of streamlines that leave the hull tangentially and continue on the free surface. At the smooth detachment of the free surface from the hull surface, both the hull boundary condition and the two free surface boundary conditions must be satisfied. Unless the detachment is in a stagnation point, this means that the flow leaves the hull tangentially.
-
the “transom flow”, occurring for immersed transoms at a sufficiently high speed. At the transom edge the hull streamlines leave the hull and continue on the free surface. The negative hydrodynamic pressure needed to make the pressure at the transom edge atmospheric is achieved by an upward curvature of the flow immediately aft of the transom edge, resulting in a more or less marked “rooster tail”.
-
The flow around a deeply immersed transom at low speed. At the sharp convex corner of the transom edge, viscous flow separation occurs and a dead-water region aft of the transom is formed.
The transitions between the various flow regimes are practically relevant, as a dead-water region is to be avoided, and a transom that is at a too high position as well. Let us further consider what phenomena determine these transitions. Suppose a regular flow type occurs, with the transom above the
water surface, and we increase the draft of the vessel. The detachment position is likely to move aft and at some moment reaches the transom edge. The streamline shape then further adjust so as to maintain a zero pressure at the edge. While in regular flow the curvature is bounded at detachment, this need not be true in the transom flow.
For a further increasing transom depth or for decreasing speed the hydrodynamic pressure coefficient required to balance the hydrostatic pressure at the transom edge increases in absolute value, and the upward curvature of the streamlines must increase. A very steep forward face of the wave aft of the transom results, eventually giving rise to a spilling breaker following the transom at a short distance. At still lower speed or greater draught this closes upon the transom and forms a dead-water zone.
From these preliminary considerations, we can list the requirements of the “ultimate” nonlinear potential flow model:
-
it should contain a model for at least the regular and the transom flow;
-
it should indicate the transition from a regular to a transom flow and reversely;
-
it should preferably indicate the transition from transom flow to dead-water flow.
If not all transitions can be incorporated in the code, one may try both flow regimes and check for anomalies. We can immediately note that point III will perhaps still be impossible to realize. If it is true that wave breaking determines this transition, a proper breaking criterion will be indispensable. Furthermore one should be aware of possibly large viscous effects on this transition. Moreover, point II requires the ability to compute the regular flow for extremely flat afterbodies; this is a very high demand for any iterative nonlinear method, as a small change of the wave elevation then results in a very large (and destabilizing) shift of the waterline.
Below, we shall consider the modeling of the transom flow in linearized and nonlinear models, and discuss the question of the transitions.
3.2 Mathematical Modeling
There seems to be some confusion about the type of modeling appropriate for transom flows. The boundary conditions to be imposed are fairly evident: on the hull the flow again must be tangential, and on the entire free surface it must be tangential and have a zero pressure. That there are two boundary conditions on the free surface corresponds with the additional degree of freedom there, the elevation of the free surface. At the transom edge however, the confluence of boundary conditions poses some problems. The two kinematic conditions can be reconciled if the flow leaves the hull tangentially. But as the edge location is fixed, the degree of freedom due to the wave elevation seems to be lost. How to impose the dynamic boundary condition?
This apparent overspecification of the problem reminds of the flow around a lifting body, in which circulation provides the additional degree of freedom. The analogy with a Kutta condition, which also imposes an extra condition on the flow at a sharp corner, has sometimes been invoked. Consequently, trailing vortex wakes or dipole sheets are introduced, e.g. in [22]. But the success of such an implementation could not be shown convincingly; in [22] the use of source panels on the transom instead of a trailing vortex wake led to almost identical results.
Another proposal for modeling transom flows is [23], which deals with slender hulls at very high speeds. Also here the necessity of introducing trailing longitudinal vorticity on the free surface is advocated. However, this vorticity appears not to result from the presence of a transom but from the use of a reverse image of the flow above the still water surface, as is appropriate in the infinite-Froude-number limit. The same trailing vorticity would in this model be required for hulls without transom. The slender-body formulation adopted causes this boundary vorticity to extend to downstream infinity with constant strength.
To study the meaning of trailing vorticity for transom flows, let us first consider the flow around a two-dimensional body with a transom stern. The flow domain is bounded by the hull and the free surface which originates from the transom edge. Therefore the domain is singly connected, and there cannot be any unknown circulation around the body.
In a three-dimensional case the situation is similar. Is there any reason why the three-dimensionality would suddenly introduce spanwise vorticity? If it would, trailing longitudinal vorticity would in fact also be present. However, this vorticity would start at the transom edge, i.e. on the free surface, so it would remain on the free surface; on the boundary of the fluid domain therefore. There is no cut in the domain, no additional degree of freedom, and the boundary vorticity has no physical effect on the flow field in the domain at all; it just affects the form of the Fredholm equation to be solved.
Therefore, in my opinion the use of a trailing vortex wake for transom flows, although perhaps
numerically helpful in some models, cannot be given any physical meaning. Rather than pointing out the analogy with the Kutta condition we might consider free streamline theory, as applied to e.g. the cavity or wake flow behind a flat plate at large incidence. Although the neglect of gravity may well affect some of the conclusions, free-streamline theory tells that the flow leaves the transom edge tangentially, but with infinite curvature. Even more illuminating is [24], in which for a flat-ship linearization in a 2D free-surface potential flow around a semi-infinite body the behaviour at the transom edge is derived. Again, the conclusion is that the slope of the streamline is continuous (tangential flow), but that the curvature tends to infinity at the edge. Specifically, the free surface shape aft of the transom is described as follows:
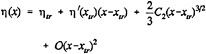
(10)
where ηtr is the height of the transom edge and the coefficient C2, which can be expressed in the hull geometry, is the degree of freedom required to satisfy the dynamic condition. Although the details of this result may be a consequence of the necessary simplifications and linearization, this study suggests that all transom conditions can be satisfied without any physical vorticity; that the additional degree of freedom is the streamline shape at the transom edge; and that a more or less singular behaviour at the edge may result.
3.3 Implementation
We shall now discuss the implementation of transom conditions. Because of the mentioned lack of general agreement on the proper modeling it seems useful to study the implementation in a linearized method as well. This has been used already for several years in the DAWSON code and provided good guidelines for the nonlinear implementation which we shall consider subsequently.
It is interesting to note that implementing transom conditions in a linearized method is basically inconsistent. Linearization assumes that the variation of the hull shape near the undisturbed waterline is small; i.e. a small curvature, and in slow-ship theory also a small slope of the sections and buttocks. Only then the exact position of the hull—free surface intersection has a negligible effect on the flow and linearization is permitted. However, at a transom edge the hull curvature is infinite, and we want to have a particular hull—free surface intersection. Nevertheless a quite reasonable representation of transom flows appears to be possible in linearized methods as well.
In the hull paneling the transom is left open. The free surface panel distribution is adapted to the transom by the addition of a few extra strips of panels aft of the transom. One might think of imposing transom conditions in points right at the transom edge; but with the usual constant-strength source panels on the hull the velocity field is singular here in the discretized formulation. Therefore transom conditions are to be imposed in the first collocation points aft of the transom.
In the linearized problem we can only impose one single FSC, a combination of the kinematic and dynamic FSC. The usual FSC is derived by expressing the term ηx in the kinematic condition in the wave elevations η in the point considered and a few upstream points using a difference scheme; and expressing these η's in the velocities through the dynamic condition. In this process any abritrary pressure added to the dynamic condition drops out; in other words, the combined form actually means that in the free surface collocation points the velocity must be parallel to the isobar surface passing through that point, but the pressure corresponding to that isobar surface is eliminated. The wave elevation is only retrieved afterwards from the dynamic FSC. Thus the ordinary form of the FSC makes it impossible to impose any condition on the wave elevation at or near the transom itself, and the free surface will most likely start somewhere at the transom face.
The solution of this difficulty is well known: the FSC must be modified so as to avoid elimination of the pressure level. This is easily achieved by imposing in the first collocation points the condition that the velocity must be directed parallel to a line from the transom edge to the wave elevation at the point, e.g.
(11)
The same transom condition can be derived by substituting into the usual FSC the velocity required for zero pressure at the transom edge.
Instead of the two-point formula for ηx, higher-order expressions may be used. These require that an assumption is made on the local behaviour at the edge. Two alternatives have been tried:
-
the behaviour according to Schmidt [24], (10)
-
a simple Taylor expansion in the transom edge point
The former has been derived from a flat-ship linearization and is, therefore, not necessarily appropriate here; but it allows an infinite curvature at the edge. The second formulation is generally applicable to regular behaviour aft of the transom edge.
With this simple modification the transom conditions to be imposed in the first points of the free surface strips aft of the transom are in principle complete for a linearized method. For the second points, in the FSC the same three-point difference scheme is used as everywhere else. This involves again the transom edge height. For all downstream points no modification is needed.
One should notice that in principle this treatment of the transom conditions does not guarantee that the solution satisfies the zero-pressure condition at the transom edge; and if not, it does not satisfy the kinematic condition in the first free surface point either. However, a mechanism that physically governs the transom flow is incorporated. The inherent continuity of solutions of the Laplace equation will make the flow leave the transom more or less tangentially. If the wave elevation in the first free surface points aft of the transom deviates from this tangent, a large streamline curvature at the transom edge results, inversely proportional to the square of the distance from the transom to the first points. This curvature adjusts the pressure at the edge and the wave elevation. Thus upon panel refinement the wave height at the first free surface collocation points will be forced to approach the transom edge. How appropriate this FSC is for finite panel sizes can only be deduced by numerical experimentation. The quality of the linearized predictions will be studied in Section 3.4
The implementation of the transom edge conditions in the nonlinear method is actually quite similar to that outlined above. As again no collocation point can be located at the transom edge itself, the free surface conditions are imposed at a small distance aft of the transom. Again, the free surface slope to be substituted in the FSC is expressed in the difference between the transom edge height and the Bernoulli expression for the collocation point, through one of the alternative expressions. The free-surface boundary conditions are now linearized with respect to the previous iteration; and the iterative procedure will converge to the fully nonlinear solution.
It was found that the convergence of the iterative procedure is excellent. As the transom edge is a fixed point in the result, extremely large errors in the dynamic and kinematic boundary conditions are found initially if one starts from a flat free surface. But the fact that this point is fixed also appears to stabilize the results locally, and convergence presents no problem at all.
Although basically the linearized and nonlinear treatment of the transom conditions is similar, it is a significant advantage of the latter that the nonlinear terms and transfer terms are fully included. These can be very large, in particular for low transom depth Froude numbers, when large vertical velocities and large free surface curvature occur near the transom. Moreover, since the nonlinear method imposes the exact free surface boundary conditions, we can be more confident that the physical mechanisms governing the transom flow are fully included.
3.4 Results
As the actual behaviour at the transom edge in a 3D nonlinear case is not known, I have chosen the following path for verifying the method. I see two possible causes why it might give erroneous results. The first is discretization; therefore careful grid refinement studies have been carried out. The second would be an incorrect modeling of some kind of singularity at the transom edge. The importance of this will be studied by comparing the results found with different assumptions on the flow behaviour at the edge.
For the panel refinement study, the test case (Fig. 4) is a mathematical hull form with rectangular sections with a rounded bilge; parabolic waterlines in the forebody; an afterbody that is prismatic up to x =0.25 L, and has a bottom slope of 1: 0.16 aft of this point.
Figure 4. Mathematical hull form with transom
The panel refinement study discussed here addressed a case with a Froude number of 0.40 and a transom immersion of 0.01 L. The Froude number based on transom depth is 4.0, which may be just sufficient to make the flow clear the transom.
Let us first look at the results of the linearized
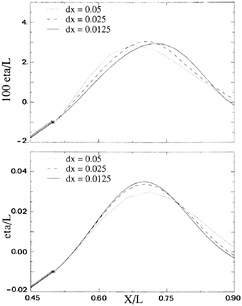
Figure 5. Wave profile behind transom, for 3 panel densities; linearized (top) and nonlinear (bottom)
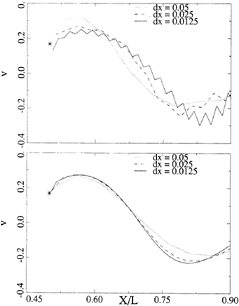
Figure 6. Vertical veloctiy behind transom, for 3 panel densities; linearized (top) and nonlinear (bottom)

Figure 7. Calculated wave pattern for transom stern hull; nonlinear method
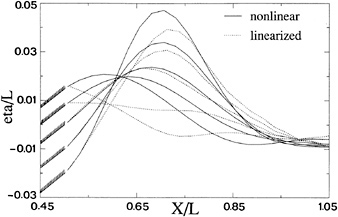
Figure 8. Wave profile for varying transom edge height; linearized and nonlinear method
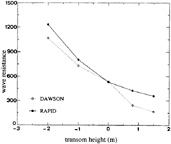
Figure 9. Wave resistance against transom edge height; linearized and nonlinear method
(DAWSON) code. Fig. 5 (top) shows the predicted free surface shape aft of the transom on the line of collocation points closest to the centerline, for hull and free surface panel lengths of 0.05 L, 0.025 L and 0.0125 L respectively. Some grid dependence appears to be there, with a downstream shift of the wave crest but not too much change in amplitude. Fig. 6 (top) shows the vertical velocity on this same line. The marker indicates the value at the transom edge, deduced from the dynamic condition and the transom slope. The value found on the free surface aft of the transom is too high for the coarser panelings, and too low for the finest distribution. The latter result may be due to the large oscillations in the vertical velocity that are typical for the Dawson-type of discretization at small panel sizes. 80 panels per wavelength is, by the way, not a density one would use in practice. Anyhow, the linearized transom modeling seems to give a qualitatively correct behaviour, but its accuracy is not quite convincing.
For the corresponding nonlinear (RAPID) calculations, the results are shown in Figs. 5 and 6, and Fig. 7. The calculated flow is absolutely smooth and satisfies both transom conditions accurately: no deviation is visible on the scale of the paneling. The convergence of the wave profile for decreasing panel size is very good, and there is hardly any difference between the two finer panelings. In particular the behaviour just aft of the transom is perfect. The vertical velocity converges well and consistently matches the transom edge value indicated.
We thus find that, as panel refinement has very little effect on the solution, we can be confident that the exact FSC's are accurately satisfied in all points on the free surface (not only the collocation points) in the converged nonlinear solution. But an exception must be made for the point right at the transom edge: no collocation point is present here, and if some sort of singular behaviour occurs, panel refinement could in principle give convergence towards an erroneous solution. Therefore the effect of the choice of the flow model at the edge has been considered. But the difference between the results obtained with the Schmidt- and the Taylor expression was only quite local and too small to be distinguished on the scale of the plots. In both cases the calculated vertical velocity was continuous (tangential flow), but with a discontinuous ∂v/∂x and a discontinuous but finite curvature of the free surface streamlines. This does not exactly correspond with the Schmidt theory, but does allow a Taylor expansion.
Since, therefore, the particular assumptions on the behaviour here have only a very small and localized effect, we may conclude that this detail of the modeling is not too important and is very unlikely to lead to an erroneous solution globally. Thus the method proposed is adequate.
Next, we study the effect of the transom depth on the predictions. The draft of the ship is varied to obtain the transom heights—0.02 L, −0.01 L, 0., 0.008 L and 0.015 L (positive is above the still water level). Fig. 8 shows the wave profile on the centerline behind the transom predicted by DAWSON and RAPID. In all cases the free surface correctly starts at the edge. The wave profiles predicted by DAWSON and by RAPID are remarkably close for all immersed transoms. The nonlinear predictions have a somewhat higher and steeper stern wave, with a difference of up to 20 %. The greater the transom immersion, the stronger the nonlinearity. But, fortuitously or not, the several nonlinear contributions, each very large for the large vertical velocities occurring (up to 40 % of the ship speed), appear to cancel to a substantial extent; the difference between DAWSON and RAPID is therefore relatively moderate.
For the cases with the transom above the still water level however, the difference between DAWSON and RAPID is much larger. The rooster tail suddenly disappears in DAWSON as soon as the transom edge comes above the still water line. As the still water level is of little meaning for the local flow, there is no physical explanation for this drastic change. As opposed to this, in RAPID the height of the rooster tail continuously decreases, which must be the proper behaviour.
Similarly, all RAPID calculations display the correct free surface slope at the edge, corresponding to a tangential flow off the hull; while in the DAWSON predictions only the cases with the transom edge on or below the still water level have the correct slope. The same tendencies are found in the predicted wave resistance (Fig. 9). For DAWSON, a contribution
has been added, which in an ad hoc fashion accounts for the absence of hydrostatic pressure on the transom. Although entirely inconsistent, this correction appears to bring the resistance fairly close to the nonlinear result (which does not require such a correction because the total pressure is integrated over the hull). At zero transom immersion the two predictions are almost equal. The cases with transom above the still water surface again show a deviation in the DAWSON results.
The explanation of the bad linearized predictions for transoms above the still water level is of course that the hull must be cut off at the undisturbed water level in a linearized method. The hull paneling then ends at some point ahead of the transom. While the transom conditions in the first free surface collocation points can be imposed just as well if the transom height is positive, no boundary condition can be imposed on the part of the hull bottom above the still water level. But, because of the double-body linearization and the symmetry with respect to the still water level, imposing no boundary condition is the same as imposing a zero vertical velocity on this part of the water surface! This may be an acceptable approximation for cases with small buttock angle near the transom, but not for the present case where the vertical velocity should be around 0.16.
Summarizing, for the cases studied the results with the linearized method appear to be quite reasonable for all immersed transoms, with a moderate deviation due to nonlinear effects; but for transoms above the still water level the representation of the flow off the transom edge is relatively poor.
The RAPID solutions however are very accurate and satisfy all boundary conditions to the degree to be expected. Even for transoms above the still water level the hull shape near the transom is completely taken into account. Optimization of the transom immersion and stern shape seems to be possible now throughout the practical range.
Remains the question to what extent the transitions to the other flow regimes (dead water and early detachment) are indicated by the nonlinear calculations. As expected, the transition to a dead-water zone is not indicated as no criterion for the inception of wave breaking is included. In [25], the nonlinear stern waves behind a flat bottomed semi-infinite two-dimensional body have been studied theoretically, and it was derived that a solution with the free surface detaching from the transom edge exists only for a transom depth Froude number exceeding 2.23; and that breaking occurs for all Froude numbers below 2.26. Hoping to find anything particular I made calculations for a flat-bottomed finite-length 3D ship with a transom depth Froude number of 2.0. But again a converged solution was obtained, and no particular indication of non-existence was found. However, the result (Fig. 10) was markedly three-dimensional, so the theory of [25] does not apply and probably nothing more could be expected.
Figure 10. Calculated wave pattern for a flat-bottomed hull at transom depth Froude number 2.0
The transition to a detachment ahead of the transom is indicated by the calculations, although rather indirectly. For the highest position of the transom edge considered here, the pressure along the bottom of the hull falls below zero before the transom is reached. But on that part of the boundary only a hull condition is imposed, and passing the zero pressure level has no effect. One has to watch the pressure distribution on the hull, and as soon as this falls below zero the regular flow type is to be attempted. Geometric complications currently prevent the RAPID code to make this switch without any user intervention; and at this moment the degree of generality of the code is still insufficient to deal with regular flow around flat sterns with extremely blunt waterlines. These restrictions will hopefully be eliminated in the near future.
4. VALIDATION STUDIES
While [16] focused on the theoretical background of the RAPID-approach and discussed several studies of the numerical accuracy, grid independence and so on, in the meantime a number of validation studies has been carried out in which the predictions were compared with experimental data. Because of the availability of very detailed and accurate measurements, we first consider two standard test cases.
4.1 Wigley hull at Fn=0.316
For this case, data from the ITTC Cooperative Experimental Program are available. A comparison has been made of the wave profiles with zero trim and sinkage. Calculations were made with 624 panels on the port half of the hull and two different free surface panelings, with 1148 and 2312 panels, respectively, in an attempt to elucidate the cause of the general underprediction of the bow wave height in all published results for this particular case.
Fig. 11 shows that for both panelings the agreement of the calculated and experimental hull wave profile
is almost perfect, and far better than in most calculations published before. Grid dependence is only visible in the immediate vicinity of the bow, were the wave height is again slightly underpredicted. Further study, preferably for a simplified test case, must show whether this local effect is a consequence of incomplete resolution or of the possible bow singularity discussed before.
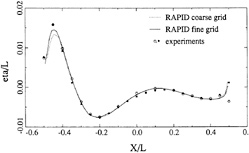
Figure 11. Hull wave profile; Wigley hull, Fn= 0.316
Fig. 12 compares the wave profiles on the line of collocation points adjacent to the hull and centerline as predicted by DAWSON, RAPID, and the first RAPID-iteration which is a Neumann-Kelvin linearization. Substantial differences are observed. Notwithstanding the slenderness of the vessel, the nonlinear method brings about a distinct improvement.
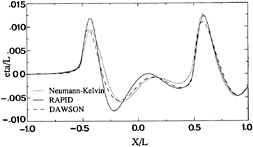
Figure 12. Wave profile, Wigley hull, Fn=0.316
4.2 Series 60 Cb=0.60 at Fn=0.316
For this case a very extensive set of measurements is available, which have been carried out at IIHR [26]. A large number of longitudinal and transverse cuts has been measured. A disadvantage of these data is that they apply to a very small model of 3 m length, in a narrow towing tank (Rn≈4 . 106). Initial calculations were made using 24*25 hull panels. Three free surface panelings have been tested: Grid I with 10 strips on each side of the hull and a panel length of 5 % of the transverse wave length; Grid II with 20 strips of 5% panels; Grid III with 10 strips of panels with a 2.5% length.
Fig. 13 compares the Neumann-Kelvin, Dawson and Rapid predictions for 2 longitudinal cuts. They all reasonably well correspond with the data, the Neumann-Kelvin results (in the present implementation) giving the worst agreement, with some phase shift in particular. While the nonlinear effects are not too large here, RAPID consistently gives the best agreement. An exception is the flow aft of the stern. The bad correlation in this region can safely be attributed to viscous effects; calculations for a displacement body in [25] in fact indicate a very important effect on stern wave amplitude.
The comparison of the nonlinear results on the 3 free surface grids showed that the first grid was somewhat less accurate, and slightly reduced the bow wave height due to an insufficient resolution. Grid II and III gave largely equivalent results, but at greater distances from the hull Grid III was marginally better due to the slightly smaller numerical damping. As the main difference between the data and the nonlinear calculation, a small, very short wave component was observed, generated at the bow and riding on top of the pattern of longer wave components. The length of this diverging wave was about 0.2 L, and the corresponding angle of the wave is 71 degrees. Although such a component is usually meaningless from the resistance point of view, the question was posed whether this deficiency was due to wave breaking, an unresolved strongly nonlinear effect or simply a lack of resolution.
Therefore grid IV has been generated, having 17 strips on the free surface and 56 panels per transverse wavelength. Besides, the hull paneling was refined to 56*15 panels. As Fig. 14 illustrates, the short wave component now actually enters (most clearly at x=0.6–0.9), and has an approximately correct phase and position, but not an entirely correct amplitude. While it apparently still is distorted by the poor resolution, this result definitely suggests that even this detail is fully contained in the mathematical model, and just requires a very fine discretization to turn up in the prediction. This short wave is, however, something of theoretical interest only.
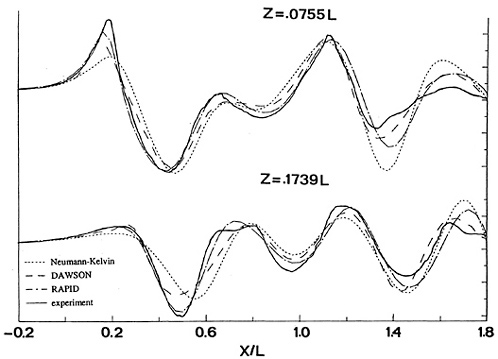
Figure 13. Longitudinal cuts, linearized and nonlinear; series 60 Cb=0.60, Fn=0.316
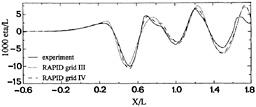
Figure 14. Grid dependence of short wave component; series 60 Cb=0.60, Fn=0.316
Fig. 15 shows the comparison of the calculation on the finest grid and the experiment, for 9 longitudinal cuts. It is noted that at the outer longitudinal cuts the agreement is not quite as good. However, these cuts are located around z=0.30L, which may have been too close to the wave absorber (at z=0.40L) and the tank wall (z=0.50L). Everywhere else the agreement is, in my opinion, extremely good and these are probably the best results for this case ever published up to now.
Also the hull wave profile (Fig. 16) corresponds quite well with the data. Grid IV represents some improvement compared to grid III; this is likely to be primarily a result of the finer hull paneling. The maximum bow wave height is accurately predicted on both grids, but the high wave elevation right at the fore perpendicular is not reproduced. As this appears to have no effect in the nearby longitudinal cut, this probably has been a very thin fluid or spray sheet in the experiment.
Summarizing, in general an excellent agreement has been obtained for this case. Panel refinement makes the results converge towards the experimental data, even for details such as the short diverging waves. There is no trace of any unresolved “strong nonlinearities ” in the near field having an effect at greater distances from the hull.
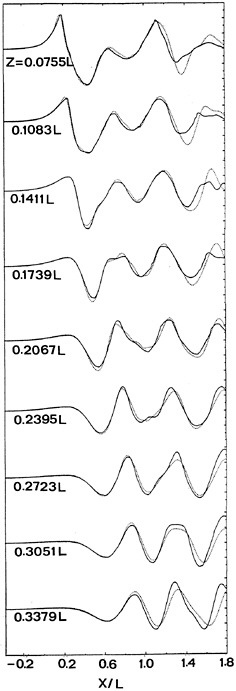
Figure 15. Longitudinal cuts, calculated (Grid IV) and experimental; series 60 Cb=60, Fn=0.316
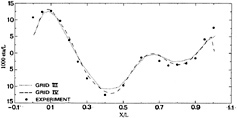
Figure 16 Hull wave profile, series 60 CB=0.60, Fn=0.316
4.3 Container ship
Of course further validations for more up-to-date hull forms are desired and will be carried out. Also, it is useful to compare linearized and nonlinear pedictions for ships exciting more diverging waves, as experience has shown that these tend to be rather poorly represented in linearized methods. Whether this is caused by numerical dispersion or damping or by the linearization was not quite clear until recently.
Our test case is a container ship with a bulbous bow, running at Fn=0.24. Two longitudinal cuts were measured during the towing tests at MARIN. DAWSON and RAPID calculations have been carried out. However, as the ship has a transom stern above the still waterline and stern sections with a very large slope, at the moment of making these calculations we were forced to modify the afterbody in the RAPID calculations. As the primary interest was in the forebody design, this was an acceptable change; but consequently the RAPID stern wave predictions cannot be compared with the data and have not been plotted. In DAWSON the transom flow model has been applied with a positive transom edge height.
Fig. 17 shows the predicted and measured longitudinal cuts for the full-draught case. At z= 0.10 L, RAPID obviously gives a far better prediction of the amplitude of the diverging bow wave system, which is severely underestimated by DAWSON. Further downstream, RAPID consistently improves upon the DAWSON results. But DAWSON is doing well for the rather transverse waves generated at the stern, notwithstanding the deficiencies in the modeling. In the second longitudinal cut, at a distance of 0.30 L from the centerplane, the agreement is slightly worse, and the bow wave system soon mixes up with the stern waves that prohibit further comparisons. But again here, RAPID is substantially closer to the data.
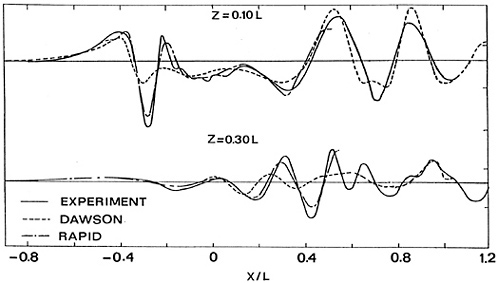
Figure 17. Longitudinal cuts for container ship, full draught
The first iteration of RAPID (a Neumann-Kelvin approximation) was quite similar to the DAWSON results, which proved that the underprediction of diverging waves is caused by neglecting nonlinear effects and not by numerical dispersion or insufficient resolution in the DAWSON results. The same has been found for other cases. It appears that the short diverging waves have a stronger tendency to steepen than the long transverse waves, and thus display stronger nonlinear effects.
For the same vessel in ballast condition the top of the bulbous bow is at 1.2 m above the still waterline (which is 15 % of the stagnation height). An important practical question is then, whether it still becomes completely immersed at the service speed; if not, a significant resistance penalty can be incurred.
This cannot be studied using a linearized method. Inherent to the linearization is the transfer of the boundary condition towards the undisturbed free surface. The greater part of the bulbous bow is above that surface and plays no role in the calculation. Therefore the predicted bow wave form is unrealistic. The same is true if the top of the bulbous bow is extremely close to the undisturbed waterplane [16]. In RAPID however, the free surface boundary conditions are applied at the actual wave surface. If the bow becomes completely submerged due to the bow wave elevation, its effect is fully included in the mathematical model. The only precaution needed is to start with an increased draught to make the bow fully submerged, and to gradually reduce this draught in the course of the iteration until the equilibrium position is reached.
RAPID here predicted that the bulbous bow would just emerge above the wave surface, by some 0.20 m. But as the free surface panel size was fairly large compared to the dimensions of the bulbous bow there was a risk of insufficient resolution of the large gradients that can occur above such bows. In fact, the towing test showed that an extremely thin sheet of water just wetted the upper side of the bulb. Immediately downstream a deep wave trough next to the hull was formed, and breaking phenomena affected the wave pattern. The less accurate prediction (Fig. 18) therefore comes as no surprise, although the major aspects of the wave pattern are captured.
The calculations for this container ship thus show that also for fairly slender vessels at moderate speed, nonlinear effects can be surprisingly large in some respects, and for diverging waves in particular. The nonlinear code gives a much better agreement with the experimental data, and additionally it permits to make calculations for surface-piercing bows; but resolution of the rather violent flow features here requires care.
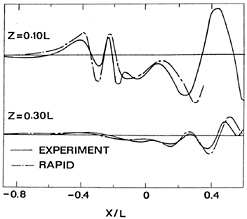
Figure 18. Longitudinal cuts for container ship, ballast draught
4.4 Frigate
In order to specifically test the transom flow modeling, linearized and nonlinear calculations have been carried out for a frigate-type hull with a wide transom, for which older experimental data were available. However, the Froude number based on the transom immersion was only 2.65, and this may well have been a case with a dead-water zone. Moreover, wave breaking near the corners of the transom was observed in corresponding wake survey data. A good agreement could therefore not be expected. As a matter of fact, both the DAWSON-and the RAPID-predictions showed a largely sinusoidal wave aft of the transom, while in the experiment a rather disturbed free surface with modest wave amplitude was observed. Accordingly, the magnitude of the diverging wave from the transom edge was substantially overestimated by both codes, and by RAPID in particular. On the other hand the diverging waves from the bow were again much better represented in RAPID. This case, therefore, turned out to be less appropriate for testing an inviscid potential flow model. Further validations will be carried out in the near future.
5. CONCLUSIONS
This paper has described part of the recent progress in the development of the RAPID-method towards a generally applicable ship design tool. In particular, attention was paid to the convergence of the iterative procedure and the applicability to flows with wave breaking; to the modeling of the flow off an immersed transom stern; and to some of the validation studies. Main conclusions are:
-
The method does not require any smoothing, filtering or damping and usually converges reliably to machine accuracy. The convergence problems typical of most steady nonlinear free surface flow solvers do not occur unless in exceptional cases.
-
A converged solution is also obtained for cases in which extensive wave breaking will occur in real flows, such as full hull forms at high speed. A separate criterion for the inception of wave breaking and a model for its effect on the flow field would be required to complete the flow picture in such cases.
-
It is argued that vorticity physically plays no role in the flow off a transom stern. The implementation of transom conditions in linearized and nonlinear methods is discussed an studied numerically. The linearized form appears to give reasonable results; the nonlinear method satisfies the transom conditions most accurately and shows very little grid-dependence. Optimization of the transom stern shape now seems possible, even for transoms above the still water line.
-
Comparisons with experimental data show that even for slender ships nonlinear effects are larger than was expected before. Diverging waves in particular are much better predicted by RAPID. Including nonlinear terms consistently improves the results. With sufficiently dense panelings very good agreement with experiments can be achieved, even for short wave components. For bulbous bows very close to the wave surface, resolution of small-scale flow phenomena requires care.
-
Future work will be directed to further experimental validation, improving the numerical and computational efficiency, and extensions to more complicated stern shapes.
ACKNOWLEDGEMENT
Computing time was provided by the Dutch National Computing Facilities Foundation (NCF) under project SC-232. Part of the development described in this paper was supported by the Netherlands Foundation for the Coordination of Maritime Research CMO, under project 91/92 B 3.15. This support is gratefully acknowledged.
REFERENCES
[1] Dawson, C.W., “A Practical Computer Method for Solving Ship-Wave Problems”, Proc. 2nd Int. Conf. Num. Ship Hydrodynamics, Berkeley, USA, 1977.
[2] Raven, H.C., “Variations on a Theme by Dawson”, Proc. 17th Symp. Naval Hydrodynamics, The Hague, Netherlands, 1988.
[3] Raven, H.C., “Adequacy of Free-Surface Conditions for the Wave-Resistance Problem ” Proc. 18th Symp. Naval Hydrodynamics, Ann Arbor, USA, 1990.
[4] Zandbergen, P.J., Broeze, J., and Van Daalen, E.F.G., “A Panel Method for the Simulation of Nonlinear Gravity Waves and Ship Motions”, in: Advances in Boundary Element Techniques, Springer Verlag, 1992.
[5] Xü, H., and Yue, D., “Computations of Fully Nonlinear Three-Dimensional Water Waves”, 19th Symp. Naval Hydrodynamics, Seoul, South-Korea, 1992.
[6] Cao, Y., “Computations of Nonlinear Gravity Waves by a Desingularized Boundary Integral Method,” Ph.D.Thesis, Univ. of Michigan, Ann Arbor, 1991.
[7] Ni, S.-Y., “A Method for Calculating Nonlinear Free Surface Potential Flows using Higher-Order Panels”, in: Ph.D.Thesis, Chalmers Univ., Gothenburg, Sweden, 1987.
[8] Larsson, L., Kim, K.J., and Zhang, D.H., “New Viscous and Inviscid CFD-Techniques for Ship Flows”, Proc. 5th Int. Conf. Numerical Ship Hydrodynamics, Hiroshima, Japan, 1988.
[9] Kim, Y.-H., and Lucas, T., “Nonlinear Ship Waves”, Proc. 18th Symp. Naval Hydrodynamics. Ann Arbor, USA, 1990.
[10] Kim, Y.-H., and Lucas, T., “Nonlinear Effects on High Block Ship at Low and Moderate Speed”, 19th Symp. Naval Hydrodynamics, Seoul, South-Korea, 1992.
[11] Delhommeau, G.,” Computation of Nonlinear Wave and Wave Resistance”, Proc. 7th Int. Workshop on Water Waves and Floating Bodies”. Val de Reuil, France, 1992.
[12] Xia, F., “A Study on the Numerical Solution of Fully Nonlinear Ship Wave Problems ”, in :Ph.D.Thesis, Chalmers Univ., Gothenburg, Sweden, 1986.
[13] Jensen, G., “Berechnung der Stationären Potentialströmung um ein Schiff unter Berücksichtigung der nichtlinearen Randbedingung an der Wasseroberfläche”, Ph.D.Thesis, IfS Bericht 484, Hamburg, 1988.
[14] Jensen, G., Bertram, V., and Soding, H., “Ship Wave-Resistance Computations”, Proc. 5th Int. Conf. Numerical Ship Hydrodynamics, Hiroshima, Japan, 1988.
[15] Raven, H.C., “The RAPID Solution of Steady Nonlinear Free Surface Problems”, Proc. 7th Int. Workshop on Water Waves and Floating Bodies, Val de Reuil, France, 1992.
[16] Raven, H.C., “A Practical Nonlinear Method for Calculating Ship Wavemaking and Wave Resistance”, 19th Symp. Naval Hydrodynamics, Seoul, South-Korea, 1992.
[17] Bertram, V., Laudan, J., and Jensen, G., “Validation Gives New Insights into Nonlinear Inviscid Flow Computations ”, 8th Int. Workshop on Water Waves and Floating Bodies, St John's, Canada, 1993.
[18] Duncan, J.H., “The Breaking and Non-Breaking Resistance of a Two-Dimensional Hydrofoil ”, Jnl. Fluid Mechanics, Vol.126, 1983, pp.507–520.
[19] Tulin, M.P., and Cointe, R., “A Theory of Spilling Breakers”, Proc. 16th Symp. Naval Hydrodynamics, Berkeley, 1986.
[20] Lin, W.M., Newman, J.N., and Yue, D.K.P, “Nonlinear Forced Motions of Floating Bodies”, Proc. 15th Symp. Naval Hydrodynamics. Hamburg, Germany, 1984.
[21] Van Daalen, E.F.G., “Numerical and Theoretical Studies of water Waves and Floating Bodies ”, Ph.D.Thesis, Twente University, Netherlands, 1993.
[22] Reed, A., Telste, J., Scragg, C, “Analysis of Transom Stern Flows”, Proc. 18th Symp. Naval Hydrodynamics, Ann Arbor, USA, 1990.
[23] Tulin, M.P., and Hsu, C.C., “Theory of High-speed Displacement Ships with Transom Sterns”, Jnl. Ship Research, Vol.30–3, 1986, pp. 186–193.
[24] Schmidt, G.H., “Linearized Stern Flow of a Two-Dimensional Shallow-Draft Ship” Jnl. Ship Research, Vol.25–4, dec. 1981, pp. 236–242.
[25] Vanden-Broeck, J.-M., “Nonlinear Stern Waves”, Jnl. Fluid Mech., Vol.96, part 3, pp.603–611.
[26] Toda, Y., Stern, F., and Longo, J., “Mean-Flow Measurements in the Boundary Layer and Wake and Wave Field of a Series 60 Cb=.6 Ship Model for Froude Number 16 and 316”, IIHR Report no. 352, Iowa, USA, 1991.
DISCUSSION
by Professor P.D.Sclavounos, MIT
1. Schmidt (1980) proves in his paper that for overhanging sterns, the coefficient C2 in the local expansion near the stern vanishes, thus establishing that the curvature of the wave profile is preserved in this case.
Author's Reply:
See common response for the above at the end of this section.
2. My question pertains to your experience with regard to the prediction of the wave resistance with your nonlinear method. Have you experienced improved predictions in the wave resistance which result from improved wave profile calculations?
Author's Reply
It has been found that slow-ship linearized methods:
-
generally predict the resistance reasonably well for relatively slender vessels at fairly high speed, with substantial wave making, but often underestimate the resistance otherwise;
-
generally predict a negative wave resistance for full hull forms at low Froude numbers. As shown in [3] this may be a result of a spurious momentum flux through the calculated free surface owing to the slow-ship linearization of the free surface boundary condition. One thus expects an improvement for a nonlinear method.
Current experience with RAPID indicates that:- for slender ships at high speed, the resistance prediction is good but not much different from that of a linearized method; -in some cases dominated by diverging waves, the resistance predicted by RAPID was much closer to experimental values;- for slow ships at low speed, the resistance is not consistently negative anymore, but it is hard to obtain an accurate prediction from pressure integration over the hull. This is due to the fact that, contrary to a linearized method, a nonlinear method requires the hydrostatic+hydrodynamic pressure to be integrated over the hull, which at low Froude numbers is a badly conditioned calculation.
More validations are, however, required. The accuracy of the resistance predictions, and possible alternative expressions for it, will be studied in the near future.
DISCUSSION
by Dr. D.Nakos, Intec Software & Consulting
In case that one of your iterations (towards the nonlinear solution) indicates that the flow separates at the stern before the ship transom, do you correct the assumed separation line?
Author's Reply:
See common response for the above at the end of this section.
DISCUSSION
by Dr. S.Kinnas, MIT
I would like to congratulate Dr. Raven for his impressive work. It appears to me that the detachment of the transom stream-surface is similar to the smooth detachment condition (Villat-Brillouin condition) for cavity flows, in which the cavity detaches at a point where the slope as well as the curvature are continuous. What are the author 's comments to this? Is this an adequate condition or we must consider the viscous flow in front of the detachment point similar to what is done for cavity flows by Arakeri, Frank, & Michel?
Author's Reply:
See common response for the above at the end of this section.
DISCUSSION
by Professor E.O.Tuck, University of Adelaide, Australia
I compliment the author on an excellent paper. My comment relates only to the minor matter raised at the end of it concerning transom sterns which are well above the undisturbed water level. This causes no extra difficulty with RAPID, apparently, which is as it should be. The only problem with this case is that the con-
verged results from RAPID passes a physically-unacceptable region of pressure less than atmospheric, just ahead of the transom. In practice, the flow would have detached prior to reaching the transom, perhaps quite next to the station where in the non-physical case studied, the pressure first goes negative (relative to atmospheric). In a similar planning context, I have had success in finding the actual detachment contour by iteration, the aim being to converge towards a final detachment contour or artificial transom on which not only the pressure but also the pressure gradient is zero. This is equivalent to requiring continuity of curvature, as well as slope, at detachment.
Author's Reply:
See common response for the above at the end of this section.
Author's Reply to Professors Sclavounos, Nakos, Kinnas, and Tuck
All above discussers address the problem of modeling the detachment of the free surface from a smooth surface, the bottom of a flat hull with the transom far above the undisturbed water level. If in a numerical solution the pressure on the hull falls below atmospheric pressure, this early detachment of the free surface may be supposed to occur physically. To model this, one should modify both the location of the detachment line and the assumed free surface behavior there. As mentioned in my paper this is not being done yet, and I had not yet given much thought to the details of this problem. The comments of the discussers are, therefore, welcomed.
As stated in Section 3.1 of the paper, in such a ‘regular flow' the curvature of the streamline at detachment is bounded. It can then be shown, at least in a 2D case, that the curvature must be equal to that of the wall, and that the pressure gradient along the wall must be zero at detachment. As Prof. Sclavounos rightly points out, this same conclusion follows from Schmidt's 2D flatship analysis, where the coefficient C2 in eq. (10) vanishes for a smooth detachment. Prof. Tuck points out that these conditions of zero pressure and zero pressure gradient at the wall permit to determine the detachment point by iteration. One could assume a detachment position and solve the problem in a way similar to the transom flow solution in RAPID (but with different local behavior at detachment). If the guessed detachment point is too far forward, there will be an infinite upward curvature of the streamline at this point, and the free surface penetrates the hull. If it is too far aft, there will be an infinite downward curvature, and the pressure along the hull ahead of the detachment point becomes negative. The correct position can thus be found, and has been found in earlier work by others.
Dr. Kinnas notes the analogy with the detachment of wall streamlines at the leading edge of a sheet cavity, where the inviscid-flow problem has almost the same properties. The conditions of continuous slope and curvature, called Villat-Brillouin condition in this field, have been imposed by e.g. Pellone and Rowe [D1], who iteratively located the detachment point from the condition of zero pressure gradient in a discretized form.
Including such an iteration in the method presented here would require much care because of the fine discretizations required and the repeated rediscretization of hull and free surface to fit the shifting intersection. But a complete description of inviscid flow off a ship afterbody may eventually require this addition.
Dr. Kinnas additionally raises the question of the importance of viscous effects. To what extent these will affect the location of smooth detachment, and the flow off an immersed transom stern as well, will depend on the hull form and the thickness of the boundary layer or wake. One expects little effect for slender high-speed vessels, but much more for slower, fuller hull forms. Some validations to be carried out now at MARIN may shed some light on this issue. If viscous effects are found to be important, I am afraid that the methods of Arakeri or Franc & Michel will be of little help, since they seem to exclusively apply to laminar separation in thin boundary layers upstream of cavity detachment on headforms and foils. But Dr. Kinnas 's remark is of course entirely justified.
References for the Replies:
[D1] Pellone, C., and Rowe, A., “Supercavitating Hydrofoils in Nonlinear
Theory”, 3rd Int. Conf. Numerical Ship Hydrodynamics, Paris, France, June 1991.
[D2] Van den Berg, W., Raven, H.C., and Valkhof, H.H., “Free-Surface Potential Flow Calculations for Merchant Vessels”, Int. Symp. on CFD and CAD in Ship Design, Wageningen, Netherlands , Sept. 1990.
[D3] Ligtelijn, J.Th, Raven, H.C., and Valkhof, H.H., “Ship Design Today: Practical Applications of Computational Fluid Dynamics”, HADMAR ‘91 Symposium, Varna, Bulgaria, Oct. 1991.
[D4] Sclavounos, P.D., and Nakos, D.E., “Stability Analysis of Panel Methods for Free-Surface Flows with Forward Speed”, 17th Symp. Naval Hydrodynamics, The Hague, Netherlands, 1988.
DISCUSSION
by Bill H.Cheng, David Taylor Model Basin
The author is commended for his contributions to nonlinear ship wave computations. MARIN's track record in applying a Dawson code to some 100 hull forms per year is impressive. I would be interested in learning more about this experience. In particular, typical examples of slender ships and full hull forms, for which Dawson codes work well and not so well, are of great interest to me.
At DTMB, the XYZFS program based on Charles Dawson's original code continues to be enhanced for use in ship design. I develop a dry transom algorithm [1] which has been successfully applied to transom-stern ships with and without bow domes [2, 3, 4, 5]. The wave resistance predictions are reasonable for moderate speeds corresponding to Froude numbers between 0.35 to 0.45. However, the predictions are less accurate outside this Froude number range since the dry transom assumption is no longer valid at lower Froude numbers and the stability and convergence become a problem at higher Froude numbers.
I am currently working on improving the stability and convergence of the Dawson method. Our outlook is more optimistic than Letcher 's assessment [6]. Our approach which uses finite difference methods to satisfy the radiation conditions is described in [7]. A new five-point upstream operator has been found to work well for fine grids corresponding to high speeds. This operator improves the stability and convergence by eliminating the spurious mode introduced by the numerics. Our latest approach is to use a family of difference operators to control the stability and convergence. A 2-D submerged source has been used as the first test case and the results show significant improvement for a wide range of Froude numbers. This finite difference method is being extended to 3-D linear problems and our results will be compared with the corresponding RAPID predictions.
References
1. Cheng, B.H., 5th Int. Conf. on Numerical Ship Hydrodynamics, Hiroshima, Japan, Sept. 1989.
2. Cheng, B.H., Dean, J.S., and Jayne, J.L., 2nd Workshop on Ship Wave Resistance Computations, DTNSRDC, Bethesda, Maryland, Nov. 1983.
3. Cheng, B.H. et al., Int. Conf. on Computer Aided Design, Manufacture and Operation in Marine and Offshore Industries, Springer-Verlag, Sept. 1986.
4. Hoyle, J.W. et. al., SNAME, Vol. 94, Nov. 1986.
5. Cheng, B.H. et al., Naval Engineers Journal, Vol. 101, No. 3, May 1989.
6. Letcher, J.S., Journal of Ship Research, Vol. 37, No. 1, Mar. 1993.
7. Strobel, K.H. and Cheng, B.H., 11th Int. Conf. on Offshore Mechanics and Arctic Engineering, Calgary, Canada, June 1992.
Author's Reply
Thanks for your comment. For some of our experience on practical applications of Dawson's method, see Refs. [D2] and [D3]. Concerning the use of linearized methods I would like to add that, although as a matter of fact the predicted wave resistance is not useful for full ships at low Froude numbers, the wave pattern predicted by our DAWSON code is qualitatively correct, as comparison with RAPID predictions has shown. In my opinion, a proper use of these linearized methods in ship design does not rely on the predicted resistance but on careful analysis of the entire flow field, pressure distribution and flow
direction. Thus handled, linearized methods are equally useful at lower Froude numbers.
I am interested in your progress in optimizing the choice of difference operators for the free surface condition. Of course, for studying the stability and accuracy of discretizations one should consider not only the effects of the difference operators, but simultaneously those due to the discretization of the singularity distribution. Note the difference in both numerical dispersion and stability of the DAWSON and RAPID implementations (see Figs 5 and 6 for example), which use identical difference schemes but different discretizations. This is one of the reasons that, like you, I do not share Letcher's conclusions. The most complete analysis is that proposed by Sclavounos and Nakos [D4], which allows to clearly identify the most promising implementations and discretizations. It will be interesting to compare the results of a linear method, optimized in this respect, with those of the nonlinear RAPID method, which has very good stability, virtually zero numerical dispersion but a numerical damping similar to that of Dawson's original method. But remember that nonlinear effects have been found to be substantial in several, sometimes unexpected, cases.
DISCUSSION
by Dr. Henry J.Haussling, David Taylor Model Basin
The author is to be commended on the development of a powerful method for the prediction of the flow about general hull geometries including nonlinear free-surface effects. I found the treatment of transom sterns interesting, as apparently did much of the audience, judging by the discussion that followed the talk. I therefore take this opportunity to recall the attention of the interested community to pertinent work, carried out some years ago at David Taylor Model Basin, that resulted in a series of publications [1– 4] on stern flows. The approach taken in that work seems to be much the same as that taken by Dr. Raven in the present paper.
The earlier work covered both the “regular” and “transom” types of flow defined in the current paper. It started with two-dimensional linearized stern flows [1] and progressed to the three-dimensional nonlinear regime [4]. It culminated in [4] with the development of a method for the computation of the wetted hull area in the vicinity of a transom or cruiser stern in such a way as to eliminate the possibility of negative pressures on the hull.
I would also like to point out that the earlier work included a careful comparison of computations of steep waves behind a two-dimensional flat-bottomed transom stern with the analytical work of Vanden-Broeck (reference [25] of the current paper). In particular, Figure 9 of [3] showed a remarkably close relationship between numerical solution behavior and Vanden-Broeck's analytic predictions in the Froude number range in which transition from non-breaking to breaking waves occurs. It was concluded that the numerical methods were accurate in the sense that they predicted the waves accurately up to the limit of breaking and that for breaking waves, where presumably a nonlinear free-surface potential flow does not exist, the numerical scheme diverged. However, Dr. Raven obtains a solution with his method even for cases in which the waves would break in reality. It is my understanding that he attributes this difference in results to his iterative scheme which is different from the time-accurate unsteady approach of the earlier work. Presumably his scheme finds a solution which is not found by the unsteady approach. If true, this would be a significant finding with important implications for nonlinear wave computations. Because of this importance, I would urge Dr. Raven to carry out careful grid refinement studies to determine the validity of his non-breaking solutions. Also, he should monitor energy conservation in his computations to make sure that he is not losing energy somewhere. Energy was carefully monitored in the earlier work. Could he repeat the two-dimensional computations of [3] with his method?
References
1. Haussling, H.J., “Two-dimensional Linear and Nonlinear Stern Waves,” Journal of Fluid Mechanics, Vol. 97, Part 4, Page 759 ( 1980).
2. Van Eseltine, R.T. and Haussling, H.J., “Flow About Transom Sterns,” Proc. of the Third Int. Conf. on Numerical Ship Hydrodynamics, Paris , Page 121 ( 1981).
3. Coleman, R.M. and Haussling, H.J. “Nonlinear Waves Behind an Accelerated Transom Stern,” Proc. of the Third Int. Conf.
on Numerical ship Hydrodynamics, Paris, Page 111 ( 1981).
4. Coleman, R.M., “Nonlinear Flow About a Three-Dimensional Transom Stern,” Proc. of the Fourth Int. Conf. on Numerical Ship Hydrodynamics, Washington , Page 234 ( 1985).
Author's Reply
Since the statements in the paper on wave breaking and its relevance for potential flow solutions are meant to stimulate a discussion on these apparently unsettled issues, I am most pleased with Dr. Haussling's discussion.
According to Vanden-Broeck's theory the steepness of the waves behind a 2D transom increases for decreasing transom Froude number. At a Froude number of 2.26, the limiting steepness of a Stokes wave is reached. The wave crests then attain stagnation height. For even lower transom Froude numbers, a steady potential flow solution does not exist.
The impressive work done by Dr. Haussling and coworkers already several years ago reproduced this. Nonlinear time-dependent calculations for 2D semi-infinite flat-bottomed transom stern hulls (his ref. [3]) at a Froude number of 2.3 and below broke down, at higher Fn they converged to a steady state. It seems obvious in this case (in absence of viscosity) that if a steady potential flow solution does not exist, wave breaking must occur. However, the converse is not true: Even while a steady potential flow exists theoretically, wave breaking may occur in reality. E.g. in Duncan's experiments and several others, wave breaking inception occurred before the limiting steepness was reached. Similarly, in this case the stern waves most likely will break already at transom Froude numbers higher than 2.26. Therefore, also in Dr. Hausslings calculations a solution was obtained in cases that wave breaking occurs in reality. In this sense, his results confirm my statement that a separate wave breaking criterion is required.
Remains the question why the result of Fig. 10 could be obtained, for a transom Froude number of 2.0. But the maximum wave height found was 80 % of the stagnation height, so the theoretical limit, which in 2D is reached at Fn=2.26, had not yet been reached here. In my opinion this is due to the three-dimensionality and not to the difference in solution methods. Most recently I triedto further increase the transom draft for the same 3D case, and did not succeed to obtain convergence below Fntr=1.77. The wave crest height then amounted to 94% of the stagnation height. This suggests that the same behaviour is found, but in 3D cases the limiting Froude number is somewhat different. Grid refinement studies and energy checks would as a matter of fact be requiredto establish the precise limits, but it seems that Vanden Broeck's theory and Dr. Haussling's and my calculations confirm rather than contradict each other. This could in fact better be studied by carrying out 2D calculations with the RAPID method, which, however, would require a substantial adaptation of the code. Similarly it is unfortunate that the results in your ref. [4] do not apply to lower transom Froude numbers in 3D flows.
In the discussion in Section 2.5 on wave breaking in more general 3D cases, wave breaking is again not defined as the nonexistence of a potential flow solution, but as the physical phenomenon. The wave pattern in Fig. 3 most likely will give rise to extensive breaking at the forward shoulder, but a steady potential flow solution may well exist (note that these are not far field waves). This calculation served to demonstrate that the convergence of the method is good enough to cover the range of wave steepnesses where wave breaking is not dominant in real flows.
Panel-Convergence of Steady Free-Surface Flow Calculations
D.Hendrix and F.Noblesse
(David Taylor Model Basin, USA)
ABSTRACT
Steady free-surface potential flow about a mathematically-defined hull form is considered. The flow is defined using the slender-ship approximation. The hull form is approximated by means of flat triangular panels within which the source strength is assumed piecewise constant. Convergence of the computed velocity potential, wave profile, and lift, moment and drag with respect to the number of panels is evaluated.
INTRODUCTION
Numerical methods for computing free-surface flows about ship forms are increasingly utilized for practical design studies. These methods are typically validated by comparisons between numerical predictions and experimental measurements. Although experimental validation of any numerical method is obviously necessary, it is not sufficient to demonstrate the reliability of the method. Indeed, experimental validation cannot be convincing unless the reliability and the accuracy of the method are established independently of comparison with experimental data. For instance, favorable comparisons between numerical predictions and experimental measurements are not meaningful if the numerical predictions depend appreciably upon some parameters such as the number and the arrangement of the panels used for representing the ship hull.
Efforts aimed at establishing the reliability and the accuracy of numerical methods are increasingly reported in the literature on numerical free-surface hydrodynamics. These efforts include studies of convergence with respect to the number of panels. As numerical methods are increasingly utilized for design studies, there is indeed a need for guidelines with respect to the number of panels that should be employed to achieve a desired accuracy.
Systematic panel-convergence studies for realistic ship forms are rendered difficult by practical limitations in computing time and computer memory, as well as by more fundamental limitations stemming from numerical uncertainties related to causes other than hull-discretization. For instance, if a numerical method relies on a solution procedure having uncertain robustness (as may be the case for the Neumann-Kelvin integral-equation) or if the required numerical calculations (such as the evaluation and panel-integration of a Green function) are performed with insufficient accuracy, it may not be meaningful to perform a panel-convergence study in which the number of panels is increased beyond a modest number.
A limited step toward the goal of developing guidelines with respect to the number of panels that must be employed to achieve a desired accuracy is made here. The present panel-convergence study is restricted to steady free-surface flow calculations based on flat triangular panels and the Green function associated with the linearized free-surface boundary condition.
FRAMEWORK OF STUDY
Specifically, the velocity potential due to a distribution of Kelvin sources on a ship's mean wetted hull surface is considered. The source strength is taken equal to the component nx of the unit vector ![]() normal to the hull along the direction of motion of the ship, according to the slender-ship approximation. The source strength thus is defined explicitly in terms of the hull geometry. Difficulties and uncertainties as-
normal to the hull along the direction of motion of the ship, according to the slender-ship approximation. The source strength thus is defined explicitly in terms of the hull geometry. Difficulties and uncertainties as-
sociated with the numerical solution of an integral equation therefore are avoided in the present panel-convergence study. The present study is in this respect simpler and less ambitious than the convergence studies reported by Doctors and Beck (1987) and others. However, the simplified approach based on the slender-ship approximation adopted here makes it possible to perform a panel-convergence analysis in which a large number of panels is employed.
Recipes for computing the velocity potential due to a piecewise-constant source distribution on a set of flat triangles within 0.1% accuracy are given in Hendrix and Noblesse (1992). This calculation method is used here. The slender-ship potential, denoted ψ, is expressed as the sum of a nonoscillatory near-field potential ψSN and a wave potential ψW corresponding to the wave field generated by the ship. We thus have
ψ=ψSN+ψW.
The potential ψSN is evaluated using a “direct” approach in which the nonoscillatory component of the Green function is computed and integrated over a panel (by means of Gauss integration rules or analytical formulas). The wave potential ψW is evaluated using an “indirect” approach based on the Fourier-Kochin representation.
All calculations are performed using Silicon Graphics (SGI) computers with 32 bit floating point arithmetic and SGI's Fortran compiler.
HULL FORM
A mathematically-defined hull form is considered for the sake of simplicity and accuracy. The hull form is depicted in Figure 1. Coordinates (x,y,z) rendered nondimensional with respect to the ship length are defined. The undisturbed waterplane is taken as the plane z=0, the ship centerplane is chosen as the plane y=0, and the ship bow and stern are located at x=1/2 and x=−1/2, respectively. The nondimensional beam and draft are denoted b and d, respectively, and are taken equal to b=0.1 and d=0.035.
The hull form is defined by means of parametric equations. The parameters, denoted λ and μ, vary within the unit square 0≤λ≤1 and 0≤μ≤1. The parameter λ is equal to 0 along the stern profile and 1 along the stern profile, and the parameter μ is equal to 0 at the static waterline and 1 at the keel. The hull form is divided into three regions, which are defined by means of different sets of parametric equations. The forebody 1/2−Lb≤x≤1/2 corresponds to 0≤λ≤Lb. The aftbody −1/2≤x≤−1/2+Ls corresponds to 1−Ls≤λ≤1. Finally, the parallel midbody −1/2+Ls≤x≤1/2−Lb corresponds to Lb≤λ≤1−Ls. The lengths of the forebody and aftbody are taken equal to Lb=0.45 and Ls =0.45.
The notation λb≡λ/Lb is used in the parametric equations defining the forebody 0≤λ≤Lb. These equations are
x=1/2−λ
z/d=−sin(πμ/2)
where the constant βb, which controls the fullness of the bow sections, is taken equal to 1.
The parallel midbody Lb≤λ≤1−Ls is defined by the parametric equations
x=1/2−λ
z/d=−sin(πμ/2).
The aftbody 1−Ls≤λ≤1 is defined by the parametric equations
x=1/2−λ+t2xs
z/d=−sin(πμ/2)
where t and xs are given by
t=1+(λ−1)Ls
and the constants ℓs , βs, and γs are taken equal to ℓs=0.15, βs=1.4, and γs=1.1. The constant ℓs determines the point at which the keel rises from the baseline toward the stern. The constants βs and γs control the fullness of the stern sections and the shape of the stern profile, respectively.
Finally, the x coordinate in the foregoing parametric equations is stretched via the linear transformation
ξ=(x−0.005)/0.99,
which yields ξ=1/2 for x=1/2 and ξ![]() −0.51 for x=−1/2. This stretching of the longitudinal coordinate x thus does not alter the location of the bow but slightly displaces the stern from x= −0.5 to ξ−0.51. A hull form having a small transom is defined by truncating the portion of the stretched hull extending beyond the station ξ=−0.5. The resulting truncated hull form is depicted in Figure 1 and used for the calculations.
−0.51 for x=−1/2. This stretching of the longitudinal coordinate x thus does not alter the location of the bow but slightly displaces the stern from x= −0.5 to ξ−0.51. A hull form having a small transom is defined by truncating the portion of the stretched hull extending beyond the station ξ=−0.5. The resulting truncated hull form is depicted in Figure 1 and used for the calculations.
Figure 1: Hull form and panel refinement scheme used in study.
PANEL ARRANGEMENT
Flat triangular panels are used to approximate the hull, as was already noted. The panels are defined so that the vertices of the panels corresponding to the coarsest panel distribution are also panel vertices of all finer distributions. The hull is divided longitudinally by constant-x stations (as is required by the theoretical formulation) and transversely by dividing each station into the same number of equal-length segments. The stations are “cosine” spaced with the minimum spacing at the bow and the stern chosen so that the aspect ratio of the panels approaches 1 at the bow for the finest panel arrangements considered in the study.
The coarsest panel arrangement used in the study, shown in the upper part of Figure 1, consists of 72 panels on one half of the hull. The lower part of Figure 1 depicts an example of a finer panel arrangement corresponding to 1152 panels. This panel arrangement is defined by subdividing each of the panels obtained in the 72-panel coarsest panel arrangement into 16 panels.
The panel distributions used in the study are listed in Table 1. In this table Nx represents the number of segments between constant-x stations and Nyz is the number of segments defining a station. The total number of triangular panels on one half of the hull is then equal to
N=2 NxNyz.
The ratio Nx/Nyz was selected so that the aspect ratio of most panels is roughly equal to five, as is apparent from Figure 1. This ratio was adjusted when necessary in order to limit the maximum aspect ratio to ten, in accordance with the restriction recommended in Hendrix and Noblesse (1992). The aspect ratio of a panel is defined here as the length of the longest side of a panel divided by the distance to the corresponding
Table 1: Panel arrangements used in study.
|
Nx |
Nyz |
N |
|
12 |
3 |
72 |
|
24 |
6 |
288 |
|
36 |
9 |
648 |
|
48 |
12 |
1152 |
|
60 |
15 |
1800 |
|
72 |
18 |
2592 |
|
84 |
21 |
3528 |
|
96 |
24 |
4608 |
|
108 |
27 |
5832 |
|
120 |
30 |
7200 |
|
132 |
33 |
8712 |
|
144 |
36 |
10368 |
|
168 |
42 |
14112 |
|
192 |
48 |
18432 |
|
216 |
54 |
23328 |
|
240 |
60 |
28800 |
|
300 |
75 |
45000 |
|
360 |
87 |
62640 |
|
420 |
90 |
75600 |
|
480 |
102 |
97920 |
|
540 |
120 |
129600 |
|
684 |
144 |
196992 |
|
1056 |
189 |
399168 |
|
1536 |
258 |
792576 |
opposite vertex. The panel configurations listed in Table 1 were not all used in all the convergence studies. These panel arrangements represent a reasonable, although not optimal, panel distribution.
SURFACE AREA
Figure 2 presents the percent relative error in the computed surface area of the hull. Five curves are shown in this figure. The curves cor-
Figure 2: Relative error in surface area.
respond to the errors determined using different assumed “exact” values of the surface area.
Specifically, the lowest curve corresponds to the assumption that the surface area computed using (approximately) 100,000 panels is exact. The next three curves were similarly determined by taking the “exact” value of the surface area as that computed using (approximately) 200,000, 400,000, and 800,000 panels. The uppermost curve was determined by means of an extrapolation based on the other four curves to obtain an estimate of the true error corresponding to an infinite number of panels Nexact=∞. The extrapolation is based on a least-squares fit to the equation
![]() .
.
Figure 2 shows that approximations to the surface area accurate within 1% and 0.1% are obtained using about 250 and 2000 panels, respectively. This figure also shows that the error ![]() decreases approximately in proportion to 1/N in the limit N→∞.
decreases approximately in proportion to 1/N in the limit N→∞.
VELOCITY POTENTIAL
The vertices of the 72 panels corresponding to the coarsest panel arrangement shown in the upper part of Figure 1 define 52 points. The velocity potential is evaluated at these 52 calculation points, which are panel vertices for all the panel arrangements considered in the study as was already noted.
Potentials ψ0 and ψ∞
The velocity potentials ψ0 and ψ∞ corresponding to the “zero” and “infinite” Froude-number limits are considered first. The upper part of Figure 3 depicts the RMS (root-mean-square) of the errors
at the 52 calculation points. Here, ψi(N) represents the value of the potential ψ, which stands for ψ0 or ψ∞, at the “calculation point” number i (with 1≤i≤52) obtained using N panels, and ![]() is the corresponding “exact” value of the potential.
is the corresponding “exact” value of the potential.
In Figure 3 the RMS of the errors at the 52 calculation points is normalized by the RMS of the “exact” values ![]() of the potential at the 52 points. Figure 3 therefore depicts
of the potential at the 52 points. Figure 3 therefore depicts
as a function of the number N of panels. The five curves shown in the figure were determined in the manner explained previously in connection with Figure 2. Thus, ![]() in the foregoing expressions is taken as ψi(N) with N (approximately) equal to 100,000, 200,000, 400,000, and 800,000 for the four lowest curves, and the uppermost curve is obtained by means of a least-squares extrapolation based on the four lower curves.
in the foregoing expressions is taken as ψi(N) with N (approximately) equal to 100,000, 200,000, 400,000, and 800,000 for the four lowest curves, and the uppermost curve is obtained by means of a least-squares extrapolation based on the four lower curves.
The upper part of Figure 3 shows that approximately 500 and 1000 panels are required to compute the potentials ψ0 and ψ∞, respectively, within a RMS accuracy of 1%, and that approximately 6,000 and 50,000 panels are required to obtain 0.1% accuracy. Thus, considerably more panels are required to compute, within the same accuracy, the potential ψ∞ than the potential ψ0.
The lower part of Figure 3 depicts the error
![]() ,
,
which is normalized by the RMS value of the potential, for each of the 52 calculation points. Here the “exact” value ![]() of the potential ψ is taken as the value ψi(N) of the potential obtained using N≈800,000 panels.
of the potential ψ is taken as the value ψi(N) of the potential obtained using N≈800,000 panels.
Considerable variation exists among the 52 curves corresponding to the various calculation points, although these curves generally follow a similar trend. A notable exception is the uppermost curve. This curve corresponds to the intersection between the stemline and the keel, where the geometry is changing rapidly and a locally more refined panel arrangement would be required. If this point is ignored, the lower part of Figure 3 shows that approximately 10,000 and
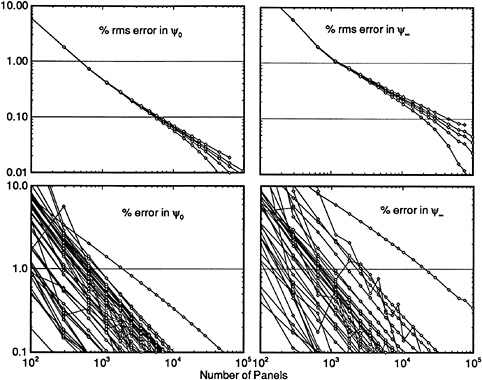
Figure 3: Relative error in velocity potential at zero and infinite Froude numbers.
30,000 panels are required to compute the potentials ψ0 and ψ∞, respectively, within a relative error of 0.1%. The upper and lower parts of Figure 3 show that errors in the calculation of the potentials ψ0 and ψ∞ decrease approximately in proportion to 1/N as the panel-number N increases.
Potentials ψ, ψW and ψSN
The velocity potential ψ considered in Figures 4 and 5 for three values of the Froude number F equal to 0.1, 0.25, and 0.5, which correspond to the top, center, and bottom rows of these two figures. The potential ψ is considered in the right columns of Figures 4 and 5 and the “nonoscillatory near-field component” ψSN and “wave component” ψW of the potential ψ are considered in the left and center columns, respectively. Figure 4 presents the RMS error, defined as in the upper part of Figure 3, in the potentials ψ, ψW and ψSN.
The left column of Figure 4 shows that approximately 500, 600 and 2,500 panels are required to compute the component ψSN at values of the Froude number F equal to 0.1, 0.25, and 0.5, respectively, within 1%, and that a greater accuracy of 0.1% requires 6,000, 30,000 and more than 100,000 panels. The number of panels required for computing the near-field potential ψSN within a specified accuracy therefore increases appreciably with the Froude number.
The center column of Figure 4 shows that approximately 1000, 500 and 300 panels are required to compute the wave component ψW within 1% for values of F equal to 0.1, 0.25, and 0.5, respectively, and that an accuracy of 0.1% requires approximately 50,000, 30,000 and 3,000 panels. The number of panels required for computing the wave potential ψW within a specified accuracy thus increases appreciably as the Froude number decreases, whereas the opposite was just found to hold for the near-field potential ψSN.
The right column of Figure 4 shows that approximately 500, 500, and 400 panels are required to compute the total potential
ψ≡ψSN+ψW
within 1% at F=0.1, 0.25, and 0.5, respectively, and that an accuracy of 0.1% requires approximately 6,000, 30,000 and 20,000 panels. The number of panels required for computing the total potential ψ within a specified accuracy is then much less affected by the Froude number than the components ψW and ψSN.
Figure 5 corresponds to the lower part of Figure 3, and depicts the error at each of the 52 calculation points. Considerable variation exists among the 52 curves, although these curves generally follow roughly a similar trend. The largest error in the left column, corresponding to the nonoscillatory potential ψSN, occurs for the point at the intersection between the stemline and the keel, as was found earlier in Figure 3. For most panel arrangements, the largest errors for the wave potential ψW considered in the center column occur at the transom. The right column of Figure 5 shows that 100,000 panels provide 3 digits of accuracy for all the 52 points and the 3 Froude numbers considered. The errors for 10,000 panels are smaller than 0.1% for most points and are no larger than 0.5%.
Figure 4 shows that errors in the calculation of the potentials ψ, ψW, and ψSN decrease roughly in proportion to 1/N. However, the RMS errors presented in Figure 4 decrease at a slower rate for large values of the panel-number N. This slow-down of the rate of convergence with increasing values of N appears to be more pronounced for larger values of the Froude number, and is also more pronounced in the center column corresponding to the wave potential ψW. The variation in the rate of decay of the RMS error may be due to the fact that the errors in Figure 5 decay at the rate 1/N at some points and at a slower rate for other calculation points. In particular, errors for most calculation points decay approximately in proportion to 1/N in the upper left corner of Figure 5, corresponding to the potential ψSN at F=0.1, while errors for most calculation points decay approximately in proportion to ![]() in the lower left grid, corresponding to ψSN at F=0.5.
in the lower left grid, corresponding to ψSN at F=0.5.
WAVE PROFILE
The wave profile is now considered. The nondimensional wave elevation for linearized po-tential flow is given by E/L=F2∂ψ/∂x, where E is the free-surface elevation, L is the ship length, and F is the Froude number based on the ship length.
The velocity component ∂ψ/∂x along the x-axis can be expressed in terms of the components (ψn,ψs,ψt) of the fluid velocity
along the unit vectors
as
∂ψ/∂x=nxψn+sxψs+txψt.
The vector ![]() is normal to the hull. The vectors
is normal to the hull. The vectors ![]() and
and ![]() are tangent to the hull, and approximately aligned with framelines and waterlines, respectively. At the plane z=0 the vector is
are tangent to the hull, and approximately aligned with framelines and waterlines, respectively. At the plane z=0 the vector is ![]() tangent to the static waterline (we then have tz=0). The components (ψn, ψs, ψt) of the velocity vector ▽ψ can be expressed in terms of the fluid velocities (∂ψ/∂n,∂ψ/∂s,∂ψ/∂t) in the directions of the vectors
tangent to the static waterline (we then have tz=0). The components (ψn, ψs, ψt) of the velocity vector ▽ψ can be expressed in terms of the fluid velocities (∂ψ/∂n,∂ψ/∂s,∂ψ/∂t) in the directions of the vectors ![]() by means of the relations ψn=∂ψ/∂n and
by means of the relations ψn=∂ψ/∂n and
ψs=(∂ψ/∂s−κ∂ψ/∂t)/(1−κ2)
ψt=(∂ψ/∂t−κ∂ψ/∂s)/(1−κ2)
where κ is defined as ![]() The normal derivative ∂ψ/∂n is taken equal to nx by virtue of the hull boundary condition. The free-surface elevation F2∂ψ/∂x is then determined in terms of the tangential derivatives ∂ψ/∂s and ∂ψ/∂t.
The normal derivative ∂ψ/∂n is taken equal to nx by virtue of the hull boundary condition. The free-surface elevation F2∂ψ/∂x is then determined in terms of the tangential derivatives ∂ψ/∂s and ∂ψ/∂t.
The free-surface elevation at the waterline is evaluated at the center of every straight waterline segment via numerical differentiation of the velocity potential. Specifically, the derivative ∂ψ/∂t is determined at the center of a waterline segment using two-point central differencing of the potential at the end-points of the waterline segment. The derivative ∂ψ/∂s at the center of a waterline segment is taken as the average of the values of the derivative ∂ψ/∂s at the end-points of the waterline segment. The derivative ∂ψ/∂s at an end-point of a waterline segment is determined using two-point one-sided differencing of the potential at the end-point of the segment and at the panel-vertex immediately below.
For a given panel distribution, the wave profile is determined using linear interpolation between the values of the free-surface elevation computed at the centers of the waterline segments. Linear extrapolation is used to determine the
wave profile at the bow and the stern. The RMS error in the wave profile is depicted in Figure 6 for three values of the Froude number F equal to 0.1, 0.25, and 0.5. The RMS error in this figure is defined as
where ψx≡∂ψ/∂x, ψx(N) is the wave-elevation obtained using N panels to approximate the hull, and ![]() represents the “exact” wave profile.
represents the “exact” wave profile.
A modification of the recipes given in Hendrix and Noblesse (1992) was made for the calculations of the wave profile using a large number of panels. Specifically, the upper limit of integration tmax in the wave integral (66) in Hendrix and Noblesse (1992) was increased in order to obtain a smooth wave profile in the immediate vicinity of the bow and stern. The upper limit of integration tmax has been multiplied by a factor taken equal to 3.5 for wave-profile calculations performed using 100,000 panels. A smaller multiplicative factor is required for a smaller number of panels.
Figure 6 corresponds to Figure 4 and the upper part of Figure 3, and likewise depicts 5 curves. The four lower curves were determined by taking the “exact” wave profile as that computed using N equal to (approximately) 10,000, 23,000, 45,000, and 100,000 panels. The uppermost curve was obtained via extrapolation of the 4 lower curves, in the manner explained previously in connection with Figure 2.
Figure 6 shows that approximately 7,000, 700, and 800 panels are required to compute the wave profile with a RMS error of 10% for values of F equal to 0.1, 0.25, and 0.5, respectively. It can also be estimated from Figure 6 that a greater accuracy of 3% requires roughly 40,000, 10,000, and 40,000 panels for F equal to 0.1, 0.25, and 0.5, respectively.
LIFT, DRAG, AND MOMENT
The hydrodynamic lift, drag, and trimming moment determined via integration of the pressure at the hull are finally considered. The pressure is taken as the linearized potential-flow approximation ρu2ψx, where ρ is the water density and u is the speed of the ship. The fluid velocity ψx is determined, using the relations given previously for the wave profile, at the centroid of every hull panel and regarded as piecewise constant within the corresponding panel. The derivatives ∂ψ/∂s and ∂ψ/∂t for a given panel are evaluated at the centers of the two shortest sides of the panel using two-point central differencing of the potential computed at the corresponding vertices of the panel.
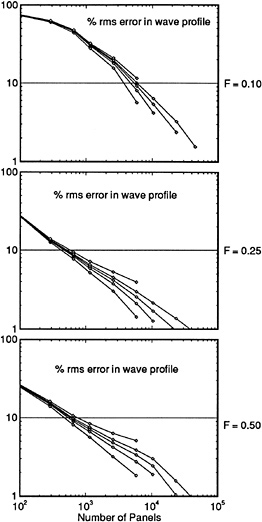
Figure 6: Root-mean-square error in the wave profile at three Froude numbers.
The lift, drag, and moment have been computed for 5 values of the Froude number F equal to 0.1, 0.2, 0.25, 0.3, and 0.5. “Exact” values of the lift, drag, and moment are determined by means of extrapolation of the corresponding values computed using 2,592, 5,832, 10,368, and 23,328 panels. The extrapolated “exact” values are obtained using a least-squares fit to the equation
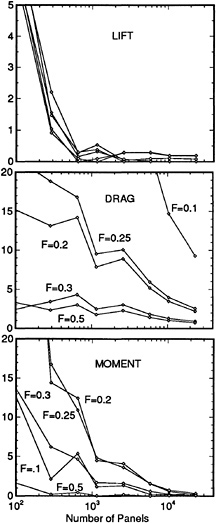
Figure 7: Percent relative error in lift, drag, and moment.
where the variable f stands for the lift, drag, or moment.
The percent relative error, defined as
![]() ,
,
corresponding to the lift, drag, and moment are depicted in the top, center, and bottom grids of
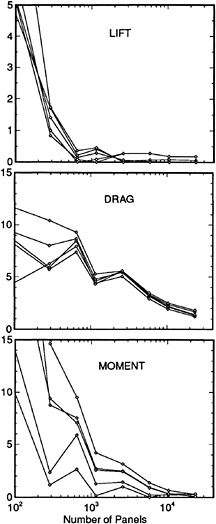
Figure 8: Percent relative error in lift, drag, and moment defined in terms of values at moderate Froude numbers.
Figure 7. This figure shows considerable variation in the errors corresponding to the drag, and to a lesser extent the moment. These variations in the errors stern largely from the large variations of the drag, and to a lesser extent the moment, with respect to the Froude number. The variation in the errors presented in Figure 7 makes it difficult to draw any conclusion with respect to the number of panels which is required for obtaining
Table 2: Number of panels required for computing various characteristics.
|
Froude Number |
|||||
|
0 |
0.1 |
0.25 |
0.5 |
∞ |
|
|
Hull area 1% |
250 panels |
||||
|
Hull area 0.1% |
2,000 |
||||
|
Potential 1% RMS |
500 |
500 |
500 |
400 |
1,000 |
|
Potential 0.1% RMS |
6,000 |
6,000 |
30,000 |
20,000 |
50,000 |
|
Wave profile 10% RMS |
8,000 |
700 |
800 |
||
|
Wave profile 3% RMS |
>40, 000 |
10,000 |
40,000 |
||
|
Lift (rel. to avg.) 1% |
500 |
||||
|
Moment (rel. to avg.) 1% |
8,000 |
||||
|
Drag (rel. to avg.) 2% |
20,000 |
- |
|||
a specified accuracy.
Figure 8 depicts the modified relative error
![]() ,
,
where ![]() is defined as the average of the values of fexact at the moderate Froude numbers F= 0.2, 0.25, 0.3. We thus have
is defined as the average of the values of fexact at the moderate Froude numbers F= 0.2, 0.25, 0.3. We thus have
![]() .
.
The large variations in the errors for the wave drag presented in Figure 7 are greatly reduced in Figure 8. This result indicates that although the lift, drag, and moment vary considerably with Froude number the absolute errors in these quantities do not vary appreciably with Froude number.
Figure 8 shows that 500 panels are sufficient to compute the lift within 1%. However, about 8,000 panels are required to compute the moment with the same accuracy, and the wave drag can be computed within about 2% using 20,000 panels.
CONCLUSION
The panel-convergence study presented in the foregoing is summarized in Table 2, which provides guidelines about the number of (flat triangular) panels that is required for predicting various flow characteristics. Table 2 shows that prediction of different flow characteristics, such as the wave drag and the hydrodynamic lift, may require widely-different numbers of panels. For instance, 500 panels are sufficient to compute the lift within 1%, but 20,000 panels are required to predict the drag within 2%.
The results summarized in Table 2 were obtained using the slender-ship approximation, in which the source density is defined explicitly in terms of the hull geometry. A greater number of panels may be required if an integral equation is solved since the variation of the source/doublet density depends on the Froude number as well as the hull geometry, and may therefore vary more rapidly than the x component nx of the unit normal vector ![]() to the hull used in the slender-ship approximation.
to the hull used in the slender-ship approximation.
The number of panels indicated in Table 2 is in most cases fairly large. Higher-order boundary element methods may therefore offer significant advantages in comparison to constant-panel methods. Table 2 also suggests that conclusions with respect to the benefits of nonlinear, or otherwise more refined, mathematical models could be questionable unless a sufficiently large number of panels is used.
ACKNOWLEDGMENTS
This study, which is a part of the first author's Ph.D. dissertation at the University of Maryland, was partly supported by the Independent Research program at DTMB.
REFERENCES
Doctors, Lawrence, and Beck, Robert, “Numerical Aspects of the Neumann-Kelvin Problem,” Journal of Ship Research, Vol. 31, No. 1, March 1987, pp. 1–13.
Hendrix, Dane, and Noblesse, Francis, “Recipes for Computing the Steady Free-Surface Flow Due to a Source Distribution,” Journal of Ship Research, Vol. 36, No. 4, Dec. 1992, pp. 346– 359.
DISCUSSION
by Professor Dr. Ing. S.D.Sharma, University of Duisburg
The authors deserve praise for a thorough and systematic study of the computational effort required to attain prescribed error margins for integral quantities of primary interest, e.g., lift, drag, and moment. This is the kind of paper one expects to see at a conference on numerical ship hydrodynamics. I would like to comment on the tremendous discrepancy in the effort required for calculating lift (500 panels for 1% error) and drag (20,000 panels for 2% error). This phenomenon is well known from all previous work, both computational and experimental, and is related to the fact that pressure drag on a ship arises from the small difference between large contributions of opposite sign from the bow and the stern. An efficient determination of pressure drag would require a uniform distribution of panels in the body plan rather than on the hull surface as seems to be the case in authors' Figure 1 . (Previous workers have even obtained a negative pressure drag as a consequence of an improper distribution of panels!) A possible solution to this problem may be to use Lagally's theorem rather than pressure integration for computing drag. Since all necessary source strengths and perturbation velocities are already generated by the authors' algorithm, this should be easily feasible. Would the authors care to give it a try?
Author's Reply
We thank Professor Sharma for his encouraging words on our efforts to quantify some of the numerical errors associated with free-surface flow calculations. We agree that it has long been recognized that wave-drag calculations by pressure integration are much more demanding than calculations of lift and moment. The magnitude of the errors associated with the prediction of wave drag using pressure integration however is not always fully appreciated. As we already noted in reply to Professor Landweber's comments, the primary aim of our study is to investigate panel convergence for conditions representing typical computational methods. Prediction of wave drag by pressure integration is commonly used, notably in Rankine source methods. Thus, pressure integration is also used in our study to estimate the corresponding errors (and for consistency with lift and moment calculations). As is emphasized by Professor Sharma, it is found that a very large number of panels must be used to obtain minimally-acceptable accuracy in wave drag by pressure integration (even though we use smaller panels near the bow and stern). Two conclusions can be drawn from this finding. One conclusion is that validation of numerical methods based on favorable comparisons between experimental data and wave-drag predictions obtained using pressure integration are in many instances questionable. Conclusions about the benefits of nonlinear, or otherwise refined, mathematical models can also be questioned, as is noted in our paper.
The other conclusion is that pressure integration is not a satisfactory method for practical wave drag calculations, and we certainly do not advocate using this method. The method based on Lagally's theorem mentioned by Professor Sharma is an alternative approach which can be expected to provide better accuracy. This method could probably be implemented fairly easily as Professor Sharma suggests, but has not been tried. Another alternative approach is the Havelock formula based on energy-flux integration. This well-known formula, made popular by the classical paper of Eggers, Sharma, and Ward (1967, Trans. SNAME, pp. 112–144), appears to offer the most general practical way of calculating wave drag. That this formula offers a means of determining wave drag more accurately than pressure integration is demonstrated by the “zeroeth-order” slender-ship approximation for the wave drag given in Noblesse (1983) J. Ship Research, pp. 13–33. In this formula the velocity potential of the flow due to the ship is simply taken equal to zero, which yields zero drag by pressure integration (a result that is better than negative drag). Nevertheless, this crudest possible approximation of the near-field flow provides a reasonable approximation to the wave drag using the Havelock formula.
DISCUSSION
by Dr. Henry T.Wang, Naval Research Laboratory
I am particularly interested in the reasons for the differences in the convergence behavior of slender ship, zero Froude number, and infinite Froude number theories. Each has been used as the starting, or basic, flow in calculating the
potential flow around surface ships. Thus, each of these flows is of special interest in its own right. Did you study the detailed variation of the potential or source strength on the hull to determine the reasons for the differences in accuracy?
Author's Reply
As Dr. Wang observes, Figure 3 in the paper shows that there are significant differences between the errors corresponding to the “zero” and “infinite” Froude-number limits, and that the errors shown in Figures 4 and 5 for free-surface flows vary between these two limiting cases. The source density in these calculations is in all cases taken equal to nx which corresponds to the slender-ship approximation. The behavior of the near-field and wave components of the velocity potential at the hull surface is significantly different. There are also significant differences in the behavior of the near-field component of the free-surface potential and its zero and infinite Froude-number limits, notable at the waterline. These differences stern from the differences in the Green functions for these cases. In particular, the Green functions for the zero and infinite Froude-number limits, given by a source and a free-surface image source or sink, result in large differences in the behavior of the corresponding potentials near the waterline. A study of the variation of these potentials at the hull surface will be presented elsewhere.
DISCUSSION
by Professor Emeritus Louis Landweber, The University of Iowa
I suggested that convergence might have been obtained with fewer panels if the authors had introduced a correction for the curvatures of the hull. This was illustrated for the case of a sphere immersed in a uniform stream. It was found, using N flat rectangular panels, that the error varied inversely as ![]() . This was presented at a symposium in honor of Ted Wu and published by World Scientific Publishing Company in 1990 on pages 415–428 of a book entitled Engineering Science. Fluid Dynamics. The title of the paper is “Properties of the Neumann Kernel and Interior Irrotational Flow for a Nearly Closed Surface,” a copy of which is being sent to the authors.
. This was presented at a symposium in honor of Ted Wu and published by World Scientific Publishing Company in 1990 on pages 415–428 of a book entitled Engineering Science. Fluid Dynamics. The title of the paper is “Properties of the Neumann Kernel and Interior Irrotational Flow for a Nearly Closed Surface,” a copy of which is being sent to the authors.
Author's Reply
The primary aim of our study is to investigate panel convergence for conditions representing typical computational methods. Flat panels are most commonly employed in current calculation methods and therefore are also used in our study. A main finding of this study is that convergence for flat panels is quite slow, as was also shown by Professor Landweber, and that a very large number of panels is required for accurate calculations. We agree with Professor Landweber that a correction for curvature, or the use of a higher order boundary-element method, would significantly reduce the required number of panels and represents a desirable improvement over existing constant-panel methods, as is noted in our conclusion.
A Higher-Order Panel Method Based on B-Splines
C.Y.Hsin, J.E.Kerwin, and J.N.Newman
(Massachusetts Institute of Technology, USA)
Abstract
A two-dimensional higher order panel method using B-splines has been developed, and the results of this method show that it is not only accurate, but also robust and efficient. In this method, both the panel geometry and singularity distributions are defined by B-splines, and Green's theorem is then applied at selected collocation points. The integrals of the influence functions are expressed in terms of polynomials of a parametric coordinate, and calculated analytically. Both the collocation method and the Galerkin method are presented to solve the system of equations.
Nomenclature
|
L |
number of panels; number of intervals between knots |
|
K |
order of polynomials |
|
Nν |
number of B-spline vertices |
|
Nc |
number of collocation points on each panel |
|
N |
degree of polynomials, N=K−1 |
|
M |
maximum number of degrees of the polynomials expansions |
|
|
inflow velocity |
|
x,y |
coordinates of the geometry |
|
z |
=x+iy |
|
velocity potential |
|
|
xν,yν |
B-spline control polygon vertices of the geometry |
|
|
B-spline control polygon vertices of the potential |
|
NK |
B-spline basis function of order K |
|
|
nth degree influence functions of the source and dipole distributions. |
1 Introduction
Panel methods have been used for aerodynamics, solid mechanics and hydrodynamics applications for decades. The principal reason for developing higher-order panel methods is to increase accuracy. However, the efficiency and robustness of higher-order methods is still debatable. In this paper, a two-dimensional higher order panel method using B-splines is presented. The results of this method show that it is not only accurate, but also robust and efficient.
The reasons for developing a higher-order panel method based on B-splines are: First, geometries can be directly passed to and from standard CAD/CAM systems, since geometries in these systems are commonly defined by B-splines. Secondly, the orders of panel geometries and singularity distributions can be arbitrary—not limited to linear, quadratic, or cubic. Also, the derivatives of the potential on the body can be directly calculated without using a numerical differencing scheme. Finally, because B-splines are naturally continuous, there is no need to impose continuity conditions at the panel boundaries.
Okan and Umpleby [6] have developed a B-spline based panel method, with similar objectives to the present work. The solution is based on the source formulation, with the velocity potential represented by a distribution of sources of unknown strength on the body surface. No details are given regarding the numerical analysis, and it is not clear how the influence functions are evaluated. The principal test computations, for the pressure distributions on two NACA foils, show significant errors near the trailing edge.
In the present work, both the panel geometry and singularity distributions are defined by B-splines, and Green's theorem is then applied. The
integrals of the influence functions are expressed in terms of polynomials of a parametric coordinate, and the polynomial coefficients are derived from the B-spline basis function. Source and normal dipole influence functions are calculated analytically so that their evaluation is both accurate and efficient.
We first present a collocation method, in which an overdetermined linear system is solved by least squares for the unknown potentials. A Galerkin method is then presented which uses the B-spline basis functions as the test functions. This method results in a square linear system for the unknown potentials. The unknowns in both methods are the polygon vertices of the B-splines representing the perturbation potentials, not the perturbation potentials themselves. The perturbation potentials and their derivatives can then be obtained from the resulting B-spline.
Two examples of uniform flow past a body have been selected to demonstrate the accuracy and efficiency of this method. The first is that of a square body section, intended to test the applicability to bodies with sharp corners, as are common with some offshore platforms. The second example is the flow past a Karman-Treftz foil, at an angle of attack, intended to test the method for use in lifting problems. In both cases comparisons are made with exact analytic results, to determine the accuracy of the numerical solutions. For a given accuracy, the computational time and storage requirements of the present method are far less than for a low order panel method.
2 B-Spline Basics
In order to show how B-splines can be applied to the solution of two-dimensional potential flow problems, we must first introduce the essential elements of B-spline curves. Rather than presenting the theory of B-splines in its most complete and general form, we will take a very simplistic approach here, and introduce only those bare essentials needed for our present purpose. More complete accounts can be found in recent texts such as [7].
Consider a two-dimensional curve expressed in parametric form
x=x(t)
y=y(t) (1)
where t is a parameter which is a monotonically increasing function of arc length along the curve, starting with a value of zero at one end and ending with a value tmax. The curve will be required to be continuously differentiate except at a set of L−1 discrete values of t which are designated as knots. In the present application, the maximum value of t will be L and the knots will be located at integral values of t,
t=1, 2, 3, …, L−1 (2)
Figure 1: Notation for B-spline representation of a two-dimensional curve
The number of intervals between knots will therefore be L. This notation is illustrated in figure 1.
Within each interval between knots, the curve x(t),y(t) will be represented as a weighted sum of Nν polynomials of order K, (degree N= K−1).
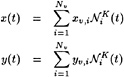
(3)
where xν,i,yν, i are the i'th weights, and ![]() is a polynomial basis function of degree K−1 associated with that weight.
is a polynomial basis function of degree K−1 associated with that weight.
B-spline curves, by definition, are generated by a particular set of basis functions. In their
most general form, the B-spline basis functions are rational functions of the parameter t, and the resulting curves are termed rational B-spline curves. In the special case when the denominators of the basis functions are constants, the basis functions become polynomials and the resulting curves are termed integral B-spline curves. In the present application, we will consider only polynomial basis functions.
While the basis functions in each interval between knots will always be required to be polynomials of the same degree, they will not generally be the same polynomials. Hence, the resulting curve will be a piecewise polynomial of specified degree in the parameter t. The degree of continuity of the basis functions at each knot boundary may be readily specified. Most frequently, one wishes the smoothest possible curve, in which case the basis functions of degree K−1 can be specified to have K−2 continuous derivatives at each knot. A B-spline curve with uniformly spaced knots, and with K−2 continuous derivatives at each knot is termed a uniform B-spline curve.
On the other hand, for shapes with sharp corners, as will be presented later in this paper, basis functions with discontinuous first derivatives at specified points can be generated. These can be generated by specifying that two or more knots have the same parameter value, t. Each additional knot at the same value of t reduces the number of continuous derivatives there by one. In that case, the knot spacing is no longer uniform, and the resulting curves are called non-uniform B-splines.
Finally, B-spline curves may either be closed and continuous, or open. The former are identified as periodic B-splines while the latter are open B-splines. Open B-splines can still form closed curves, as in the example shown in figure 1, but they are logically open in the sense that no conditions of continuity are imposed at the point of closure.
A recursive formula for generating B-spline basis functions of any order and degree of continuity was developed by Cox and de Boor, and may be found in [7]. Figure 2 shows a set of open, uniform, integral B-spline basis functions of order K=4. In this example, L=7 and Nν=10. For a given choice of K and L, Nν is not arbitrary, but must have the unique value
Nν=K+L−1 (4)
in order that all of the required conditions imposed on the basis functions be met.
Figure 2: Basis functions for an open, uniform, integral B-spline curve with K=4, L=7, Nν= 10.
A major reason for the popularity of B-splines for CAD applications may be found in the geometric interpretation of the weights, xν,yν. If one connects the weights with straight lines, one generates a polygon which can be seen, in a sense, to approximate the resulting B-spline curve, as shown in figure 1. This is in contrast to most polynomial representations of curves, where the order of magnitude of the coefficients may vary widely and where the effect of changing one or more of the coefficients is far from intuitive.
In view of this geometrical interpretation, the term weights will be replaced by control polygon vertices, or simply vertices. These are sometimes referred to in the literature as control points, but this terminology will be avoided here since this term is commonly used to designate points on a body where boundary conditions of the hydrodynamic problem are to be satisfied.
While we started the discussion of B-spline curves by introducing the concept of knots, in most cases one generates a curve by selecting a set of vertices. In this case, equation (3) can be used to evaluate the curve. The position of the knots therefore follows by setting the parameter t to 0, 1, …, L. One can, in principle, start by specifying a set of knot coordinates at which point
equation (3) becomes a set of linear equations which can be readily solved for the vertex positions. However, the relationship between knot positions and the shape of the curve between knots is not intuitive, and great care must be taken in following this approach.
In any event, once one has selected the order of the B-spline, the degree of continuity at the knots and the vertex positions, all quantities on the right hand side of equation (3) are known. One can therefore carry out the summation and represent the curve in the I′th interval between knots as a single polynomial of degree K−1,
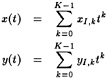
(5)
where xI,k,yI,k are constants generated by carrying out the summation in equation (3). When expressed in the form of equation (5), auxiliary geometric properties such as arc length and unit normal vectors may be readily determined. The fact that the curve was originally generated by B-spline basis functions is immaterial at this stage.
3 B-splines and Surface Potential Distributions
So far we have only discussed geometry. Our real objective, of course, is to solve for the potential flow around arbitrary two-dimensional bodies. This can be reduced to the problem of finding the distribution of velocity potential, ![]() (s) along the surface of the body. With the widespread use of potential based panel methods for both two and three dimensional flow problems, it is well known that the potential at a point on the body surface can be expressed in the form of integrals of source and dipole distributions over the body surface.
(s) along the surface of the body. With the widespread use of potential based panel methods for both two and three dimensional flow problems, it is well known that the potential at a point on the body surface can be expressed in the form of integrals of source and dipole distributions over the body surface.
This approach will be followed in the present paper. However, instead of solving directly for the potential at a discrete set of points on the body, the potential is represented in the same form as the geometry itself. Hence, equation (1) becomes
x=x(t)
y=y(t) (6)
Figure 3: B-spline representation of a two-dimensional foil, together with the potential distribution over its surface.
and equation (3) becomes
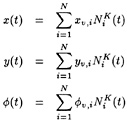
(7)
The unknowns in the hydrodynamic problem are therefore the values of the potential vertices, ![]() , which are not potentials in the physical sense. However, a given set of potential vertices, together with the appropriate B-spline basis functions, generates a continuous distribution of the physical velocity potential along the surface of the body. Discontinuities in higher derivatives of the potential will occur at the knots, in the same way as for the geometry. However, so long as at least first derivative continuity is maintained, the surface derivative of the potential, and hence velocity, is defined at all points on the body. This representation of the geometry and surface potential is shown in figure 3.
, which are not potentials in the physical sense. However, a given set of potential vertices, together with the appropriate B-spline basis functions, generates a continuous distribution of the physical velocity potential along the surface of the body. Discontinuities in higher derivatives of the potential will occur at the knots, in the same way as for the geometry. However, so long as at least first derivative continuity is maintained, the surface derivative of the potential, and hence velocity, is defined at all points on the body. This representation of the geometry and surface potential is shown in figure 3.
4 Discretized Grenn's Formula
The common basis of all panel methods is Green's theorem [4]. For a two dimensional problem, the potential based formulation can be derived from the Green's theorem as follows:
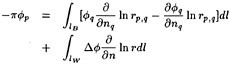
(8)
where lB is the boundary of the body, and lW is the wake surface of a lifting body, ![]() is the perturbation potential, and rp,q is the distance between point p and point q. In applications with Neumann boundary condition, the normal derivative of
is the perturbation potential, and rp,q is the distance between point p and point q. In applications with Neumann boundary condition, the normal derivative of ![]() is specified on lB, for example in the form,
is specified on lB, for example in the form,
(9)
for streaming flow with velocity ![]() past a fixed body.
past a fixed body.
The discretized form of equation (8) can then be expressed as
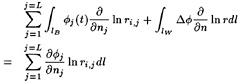
(10)
where i and j are the discretized panel indices, and L is the total number of panels.
Our purpose is to define both the geometry, lB, and the singularity strengths, ![]() ,
, ![]() , by B-splines. We already described the way to define the geometry by B-splines in the last section, and we are going to describe the way to define singularity strengths by using the B-splines.
, by B-splines. We already described the way to define the geometry by B-splines in the last section, and we are going to describe the way to define singularity strengths by using the B-splines.
In equations (8), (9) and (10), the term ![]() In r is the expression of the influence function of a two-dimensional dipole, and the term In r is the expression of the influence function of a two-dimensional source (or, Green's function). Therefore,
In r is the expression of the influence function of a two-dimensional dipole, and the term In r is the expression of the influence function of a two-dimensional source (or, Green's function). Therefore, ![]() in the Neumann boundary condition (equation (9)), can be thought of as the source strength, and the unknown perturbation potentials,
in the Neumann boundary condition (equation (9)), can be thought of as the source strength, and the unknown perturbation potentials, ![]() , can be thought of as the dipole moment. In equation (9), the normal vector
, can be thought of as the dipole moment. In equation (9), the normal vector ![]() can be written as
can be written as
(11)
where l is the arc length of the curve. Since we have expressed x and y as polynomials in the local parameter t, the normal vector can be also written as a polynomial of t by taking the derivatives of x and y (equation (5)). For panel j, the normal vectors can be expressed as follows:
(12)
The source strength, σ, is specified by the boundary condition that ![]() . Thus, the source strength on panel j, σj, can be written as
. Thus, the source strength on panel j, σj, can be written as
(13)
where σj,k is the B-spline coefficient of the source strength. M is the maximum degree of the polynomial expansions, which will be discussed in the next section. Similarly, the unknown perturbation potential strength, ![]() , on panel j can be written as
, on panel j can be written as
(14)
By inserting the equations (13) and (14) into equation (10), we have the following discretized formula:
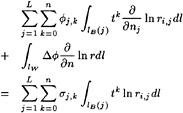
(15)
The source strength B-spline coefficients, σj,k, are known from the boundary condition, and the dipole moments are unknowns to be solved. These B-spline coefficients are functions of the B-spline polygon vertices. Therefore, the unknowns can be reduced to the B-spline polygon vertices defining the dipole moment instead of the B-spline coefficients. The terms ![]() In rdl and
In rdl and
∫ tk In rdl are the moments of the influence functions, and their evaluations are described in the next section.
5
Calculations of the influence functions
5.1
Introduction
Both the panel geometry and the basis functions for the singularity distributions are defined by polynomials of the general form
(16)
where the parametric coordinate t is in the range t1≤t≤t2. As t varies in this range, the coordinates of the panel are generated in the complex plane z=x+iy, in accordance with the representation
(17)
The end points of the panel are defined by the coordinates Z1=z(t1) and Z2=z(t2).
The required influence functions are defined in the forms
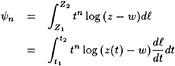
(18)
for the source distribution, and
(19)
for the normal dipole distribution. In both integrals the field point w is arbitrary, with special provisions in the limiting case where it is on the panel. Only the real parts of (18)–(19) are required in applications. The normal derivative in (19) is defined with respect to the source coordinate z along the panel contour.
By assumption the range (t1,t2) is sufficiently small that the polynomials are accurate to some useful tolerance. To be as general as possible M will be unrestricted here, and recursion formulae will be used to permit the results to be derived for arbitrary values of M. It will turn out that higher-order polynomials of degree N>M are required in the intermediate analysis to follow, to give controlled accuracy of the influence functions. Thus two independent parameters M and N are retained in (16)–(17), with the understanding that M corresponds to the specified geometrical representation, and N corresponds to the series expansions which are required for the analysis. The maximum degree n of the integrals (18)–(19) is expected to be between M (or possibly M−1), and N, and is not restricted in the analysis.
Two distinct regimes are dealt with in the following analysis. Most straightforward is the regime where the field point w is sufficiently far from the panel so that multipole expansions can be utilized. These are equivalent to expansions of (18)–(19) in descending negative powers of w, with coefficients which depend on the panel geometry and can be pre-evaluated. (The source integral (18) must also include one term proportional to the logarithm of w.) Numerical experiments indicate that these multipole expansions are effective outside a circle, centered on the mid-point of the panel, with a radius on the order of 1.5 times the length of the panel. Thus for a succession of panels of approximately equal length, along a slowly varying arc, with collocation points in the interior of each panel, the only evaluations where the multipole expansion is not effective are for the panel itself and its two contiguous neighbors.
For the contiguous neighbors, and more generally for any field point which is not on the panel, the same multipole expansions can be used provided the panel is sub-divided into a set of subpanels, with the maximum length of each subpanel chosen to satisfy the minimum radius requirement above, i.e. its length is less than or equal to two-thirds of the distance from its center to the field point. In this manner the utility of the multipole expansions is extended to apply in all cases except that where the field point is on the panel itself.
A separate analysis is required when the field point is on the panel. In this case it is possible to use the same polynomial representation (17) for both the source and field points, and to write the difference (z−w) as a polynomial with a prescribed zero, say at the point t=t0, which can be factored and treated analytically. The remaining factor is non-zero on the panel, and thus its logarithm or inverse can be expanded in polynomials. This leads to the desired relations for the special case where the field point is on the panel,
and complements the multipole expansions.
The analysis is based on a sequence of recursion formulae which are outlined in the following section.
5.2
Recursion Formulae
Given a truncated series of the form (16), the square of this series can be expanded in the form
(20)
where
(21)
More generally, for any integer power m,
(22)
where
(23)
and ![]()
In the derivations of the multipole expansions (22)–(23) will be used to evaluate higher powers of the polynomial
(24)
in the form
(25)
where, from (23),
(26)
The coefficients ![]() are non-zero only within the triangular matrix (m≤n).
are non-zero only within the triangular matrix (m≤n).
If m=0, (22) remains valid with the convention that ![]() . (Here the Kroenecker delta function is defined such that δnn=1 and δmn=0 if m≠n.)
. (Here the Kroenecker delta function is defined such that δnn=1 and δmn=0 if m≠n.)
Equation (23) can be used with m=0 to find the coefficients ![]() for the inverse 1/f of the original polynomial (16). The required coefficients are found recursively, from the first term in the sum of (23):
for the inverse 1/f of the original polynomial (16). The required coefficients are found recursively, from the first term in the sum of (23):
(27)
(28)
The square-root of a truncated series can be expanded in a similar form, using (21) to find the coefficients fn from given values of ![]() . Thus if the given series is of the form (20), successive coefficients of its square-root (16) can be found from the relations
. Thus if the given series is of the form (20), successive coefficients of its square-root (16) can be found from the relations
(29)
(30)
5.3
The Source Integral
The objective is to evaluate the real part of the integral
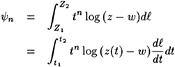
(31)
Here dℓ is the differential element of arc length along the contour:
(32)
Thus
(33)
The separate derivatives dx/dt, dy/dt are obtained directly from (17). The sum of their squares is then given in the form
(34)
where
(35)
(n=0,1,2, …2M—2)
The only non-zero terms in (35) are in the range max(0,n−2)≤v≤min(2,n).
Forming the square-root of (34) as indicated in (29)–(30), the coefficients of (33) are given by
(36)
(37)
Thus the source integral (18) is transformed in the form
(38)
5.4
The Dipole Integral
Next consider the normal-dipole integrals (19). The normal derivative can be written as
(39)
where the normal vector has been defined in equation (11), and
(40)
From these relations it follows that the dipole integral can be evaluated in the form
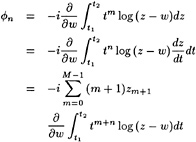
(41)
5.5
Multipole expansions
For sufficiently large values of ![]() the logarithmic function in (38) and (41) can be expanded in Taylor series, about the point z=z0, and integrated term-by-term:
the logarithmic function in (38) and (41) can be expanded in Taylor series, about the point z=z0, and integrated term-by-term:
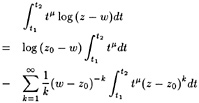
(42)
Using (25),
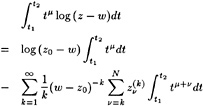
(43)
The integrals which remain in (43) are elementary:
(44)
With this definition (43) can be evaluated in the form
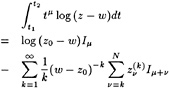
(45)
To simplify these evaluations, define the following coefficients
![]() (n=0, 1, 2, …) (46)
(n=0, 1, 2, …) (46)
(47)
(48)
(49)
Interchanging the order of summation in (43) and truncating the Taylor series, it follows that
(50)
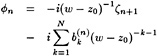
(51)
The coefficients (48–49), which depend only on the geometric properties of each panel, can be pre-evaluated and stored for subsequent use. Thus the evaluation of equations (50–51) for multiple field points can be affected with relatively small computational cost.
When the field point is too close to the panel for the direct use of these expansions, subdivision is necessary. The limits (t1,t2) of each sub-divided panel are within the domain of the original panel, and the only change required is to evaluate the Taylor expansion about a shifted reference ![]() , situated at an arbitrary point in the panel. There are various ways to make this generalization using the binomial theorem. The following appears to be relatively robust.
, situated at an arbitrary point in the panel. There are various ways to make this generalization using the binomial theorem. The following appears to be relatively robust.
With the definition ![]() of the parametric point t0 corresponding to the shifted origin, shifted coefficients
of the parametric point t0 corresponding to the shifted origin, shifted coefficients ![]() are defined for the expansion of
are defined for the expansion of ![]() in powers of the shifted parameter
in powers of the shifted parameter ![]() . Equations (42–43) then can be replaced by
. Equations (42–43) then can be replaced by
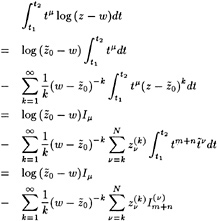
(52)
where, from the binomial theorem,
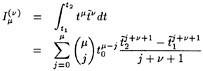
(53)
The integrals (53 ) can be evaluated from the recursion relations
(54)
and
(55)
If t0 is situated at the mid-point between t1 and t2 on the sub-divided panel, the only non-zero terms in (54) are those where ν is even.
From (38) it follows that
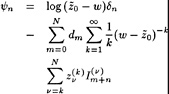
(56)
Similarly, from (41),
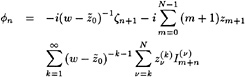
(57)
To facilitate the evaluation of (56)–(57) it is useful to define the sums
(58)
and
![]() (ν=1, 2, …, N) (59)
(ν=1, 2, …, N) (59)
The local multipole expansions for the subdivided panel are then evaluated in the forms
(60)
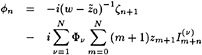
(61)
The latter forms reduce the number of nested loops, with a resulting improvement in computational efficiency.
5.6
Field point on the panel
Consider first the case where the field point is at w=z0 in physical coordinates, corresponding to t=0 in parametric coordinates. In this case
(62)
and the logarithm can be decomposed in the form
(63)
If the last term is expanded in a Taylor series the formal result is
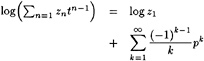
(64)
where
(65)
With the coefficients of (65) denoted by pn, successive powers of p can be expanded using the algorithm (25–26). Thus
(66)
where
![]() (k=2,3 …N; j=k, …, N) (67)
(k=2,3 …N; j=k, …, N) (67)
and
![]() (n=1,2, …, N–1) (68)
(n=1,2, …, N–1) (68)
Substituting (66) for each term in the series of (64), and collecting the homogeneous coefficients, gives the desired result
(69)
where
q0=log z1 (70)
and
![]() (j=1,2, …, N) (71)
(j=1,2, …, N) (71)
The source integral can be evaluated using (69), with the result
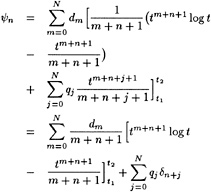
(72)
The normal dipole integral requires a separate analysis. Evaluating the indicated derivative in (44), and using (66),
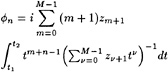
(73)
To evaluate the inverse of the series in (73), (27 –28) are used to find the coefficients ![]() , with
, with ![]() , and
, and ![]() . The resulting coefficients are
. The resulting coefficients are
(74)
and
![]() (n=1, 2, …, N) (75)
(n=1, 2, …, N) (75)
The normal dipole integral is then given as
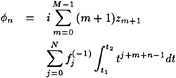
(76)
Except for the singular case j+m+n=0 the integrals are elementary, with the result
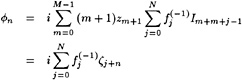
(77)
where the integrals Iμ are defined by (44). The singular case occurs only for n=0, where the contribution from the term where m=0 and j= 0 is given by
(78)
Thus, when n=0, (77) applies in the modified form
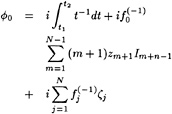
(79)
Depending on the definition of ϕ0 (as a principal-value integral or as the limit where w→z0 on a specified side of the panel), the integral in (79) is either real, or differs from a real quantity by ±πi. The only contribution to the real part of (79) is in the latter case.
For the more general case where the field point is on the panel at w=z(t0), with t0 an arbitrary point in parametric space in the open interval (t1,t2), the results above can be extended using the binomial theorem. Hereafter a tilde is used to denote the shifted variable t̃̈=t−t0, or the coefficients in a series involving this variable. Thus the panel is defined in physical space by analogy with (17), in the form
(80)
where
![]() (n=0,1,2, …, M) (81)
(n=0,1,2, …, M) (81)
In place of (69) we write
(82)
where the coefficients q̄n are evaluated from the relations
![]() (n=1, 2, …, M−1) (83)
(n=1, 2, …, M−1) (83)
![]() (k=2, 3, …, N; j=k, …, N) (84)
(k=2, 3, …, N; j=k, …, N) (84)
(85)
![]() (j=1, 2, …, N) (86)
(j=1, 2, …, N) (86)
The contribution to the source integral from the logarithmic singularity in (82) is
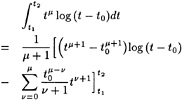
(87)
The contribution from the remaining terms in (82) is
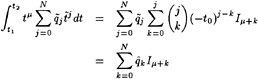
(88)
where
![]() (k=0,1,2, …, N) (89)
(k=0,1,2, …, N) (89)
Thus the source integral is evaluated in the more general form
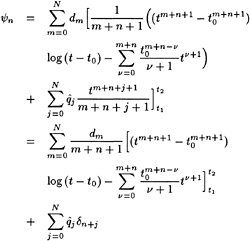
(90)
Following a similar generalization for the normal dipole integral, (73)–(76) are replaced by
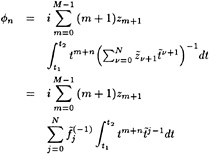
(91)
where
(92)
![]() (n=1,2, …, M−1) (93)
(n=1,2, …, M−1) (93)
The singular case j=0 simplifies again, as a result of the identity
(94)
Thus
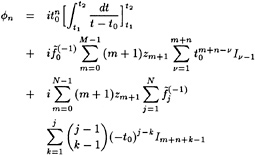
(95)
This equation can be simplified by extending the definition (46) of the coefficients ζn, with the final result
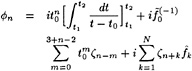
(96)
where
![]() (k=1, 2, …, N) (97)
(k=1, 2, …, N) (97)
Here the coefficients ζn are defined for n= 0, −1, −2,… as in (46), but with the lower limit of the sum m=1−n.
As in the discussion following (79), the only contribution to the real part of the dipole potential from the singular integral which in (95–96) is from the residue.
6
System of Equations
We have discussed the B-spline defined singularity strengths and calculations of the influence functions in the above sections. In this section, we are going to discuss the implementations of the system of equations. The collocation method will be discussed first, and then the Galerkin method.
6.1
The Collocation Method
In this system of equations, the boundary condition is satisfied at collocation points, and the unknowns to be solved are the B-spline polygon vertices of the dipole moments. The number of
collocation points on each panel can be arbitrary subject to the condition that the system is not underdetermined.
Consider the discretized Green's formula (15). The influence of the dipole singularities on the collocation point i is
(98)
where ![]() j,k is the kth degree B-spline coefficient of the dipole moment on the jth panel. The moments of the influence functions can be evaluated as described in the last section, and we will define
j,k is the kth degree B-spline coefficient of the dipole moment on the jth panel. The moments of the influence functions can be evaluated as described in the last section, and we will define ![]() as the kth moment of the dipole influence function on collocation point i by panel j. Therefore, the dipole influence of panel j on collocation point i can be written as,
as the kth moment of the dipole influence function on collocation point i by panel j. Therefore, the dipole influence of panel j on collocation point i can be written as,
(99)
From section 3, ![]() j,k is a function of the B-spline polygon vertices, therefore, (99) can be further expanded as follows:
j,k is a function of the B-spline polygon vertices, therefore, (99) can be further expanded as follows:
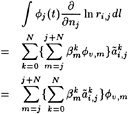
(100)
where ![]() ν,m is the mth B-spline vertex of the dipole moment, and the coefficients
ν,m is the mth B-spline vertex of the dipole moment, and the coefficients ![]() can be obtained by expanding the basis functions
can be obtained by expanding the basis functions
(101)
Now the left-hand-side of the discretized Green's formula (10) can be rewritten as follows:
(102)
Hence, the left-hand-side of the system of equations has been established.
We can calculate the influence of the sources, the right-hand-side of the system of equations, in a similar way. Since the strengths of the sources are known, the calculations are relatively simple.
Starting with equation (13), the source strength of panel j, σj, can be expressed as ![]() . We next define the source influence function
. We next define the source influence function ![]() such that
such that ![]() , where
, where ![]() is the kth moment of the source influence function on the collocation point i by the panel j. Then the total source influence on the collocation point i will be,
is the kth moment of the source influence function on the collocation point i by the panel j. Then the total source influence on the collocation point i will be,
(103)
Equation (103) gives the right-hand-side of the system of equations.
Therefore, the discretized Green's formula becomes,
(104)
Equation (104) is the complete formulation for non-lifting problems. The effect of the wake and the Kutta condition on the formulation of the lifting problem will be discussed later in this section.
Defining ![]() , and
, and ![]() , we obtain the system of equations in the matrix form [A][Φν]= [RHS]. In this system, there are L+N unknowns, and L*Nc equations (Nc is number of collocation points per panel). Therefore, we need more than one collocation point per panel to avoid an underdetermined system. Increasing the number of collocation points per panel, Nc, increases the computational time but also improves the stability of the solution. Based on numerical experiments we have selected Nc =3. Using a cubic B-spline with three collocation points on each panel, the left-hand-side matrix [A] is,
, we obtain the system of equations in the matrix form [A][Φν]= [RHS]. In this system, there are L+N unknowns, and L*Nc equations (Nc is number of collocation points per panel). Therefore, we need more than one collocation point per panel to avoid an underdetermined system. Increasing the number of collocation points per panel, Nc, increases the computational time but also improves the stability of the solution. Based on numerical experiments we have selected Nc =3. Using a cubic B-spline with three collocation points on each panel, the left-hand-side matrix [A] is,

(105)
and the unknowns are
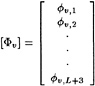
(106)
This is an overdetermined system, which can be solved by a least squares approach. The solution of this least squares system initially was carried out by both the Householder method and the normal equation approach [2], and both methods gave the same solution. In the present method, the Householder method is used.
To solve a lifting problem, the influence of the wake must also be included. For a two-dimensional, steady lifting problem, the strength of the wake sheet dipole is equivalent to a point vortex at the trailing edge, and the strength of this vortex should satisfy the Kutta condition. As shown by Morino [5], the strength of this vortex Г is equal to the the potential jump at the trailing edge,
(107)
where ![]() + is the dipole moment at the trailing edge of upper side (suction side), and
+ is the dipole moment at the trailing edge of upper side (suction side), and ![]() − is the dipole moment at the trailing edge of lower side (pressure side). The system of equations thus becomes,
− is the dipole moment at the trailing edge of lower side (pressure side). The system of equations thus becomes,
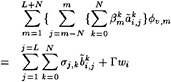
(108)
where wi is the wake influence function, i.e. the contribution from the last term of equation (8) to the ith panel on the foil.
When applying B-splines to define the dipole moment, these two values are the dipole moments at the “end points” of the B-spline, and are therefore equal to the first and the last of the B-spline polygon vertices.
(109)
Therefore, the wake influence functions can be coupled into the left-hand-side of the least squares system. However, this will cause the system of equations to become more ill-conditioned, and will therefore increase the numerical error in the solution. In the present method, we first guess the initial solution Г0, and then impose a pressure Kutta condition to get the final solution iteratively. The pressure Kutta condition used here was first introduced by Kerwin, et al. [3] for threedimensional propeller problems, and it requires the equality of the pressures on the upper and lower sides of the trailing edge. This non-linear pressure Kutta condition has been described in [ 3], and it can be simplified for two-dimensional problems. It is found that by using this approach, the solution procedure is more stable and more accurate. In the present paper, we used the two-dimensional flat plate solution (2πα, where α is the angle of attack) to be our initial solution, however, the selection of the initial solution (including zero) will not affect the final solution since the satisfaction of the Kutta condition should provide a unique solution.
For non-lifting problems, the accuracy is improved by imposing a continuity condition at the two ends of the B-splines. That is,
(110)
Although solving a least squares system sometimes is less accurate and robust than solving a square linear system, it provides more freedom to set up the system of equations. The selection of the number of collocation points on each panel is one example, and the applications of the Kutta condition and the continuity condition described above further demonstrate the flexibility of the present method. However, the size of the matrix is increased by the number of collocation points. This issue will be discussed later.
6.2
The Galerkin Method
The Galerkin method used here is the Bubnow-Galerkin method, in which the test functions are selected to be the same as the interpolation functions.
Applying the Galerkin method to the integral equation expressed in equations (8) and (9), we will have,
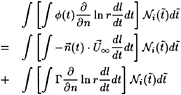
(111)
where the dipole moment, ![]() (t), can be expressed in terms of the B-spline basis functions as equation (7).
(t), can be expressed in terms of the B-spline basis functions as equation (7).
The inner integrals in the equation (111) are exactly the same as the collocation method described in the last section, therefore, the discretized form of equation (111) can be derived similarly. Let us define functions ![]() , and
, and ![]() as the discretized forms of the inner integrals of the left-hand-side and the right-hand-side of the equation (111), where li stands for the lth collocation point of panel i. Therefore, they represent the total influence on the collocation point l of the panel i of the dipole and source (plus the wake effect for the lifting problems) separately. From equation (108), we have,
as the discretized forms of the inner integrals of the left-hand-side and the right-hand-side of the equation (111), where li stands for the lth collocation point of panel i. Therefore, they represent the total influence on the collocation point l of the panel i of the dipole and source (plus the wake effect for the lifting problems) separately. From equation (108), we have,
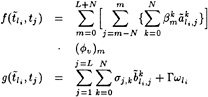
(112)
Equation (111) becomes the following equation by replacing these two functions with the inner integrals:
(113)
By applying a quadrature rule to this equation, we then have,
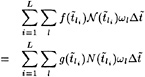
(114)
where ωl is the weighting function of the numerical integration. The resultant system of equations is an L+N by L+N linear system for a degree N higher order panel method. If we expressed the matrix system as equation (105–106), the matrix system of the Galerkin method will then be [Q][A][Φν]=[Q][B], and the matrix [Q] is,
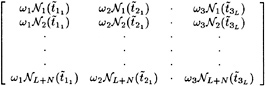
(115)
if the number of collocation points is selected as 3.
The Galerkin method utilized here uses the exact form for the inner integrals, and a numerical integration for the outer integrals. Chandler and Sloan [1] called this a “qualocation” method.
The numerical examples shown later show that the Galerkin method has almost the same accuracy and efficiency as the collocation method. However, the left-hand-side matrix size of the Galerkin method will be smaller than that of the collocation method. For a cubic higher order panel method, with L panels and Nc collocation points, the collocation methods will give an L*Nc by L+3 left-hand-side matrix, and the Galerkin method will give an L+3 by L+3 left-hand-side matrix. If we used a Householder least squares solution for the collocation method, then it needs 2(L+3)2(L*Nc−(L+3)/3) flops. On the other hand, the Galerkin method needs 2(L+3)3/3 flops to solve the matrix system by using Gaussian elimination. The collocation method needs about 3(Nc−1) times more computational time than the Galerkin method. This factor is not important for two-dimensional problems because only a small portion of the computational time is spent on solving the matrix (less than 10%).
In the next section, we will show results for both the non-lifting and lifting problems by applying the present method.
7
Computational Results
In this section, several numerical examples will be shown for the present method. We will first show results of the collocation method for all the cases, and then compare the solutions of the Galerkin method to the solutions of the collocation method.
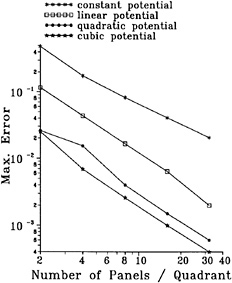
Figure 4: The number of panels used on one quadrant vs. the maximum error of the solutions of different order panel methods for the case of a uniform inflow past a square.
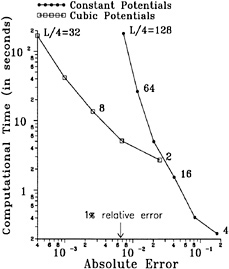
Figure 5: The absolute error (maximum error of the solutions) of the case a uniform inflow past a square, vs. the computational time of different order panel methods. The computational time is measured on a SiliconGraphics Iris 4D25 machine.
The first case we tested is that of uniform flow past a square. Since the present method is a general higher order method, we will present the results of linear potentials, quadratic potentials, and cubic potentials, and compare these results to the analytical results and results of a low order panel method.
Due to the sharp corners of the square, a non-uniform B-spline curve is used to define the geometry. An end condition is applied for the continuity as described in (110), such that the first B-spline control point coincides with the last B-spline control point. The error of this test case is defined as the maximum difference between the computational results and the analytical solution. Figure 4 shows the results of linear potential, quadratic potential, and cubic potential from the present method, along with the results from a two-dimensional constant potential panel method. The accuracy of the higher order panel method is much better than that of the low order panel method. Figure 5 shows the errors vs. the computational time (run on a SiliconGraphics Iris 4D25 machine) by using the cubic potentials and constant potentials. For a 1% error, the computational time of the constant potential method is about 36 times longer than that of the cubic potential method. This means that the present method is not only accurate, but also efficient.
The second case we tested is a symmetrical Karman-Treftz foil with a thickness/chord ratio of 25% and a tail angle of 45º (as shown in figure 1). The angle of attack is selected as 5 degrees. The error in this case is defined as the difference between the computational circulation and the analytical solution. Figure 6 shows the errors by using the different order of panel methods. It shows the similar trend as the square case. One of the advantages of applying the B-splines to define the solutions is that the derivatives of solutions can be directly calculated from the B-spline basis functions and solved B-spline polygon vertices. That is, the velocities can be computed directly without using finite differencing schemes. Figure 7 shows the calculated pressure distribution of this foil by using cubic potentials compared to the analytical results. It shows that even 10 panels gives a very good result for the pressure distribution. Notice that although we only show the pressure coefficients on the panel boundaries, in fact the solutions are continuous because they are defined by B-splines. Figure 8 again shows the error vs. the computational time of this case, and for the 1% error, the computational time of
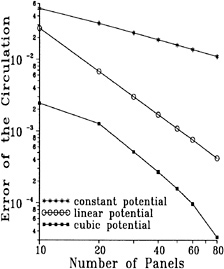
Figure 6: The number of panels used vs. the error of the solutionsof different order panel methods for the Karman-Treftz foil case.
Figure 7: The pressure distribution of calculated results and analytical solutions of the Karman-Treftz foil case.
Figure 8: The absolute error (error of the calculated circulation) vs. the computational time of different order panel methods for the hydrofoil case. The exact solution is 0.33. The computational time is measured on a SiliconGraphics Iris 4D25 machine.
the constant panel method is 41 times that of the cubic potential method. Notice that the constant potential method needs 480 panels to get a result within 1% error, and the cubic potential method only needs 10 panels.
To explore alternative solution techniques we have compared the results based on the collocation and Galerkin methods. Three collocation points are used on each panel, which were selected initially to provide uniform spacing in the parametric coordinate t, at the points 1/6, 1/2, 5/6 of the distance between each pair of vertices. The Galerkin scheme was implemented using the same integration nodes with equal weights. Subsequently, to refine the Galerkin integration, Gauss nodes were substituted in both methods. As shown in Figure 9, the improved accuracy of the Galerkin method is practically insignificant, while the use of Gauss nodes reduces the error in both methods by a factor of order two.
Figure 10 demonstrates the error em vs. the number of elements in the LHS matrix (hereafter refer to as the “matrix size”) of the constant potential method, and higher order (cubic) collocation method and higher order Galerkin method.
Figure 9: The error of computational results from the collocation method and the Galerkin method. The test case is the Karman-Treftz foil
Figure 10: The error vs. the matrix size of different order panel methods for the Karman-Treftz foil case.
The matrix size of the constant potential method is the square of the number of panels, L, the matrix size of the higher order collocation method is 3*L (for three collocation points each panel), multiplied by L+3, and the matrix size of the higher order Galerkin method is the square of L+3. From figure 10, one can see that 480 panels of the constant potential, 10 panels of the collocation and Galerkin higher order methods have similar errors (about 0.7% of the exact value). However, the number of elements in the matrix of these methods are 230400, 390 and 169 separately. That is, for the same error, the matrix size that the constant potential method needs is about 600 times larger than that of the higher order collocation method, and 1400 times larger than that of the higher order Galerkin method! Therefore, the presented method also has the advantage of using less computer resources.
8
Conclusion
We have presented a higher order panel method by using B-splines to define both the geometry and solutions. The test solutions show that for a given number of panels, the present method is more accurate than the low order method, and for a given accuracy, the computational time is far less than that of a low order panel method. The solutions are naturally continuous, and the derivatives of potentials can be directly calculated from the B-spline polygon vertices and B-spline basis functions. Also this method needs far less computer storage space or memory than the low order method, which will be significant advantage when solving three dimensional problems.
This method has been implemented by both the collocation method and the Galerkin method. The accuracies of both methods are equally good. The left-hand-side matrix of the Galerkin method is smaller than the collocation method. The resulting savings of the computational time, memory, and storage space are relative minor in solving two-dimensional problems; however, these savings are expected to be substantial in solving three-dimensional problems.
The extension of this method to solve three dimensional problems is under research. The problems of three-dimensional geometries are much more complicated, such as the connection of two surfaces, or the intersection of two surfaces. These complexities have to be well defined, and carefully incorporated into the solution
matrix system. The calculations of the influence functions are also much more difficult than the two-dimensional problems. It is hoped that this method will not only be able to provide more accurate solutions than the low order panel method, but also be more effective of solving problems such as wave body interactions, and lifting problems.
Acknowledgements
This work was performed as part of the Joint Industry Project “Wave effects on offshore structures”, and also under the MIT Sea Grant College Program with support provided by the David Taylor Model Basin. The authors would like to thank Mr. Seamus Tuohy, a graduate student in MIT Ocean Engineering Design Laboratory, for his help in answering our questions about B-splines.
References
[1] G.A.Chandler and I.H.Sloan. Spline qualocation methods for boundary integral equations. Numer. Math., 58, pp. 537–567, 1990.
[2] G.H.Golub and C.F.Van Loan. Matrix Computations. The Johns Hopkins University Press, Baltimore, Maryland, 1989.
[3] J.E.Kerwin, S.A.Kinnas, J-T Lee, and W-Z Shih. A surface panel method for the hydrodynamic analysis of ducted propellers . Trans. SNAME, 95, 1987.
[4] Sir Horace Lamb. Hydrodynamics. Cambridge University Press, sixth edition, 1932.
[5] Luigi Morino and Ching-Chiang Kuo. Subsonic potential aerodynamic for complex configurations: a general theory. AIAA Journal, vol 12, no 2, pp. 191–197, February 1974.
[6] M.B.Okan and S.M.Umpleby. The use of B-splines for the calculation of two-dimensional potential around arbitrary bodies. Int. Ship-building Progress, 32, June 1985.
[7] D.F.Rogers and J.A.Adams. Mathematical Elements for Computer Graphics. McGraw-Hill, Inc., New York, 1990.