Appendix C: Basic Concepts of Probability and Reliability
BACKGROUND
An evaluation of the usefulness and role of reliability in geotechnical engineering cannot be made without a clear understanding of the probability and risk assessment principles and methods that are used. Accordingly, a brief overview of some basic concepts is presented in this appendix. Although a text on basic probability and reliability concepts specifically written for geotechnical engineers is currently not available (with the possible exception of Harr, 1977), several texts (Benjamin and Cornell, 1970; Ang and Tang, 1975, 1984; Harr, 1987) that pertain to civil engineering as a whole can be referred to for a comprehensive and detailed treatise of the subject.
DESCRIPTION OF UNCERTAINTIES AND PROBABILITY ASSESSMENT
Geotechnical engineers are very familiar with uncertainties. The uncertainty may be in the form of a lack of information about the subsurface soil profile or a large scatter in the soil test results, or it may be associated with a substantial deviation of the measured field performance from its predicted value. When measurements on a given random variable are available, a histogram is often used to portray the uncertainties associated with the variable. The graph is a plot of the number of observed values for respective intervals of values of the variable. An example of such a plot is Figure C-1, which shows a histogram of the undrained shear strength measured from laboratory testing of a set of soil samples collected from a site. This plot shows that the measured soil strengths for this soil range from 0.8 to 1.6 ksf. The measured strengths are roughly symmetrical about the central value of 1.2 ksf. Figure C-2 shows a histogram of the ratio, N, of the measured-versus-predicted pile capacity from a set of pile load tests1. The actual capacity of a test pile ranges from as low as 40 percent of the value predicted to as great as twice that predicted value. The shape of the histogram is skewed toward higher values of the ratio
|
1 |
The pile tests were all in clay, and their capacities were predicted according to the procedures in the 16th edition of Recommended Practice 2A of the American Petroleum Institute (1986). To assure consistency, the soil strength for all the test piles are based on unconfined compressive strengths on pushed samples or equivalent. |
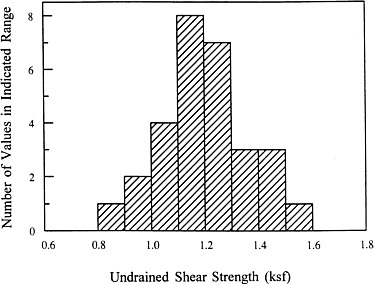
Figure C-1 An example histogram of soil strength data.
N, which implies that exceptionally large ratios may be observed. Besides drawing the histogram, statistical measures can be calculated from a given a set of observed data to gain a better understanding of the distribution of the variable.
A common statistic, the sample mean, is mathematically defined as the average of the observed values. It is a measure of the central tendency of the random variable. For the above case of pile capacity, if the prediction model does not contain any systematic bias, the mean value of the observed ratios will be approximately 1.0. Any deviation of the computed mean of N from 1.0 indicates that bias may be present in the model, which could mean either consistent overprediction or underprediction by the model. The sample variance, which is defined as the average of the squared deviation from the sample mean for all observed values, describes the amount of dispersion of the variable from the central value. Because the variance has a dimension that is a square of the dimension of the mean, the sample standard deviation, which is the square root of the variance, may be used to measure the average dispersion of the variable from its mean value. An even more convenient measure of the dispersion is given by the coefficient of variation (c.o.v.), which is the ratio of standard deviation to the mean and is a dimensionless quantity. Typical c.o.v. values for shear strength of soil are 20 to 40 percent, whereas the value for the soil density is smaller, around 5 percent.
In the above examples, the values observed represent only one set of observations. Another set of observations would not likely give exactly the same individual values. Thus, the histogram, as well as the sample statistics defined above, is subject to variation
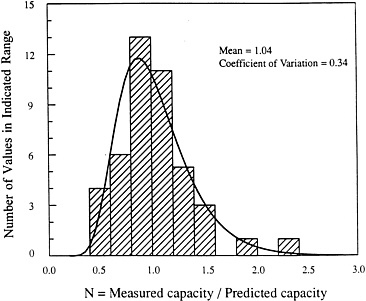
Figure C-2 Histogram of pile-test data. (The pile tests are all in clay, and their axial capacities are predicted according to the 16th edition of American Petroleum Institute, Recommended Practice 2A, 1986. Source: Tang, 1988).
between sets of observations. This is particularly true if the number of observations in each set is small. In fact, the measured data, such as those cited above, only serve to provide some information on the nature of the uncertainties associated with the variable under consideration. Besides the directly measured data at a given site, an engineer often has a strong feeling about which values a geotechnical variable will likely have on the basis of judgment and prior experience. Indeed, this subjective information is most useful in augmenting a small data base or (in the absence of measured data) in determining a probability model for the geotechnical variable.
A probability density function (PDF) may be introduced to model the relative likelihood of a random variable. The PDF describes the relative likelihood that the variable will have a certain value within the range of potential values . In a case where the engineer believes that a given set of measured data does represent a set of realistic sample values of the engineering variable and no other information is available, a PDF can be fitted over the frequency diagram, which is a modified histogram whose ordinate has been scaled, so that the area under the histogram is unity. For instance, a normaldistribution is a common probability distribution model used to fit a symmetrical bell-shaped histogram. If the engineer adopts a normal distribution to model the undrained shear strength in Figure C-1, the parameters of the normal distribution, namely µ and (σ, can be estimated by the sample mean and sample standard deviation, respectively.
In most situations, however, the choice of the PDF will be based on engineering judgment instead of a histogram, because either the sample size of the observations is
small, or the engineer believes that the values measured are not representative of the values of the pertinent variable, as is discussed further in the next section. In a broad sense, the PDF may be used to express the overall feeling of the engineer on the basis of all the evidence that is available. The evidence may include results of various types of tests, geological history, geotechnical performance in similar soils, and the engineer's intuition. The mean value of the PDF represents the engineer's best estimate of the random variable without the addition of conservative assumptions, and the standard deviation, or c.o.v., of the PDF represents the engineer's assessment of the uncertainty. A convenient probability-distribution type (e.g., normal or lognormal) may be selected, and calibrated with those mean values and standard deviations that are consistent with the engineer's judgment, to yield the judgmentally based PDF of the variable. If an engineer is only confident with the maximum and minimum values of a variable, a uniform distribution over the range may be used as a conservative PDF, whereas a triangular distribution can model approximately the engineer's perception of the relative likelihood over the given range of values. The PDF associated with an engineer's belief can change with time, especially when there is new evidence that is contrary to the engineer's previous opinion. The subject of updating probability with additional information will be discussed in a later section.
Once the PDF of a random variable is established, it can be used to calculate the probability of an event associated with a range of values of the variable. For instance, suppose that the undrained shear strength of the soil at a site is modeled by a normal distribution with parameters µ and σ equal to 1.2 and 0.17 ksf, respectively. The probability that the undrained shear strength, for example, for the next test specimen from the site, will be less than 1.03 ksf is given by 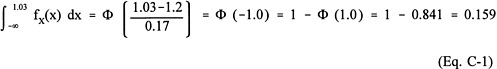 where f x(x) is the PDF of the random undrained shear strength, and Φ(x) is the probability of a standard normal variate (i.e., with mean 0 and standard deviation 1.0) less than x. Some typical values of the function are presented in Table C-1; for negative values of x, the function Φ(x) = 1 − Φ(−x).
where f x(x) is the PDF of the random undrained shear strength, and Φ(x) is the probability of a standard normal variate (i.e., with mean 0 and standard deviation 1.0) less than x. Some typical values of the function are presented in Table C-1; for negative values of x, the function Φ(x) = 1 − Φ(−x).
The advantage of the probability model is that with appropriate judgment of the engineer the PDF extends beyond the information portrayed by the observed data. The PDF incorporates the engineer's judgment on the applicability of the data for the specific site, as well as any other pertinent factors. Caution has to be exercised, however, to ensure the appropriateness of the PDF in representing the engineer 's state of belief. Judgment of the engineer should also play a significant role in the appropriate use of the probability estimated from the chosen PDF.
Table C-1 Values of Cumulative Distribution Function of the Standard Normal Variable
|
x |
Φ(x) |
|
0 |
0.5 |
|
0.5 |
0.691 |
|
1.0 |
0.841 |
|
1.5 |
0.933 |
|
2.0 |
0.977 |
|
2.5 |
0.9938 |
|
3.0 |
0.9987 |
|
3.5 |
0.99977 |
|
4.0 |
0.999968 |
|
5.0 |
0.9999997 |
An engineer may also estimate the likelihood of a given event directly, that is without going through the PDF, based on judgmental information. Vick (1992) suggested a workable procedure for encoding probabilities from engineers (see Example 3 in Chapter 2). As described in the approach adopted here to model uncertainties, a judgmental probability or probability distribution should be more valuable than one estimated strictly from observed data. It quantifies the engineer's opinion based on his or her experience and interpretation of the available information. By using these judgmental probabilities, engineers can be assured that judgment, the most important element in a reliability evaluation of geotechnical performance will not be ignored but instead will be enhanced.
FROM SOIL SPECIMAN TO IN SITU PROPERTY
The random variable in the first example (see Figure C-1) is the undrained shear strength of soil. However, the measured data represent only the undrained shear strengths of discrete soil specimens, which are determined using a given test procedure. This is not necessarily the strength that governs the performance at the site. In fact, the pertinent soil property controlling the performance of a foundation system often involves a much larger volume of soil. For instance, the average shear strength along a potential slip surface will control the failure of a slope, and the average compressibility of a volume of soil beneath a footing will control the settlement of the footing. In these two cases, the soil properties from each of the many points that constitute the domain of influence will contribute to the performance. Hence a domain-average property is needed instead of the property of discrete soil specimens. Sometimes, extreme low or high values of the soil property within a small local region may also govern system performance. Examples include the initiation of progressive failure in a slope by a local zone of weak material and piping failure in an
earth dam that is induced by a small zone of highly permeable material. Even in these cases, the local zone involved is often much larger than the size of a typical soil specimen. In any event, the pertinent soil property is the average soil property over an appropriate spatial domain, large or small; this soil property is referred to as the “spatial average property”. To evaluate correctly the site performance, the probabilistic description (e.g., mean value and c.o.v.) of the spatial average property must be determined.
Two factors are involved here. First, there is a size effect. The law of averaging would imply that the average soil property over a given volume or area will exhibit a smaller scatter than the properties at individual locations. Hence, in many circumstances there is a reduction in variability that depends on the size of the domain to be averaged, Although in some circumstances, increasing the size of this domain may actually increase the variability. In addition, the correlational structure of the soil property will also affect the amount of reduction in variability. To study the effect of correlation, observe first that soil samples collected adjacent to each other are likely to have properties that are similar to each other compared with the relationships between those collected at large distances apart. Also, soil specimens tested by the same device will likely show less scatter in the measured values than if they were tested by different devices in separate laboratories. The degree of correlation as a function of separation distance between soil samples depends on the specific soil type and deposit characteristics and on the property considered. Nevertheless, the more erratic the variation (i.e., less correlated) of the soil property with distance and the larger the soil domain considered, the larger the reduction in the variability of the average property will be. This phenomenon is a result of the increasing likelihood that unusually high property values at some points will be balanced by low values at other points; therefore, the average property is less likely to take on exceptionally high or low values.
Second, the in situ soil property at incipient failure is not necessarily duplicated by the sampling and testing procedure performed on the soil specimen. Some of the causes of variance are sample disturbance, different stress conditions, and macrofeatures that may not be well represented by a small specimen. Each of these causes can yield test results that are consistently lower or higher than the in situ value; for example, a fissured clay might have a lower in situ strength than that measured in small samples. Hence, a bias may exist that needs to be corrected and incorporated into the overall uncertainty evaluation.
To account for the effect of the two factors described in the last paragraph, Tang (1984) proposed the following expressions for relating the mean and c.o.v. of the average soil property in situ to those of the tested soil specimens:
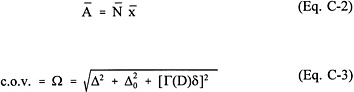
where the mean soil property estimated from laboratory or field tests, ![]() ,is modified by the mean bias,
,is modified by the mean bias, ![]() , of the respective test to yield the mean average soil property, Ā . For the first c.o.v. on the right side of Eq. C-3, Δ denotes the uncertainty in the bias caused by the discrepancy between specimen and in situ property. The value of
, of the respective test to yield the mean average soil property, Ā . For the first c.o.v. on the right side of Eq. C-3, Δ denotes the uncertainty in the bias caused by the discrepancy between specimen and in situ property. The value of ![]() and Δ can be assessed subjectively by the engineer after the factors causing the discrepancy are identified and evaluated. The second c.o.v., Δ0, denotes the uncertainty contribution from taking a limited number of samples, which can be expressed as a function of the sample size. The third term is the squared product of δ; the c.o.v. of property values from tests on specimens; and Γ(D), a reduction factor depending on the size of the averaging domain D and the spatial correlation characteristics of the soil properties (Vanmarcke, 1977). Uncertainty contributed by the first two components is often termed “systematic ” in contrast to the last component, which is termed “random”. Systematic uncertainties impose the same effect (or discrepancy) on each soil element throughout the spatial domain considered and hence are not subject to the averaging effect, unlike the spatial variability in the last term. It should be emphasized that the c.o.v. values reported in the literature are often estimated from measured test values for small soil specimens, which generally are not representative of the in situ soil properties governing geotechnical performance. Therefore, these c.o.v. values are essentially those denoted by δ in Eq. C-3. They generally cannot be used directly in reliability analysis; they need to be modified by factors to account for the spatial averaging reduction and the hidden systematic bias and error associated with the given type of test procedure for determining that property. As shown in Figure C-3 for a case where the test strength has a conservative bias, the
and Δ can be assessed subjectively by the engineer after the factors causing the discrepancy are identified and evaluated. The second c.o.v., Δ0, denotes the uncertainty contribution from taking a limited number of samples, which can be expressed as a function of the sample size. The third term is the squared product of δ; the c.o.v. of property values from tests on specimens; and Γ(D), a reduction factor depending on the size of the averaging domain D and the spatial correlation characteristics of the soil properties (Vanmarcke, 1977). Uncertainty contributed by the first two components is often termed “systematic ” in contrast to the last component, which is termed “random”. Systematic uncertainties impose the same effect (or discrepancy) on each soil element throughout the spatial domain considered and hence are not subject to the averaging effect, unlike the spatial variability in the last term. It should be emphasized that the c.o.v. values reported in the literature are often estimated from measured test values for small soil specimens, which generally are not representative of the in situ soil properties governing geotechnical performance. Therefore, these c.o.v. values are essentially those denoted by δ in Eq. C-3. They generally cannot be used directly in reliability analysis; they need to be modified by factors to account for the spatial averaging reduction and the hidden systematic bias and error associated with the given type of test procedure for determining that property. As shown in Figure C-3 for a case where the test strength has a conservative bias, the
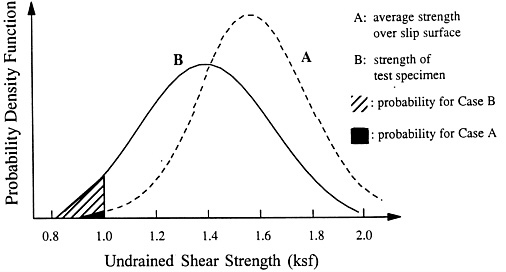
Figure C-3 Discrepancy between distribution of in situ property and those of specimen property.
probabilities calculated for an event, for example, undrained shear strength less than 1.0 ksf, can be substantially different using the probability distribution based on the test specimen statistics (curve B) rather than using that based on the average strength along a slip surface (curve A).
The discussion in this section considers a soil medium consisting of a single material type. In problems such as instability of rock slopes that is induced by the most unfavorably oriented joint, specific localized properties will affect the performance instead of the average property. In this case, undesirable extreme conditions are more likely to occur as the volume of the soil or rock increases. Another case is the phenomenon of progressive failure initiated at some local weak zone. The larger the domain of soil considered, the more adverse it will become. If the soil stratum consists of other materials whose properties are drastically different from those of the main soil material (such as the presence of slickensides in Example 9 in Chapter 2), it will require a different model and analysis procedure.
Example
The average density of a 10-m-thick soil layer is estimated based on the following information:
-
Nine soil samples taken at widely scattered locations have been tested for their densities, which yielded a mean of 1,800 kg/m3 and a standard deviation of 200 kg/m3. Assume random test error is negligible compared with spatial variability.
-
Assume perfect correlation among soil densities in the horizontal plane and an exponential correlation model with parameter 0.3 m in the vertical direction.
-
From long experience, the densities measured at this laboratory exhibit some discrepancy from those in situ. This discrepancy could range between 0.9 and 1.06; that is, the true in situ density may be from 90 to 106 percent of the laboratory-measured values.
The c.o.v., δ, denoting the inherent spatial variability of density between specimens is 200/1,800 or 0.111. For the given exponential correlation model and the averaging domain of 10 m, the factor Γ(D) is estimated to be 0.241 (Tang, 1984). The error due to limited samples is given by ![]() or 0.037 by assuming that the nine sample values are statistically independent. Lastly, the error due to systematic bias can be evaluated by assuming a uniform distribution between 0.9 and 1.06 for the correction factor N, which yields a mean value,
or 0.037 by assuming that the nine sample values are statistically independent. Lastly, the error due to systematic bias can be evaluated by assuming a uniform distribution between 0.9 and 1.06 for the correction factor N, which yields a mean value, ![]() , of 0.98 and a c.o.v., Δ, of 0.047. Incorporating all of these component statistics into Eq. C-2 and Eq. C-3, the mean and overall c.o.v. of the spatial average density are
, of 0.98 and a c.o.v., Δ, of 0.047. Incorporating all of these component statistics into Eq. C-2 and Eq. C-3, the mean and overall c.o.v. of the spatial average density are
Ā=0.98x1800=1764 kg/m3
(Eq. C-4)
and
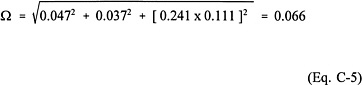
FROM FIELD-TEST TO FIELD PERFORMANCE
Geotechnical engineers often have collected data on field-test performance and compared these data with those predicted according to a geotechnical model. The field tests may involve actual full-size foundation systems or simply scaled-down field tests or even laboratory model tests. An example has been shown in Figure C-2 for the case of axial pile capacity based on a large number of pile tests. In principle, the probability distribution of this ratio, especially that established on the basis of high-quality field tests, can be used to determine the uncertainty associated with a given performance prediction model, which in turn may be used to estimate the probability of failure of the given geotechnical system. However, the applicability of this procedure depends on the performance of the geotechnical system under consideration being representative of the population of the field-test systems used in assessing the model bias and c.o.v. If there is a discrepancy, additional factors are required to modify the predicted performance. The bias and c.o.v. associated with each of the factors can be estimated from reported research studies or can be based on judgment of the engineer. An example of the use of pile test data in Figure C-2 for evaluating the in situ capacity of an offshore pile is given below.
Example
A large database from test piles was compiled by Olson and Dennis (1982) from which the discrepancies between the measured capacity and that predicted by a given pile- capacity prediction model were analyzed (Tang, 1988). Large scatter in the ratio of predicted-versus-measured capacity was observed, as shown in Figure C-2 for piles in clay. To apply this result to the evaluation of the axial capacity of an offshore pile, corrections are needed to account for the effects of factors such as
-
loading rate, because the strain rate in most pile tests is a fraction of 1 mm/minute, whereas that during a severe storm could be much larger, on the order of 200 mm/second or 10,000 mm/minute;
-
pile compressibility, because offshore piles are generally much longer than short piles tested on land;
-
consolidation level, because the time at which the critical storm hits could be years after the installation of the piles, whereas test piles normally are tested within months of installation; so the soil surrounding the test piles may have been subject to a different degree of consolidation relative to the actual pile; and
-
the specific sampling/testing procedure used for soil strength determination at the given site, which may be in contrast to that used for determining the statistics of the model bias and c.o.v. The bias and c.o.v associated with each of these factors have been assessed and then combined through a first-order probability model to yield the overall bias and c.o.v. of the in situ pile capacity (Tang, 1989) as
and where
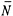 i and Ωi denote the respective bias (i.e., mean and c.o.v.) of the individual correction factor for the ith effect. The values of
i and Ωi denote the respective bias (i.e., mean and c.o.v.) of the individual correction factor for the ith effect. The values of 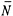 i and Ωi depend on the dimension of the pile, the sampling/testing procedure for soil strength determination, and the environmental conditions at the proposed site (Tang, 1988). For a 300-ft pile in a typical site at the Gulf of Mexico, with soil strengths determined by unconfined compression tests on driven samples, the overall mean bias is estimated to be 2.15, and overall c.o.v. is about 0.432. This implies that the pile capacity is expected to be 2.15 times the predicted value. On the other hand, if unconfined, unconsolidated strength tests on pushed samples were used for determining the soil strengths, the corresponding overall bias and c.o.v. would be 0.865 and 0.197, respectively.
i and Ωi depend on the dimension of the pile, the sampling/testing procedure for soil strength determination, and the environmental conditions at the proposed site (Tang, 1988). For a 300-ft pile in a typical site at the Gulf of Mexico, with soil strengths determined by unconfined compression tests on driven samples, the overall mean bias is estimated to be 2.15, and overall c.o.v. is about 0.432. This implies that the pile capacity is expected to be 2.15 times the predicted value. On the other hand, if unconfined, unconsolidated strength tests on pushed samples were used for determining the soil strengths, the corresponding overall bias and c.o.v. would be 0.865 and 0.197, respectively.
FACTOR OF SAFETY
Satisfactory performance of a geotechnical system often depends on its capacity relative to the applied load. For a pile foundation system, a pile fails by plunging if the axial capacity of the pile provided by the surrounding soil is less than the axial load from the superstructure. Slope failure occurs if the total sliding resistance along a potential slip surface is less than the driving force caused by the soil weight and other loads. Hence, in the simplest case, a safety factor can be defined as the ratio of the available resistance, R, to the applied load, L, or
F = R/L (Eq. C-8)
such that failure is given by the event {F < 1}. For the case where the applied load is known, or if an engineer would like to assess the safety subject to a prescribed design load, L is a constant and F can be alternatively defined as the factor by which the available resistance must be divided to cause failure. The definition of safety factor in Eq. C-8 should not be confused with the traditional design safety factor, which is treated deterministically as the ratio of the nominal resistance to the nominal load. Further discussion of the traditional design safety factor is presented at the end of this subsection.
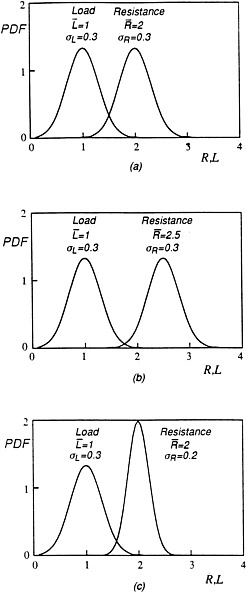
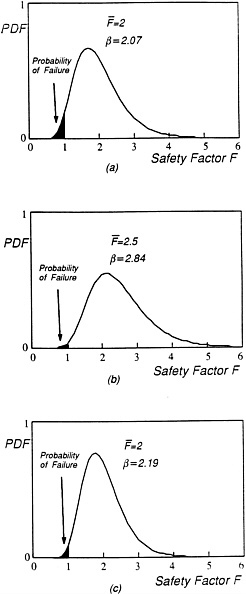
Since the available resistance and available load are each subject to uncertainties, they should be modeled as random variables; thus, F, in turn, will also be a random variable. The relationship between the probability of failure and the probability distributions of R and L is shown in Figure C-4a. The resistance can take on any value covered by the extent of the PDF of R, that is, fR(r), whereas the load can take on any value covered by the extent of the PDF of L, that is, fL(l). The region under the overlapping portion of the two PDF curves denotes the zone where the resistance may be less than the load. Although the area of overlap is not the probability of failure, the relative size of the overlapping region may be used as a rough comparison of the relative likelihoods of failure. As the mean resistance increases (Figure C-4b), likelihood of the failure decreases as expected. A decrease in the likelihood of failure can also be achieved by reducing the dispersion or uncertainty in the resistance (Figure C-4c). Mathematically, the probability of failure is calculated from the convolution integral as follows where the
![]() (Eq. C-9)
(Eq. C-9)
probability of the resistance being less than a given load value l, which is given by the bracket within the integral, is weighted by the PDF of the load over all possible values of l. A reliability index, β, has been commonly used in the reliability literature to denote the reliability level without the explicit determination of the probability of failure. For the
safety factor, F, as defined in Eq. C-8, ß is approximately the ratio of the natural logarithm of the mean F (which is approximately equal to the ratio of mean resistance over mean load) to the c.o.v. of F2; a large value of ß represents a higher reliability or smaller probability of failure. The reliability level associated with a reliability index ß is approximately given by the function Φ( ), evaluated at ß, from Table C-1. The probability of failure is simply 1-Φ (ß). As shown in figures C-5a through C-5c, the distribution of the safety factor corresponding to the cases of figures C-4a, through C-4c may be used to determine the respective probabilities of failure, namely the probability that F is less than 1. The value of ß is larger for cases b and c relative to that for case a. By reducing the uncertainty of the resistance, the spread of the safety factor distribution decreases as shown in Figure C-5c, yielding a smaller probability of failure. Moreover, as the mean safety factor increases, the PDF shifts to the right (Figure C-5b) and the probability of failure decreases.
The conventional factors of safety commonly used by engineers are based on nominal values of resistance and load. They are not mean safety factors. The conventional safety factor depends on the physical model, the method of calculation, and most importantly, on the choice of soil parameters. Usually there is a lack of consensus on these choices, and a large range of levels of conservatism on the choice of soil strength and methods of analysis is common. The uncertainty level associated with the resistance and load is not explicitly considered. Consequently, inconsistency is likely to exist among engineers and between applications for the same engineer. The same conventional safety factor can be associated with a large range of reliability level and thus is not a consistent measure of safety, as demonstrated in the following example. The use of a reliability index, ß, such as that introduced earlier in this section, can provide significant improvement over the use of the traditional design safety factor in measuring the relative safety between designs.
Example
In dam design, structural engineers designing concrete gravity dams use F=3.0 for foundation design with respect to sliding failure, while geotechnical engineers designing earth dams use F=1.5 for similar foundation design. Does this mean that concrete gravity dams are twice as safe as earth dams in regard to sliding? The answer is probably “no.” The reasons are (1) geotechnical engineers tend to be more conservative in selecting soil strength parameters, and (2) the value of F is generally not directly related to the likelihood of failure. Reliability methods offer a tool
|
2 |
This definition of ß is not the standard definition of ß associated with the first order reliability method, which is presented later in this section, but it serves to demonstrate the relationship between the mean safety factor, uncertainties of load and resistance, and the probability of failure without using a more elaborate formulation. |
to compare the relative safety between the two design methods. Consider a simple case in which a dam is 600 ft wide at the base with a height, h, in ft to be designed. The average undrained strength of the soil supporting the dam is 1,000 psf based on unconfined-compression tests on pushed samples. Suppose the dam is designed with respect to the sliding mode at the base to resist a lateral hydrostatic pressure of 0.5 × 62.5 × h2psf.
For a concrete dam, the design height of the dam can be obtained by equating the ratio of nominal resistance to nominal load, that is, (1,000 × 600)/(0.5 × 62.5 × h2) to 3.0, yielding a height of 80 ft. Similarly, for an earth dam, if the geotechnical engineer adopted a conservative undrained soil strength equal to two-thirds of the average value measured, the design height can be obtained by equating the ratio (0.67 × 1,000 × 600)/(0.5 × 62.5 × h2) to 1.5, yielding a height of 87 ft.
To evaluate the reliability of each of these two designs with respect to the sliding-failure mode, assume for simplicity that the in situ undrained soil strength is 0.9 of that measured and that its uncertainty is represented by a c.o.v. of 30 percent. The mean safety factor for the concrete dam is estimated by (0.9 × 1,000 × 600)/(0.5 × 62.5 × 80 2), that is, 2.7. Hence its reliability index is (ln 2.7)/(0.3) = 3.31. Similarly, the reliability index for the earth dam is estimated as 2.75, which is substantially more than half of the value of ß for the concrete dam. The probability of sliding failure for the concrete dam is 0.00047, compared with 0.00347 for the earth dam. In other words, for the values assumed in this example, the earth dam is about seven times more likely to slide than a concrete dam. On the other hand, if the geotechnical engineer had adopted a very conservative undrained soil strength equal to 40 percent of the average value measured, the design height of the earth dam would be 71 ft and the corresponding probability of sliding failure of the earth dam would be 0.00002. In spite of its smaller factor of safety, the earth dam would be only about one-twentieth as likely to fail as the concrete dam for this case.
The simple expression of R/L used in defining the factor of safety may not be obvious at times. For instance, in the stability analysis of a slope, the weight of the soil at the toe can act as counterweight to resist the driving moment caused by the main mass of the soil slope. This contribution can be either treated as additional resistance or reduced load. Depending on how this contribution is treated, it may introduce a discrepancy in the evaluation of the reliability index according to the approximate procedure presented earlier. To overcome this problem, a generalized safety factor, F, may be used to define the satisfactory performance of a geotechnical system. The safety factor can be represented by a general performance function
F=g(X1, X2, ..., Xm) (Eq. C-10)
where Xis are the component variables. In fact, this formulation is more general, because the resistance is usually a function of soil properties and geometric variables, and the load may be a function of some of the same variables plus other variables. Moreover, performance pertaining to settlement or leakage rate may be more conveniently expressed as a function of the loads, hydraulic head, soil, and other geometric variables instead of the ratio R/L.
In principle, for given PDF of each of the component variables in the performance function in Eq. C-10, the probability that {F < 1} can be calculated. However, the calculation can be mathematically cumbersome, involving many levels of analytical or numerical integration. Moreover, the engineer may be able to estimate perhaps only the mean value and the c.o.v. (but not the PDF) of most of the component variables due to a general lack of data. As a result, one may need to resort to approximate procedures for evaluating the probability of failure.
Consider first the case where the PDF of each component variable is satisfactorily prescribed by the engineer. The mathematical problem of performing the multiple integration can be avoided by using Monte Carlo simulation. By this procedure, values of the component variables are randomly generated according to their respective PDFs; these values are then used to calculate the value of the safety factor. By repeating this process many times, the probability of failure can be estimated by the proportion of times that the safety factor is less than one. The estimate is reasonably accurate only if the number of simulations is very large; also, the smaller the probability of failure, the larger the number of simulations that will be required. When the PDF of some (or even all) of the component variables are not prescribed but their mean values and c.o.v.s are available, the first-order reliability method may be used to determine the reliability index and the corresponding probability of failure approximately. The method is based on the truncation of the Taylor series expansion of the safety factor beyond the first-order term. Therefore, the method will yield a good approximation if the function g( ) is nearly linear or if the uncertainties of the component variables are small, for example if the c.o.v. is less than 15 percent. Otherwise, the results may be inaccurate or difficult to obtain. The second-order reliability method has been successful in improving the accuracy of the results in some cases. Essentially, this method retains one more term in the Taylor series expansion; hence, it can approximate some nonlinear g( ) better. However, the method generally requires additional information about the component variables beyond their mean and c.o.v. values, for instance their probability distribution type. For more details of the first-order and second-order reliability method procedures, refer to Ang and Tang (1984) and Madsen et al. (1986).
A simpler use of the first-order method is to relate the c.o.v. of the safety factor to the c.o.v.s of the component variables. For instance, the c.o.v. of the safety factor in Eq. C-10 is approximately equal to
![]()
where Ωi is the c.o.v. of each variable X i, and Si is the sensitivity factor denoting the percent change in safety factor for each percent of change in the value of Xi. The sensitivity factor may be determined analytically or numerically by taking the partial derivative of the function g( ) with respect to each variable. Both the sensitivity factor and the c.o.v. of the component variable are important in determining the contribution of a given variable to the c.o.v. of F. The benefit of an uncertainty analysis, such as that in Eq. C-11, is that the relative contribution of uncertainties from each variable, including the model error, can be compared on a consistent basis. This information can help the allocation of future research efforts or additional site explorations, because one can identify the variables that have the most effect on (or contribution to) the overall c.o.v. of the safety factor. Reduction of the c.o.v. in these variables will likely yield the largest improvement in the reliability of the current system as well as similar systems in the future. Finally, for a geotechnical system whose performance involves complex numerical procedures in lieu of an analytical function, the point estimate method proposed by Rosenblueth (1975) can be used efficiently to obtain approximate estimates of the mean and c.o.v. of the safety factor.
RELIABILITY-BASED DESIGN
The discussion thus far has focused on evaluating the reliability of a geotechnical system when the uncertainties of the pertinent variables are defined. In a design situation, one would be interested in choosing a design that will achieve a desired or prescribed level of safety. As shown earlier in figures C-4 and C-5, a geotechnical engineer can increase the reliability by increasing the mean resistance, by reducing the c.o.v. of the resistance, or by decreasing the loads. To obtain a higher ratio of mean resistance to the design load, one can deliberately adopt a low or conservative value as the design resistance to be checked against the designed load. This in turn will yield a mean resistance that has a high value relative to the design load. For instance, the design resistance may be a fraction of the mean resistance, which can be obtained by introducing a resistance factor φ (smaller than one) to be multiplied by the mean resistance. By applying the first-order reliability method, one can determine the appropriate value of the resistance factor from the following equation
φi = 1 − αi* β Ωi (Eq. C-12)
which shows that the resistance factor φ i depends on the uncertainty level of the ith variable (given by c.o.v., Ωi), the desired level of reliability (given by ß), and a coefficient αi* that measures the sensitivity of the ith variable relative to the other component variables. With this approach, the more uncertain variables (i.e., those with large Ω i) or the more important variables (i.e., those with large αi*) will have relatively smaller resistance factors φi. An example of this factor is the ratio Sd/(![]() used in Example 9 of Chapter 2 in this case, it represents the resistance factor for the undrained shear strength of soil.
used in Example 9 of Chapter 2 in this case, it represents the resistance factor for the undrained shear strength of soil.
Alternatively, the design resistance can be obtained by dividing the mean resistance by a factor γ (larger than one). The relationship between the two factors is simply γ = 1/φ. Eurocode No. 7, Geotechnics, as presented in Chapter 3 of this report, prefers to use γ as the resistance factor.
In determining the resistance factors for geotechnical design in the proposed design code based on Load and Resistance Factor Design procedures, a value of β should be used that is about the same as the average β associated with the current design. In other words, it is implicitly assumed that the average reliability level of the current designs is found to be acceptable and desirable.
MULTIPLE MODES OF FAILURE
Safety of a geotechnical system may involve its satisfactory performance with respect to several modes of failure. For instance, a retaining wall could fail by overturning, sliding, or inadequate bearing capacity. Realistically, each of the failure modes could happen, producing failure of the system. The probability of foundation failure will generally increase with the number of potential modes. Pertinent questions include: “Which mode is critical, or most likely to occur? ” and “How much additional risk is contributed by the noncritical failure modes?” Probabilistic analysis can provide answers to these questions by evaluating the probability of failure of each mode and can further calculate the probability that at least one mode will fail (i.e., system failure). For example, in the case of a foundation subject to two modes of failure, the probability of system failure is given by the probability of the union of the two failure events E1 and E2, namely
P(E1∪ E2) = P(E1) + P(E2) − P(E1E2)(Eq. C-13)
which is the sum of the individual failure probabilities after subtracting the probability that both modes occur. The last term in Eq. C-13 will be simply the product of P(E1) and P(E2) if the two failure modes are statistically independent or unrelated. It is recognized that the consequences, such as physical damages, of these failure modes are not necessarily the same. Hence, to assess the potential losses or damages in addition to the overall failure probability, one should assess the probability of individual failure modes,
weigh each by the respective loss, and combine each contribution to determine the overall expected loss. On the other hand, the failure of a geotechnical system may sometimes require the failure of a number of component events together. For instance, in the example on dam design in karst terrain (Example 3 in Chapter 2), the event of failure is the uncontrolled reservoir release, which requires the occurrence of the following five events: (1) existence of a foundation sinkhole; (2) collapse of sinkhole; (3) dike fill cracks; (4) piping, and (5) dike breaching. The probability of the failure event in this case is the product of the five component probabilities, which is much smaller than any of the individual component probabilities.
Consider next the case of a geotechnical system consisting of several components. For instance, the foundation of an offshore platform may consist of many similar piles. For a given direction of wave loading, the pile subjected to the largest load (defined as the critical pile) may not necessarily be the first to fail; in fact, each of the piles could be the first to fail. Again, one would be interested in how much additional risk is contributed by the noncritical piles toward initial failure of the pile system. Fortunately, the failure of the first pile in this case is not likely to lead to collapse of the platform system. It may require the failure of several more piles before the pile system fails completely. A pertinent question is “What is the additional reserve implicit in the pile system beyond the failure of the first pile?”, or, in other words, “What is the redundancy associated with the given pile system?” Probabilistic methods can be used to evaluate the relative likelihood of various failure-path scenarios. Moreover, these methods can provide a measure of the redundancy accounting for the combined effect of the expected reserve capacity as well as the uncertainties in the system. For example, a redundancy factor can be defined as the ratio of probability of initial failure to the probability of complete system failure. In other words, if there is only a small likelihood of system failure given that a component has already failed, or if system failure is very unlikely compared with initial failure, the redundancy factor will assume a large value as expected.
The importance of system consideration in reliability evaluation cannot be understated. In the case of slopes, sliding can occur along one of the many slip surfaces. For a long tunnel system, collapse also can occur at any section. Because most of the reliability analysis is based on the critical slip surface or the critical cross section of the tunnel, procedures are needed to extrapolate these critical component probabilities to those of the entire geotechnical system. Probabilistic methods can provide the necessary analytical framework.
UPDATING OF INFORMATION
Geotechnical engineers traditionally have used the observational method to help them deal with uncertainties in site conditions or performance behavior. The engineer will begin with a few hypotheses about the site conditions, and field observations are then gathered to pinpoint the correct hypothesis. This procedure can be formalized by applying probability theory. Whenever there is additional information about the site, be it from a site exploration program for a new site, measurements from nondestructive diagnostic tests for an existing infrastructure, or observations during an early phase of construction,
Bayesian probability procedures provide a logical basis for revising the engineer's judgment of the site characteristics. Conceptually, the updated probability of a given hypothesis, H1, based on observation, E, is determined from Bayes' theorem as
P″(H1) = k L(E ∣ H1) P′(H1) (Eq. C- 14)
where P'(H1) may represent the estimated probability of Hypothesis 1 prior to the observation; L(E ∣ H1), commonly referred to as the likelihood function, is the likelihood of Hypothesis 1 producing the observation, and k is a normalizing constant such that the sum of the updated probabilities of all potential hypotheses will be 1.0. Essentially, the likelihood function represents information from the observation; it is used to modify the prior judgmental probabilities to obtain the updated probabilities. Bayes ' theorem thus furnishes a systematic means of quantifying relative likelihood of the respective conceptual models in light of the observations and the respective reliability associated with each observation scheme. These probability values can be used to discriminate between contending models; they also can be used to update the performance reliability of a proposed geotechnical system. More importantly, by explicitly considering the relative reliability of respective observation schemes and relative likelihood of the conceptual models before and after the observations, the usefulness of each observation scheme in improving the overall system performance can be compared beforehand. This will facilitate the selection of what to measure or observe. Waste-remediation decisions, which increasingly involve geotechnical engineers, can benefit greatly from the above-described probabilistic observational method; this is also true for many other geotechnical applications, ranging from dam safety to repair/maintenance decisions concerning deteriorating infrastructures.
Hachich and Vanmarcke (1983) demonstrated an application of Bayesian methods to update the relative likelihood of two hypotheses of the drainage conditions of a dam based on piezometer measurements. The method was used by Tang et al. (1994) to update the coefficient of compression of waste material based on a set of settlement plates installed at a landfill site. These authors also showed how the Bayesian updating procedure could be incorporated in a probabilistic observational method to facilitate decisions associated with a landfill cover design. The following simple example demonstrates the essence of the Bayesian updating procedure:
Example
Leakage of contaminated material is suspected from a given landfill. Monitoring wells are proposed to verify if leakage has occurred. The locations of two wells are shown in Figure C-6. For simplicity, suppose that if leakage has occurred, the engineer estimates that the probability that it will be observed by well A is 80 percent, whereas well B is 90 percent likely to detect the leakage. Assume that neither well will
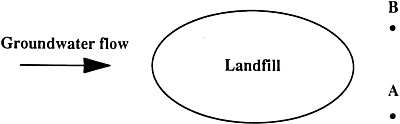
Figure C-6 Locations of monitoring wells for potential leakage of contaminants from a landfill.
erroneously register any contamination if there is no leakage from the landfill. Before any of these wells is installed, the engineer believes that there is a 70 percent chance that the leakage has happened. Consider first the case that well A has been installed and no contaminants have been observed. Clearly, the engineer's belief that leakage had occurred will decrease. With this observation, Bayes theorem yields
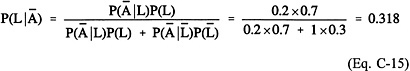
where L denotes the event of leakage, ![]() denotes the event of no leakage, A denotes the event of well A detecting contamination, Ā denotes the event of well A not detecting contamination, and P(L) is the engineer's estimate of leakage probability. In probability theory, P(L¦Ā) represents the conditional probability, namely the probability of leakage given that well A did not detect contaminants. Although the observation from well A seems to support the hypothesis that leakage has not occurred, the hypothesis cannot be fully substantiated because of the imperfect detectability of well A and also because of the engineer 's prior judgment. By considering these factors, the engineer would now believe that there is only a 31.8 percent chance that leakage has occurred.
denotes the event of no leakage, A denotes the event of well A detecting contamination, Ā denotes the event of well A not detecting contamination, and P(L) is the engineer's estimate of leakage probability. In probability theory, P(L¦Ā) represents the conditional probability, namely the probability of leakage given that well A did not detect contaminants. Although the observation from well A seems to support the hypothesis that leakage has not occurred, the hypothesis cannot be fully substantiated because of the imperfect detectability of well A and also because of the engineer 's prior judgment. By considering these factors, the engineer would now believe that there is only a 31.8 percent chance that leakage has occurred.
Suppose well B also has been installed, and it also fails to detect any contamination. By applying Bayes' theorem again, the probability of leakage based on the combined observations that both wells did not detect contamination is
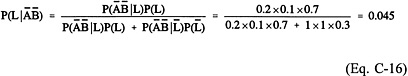
In the above calculation, the detectabilities between the wells have been assumed independent for simplicity. Hence, P(Ā![]() ¦L) is simply the product of P(Ā¦L) and P(
¦L) is simply the product of P(Ā¦L) and P(![]() ¦L). The results show that the observations from the two monitoring wells apparently imply that there is practically no likelihood of a leak. However, because of the imperfect reliability of the wells in diagnosing the leakage event, there is still a probability, though very small, that leakage has indeed happened.
¦L). The results show that the observations from the two monitoring wells apparently imply that there is practically no likelihood of a leak. However, because of the imperfect reliability of the wells in diagnosing the leakage event, there is still a probability, though very small, that leakage has indeed happened.
UNCERTAINTY IN MAPPING OF MATERIAL TYPES
Uncertainty in mapping arises when it is necessary to infer the type of soil material that exists at unobserved points from data obtained at points of observation. An example is the inference of the soil profile from borehole information during the characterization phase of a site. The question is, “What is the probability of finding a specific material type at a point, given that the material has been found or not found at another point or points?” The probability can be evaluated with the application of Bayesian methods, given a geological model of the spatial distribution of the material type. Wu et al. (1989) presented contour maps showing the probability of encountering clay at a given point in a soil stratum based on borehole samples and cone penetration records collected at a North Sea site. In fact, Bayes' theorem has been used extensively in conjunction with site characterization (e.g., Baecher, 1972; Wu and Wong, 1981). For instance, the unexpected presence of geologic anomalies, such as pockets of weak material in a stiff soil stratum or sand lenses in an otherwise impermeable clay stratum, can cause geotechnical failures. Even if a given site exploration program has not encountered such geologic anomaly, the experience of the engineer with the geology of the region may suggest that it could still be present at the site. In this case, the engineer's judgment can be combined with the level of site exploration efforts spent (e.g., number of borings) by means of the Bayesian procedure to estimate the likelihood of anomaly presence and the probability distribution of its size and location (Halim and Tang, 1993). The effects of these potential geologic anomalies then can be incorporated in the reliability evaluation of the geotechnical system.
DECISION UNDER UNCERTAINTY
Very often, engineers—or more appropriately, their clients—have to decide between alternatives that comprise different levels of expenditure and different probabilities of success. To rank a set of design alternatives, the potential risk associated with a given alternative should be considered, as well as the capital cost of the alternative. A decision tree, such as that shown in Figure C-7 for a landslide mitigation decision at a given site, can be used. The procedure identifies first the available alternatives of action and the possible outcomes, or sequences of outcome events associated with each alternative. Then the respective consequences or costs for each scenario or path can be assessed. The probability of each branch of outcome can be determined either from probabilistic models or by the engineer's judgment based on the available information. The probability of a path is simply the product of the respective probabilities. The expected cost of each alternative is the summation of the path probability multiplied by the path consequence over all outcome scenarios for that alternative. The alternative with the least expected cost is considered optimal if the commonly used expected value criteria is adopted for the decision. In this example, the optimal alternative for landslide mitigation at the site is to install a drainage system.
When the input probabilities and costs to the above decision analysis are only crude estimates, a sensitivity analysis should be performed to check if the optimal alternative will change within the estimated range of values for each probability or cost (see, e.g., Vick and Bromwell, 1989; Massmann et al., 1991).
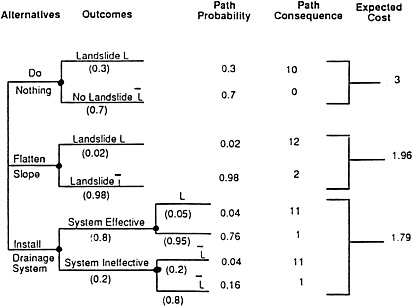
Decision tree for landslide mitigation.
REFERENCES
American Petroleum Institute. 1986. Recommended Practice for Planning, Design and Constructing Fixed Offshore Platforms. API Recommended Practice 2A, Sixteenth Edition. Washington, D.C.: API.
Ang, A.H.-S., and W.H. Tang. 1975. Probability Concepts in Engineering Planning and Design, Vol. 1: Basic Principles. New York: John Wiley & Sons.
Ang, A.H.-S., and W.H. Tang. 1984. Probability Concepts in Engineering Planning and Design, Vol. II: Decision, Risk and Reliability. New York: John Wiley & Sons. Currently distributed by BookMasters, Inc., Ohio.
Baecher, G.B. 1972. Site Exploration: A Probabilistic Approach. PhD Dissertation. Massachusetts Institute of Technology, Cambridge, Massachusetts.
Benjamin, J.R., and C.A. Cornell. 1970. Probability, Statistics and Decision for Civil Engineers. New York: McGraw-Hill.
Hachich, W., and E.H. Vanmarcke. 1983. Probabilistic updating of pore pressure fields. Journal of Geotechnical Engineering, American Society of Civil Engineers 109(3): 373–385.
Halim, I.S., and W.H. Tang. 1993. Site exploration strategy for geologic anomaly characterization. Journal of Geotechnical Engineering, American Society of Civil Engineers 119(2): 195–213.
Harr, M.E. 1977. Mechanics of Particulate Media. New York:McGraw-Hill.
Harr, M.E. 1987. Reliability-Based Design in Civil Engineering. New York: McGraw-Hill.
Madsen, H.O., S. Kwenk, and N.C. Lind. 1986. Methods of Structural Safety. Englewood Cliffs, New Jersey: Prentice-Hall, Inc.
Massmann, J., R.A. Freeze, L. Smith, T. Sperling, and B. James. 1991. Hydrogeologic decision analysis: 2. Applications to ground-water contamination. Ground Water 29(4): 536–548.
Olson, R.E., and N.D. Dennis. 1982. Review and compilation of pile test results, axial pile capacity. Geotechnical Engineering Report CR83-4. Austin, Texas: University of Texas, Department of Civil Engineering.
Rosenblueth, E. 1975. Point estimates for probability moments. Proceedings of National Academy of Sciences of the United States of America 72(10): 3812–3814.
Tang, W.H. 1984>.Principles of probabilistic characterization of soil properties. Pp. 74–89 in Probabilistic Characterization of Soil Properties, D.S. Bowles and Hon-Kim Ko, eds. New York: ASCE.
Tang, W.H. 1988. Offshore Axial Pile Design Reliability. Final Report for Project PRAC 86-29B sponsored by the American Petroleum Institute. Copies of this report may be obtained from the American Petroleum Institute, Washington, D.C.
Tang, W.H. 1989. Uncertainties in offshore axial pile capacity. Pp. 833–847 in Foundation Engineering: Current Principles and Practice, F.H. Kulhawy>, ed. New York: American Society of Civil Engineers.
Tang, W.H., R.B. Gilbert, M. Angulo, and R.S. Williams. 1994. Probabilistic observation method for settlement-based design of a landfill cover. Pp. 1573–1589 in Vertical and Horizontal Deformations of Foundations and Embankments , eds. Yeung and Felio. Geotechnical Special Publication No. 40, American Society of Chemical Engineers. New York: ASCE.
Vanmarcke, E.H. 1977. Probabilistic modeling of soil profiles. Journal of Geotechnical Engineering, American Society of Civil Engineers 103 (GT11): 1247–1266.
Vick, S.G. 1992. Risk in geotechnical practice. Pp. 41–62 in Geotechnique and Natural Hazards. Richmond, British Columbia: BiTech Publishers, Ltd.
Vick, S.G., and L.G. Bromwell. 1989. Risk analysis for dam design in karst. Journal of Geotechnical Engineering, American Society of Civil Engineers 115(6): 819–835.
Wu, T.H., and K.F. Wong. 1981. Probabilistic soil exploration: Case history. Journal of Geotechnical Engineering Division, American Society of Civil Engineers 107(GT12): 1693–1711.
Wu, T.H., O. Kjekstad, I.M. Lee, and S. Lacasse. 1989. Reliability analysis of foundation stability for gravity platforms in the North Sea. Canadian Geotechnical Journal 26: 359–368.