10
DEVELOPING PROFICIENCY IN TEACHING MATHEMATICS
In the previous chapter, we examined teaching for mathematical proficiency. We now turn our attention to what it takes to develop proficiency in teaching mathematics. Proficiency in teaching is related to effectiveness: consistently helping students learn worthwhile mathematical content. Proficiency also entails versatility: being able to work effectively with a wide variety of students in different environments and across a range of mathematical content.
What Does It Take to Teach for Mathematical Proficiency?
Teaching in the ways portrayed in chapter 9 is a complex practice that draws on a broad range of resources. Despite the common myth that teaching is little more than common sense or that some people are just born teachers, effective teaching practice can be learned. In this chapter, we consider what teachers need to learn and how they can learn it.
Despite the common myth that teaching is little more than common sense or that some people are just born teachers, effective teaching practice can be learned.
First, what does it take to be proficient at mathematics teaching? If their students are to develop mathematical proficiency, teachers must have a clear vision of the goals of instruction and what proficiency means for the specific mathematical content they are teaching. They need to know the mathematics they teach as well as the horizons of that mathematics—where it can lead and where their students are headed with it. They need to be able to use their knowledge flexibly in practice to appraise and adapt instructional materials, to represent the content in honest and accessible ways, to plan and conduct instruction, and to assess what students are learning. Teachers need to be able to hear and see expressions of students’ mathematical ideas and to design
|
A Chinese teacher on how a profound understanding of fundamental mathematics is attained One thing is to study whom you are teaching, the other thing is to study the knowledge you are teaching. If you can interweave the two things together nicely, you will succeed…. Believe me, it seems to be simple when I talk about it, but when you really do it, it is very complicated, subtle, and takes a lot of time. It is easy to be an elementary school teacher, but it is difficult to be a good elementary school teacher. SOURCE: Ma, 1999, p. 136. Used by permission from Lawrence Erlbaum Associates. |
appropriate ways to respond. A teacher must interpret students’ written work, analyze their reasoning, and respond to the different methods they might use in solving a problem. Teaching requires the ability to see the mathematical possibilities in a task, sizing it up and adapting it for a specific group of students. Familiarity with the trajectories along which fundamental mathematical ideas develop is crucial if a teacher is to promote students’ movement along those trajectories. In short, teachers need to muster and deploy a wide range of resources to support the acquisition of mathematical proficiency.
In the next two sections, we first discuss the knowledge base needed for teaching mathematics and then offer a framework for looking at proficient teaching of mathematics. In the last two sections, we discuss four programs for developing proficient teaching and then consider how teachers might develop communities of practice.
The Knowledge Base for Teaching Mathematics
Three kinds of knowledge are crucial for teaching school mathematics: knowledge of mathematics, knowledge of students, and knowledge of instructional practices.1 These can be seen in the instructional triangle (Box 9–1 in chapter 9 and below).2 Mathematics and students are two of the triangle’s vertices, and instructional practices are the interactions portrayed by the arrows.
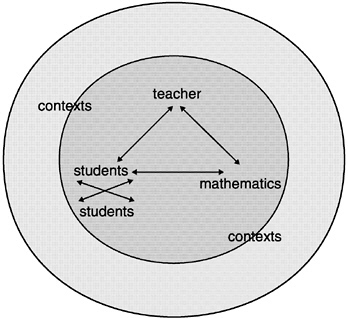
Mathematical knowledge includes knowledge of mathematical facts, concepts, procedures, and the relationships among them; knowledge of the ways that mathematical ideas can be represented; and knowledge of mathematics as a discipline—in particular, how mathematical knowledge is produced, the nature of discourse in mathematics, and the norms and standards of evidence that guide argument and proof. In our use of the term, knowledge of mathematics includes consideration of the goals of mathematics instruction and provides a basis for discriminating and prioritizing those goals. Knowing mathematics for teaching also entails more than knowing mathematics for oneself. Teachers certainly need to be able to understand concepts correctly and perform procedures accurately, but they also must be able to understand the conceptual foundations of that knowledge. In the course of their work as teachers, they must understand mathematics in ways that allow them to explain and unpack ideas in ways not needed in ordinary adult life. The mathematical sensibilities they hold matter in guiding their decisions and interpretations of students’ mathematical efforts.
Knowledge of students and how they learn mathematics includes general knowledge of how various mathematical ideas develop in children over time as well as specific knowledge of how to determine where in a developmental trajectory a child might be. It includes familiarity with the common difficul-
ties that students have with certain mathematical concepts and procedures, and it encompasses knowledge about learning and about the sorts of experiences, designs, and approaches that influence students’ thinking and learning.
Knowledge of instructional practice includes knowledge of curriculum, knowledge of tasks and tools for teaching important mathematical ideas, knowledge of how to design and manage classroom discourse, and knowledge of classroom norms that support the development of mathematical proficiency. Teaching entails more than knowledge, however. Teachers need to do as well as to know. For example, knowledge of what makes a good instructional task is one thing; being able to use a task effectively in class with a group of sixth graders is another. Understanding norms that support productive classroom activity is different from being able to develop and use such norms with a diverse class.
Knowledge of Mathematics
Because knowledge of the content to be taught is the cornerstone of teaching for proficiency, we begin with it. There is a substantial body of research on teachers’ mathematical knowledge, and teachers’ knowledge of mathematics is prominent in discussions of how to improve mathematics instruction. Improving teachers’ mathematical knowledge and their capacity to use it to do the work of teaching is crucial in developing students’ mathematical proficiency.
Many recent studies have revealed that U.S. elementary and middle school teachers possess a limited knowledge of mathematics, including the mathematics they teach. The mathematical education they received, both as K-12 students and in teacher preparation, has not provided them with appropriate or sufficient opportunities to learn mathematics. As a result of that education, teachers may know the facts and procedures that they teach but often have a relatively weak understanding of the conceptual basis for that knowledge. Many have difficulty clarifying mathematical ideas or solving problems that involve more than routine calculations.3 For example, virtually all teachers can multiply multidigit numbers, but several researchers have found that many prospective and practicing elementary school teachers cannot explain the basis for multidigit multiplication using place-value concepts and the underlying properties for adding and multiplying.4 In another study,5 teachers of fourth through sixth graders scored over 90% on items testing common decimal calculations, but fewer than half could find a number between 3.1 and 3.11.
Teachers frequently regard mathematics as a fixed body of facts and procedures that are learned by memorization, and that view carries over into their instruction. Many have little appreciation of the ways in which mathematical knowledge is generated or justified. Preservice teachers, for example, have repeatedly been shown to be quite willing to accept a series of instances as proving a mathematical generalization.6 Nowhere in their education have they had opportunities to study and experience the nature and role of justification in mathematics, a notion central to developing mathematical knowledge.
Although teachers may understand the mathematics they teach in only a superficial way, simply taking more of the standard college mathematics courses does not appear to help matters. The evidence on this score has been consistent, although the reasons have not been adequately explored. For example, a study of prospective secondary mathematics teachers at three major institutions showed that, although they had completed the upper-division college mathematics courses required for the mathematics major, they had only a cursory understanding of the concepts underlying elementary mathematics.7 The mathematics of the elementary and middle school curriculum is not trivial, and the underlying concepts and structures are worthy of serious, sustained study by teachers. To develop prospective teachers’ understanding of the mathematics they will teach, careful attention must be given to identifying the mathematics that teachers need in order to teach effectively, articulating the ways in which they must use it in practice and what that implies for their opportunities to learn mathematics. This sort of attention to teachers’ mathematical knowledge and its central role in practice is crucial to ensure that their study of mathematics provides teachers with mathematical knowledge useful to teaching well.
Teachers’ mathematical knowledge and student achievement. Conventional wisdom asserts that student achievement must be related to teachers’ knowledge of their subject. That wisdom is contained in adages such as “You cannot teach what you don’t know.” For the better part of a century, researchers have attempted to find a positive relation between teacher content knowledge and student achievement. For the most part, the results have been disappointing: Most studies have failed to find a strong relationship between the two.
Many studies, however, have relied on crude measures of these variables. The measure of teacher knowledge, for example, has often been the number of mathematics courses taken or other easily documented data from college
transcripts. Such measures do not provide an accurate index of the specific mathematics that teachers know or of how they hold that knowledge. Teachers may have completed their courses successfully without achieving mathematical proficiency. Or they may have learned the mathematics but not know how to use it in their teaching to help students learn. They may have learned mathematics that is not well connected to what they teach or may not know how to connect it. Similarly, many of the measures of student achievement used in research on teacher knowledge have been standardized tests that focus primarily on students’ procedural skills. Some evidence suggests that there is a positive relationship between teachers’ mathematical knowledge and their students’ learning of advanced mathematical concepts.8 There seems to be no association, however, between how many advanced mathematics courses a teacher takes and how well that teacher’s students achieve overall in mathematics.9 In general, empirical evidence regarding the effects of teachers’ knowledge of mathematics content on student learning is still rather sparse.
In the National Longitudinal Study of Mathematical Abilities (NLSMA), conducted during the 1960s and still today the largest study of its kind, there was essentially no association between students’ achievement and the number of credits a teacher had in mathematics at the level of calculus or beyond.10 Commenting on the findings from NLSMA and a number of other studies of teacher knowledge, the director of NLSMA later said,
It is widely believed that the more a teacher knows about his subject matter, the more effective he will be as a teacher. The empirical literature suggests that this belief needs drastic modification and in fact suggests that once a teacher reaches a certain level of understanding of the subject matter, then further understanding contributes nothing to student achievement.11
The notion that there is a threshold of necessary content knowledge for teaching is supported by the findings of another study in 1994 that used data from the Longitudinal Study of American Youth (LSAY).12 There was a notable increase in student performance for each additional mathematics course their teachers had taken, yet after the fifth course there was little additional benefit.13
Data from the 1996 NAEP on teachers’ college major rather than the number of courses they had taken provide a contrast to the general trend of this line of research. The NAEP data revealed that eighth graders taught by teachers who majored in mathematics outperformed those whose teachers
majored in education or some other field. Fourth graders taught by teachers who majored in mathematics education or in education tended to outperform those whose teachers majored in a field other than education.14
Although studies of teachers’ mathematical knowledge have not demonstrated a strong relationship between teachers’ mathematical knowledge and their students’ achievement, teachers’ knowledge is still likely a significant factor in students’ achievement. That crude measures of teacher knowledge, such as the number of mathematics courses taken, do not correlate positively with student performance data, supports the need to study more closely the nature of the mathematical knowledge needed to teach and to measure it more sensitively.
The persistent failure of the many efforts to show strong, definitive relations between teachers’ mathematical knowledge and their effectiveness does not imply that mathematical knowledge makes no difference in teaching. The research, however, does suggest that proposals to improve mathematics instruction by simply increasing the number of mathematics courses required of teachers are not likely to be successful. As we discuss in the sections that follow, courses that reflect a serious examination of the nature of the mathematics that teachers use in the practice of teaching do have some promise of improving student performance.
Teachers need to know mathematics in ways that enable them to help students learn. The specialized knowledge of mathematics that they need is different from the mathematical content contained in most college mathematics courses, which are principally designed for those whose professional uses of mathematics will be in mathematics, science, and other technical fields. Why does this difference matter in considering the mathematical education of teachers? First, the topics taught in upper-level mathematics courses are often remote from the core content of the K-12 curriculum. Although the abstract mathematical ideas are connected, of course, basic algebraic concepts or elementary geometry are not what prospective teachers study in a course in advanced calculus or linear algebra. Second, college mathematics courses do not provide students with opportunities to learn either multiple representations of mathematical ideas or the ways in which different representations relate to one another. Advanced courses do not emphasize the conceptual underpinnings of ideas needed by teachers whose uses of mathematics are to help others learn mathematics.15 Instead, the study of college mathematics involves the increasing compression of elementary ideas into the more and more powerful and abstract forms needed by those whose professional uses of mathematics will be in scientific domains. Third, advanced mathematical
study entails using elementary concepts and procedures without much conscious attention to their meanings or implications, thus reinforcing the making of prior learning routine in the service of more advanced work. While this approach is important for the education of mathematicians and scientists, it is at odds with the kind of mathematical study needed by teachers.
Consider the proficiency teachers need with algorithms. The power of computational algorithms is that they allow learners to calculate without having to think deeply about the steps in the calculation or why the calculations work. That frees up the learners’ thinking so that they can concentrate on the problem they are trying to use the calculation to solve rather than having to worry about the details of the calculation. Over time, people tend to forget the reasons a procedure works or what is entailed in understanding or justifying a particular algorithm. Because the algorithm has become so automatic, it is difficult to step back and consider what is needed to explain it to someone who does not understand. Consequently, appreciating children’s difficulties in learning an algorithm can be very difficult for adults who are fluent with that algorithm.
The necessary compression of ideas in the course of mathematical study also shortchanges teachers’ mathematical needs. Most advanced mathematics classes engage students in taking ideas they have already learned and using them to construct increasingly powerful and abstract concepts and methods. Once theorems have been proved, they can be used to prove other theorems. It is not necessary to go back to foundational concepts to learn more advanced ideas. Teaching, however, entails reversing the direction followed in learning advanced mathematics. In helping students learn, teachers must take abstract ideas and unpack them in ways that make the basic underlying concepts visible.16 For example, most adults have lost sight of the fact that there are different interpretations of division. For adults, division is an operation on numbers. Division, however, is rooted in quite different physical situations, and distinctions among those situations are important for understanding children’s thinking, developing their understanding of the meaning of division, and helping them apply that understanding to solve problems.17 For example, although both of the following problems can be represented as dividing 24 by 6, young children think about them in very different ways and use quite different strategies to solve them:18
Jane has 24 cookies. She wants to put 6 cookies on each plate. How many plates will she need?
Jeremy has 24 cookies. He wants to put all the cookies on 6 plates. If he puts the same number of cookies on each plate, how many cookies will he put on each plate?
These two problems correspond to the measurement and sharing models of division, respectively, that were discussed in chapter 3. Young children using counters solve the first problem by putting 24 counters in piles of 6 counters each. They solve the second by partitioning the 24 counters into 6 groups. In the first case the answer is the number of groups; in the second, it is the number in each group. Until the children are much older, they are not aware that, abstractly, the two solutions are equivalent. Teachers need to see that equivalence so that they can understand and anticipate the difficulties children may have with division.
To understand the sense that children are making of arithmetic problems, teachers must understand the distinctions children are making among those problems and how the distinctions might be reflected in how the children think about the problems. The different semantic contexts for each of the operations of arithmetic is not a common topic in college mathematics courses, yet it is essential for teachers to know those contexts and be able to use their knowledge in instruction. The division example illustrates a different way of thinking about the content of courses for teachers—a way that can make those courses more relevant to the teaching of school mathematics.
A recent study indicates that teachers’ performance on mathematical tasks that have been set in the context of teaching practice is positively related to student achievement.19 In the study, teachers’ ability to interpret four student responses to a ratio problem and to determine which were correct was strongly related to their students’ mathematics achievement.
Teachers’ mathematical knowledge and their teaching practice. Conventional wisdom holds that a teacher’s knowledge of mathematics is linked to how the teacher teaches. Teachers are unlikely to be able to provide an adequate explanation of concepts they do not understand, and they can hardly engage their students in productive conversations about multiple ways to solve a problem if they themselves can only solve it in a single way.
In the last 15 years, researchers have investigated how teachers’ mathematical knowledge shapes the way they teach. Most of the investigations have been case studies, almost all involving fewer than 10 teachers, and most only one to three teachers. In general, the researchers found that teachers
with a relatively weak conceptual knowledge of mathematics tended to demonstrate a procedure and then give students opportunities to practice it. Not surprisingly, these teachers gave the students little assistance in developing an understanding of what they were doing.20 When the teachers did try to provide a clear explanation and justification, they were not able to do so.21 In some cases, their inadequate conceptual knowledge resulted in their presenting incorrect procedures.22
Some of the same studies contrasted the teaching practices of teachers with low levels of mathematical knowledge with the teaching practices of teachers who had a better command of mathematics. These studies indicate that a strong grasp of mathematics made it possible for teachers to understand and use constructively students’ mathematical solutions, explanations, and questions.23 Several researchers found, however, that some teachers with strong conceptual knowledge did not necessarily use that knowledge to understand their students’ mathematical explanations, preferring instead to impose their own explanations.24
Knowledge of Students
Knowledge of students includes both knowledge of the particular students being taught and knowledge of students’ learning in general. Knowing one’s own students includes knowing who they are, what they know, and how they view learning, mathematics, and themselves. The teacher needs to know something of each student’s personal and educational background, especially the mathematical skills, abilities, and dispositions that the student brings to the lesson. The teacher also needs to be sensitive to the unique ways of learning, thinking about, and doing mathematics that the student has developed. Each student can be seen as located on a path through school mathematics, equipped with strengths and weaknesses, having developed his or her own approaches to mathematical tasks, and capable of contributing to and profiting from each lesson in a distinctive way.
Teachers also need a general knowledge of how students think—the approaches that are typical for students of a given age and background, their common conceptions and misconceptions, and the likely sources of those ideas. Over the last decade, researchers have produced an impressive body of evidence about how children’s thinking about various mathematical concepts progresses over time. We have described some of those progressions in chapters 6 through 8. Using that body of evidence, researchers have also
studied how teachers’ knowledge of students’ mathematical thinking is related to how they teach and to how well their students achieve.
From the many examples of misconceptions to which teachers need to be sensitive, we have chosen one: An important mathematical notion that poses a major stumbling block when students are moving from arithmetic to algebra is the role played by “=,” the sign for equality.25 As we discussed in chapter 8, many if not most elementary school children have the misconception that the equality sign is a signal to do something, to carry out the calculation that precedes it.26 The number immediately after the equal sign is seen as the answer to the calculation. For example, in the number sentence 8+4=□+5, many students would put 12 in the box. Children can develop this impression because that is how the notation is often described in the elementary school curriculum and most of their practice exercises fit that pattern. Few teachers realize the degree of their students’ misunderstanding of such sentences.27 Moreover, although most teachers have some idea that equality is a relation between two numbers, few realize how important it is that students understand equality as a relation, and few consider this need for understanding when they use the equals sign.
Knowledge of Classroom Practice
Knowing classroom practice means knowing what is to be taught and how to plan, conduct, and assess effective lessons on that mathematical content. It includes a knowledge of learning goals as expressed in the curriculum and a knowledge of the resources at one’s disposal for helping students reach those goals. It also includes skill in organizing one’s class to create a community of learners and in managing classroom discourse and learning activities so that everyone is engaged in substantive mathematical work. We have discussed these matters in chapter 9. This type of knowledge is gained through experience in classrooms and through analyzing and reflecting on one’s own practice and that of others.
In the sections that follow, we consider how to develop an integrated corpus of knowledge of the types discussed in this section. First, however, we need to clarify our stance on the relation between knowledge and practice. We have discussed the kinds of knowledge teachers need if they are to teach for mathematical proficiency. Although we have used the term knowledge throughout, we do not mean it exclusively in the sense of knowing about. Teachers must also know how to use their knowledge in practice. Teachers’ knowledge is of value only if they can apply it to their teaching; it cannot be
divorced from practice. Effective programs of teacher preparation and professional development cannot stop at simply engaging teachers in acquiring knowledge; they must challenge teachers to develop, apply, and analyze that knowledge in the context of their own classrooms so that knowledge and practice are integrated.
Proficient Teaching of Mathematics
In chapter 4 we identified five components or strands of mathematical proficiency. From that perspective, successful learning is characterized by comprehension of ideas; ready access to skills and procedures; an ability to formulate and solve problems; a capacity to reflect on, evaluate, and adapt one’s knowledge; the ability to reason from what is known to what is wanted; and a habitual inclination to make sense of and value what is being learned. Teaching is a complex activity and, like other complex activities, can be conceived in terms of similar components. Just as mathematical proficiency itself involves interwoven strands, teaching for mathematical proficiency requires similarly interrelated components. In the context of teaching, proficiency requires:
-
conceptual understanding of the core knowledge required in the practice of teaching;
-
fluency in carrying out basic instructional routines;
-
strategic competence in planning effective instruction and solving problems that arise during instruction;
-
adaptive reasoning in justifying and explaining one’s instructional practices and in reflecting on those practices so as to improve them; and a
-
productive disposition toward mathematics, teaching, learning, and the improvement of practice.
Like the strands of mathematical proficiency, these components of mathematical teaching proficiency are interrelated. In this chapter we discuss the problems entailed in developing a proficient command of teaching. In the previous section we discussed issues relative to the knowledge base needed to develop proficiency across all components. Now we turn to specific issues that arise in the context of the components.
Understanding of Core Knowledge
It is not sufficient that teachers possess the kinds of core knowledge delineated in the previous section. One of the defining features of conceptual understanding is that knowledge must be connected so that it can be used intelligently. Teachers need to make connections within and among their knowledge of mathematics, students, and pedagogy.
The kinds of knowledge that make a difference in teaching practice and in students’ learning are an elaborated, integrated knowledge of mathematics, a knowledge of how students’ mathematical understanding develops, and a repertoire of pedagogical practices that take into account the mathematics being taught and how students learn it. The implications for teacher preparation and professional development are that teachers need to acquire these forms of knowledge in ways that forge connections between them. For teachers who have already achieved some mathematical proficiency, separate courses or professional development programs that focus exclusively on mathematics, on the psychology of learning, or on methods of teaching provide limited opportunities to make these connections. Unfortunately, most university teacher preparation programs offer separate courses in mathematics, psychology, and methods of teaching that are taught in different departments. The difficulty of integrating such courses is compounded when they are located in different administrative units.
The professional development programs we discuss later in this chapter all situate their portrayals of mathematics and children’s thinking in contexts directly relevant to the problems teachers face daily in teaching mathematics.28 This grounding in reality allows knowledge of mathematics and knowledge of students to be connected in ways that make a difference for instruction and for learning. It is not enough, however, for mathematical knowledge and knowledge of students to be connected; both need to be connected to classroom practice. Teachers may know mathematics, and they may know their students and how they learn. But they also have to know how to use both kinds of knowledge effectively in the context of their work if they are to help their students develop mathematical proficiency.
Similarly, many inservice workshops, presentations at professional meetings, publications for teachers, and other opportunities for teacher learning focus almost exclusively on activities or methods of teaching and seldom attempt to help teachers develop their own conceptual understanding of the underlying mathematical ideas, what students understand about those ideas, or how they learn them. Alternative forms of teacher education and professional development that attempt to teach mathematical content, psychology
of learning, and methods of teaching need to be developed and evaluated to see whether prospective and practicing teachers from such programs can draw appropriate connections and apply the knowledge they have acquired to teach mathematics effectively.
Instructional Routines
The second basic component of teaching proficiency is the development of instructional routines. Just as students who have acquired procedural fluency can perform calculations with numbers efficiently, accurately, and flexibly with minimal effort, teachers who have acquired a repertoire of instructional routines can readily draw upon them as they interact with students in teaching mathematics. Some routines concern classroom management, such as how to get the class started each day and procedures for correcting and collecting homework. Other routines are more grounded in mathematical activity. For example, teachers need to know how to respond to a student who gives an answer the teacher does not understand or who demonstrates a serious misconception. They need to know how to deal with students who lack critical prerequisite skills for the day’s lesson. Teachers need businesslike ways of dealing with situations like these that occur on a regular basis so that they can devote more of their attention to the more serious issues facing them. When teachers have several ways of approaching teaching problems, they can try a different approach if one does not work.
Researchers have shown that expert teachers have a large repertoire of routines at their disposal.29 They can choose among a number of approaches for teaching a given topic or responding to a situation that arises in their classes. Novice teachers, in contrast, have a limited range of routines and often cannot respond appropriately to situations. Expert teachers not only have access to a range of routines, they also can apply them flexibly, know when they are appropriate, and can adapt them to fit different situations.
Strategic Competence
The third component of teaching proficiency is strategic competence. Although teachers need a range of routines, teaching is very much a problem-solving activity.30 Like other professionals, teachers are constantly faced with decisions in planning instruction, implementing those plans, and interacting with students.31 Useful guidelines are seldom available for figuring out what to teach when, how to teach it, how to adapt material so that it is appropriate for a given group of students, or how much time to allow for an activity. On
the spot, teachers need to find out what a student knows, choose how to respond to a student’s question or statement, and decide whether to follow a student’s idea. These are problems that every teacher faces every day, and most do not have readymade solutions.
Conceptual understanding of the knowledge required to teach for proficiency can help equip teachers to deal intelligently with these problems. It is misleading to claim that teachers actually solve such problems in the sense of solving a mathematical problem. There is never an ideal solution to the more difficult problems of teaching, but teachers can learn to contend with these problems in reasonable ways that take into account the mathematics that students are to learn; what their students understand and how they may best learn it; and representations, activities, and teaching practices that have proven most effective in teaching the mathematics in question or that have been effective in teaching related topics.
Teacher education and professional development programs that take into account the strategic decision making in teaching can help prepare teachers to be more effective in solving instructional problems. Rather than being designed to resolve teachers’ problems, programs of teacher education and professional development can engage prospective and practicing teachers in the analysis of instructional problems and potential ways of dealing with them. Teachers can learn to recognize that teaching involves solving problems and that they can address these problems in reasonable and intelligent ways.
Adaptive Reasoning
The fourth component of teaching proficiency is adaptive reasoning. Teachers can learn from their teaching by analyzing it: the difficulties their students have encountered in learning a particular topic; what the students have learned; how the students responded to particular representations, questions, and activities; and the like.32 Teachers can become reflective practitioners, and reflection is essential in improving their practice. The focus of teachers’ reflection and the tools they use shape the nature of that reflection and affect whether, what, and how they learn from it. Many successful programs of teacher education and professional development engage teachers in reflection, but the reflection, or perhaps more appropriately the analysis, is grounded in specific examples. In those programs, teachers engage in analyses in which they are asked to provide evidence to justify claims and assertions. As with other complex activities, teacher learning can be enhanced by making more visible the goals, assumptions, and decisions involved in the practice of
teaching.33 The implications for teacher education and professional development is that teachers engage not only in learning methods of teaching but also in reflecting on them and justifying and explaining them in relation to such matters as the mathematics being taught, the goals for students, the conceptions and misconceptions that students have about the mathematics, the difficulties they have in learning it, and the representations that are most effective in communicating essential ideas.
One of the ways that the professional development programs described below foster teachers’ ability to justify and explain classroom practices is that teachers examine familiar artifacts from practice, and those artifacts help them focus their attention and develop a common language for discussion. In some cases the program leaders provide the artifacts; in others the artifacts come from the teachers’ classrooms. Teachers are often asked to pose a particular mathematical problem to their classes and to discuss the mathematical thinking that they observe.
Productive Disposition
The final component of teaching proficiency is a productive disposition about one’s own knowledge, practice, and learning. Just as students must develop a productive disposition toward mathematics such that they believe that mathematics makes sense and that they can figure it out, so too must teachers develop a similar productive disposition. Teachers should think that mathematics, their understanding of children’s thinking, and their teaching practices fit together to make sense and that they are capable of learning about mathematics, student mathematical thinking, and their own practice themselves by analyzing what goes on in their classes. Teachers whose learning becomes generative perceive themselves as in control of their own learning.34 They learn by listening to their students and by analyzing their teaching practices. Not only do they develop more elaborated conceptions of how students’ mathematical thinking develops by listening to their students, but they also learn mathematical concepts and strategies from their interactions with students. The teachers become more comfortable with mathematical ideas and ripe for a more systematic view of the subject.
Teachers whose learning becomes generative see themselves as lifelong learners who can learn from studying curriculum materials35 and from analyzing their practice and their interactions with students. Programs of teacher education and professional development that portray to the participants that they are in control of their own learning help teachers develop a productive dispo-
sition toward learning about mathematics, student mathematical thinking, and teaching practice. Programs that provide readymade, worked-out solutions to teaching problems should not expect that teachers will see themselves as in control of their own learning.
Programs to Develop Proficient Teaching
In a teacher preparation program, teachers clearly cannot learn all they need to know about the mathematics they will teach, how students learn that mathematics, and how to teach it effectively. Consequently, some authorities have recommended that teacher education be seen as a professional continuum, a career-long process.36 Hence, teachers need a basis for ongoing learning. They need to be able to adapt to new curriculum frameworks, new materials, advances in technology, and advances in research on student thinking and teaching practice. They have to learn how to learn, whether they are learning about mathematics, students, or teaching. Teachers can continue to learn by participating in various forms of professional development. But formal professional development programs represent only one source for continued learning. Teachers’ schools and classrooms can also become places for teachers as well as students to learn.37 Professional development programs that engage teachers in inquiry in their classrooms can provide the basis for teachers’ learning to become generative so that their knowledge, conceptions, and practice continue to grow and evolve.38
Programs of teacher education and professional development based on research integrate the study of mathematics and the study of students’ learning so that teachers will forge connections between the two. Some of these programs begin with mathematical ideas from the school curriculum and ask teachers to analyze those ideas from the learners’ perspective. Other programs use students’ mathematical thinking as a springboard to motivate teachers’ learning of mathematics. Still others begin with teaching practice and move toward a consideration of mathematics and students’ thinking. We consider below examples of four such program types that represent an array of alternative approaches to developing integrated proficiency in teaching mathematics.39
Focus an Mathematics
Some teacher preparation and professional development programs attempt to enhance prospective and practicing teachers’ knowledge of mathematics by having them probe more deeply fundamental ideas from elementary school
mathematics, often through problem solving. For example, prospective elementary school teachers may take a mathematics course that focuses, in part, on rational numbers or proportionality rather than the usual college algebra or calculus. Such courses are offered in many universities, but they are seldom linked to instructional practice. The lesson depicted in Box 10–1 comes from a course in which connections to practice are being made.
|
Box 10–1 Investigating Division of Fractions in a Mathematics Course The prospective teachers stare at the board, trying to figure out what the instructor is asking them to do. After calculating the answer to a simple problem in the division of fractions The instructor proposes a new task: “See if you can make up a story problem, devise a real-world context, or draw a picture that will go with one and three fourths divided by a half. Can you come up with an example or a model that shows what is going on with dividing one and three fourths by one half?” The prospective teachers set to work, some in pairs, some alone. The instructor walks around, watching them work, and occasionally asking a question. Most have drawn pictures like those below: |
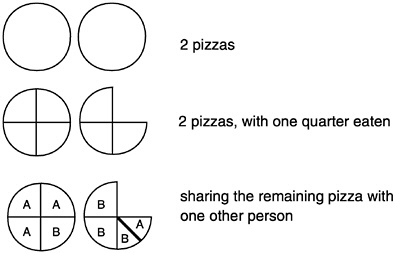 They have written problems like the following: I have two pizzas. My little brother eats one quarter of one of them and then I have one and three quarters pizzas left. My sister is very hungry, so we decide to split the remaining pizza between us. We each get One pair of students has a different problem: I have And another pair has envisioned filling After about 10 minutes, the instructor invites students to share their problems with the rest of the class. One student presents the pizza situation above. Most students nod appreciatively. When a second student offers the sesame cracker problem, most nod again, not noticing the difference. The instructor poses a question: How does each problem we heard connect with the original computation? Are these two problems similar or different, and does it matter? Through discussion the students gradually come to recognize that, in the pizza problem, the pizza has been divided in half and that the answer is in terms of fourths—that is, that the |
|
The instructor moves into a discussion of different interpretations of division: sharing and measurement. After the students observe that the successful problems— involving the sesame crackers and the liters of water—are measurement problems, she asks them to try to develop a problem situation for For homework, the instructor asks the students to try making representations for several other division situations, which she chooses strategically, and finally asks them to select two numbers to divide that they think are particularly good choices and to say why. She also asks them to try to connect what they have done in class today with the familiar algorithm of “invert and multiply.” |
In this excerpt from a university mathematics course, the prospective teachers are being asked to unpack familiar arithmetic content, to make explicit the ideas underlying the procedures they remember and can perform. Repeatedly throughout the course, the instructor poses problems that have been strategically designed to expose concepts on which familiar procedures rest.
One principle behind the instructor’s efforts is to engage the prospective teachers in a kind of mathematical work that focuses on developing their proficiency with the mathematical content of the elementary school curriculum. A second principle is to link that work with larger mathematical ideas and structures. For example, the lesson on the division of fractions is part of a larger agenda that includes understanding division, its relationship to fractions and to multiplication, and the meaning and representation of operations. Moreover, throughout the development of these ideas and connections, the prospective teachers work with whole and rational numbers, considering how the mathematical world looks inside these nested systems.
The overriding purpose of a course like this is to provide prospective teachers with ample opportunities to learn fundamental ideas of school mathematics, how they are related, and how students come to learn them. The
ways in which the prospective teachers’ opportunities to learn are designed may at times situate the mathematical questions within apparently pedagogical contexts (e.g., make a story problem), so that the kind of mathematical work they do in the course helps them develop mathematical proficiency in ways they can use in teaching. But the course is not about how to teach, nor about how children learn. It is explicitly and deliberately a sustained opportunity for prospective teachers to learn mathematical ideas in ways that will equip them with mathematical resources needed in teaching.
Focus on Student Thinking
The successful programs that focus on mathematics and children’s thinking are programs grounded in practice. Teachers do not learn abstract concepts about mathematics and children. In the programs, teachers look at problem-solving strategies of real students, artifacts of student work, cases of real classrooms, and the like. Furthermore, the teachers in these programs are challenged to relate what they learn to their own students and their own instructional practices. They learn about mathematics and students both in workshops and by interacting with their own students. Specific opportunity is provided for the teachers to discuss with one another how the ideas they are encountering influence their practice and how their practice influences what they are learning. Discussions in these programs are conducted in a spirit of supporting the teachers’ inquiry. The analysis of children’s thinking is not presented as a fixed body of knowledge, and the teachers engage not only in inquiry about how to apply knowledge about students’ thinking in planning and implementing instruction but also in inquiry to deepen their understanding of students’ thinking.40
The workshop described in Box 10–2 forms part of a professional development program designed to help teachers develop a deeper understanding of some critical mathematical ideas, including the equality sign. The program, modeled after Cognitively Guided Instruction (CGI), which has proven to be a highly effective approach,41 assists teachers in understanding how to help their students reason about number operations and relations in ways that enhance the learning of arithmetic and promote a smoother transition from arithmetic to algebra.42 This particular workshop was directed at illuminating students’ misconceptions about equality and considering how those misconceptions might be addressed.
Several features of this example of professional development are worth noting. The teachers focus on children’s thinking about a critical mathematical idea. Although they begin by considering how children think, the teachers
|
Box 10–2 Investigating the Concept of Equality in a Professional Development Group Before attending the workshop, participating teachers ask their students to find the number that they could put in the box to make the following open-number sentence a true number sentence: 8+4=□+5. At the workshop, the teachers share their findings with the other participants. Fewer than 10% of the students in any teacher’s class solved the problem correctly.* The majority of the incorrect responses were 12, with a number of responses of 17. These findings, which surprised most teachers, have led them to begin to listen to their students, and a number of teachers have engaged their students in a discussion of the reasons for their responses. The teachers’ experiences have precipitated a discussion in the workshop of how students are thinking about equality and how these misconceptions might have been acquired. The discussion generates insights about how children are thinking and what teachers can learn by listening to their students. Although the teachers recognize the students’ errors on this problem, however, they do not have a good idea of how they would address the misconception. The workshop leader introduces several true and false number sentences as a context to challenge children’s incorrect notions of equality. Examples include 8=3+5, 17+9=36, 23=23, 17+26=27+16, and 76+7=76. The task is to decide whether the sentence is true or false. Sometimes the decision requires calculation (e.g., 74–57=17), and sometimes it does not (e.g., 67+96=96+67). The teachers work in small groups to construct true and false number sentences they might use to elicit various views of equality. Using these sentences, their students could engage in explorations that might lead to understanding equality as a relation. The sentences could also provide opportunities for discussions about how to resolve disagreement and develop a mathematical argument. The teachers work together to consider how their students might respond to different number sentences and which number sentences might produce the most fruitful discussion. SOURCE: Falkner, Levi, and Carpenter, 1999. Used by permission of the authors. |
must also examine their own conceptions. Properties of equality that the teachers have not usually examined carefully before emerge in their discussions of students’ conceptions and misconceptions in using the equals sign. The teachers also begin to ponder how notation is used and how ideas are justified in mathematics. A central feature of their discussion is that math-
ematics and children’s thinking are set in a context that relates to their practice. The mathematical ideas and how children think about them are seen in classroom interactions. The problems discussed in the workshop are problems that the teachers can and do use in their classes; the interactions about mathematics that occur in the teachers’ classes provide a setting for workshop discussion of mathematical ideas and children’s thinking. The activities taking place in the workshop and in the teachers’ classrooms have the same goals. In both places the teachers engage in inquiry to gain a deeper understanding of mathematics, students’ thinking about that mathematics, and how to plan their instruction so as to foster the development of students’ mathematical thinking.
Before beginning a professional development program similar to the one described above, teachers participating in the program found that fewer than 10% of their students at any grade demonstrated a relational concept of equality. After one year of the program, the percentage of students in their classes who demonstrated a relational concept of equality ranged from 66% in first and second grades to 84% in sixth grade.43
Although these programs place a heavy emphasis on children’s thinking, understanding children’s mathematical thinking depends upon understanding the mathematics with which that thinking is engaged. The programs do not deal with general theories of learning. They concentrate instead on understanding children’s thinking in specific domains of mathematical content. Understanding the mathematics of the domain being studied is a prerequisite to understanding children’s thinking in that domain. For example, to understand the different strategies that children use to solve different problems, teachers must understand the semantic differences between problems represented by the same operation, as illustrated by the sharing and measurement examples of dividing cookies described above in Box 10–1. In programs focusing on children’s mathematical thinking, teachers learn to recognize and appreciate the mathematical significance of children’s informal methods for solving problems, how these methods evolve into more abstract and more powerful methods, and how the informal methods could serve as a basis for students to learn formal concepts and procedures with understanding.
Professional development programs focusing on helping teachers understand both the mathematics of specific content domains and students’ mathematical thinking in that domain have consistently been found to contribute to major changes in teachers’ instructional practices that have resulted in significant gains in students’ achievement.44 For example, in an experimental study of CGI with first-grade teachers, teachers who had taken a month-long
workshop on children’s development of addition and subtraction concepts taught problem solving significantly more and number facts significantly less than did teachers who had instead taken two 2-hour workshops on nonroutine problem solving. Students in the CGI teachers’ classes performed as well as students in the comparison teachers’ classes on a standardized computation test and outperformed students in the comparison teachers’ classes on complex addition and subtraction word problems.45 After teachers have studied the development of children’s mathematical thinking, they tend to place a greater emphasis on problem solving, listen to their students more and know more about their students’ abilities, and provide greater opportunity for their students to use a variety of solution methods. Gains in student achievement generally have been in the areas of understanding and problem solving, but none of the programs has led to a decline in computational skills, despite their greater emphasis on higher levels of thinking.
Focus an Cases
Case examples are yet another way to build the connections between knowledge of mathematics, knowledge of students, and knowledge of practice. Although the cases focus on classroom episodes, the discussions the teachers engage in as they reflect on the cases emphasize mathematics content and student thinking. The cases involve instruction in specific mathematical topics, and teachers analyze the cases in terms of the mathematics content being taught and the mathematical thinking reflected in the work the children produce and the interactions they engage in. Cases can be presented in writing or using multiple media such as videotapes and transcriptions of lessons. The episode in Box 10–3 is taken from a case discussion in which the case is presented through video recordings of lessons from an entire year that were captured on computer disks, together with the teacher’s plans and reflections and with samples of student work.
Notable in this example is how the teachers’ opportunities to consider mathematical ideas—in this case, functions—are set in the context of the use of those ideas in teaching. These teachers are probing the concept of functions from several overlapping perspectives. They dig into the mathematics through close work on and analysis of the task that the teacher posed. They also explore the ideas by investigating students’ work on the problem. And they revisit the mathematical ideas by looking carefully at how the teacher deals with the mathematics during the lesson.
|
Box 10–3 Investigating Mathematical Tasks Using Cases from Real Practice A dozen teachers are gathered around a table. They have read a case of a teacher teaching a lesson on functions. The written case includes the task the teacher used and a detailed narrative account of what happened in the class as students worked on the problem. The teacher used the following task: Sara has made several purchases from a mail-order company. She has found that the company charges $12.90 to ship an 8-kg package, $6.40 to ship a 3-kg package, and $9.00 to ship a 5-kg package. Sara decides that the company must be using a simple rule to determine how much to charge for shipping. Help her figure out how much it would most likely cost to ship a 1-kg package and how much each additional kilogram would cost. Photocopies of students’ work are available, as are pages from the curriculum materials being used. Before the teachers studied the case and the accompanying materials, they solved the mathematical problem themselves. To begin the discussion, the workshop leader asks the teachers to look closely at one segment of the lesson in which two students are presenting solutions to the problem. She asks them to interpret what each student did and to compare the two solutions. This request precipitates an animated discussion in which the teachers probe the students’ representations and explanations. One teacher notes that a third student has a method that is similar to the first student’s, but several others argue that the method is not similar. The teachers continue to analyze the students’ thinking, with repeated careful use of the reproductions of the students’ work. At one point one teacher raises a mathematical point, asking whether there might be something particularly significant in one student’s idea. The teachers launch into a discussion of the mathematics for several minutes. They note that if the given values (weight, cost) are graphed, the points lie on the same straight line. Reading the graph provides a solution. Also, by asking how much each additional kilogram would cost, the problem suggests there is a constant difference that can be used in solving it. Since the 2-kg difference between 5 kg and 3 kg is $2.60, and the 3-kg difference between 8 kg and 5 kg is $3.90, the simplest rule would be that each additional kilogram costs $1.30. A linear function (y=1.30x+2.50) fits the three values, and one can use constant differences or a graph to find this function (although that is not necessary to answer the two questions). After a much-needed break, the leader refocuses the discussion on the teacher’s moves throughout the episode that they have been discussing. At first, several |
|
teachers comment that the teacher doesn’t seem to be doing much. “She is more of a guide,” one teacher remarks. “It is really a student-centered class.” “Is it?” asks the leader. She asks them to analyze the text closely and try to categorize what the teacher is doing. This discussion yields surprises for most of the teachers. Suddenly the intricate work that the teacher is doing becomes visible. They see her posing strategic questions, using particular aspects of the students’ solutions to focus the class discussion, providing direction at some moments and letting the students struggle a bit at others. They begin to describe and name the different moves she makes. One teacher becomes intrigued with how the teacher helps students express their ideas by asking questions to support their explanations before she asks other students to comment. It is quite clear that this is no generic skill, for the mathematical sensitivity and knowledge entailed are quite visible throughout. Another teacher notices how the teacher’s own mathematical knowledge seems to shape her skilled questioning. The teachers become fascinated with what looks like an important missed opportunity to unpack a common misconception about function. Speculating about why that happened leads them to a productive conversation about what one might do to seize and capitalize on the opportunity. The session ends with the teachers agreeing to bring back one mathematical task from their own work on functions and compare it with the task used in the case. Several are overheard to be discussing features of this problem that seem particularly fruitful and that have them thinking about how they frame problems for their students. The group briefly discusses some ways to vary the problem to make it either simpler or more complex. The leader then closes by summarizing some of the mathematical issues embedded in the task. She points out that it is not obvious what the value of 2.50 means in the algebraic expression of the function. It is the cost of sending a package of zero weight, an idea that does not appear anywhere in the problem itself or in real life. She also says that it is important to understand that x refers to whole numbers only. Finally, she notes that with a different function, the differences might not be constant. The assumption of constant differences is one suggested by the problem and common in situations like those involving shipping costs, but it is not necessarily always warranted. |
Studies of teachers’ learning in professional development programs that have used classroom cases show that the teachers learned mathematics from studying such cases. They gained a greater repertoire of ways to represent mathematical ideas, were able to articulate connections among mathematical ideas, and developed a deeper understanding of mathematical structures.46
As a result of their work in this program, the teachers became more likely to bring out students’ reasoning in discussions and to invite both public and private reflection on the students’ ideas. At least some of the teachers continued the process of learning mathematics by examining the mathematical work of their own students in their own classrooms.
The case-based programs that focus on classroom instruction treat the cases as problematic situations that serve as a basis for discussion and inquiry rather than as models of instruction for the teachers to emulate. Teachers analyze classes not to figure out how they can do what the teacher in the case example did; instead, the case discussions provide models for inquiry that teachers may apply to analyze their own students’ mathematical thinking and their own teaching practices.
Focus on Lesson Study
A somewhat different approach to professional development is represented by so-called lesson study groups, which are used in Japan (see Box 10–4). These study groups focus on the development and refinement of one specific mathematical lesson, called a “research lesson.” Teachers work together to consider a specific difficulty entailed in teaching some important piece of mathematics. They design a lesson, and one member of the group teaches it while the others watch. Afterwards they discuss what happened in light of their anticipations and goals. Based on this experience, the group revises the lesson and someone else teaches it. The cycle continues of trying the lesson, discussing and analyzing how it worked, and revising it. Through such lesson study groups, teachers engage in very detailed analyses of mathematics, of students’ mathematical thinking and skill, of teaching and learning. Although the process results in a well-crafted lesson, in the process of developing and refining the lesson, teachers work on analyzing students’ responses and learn from and revise their own teaching practices. Their knowledge becomes a basis for further learning through the study of a lesson.47
Lesson study groups might follow somewhat different formats and schedules than the one described above, but most meet regularly during the year and focus on improving a very few lessons with clear learning goals. Using the lesson as the unit of analysis and improvement, the teachers are encouraged to improve their knowledge of all aspects of teaching within the context of their own classrooms—knowledge of mathematics, of students’ thinking, of pedagogy, of curriculum, and of assessment. Although the year’s activity yields a collective product that can be shared with other teachers (the group’s written report), Japanese teachers say that the primary value of lesson study
|
Box 10–4 The Japanese Lesson Study Small groups of teachers form within the school around areas of common teaching interests or responsibilities (e.g., grade-level groups in mathematics or in science). Each group begins by formulating a goal for the year. Sometimes the goal is adapted from national-level recommendations (e.g., improve students’ problem-solving skills) and is translated into a more specific goal (e.g., improve students’ understanding of problems involving ratios). The more specific goal might focus on a curriculum topic that has been problematic for students in their classrooms. A few lessons then are identified that ordinarily deal with that topic, and the group begins its yearlong task to improve those lessons. Lesson study groups meet regularly, often once a week after school (e.g., 3:00 to 5:00 pm), to develop, test, and refine the improved lessons. Some groups divide their work into three major phases, each taking about one third of the school year. During the first phase, teachers do research on the topic, reading and sharing relevant research reports and collecting information from other teachers on effective approaches for teaching the topic. During the second phase, teachers design the targeted lessons (often just one, two, or perhaps three lessons). Important parts of the design include (a) the problems that will be presented to students, (b) the teachers’ predictions about how students will solve the problems, and (c) how these different solution methods are to be integrated into a productive class discussion. During the third phase, the lessons are tested and refined. The first test often involves one of the group members teaching a lesson to his or her class while the other group members observe and take notes. After the group refines the lesson, it might be tested with another class in front of all the teachers in the school. In this case, a follow-up session is scheduled, and the lesson study group engages their colleagues in a discussion about the lesson, receiving feedback about its effectiveness. The final task for the group is to prepare a report of the year’s work, including a rationale for the approach used and a detailed plan of the lesson, complete with descriptions of the different solution methods students are likely to present and the ways in which these can be orchestrated into a constructive discussion. |
is teacher development. Working directly on improving teaching is their means of becoming better teachers.
Communities of Practice
Learning in ways that continue to be generative over time is best done in a community of fellow practitioners and learners, as illustrated by the Japanese lesson study groups. The foregoing discussion of teacher proficiency focused on individual teachers’ knowledge, but teaching proficiency does not easily develop and is not generally sustained in isolation. Studies of school reform efforts suggest that professional development is most effective when it extends beyond the individual teacher.48 Collaboration among teachers provides support for them to engage in the kinds of inquiry that are needed to develop teaching proficiency. Professional development can create contexts for teacher collaboration, provide a focus for the collaboration, and provide a common frame for interacting with other teachers around common problems. When teachers have opportunities to continue to participate in communities of practice that support their inquiry, instructional practices that foster the development of mathematical proficiency can more easily be sustained.
Professional development can create contexts for teacher collaboration, provide a focus for the collaboration, and provide a common frame for interacting with other teachers around common problems.
The focus of teacher groups matters for what teachers learn from their interactions with others. When sustained work is focused on mathematics, on students’ thinking about specific mathematical topics, or on the detailed work of designing and enacting instruction, the resources generated for teachers’ own practice are greater than when there is less concrete focus. For example, general sharing, or discussion of approaches, ungrounded in the particulars of classroom artifacts, while possibly enjoyable, less often produces usable knowledge that can make a difference for teachers’ work.
Mathematics Specialists
Because of the specialized knowledge required to teach mathematics, there has been increased discussion recently of the use of mathematics specialists, particularly in the upper elementary and middle school grades. The Learning First Alliance, comprising 12 major education groups, recommends that mathematics teachers from grades 5 through 9 have “a solid grounding in the coursework of grades K-12 and the teaching of middle grades mathematics.”49 The Conference Board of the Mathematical Sciences recommends in its draft report that mathematics in middle grades should be taught by mathematics specialists, starting at least in the fifth grade.50 They further recommend that teachers of middle school mathematics have taken 21 semester
hours of mathematics, 12 of which are on fundamental ideas of school mathematics appropriate for middle school teachers.
Implicit in the recommendations for mathematics specialists is the notion of the mathematics specialist in a departmental arrangement. In such arrangements, teachers with a strong background in mathematics teach mathematics and sometimes another subject, depending on the student population, while other teachers in the building teach other subject areas. Departmentalization is most often found in the upper elementary grades (4 to 6). Other models of mathematics specialists are used, particularly in elementary schools, which rarely are departmentalized. Rather than a specialist for all mathematics instruction, a single school-level mathematics specialist is sometimes used. This person, who has a deep knowledge of mathematics and how students learn it, acts as a resource for other teachers in the school. The specialist may consult with other teachers about specific issues, teach demonstration lessons, observe and offer suggestions, or provide special training sessions during the year. School-level mathematics specialists can also take the lead in establishing communities of practice, as discussed in the previous section. Because many districts do not have enough teachers with strong backgrounds in mathematics to provide at least one specialist in every school, districts instead identify district-level mathematics coaches who are responsible for several schools. Whereas a school-level specialist usually has a regular or reduced teaching assignment, district-level specialists often have no classroom teaching assignment during their tenure as a district coach. The constraint on all of the models for mathematics specialists is the limited number of teachers, especially at the elementary level, with strong backgrounds in mathematics. For this reason, summer leadership training programs have been used to develop mathematics specialists.
Effective Professional Development
Perhaps the central goal of all the teacher preparation and professional development programs is in helping teachers understand the mathematics they teach, how their students learn that mathematics, and how to facilitate that learning. Many of the innovative programs described in this chapter make serious efforts to help teachers connect these strands of knowledge so that they can be applied in practice. Teachers are expected to explain and justify their ideas and conclusions. Teachers’ ideas are respected, and they are encouraged to engage in inquiry. They have opportunities to develop a productive disposition toward their own learning about teaching that contrib-
utes to their learning becoming generative. Teachers are not given readymade solutions to teaching problems or prescriptions for practice. Instead, they adapt what they are learning and engage in problem solving to deal with the situations that arise when they attempt to use what they learn.
Professional development beyond initial preparation is critical for developing proficiency in teaching mathematics. However, such professional development requires the marshalling of substantial resources. One of the critical resources is time. If teachers are going engage in inquiry, they need repeated opportunities to try out ideas and approaches with their students and continuing opportunities to discuss their experiences with specialists in mathematics, staff developers, and other teachers. These opportunities should not be limited to a period of a few weeks or months; instead, they should be part of the ongoing culture of professional practice. Through inquiry into teaching, teacher learning can become generative, and teachers can continue to learn and grow as professionals.
Notes
References
Ball, D.L. (1988). The subject matter preparation of prospective mathematics teachers: Challenging the myths (Research Report 88–3). East Lansing: Michigan State University, National Center for Research on Teacher Learning. Available: http://ncrtl.msu.edu/http/rreports/html/rr883.htm. [July 10, 2001].
Ball, D.L. (1990). The mathematical understandings that prospective teachers bring to teacher education. Elementary School Journal, 90, 449–466.
Ball, D.L. (1991). Research on teaching mathematics: Making subject matter knowledge part of the equation. In J.Brophy (Ed.), Advances in research on teaching, Vol. 2: Teachers’ knowledge of subject matter as it relates to their teaching practice (pp. 1–48). Greenwich, CT: JAI Press.
Ball, D.L., & Bass, H. (2000). Interweaving content and pedagogy in teaching and learning to teach: Knowing and using mathematics. In J.Boaler (Ed.), Multiple perspectives on the teaching and learning of mathematics (pp. 83–104). Westport, CT: JAI/Ablex.
Barnett, C. (1991). Building a case-based curriculum to enhance the pedagogical content knowledge of mathematics teachers. Journal of Teacher Education, 42, 263–272.
Barnett, C. (1998). Mathematics teaching cases as a catalyst for informed strategic inquiry. Teaching and Teacher Education, 14(1), 81–93.
Begle, E.G. (1972). Teacher knowledge and student achievement in algebra (SMSG Reports No. 9). Stanford, CA: Stanford University, School Mathematics Study Group.
Begle, E.G. (1979). Critical variables in mathematics education: Findings from a survey of the empirical literature. Washington, DC: Mathematical Association of America and National Council of Teachers of Mathematics.
Behr, M., Erlwanger, S., & Nichols, E. (1976). How children view equality sentences (PMDC Technical Report No. 3). Tallahassee: Florida State University. (ERIC Document Reproduction Service No. ED 144 802).
Behr, M., Erlwanger, S., & Nichols, E. (1980). How children view the equals sign. Mathematics Teaching, 92, 13–15.
Borko, H., Eisenhart, M., Brown, C.A., Underhill, R.G., Jones, D. & Agard, P.C. (1992). Learning to teach hard mathematics: Do novice teachers and their instructors give up too easily? Journal for Research in Mathematics Education, 23, 194–222.
Brown, J.S., Collins, A., & Duguid, P. (1989). Situated cognition and the culture of learning. Educational Researcher, 18(1), 32–42.
Campbell, P.F. (1996). Empowering children and teachers in the elementary mathematics classrooms of urban schools. Urban Education, 30, 449–475.
Carpenter, T.P. (1988). Teaching as problem solving. In R.I.Charles & E.A.Silver (Eds.), The teaching and assessing of mathematical problem solving (pp. 187–202). Reston, VA: National Council of Teachers of Mathematics.
Carpenter, T.P., Fennema, E., & Franke, M.L. (1996). Cognitively Guided Instruction: A knowledge base for reform in primary mathematics instruction. Elementary School Journal, 97, 3–20.
Carpenter, T.P., Fennema, E., Franke, M.L., Empson, S.B., & Levi, L.W. (1999). Children’s mathematics: Cognitively guided instruction. Portsmouth, NH: Heinemann.
Carpenter, T.P., Fennema, E., Peterson, P.L., Chiang, C.P., & Loef, M. (1989). Using knowledge of children’s mathematics thinking in classroom teaching: An experimental study. American Educational Research Journal, 26, 499–531.
Carpenter, T.P., & Levi, L. (1999, April). Developing conceptions of algebraic reasoning in the primary grades. Paper presented at the meeting of the American Educational Research Association, Montreal.
Clark, C.M., & Peterson, P.L. (1986). Teachers’ thought processes. In M.C.Wittrock (Ed.), Handbook of research on teaching (3rd ed., pp 225–296). New York: Macmillan.
Cobb, P., Wood, T., Yackel, E.Nicholls, J., Wheatley, G., Trigatti, B., & Perlwitz, M. (1991). Assessment of a problem-centered second-grade mathematics project. Journal for Research in Mathematics Education, 22, 3–29.
Cohen, D.K., & Ball, D.L. (1999). Instruction, capacity, and improvement (CPRE Research Report No. RR-043). Philadelphia: University of Pennsylvania, Consortium for Policy Research in Education.
Cohen, D.K., & Ball, D.L. (2000, April). Instructional innovation: Reconsidering the story. Paper presented at the meeting of the American Educational Research Association, New Orleans.
Conference Board of the Mathematical Sciences. (2000, September). CBMS Mathematical Education of Teachers Project draft report [On-line]. Available: http://www.maa.org/cbms/metdraft/index.htm. [January 3, 2001].
Davenport, L. (in press). Elementary mathematics curricula as a tool for mathematics education reform: Challenges of implementation and implications for professional development. In P.Smith, A.Morse, & L.Davenport (Eds.), Teacher learning and curriculum implementation. Newton, MA: Education Development Center, Center for the Development of Teaching.
Erlwanger, S., & Berlanger, M. (1983). Interpretations of the equal sign among elementary school children. In J.C.Bergeron & N.Herscovics (Eds.), Proceedings of the Fifth Annual Meeting of the North American Chapter of the International Group for the Psychology of Mathematics Education (vol. 1, pp. 250–258). Montreal: University of Montreal. (ERIC Document Reproduction Service No. ED 289 688).
Falkner, K.P., Levi, L., & Carpenter, T.P. (1999). Children’s understanding of equality: A foundation for algebra. Teaching Children Mathematics, 6, 232–236.
Fennema, E., Carpenter, T.P., Franke, M.L., Levi, L., Jacobs, V., & Empson, B. (1996). A longitudinal study of learning to use children’s thinking in mathematics instruction. Journal for Research in Mathematics Education, 27, 403–434.
Fernández, E. (1997). The “‘Standards’-like” role of teachers’ mathematical knowledge in responding to unanticipated student observations. Paper presented at the meeting of the American Educational Research Association, Chicago. (ERIC Document Reproduction Service No. ED 412 261).
Franke, M.L., Carpenter, T.P., Fennema, E., Ansell, E., & Behrent, J. (1998). Understanding teachers’ self-sustaining, generative change in the context of professional development. Teaching and Teacher Education, 14(1), 67–80.
Franke, M.L., Carpenter, T.P., Levi, L. & Fennema, E. (in press). Capturing teachers’ generative change: A follow up study of teachers’ professional development in mathematics. American Educational Research Journal.
Gordon, A., & Heller, J. (1995, April). Traversing the web: Pedagogical reasoning among new and continuing case methods participants. Paper presented at the meeting of the American Educational Research Association, San Francisco.
Greer, B. (1992). Multiplication and division as models of situations. In D.Grouws (Ed.), Handbook of research on mathematics teaching and learning (pp. 276–295). New York: Macmillan.
Hargreaves, A. (1994). Changing teachers, changing times: Teacher work and culture in the postnuclear age. New York: Teachers College Press.
Hawkins, E.F., Stancavage, F.B., & Dossey, J.A. (1998). School policies and practices affecting instruction in mathematics (NCES 98–495). Washington, DC: National Center for Education Statistics. Available: http://nces.ed.gov/spider/webspider/98495.shtml. [July 10, 2001].
Kieran, C. (1981). Concepts associated with the equality symbol. Educational Studies in Mathematics, 12, 317–326.
Learning First Alliance. (1998). Every child mathematically proficient: An action plan. Washington, DC: Author. Available: http://www.learningfirst.org/publications.html. [July 10, 2001].
Leinhardt, G., & Smith, D.A. (1985). Expertise in mathematics instruction: Subject matter knowledge. Journal of Educational Psychology, 77, 247–271.
Lewis, C., & Tsuchida, I. (1998). A lesson is like a swiftly flowing river: How research lessons improve Japanese education. American Educator, 22(4), 12–17, 50–52.
Lewis, J.M., & Ball, D.L. (2000, April). Making teaching visible. Paper presented at the meeting of the American Educational Research Association, New Orleans.
Little, J.W. (1993). Teachers’ professional development in a climate of educational reform. Educational Evaluation and Policy Analysis, 15, 129–151.
Loucks-Horsley, S., Hewson, P.W., Love, N., & Stiles, K.E. (1998). Designing professional development for teachers of science and mathematics. Thousand Oaks, CA: Corwin Press.
Lubinski, C.A., Otto, A.D., Rich, B.S., & Jaberg, P.A. (1998). An analysis of two novice K-8 teachers using a model of teaching-in-context. In S.Berenson, K.Dawkins, M. Blanton, W.Coulombe, J.Kolb, K.Norwood, & L.Stiff (Eds.), Proceedings of the Twentieth Annual Meeting of the North American Chapter of the International Group for the Psychology of Mathematics Education (vol. 2, pp. 704–709). Columbus, OH: ERIC Clearinghouse for Science, Mathematics, and Environmental Education. (ERIC Document Reproduction Service No. ED 430 776).
Ma, L. (1999). Knowing and teaching elementary mathematics: Teachers’ understanding of fundamental mathematics in China and the United States. Mahwah, NJ: Erlbaum.
Matz, M. (1982). Towards a process model for school algebra errors. In D.Sleeman & J. S.Brown (Eds.), Intelligent tutoring systems (pp. 25–50). New York: Academic Press.
Martin, W.G., & Harel, G. (1989). Proof frames of preservice elementary teachers. Journal for Research in Mathematics Education, 20, 41–51.
Monk, D.H. (1994). Subject area preparation of secondary mathematics and science teachers and student achievement. Economics of Education Review, 13, 125–145.
Mullens, J.E., Murnane, R.J., & Willett, J.B. (1996). The contribution of training and subject matter knowledge to teaching effectiveness: A multilevel analysis of longitudinal evidence from Belize. Comparative Education Review, 40, 139–157.
Nathan, M.J., & Koedinger, K.R. (2000). An investigation of teachers’ beliefs of students’ algebra development. Cognition and Instruction, 18, 209–237.
National Research Council. (2000). Educating teachers of science, mathematics, and technology: New practices for the new millennium. Washington, DC: National Academy Press. Available: http://books.nap.edu/catalog/9832.html. [July 10, 2001].
National Research Council. (2001). Knowing and learning mathematics for teaching: Proceedings of a workshop. Washington, DC: National Academy Press. Available: http://books.nap.edu/catalog/10050.html. [July 10, 2001].
Post, T.R., Harel, G., Behr, M.J. & Lesh, R. (1991). Intermediate teachers’ knowledge of rational number concepts. In E.Fennema, T.P.Carpenter, & S.J.Lamon (Eds.), Integrating research on teaching and learning mathematics (pp. 194–217). Albany: State University of New York Press.
Putnam, R.T., & Borko, H. (2000, January-February). What do new views of knowledge and thinking have to say about research on teacher learning? Educational Researcher, 29(1), 4–15.
Putnam, R.T., Heaton, R.M., Prawat, R.S., & Remillard, J. (1992). Teaching mathematics for understanding: Discussing case studies of four fifth-grade teachers. Elementary School Journal, 93, 213–228.
Rowan, B., Chiang, F.S., & Miller, R.J. (1997). Using research on employee’s performance to study the effects of teachers on student achievement. Sociology of Education, 70, 256–284.
Saenz-Ludlow, A., & Walgamuth, C. (1998). Third graders’ interpretation of equality and the equal symbol. Educational Studies in Mathematics, 35, 153–187.
Sarason, S.B. (1990). The predictable failure of educational reform: Can we change course before it’s too late? San Francisco: Jossey Bass.
Sarason, S.B. (1996). Revisiting “The culture of school and the problem of change.” New York: Teachers College Press.
Schon, D. (1987). Educating the reflective practitioner: Toward a new design for teaching and learning in the professions. San Francisco: Jossey Bass.
Schoenfeld, A.H. (1998). Toward a theory of teaching-in-context. Issues in Education, 4(1), 1–94. Available: http://www-gse.berkeley.edu/faculty/aschoenfeld/TeachInContext/teaching-in-context.html . [July 10, 2001].
Shimahara, N.K. (1998). The Japanese model of professional development: Teaching as a craft. Teaching and Teacher Education, 14, 451–462.
Shulman, L.S. (1987). Knowledge and teaching: Foundations of the new reform. Harvard Educational Review, 57, 1–22.
Silver, E.A., & Stein, M. (1996). The QUASAR Project: The “revolution of the possible” in mathematics instructional reform in urban middle schools. Urban Education, 30, 476–521.
Simon, M.A., & Blume, G.W. 1996). Justification in the mathematics classroom: A study of prospective elementary teachers. Journal of Mathematical Behavior, 15(1), 3–31.
Stigler, J.W., & Hiebert, J. (1999). The teaching gap: Best ideas from the world’s teachers for improving education in the classroom. New York: Free Press.
Tharp, R.G., & Gallimore, R. (1988). Rousing minds to life: Teaching, learning, and schooling in a social context. New York: Cambridge University Press.
Thompson, A.G., & Thompson, P.W. (1996). Talking about rates conceptually, Part 2: Mathematical knowledge for teaching. Journal for Research in Mathematics Education, 27, 2–24.
Thompson, P.W., & Thompson, A.G. (1994). Talking about rates conceptually, Part 1: A teacher’s struggle. Journal for Research in Mathematics Education, 25, 279–303.
Tirosh, D., Fischbein, E., Graeber, A.O. & Wilson, J.W. (1999). Prospective elementary teachers’ conceptions of rational numbers. Available: http://jwilson.coe.uga.edu/Texts.Folder/tirosh/Pros.El.Tchrs.html. [July 10, 2001].
Villasenor, A., & Kepner, H.S. (1993). Arithmetic from a problem-solving perspective: An urban implementation. Journal for Research in Mathematics Education, 24, 62–69.






































