Appendix C
The Statistical Power of National Data to Evaluate Welfare Reform
John Adams and V.Joseph Hotz
As discussed in Chapter 4, a common form of analysis for assessing welfare reform is to use cross-state (as well as over time) variation to identify the overall effects as well as specific components of welfare reforms that have occurred over the last 20 years. As summarized in Chapter 2, a number of recent studies have used the cross-state variation in waivers granted to states in their administration of the AFDC program to assess the extent to which these particular reforms could account for the decline in the AFDC caseloads that occurred during the 1990s, as well as trends in labor force participation, earnings and poverty rates among welfare-prone groups in the population (see, e.g., Bartik and Eberts, 1999; Blank, 1997, 1999; Council of Economic Advisers, 1997; Figlio et al., 2000; Moffitt, 1999; Schoeni and Blank, 2000; Ziliak and Figlio, 2000; Ziliak et al., 2000). This approach takes as the unit of analysis a state in a given year. For example, the dependent variable might be the AFDC caseload in a state for a particular year. The independent variables could be state indicators, time trends, measures of a state’s economic conditions, as well as measures of the particular components of a state’s AFDC program granted under the waiver process.
A key question that must be addressed in evaluating the results of such analyses is the statistical power of such analyses to detect the effect: whether an indicator variable for a feature of a state’s welfare policy (or any other state-specific provision) has a statistically significant effect on a particular outcome being analyzed. Typically these analyses are conducted using regression analyses, either ordinary regression models, logistic regression models, or Poisson regression models. The question of statistical power for regression models is whether there is sufficient information to determine if a regression coefficient is
different from zero. The regression coefficients of greatest policy relevance are for the indicator variables describing state policy. The simplest form of this analysis would be a single indicator variable for the state having welfare reform in place.
In this paper, we examine the statistical power of analyses to detect the effects of these indicators of state-level welfare policy reforms that are associated with alternative types of statistical analyses. Mirroring the existing literature, we examine the effects of state-level AFDC waivers on several different outcome measures with data for the pre-PRWORA era. These analyses will have the flavor of post-hoc power analysis, which researchers sometimes do after developing a regression model. But we also intend these analyses to serve as examples, or given the relatively large effects, optimistic estimates of the potential of this type of analysis to detect the effects of future changes.
THE MODELS CONSIDERED
The most widely circulated study in this genre is a 1997 report by the Council of Economic Advisers (CEA) (Council of Economic Advisers, 1997). This report used the aggregate state level AFDC caseload rate as the outcome variable. The unemployment rate and state waiver activity were used as independent variables. In this paper we focus on a variant of the CEA analysis, using data from various waves of the Current Population Surveys (CPS) as implemented in Moffitt (1999). The extensions in Moffitt (1999) make it easy to explore some refinements and more thoroughly capture the range of models used by analysts.
Moffitt (1999) implements the CEA model using CPS data. The advantage of this approach is that the CPS data can be subdivided to finer subsets of the population. For example, the data on outcomes can be disaggregated by age and education status. Furthermore, the CPS data includes alternative outcome variables, such as weeks worked and earnings. Although the future pattern of welfare reform is unknown, we believe that the power of these future analyses to measure the effects will probably be similar.
The outcome variables we consider (as in Moffitt, 1999) are AFDC caseload, annual weeks worked, annual hours worked, annual earnings, and weekly earnings. The focal independent variable was whether there was any waiver in place in the state in a given year. This variable was coded 0 or 1. If the waivers were in place for a fraction of the year, the variable was set to that fraction. Other dependent variables include the unemployment rate, the lagged unemployment rate, state indicators, and state trends to account for other factors that may explain the cross-state and temporal variation in outcomes. The substate demographic cell versions of these models also included education status, age, and waiver by education interaction terms. These variables were binned and entered as indicator variables (see Moffitt, 1999).
For the power calculations, all we require from these analyses are the effect size estimates and their standard errors. These statistics appear in Table C-1. The CEA analyses use log AFDC caseload rate as the outcome variable. In the log scale the effect estimates have a percentage interpretation. The CPS analyses for the AFDC participation rates do not use a log transformation. These effects were reported in the Council of Economic Advisers (1997) and Moffitt (1999) papers as rates. Here, the corresponding estimates are converted to percentages to
TABLE C-1 Models and Effect Sizes
|
Model |
Outcome |
Focal Independent Variable |
Effect Estimatea |
Standard Error Estimate |
|
CEA |
Log(AFDC rate) |
Any waiver |
−5.751 |
2.6 |
|
CEA |
Log(AFDC rate) |
JOBS sanctions |
−2.043 |
5.641 |
|
CEA |
Log(AFDC rate) |
JOBS exemptions |
5.733 |
4.695 |
|
CEA |
Log(AFDC rate) |
Termination time limits |
−6.79 |
7 |
|
CEA |
Log(AFDC rate) |
Work requirement time limits |
−9.211 |
5.6 |
|
CEA |
Log(AFDC rate) |
Family cap |
−10.58 |
4.751 |
|
CEA |
Log(AFDC rate) |
Earnings disregard |
−4.569 |
4.318 |
|
CPS |
AFDC rate |
Any waiver |
−1.007 |
0.3673 |
|
CPS Doubledb |
AFDC rate |
Any waiver |
−1.007 |
0.2597 |
|
CPS-Disaggregated |
AFDC rate |
Waiver by education < 12 interaction |
−1.67 |
0.6064 |
|
CPS-Disaggregated |
AFDC rate |
Waiver by education = 12 interaction |
−0.947 |
0.6064 |
|
CPS-Disaggregated |
AFDC rate |
Waiver by education = 13–15 interaction |
−0.662 |
0.6064 |
|
CPS-Disaggregated |
AFDC rate |
Waiver by education = 16+ interaction |
−0.751 |
0.6065 |
|
CPS |
Annual Weeks Worked |
Any waiver |
9.837662 |
8.766234 |
|
CPS |
Annual Hours Worked |
Any waiver |
13.72197 |
10.49327 |
|
CPS |
Annual Earnings |
Any waiver |
27.68749 |
16.33189 |
|
CPS |
Weekly Earnings |
Any waiver |
16.84836 |
11.89296 |
|
aDue to different definitions of the dependent variable CEA and CPS AFDC effect estimates are not directly comparable; see discussion for details. bThe effect estimate is taken from the same analysis as the CPS row. The standard error estimate is the CPS row standard error estimate divided by |
||||
facilitate comparison to the CEA analyses. The CPS analyses were done at the state level and at the disaggregated level where the state was disaggregated by women’s age and educational attainment. In addition, other CPS based models for other outcome variables are included.
AN INTRODUCTION TO REGRESSION POWER CALCULATIONS
Statistical power is the probability of detecting an effect of a certain size if that effect does exist. To perform power calculations, one needs an estimate of effect size1 and an estimate of the variance or standard error of the effect. Power calculations for regressions require an estimate of the regression coefficient of interest (β), an estimate of the variance of the error (σ), and an estimate of the variance-covariance matrix of the independent variables. Using these quantities, an estimate of the variance of a regression coefficient vector is
VÂR(β̂)=σ̂2(X′X)−1.
It is usually only possible to perform regression power calculations if a similar regression is available, as we have in the analyses considered here.
Note that all of the quantities involved can affect the power. Larger regression coefficients are easier to detect. Incorporating important variables can reduce the estimated variance. Less obviously, the correlations between the independent variables can reduce power. In this paper we condition on the observed values of the variance estimates and independent variables. We then explore the power over plausible ranges of effect sizes and total sample sizes.2
THE POWER OF CEA MODELS TO DETECT WAIVER EFFECTS AND COMPONENT EFFECTS ON AFDC CASELOADS
The CEA models use the log of the AFDC case rate as the dependent variable. The rate is defined as the AFDC caseload divided by the state population. The log transformation gives the coefficient estimates in Table C-1 a convenient percent change interpretation. For example, the −5.75 in the first “any waiver” row corresponds to a decrease of 5.75 percent in caseload if a state has a waiver.
The CEA effect estimates in Table C-1 come from two models. The first model has an indicator for the state’s waiver status in a given year. We label these as “any waiver” models. The second model replaces this waiver indicator
with a collection of indicators describing the particular components of a state’s AFDC program. These included: (1) whether a state imposed sanctions for failure of AFDC recipients to participate in the state’s Job Opportunity and Basic Skills (JOBS) program; (2) whether a state exempted various groups from the JOBS program; (3) whether a state imposed time limits on receipt of cash assistance from the AFDC program; (4) whether a state had time limits on the work requirements of AFDC recipients; (5) whether the state imposed a family cap on an assistance unit’s monthly AFDC benefit; and (6) whether the state disregarded some amount of earnings of an assistance unit when calculating the AFDC monthly cash benefit. In addition to an indicator for waiver status or a collection of component indictors as independent variables, the models include state indicators and trends, unemployment rate and lagged unemployment rate, and the log of the maximum AFDC benefit for a family of three.
Figure C-1 presents power curves for the CEA models. Each curve shows the power of the models to detect an effect over a range of potential effect sizes.
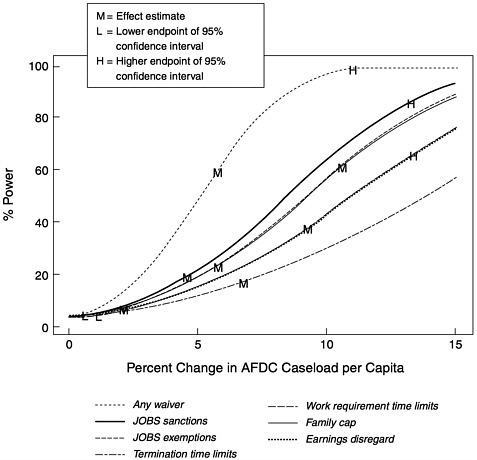
FIGURE C-1 Power for the CEA models.
All power curves in this figure use the absolute value of the effect size. For reference, each curve has been labeled with estimates of the effect sizes from the CEA models. The “M” corresponds to the effect estimate. The “L” and “H” correspond to the lower and upper endpoints of a 95 percent confidence interval for the effect size. Note that the L and H may not appear on some curves if they are out of the range of the figure. In particular, effects that were not significantly different from zero will have lower bounds below zero.
For the CEA models, only the any waiver effect has substantial power for this observed effect size, sample size, state sample allocation, and pattern of waivers across the states and over time. The roughly 60 percent power at the observed effect size (5.75) suggests that an effect of this size could be detected in 6 out of 10 similar situations. This is not a very encouraging power for one of the larger welfare reforms in recent history. The power to detect component effects is typically smaller. The exception is the family cap indicator, which has a somewhat larger power than the any waiver indicator. A decomposition of a bundle of features can have larger power for some or even all of the components if the components have substantial effect sizes and are not too correlated with each other.
The usefulness of Figure C-1 goes beyond simply assessing the statistical power associated with the observed effects. The figure can also be used to understand the power to detect other effect sizes with a similar pattern of state “roll out” over time. Consider a reform hypothesized to have a similar roll out pattern but only half the any waiver effect size: the Figure C-1 suggests that the power to detect this effect would be only 20 percent.
THE POWER OF CPS MODELS TO DETECT WAIVER EFFECTS ON AFDC CASELOADS AND CASELOADS IN SUBSETS OF THE POPULATION
In his paper, Moffitt (1999) modifies the CEA analysis by using CPS data in place of the size of state caseloads in a given year. There are two motivations for this modification. The first motivation is to move below the state level of aggregation and explore the effects of reform in subsets of the population. Here, we focus on the disaggregation by educational attainment. The second motivation is to capitalize on the availability of other outcome measures in the CPS. We address these other outcome measures in the next section.
In the CPS analyses, the definition of the dependent variable is different from the definition used in the CEA analyses in three ways. First, the denominator (population) definition in the AFDC case rate calculation is changed to women age 16 to 54. Second, the caseload is estimated from the CPS rather than the CEA estimates. Third, no log transformations of outcome measures are used. An effect in the CPS models is the percent change in women aged 16–54 on AFDC. The models in the original work reported results as rates. Here we have multi-
plied the rates by 100 to yield percentage. Note that these percentage are of women aged 16–54, not percentage changes in caseload.
Figure C-2 presents power curves for a model with a single any waiver indicator and a model that replaces the any waiver indicator by the indicators for the interactions of any waiver with different levels of educational attainment. Additional independent variables are state indicators and trends, unemployment rate, lagged unemployment rate, and the log of the maximum AFDC benefit for a family of three.
As in Figure C-1, each curve has been labeled with estimates of the effect sizes from the CEA models. The “M” corresponds to the observed effect estimate. The “L” and “H” correspond to the lower and upper endpoints of a 95 percent confidence interval for the effect size. Note that the L and H may not appear on some curves if they are out of the range of the figure. In particular effects that were not significantly different from zero will have lower bounds below zero.
The any waiver curve in Figure C-2 shows the larger power, approximately 80 percent, at the observed effect size than the CEA model. We speculate that this is due to the combination of the more targeted population (women aged 16– 64) for which the outcome is assessed and the disaggregation of the model into age and education cells. After disaggregation, there are 15,504 cells, quadrupling the number of cells. Since this disaggregation almost certainly reduces bias, this is a more defensible and a more powerful model. The power curves for the any
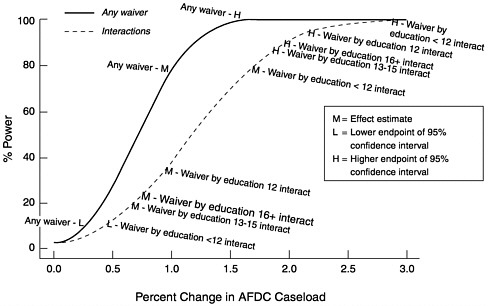
FIGURE C-2 Power for models with CPS data.
waiver by educational attainment interactions are all superimposed in Figure C-2. This is a consequence of the model’s having the same structure for each education group. Note that the least educated group has the largest observed effect size. Despite the lower power curves for the population subsets this larger effect size results in more power at the observed effect size than the any waiver model. This result illustrates the valuable power consequences of finding an appropriate desegregation of the data. It is possible for the average effect in the aggregate data to be the result of a more pronounced result in a subset of the data averaged with smaller effects.
As discussed for Figure C-1, these curves provide information on more than just the statistical power for the observed effects. The figure also helps one to understand the power to detect other effect sizes with a similar pattern of state roll out over time. The interaction curves should be of particular interest to anyone trying to understand the power to evaluate interventions that focus on a subset of the eligible population.
THE POWER OF CPS MODELS TO DETECT WAIVER EFFECTS ON OTHER OUTCOME MEASURES
Another advantage of the use of CPS data rather than aggregate caseload size is the availability of other outcome measures of welfare reform. Using the same model specification as the any waiver CPS model presented in the previous section, Moffitt considered four other outcome measures: annual weeks worked, annual hours worked, annual earnings, and weekly earnings. Figure C-3 presents power curves for these other outcomes. Note that the units are different for the different outcome measures and that none of the observed effect sizes have a power of more than 50 percent. The lower powers here are a consequence of the higher error variance for these outcomes. This result suggests that these outcome measures would be difficult to use for welfare reform evaluation unless the reform was expected to have a substantially larger effect on these measures than waivers or a larger data set was available.
OBTAINING MORE POWER
Despite the seemingly important changes that waivers brought to the welfare system, the above analyses imply that the basic CEA analysis barely has enough statistical power to detect an effect of waivers on the size of state AFDC caseloads. Clearly, more statistical power is needed to maximize the usefulness of this type of analysis to inform future welfare policy issues. The analyses presented above suggest two possible methods for obtaining more power—improved modeling and increased sample size.
Improved modeling is the most economical way to improve statistical power. Moffitt’s success in getting more power out of the same policy shift is exemplary.
More detailed modeling, if there are data to support the additional detail, can improve power with no increase in data collection costs. Further disaggregation also appears to be a promising direction. Perhaps more geographical detail (e.g., urban versus rural) could be obtained. Similarly, more detailed decomposition of the features of reform hold the promise of additional power potential.
The other key driver of statistical power is total sample size. In Figure C-4, we present an additional power curve for a hypothetical doubling of the size of the CPS samples in every state. The power for the observed effect size increases to approximately 95 percent. In study design problems, one frequently sees power curves where doubling the sample size increases the power from inadequate to slightly less inadequate. This is not the case here. A doubling of the CPS sample size would add substantially to the ability to measure the effects of welfare reform. However, a simple doubling of the sample sizes for each state is not necessarily the optimal way to allocate a doubling of sample size. Although the optimal allocation depends on the pattern of reform roll out in a future evaluation, it is likely that the best use of resources is to more than double sample sizes in the smaller states at the expense of less than doubling them in the larger states.
Several caveats should be made when interpreting the power analyses we have presented in this paper. First, a different pattern of roll out for the waivers
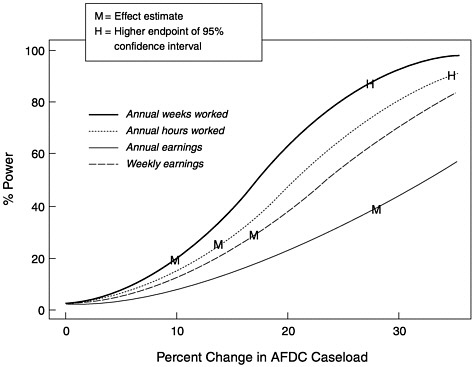
FIGURE C-3 Power for CPS models of additional outcomes.

FIGURE C-4 Power for the CPS model if sample sizes are doubled.
could result in a different power. Second, the other variables in the model (e.g., unemployment rate) can affect power as well. Different patterns in the future could confound with changes, reducing power. Third, there are other functional forms (e.g., first differences) that could have better or worse power. Fourth, we have not incorporated any elaborate error structure in the modeling herein. Correlated errors could further reduce power.
One of the advantages of this style of analysis is that it does fit one model for the entire United States. Models of this type can set the context for other analyses of more limited scope. With further improvements in disaggregation and increased sample sizes, this style of analysis could increase its contribution to the reform analysis portfolio of methods.
REFERENCES
Bartik, Timothy, and Randall Eberts 1999 Examining the effect of industry trends and structure on Welfare caseloads. Pp. 119–157 in Economic Conditions and Welfare Reform. Sheldon Danziger, ed. Kalamazoo, MI: Upjohn Institute.
Blank, Rebecca M. 1997 What Causes Public Assistance Caseloads to Grow? Working Paper #2, Joint Center for Poverty Research, University of Chicago and Northwestern University.
1999 What Goes Up Must Come Down? Explaining Recent Changes in Public Assistance Caseloads. Working Paper # 78, (March). Joint Center for Poverty Research, University of Chicago and Northwestern University.
Council of Economic Advisers 1997 Technical Report: Explaining the Decline in Welfare Receipt, 1993–1996. Washington, DC: U.S. Government Printing Office.
Figlio, David, Craig Gundersen, and James Ziliak 2000 The effects of the macroeconomy and welfare reform on food stamp caseloads. American Journal of Agricultural Economics, Forthcoming.
Moffitt, Robert 1998 The effect of pre-PRWORA waivers on AFDC caseloads and female earnings, income and labor force behavior. Pp. 91–118 in Economic Conditions and Welfare Reform, Sheldon Danziger, ed. Kalamazoo, MI: Upjohn Institute.
Schoeni, Robert F., and Rebecca M.Blank 1999 What has Welfare Reform Accomplished? Impacts on Welfare Participation, Employment, Income, Poverty, and Family Structure. Working Paper No. W7627, National Bureau of Economics Research (March) .
Ziliak, James P., and David N.Figlio 2000 Geographic Differences in AFDC and Food Stamp Caseloads in the Welfare Reform Era. Working Paper # 180, Joint Center for Poverty Research, University of Chicago and Northwestern University (May).
Ziliak, James P., David N.Figlio, Elizabeth Davis, and Laura Connolly 2000 Accounting for the decline in AFDC caseloads: Welfare reform or the economy? The Journal of Human Resources 35(3):570–586.












