3
Recent Advances in Computational Thermochemistry and Challenges for the Future
Larry A. Curtiss,
Argonne National Laboratory
and
John A. Pople,
Northwestern University
Introduction
Knowledge of the thermochemistry of molecules is of major importance in the chemical sciences and is essential to many technologies. Thermochemical data provide information on stabilities and reactivities of molecules that are used, for example, in modeling reactions occurring in combustion, the atmosphere, and chemical vapor deposition. Thermochemical data are a key factor in the safe and successful scale-up of chemical processes in the chemical industry. Despite compilations of experimental thermochemical data for many molecules, there are numerous species for which there are no data. In addition, the data in the compilations are sometimes incorrect. Experimental measurements of thermochemical processes are often expensive and difficult, so it is highly desirable to have computational methods that can make reliable predictions.
Since the early 1970s when ab initio molecular orbital calculations became routine, one of the major goals of modern quantum chemistry has been the prediction of molecular thermochemical data to chemical accuracy (±1 kcal/mol). One of the problems was that the Hartree-Fock calculations done in the 1970s gave large errors (up to 100 kcal/mol) in bond energies. Prediction of accurate thermochemical data required going beyond Hartree-Fock theory to include a sophisticated treatment of electron correlation, which made the calculations very difficult. After several decades of work, considerable progress has been made in attaining the goal of a ±1 kcal/mol accuracy through advances in theoretical methodology, development of computer algorithms, and increases in computer power. It is now possible to calculate reliable thermochemical properties for a fairly wide variety of molecules.
At the ab initio molecular orbital level, the methods currently used for computing thermochemical data range from very high levels of theory to those that combine moderate levels of theory with some form of empirical input. The former is limited to smaller molecules and can attain accuracies of ±0.5 kcal/ mol, while the latter methods can be applied to larger molecules with somewhat less accuracy. The Gaussian-n methods1 that we have developed fall in the latter category and have been widely used for
predicting thermochemical data of molecules. In the second section of this paper we summarize current state-of-the-art methods in computational thermochemistry. In the third section we describe in more detail the Gaussian-n approach and then discuss a recent development in this area, Gaussian-3 (G3) theory, which achieves a new level of accuracy. Finally, in the fourth section we assess prospects for the future of computational thermochemistry.
Current State of the Art in Computational Thermochemistry
The available methods for computing thermochemical data range from empirical schemes to ab initio molecular orbital theory.2 In this paper we restrict our discussion to the ab initio based methods. They can be roughly divided into three types: (1) very high level quantum chemical calculations with no experimental input; (2) composite techniques that combine moderate level ab initio quantum chemical calculations with some form of molecule-independent empirical parameters; and (3) techniques that use molecule-dependent empirical parameters obtained from accurate experimental data in combination with moderate level ab initio quantum chemical calculations. In this section we discuss some examples of these different approaches.
In principle it is known how to compute the thermochemical properties of most molecules to very high accuracy (0.5 kcal/mol). This can be achieved by using very high levels of correlation, such as are obtained with coupled clustered [CCSD(T)] or quadratic configuration [QCISD(T)] methods, and very large basis sets. The results of these calculations are then extrapolated to the complete basis set limit and corrected for some smaller effects such as core-valence effects and atomic spin-orbit effects. Unfortunately, this approach is limited to small molecules because of the ˜n7 scaling (with respect to the number of basis functions) of the correlation methods and the large basis sets used. This methodology has been used by Dunning, Feller, and coworkers3,4 at Pacific Northwest National Laboratory to systematically study a large number of small molecules having one and two non-hydrogen atoms. They have applied these very high level calculations to a diverse enough set of molecules to show that the methodology does perform to a very high level of accuracy.
Other groups have also used this type of approach to computational thermochemistry. Grey, Janssen, and Schaefer5 have used CCSD(T) with large basis sets to study the thermochemistry of CHn and SiHn hydrides, and some of their cations. They achieved bond energies accurate to 0.5 kcal/mol without any empirical corrections for these small molecules. Petersson and coworkers6 have used QCISD(T) with very large basis sets and have obtained a mean absolute deviation of 0.53 for a subset of the G2 test set of reaction energies. Bauschlicher, Langhoff, Taylor, and coworkers7 have used an approach based on converging to the one-particle limit through the use of atomic natural orbitals at a moderate level of correlation treatment. The correlation treatment is calibrated against full configuration interaction calculations on smaller systems or against accurate experimental data, in some cases. They have achieved accuracies of 1 kcal/mol or better using these methods.
Since the very high level calculations are difficult to extend to larger molecules, an alternative
approach is to use a series of high-level correlation calculations [e.g., QCISD(T), MP4, CCSD(T)] with moderate sized basis sets to estimate the result of a more expensive calculation. The Gaussian-n8 series described in the next section exploits this idea to predict thermochemical data. In addition, molecule-independent empirical parameters are used in these methods to estimate the remaining deficiencies in the calculation. This will work if the remaining deficiencies are systematic and scale as the number of pairs of electrons. Such an approach has been quite successful in the Gaussian-n series and the latest version, Gaussian-3 theory, achieves an overall accuracy of 1 kcal/mol and is computationally feasible for molecules containing up to about eight non-hydrogen atoms.
Petersson et al.9 have developed a related series of methods, referred to as complete basis set (CBS) methods, for calculating energies of molecular systems. The central idea in the CBS methods is an extrapolation procedure to determine the projected second-order (MP2) energy in the limit of a complete basis set. This extrapolation is performed pair by pair for all the valence electrons, and is based on the asymptotic convergence properties of pair correlation energies for two-electron systems in a natural orbital expansion. As in the Gaussian-n methods, the higher-order correlation contributions are evaluated by a sequence of calculations with a variety of basis sets. Several empirical corrections, similar in spirit to the higher-level correction used in G2 theory, are added to the resulting energies in the CBS methods to remove systematic errors in the calculations
The third approach is the use of molecule-dependent empirical parameters in combination with a moderate level ab initio molecular orbital method. The use of isodesmic reactions is a primary example of this approach, which can be quite accurate for molecules having no unusual bonding. In the isodesmic approach, a reaction is chosen with the same number of chemical bonds of each formal type (e.g., C-C, C=C, C-N, C-H) on both sides of the reaction, and all of the species have accurate experimental thermochemical data available except the species of interest.10 A moderate level of theory is used to calculate the reaction energy, and the enthalpy of formation of the unknown species is then extracted. Use of specially chosen reactions can give quite accurate enthalpies of formation because of cancellation of correlation effects and also because they make use of accurate experimental data. However, suitable reference molecules are often not available, making this method inapplicable in many cases.
An extension of the isodesmic reaction scheme is the use of bond additivity corrections. An example of this method is the BAC-MP4 method of Melius and coworkers11 that uses a computationally inexpensive molecular orbital method and combines it with a bond additivity correction. This procedure uses a set of accurate experimental data to obtain a correction for different types of bonds that is then used to adjust calculated thermochemical data such as enthalpies of formation. Quite accurate results can be obtained if suitable reference molecules are available and if the errors in the calculation are systematic. The bond additivity approach can also be used in combination with computationally more demanding methods such as G2 or G3 theory. In these cases an accuracy of 0.5 kcal/mol can be achieved for large molecules.
Gaussian-N Theory
Ideally, a method for computation of thermochemical data has several requirements to be successful. (1) It should be applicable to any molecular system in an unambiguous manner. (2) The method needs to be computationally efficient so that it can be widely applied. (3) It should be able to reproduce known experimental data to a prescribed accuracy and be applied with similar accuracy to species having larger uncertainty or for which data are not available. The Gaussian-n methods12 were developed with these objectives in mind.
Gaussian-2 (G2) theory13 was the second in this series of methods. G2 theory is a composite technique in which a sequence of well-defined calculations is performed to arrive at a total energy of a given molecular species. It was developed for predicting molecular systems containing the elements H and C1, and extended subsequently to third-row non-transition metal elements. The goal was an accuracy of ±2 kcal/mol. There are several steps to G2 theory:
|
1. |
Geometries are determined using second-order Møller-Plesset perturbation theory (MP2) with the 6-31G(d) basis set. |
|
2. |
Zero-point energies are determined at the Hartree-Fock level and scaled to account for known differences between experiment and theory. |
|
3. |
A series of correlation-level calculations are done using perturbation theory up to fourth-order and quadratic configuration interaction. Large basis sets including polarization and diffuse functions with 6-311G(d,p) as the starting point are used in the correlation calculations. The energies are added together to obtain a total energy. |
|
4. |
A higher-level correction is added to the total energy in step 3 to account for systematic errors in the energy calculation that scale as the number of pairs of electrons. This is a single molecule-independent empirical parameter that is chosen by fitting to a set of accurate experimental data. |
|
5. |
The zero-point energy is added to the energy in step 4 to obtain a final total energy that is used to calculate thermochemical properties. |
A test set of 125 reaction energies having well-established experimental values, referred to as the G2 test set, was used to assess the reliability of G2 theory. The test set was limited to molecules containing one or two non-hydrogen atoms. Since its publication in 1991, G2 theory has been widely used for the prediction of thermochemical data such as enthalpies of formation, bond energies, ionization potentials, electron affinities, and proton affinities.
Evaluation of G2 theory indicates that it meets the first requirement listed at the beginning of this section, but only partially meets the second and third ones. Since G2 theory needs no empirical input that depends on the type of molecule, it can be unambiguously applied to any molecular system. Due to its computationally intensive correlation treatment, G2 theory can handle systems with up to five or six non-hydrogen atoms, but becomes prohibitive beyond about benzene because of the ˜n7 scaling of these methods. On the G2 test set of small molecules, G2 theory is able to reproduce adequately (average absolute deviation of 1.2 kcal/mol) the experimental data; however, on certain larger molecules it fails.
The G2/97 test set of larger molecules (302 reaction energies) was recently developed14 to provide a more stringent test of G2 theory and other methods. An assessment of G2 theory on this test set indicated that it failed for certain types of molecules such as halogen-containing species and systems with unsaturated rings. For example, the G2 enthalpy of formation for SiF4 is off by 7.1 kcal/mol, and for benzene it is off by 3.9 kcal/mol. Hence, although the average errors in G2 theory are less than 2 kcal/mol, the maximum errors are too large to allow for full confidence in the method.
We recently developed Gaussian-3 (G3) theory,15 which is significantly more accurate than G2 theory and eliminates most of its deficiencies. G3 theory is a composite technique similar in spirit to G2 theory, but with some new features. Steps 1 and 2 in G2 theory remain the same. Step 3 is modified with different basis sets that are more uniform, yet are smaller so that the calculations require fewer computational resources (although they still scale as ˜n7). The higher-level correction in step 4 is reformulated in terms of four parameters, but remains molecule-independent and is obtained by fitting to a larger set of accurate experimental data. Two new steps are added: a correction for core correlation at the second-order perturbation level using a new basis set, G3 large, and a correction for spin-orbit effects in atoms.
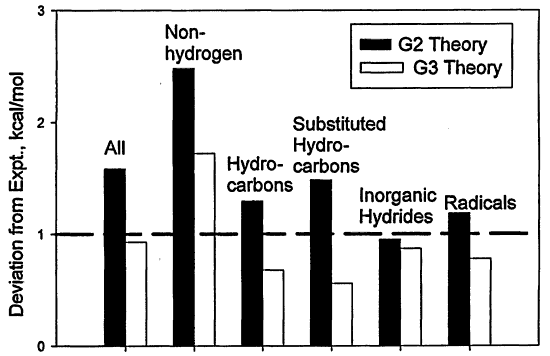
G3 theory was assessed on a total of 299 energies (enthalpies of formation, ionization energies, electron affinities, and proton affinities) in the G2/97 test set.16 The average absolute deviation from experiment of G3 theory for the 299 energies is 1.01 kcal/mol. For the subset of 148 neutral enthalpies of formation the average absolute deviation is 0.93 kcal/mol. The corresponding deviations for G2 theory are 1.49 and 1.56 kcal/mol, respectively. The improvement over G2 theory is shown in Figure 3.1 for different types of molecules in the G2/97 test set. Many of the deficiencies in G2 theory for the G2/97 test set have been eliminated. Of particular importance is the improvement for 35 non-hydrogen systems, such as SiF4 and CF4, for which the average absolute deviation decreases from 2.54 kcal/mol (G2 theory) to 1.72 kcal/mol (G3 theory). Another significant improvement is found for the 47 substituted hydrocarbons in the test set, for which the average absolute deviation decreases from 1.48 to 0.56 kcal/mol. The deviations from experiment for a series of hydrocarbons are given in Figure 3.2 and show excellent agreement with experiment.
In summary, the Gn approach uses a moderate level of ab initio molecular orbital calculation, combined with molecule-independent parameters to account for systematic deficiencies in the calculations. The latest method in this series, G3 theory, gives thermochemical data accurate to 1 kcal/mol with small maximum deviations for molecules containing up to about eight non-hydrogen atoms. The applicability to larger molecules remains to be investigated.
Future Outlook
All three approaches to computational thermochemistry discussed above will play important roles in the future. It should be stressed that, despite the successes, much remains to be clone in the development of computational thermochemistry methods.
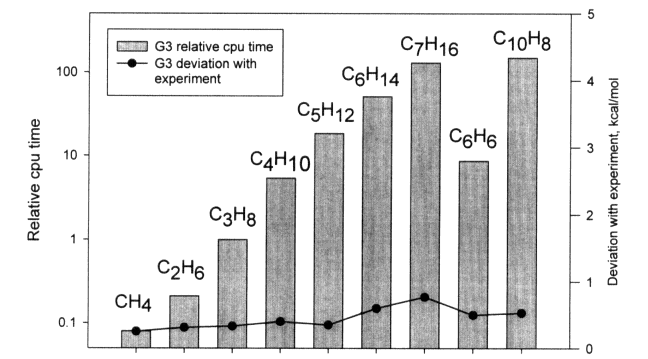
One of the major challenges for these methods is the ~n7 scaling and how it limits the size of molecules for which thermochemical data can be computed. The increase in computer time with size for some typical hydrocarbons is shown in Figure 3.2. Current limitations and capabilities of the various
TABLE 3.1 Accuracy and Applicability of Different Approaches to Computational Thermochemistrya
|
Approach |
Example |
Accuracy, kcal/mol |
Types of Molecules |
Size Limitb |
|
Direct calculation |
CCSD(T) with very large basis sets |
0.5 |
All |
2 |
|
Composite techniques with molecule-independent empirical parameters |
G3 theory |
1 |
All |
8 |
|
Composite techniques with molecule-dependent empirical parameters |
G3 theory combined with isodesmic reactions or bond additivity parameters |
0.5 |
Limited |
8 |
|
a For molecules containing first- and second-row elements. The accuracy and size limits are approximate and are based on current workstation capabilities. b The size limits refer to the number of non-hydrogen atoms and are somewhat dependent on the symmetry of the molecule and number of hydrogen atoms. |
||||
approaches are summarized in Table 3.1. In the future, thermochemical data for very large molecules will be needed for modeling studies. An example is the simulation of combustion in diesel engines that involves hydrocarbons containing up to 24 carbon atoms. Thus, the scaling problem in computational thermochemistry will have to be addressed in order to make predictions of thermochemical data needed in this area of research. The development of massively parallel computers in the teraflops-speed range, and the software to run on them, will provide computational chemists the opportunity to greatly extend the size of molecules to which the current methods of computational thermochemistry can be applied. However, even this new generation of computers will not be able to handle the very large molecules, so methods to reduce the n7 scaling will be needed. There are a number of ways by which this might be accomplished: (1) application of scale reduction techniques to coupled cluster and other high-order correlation methods; (2) development of correlation methods that exploit the locality of molecular interactions; (3) modifications to composite methods such as G3 to reduce computational time; and (4) development of density functional methods with improved accuracy.
Another challenge for the current computational thermochemical methods is remaining problem areas, i.e., failures for certain molecules and lack of the required accuracy for others. Work in the future will focus on determining causes for the failures and how to correct the problems. An important aspect of this work will be the development of expanded test sets of accurate experimental data such as the G2/97 test set. The existence of these test sets will be very important to finding weaknesses of current methodologies as well as developing new and more accurate methods. In addition, contributions to molecular energies that have been neglected as small in the past will be considered in the future in order to attain the required accuracy in larger molecules. These include relativistic effects, nuclear motion, etc. Methods will be developed to account for these effects.
Most of the computational thermochemistry methods that have been developed so far have focused on molecules containing first- and second-row elements. Thermochemical data on compounds containing elements beyond the second row are important but are more difficult to predict accurately because of the increased importance of relativistic and correlation effects; lack of adequate basis sets; and lack of accurate experimental data for assessments. In the future, new developments should provide methods that can handle these more difficult species.
Summary
The thermochemistry of molecules is of major importance in the chemical sciences and is essential to many technologies. It is now possible to compute reliable thermochemical data for a fairly wide variety of molecules through recent advances in theoretical methodology, computer algorithms, and computer power. This paper reviews the current state of the art in computational thermochemistry and describes the Gaussian-n series of methods that have been widely used for thermochemical predictions. The latest in this series, Gaussian-3 theory, gives thermochemical data accurate to 1 kcal/mol with small maximum deviations. Despite the successes, much remains to be done in the future to further develop capabilities for accurate prediction of thermochemical data. Among the challenges will be extension of the methods to larger molecules, increased accuracy in predictions, and extension to heavier elements. The increase in computing power obtainable from new generations of computers, such as those with massively parallel architectures, will play an important role in meeting these challenges.
Discussion
Jack Kay, Drexel University: Could you indicate for which types of molecules the Gaussian methods do the poorest job, and for which types it would do the best job?
John Pople: Well, the poorest ones I showed. They were molecules such as SO2 and PF3, generally second-row molecules where we are probably not doing as well as for the first-row ones. The best job is certainly done on the simplest hydrocarbons, which are well known from an empirical point of view, to have great regularities. And if you get a theory that does well on ethane and propane it is going to do well on butane and so forth. That is not surprising. So those are the better examples. Generally, moving toward the right of the periodic table and down in the periodic table makes things more and more difficult.
Jack Kay: How much luck have you had applying that to the metallic elements?
John Pople: Well, the theory is tested against all the known facts, and that includes the molecules like Li2 and Na2. It includes completely ionic molecules like lithium chloride and sodium chloride, and completely homoprotic ones like the hydrocarbons. We have, without bias, taken everything that we could find in the literature.
Jack Kay: What about transition-metal compounds?
John Pople: Transition-metal compounds analysis is really just starting. We have developed now the same basis sets for transition metals so we can begin to examine transition-metal compounds. A difficulty there is that the good experimental data is quite limited. Part of the trouble is that doing thermochemistry experimentally went out of fashion some time ago and there is less new material appearing than used to be there. So there is a need for more.
Jack Kay: I was wondering about relativistic corrections and things of that sort.
John Pople: That is another very pertinent question. The theory as I have described it does not include any relativistic corrections apart from the spin-orbit corrections applied to the separated atoms. You can
ask how this changes if relativity is included. And very recently we have generalized the theory to the leading term in the relativistic expansion. You can treat relativity as a perturbation on non-relativity by using the inverse of the speed of light as an expansion parameter and just work out the leading term.
The results are not big but they are not insignificant. The biggest relativistic correction that we have found is for silicon tetrafluoride, which is about 3 kcal/mole. So, if you include relativity you would have to reparameterize these small parameters. But those corrections will get bigger without doubt when we get into transition-metal compounds.