J
Probabilities in Estimation of Fuel Consumption Benefits and Costs
The committee estimated cumulative fuel consumption by successively multiplying the base fuel consumption by one less the estimated fractional reductions associated with specific technologies. The estimates of cumulative cost impacts are obtained by successively adding individual retail price equivalent change estimates. The committee has provided rough confidence intervals for the individual fractional reductions. The confidence intervals are based on the committee’s judgment and have not been derived in a rigorous, reproducible method. The committee’s intent in providing the confidence intervals is to convey its opinion that all such estimates are subject to uncertainty. The committee believes it is important to communicate the degree of uncertainty in estimates of fuel consumption potential and cost even though it cannot make these estimates with precision or scientific rigor. Given the judgmental nature of our fuel consumption and cost estimates, the committee has attempted to aggregate them with an appropriate degree of mathematical rigor. The following describes the method used by the committee to aggregate its estimates of uncertainty for individual technologies to estimate the confidence intervals for the full technology pathways shown in Chapter 9.
Assuming the individual estimates of cost impacts are independent, the variance of the sum of n cost estimates is equal to the sum of the variances. Thus the standard deviation of the sum is the square root of the sum of the squared standard deviations. Let ±1.64ω be the committee’s estimated confidence interval for the retail price impact of technology i. The confidence interval for the sum of i price impact estimates would be ± 1.64ω, where ωn is defined as follows.
Equation 1
Let fi be the impact of technology i on fuel consumption, where fi = 1 – ∆I and ΔI is the expected fractional reduction expected from technology I, and let pi be the expected increase in retail price equivalent. Let ± 1.64σi be the committee’s estimated confidence interval for technology i and assume that ![]() is a reasonable estimate of the variance of the estimate, whose distribution is assumed to be symmetric. Furthermore, it is assumed that the individual technology estimates are independent. The exact formula for the variance of the product of n independent random variables was derived by Goodman (1962), who also pointed out that if the square of the coefficients of variation
is a reasonable estimate of the variance of the estimate, whose distribution is assumed to be symmetric. Furthermore, it is assumed that the individual technology estimates are independent. The exact formula for the variance of the product of n independent random variables was derived by Goodman (1962), who also pointed out that if the square of the coefficients of variation ![]() of the variables is small, then an approximation to the exact variance should be reasonably accurate. The committee’s estimates of fuel consumption reduction are on the order of f = 1 − 0.05, in general, while its estimates of the confidence intervals 1.64σ are on the order of 0.02. Thus the square of the coefficients of variation are on the order of 0.00015/0.9025 = 0.00016. However, Goodman also notes that his approximate formula tends to underestimate the variance, in general. As a consequence, we use his exact formula, shown below in Equation 2.
of the variables is small, then an approximation to the exact variance should be reasonably accurate. The committee’s estimates of fuel consumption reduction are on the order of f = 1 − 0.05, in general, while its estimates of the confidence intervals 1.64σ are on the order of 0.02. Thus the square of the coefficients of variation are on the order of 0.00015/0.9025 = 0.00016. However, Goodman also notes that his approximate formula tends to underestimate the variance, in general. As a consequence, we use his exact formula, shown below in Equation 2.
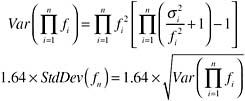
Equation 2
Equation 1 can be used to calculate a confidence interval for either the cumulative fuel consumption or cumulative cost impacts by calculating the square root of the variance and multiplying by 1.64. The committee believes that its 1.64σi bounds represent, very approximately, a 90 percent confidence interval. Assuming that the cost and fuel consumption estimates are also independent, the probability that fuel consumption is within its 90 percent confidence bounds and cost is within its confidence bounds at the same time implies that the joint confidence interval is an 81 percent confidence interval.
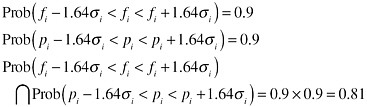
The committee did not address what specific probability distribution the uncertainty about fuel consumption and cost impacts might take. However, if one assumes they follow a normal distribution, then the ratio of a 90 percent confidence interval to an 81 percent confidence interval would be approximately 1.64/1.31 = 1.25. Thus, an appropriately rough adjustment factor to convert the individual confidence intervals to a joint confidence interval of 90 percent would widen them by about 25 percent.
REFERENCE
Goodman, L.A. 1962. The variance of a product of K random variables. Journal of the American Statistical Association 57(297):54-60.


