C
Exoplanet Detection Methods
This appendix describes in more physical and mathematical detail the primary methods of detecting planets. However, no attempt is made to be thorough or comprehensive. For more complete and detailed reviews, along with relevant references, see the book chapter “Exoplanet Detection Methods,” by Wright and Gaudi (2013), and the textbooks Exoplanets, edited by S. Seager (Dotson, 2010), and The Exoplanet Handbook, edited by M. Perryman (2011).
The remainder of this appendix adopts the following notation. The primary host has a mass M*, radius R*, density ρ*, and luminosity L*. The companion exoplanet has a mass Mp, radius Rp, density ρp, luminosity Lp, orbit with semimajor axis a, period P, and inclination i (where sin(i) = 1 is edge-on). For noncircular orbits, depending on the detection technique, it may be possible to measure the eccentricity e, argument of periastron (which differ for the planet and host by π), the time of periastron, and longitude of the ascending node, but for simplicity this appendix will typically assume circular orbits.
RADIAL VELOCITY
The radial velocity (RV), or Doppler technique, is an indirect method that relies on measuring the Doppler shift of the star as it orbits the center of mass of the planet/star system. Since it is measuring the line-of-sight RV of the star, it is most sensitive to edge-on planetary systems. For a circular orbit, the general observables are the stellar velocity semiamplitude K and the period (as well as the time of periastron and the systemic velocity of the system). For a circular orbit the radial velocity curve as a function of time is a sinusoid; for eccentric orbits K depends on the eccentricity, and the precise shape of the curve reveals the eccentricity and argument of periastron.
The velocity semiamplitude is given by
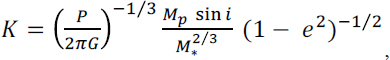
where it is assumed that MP<<M*, K ~ 13 m/s, and P ~ 12 years for an edge-on Jupiter analogue orbiting a Sun-like star. For an edge-on Earth analogue orbiting a Sun-like star, K ~ 10 cm/s and P ~ 1 year. For a “hot Jupiter” with a period of ~3 days, K ~ 150 m/s. Therefore, to detect Jovian analogues generally requires RV accuracies of
1-10 m/s, Neptune-mass planets (~17 M⊕) on ~100 day orbits require ~1 m/s accuracies, and true Earth analogues require better than ~10 cm/s Doppler precision.
Generally, the intrinsic Doppler information content in the spectral lines of quiet late F, G, K, and M stars, if observed at sufficiently high resolution of R ~ 60,000 to resolve the lines, is sufficient to achieve precision of a few m/s for reasonable exposure times on currently existing 3-10 m telescopes. The primary difficulty is therefore calibrating the wavelength of the spectral lines to the position on the detector to an accuracy that is much better than the precision. There have been two basic approaches to accomplish this. The first is to pass the starlight through a gas cell, whereby the lines of the gas in the cell (which have known rest wavelengths) are imprinted on the stellar spectra. The second is to build extremely stable spectrographs and use noncommon path calibration lamps. Both of these methods have been used to achieve Doppler precisions and accuracies of a few m/s.
Achieving precisions below this requires dealing with a host of additional systematics, which are described in detail in Chapter 4, in the section “Exoplanet Masses.” Many of these can be dealt with by constructing ever more stable spectrographs and designing ever more precise and stable wavelength calibration methods, but it may well be that the ultimate limit in the accuracy of RV measurements is set by the intrinsic stellar variability, which causes what is colloquially referred to as “RV jitter.”
The relatively weak function of K on P makes the RV method able to detect planets over a broad range of parameter space, although it is generally limited to detecting planets around slowly rotating stars (which largely eliminates main-sequence stars above the Kraft break of ~1.2 Msun as good targets), and, at least to date, old, relatively inactive stars. Furthermore, unless the planet also transits or is directly detected, RV observations provide little detailed information about the detected planet itself. Other than the period and eccentricity of the orbit, RV observations alone only provide the minimum mass of the planet. A priori, the cosine of the inclination angle is uniformly distributed, implying that the true mass is typically close to the minimum mass. However, this statement assumes a uniform prior on the logarithm of the true mass, which may be a poor assumption for some regimes of the planet mass function (Ho and Turner, 2011).
TRANSITS
In many ways, the transit technique is conceptually one of the simplest techniques to detect exoplanets, as it relies on the planet blocking a small amount of stellar light as the planet passes between the observer and the planet’s host star. For exoplanets with nearly edge-on inclinations, or more specifically in the case of circular orbits when the impact parameter in units of the stellar radius satisfies the inequality
![]()
where 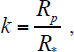 the planet will pass in front of its parent star (transit) once per orbit, thereby blocking part of the light from the star. Assuming no limb darkening of the star and that the transit is complete—for example, b < 1 –k —then the fractional depth of the transit is simply k2. Again for a circular orbit, the transit duration is
the planet will pass in front of its parent star (transit) once per orbit, thereby blocking part of the light from the star. Assuming no limb darkening of the star and that the transit is complete—for example, b < 1 –k —then the fractional depth of the transit is simply k2. Again for a circular orbit, the transit duration is
![]()
where the equatorial transit duration is
![]()
Given that cos(i) is uniformly distributed for randomly oriented orbits, the a priori transit probability is ![]()
again assuming circular orbits and Rp << R*. Note that the duty cycle of the transit—that is, the fraction of the planet’s orbit that it is passing in front of its parent star—is roughly ![]() for an equatorial transit.
for an equatorial transit.
For a hot Jupiter orbiting a solar-type star, the transit probability is ~10 percent, the duty cycle is ~3 percent, the depth is of the transit ~1 percent, and it lasts for a few hours. For an Earth analogue, the transit probability is roughly ![]() percent, the depth is
percent, the depth is 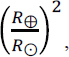 or roughly 0.01 percent, and the duration is about 10 hours, corresponding to a duty cycle of only 0.15 percent.
or roughly 0.01 percent, and the duration is about 10 hours, corresponding to a duty cycle of only 0.15 percent.
The challenges of detecting hot Jupiters via transits are clearly very different from the challenges of detecting Earth analogues. In general, 1 percent relative photometry on bright stars can be achieved from the ground with relatively small-aperture telescopes. Indeed, smaller telescopes are preferred because they typically have larger fields of view for a fixed detector size. Therefore, essentially all of the hot Jupiters orbiting bright (V < 12) stars have been found by relatively small-aperture telescopes with diameters less than 20 cm and wide fields of view (many degrees), or arrays of such telescopes. On the other hand, it is generally exceptionally difficult to achieve relative photometric precisions of <0.1 percent from the ground, particularly simultaneously for a large number of stars.
Therefore, to detect true Earth analogues, space-based missions are required. Given the long periods, small duty cycles, and the low a priori transit probabilities, these missions need to not only achieve exquisite (10 micromagnitude) relative photometric precision, they need to do so for a large number (tens of thousands) of stars essentially continuously for several years. These requirements drove the design of NASA’s Kepler space telescope, and similar considerations drove the requirements for NASA’s recently launched Transiting Exoplanet Survey Satellite (TESS; although TESS will be sensitive to true Earth analogues over only a limited region of the sky), and is driving the design of the European Space Agency’s (ESA’s) Planetary Transits and Oscillations of Stars (PLATO).
The detection of transits of a planet alone yield only the period of the planet orbit and the radius of the planet (given a measurement of the radius of the star, which has fortunately now become routine for bright stars with Gaia). However, with sufficiently precise radial velocity follow-up, it is also possible to measure the density of the star and, when combined with R* and M*, to measure Mp, and Rp (Seager and Mallen-Ornelas, 2003). Thus, for transiting planets with radial velocity follow-up, it is possible to infer the density of the planet, which is the first step in determining its basic nature.
Finally, it is also possible to detect the existence of additional, nontransiting planets in transiting systems by searching for transiting timing variations. The detection of transit timing variations in multiple-planet systems also enables the measurement of the masses of the planets without measuring the reflex radial velocity they induce on their parent star.
DIRECT IMAGING
Detecting exoplanets via direct imaging generally refers to resolving the light from an orbiting exoplanet from its parent star (rather than, e.g., the detection of the thermal emission of a transiting planet from eclipse spectroscopy). The challenges of direct imaging are generally the large flux ratio between the planet and the star, and the small angular separation between the planet and the much brighter host star.
The angular separation of a planet from its host star depends on all the Keplerian orbital elements, as well as on the epoch of observation and the distance to the system. For simplicity, one assumes a circular, face-on orbit, for which the angular separation is simply ![]() where d is the distance to the system.
where d is the distance to the system.
For planets reflecting starlight, the planet/star flux ratio depends on the geometric albedo Ag, the phase and phase curve f of the planet, the radius of the planet, and the separation of the planet from the star,
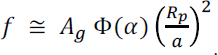
For planets emitting in thermal emission, the flux ratio in the Rayleigh-Jeans tail (where the contrast is the largest) is
![]()
For planets for which the thermal emission arises from reprocessed starlight, simple energy balance gives
![]()
where f accounts for the fraction of the planet surface over which the absorbed energy is reemitted, and AB is the Bond (or total) albedo. In all the cases where planets have been directly imaged to date, however, the detections are of young (<300 Myr) giant (>2 MJ) planets whose luminosity and temperature are driven by released gravitational potential energy, and the planet’s spectrum is significantly different from a black body, resulting in near-infrared planet-to-star flux ratios for young planets (<300 Myr) of 104 to 106. Although this flux ratio is large, it can be overcome with combinations of large ground-based telescopes, advanced adaptive optics, sophisticated image processing, and coronagraphy. However, young stars are almost inevitably moderately distant from Earth and the necessary sensitivity is possible only beyond a few tenths of an arcsecond from the parent star; hence, almost all the imaged planets are giant (>2 MJ) planets orbiting at 20 AU or farther. As these planets are directly detected, it is also possible to obtain their spectra, which allows for inferences about their atmospheric composition. Also, these planets orbit far from young stars for which precision Doppler measurements are impossible, and therefore inferring their mass requires both an estimate of the age of the system and (generally poorly calibrated) evolutionary models. Astrometric measurements with Gaia should change this situation and in turn calibrate the models.
Directly detecting mature planets that are in equilibrium with their host stars via either reflected light or reprocessed thermal emission is generally much harder, and is expected to require space-based missions. This is simply due to the astonishingly small flux ratios between the planets and their host stars, and their small angular separation. Consider an Earth analogue orbiting a Sun-like star at a distance from Earth of 10 pc. The flux ratio of Earth to the star in reflected light (depending on albedo and phase) is roughly 10–10, and the maximum angular separation is about 0.1 arcsecond (at quadrature)—that is, this requires detecting a 30th magnitude object located 0.1 arcsecond away from a 5th magnitude star. For a Jupiter analogue in the same system, the flux ratio is only (10/5.2)2 ~3.7 times larger, since Jupiter is about 10 times larger than Earth but is roughly 5.2 times farther away. The fact that the separation is about 5 times larger at quadrature does relax the requirements for detecting Jupiter analogues in reflected light considerably. Directly detecting such a system generally not only requires going to space, but also requires sophisticated techniques to suppress the light from the star, as the wings of the Airy pattern of an unobstructed stellar point spread function are orders of magnitude larger than the brightness of the planet. Two promising techniques, which are described in detail in the section “The Case for Imaging,” in Chapter 4, are internal coronagraphs and external occulters (starshades). These techniques have been mathematically demonstrated to allow the detection of Earth and Jupiter analogues around the most nearby stars with telescopes as small as 4 m. However, they are nevertheless relatively immature technologies, and significant investment is needed to mature them to the point where they can confidently be flown on a future direct imaging mission.
Detecting mature planets in thermal emission is easier in terms of flux ratio than detecting them in reflected light, as the flux ratios are generally more favorable by about 104 orders of magnitude. However, for an Earth-like planet this emission peaks at approximately 10 microns. The diffraction limit of a 20 m telescope at 10 microns is 0.1 arcsecond. Constructing a diffraction-limited 20 m class space telescope that would be cold enough to operate at 10 microns is considered exceptionally difficult. Indeed, most credible paths toward achieving the resolution needed to detect Earth analogues in thermal emission employ a nulling interferometer, which uses smaller apertures separated by tens of meters, and provides a natural way to suppress the light from the primary star. Furthermore, interferometry is generally believed to be easier at longer wavelengths. Nevertheless, the former method (detecting the planets in reflected light) is currently generally believed to be the more straightforward path. That said, the
common (although often unspoken) belief is that such a nulling, near-infrared interferometry would be a necessary follow-up to any reflected light direct imaging mission, as detecting the exoplanet in thermal emission is not only required to measure the temperature of the planet but is also needed to measure its radius, and so (with an astrometric or radial velocity detection of the reflex motion of its host star and thus the mass of the planet) measure its density and thus determine if it is truly terrestrial.
The committee concludes this section by mentioning other avenues of directly detecting and studying potentially habitable, mature exoplanets from the ground using the next generation of ground-based large-aperture telescopes (giant segmented mirror telescopes [GSMTs]; for further discussion, see the section “Ground-Based Studies,” in Chapter 4). The next generation of ground-based telescopes (ELT, GMT, and TMT) will have apertures of 30 to 40 m. At wavelengths of 1 micron, these telescopes will have a diffraction limit of about 0.005 arcsecond. Terrestrial planets orbiting in the habitable zones of nearby (few parsecs) M dwarfs will have maximum angular separations of their host star of several times larger than this. Furthermore, habitable planets orbiting M dwarfs have reflected-light flux ratios that are orders of magnitude larger than Earth analogues. It may also be possible to detect potentially habitable planets in thermal emission for several nearby systems. These systems can be discovered either by transit surveys (which are sensitive only to edge-on, and therefore generally more distant, systems) or radial velocity surveys. As discussed in the section “Ground-Based Studies,” it may also be possible to detect and characterizing planets in the thermal infrared (3-13 microns) using GSMTs.
MICROLENSING
Microlensing is an indirect method of detecting exoplanets that is primarily useful for the statistical characterization of the demographics of exoplanets over a broad range of host star and exoplanet parameter space. As described below, it is not optimal for characterizing individual exoplanets or exoplanetary systems.
The basics of the microlensing method are quite simple. It relies on the fact that gravity bends light, by an amount that can be quantitatively derived (to within a factor of 2) with Newtonian dynamics (the additional factor of 2 requires general relativity). Consider a star at a distance ds (in this case, the star is typically in the galactic bulge). If another star, in the foreground galactic disk or galactic bulge, at a distance dl, passes within roughly one milliarcsecond of the background star, it will split the light from that background star into two images, with separation of order of the Einstein ring radius θE
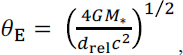
where drel=dl-1-ds-1 is proportional to the relative lens-source parallax. For typical parameters θE =1 mas, and thus two images are unresolved. However, the background stars are also magnified, by an amount that ranges from a few millimagnitudes to factors of thousands. The closer the alignment of the lens and source, the larger the magnification. The images pass by the lens at a distance of order of the Einstein ring radius, and is thus
![]()
which is typically a few to 5 AU for host stars with masses of roughly the mass of a typical M dwarf to a solar-mass star. The durations of the primary microlensing events are ![]() where μrel is the relative proper motion between the lens and source, which is typically 5-10 milliarcseconds per year, and thus the typical durations of microlensing events due to stars are a few days to hundreds of days.
where μrel is the relative proper motion between the lens and source, which is typically 5-10 milliarcseconds per year, and thus the typical durations of microlensing events due to stars are a few days to hundreds of days.
In order to detect a planet with microlensing, the projected planet separation of the microlensing event needs to coincide with the location of the images. Thereby, the gravitational field of the planet further perturbs the images, revealing the existence of the planet. This leads to detection probabilities (given the presence of a planet) of about 1 percent for an Earth-mass planet up to 20 percent for a Jupiter-mass planet. Fortunately, the signals
induced from these planets are typically large and unambiguous, unless the angular Einstein ring radius of the planet is substantially smaller than that of the angular size of the source, which generally occurs only for planets less massive than Earth.
Because of the low probability of detecting a stellar-mass microlensing event, and the lower probability of detecting the planetary perturbation even in the case that the microlensing event is detected and assuming the planetary companion exists, microlensing surveys for exoplanets generally require continuously monitoring hundreds of millions of stars on daily time scales to detect the microlensing events, and then monitoring the known microlensing events on hourly to daily time scales to detect the planetary perturbations. Recently, large-format (several square degree) detectors have been available, such that these goals can be simultaneously achieved with the same observatory setup, although round-the-clock (and thus several longitudinally distributed) telescopes are required.
As explained in the section “Expanding the Statistical Census of Exoplanets,” in Chapter 4, realizing the true potential of microlensing ultimately requires a space-based mission. Such a mission is essential in that it would enable the competition of the statistical census of exoplanets begun by Kepler.
Planets detected via microlensing routinely measure the mass-ratio between the planet and the star, and the instantaneous projected separation between the planet and host star in units of the Einstein ring radius. Fortunately, there are many methods of breaking these degeneracies, and the microlensing survey with the Wide-Field Infrared Survey Telescope will enable the routine measurement of the host star and planet mass.
PULSAR TIMING
Pulsar timing relies on the exquisite timing that can be achieved by monitoring pulsars to search for deviations from nonuniform period. As described in Chapter 2, timing of the pulsar PSR 1257+12 by Wolszczan and Frail led to the discovery of the first pulsar planetary system, as well as the lowest-mass exoplanet yet discovered. Unfortunately, it turns out that pulsar planetary systems are quite rare, and thus do not provide significant insight into the formation of planetary systems.
ASTROMETRY
Astrometry, in some sense, provides the “ideal” method of detecting planetary systems, in that it is sensitive to planets regardless of their inclination. Conversely, astrometry has many hindrances. First, the astrometric signals of planetary systems are incredibly small. For an Earth analogue at a distance of 10 pc, the astrometric signal is
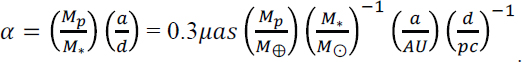
This is well below any realistic astrometric accuracy achievable from the ground. Furthermore, the astrometric detection of a planet with period P is very difficult unless the survey has a duration of at least P. Combined with the fact that astrometric surveys are inherently the most sensitive to planets with periods at the limit of the survey implies that generally only the most massive planets with periods slightly less than the survey duration can be found in astrometric surveys.
An excellent example of this reality is the Gaia mission. While Gaia will have the most exquisite astrometric accuracy to date (<10 microarcseconds for V < 12), it will not open up a new region of exoplanet parameter space, as it will be sensitive only to planets with mass several times the mass of Jupiter at separations of several AU. While it will detect such planets in unprecedented numbers, it will not reveal new knowledge about the demographics of exoplanets. That said, Gaia will measure the true mass of the planets it detects (not just the minimum mass measured by radial velocity), it will provide knowledge of the coplanarity of exoplanet systems, and it will discover extremely rare (and valuable) planetary system “oddballs.”
DISK PERTURBATIONS
In principle, planets too small to be directly observed in other ways could be inferred from their perturbations on their disks. Young planets perturb both gas and dust, including opening gaps and driving spiral arms; old planets can pile dust into resonances. Ground truth for the former is seen in the detection of planets around LkCa 15 and PDS 70 inside gaps (Sallum et al., 2018). Ground truth for the latter exists in the planet around Beta Pictoris, which was first predicted from the inclined inner disk and then discovered with direct imaging (Augereau et al., 2001).
OTHER METHODS
A variety of other methods have been proposed to detect exoplanets. One prominent example includes the detection of their radio emission. Unfortunately, despite their promise, to date none of these methods have led to the definitive detection of an exoplanet. Nevertheless, the committee concludes that these methods hold promise, and should continue to be explored.
REFERENCES
Augereau, J.C., R.P. Nelson, A.M. Lagrange, J.C.B. Papaloizou, and D. Mouillet. 2001. Astronomy and Astrophysics 370:447.
Dotson, R. 2010. Exoplanets (S. Seager, ed.). University of Arizona Press, Tucson, Ariz.
Ho, S., and E.L. Turner. 2011. The posterior distribution of sin(i) values for exoplanets with MT sin(i) determined from radial velocity data. Astrophysical Journal 739(1):26.
Perryman, M. 2011. The Exoplanet Handbook. Cambridge University Press, U.K.
Sallum, S., K.B. Follette, J.A. Eisner, L.M. Close, P. Hinz, K. Kratter, J. Males, et al. 2018. Discovery of a planetary-mass companion within the gap of the transition disk around PDS 70. Astronomy and Astrophysics, in press.
Seager, S., and G. Mallen-Ornelas. 2003. A unique solution of planet and star parameters from an extrasolar planet transit light curve. Astrophysical Journal 585(2):1038.
Wright, J.T., and B.S. Gaudi. 2013. Exoplanet detection methods. Pp. 489-549 in Planets, Stars and Stellar Systems (T.D. Oswalt, L.M. French, and P. Kalas, eds.). Springer, Netherlands.







