Appendix D
Using Bayes Analysis for Hypothesis Testing
After a study is conducted that produces a scientific conclusion, what is the probability1 that the conclusion is correct? In the case of research that involves hypothesis testing, the scientific result may point to the null or to the alternative hypothesis. An estimate of the likelihood that the scientific conclusion is correct is represented by the post-experimental (a posteriori) probability of, or the odds favoring, the particular hypothesis. These odds or, equivalently, the probability, can be obtained from the Bayes formula.
For purposes of exposition, it is convenient to express the Bayes formula using likelihood ratios in the simplified context of observing a data point xo and using it to test null hypothesis H0 versus the alternative hypothesis H1, as shown in Equation D.1. For a study comparing two groups, H0 would typically be the hypothesis of no difference between the groups, H1 would specify a difference of a particular size, and the observed data point would be the difference in the group means.
In mathematical terms, the Bayes formula is represented as follows, Equation D.1:
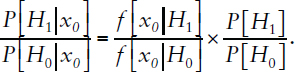
___________________
1 Text modified December 2019. In discussions related to the p-value, the original report used “likelihood” rather than “probability.” Although the words probability and likelihood are interchangeable in everyday English, they are distinguished in technical usage in statistics. This change was made, when relevant, on pages 224, 225, and 228.
In this representation:
P[H1|xo] is the probability that H1 (the alternative hypothesis) is correct given the observed findings (xo).
P[H0|xo] is the probability that H0 (the null hypothesis) is correct given the observed findings (xo).
P[H1] is the prior (pre-experimental2) probability of H1.
P[H0] is the prior (pre-experimental) probability of H0.
f[xo|H1] is the likelihood of xo under the alternative hypothesis, assumed here to follow a normal distribution.
f[xo|H0] is the likelihood of xo under the null hypothesis, assumed here to follow a normal distribution.
It is assumed that P[H0] + P[H1] = 1.0, which also implies P[H0|xo] + P[H1|xo] = 1.0. The ratio of P[H1] to P[H0] is the prior odds favoring the alternative hypothesis H1, while the ratio of P[H1|xo] to P[H0|xo] is the posterior odds favoring the alternative hypothesis. The ratio of f[xo|H1] to f[xo|H0] is called the Bayes factor.
In words, the Bayes formula (see Equation D.1) shows that the post-experimental odds favoring a hypothesis depends on the pre-experimental odds favoring the hypothesis and the relative likelihood of observing the results when the hypothesis is true, in comparison to the relative likelihood when the hypothesis is false.
The p-value, in classical statistics, is defined as the probability of finding an observed, or more extreme, result under the assumption that the null hypothesis is true. The p-value is thus related to the expression f[xo|H0] in that the p-value represents one or both outer segments of the curve defined by the possible, observed results when the null hypothesis is true. It is assumed that the possible results under the null hypothesis (H0) and under the alternative hypothesis (H1) have normal distributions with the same variance (σ3) but different means (μ).2 In the case of a two-group comparison, the mean under the null hypothesis would be zero and under the alternative hypothesis non-zero. With these assumptions, and the p-value calculated on the basis of the results observed in an experiment, one can
___________________
2 Pre-experimental or prior probability may also be referred to as “a priori probability.” We chose to use “prior probability” throughout this appendix.
3 The height of a normal curve is defined as: 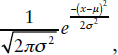 where μ is the mean and σ is the standard deviation (σ2 is the variance); π is a constant representing the ratio of the circumference to the diameter of a circle and is ≅ 3.14159; and e is the base of natural logarithms and is ≅ 2.718282.
where μ is the mean and σ is the standard deviation (σ2 is the variance); π is a constant representing the ratio of the circumference to the diameter of a circle and is ≅ 3.14159; and e is the base of natural logarithms and is ≅ 2.718282.
apply a Bayesian approach to estimate the post-experimental odds favoring the alternative or the null hypothesis based on the pre-experimental odds and the measured p-value. The pre- and post-experimental odds may be equivalently expressed as probabilities.4
In principle, under a Bayesian approach, the alternative hypothesis (H1) may take on any value (indicating the distance of its mean from the H0 mean) and any prior (pre-experimental) probability (subject to the constraint that the sum of the probabilities of the null and the alternative equal 1.0). The pre-experimental probabilities of the hypotheses (P[H0] and P[H1] in Bayes formula) reflect the prior expectation that a hypothesis would be true. If an inference from a study is very surprising, this means that the pre-experimental probability of the corresponding hypothesis was low. If a particular inference was highly anticipated, this indicates that the pre-experimental probability of its corresponding hypothesis was high.
As noted above, in a study that compares an experimental and a control group, the null hypothesis specifies that the difference between the means of the experimental and control group is zero. The alternative hypothesis can specify that the difference in means can take on any pre-experimental value reflecting the degree of effect that the experimenter posits. For example, there may be a threshold for action that the experimenter identifies, and the experimenter wishes to test whether this threshold has been exceeded.
For purposes of illustration here, consider an alternative hypothesis where the underlying mean effect size (μ1) is the same as the effect size actually observed (xo). This for expository purposes only; this choice of value for the mean effect size of the alternative hypothesis illustrates the maximum degree to which the observed results of the study can diminish the post-experimental probability of the null hypothesis. Put another way, if the observed results happened to coincide with the mean value of the previously chosen alternative hypothesis, one would obtain the maximum possible change in the a posteriori (post-experiment) probability of the experimental hypothesis in comparison with the null hypothesis.
One can use the ratio of the two likelihood functions (for H1 and for H0) at the observed results (xo) to estimate the odds favoring the more likely (higher) hypothesis given the observed effect. This ratio,
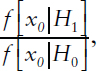
at the observed effect, gives the Bayes factor that pertains to this study. When we specify an effect size that generates a particular p-value under the
___________________
4 To convert from odds to probabilities, divide the odds by one plus the odds. To convert from a probability to odds, divide the probability by one minus that probability. An odds ratio of 3 (or 3 to 1 in favor) thus converts to a probability of 3 ÷ 4 = 0.75.
assumption that the null hypothesis is correct, such as p = 0.05 for H0, this determines the Bayes factor ratio for that p-value, namely,
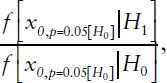
in the case of p = 0.05.
Under the assumption of normal distributions with the same variance for the data under the null and alternative hypotheses, with μ1 = xo, the Bayes factor does not depend on the specific values of μ0, μ1, or s (the means or standard deviation of the distributions). Rather, the Bayes factor reduces to a function of the standard deviate units (z) that correspond to the specified p-value in each case: specifically, under these assumptions, the Bayes factor = e(z/2). The z-score for any specified p-value may be found in any table of standard normal probabilities: for example, a p-value of 0.05 corresponds to z = 1.645. Under our assumptions, the Bayes factor for p = 0.05 is e(1.6252/2) = 3.87.
Importantly, only if one also knows the pre-experimental (prior) odds favoring the experimental hypothesis, expressed as
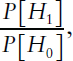
can one calculate the post-experimental probability that the alternative hypothesis is true on the basis of the results of a specific study. In principle, one would want to specify the prior odds without knowing the specific results of the study, based only on knowledge obtained prior to the study. One is expressing the odds as favoring the experimental or alternative hypothesis, but one could equivalently use the same results to estimate the post-experimental odds favoring the null hypothesis based on pre-experimental odds of
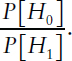
Consider the case in which a study produces results with a one-tailed test of statistical significance at p = 0.05, and the pre-experimental probability that the experimental hypothesis is true was 25 percent. With these assumptions, the post-experimental probability that the experimental hypothesis is true rises only to about 56 percent, see Table D-1 (Posterior odds in favor of 1.289 are equivalent to a probability of about 56%.)
One of the most striking lessons from Bayesian analysis is the profound effect of the pre-experimental odds that a hypothesis is true on the post-experimental odds. Similar calculations show, for example, how the a posteriori probability of a disease following a positive test result depends crucially on the prior probability. For any given level of statistical significance observed in a study, the probability that an inference is correct can vary widely depending on the probability it was true before the experiment. For example, if an experiment resulted in a one-sided p-value of 0.01, the post-experimental probabilities the hypothesis is true range from about 13 percent, if the prior probability was as low as 1 percent, to nearly 94 percent, if the prior probability was as high as 50 percent.
Another way of thinking about this is that if one had done a series of studies in which the prior probability of each experimental hypothesis was only 1 percent, and the results were statistically significant at the 0.01 level, only about one in eight of those study results would be likely to hold up as true. In contrast, if the prior probability was as high as 25 percent, then the post-experimental probability would rise to about 83 percent, and one would expect more than four of five such studies to hold up over time. It is clearly inappropriate to apply the same confidence to the results of a study with a highly unexpected and surprising result as in a study in which the results were a priori more plausible. If one quantifies the prior expectations, then Bayes formula can be used to calculate the appropriate adjustment to the post-experimental probabilities.
If study results are significant only at the 0.05 level (rather than 0.01 level), then the post-experimental probabilities of the experimental hypothesis (P[H1|xo]) would range from under 4 percent, when the pre-experimental probability was 1 percent, to nearly 80 percent, when the pre-experimental probability was 50 percent. Comparisons across levels of significance show the degree to which more statistically significant results affect the likelihood that the experimental hypothesis is correct: see Tables D-1, D-2, D-3, and D-4. However, the effect of the observed level of statistical significance is indirect, affected by sample size and variance, and mediated by the Bayes factor and the prior probabilities of the null and experimental hypotheses.
TABLE D-1 Posterior Odds Based on Bayes Formula for p = 0.05, 1-Sided Test, z ≈ 1.645
| [H1] | [H0] | Prior Odds P[H1] / P[H0] |
P[H1|xo] | P[H0|xo] | Posterior Odds P[H1|xo] / P[H0|xo] |
|---|---|---|---|---|---|
| 0.01 | 0.99 | 0.010 | 0.038 | 0.962 | 0.039 |
| 0.05 | 0.95 | 0.053 | 0.169 | 0.831 | 0.204 |
| 0.1 | 0.9 | 0.111 | 0.301 | 0.699 | 0.430 |
| 0.2 | 0.8 | 0.250 | 0.492 | 0.508 | 0.967 |
| 0.25 | 0.75 | 0.333 | 0.563 | 0.437 | 1.289 |
| 0.3 | 0.7 | 0.429 | 0.624 | 0.376 | 1.658 |
| 0.4 | 0.6 | 0.667 | 0.721 | 0.279 | 2.579 |
| 0.5 | 0.5 | 1.000 | 0.795 | 0.205 | 3.868 |
NOTES: In this table:
Bayes factor: 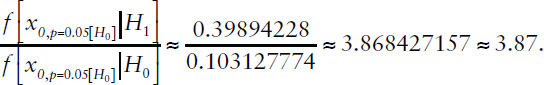
Bayes factor (simplified calculation): e(1.6452/2) ≈ 3.87.
TABLE D-2 Posterior Odds Based on Bayes Formula for p = 0.025, 1-Sided Test, z ≈ 1.96
| [H1] | [H0] | Prior Odds P[H1] / P[H0] |
P[H1|xo] | P[H0|xo] | Posterior Odds P[H1|xo] / P[H0|xo] |
|---|---|---|---|---|---|
| 0.01 | 0.99 | 0.010 | 0.065 | 0.935 | 0.069 |
| 0.05 | 0.95 | 0.053 | 0.264 | 0.736 | 0.359 |
| 0.1 | 0.9 | 0.111 | 0.431 | 0.569 | 0.758 |
| 0.2 | 0.8 | 0.250 | 0.631 | 0.369 | 1.707 |
| 0.25 | 0.75 | 0.333 | 0.695 | 0.305 | 2.275 |
| 0.3 | 0.7 | 0.429 | 0.745 | 0.255 | 2.926 |
| 0.4 | 0.6 | 0.667 | 0.820 | 0.180 | 4.551 |
| 0.5 | 0.5 | 1.000 | 0.872 | 0.128 | 6.826 |
NOTES: In this table:
Bayes factor: 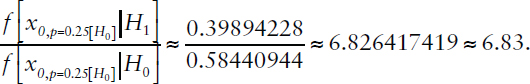
Bayes factor (simplified calculation): e(1.962/2) ≈ 6.83.
TABLE D-3 Posterior Odds Based on Bayes Formula for p = 0.01, 1-Sided Test, z ≈ 2.325
| [H1] | [H0] | Prior Odds P[H1] / P[H0] |
P[H1|xo] | P[H0|xo] | Posterior Odds P[H1|xo] / P[H0|xo] |
|---|---|---|---|---|---|
| 0.01 | 0.99 | 0.010 | 0.132 | 0.868 | 0.151 |
| 0.05 | 0.95 | 0.053 | 0.441 | 0.559 | 0.789 |
| 0.1 | 0.9 | 0.111 | 0.625 | 0.375 | 1.666 |
| 0.2 | 0.8 | 0.250 | 0.789 | 0.211 | 3.748 |
| 0.25 | 0.75 | 0.333 | 0.833 | 0.167 | 4.997 |
| 0.3 | 0.7 | 0.429 | 0.865 | 0.135 | 6.425 |
| 0.4 | 0.6 | 0.667 | 0.909 | 0.091 | 9.994 |
| 0.5 | 0.5 | 1.000 | 0.937 | 0.063 | 14.991 |
NOTES: In this table:
Bayes factor: 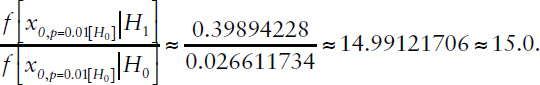
Bayes factor (simplified calculation): e(2.3252/2) ≈ 14.9.
TABLE D-4 Posterior Odds Based on Bayes Formula for p = 0.005, 1-Sided Test, z ≈ 2.575
| [H1] | [H0] | Prior Odds P[H1] / P[H0] |
P[H1|xo] | P[H0|xo] | Posterior Odds P[H1|xo] / P[H0|xo] |
|---|---|---|---|---|---|
| 0.01 | 0.99 | 0.010 | 0.218 | 0.782 | 0.279 |
| 0.05 | 0.95 | 0.053 | 0.592 | 0.408 | 1.453 |
| 0.1 | 0.9 | 0.111 | 0.754 | 0.246 | 3.067 |
| 0.2 | 0.8 | 0.250 | 0.873 | 0.127 | 6.900 |
| 0.25 | 0.75 | 0.333 | 0.902 | 0.098 | 9.201 |
| 0.3 | 0.7 | 0.429 | 0.922 | 0.078 | 11.829 |
| 0.4 | 0.6 | 0.667 | 0.948 | 0.052 | 18.401 |
| 0.5 | 0.5 | 1.000 | 0.965 | 0.035 | 27.602 |
NOTES: In this table:
Bayes factor: 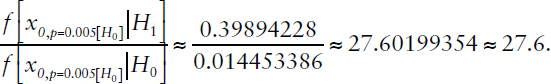
Bayes factor (simplified calculation): e(2.5752/2) ≈ 27.5.
If the observed results produce a p-value equal to 0.005 and the prior probability of the experimental hypothesis is 0.25, then the post-experimental probability that the experimental hypothesis is true is about 90 percent. It is reasoning such as this (using different assumptions in applying the Bayes formula) that led a group of statisticians to recommend setting the threshold p-value to 0.005 for claims of new discoveries (Benjamin et al., 2018). One drawback with this very stringent threshold for statistical significance is that it would fail to detect legitimate discoveries that by chance had not attained the more stringent p-value in an initial study. Regardless of the threshold level of p-value that is chosen, in no case is the p-value a measure of the probability that an experimental hypothesis is true.
When the prior probability of an experimental hypothesis (P[H1]) is 0.3 (meaning its pre-experimental probability of being true is about 1 in 3) and the p-value is 0.05, Table D-1 shows the post-experimental probability to be about 62 percent (posterior odds favoring H1 of 1.658 are equivalent to a probability of about 62%). If replication efforts of studies with these characteristics were to fail about 40 percent of the time, one would say this is in line with expectations, even assuming the studies were flawlessly executed.
When a study fails to be replicated, it may be because of shortcomings in study design or execution, or it may be related to the boldness of the experiment and surprising nature of the results, as manifested in a low pre-experimental probability that the scientific inference is correct (Wilson and Wixted, 2018). For this reason, failures to replicate can be a sign of error, may relate to variability in the data and sample size of a study, or they may signal investigators’ eagerness to make important, unexpected discoveries and represent a natural part of the scientific process.
Without losing sight of the importance of errors in experimental design and execution or instances of fraud as sources of non-replicability, this excursion into Bayesian reasoning demonstrates how non-replicability can reflect the probabilistic nature of scientific research and be an integral part of progress in science. Just as it would be wrong to assume that any particular instance of non-replicability indicates a fundamental problem with that study or with a whole branch of science, it is equally wrong to ignore sources of non-replicability that are avoidable and the result of error or malfeasance. It is incumbent on those who produce scientific results to use sound research design and technique and to be clear, precise, and accurate in depicting the uncertainty inherent in their results; those who use scientific results need to understand the limitations of any one study in demonstrating that a scientific hypothesis is more or less likely to be correct.
REFERENCES
Benjamin, D.J., Berger, J.O., Johannesson, M., Nosek, B.A., Wagenmakers, E.-J., Berk, R., Bollen, K.A., Brembs, B., Brown, L., Camerer, C., et al. (2018). Redefine Statistical Significance. Nature Human Behaviour, 2, 6-10. Available: https://www.nature.com/articles/s41562-017-0189-z [July 2019].
Wilson, B.M., and Wixted, J.T. (2018). The Prior Odds of Testing a True Effect in Cognitive and Social Psychology. Advances in Methods and Practices in Psychological Science, 1(2), 186-197.
This page intentionally left blank.










