3
Developmental Mathematics Students and Their Experiences
As part of the guiding questions for the workshop, Howard Gobstein shared that in order to make continual improvements to provide equitable learning opportunities to all students and increase their chances of success, it is essential to understand who is enrolled in developmental mathematics, which approaches work for whom, and who is still being left behind. In light of these questions, workshop participants considered data on student demographics and methods to measure student outcomes that together highlight which of the reforms discussed in Chapter 2 are yielding better results for specific subpopulations of students. Additionally, workshop presenters and participants discussed pre- and postreform data on the characteristics of developmental mathematics students and their experiences, from both national and state-level datasets, as a way to better understand how reforms could enhance outcomes for all students, to assess if progress has been made, and to determine what additional research might be needed.
UNDERSTANDING THE DEVELOPMENTAL MATHEMATICS STUDENT POPULATION
Michelle Hodara, a manager of research and evaluation at Education Northwest, provided an overview of “Understanding the Developmental Mathematics Student Population: Findings from a Nationally Representative Sample of First-Time College Entrants,”1 a paper commissioned by the
___________________
1 To read Hodara’s commissioned paper, see http://sites.nationalacademies.org/cs/groups/dbassesite/documents/webpage/dbasse_191821.pdf.
workshop planning committee; this paper highlights the characteristics of developmental mathematics students nationwide across institution types. She explained that her research was motivated by a series of questions from the workshop planning committee:
- How many students take developmental mathematics at 2- and 4-year institutions?
- What is known about these students?
- Has the population changed over the past decade?
- How can we better characterize this population of students?
She noted that because limited data are currently available, these are difficult questions to answer; as a result, this study should be considered as just the beginning of a research agenda to understand developmental mathematics students in the United States.
Hodara’s study was informed by two datasets from the Beginning Postsecondary Students (BPS) Longitudinal Study,2 which is the only national dataset that contains information about developmental education enrollment patterns, among other student data. The first dataset focused on first-time college entrants (n = 16,684) across 2- and 4-year institutions in 2003–2004. These students were interviewed in 2004, 2006, and 2009, and their course transcripts were collected. The second dataset concentrated on first-time college entrants (n = 24,766) across 2- and 4-year institutions in 2011–2012 (see Table 3-1 for the demographic characteristics of students in this cohort). These students were interviewed in 2012 and 2014, but no course transcripts were collected. The 2011–2012 dataset is thus limited to students’ self-reported data, which presents three limitations in the research findings: (1) students could have neglected to report taking developmental education courses; (2) certain groups of students could have been less likely to report their enrollment in developmental courses; and (3) some students may not have enrolled in developmental courses until their second year of college. As Hodara explained in her research, “We may not have a complete picture of the full population of developmental mathematics students in the 2011–2012 cohort. Nevertheless, there is still much to learn from this BPS dataset about the developmental mathematics student population, despite these limitations” (Hodara, 2019).
___________________
2 The BPS Longitudinal Study was conducted by the U.S. Department of Education at the National Center for Education Statistics and is a nationally representative sample drawn from the National Postsecondary Student Aid Study. This includes students’ background characteristics, levels of high school preparation, college experiences, financial aid data, and postsecondary outcomes.
TABLE 3-1 Demographic Characteristics of Students Who Entered Public 2- and 4-Year Institutions in 2011–2012 and Took Developmental Mathematics (in percentage)
| Public 2-Year | Public 4-Year | |
|---|---|---|
| Female | 58 | 61 |
| Student of Color | 51 | 56 |
| First Learned to Speak a Language Other Than English | 19 | 19.5 |
| Foreign Born or Had Foreign-Born Parents | 28 | 32 |
| Parents Whose Highest Degree Was a High School Diploma or Less | 47 | 34 |
| Pell Grant Recipient | 70 | 63 |
SOURCE: Adapted from Hodara (2019).
Because the most recent available data are from 2011–2012, which was an early year of developmental mathematics education reform, this analysis serves as a “baseline picture of the developmental mathematics student population” (see Box 3-1). She asserted that more research is needed to understand the student population being served by the new models of developmental education. Hodara found that across “all institution types, 42 percent of students who started college in 2003–2004 took developmental mathematics.” The largest proportions were enrolled at public 2-year institutions and private nonprofit 2-year institutions. By 2011–2012, this rate had not changed substantially, except for an increase at private for-profit 4-year institutions and public 2-year institutions. She noted that the for-profit 4-year sector grew more than 200 percent during this time period, which might explain the increase at these institution types. She presented demographic characteristics of students who entered public 2-year institutions and public 4-year institutions in 2011–2012 and took developmental mathematics, emphasizing that a very diverse group of students is reflected in these populations (refer to Table 3-1).
Hodara observed that the developmental mathematics students in the 2011–2012 cohort were more likely to be female, from historically underrepresented groups, first-generation college students, and Pell Grant recipients compared to their peers in the same institution type who did not take developmental education in their first year of college (see Figure 3-1). She also found that developmental mathematics students in the 2011–2012 cohort were more likely to be from historically underrepresented groups, first-generation college students, and Pell Grant recipients, in addition to being foreign born or having foreign-born parents and first speaking a language other than English, compared to the developmental mathematics
students in the 2003–2004 cohort (see Figure 3-2). The 2003–2004 cohort was slightly more likely to be female compared to the 2011–2012 cohort.
Using a composition index, Hodara evaluated how the percentage of students in a particular group within the developmental mathematics population compares to the percentage of that particular group in the overall population. This standard measure can reveal the extent to which even small populations are overrepresented in developmental mathematics—for example, a higher proportion of American Indian/Alaska Native students was enrolled in developmental mathematics than was represented in the overall college student population in 2011–2012 (see Figure 3-3). Hodara noted that “overrepresentation for students of color and low-income students is more problematic at 4-year public colleges than 2-year public colleges” (refer to Box 3-1 and Figure 3-3). She suggested that the issue of overrepresentation of students of color and low-income students in
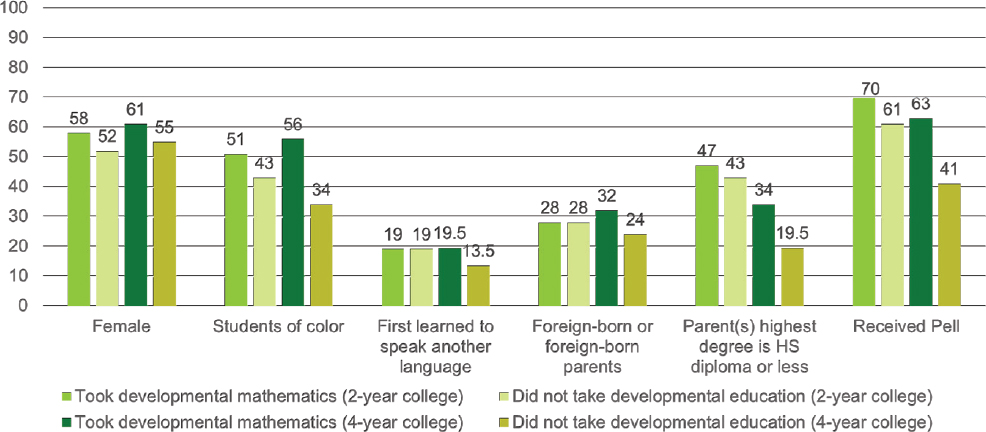
SOURCE: Hodara (2019, slide 10).
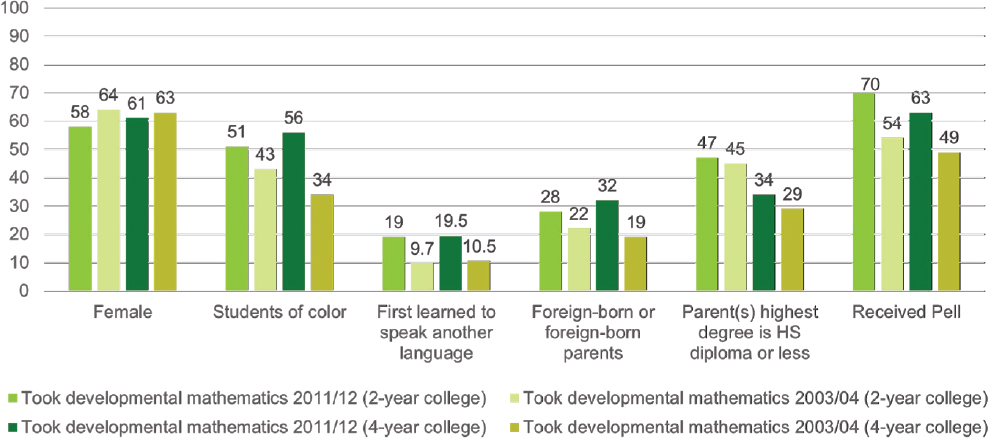
SOURCE: Hodara (2019, slide 11).
developmental mathematics should prompt critical thought and action from both researchers and educators.
To delve deeper into these questions about overrepresentation, Hodara examined the proportion of students from each racial/ethnic group who took developmental mathematics and had the same level of college readiness. In her analysis, she defined college readiness in the same way that it would be defined based on new multiple measures assessment policies:
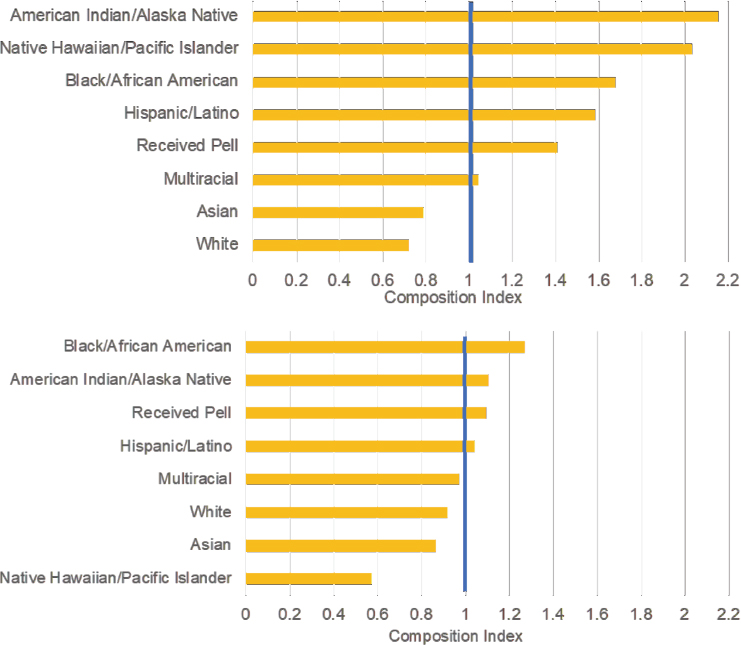
SOURCE: Hodara (2019, slides 14 and 15).
students are considered college ready if they (1) completed Algebra 2 or higher in high school and (2) had a 2.6 high school grade point average (GPA) (the equivalent of a B–) or higher. Although percentages within each racial/ethnic group varied, she found that overall, 68 percent of the developmental mathematics population in the 2011–2012 cohort completed Algebra 2 in high school and 55 percent had a B– or higher GPA across public 2- and 4-year institutions. Given that these features reflect actual preparedness for college, Hodara was surprised that students with this level of preparation were a part of the developmental mathematics population.
Hodara’s additional analyses of student outcomes reflected in the BPS datasets revealed that across all institution types, developmental
mathematics students were 3 percentage points more likely to report a decline in mental health from 2012–2014 than students who did not take developmental education during their first year. Developmental mathematics students left their science, technology, engineering, and mathematics (STEM) majors at higher rates than students who did not take developmental education in their first year. Because the relationships between mental health and developmental mathematics and between STEM persistence and developmental mathematics are understudied, it can be difficult to understand how to best address the challenges students experience in their efforts to complete college. Developmental mathematics students were generally less likely to have attained a degree and/or still be enrolled in college after 3 years than students who did not take developmental education in the first year; however, in order to make any significant conclusions about persistence and attainment, students would need to be tracked for much longer than 3 years, she explained.
Hodara concluded with three suggested areas for future research in developmental mathematics education:
- Developmental mathematics enrollment rates in current models and over time.
- Characteristics of developmental mathematics student populations in new models.
- Qualitative and quantitative research on students, especially those in developmental mathematics in the 4-year sector.
She also suggested that causal research should disaggregate impacts by race and ethnicity and other student categories to understand for whom certain reform models are working.
DISCUSSION
Discussion moderator Tatiana Melguizo, associate professor in the Rossier School of Education at the University of Southern California, highlighted the connections between Hodara’s research and the importance of the multiple measures assessments previously described by Elizabeth Zachry Rutschow (see Chapter 2). Observing that the data appeared to suggest that community colleges have more rigorous placement requirements than 4-year institutions, Melguizo and Linda Braddy championed Hodara’s suggestion to expand research in the 4-year sector. As one possible explanation of these data, Hodara referenced a pre-reform era paper by Fields and Parsad (2012). Their research included a national survey of placement scores across the United States, which showed cutoffs to be higher at 2-year institutions than 4-year institutions—that is, a student with
the same score could more likely be placed in developmental mathematics at a 2-year institution than at a 4-year institution. Melguizo noted that California is working to eliminate this issue by setting standards for validating the knowledge that students accumulate in high school. She encouraged using multiple measures assessments more often at 4-year institutions as well as “thinking about how to change the mindsets of the mathematics faculty who are implementing these incredible reforms but might not have kept pace with all of the work from the pathways and the way that the field has been trying to move and shift the way they think about math.” Cammie Newmyer, 2018–2019 Albert Einstein Distinguished Educator Fellow, highlighted Colorado’s work to standardize community college programs so that the coursework is transferable to universities throughout the state, which, she argued, demonstrates the commitment to rigor in the community college space. Tristan Denley, executive vice chancellor for academic affairs and chief academic officer at the University System of Georgia, noted that around 2011–2012 many states declared that students in 4-year settings were not allowed to be in developmental mathematics, which could heighten misunderstandings of rigor as it relates to mathematics placement requirements.
Philip Uri Treisman pointed out that some of the students in the 2011–2012 BPS cohort might have enrolled in college as a result of the high unemployment rate in the United States—these students would have been older and had more time lapse since they took Algebra 2 than members of the 2003–2004 cohort. Performing an age disaggregation to better understand similarities and differences between the 2003–2004 cohort and the 2011–2012 cohort, he continued, could help academic institutions understand how to better serve students who might be drawn back into higher education during recessions, especially with the anticipation of another recession. Mary Heiss, senior vice president of academic and student affairs at the American Association of Community Colleges, seconded Treisman’s suggestion and added that 51 percent of community college students are under age 21, 39 percent are between the ages of 22 and 39, and 10 percent are over age 40. Hodara noted that the students in the cohorts of the BPS study were, on average, age 19 at public 4-year institutions and age 21 at public 2-year institutions, which might be lower ages than what institutions have experienced. Amy Kerwin, vice president of education philanthropy at Ascendium Education Group, advocated for an additional research area that focuses on best serving students who are not first-time entrants, especially if the main reason they withdrew is because they were unsuccessful in fulfilling the mathematics requirement. These students could be described as having some college education but no degree, and thus they represent a separate cohort of students that is worthy of examination, she continued.
John Hetts, senior director of data science at the Educational Results Partnership, highlighted the challenges of understanding overrepresentation on campuses where the general population is predominantly composed of students of color (e.g., community colleges), whose placement into developmental mathematics “sets the standard” for these institutions. In response, Hodara advised institutions to think carefully about their individual equity goals when using the composition index as a measure to understand overrepresentation. Aditya Adiredja pointed out that Hodara’s data on college readiness challenges the traditional narrative that students are arriving to campus unprepared and refocuses the problem on the structural and policy issues at play. He also wondered if it would be possible to “conceptualize the problem a little bit differently and focus on the students who made it through or the students who persisted” and understand the characteristics of these students. Heidi Schweingruber, director of the Board on Science Education at the National Academies, suggested that if 43 percent of students are beginning college in developmental mathematics, then the definition of college-level mathematics might need to be revisited. “As an educator,” she continued, “my philosophy is you meet students where they are and you create opportunities for them to learn and move forward. So it just opens up this whole philosophical question for me about what we are doing.” Denley echoed this point and added that many students have overcome considerable obstacles just to attend college, only to be given the message that they are not “college material.” Because this impacts the way that students then view their experiences as they progress through developmental education, it is an important issue for the mathematics education community to consider, he continued.
EXPERIENCES FROM FOUR DIFFERENT STATE CONTEXTS
Susan Bickerstaff, senior research associate at the Community College Research Center and panel moderator, introduced the next panel, in which participants explored in greater depth the questions around student outcomes posed during Hodara’s presentation, using data from particular state contexts. Bickerstaff reiterated that change in the developmental and introductory mathematics education space is happening quickly, national data are limited, and reforms have differential outcomes for students. Four panelists, each of whom is doing research on developmental mathematics reform in diverse state contexts with various populations of students, shared their findings.3
___________________
3 Background resources on these presentations can be found at https://sites.nationalacademies.org/DBASSE/BOSE/devmathhandouts/index.htm.
Student Preparation and Developmental Mathematics in Tennessee
Angela Boatman, assistant professor of public policy and higher education in the Department of Leadership, Policy, and Organizations at Vanderbilt University, shared research on the relationship between student preparation and success in developmental mathematics in Tennessee. Boatman discussed the differential impacts of developmental mathematics, focusing specifically on students with the lowest standardized test scores in the state of Tennessee, and whether impacts on these students vary by instructional method. Standardized tests are commonly used for efficient placement, becoming the gatekeeper to college-level mathematics. However, these exams are noisy measures of students’ abilities, and high degrees of variation exist in what is considered “remedial” across institutions in Tennessee. Remediated students often have no better, and sometimes worse, outcomes than their peers who are placed directly into college-level courses, according to Boatman.
Boatman explained that prior to the era of reform in Tennessee, approximately 19 percent of students with a score of 18 on the mathematics section of the ACT and entering community college in Fall 2012 passed college mathematics in their first three semesters. Students in that same cohort with a score of 13 on the mathematics section of the ACT passed college mathematics in the first three semesters at a rate of only 5 percent. After a series of reforms were implemented (e.g., the co-requisite model), approximately 25 percent of students with a score of 18 on the mathematics section of the ACT and entering community college in Fall 2014 passed college mathematics in their first three semesters. However, students with a score of 13 on the mathematics section of the ACT still only passed college mathematics in their first three semesters at a rate of 5 percent. When the lowest-scoring students were placed into basic mathematics courses prior to the initial implementation of reforms, she continued, they passed college mathematics within 2 years at a rate of only 8 percent, which raises questions about the value of developmental mathematics for all student groups (see Figure 3-4).
Boatman shared competing hypotheses for how low-scoring students might be harmed or could benefit from developmental mathematics courses: (1) multiple developmental mathematics course sequences slow student progress, which could lead to lower self-esteem, higher frustration, and higher drop-out rates, as well as more time and money needed to complete college (although the effect may not be as prominent at colleges where the majority of peers have similar levels of preparedness) or (2) basic, foundational skills taught in lower-level developmental mathematics courses could be more beneficial for student success in subsequent college courses
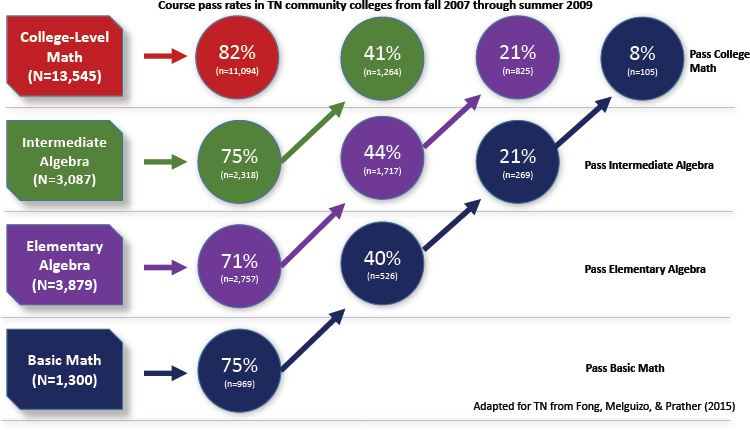
SOURCES: Boatman (2019, slide 6); data from Tennessee Board of Regents.
compared to the lessons taught in courses just below college level, and thus community colleges might focus more supports on students placed in these lower-level courses.
Additionally, Boatman shared findings from a study by Xu and Dadgar (2018) across 23 community colleges in Virginia, which revealed that when assigned to three rather than two remedial mathematics courses, students experienced no benefit for completing a college-level mathematics course or an associate’s degree. The study also showed that students at the lowest levels of academic preparedness would have also benefitted from skipping the third remedial mathematics course. Boatman and Long (2018) studied 13 community colleges in Tennessee and found that the largest negative effects on college completion occurred among students who needed and were assigned to only one developmental mathematics course. In alignment with these findings, eliminating the higher-level developmental mathematics course and placing students directly into college-level mathematics led to greater success for students in both Tennessee and Virginia. For students with the lowest scores (i.e., below 16 on the mathematics section of the ACT), they observed small positive effects (e.g., increases in degree or certificate completion) over a long period of time. The key takeaways from both studies, Boatman explained, are that developmental education students are
not a homogeneous group and developmental courses affect students differently depending on their levels of academic preparedness.
To address issues of college readiness, the Tennessee Seamless Alignment and Integrated Learning Support (SAILS) Program was created in 2013. This early assessment program affords the completion of a college developmental mathematics course during a student’s senior year of high school. This online program is modular and self-paced, delivering all of the content while teachers serve more as tutors. An evaluation of some of the early SAILS cohorts showed generally positive effects in earning college credits and passing college-level mathematics after taking the SAILS course, and those effects were driven by the lowest-scoring students. Boatman also described the Emporium model, another online program that is similar to the SAILS program except that the developmental course is taken in college instead of in high school. Concerns remain about self-paced online learning, and researchers continue to investigate its value. For example, Xu and Jaggars (2014) found that, in general, students with lower GPAs tended to perform worse in courses that are offered online or are technology driven. Similarly, in a study looking at the adoption of the Emporium model across the state of Tennessee, Boatman has so far seen more negative outcomes for the lowest-scoring students, older students, and Pell Grant recipients, as well as more negative effects for students in 2-year institutions. This suggests that online, self-paced learning might not be the best approach in the college setting, which aligns with the findings presented by Zachry Rutschow (see Chapter 2). Boatman reiterated that more research needs to be conducted on the range of the academic needs of students in developmental mathematics, and that it is important for students to develop fundamental skills, but it is equally important not to delay their progress to college completion.
Reform for Developmental Mathematics Requirements in Florida
Toby Park-Gaghan, associate professor of economics of education and education policy and associate director of the Center for Postsecondary Success at Florida State University,4 shared his research on student outcomes pre- and postreform of developmental education enrollment requirements in Florida. Park-Gaghan discussed the path to eliminating developmental mathematics requirements in the state of Florida through a statewide
___________________
4 The Center for Postsecondary Success (CPS) is a research center dedicated to identifying and evaluating institutional, state, and federal policies and programs that may serve to improve student success. CPS provides support for, and fosters collaboration, among those who are interested in conducting research on student success in postsecondary education. For more information on CPS, see http://centerforpostsecondarysuccess.org.
initiative. Florida Senate Bill 1720,5 implemented in Fall 2014, made placement tests optional and created an exempt student category, which gave those students the option to bypass developmental education and enroll directly into college-level coursework. Exempt students include students who entered a Florida high school in 2003 (or later) and graduated with a standard diploma, as well as active-duty members of the U.S. Armed Services. This bill also changed the way that Florida postsecondary institutions taught developmental education, with the implementation of co-requisite and compression models.
Using a comparative interrupted time series and data on cohorts of first-time-in-college students from the Florida Department of Education’s longitudinal record system, Park-Gaghan and his team explored how removing the “roadblock” of developmental education, especially for students of traditionally underrepresented races and ethnicities, would impact student success (Hu et al., 2019). Ultimately, they wanted to understand whether more students were successfully enrolling in and passing gateway mathematics courses (i.e., college-level courses required to pass for a program of study) as a direct result of Florida Senate Bill 1720. Starting with the 2014 cohort of students, a significant and positive increase was apparent in the number of students enrolled in gateway mathematics courses; additionally, black and Hispanic students were enrolling at faster rates in these courses than their white counterparts. Even with increased enrollment rates, course-based passing rates—the share of students enrolled in the courses who passed the class—remained similar to what they were previously except for black students, who experienced a slight decrease in passing rates.
While not all students who chose to enroll in gateway courses were successful in passing the course, cohort-based passing rates—the share of incoming students who passed a gateway mathematics course—increased since the implementation of Florida Senate Bill 1720, with black and Hispanic students having greater gains than white students, Park-Gaghan explained. Thus, overall achievement has been raised for everyone and, in some cases, even more so for black and Hispanic students. All of these findings suggest that Florida Senate Bill 1720 is having a consistent, substantive, and positive impact on student success; the reform seems to have helped to mitigate the performance gap between white and underrepresented students, contributing to equalizing postsecondary educational outcomes. Furthermore, Park-Gaghan explained, the regression-adjusted analyses substantiate that the changes observed pre- and postreform are not occurring purely due to random chance. Implications for practice, he continued, include redefining
___________________
5 For more information on Florida Senate Bill 1720, see https://www.flsenate.gov/Session/Bill/2013/1720.
who is required to take developmental education and how it is taught, which requires attention to both the instructional practices and the structure of college-level courses. Additionally, he asserted that increased advising and enhanced student support services are integral parts of developmental education reform and overall student success. He concluded by emphasizing that research could play an important role in informing policy related to the implementation of developmental mathematics reforms (e.g., how to redesign mathematics pathways and revise institutional approaches to course offerings).
Assessment and Placement Reform in California
Hetts discussed the implementation of assessment and placement reform in California and its impacts on student outcomes. He observed that when students move from the K–12 system to the community college system in California, approximately 75 percent have to repeat one or more courses that they successfully completed in high school. That impact falls disproportionately on people of color, women (specifically in the case of mathematics), and low-income students. Approved in 2017, California Law AB-7056 requires educational institutions to justify their decisions about who is placed into a developmental education pathway: students have to be highly unlikely to succeed in a college-level course, and the institution has to demonstrate that placing them into a developmental mathematics sequence will increase their likelihood of completing a college-level mathematics course. In light of this new policy and given the fact that so many students are repeating courses that they already successfully completed in high school, educational leaders have been inspired to identify a new method for placing students into courses.
The Multiple Measures Assessment Project7 is an ongoing, collaborative effort of the California Community Colleges Chancellor’s Office, Common Assessment Initiative, Cal-Partnership for Achieving Student Success Plus, the RP Group, and more than 90 pilot community colleges in California to assess and place students more accurately into mathematics and English sequences—not only in developmental education but also in courses such as calculus and Calculus 2. The multiple measures data that are identified, analyzed, and validated include students’ high school transcript data, noncognitive variable data (e.g., students’ motivation or perceptions of their own skill levels), and self-reported high school transcript data.
___________________
6 For more information about California AB-705, see https://leginfo.legislature.ca.gov/faces/billNavClient.xhtml?bill_id=201720180AB705.
7 For more information about the Multiple Measures Assessment Project, see https://rpgroup.org/All-Projects/ArticleView/articleId/118.
Hetts explained that results from an analysis to predict course success indicated that students with a high school GPA greater than 3.0 (or students with a slightly lower GPA but who progressed further in mathematics) are likely to succeed in courses such as statistics if they begin at the level of college statistics. Students with a GPA of 3.4 or higher and at least Algebra 2 (or with a slightly lower GPA and successful completion of calculus in high school) are likely to succeed in precalculus if they begin at the level of precalculus. However, historically, only 15 percent of students in the California community colleges were placed directly into a college-level mathematics course. Using these new standards for multiple measures assessments, he estimated that 40 percent of students could be placed directly into college-level courses and thus given a better opportunity to succeed.
Students in the Multiple Measures Assessment pilot programs completed college courses at a rate of 67 percent, which is the same rate of success as students with traditional placement into college-level courses. In comparison, students at these same colleges who started one level below college-level mathematics succeeded at a rate of 27 percent, and students who started two levels below succeeded at a rate of 16 percent. Multiple measures assessments have helped to identify students who are most likely to succeed, yet 60 percent of students are still not included in that category. Looking more closely at this remaining population of students who would be described as “least likely to succeed,” and employing the analysis used to predict course success, Hetts observed that their success rates in a college-level mathematics course is approximately 40 percent (MMAP Team, 2018; see Figure 3-5). However, if these same students start just one level below college-level mathematics, only 10 to 15 percent of them are successful.
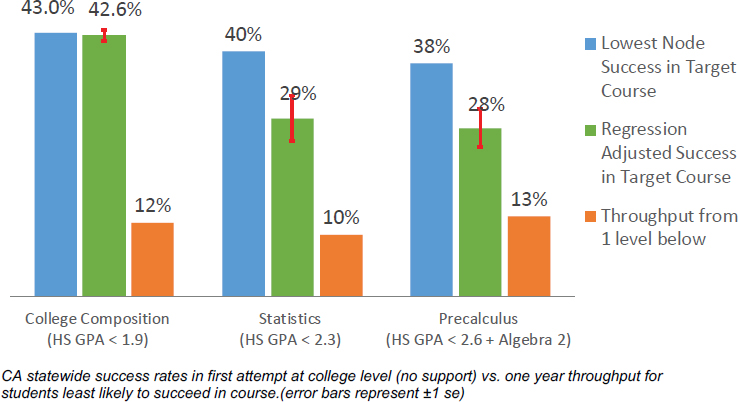
SOURCE: Modified from MMAP Team (2018).
Taken together, he continued, these findings illustrate that placement leads to differential outcomes for students in terms of the completion of college-level mathematics. Furthermore, all students essentially benefit from a pathway that starts at the college level, and these patterns hold across (1) race/ethnicity, (2) gender, (3) Extended Opportunity Programs and Services status, (4) Disabled Student Programs and Services status, (5) English language learner status, and (6) Pell Grant eligibility, he continued.
Initial data from a selection of California community colleges on student success rates in an open-access co-requisite statistics course by GPA band show that high school GPA is indeed highly predictive of performance. Students at the lowest level of performance (as defined by high school GPA) who start in this gateway college-level mathematics course with supports can complete it successfully 50–60 percent of the time. Without the support, the success rate might have been 30 percent, and starting at just one level below might have reduced the completion rate to 10 percent. “College-level mathematics is for everyone,” Hetts reiterated, and the next step is to determine how to best support all students in the appropriate mathematics classes.
Student Access to Reform in Texas
Lauren Schudde, assistant professor in the Department of Educational Leadership and Policy at The University of Texas at Austin, shared her
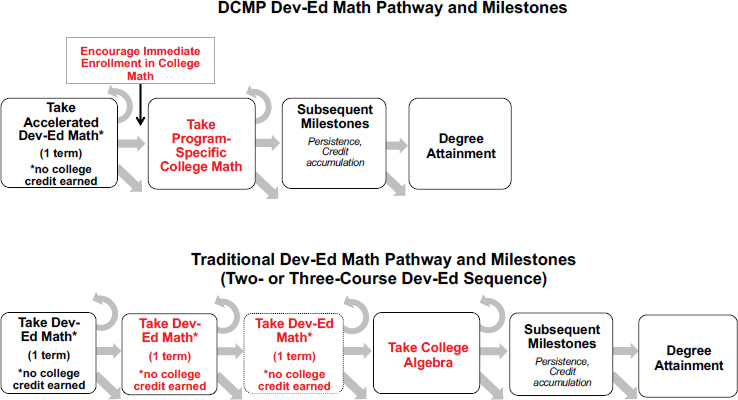
SOURCE: Modified from Schudde and Keisler (2019).
findings on student access to new approaches to developmental mathematics education in the state of Texas. She observed that although much reform is under way, it is not being done fully at scale (i.e., some colleges roll out the reformed models while still primarily offering traditional developmental mathematics sequences) and many students are being left behind.
Schudde’s discussion focused on the Dana Center Mathematics Pathways (DCMP) model,8 a model that combines the structural reform of developmental mathematics education with curricular and advising reform into pathways that offer students field-specific college mathematics. It includes a one-term accelerated developmental education course (noncredit bearing) paired with an optional success course that prepares students for college-level mathematics, including statistics, quantitative reasoning, and algebra courses. Additionally, this model encourages immediate enrollment in college-level mathematics upon passing the developmental mathematics course, uses student-centered approaches and real-world examples to teach mathematics concepts, and is dramatically shorter in duration than a traditional developmental mathematics pathway (see Figure 3-6).
To understand who participates in DCMP (compared to traditional developmental mathematics education) as well as the outcomes associated with this model, Schudde evaluated statewide student-level longitudinal
___________________
8 For more information on the DCMP model, see https://dcmathpathways.org.
data in Texas from Fall 2014, 2015, and 2016. For this presentation, she focused on the Fall 2015 cohort because it is the most recent cohort with available 2-year follow-up data to demonstrate how patterns endure over time. She used covariate adjustment to model how students were selected into DCMP and to examine the relationship between DCMP status and outcomes (e.g., persisting in college, passing developmental mathematics, enrolling in college mathematics, and passing college mathematics), while trying to control for the fact that DCMP students are quite different from those in a traditional mathematics pathway (Schudde and Keisler, 2019). In the Fall 2015 cohort (see Figure 3-7), students in DCMP were much more likely to be white than their counterparts in the traditional developmental mathematics pathway (44% versus 26%). There is a slightly higher representation of black students in DCMP than in traditional developmental education. However, Hispanic students were highly underrepresented in DCMP compared to traditional developmental education, which is of great concern given the high population overall of Hispanic students enrolled in Texas postsecondary institutions. DCMP students were also more likely to
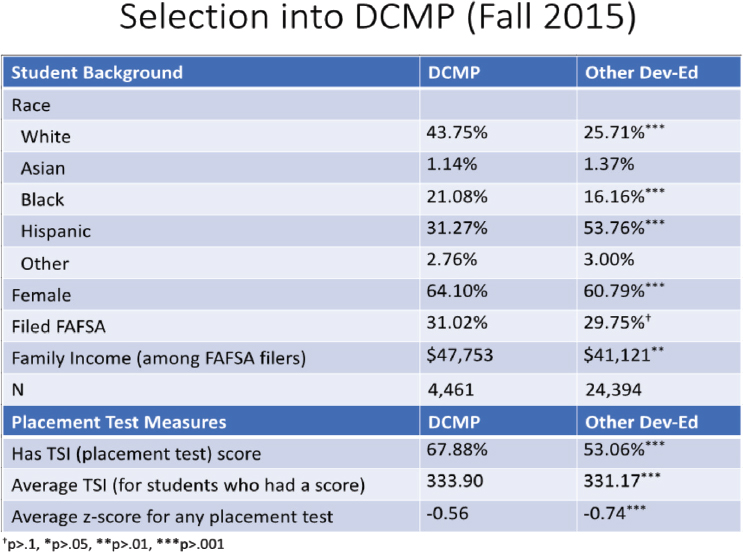
SOURCES: Schudde (2019, slides 11 and 12); data from Texas Higher Education Coordinating Board.
be women, to have higher income, and to have performed better on placement tests.
Schudde emphasized that these patterns of selection should be a cause for concern, especially because students who are enrolled in DCMP tend to have better outcomes than those in traditional pathways. DCMP students are more likely to enroll in college mathematics in the subsequent semester by 16 percentage points and are more likely to pass college mathematics by the end of that semester by 4 percentage points, and these patterns persisted over a 2-year span. Additionally, there is little evidence of differential effects, indicating that “everyone benefits,” according to Schudde. These findings, she continued, align with those of the randomized control trial discussed by Zachry Rutschow (see Chapter 2) and hold true even at institutions that did not agree to a randomization study, suggesting that DCMP is working in a variety of contexts. But, essentially, “students who probably would have been more likely to get access to better opportunities anyway” are the ones who have the greatest access to DCMP, she explained. DCMP is intended for students who need acceleration (i.e., they placed two or three levels below college-level mathematics) and not necessarily intended for students who need only one semester. While the latter population of students might benefit from the curricular reform, they do not necessarily need the structural reform. Thus, Schudde commented that more research is needed, including a close examination of selection procedures to better understand the messages faculty and advisers are giving students about developmental mathematics and reform options, the role of implicit bias, and how students view mathematics placement in light of their beliefs about their mathematical abilities. Additionally, she emphasized the need to change current procedures and cultures that create inequitable opportunities for students: the goal is to ensure that students, advisers, and faculty are all informed about the negative effects of prolonged developmental education on student success and, as a result, to shift student course enrollment toward alternative pathways.
DISCUSSION
Building on Boatman’s assertions about the outcomes for the Fall 2014 cohort of students, Denley commented that the structural changes via the co-requisite model had not been implemented at that time, and so more recent data indicate that both pedagogical and structural changes are needed to make the most beneficial gains for student success, especially for students at the low end of the preparation spectrum. Julie Phelps noted that Park-Gaghan’s research motivated Florida postsecondary institutions to study their own data; mathematics faculty at Valencia College are now meeting once every other month to discuss these data, emerging questions,
and possible reforms that better support students and close achievement gaps. Denley observed that front-line faculty in Georgia and Tennessee were initially unaware of the data they needed to enable reforms, and he reiterated Phelps’s assertion that academic institutions need to have access to data about their own students. Melguizo emphasized the value of involving community college faculty in this work, which will inform practice, and engaging student voices in advocacy for reform.
Recalling her panel’s discussion on equitable opportunities for students, Pamela Burdman asked these panelists if their research has illustrated anything about the theory behind versus the actual implementation of mathematics pathways. Schudde said that comparable numbers of students are actually pursuing the different pathway options and that instead of limiting students, mathematics pathways might be prompting them to enroll in more mathematics courses. Amy Getz, manager of systems implementation for higher education at the Charles A. Dana Center at The University of Texas at Austin, observed that Schudde’s data provide evidence for supporting a 1-semester model instead of a 1-year model and for implementing reforms at full scale.
Denley cautioned reform advocates about stressing the “accelerated” nature of reform efforts, such as the co-requisite model, as that language can increase both student and faculty skepticism about their success; in reality, the co-requisite model is successful because parallel remediation is more effective than serial remediation. Hetts agreed that labeling courses (e.g., as “stretch” or “accelerated”) could be dangerous because it signals incorrectly to students that one course could be easier than the other.
Zachry Rutschow referenced a soon-to-be-released randomized control trial study that she led on the mathematics pathways model. Noting that it was difficult to identify institutions willing to implement this curriculum at a high level, she confirmed how challenging it is to change instructor practice. Furthermore, a survey of a randomized group of students revealed that the mathematics pathways approach led to a 40 to 50 percent increase in students’ positive experiences of how they learned mathematics, in their comprehension of how mathematics applies to their life experiences, and in their work with other students in small groups, as well as a decrease in the amount of traditional classroom lecture that they received. Schudde hypothesized that even more substantial positive effects might be observed if it were possible to control for students enrolled in other developmental mathematics education reforms (e.g., co-requisite model) in the research. Boatman shared similar findings from qualitative observations of the high school students in the Tennessee SAILS program: they felt better prepared for college upon completion of the program, and they better understood the usefulness of mathematics compared to students not enrolled in the program.
Treisman observed that when faculty recognize that students can succeed in college-level mathematics courses without taking prerequisite courses (i.e., developmental mathematics education courses), the powerful reality of “intelligent co-requisite design” becomes attainable. He pointed out that while faculty are essential components of pedagogical reform, structural reforms at scale are what lead to the dramatic increases in student success rates. Hetts shared a slightly different perspective in that faculty professional development opportunities have opened faculty members’ minds to greater change, thus enabling structural reform at many institutions. Echoing Denley’s earlier comment, Mesa emphasized that individual faculty cannot change the landscape of developmental mathematics education on their own; instructional reform must be paired with structural reform in order to enhance success for students. She explained that faculty professional development should be combined with a “structural understanding of how the system works, how we bias students into courses, how we do not listen in advising, and how we do not understand the needs that people have” in order to make full-scale improvements in mathematics education.
REFLECTIONS FROM DAY 1 OF THE WORKSHOP
After a series of thought-provoking presentations and panel discussions throughout the first day of the workshop, Phelps asked participants to reflect on these conversations and to share their perspectives about the current and future states of developmental mathematics education. Zachry Rutschow expressed her disappointment that despite the data that exist on reform, many 2-year institutions are still implementing mathematics reforms alongside traditional prerequisite sequences; thus, much work remains to be done to scale these reforms. Denley added that students do not need to be “fixed;” instead, structure, policy, and pedagogy need to be reformed to improve students’ experiences, especially given that new approaches to delivering mathematics content seem to eliminate equity gaps. Treisman called for research specifically focused on the one-third of students who are still not being well served by mathematics reforms. Mark Green echoed Treisman’s suggestion to consider why those students are not being well served and added that for the two-thirds of students who are already succeeding, additional support could be implemented to help them graduate and start successful careers. Zachry Rutschow agreed that instead of focusing only on methods to get students through college mathematics, educators should focus on how to get students interested in mathematics courses and careers. Thus, research is needed on how instructional reforms could change students’ experiences with mathematics in these ways.
Phelps argued that connection and direction for students are imperative for student success, and faculty can learn lessons both from their colleagues
and from data about how to impact futures by creating equitable outcomes for all students. Boatman added that academic institutions need guidance to understand how the data illuminate issues on their individual campuses, and Phelps urged workshop participants to replace the phrase “faculty buy-in” with “faculty engagement and ownership” when talking about faculty involvement with reform initiatives. Denley shared that a faculty community of instructional practice around reform initiatives is one approach that could help change this mentality about reform. As is the case in Georgia, by participating in these learning communities, faculty begin to share their experiences around implementation, change their mindsets, and own these structural changes, Denley explained.
Mesa pointed out that true reform takes time and involves politicians, legislators, and faculty alike. In the meantime, educators have the power to influence students’ experiences in positive ways, Adiredja proposed. Schweingruber raised the issue of systemic reform, emphasizing that more research is needed to understand how to bring these reforms to scale (i.e., who the actors are and how to motivate policy change), and Treisman observed that periods of change offer opportunities to create new norms for responsible practice. For example, because eliminating barriers is not the same as achieving ultimate outcomes (e.g., earning high-value degrees in nursing, business accounting, information technology, etc.), a higher class of equity problems should be targeted and subjected to critical research study.
Other areas for opportunity include increased partnerships and participation across the K–12 and higher-education spaces, according to Schweingruber. Hetts agreed and emphasized the need to recognize K–12 colleagues for the high-quality instruction that they provide to students. Rebecca Fitch added that postsecondary institutions need to place more confidence in the K–12 system and its assessments of students (i.e., high school transcripts) instead of relying on standardized test scores for placement in college or developmental courses, since research has proven that those measures are ineffective and often lead to negative consequences.
To conclude the first day of the workshop, Amy Kerwin provided her reflections. She explained that Ascendium Education Group, the sponsor of the workshop, concentrates on learners from populations that are historically underrepresented in both postsecondary education and workforce training, especially those from low-income backgrounds. She thanked the Board on Science Education, the planning committee members, and the workshop speakers for their work to organize the workshop and to help create a set of important research questions to move reform efforts in the field forward. She reiterated the need to focus further research and reform initiatives on the three cohorts of students who are not being well served in the era of developmental mathematics education reform: (1) the 30 to 40
percent of students who are still not succeeding in current developmental mathematics sequences, (2) the students who are “structurally prevented” from accessing a developmental education reform pathway (e.g., an institution does not offer enough sections of the reform or offers biased advising), and (3) the students who cannot access any reform (e.g., students enrolled in a community-based adult basic education program). Kerwin championed the notion of implementing reforms “with a sense of fidelity to the spirit of the reform and not simply to the structure of the reform,” but she cautioned that biases maintained by students, faculty, and advisers alike can interfere with achieving this vision. She emphasized that the mathematics education community has an opportunity to create a research agenda that “sends a clear signal to policy makers, to college and university leaders, to faculty, and ultimately to others in philanthropy that we really and truly do believe that math is for everyone.” She lauded the many ideas about future areas of research that emerged from the panel discussions and presentations and shared her commitment to thinking collaboratively about the next steps following the workshop.
This page intentionally left blank.
























