Investigating Alternative Approaches to Helping Teachers Learn Mathematics
Participants attended two of four concurrent sessions in which they engaged in activities to help them understand how opportunities might be designed to enable preservice teachers to learn the mathematics they will need to teach well.
SESSIONS
Curriculum Materials
Shin-ying Lee, Michigan State University
Marco Ramirez, Tucson Public Schools
Case Materials
Carne Barnett, WestEd
Programs and Practices
Virginia Bastable, SummerMath for Teachers
Jill Lester, Mount Holyoke College
Deborah Schifter, Education Development Center
Video as a Delivery Mechanism
Bradford Findell, Mathematical Sciences Education Board
Deborah Ball, University of Michigan
Student Curriculum Materials: Japanese Teachers' Manuals
Shin-ying Lee
SESSION GOALS
The session, focused on the use of curriculum materials as a way to help teachers learn mathematics, offered participants the opportunity to closely examine the information presented in two sample teachers ' manuals and to think carefully about how materials like these may or may not provide resources for teachers or prospective teachers to acquire mathematical knowledge as well as how to teach mathematics. In the first part, participants considered a lesson on weight using a Japanese teacher's manual.
OVERVIEW
There is a strong need for capable, well-trained mathematics teachers if there is to be improvement in the mathematics achievement of American students. Evidence from studies has shown that the mathematical knowledge and teaching skills of typical American school teachers are lower than they should be and lower than that of many of their counterparts in the rest of the world. In addition, teachers' working conditions do not foster the professional growth necessary for effective institutional practices (Lee, 1998). Teachers need to have a conceptual understanding of mathematical knowledge to facilitate the quantitative reasoning ability of their students. It is unlikely that teachers will change their teaching practices unless they have acquired an in-depth understanding of the mathematics they have to teach and have had opportunities to develop the pedagogical strategies necessary for effective teaching (Ball & Cohen, 1996). It is critical to engage in discussion and to suggest practices that could lead to the improvement of American teachers' mathematics knowledge.
This Workshop addressed the nature of the problem and possible solutions by focusing on two questions: What mathematical knowledge do teachers need to have in order to teach well? How do teachers obtain that knowledge? Participants had opportunities to think of new ways to improve teachers' mathematical content knowledge and pedagogical content knowledge at the preservice and inservice level. One possible avenue is to examine the teacher training practices of countries that demonstrate effective instruction in mathematics. Japan is one such country. In comparative studies, Japanese teachers have consistently
demonstrated that they teach mathematics in a clear, coherent, and in depth fashion (Stevenson & Lee, 1995). They facilitate students ' conceptual understanding of mathematics in an interactive and effective way. The types of instruction observed in these studies illustrate teachers' thorough understanding of the mathematical topics and their knowledge of the elements of effective math lessons. Teachers' manuals for the curriculum provide a significant source of information that may contribute to their knowledge base for teaching mathematics (Gill & McPike, 1995).
Japanese teachers' manuals differ from American curricular materials in several ways. The primary focus is on the fundamentals of mathematics. The mathematics content knowledge and pedagogical knowledge are organized in a systematic and thorough way to facilitate the teaching and learning processes. The Ministry of Monbusho develops curricular guidelines (Course of Study) that comprise the national educational standards in mathematics for each grade level. The Course of Study succinctly outlines the mathematical topics of study as well as the desired structure and sequence of instruction for each year. These guidelines are made widely available and used by local boards of education, schools, teachers, and textbook publishers to develop curricular materials and instructional plans.
Textbooks published by private companies have to be reviewed and approved by the Ministry for conformity to the Course of Study. Companies that publish student textbooks also publish teachers' manuals (Kyoushiyou Shidousho). Using the content of students' textbooks as the guideline, the manuals provide a coherent body of subject matter knowledge and offer pedagogical suggestions on how to teach the lessons. The use of the manuals is not mandatory for teachers. However, the manuals are usually written by expert teachers who have not only demonstrated effective teaching but are also experienced in working with novice teachers. The mathematical knowledge and the suggestions for teaching are practical and realistic, often including content and activities that have been used in research lessons to demonstrate their effectiveness in guiding students to meet the particular lesson goals.
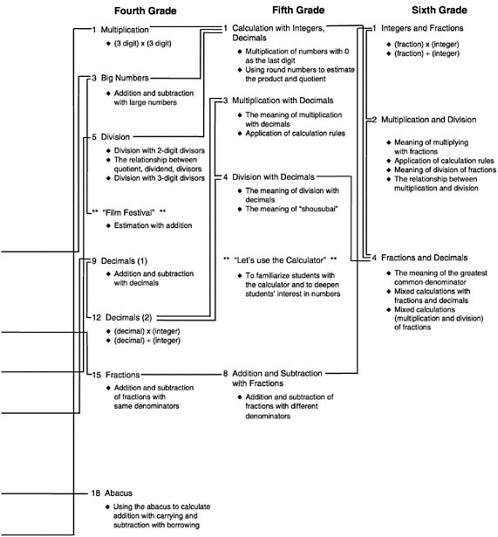
Effective teaching requires that teachers have a thorough understanding of the structure of mathematics at the level at which they are teaching (National Council of Teachers of Mathematics, 1991; Leitzel, 1991). Japanese elementary school teachers can acquire a clear idea of the structure of elementary mathematics through the scope and sequence chart in the teachers' manuals. The scope and sequence Systematic Charts included at the back of every teacher's manual lay out the sequence of all the mathematics concepts students should learn in the four mathematics content areas over the elementary school years. The four strands are identified in the Japanese Course of Study for Elementary School: numbers and operations, quantities and measurement, geometrical figures, and quantitative relations. Each strand is presented in a one-page “Systematic Chart.” The same charts are included in the teachers' manuals for all different grade levels. Those charts could serve as the cognitive maps for teachers to understand the structure and connectedness of the entire elementary mathematics system.
Figure 1 shows the systematic chart for numbers and operations. The development of numbers and operations within a particular grade and how it lays the groundwork for concepts in later years are presented in a flowchart format. For
example, in the learning of addition and subtraction, the instructional system involves not only gradually increasing the number of digits over time but also takes into consideration the concept of place value. The process of regrouping is systematically introduced in the operations. All the possibilities are laid out in a specific order. Moreover, addition and subtraction are introduced first in separate units and then mixed together in the same unit to facilitate the complementary relationship between addition and subtraction.
Beyond the overall structure of elementary mathematics, Japanese teachers' manuals also lay out coherent information on the mathematical content and pedagogical knowledge for every unit. The overview of the mathematics content and goals, the instructional system, and the instructional plan, as well as key points for instruction, are clearly presented. The mathematical information is always explained in the context of the critical pedagogical issues. Using the unit on weight in the third-grade teachers' manual as an example (see Appendix F), the learning goals of the unit are clearly identified, and a thorough and in-depth treatment of the topic of weight is clearly reflected in these goals. The mathematical components are always presented in the context of teaching. For example, it is pointed out that the concept of weight is more difficult to understand than length or volume because weight is impossible to estimate or judge from the appearance of the objects, therefore making it important to provide students with different manipulative experience. The steps for developing the concepts should go from direct comparison, to indirect comparison, then to measuring by arbitrary unit, and finally to measuring by universal units.
In Japanese teachers' manuals, the common difficulties and mistakes students may have are always illustrated for the teachers. Instructional activities are suggested to clarify those misconceptions. For example, it is common for students at this age to believe that an object's weight changes when the physical position or the shape of the object changes. Therefore, it is imperative to engage students in specific activities, such as weighing an object after changing its position and weighing clay after changing its shape to provide opportunities to discuss the misconceptions. In addition, the key points of the discussion address the particular features of the mathematics being taught in the lesson, the developing nature of the mathematical thinking of the students, and the critical mathematical ideas students should learn from the activity. The conceptual basis is illustrated, along with a good lesson script, for every lesson in the curriculum. The connections among mathematical content, students, and teaching are always made explicit.
ACTIVITIES
Participants were first asked to think about the concept of weight for a few minutes. What do they know about the concept and how would they plan their lessons if they were to teach a class of third-grade students the concept of weight? What are the elements that are important for the students to learn? By putting themselves in the role of a classroom teacher and focusing on teaching one specific mathematical topic, the participants were set to evaluate how the Japanese materials may or may not be helpful for American teachers to learn to teach.
Next, the translated materials from the Japanese teachers' manuals for the unit on
weight in third-grade mathematics were handed to the participants (Shinpan Sansu 3: Kyoushiyou Shidousho, 1993; refer to Appendix F for the translation). They were given time to read individually and then, in small groups, discuss their assessment of the materials. The participants discussed whether the materials actually expanded their mathematical knowledge about the concept of weight and how the materials may or may not help them to teach the concept.
Finally, the whole group was brought together to discuss whether materials like this would be helpful for teachers—to build their mathematical content knowledge and to help them conduct lessons that would lead to students' understanding of the topic. Questions of how materials of this nature could be used at preservice or inservice training for teachers and what other information would be needed were also raised.
DISCUSSION SUMMARY
The discussion ranged from general concerns about the differences between Japanese and American societies to specific questions about the amount of classroom time devoted to a particular lesson.
Participants asked questions about general Japanese background, the national curriculum, the textbook and curriculum development processes, and preservice and inservice teacher training. Such information was necessary for the participants to place the Japanese teachers' manuals in perspective. An example of one Japanese scope and sequence chart and its English translation were shown to illustrate the sequential and systematic approach to the mathematical concepts throughout the elementary school curriculum (see Figure 1).
There seemed to be a consensus among the participants that materials similar to the Japanese materials would be very helpful. They pointed out that the Japanese materials have more mathematical knowledge and guidance for teaching than most currently available American curriculum materials. The notes in the Japanese teachers' manuals that anticipated how students might respond to questions or activities and the common misconceptions of the students would be particularly helpful for inservice training. Such materials can also be used in preservice training and in the teacher preparation process in the first few years of teaching. Teachers can use the activities suggested in the curriculum to talk with each other about teaching. The diagram of the sequence of concepts within a grade and across different grades clearly shows what mathematical concepts come before and after the current concept. It offers an explicit mathematical knowledge structure that is easy for teachers to follow.
The difficulties American teachers might have using the materials were also addressed. For example, for this unit on weight, Japanese manuals suggest spending 8 hours discussing 14 questions. Given the typical U.S. curriculum and texts, U.S. teachers are accustomed to using many more problems to “fill” time. Japanese lessons tend to use one good leading question with the specific mathematical goal in mind for a discussion of the entire lesson. American teachers may have difficulties with this approach. American teachers need to learn how to ask questions and how to lead a discussion about mathematics ideas in an in-depth approach. They need to have knowledge of mathematical content, and also know how to develop a climate of
inquiry. Additional information, such as the diagram in Figure 2, would be helpful for further explicit guidance about how each of the activities in this unit helps facilitate students' thinking and learning about the topics. These kinds of information could provide another piece of mathematical knowledge for thinking about pedagogy.
There were concerns about the different cultural expectations between Japan and the United States. Japanese culture has elements that support teaching and learning. There is an assumption about parent involvement in education that does not necessarily hold true for this country. In the United States, teachers need materials to support communication with parents. There are also issues related specifically to the American context. For example, it is necessary to assist teachers who have students who speak primarily in a language other than English.
Some participants chose to focus the discussion on issues embedded in the American system or their own particular institutions, for example, the lack of good mathematics textbooks at the college level. Therefore, some college teachers choose to write their own teaching
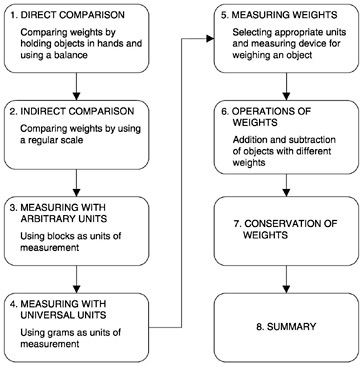
Figure 2. Understanding and Teaching the Concept of Weight
materials and activity books for their classes. Similarly, some elementary curricular materials are not useful for teaching mathematics. There were also concerns about the differences between math content and method courses at the preservice level. Different states require prospective teachers to take different numbers of hours in math courses, and there are also very different expectations of the content of those courses. The college structure of two separate departments —mathematics and mathematics education, both of which are involved in the training of prospective elementary school teachers—may not be the best way to enhance the mathematical knowledge of future teachers. Professors in the mathematics department are not likely to teach content necessary for elementary mathematics nor to understand mathematics in the setting of elementary classroom practices.
During the discussion, most people focused on the materials and carefully examined the content in terms of the mathematical knowledge provided and the issues involved in teaching the concept. Others seemed to focus on questions beyond the materials and beyond the two main questions raised in the workshop. Those people were more concerned about the specific circumstances with which they themselves have to deal in their own work.
Ball, D. L., & Cohen, D. K. ( 1996). Reform by the book: What is—or might be—the role of curriculum materials in teacher learning and instructional reform. Educational Researcher, 25(9), 6-8, 14.
Gill, A., & McPike, L. ( 1995). What we can learn from Japanese teachers' manuals? American Educator, 19(1), 14-24.
Lee, S. Y. ( 1998). School context and mathematics learning. In S. Paris & H. Wellman (Eds.), Global prospects for education: Development, culture, and schooling (pp. 45-77). Washington, DC: American Psychological Association.
Leitzel, J. R. C. (Ed.) ( 1991). A call for change: Recommendations for mathematical preparation of teachers of mathematics. Washington, DC: The Mathematical Association of America, Committee on the Mathematical Education of Teachers.
National Council of Teachers of Mathematics. ( 1991). Professional standards for teaching mathematics. Reston, VA: Author.
Shinpan Sansu 3: Kyoushiyou Shidousho. ( 1993). [New edition of arithmetic 3: Teachers' guidance] Tokyo: Kyouiku Shuppan, Inc. (in Japanese).
Stevenson, H. W., & Lee, S. Y. ( 1995). The East Asian version of whole-class teaching. Educational Policy, 9(2), 152-168.
Student Curriculum Materials: Investigations in Number, Data, and Space
Marco Ramirez
SESSION GOALS
The session, focused on the use of curriculum materials as a way to help teachers learn mathematics, offered participants the opportunity to closely examine the information presented in two sample teachers ' manuals and to think carefully about how materials like these may or may not provide resources for teachers or prospective teachers to acquire mathematical knowledge as well as how to teach mathematics. In the second part of the session, participants considered a lesson on 3-dimensional geometry from Investigations in Number, Data, and Space, an elementary mathematics program in the United States.
OVERVIEW
What kind of mathematical support do curriculum materials provide teachers? Curriculum materials in the United States address teachers ' needs in a variety of ways. Traditionally, some teacher-support materials provide just the answers to problems, while others display worked out solutions. As the curriculum has expanded to cover more than arithmetic topics, however, curriculum developers found that teachers needed more and better resources to support their understanding of the underlying mathematical ideas in the new content and in developing approaches to teaching this new content.
In Investigations in Number, Data, and Space, a curriculum project funded by the National Science Foundation and developed by TERC, one of the four goals is to communicate mathematics content and pedagogy to teachers. To achieve this goal, the project has extensive teacher-support materials designed to enable teachers to move comfortably through the curriculum even though they may be teaching unfamiliar mathematical ideas (Appendix G). Key mathematical concepts in data, number, and space are outlined for each grade level, so teachers can follow the development of the ideas throughout the grades. The curriculum is presented through a series of teacher books. Each book provides lesson plans; description of the mathematical emphasis of the lesson; the materials preparation needed; reproducible student sheets for activities and games; a family letter; homework suggestions; opportunities for skill and practice; assessment activities; notes to the teacher including vocabulary, notation, and a discussion of the mathe-
matics students are encountering; samples of the unit translated into other languages; dialogue boxes containing teacher-to-teacher discussions from teachers who piloted the project.
ACTIVITIES
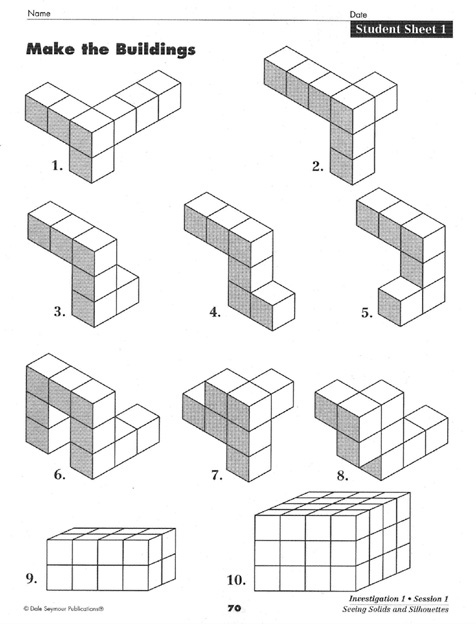
Participants worked through a lesson from a fourth-grade unit on three-dimensional geometry, Seeing Solids and Silhouettes (Battista & Clements, 1998). The goals of the unit are to have students explore the relationship between three-dimensional objects and their two-dimensional representations and to investigate what objects look like from different perspectives. Students are to use interlocking cubes to construct cube buildings shown in drawings and describe how they mentally see the buildings (see Figure 1). The conceptual development of two- and three-dimensional representations in the program is laid out as follows: noticing shapes in the environment; observing, describing and comparing two-dimensional shapes; developing vocabulary to describe two-dimensional shapes; becoming familiar with the names of two-dimensional shapes; describing characteristics of triangles; grouping shapes according to common characteristics; composing and decomposing shapes; noticing relationships among shapes; using rotation and reflection to arrange shapes; filling a certain region with shapes; visualizing and representing two-dimensional shapes; counting, comparing, and adding quantities; building a pattern by repeating a square unit; seeing how changing the unit affects the whole pattern; constructing, observing, describing, and comparing three-dimensional shapes and objects and their characteristics; creating and using two-dimensional representations of three-dimensional shapes and objects. After working with the cubes, participants read the teacher's materials for that lesson and discussed the role such materials would play in enabling teachers to conduct the lesson meaningfully and in helping teachers understand the mathematics involved.
DISCUSSION SUMMARY
The discussion focused on how such materials would facilitate a teacher 's knowledge of mathematics and facilitate the teaching of mathematics. Many of the participants felt a strength of the Japanese materials was the clear presentation of the scope and sequence that would facilitate a teacher's understanding about the mathematical direction of the unit. The participants identified strengths of Investigations as: teachers' notes, mathematical emphasis, classroom routines, and translations. Participants considered the degree of support necessary for teachers and spent some time commenting on the reality of teaching from a school perspective, raising issues of teacher preparation in mathematics, credentialing and licensing procedures, time for planning lessons, diverse nature of students' mathematical and cultural backgrounds, home environment and support, and language. If such a reality does in fact exist, participants questioned what type of curriculum-support mechanisms are needed to address the situation in mathematics classrooms. One unresolved issue is the extent to which teacher materials, such as the Japanese or Investigations materials, can be used successfully by teachers on an individual basis with little or no leadership support from colleagues.
Case Materials
Carne Barnett
SESSION GOALS
Participants in this session explored the potential of using narrative case materials, similar to those used in the business, law, and medical professions, as a learning tool for mathematics teachers. The session highlighted the cases and processes developed by the Mathematics Case Methods Project at WestEd as an example for participants to examine and discuss.
On-going studies of the professional development offered by the Mathematics Case Methods Project have shown that involvement in case discussions can have a positive influence on teachers' understanding of mathematics and how they planned their lessons (Barnett, 1998; Gordon & Heller, 1995; Gordon, Heller, & Lee, 1994).
One goal of the presenter was to illustrate how a deliberately facilitated case discussion can help teachers acquire an advanced and flexible knowledge of the mathematics content they teach. Another goal was to demonstrate how deep analysis of the mathematics—in the context of a classroom situation—can prepare teachers to make informed and strategic teaching decisions.
OVERVIEW
The session began with a brief history of the Mathematics Case Methods Project, which started in 1987 as a pilot study in collaboration with Lee Shulman of Stanford University. Shulman's ideas had a strong influence on the project. Most importantly, he pointed out that teachers need a special kind of content knowledge, which he called pedagogical content knowledge. With this in mind, the Mathematics Case Methods Project designed a set of cases to build teachers' understanding of rational numbers that merged with the teaching decisions and learning challenges related to these concepts. Other projects, such as the Developing Mathematical Ideas Project at the Educational Development Center and the budding Science Cases Project at WestEd, are developing similar materials to promote content learning that is grounded in classroom practice.
The Mathematics Case Methods Project is a comprehensive program that includes the development of cases, the creation of videotapes and materials to support the use of cases, and the large-scale dissemination of the case discussion
approach. This project primarily serves practicing teachers.
The casebook created by the project—Fractions, Decimals, Ratios, and Percents (Barnett, Goldenstein, & Jackson, 1994)—contains teacher-authored narratives that are studied as a collection. The cases describe dilemmas that occurred in lessons on rational number concepts. The accompanying facilitator's guide describes the key mathematical and pedagogical issues that typically arise in each discussion. A second casebook, featuring primary-grade mathematics topics, is in development. During the next part of the session, the presenter modeled how case discussions in the Mathematics Case Methods Project would be introduced to teachers. First, four purposes for discussing cases, related to the mathematics, children's thinking, instruction, and language issues, were presented. (Refer to Appendix H for copies of the overhead transparencies that were used.) Next, participants were invited to take part in a discussion of the case titled “Six-Tenths or Four-Fifths of a Dollar.” The presenter modeled a step-by-step process, developed by the Mathematics Case Methods Project, which provides a familiar routine for discussing cases and for focusing the discussion on productive issues. After reading the case but before the discussion, participants worked on a “Starter Problem” related to the case, designed to help them think about what might be difficult or confusing for a child. Then, participants quickly called out factual information from the case. This part of the process helps to keep important pieces of background information from being overlooked. After listing important facts, participants worked in pairs to formulate discussion issues and put them in a question format. Working in pairs helps those who might be intimidated by the mathematics feel a little more comfortable. As the issues were read to the group, they were recorded on chart paper in the front of the room. Two of the issues brought up in this session, for example, were: “Is it appropriate to use the area model rather than a set model?” and “Were fifths confused with nickels in this lesson? ”
These issues are typical for this case and commonly lead to a discussion about the contrasts among various fraction representations and applications. For example, this case elicits examination of the fraction kit used in the case and its limitations for understanding a fraction as a comparison, rather than two separate numbers. It also addresses the limitations of relying on only one representation, such as an area model, and assuming that the students' understandings will transfer to other situations, such as set models or the number line. It also stimulates discussion about whether, when, and how other representations should be introduced.
During the discussion of the issues posed by the group, participants were invited to illustrate their ideas on the chart in the front of the room or with various materials distributed among the tables. By seeing how someone else interprets an idea or solves a problem, each participant's own understanding is enhanced. The public display of these ideas stimulates additional ideas and questions.
During the discussion, the presenter modeled how to invite comments on the issues being discussed, help participants focus on one idea long enough to examine it deeply, and ask questions to elicit justification or evaluation of an idea or to challenge the thinking of the group. These techniques have proven to be helpful in deepening the reflection and inviting careful analysis by members of the group.
Only a short discussion was possible during this session; thus many of the mathematical issues embedded in the case were only touched upon or were not discussed. The section below called “Opportunities Afforded by this Approach” identifies some of the other mathematical ideas that could be discussed in a longer time frame
DISCUSSION SUMMARY
Pitfalls of this approach
The facilitator of a case discussion must be very knowledgeable about the mathematics in the case and have skills to know how to advance the thinking of the group members. Facilitators new to cases should be encouraged to learn from others with more experience.
Participants asked how the process might be used with preservice teachers. They were also concerned about finding the time to cover the content required in prescribed math courses. They were referred to Joanne Lobato at San Diego State University, who has successfully integrated cases into her mathematics course. She designed questions for each rational number case to which students respond in writing and bring to class. This eliminates much of the time needed for discussants to pick out the issues to discuss among themselves. The drawback is that practicing teachers claim that the process of generating the issues themselves is one of the more beneficial parts of the discussion.
There was also concern that many course instructors might integrate a case discussion here and there without realizing that learning from cases can be very different from learning from other materials. The mathematics Case Methods cases, for example, are designed to build interconnected knowledge about rational numbers and are best discussed as a collection.
Opportunities afforded by this approach
Many participants agreed that cases offer a site for discussing complex mathematical concepts. A mathematician in the group pointed out that mathematics courses are specifically designed for architects and engineers, using problems faced by architects and engineers in their work. The mathematics courses designed for teachers teach the mathematics apart from teaching practice. Case discussions were thought to be a potential candidate for such a course.
It was also pointed out that a single case, such as the one discussed during the session, can offer a platform on which to examine several central ideas of mathematics very closely. For example, there were opportunities to examine the relationship of division to fractions, the difference between discrete and continuous representations, and different models of division. The added benefit of the case discussion approach was that these ideas can be discussed in the context of how they might be taught, learned, or misunderstood by students.
Cases also offer opportunities to examine the role of oral, written, and symbolic language in learning and teaching mathematics. The case discussion in this presentation illustrated that mathematics learning can either be impeded or facilitated by how language is used or interpreted. This is particularly important for teachers who view mathematics as language free and for teachers of limited English speakers.
One advantage of case discussions is that they can be very engaging, as was demonstrated during this session. Partici-
pants want to resolve their own confusion and are anxious to have their ideas discussed. Sometimes it is difficult, however, for the facilitator to slow the discussion and allow ample time for reflection and deep examination of others' ideas. The facilitator must focus the discussion and coordinate the ideas offered by the participants to make the discussion useful. As case discussion participants gain experience, they learn the importance of carefully analyzing one idea before moving on to the next.
Barnett, C. ( 1998). Mathematics teaching cases as a catalyst for informed strategic inquiry . Teaching and Teacher Education, 14 (1), 81-93.
Barnett, C., Goldenstein, D., & Jackson, B. ( 1994). Fractions, decimals, ratios, and percents: Hard to teach and hard to learn? Portsmouth, NH: Heinemann.
Gordon, A., & Heller, J. ( 1995). Traversing the web: Pedagogical reasoning among the new and continuing case methods participants. Paper presented at the annual meeting of the American Educational Research Association, San Francisco, CA.
Gordon, A., Heller, J., & Lee, G. ( 1994). Mathematics case methods: External longitudinal evaluation. Unpublished Manuscript.
Programs and Practices
Deborah Schifter, Virginia Bastable, and Jill Bodner Lester
SESSION GOALS
The session centered on excerpts from Developing Mathematical Ideas (DMI), a mathematics inservice program for elementary and middle-grade teachers created by the Center for the Development of Teaching at the Education Development Center, Inc., in Newton, MA. DMI was designed to help preservice and inservice teachers think through the major ideas of K-6 mathematics and examine how children develop those ideas. The goal of the session was to illustrate a model of a program designed to provide teachers with opportunities to learn mathematics.
OVERVIEW
At the heart of the DMI materials are sets of classroom episodes (cases) illustrating student thinking as described by their teachers. In addition to case discussions, the curriculum offers teachers opportunities to explore mathematics in lessons led by facilitators; share and discuss the work of their own students; plan, conduct, and analyze a mathematics interview of one of their own students; view and discuss videotapes of mathematics classrooms and mathematics interviews; write their own classroom episode; analyze lessons taken from innovative elementary mathematics curricula; and read overviews of related research. When DMI is used with undergraduates, students are assigned to elementary classrooms to complete their assignments.
When completed, the curriculum will comprise a series of five seminars, each designed for 24 hours of class time and organized around a particular mathematical theme. Two seminars have been developed so far: Number and Operations: Building a System of Tens, and Number and Operations: Making Meaning for Operations. Three seminars under development are Examining Features of Shape; Measuring Space in One, Two, and Three Dimensions; and Working with Data.
BUILDING A SYSTEM OF TENS
This seminar begins with cases from second- and sixth-grade classrooms focusing on the methods children use for adding and subtracting two-digit numbers when, building on their knowledge of the number system, they construct their own procedures. What are the various ways
children naturally tend to think about separating and combining numbers? And what must they understand in order to work with numbers in these ways? These questions motivate the rest of the module. The focus of the last half of the seminar is how these basic concepts are applied and extended in the middle-grade years through multidigit multiplication and division and work with decimal fractions.
As seminar participants investigate children's thinking, they also engage in the mathematics for themselves, practicing mental arithmetic, and sharing their strategies for adding, subtracting, multiplying, and dividing multidigit numbers. In our experience, many who come to the seminar believe that the algorithms they teach offer the only valid methods of computation. And those who invent their own strategies often feel sheepish, as if they are “cheating ” by using “less sophisticated” methods. At first, then, teachers need to loosen their hold on these beliefs. As they more fluently maneuver in our number system, they also begin thinking about properties of the operations. In particular, they develop models for multiplication and division and work through how the distributive property is involved when multiplying or dividing multidigit numbers. Toward the end of the module, seminar participants consider representations of, and operations with, decimal fractions and examine how ideas of place value, which they have been studying since the beginning of the course, play out when applied to the right of the decimal point.
MAKING MEANING FOR OPERATIONS
This module, which examines the actions and situations modeled by the four basic operations, begins with a view of young children' s counting strategies as they address problems they would later solve by either adding, subtracting, multiplying, or dividing. It then looks at different situations modeled by whole-number addition/subtraction and multiplication/division. The latter part of the module revisits the operations in the context of rational numbers. Which ideas, issues, and generalizations need to be refined or revised once the domain under consideration is extended to include rational numbers? For example, how does one make sense of multiplication and division when the numbers being operated on—fractions—already have an implied division?
As in the first seminar, while teachers work through the cases to learn how children confront these mathematical issues, they also work through the mathematics for themselves. Since most teachers are products of an education that emphasizes rote memorization of math facts, they, too, need to think through the variety of situations modeled by addition and subtraction, and they, too, need to examine various representations of multiplication and division. Especially challenging for teachers is the work on operations with fractions.
WORKSHOP ACTIVITIES: THE BREAK-OUT SESSION
In the teacher preparation workshop, we drew mainly on material from Building a System of Tens, showing examples of videotape, print cases, mathematical explorations, and seminar participants' writing assignments to illustrate the flow of ideas and demonstrate how the various strategies provide different windows on the same or related ideas. Having talked
the group through the issues that arose in the sessions on the base-10 structure of number and addition/subtraction multidigit computation, we stopped to work together on the session devoted to multidigit multiplication. Specifically, we showed video cases of two children who explain their methods for solving 12 × 29 and 17 × 36, respectively, and of one child, Thomas, who presents a strategy for 17 × 36 that does not work. This is what Thomas did to multiply 17 × 36,
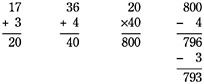
Our purpose for including the latter case in our curriculum is that, though mistaken, this child's strategy has strong elements of logic. By taking apart Thomas's solution methods and identifying what is solid in his thinking—it would be an effective strategy for adding 17 + 36—and where his logic has gone awry, and comparing elements of strategies to those of his classmates, teachers can practice important pedagogical skills while working out for themselves concepts of multidigit multiplication. This case illustrates how teachers can transform student error into a learning opportunity for their classes.
DISCUSSION SUMMARY
In Sunday's DMI break-out session, some participants became involved in sorting out for themselves the issues that the Thomas video case presented and could see its value for teacher learning. But other members were unwilling to accept the premise that a child's incorrect method is worth examining. Instead, they argued that Thomas's teacher should have been teaching in such a way that none of her pupils would make such an error.
This impulse to “fix” child or teacher whenever a mistake is made is prevalent in the culture of mathematics education. In fact, teachers and teacher educators often believe that successful teaching means an absence of error. But mathematicians will say that doing mathematics entails making mistakes and learning from them. One aspect of our work with teachers is to help them explore error as a vehicle for further learning. Therefore, we believe the impulse to “fix” must be checked if classrooms are to become contexts for the development of mathematical habits and for building from an analysis of common error.
Other participants' comments that emerged from the session included the following:
-
Pedagogical strategies—manipulative use, for example—don't need to be taught separately; they can arise naturally in the contexts of the cases and mathematical explorations.
-
In teacher education courses, different strategies should be used complementarily. For example, print and video cases each have their respective advantages. Also, after examining children's thinking in the written cases, it is important that teachers check out similar ideas with “live” children in their classes.
-
When undergraduates have only one mathematics course to prepare them for teaching, dedicating so much time to one theme only is difficult. For example, in the DMI course materials, prime and composite numbers are not specifically addressed.
-
When inquiry is the style of the class, participants' thinking is validated, appreciated, and valued (as opposed to settings in which all ideas come from the instructor). And with specific reference to preservice courses, undergraduates have the opportunity to ask questions related to their fears about teaching.
Video as a Delivery Mechanism
Bradford Findell, Deborah Loewenberg Ball
SESSION GOALS
The session “Video as a Delivery Mechanism” focused on using video as an alternative approach to help teachers learn mathematics. The goal of the session was to consider how video can be used to provide opportunities for learning mathematics. The session was organized around two video clips. The first video excerpt was a 5-minute teacher-directed class discussion of student solutions to a mathematical problem. The second excerpt was the beginning of a 30-minute lecture prepared as part of a video course on arithmetic for prospective elementary teachers.
For each video, participants were asked to identify and discuss opportunities and pitfalls presented by the video. In particular, what opportunities for learning mathematics are afforded by the video and how might they be exploited? What potential pitfalls does the video bring and how might they be mitigated? The intent was to think about characteristics of a video that make it productive for engaging in discussions of the mathematical problems of teaching.
A VIDEO CASE: CINDY
The first video came from the VideoCases for Mathematics Professional Development project, directed by Nanette Seago.1 In their work, they found that it was important to ask participants to engage in the mathematics before viewing the video. To that end, the participants were asked to solve the problem in Figure 1, trying to anticipate also how a middle-school student might approach the problem.
Some participants used a table to arrive at a solution, others used general algebraic approaches, and most arrived at a formula such as P = T + 2, where P is the perimeter and T is the number of triangles. Some participants were concerned about what units of length might be used to measure the perimeter. In the problem statement, there is no mention of the length of a side of a triangle. The simplest approach is to assume the length is one unit. But this assumption doesn't completely resolve the problem because the resulting formula obscures a neces-
|
1 |
Judith Mumme and Nicholas Branca are Principal Investigators for the project. |
Figure 1. Polygons All in a Row
If equilateral triangles are placed in a row, as shown below, how does the perimeter vary with the number of triangles? What would the perimeter be if 100 triangles were placed in such a row?
Can you come up with a general method and express it algebraically? Explain your reasoning.
sary unit conversion: T is a number of triangles, whereas P is a length.
The emphasis in the discussion was that different approaches yield solutions that look different but are algebraically equivalent. Some participants wondered whether the solutions would have been different if they had been asked to think about how preservice or inservice teachers would approach the task. Which approach, they wondered, would provide more direct access to the mathematics? And for whom would such an approach work?
Participants then watched a video segment from an eighth-grade class engaged in the same triangle problem. Participants were asked to look in particular for the mathematics in the video in order to focus the subsequent discussion toward the mathematical opportunities and pitfalls.
SUMMARY OF CINDY VIDEO
In this excerpt, Cindy, the teacher, brings the class together to discuss their solutions to the triangle problem. She points out that the class has noticed two rules: a “plus one” rule that describes how the perimeter changes with each additional triangle, and a “plus two” rule that describes the relationship between the number of triangles and the perimeter. She illustrates these rules in a table (see Figure 2).
To describe the “plus two” rule, a student suggests the equation T + 2 = perimeter, where T = the number of triangles. Cindy points out that every new triangle adds three edges and asks why the rule should be “+2” and not “+3”. One student shows that when a triangle is added, some of the edges get “closed up.” Another student suggests that the triangles account for the top and bottom edges, and the “+2” comes from the two ends. Then Lindsay asks, since there are two ends with two edges each, “shouldn't it be +4?” In response to Lindsay's question, one student proposes what it might be like with squares. Cindy puts Lindsay's
question on hold and poses versions of the problem that replace the triangles with squares, regular pentagons, and regular hexagons.
DISCUSSION SUMMARY
Participants identified opportunities and pitfalls of using the video as listed in Table 1. Several of these provoked extended discussion. In particular, participants noted that the video case could be used with many different audiences for many different purposes, but that a facilitator would probably be required, especially if the goal was to learn some mathematics.
Participants were concerned about the mathematical focus of the lesson. Was the purpose to look for patterns or to analyze perimeter? Was this a lesson in geometry or in patterns and algebra? The lesson was supposed be part of a unit on functions, where the specific purpose is to use the context to get data from which a rule can be generated. Some participants viewed the vagueness of the goal as a potential pitfall; others suggested that the vagueness might present an opportunity to discuss the importance of setting clear goals for lessons and keeping the goal in focus during the lesson.
There was some sentiment that the purpose and the mathematics were somewhat confused in this episode, and that the confusion was compounded by the several ideas that seemed to contribute to “rules.” The “plus one” and “plus two” rules could be used to highlight the vertical and horizontal relationships in the table, providing opportunities for distinguishing between recursive and “closed form” representations of functions. The “plus 3” and “plus 4” ideas, on the other hand, were tied more to the geometry of the situation. With so many ideas in such a short time, unless the teacher is able to lead the class toward a synthesis of the ideas, it will be difficult for students to form clear understandings that will support deeper learning about function. Also, unless the teacher has a clear understanding of the mathematics, it will be difficult for her to lead the class toward such a synthesis. The teacher needs to explore the mathematical territory of the problem prior to teaching it.
The Cindy video can be used to discuss teacher decision making: Why, for example, did Cindy choose to postpone responding to Lindsay' s question? And how are teachers' decisions influenced by what they see as the goal of the lesson?
A VIDEO LECTURE: HERB GROSS
The second video excerpt was a portion of “Gateways to Arithmetic, Lecture #7: Subtracting Whole Numbers” from a 51-lecture collection on mathematics content. In each 30-minute videotape, Herb Gross lectures for a video audience, sometimes speaking directly to the camera. He writes notes and solutions as he proceeds through the content.
SUMMARY OF VIDEO LECTURE
This lecture begins with a short discussion of some pointers on how to use the video. The professor announces, “I have made the decision to jam the tape full of information. You can always rewind the tape and watch it again” whenever the verbal description is too fast. He explains that whether a fill-in-the-blank question is easy or hard depends on where the blank is. In Figure 3a, for example, the second question is easier because one associates
Table 1. Opportunities and Pitfalls of the Cindy Video
|
Opportunities |
Potential Pitfalls |
|
Using the Video
|
Using the Video
|
|
Mathematics
|
Mathematics
|
|
Teacher Decisions
|
|
|
Students
|
Figure 3. Comparing Fill-in-the-Blank Questions
Sacramento with California even if one does not know that it is the capital. In the first question, on the other hand, one might associate California with many cities. Similarly, in Figure 3b, the first question is easier because one can get the answer by association or by pressing keys on a calculator. The second question, however, requires some understanding.
Gross doesn't like the “take-away” concept and instead emphasizes the connection between addition and subtraction, pointing out that, in technical terms, subtraction is called “inverse addition.” He shows (Figure 4a) how one might give change from a $500 bill for a $279 purchase. So 500 − 279 means the number we have to add to 279 to get 500. He shows connections to more traditional written procedures for subtraction (Figure 4c) by showing how one might trade a $100 bill for ten $10 bills and then trade one of those for ten $1 bills (see Figure 4b). Borrowing is to subtraction, what carrying is to addition.
DISCUSSION SUMMARY
Again, the participants identified opportunities and pitfalls (see Table 2), several of which provoked extended discussion. In particular, several participants voiced their perspectives that presenting a lecture as a means of instructing preservice teachers is in conflict with what they feel teachers should be prepared to do in their classrooms. But because the video can be paused and viewed again, and because there is no interaction, viewing the video is not the same as sitting in a lecture.
Although some participants suggested that the video could be used without a facilitator, others wondered what a viewer has to know about subtraction and place-
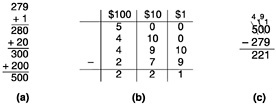
Figure 4. Methods for Computing 500 − 279
Table 2. Opportunities and Pitfalls of the Herb Gross Video
|
Opportunities |
Potential Pitfalls |
|
Use
|
Use
|
|
Mathematics
|
Mathematics
|
value for the video to make sense. Although the video provides a useful synthesis of some mathematical ideas, some conceptual difficulties are omitted. Some participants suggested that the lecture might be used as a source of mathematical questions for deeper consideration and reflection.
CONCLUSION
In keeping with the guiding principles of the second day of the Workshop, we looked at these videos as sources for mathematical questions. The perspective was to ask how video can serve as a tool in the mathematics learning process. We were able to shed some light on two very different uses of video with preservice teachers, perhaps leading to consideration of different types of video to serve different learning goals for teachers. Furthermore, by exploring both opportunities and pitfalls in each of the videos, participants were able to move beyond quick conclusions about the quality of the video to ask questions about the potential for mathematics learning.