4
The Simplified Stress-Based Approach to Triggering Assessment
Liquefaction is triggered when the generation of large porewater pressures forces a soil to lose significant stiffness and strength and, under some circumstances, to behave like a viscous fluid (see Chapter 2). A first step in a liquefaction evaluation is to assess whether the expected seismic shaking is large enough to trigger liquefaction. The evaluation usually includes site characterization: that is, studying the geologic, hydrologic, and geotechnical conditions that influence the liquefaction potential of a site. The quantitative component of the evaluation is usually calibrated to the shaking levels and soil properties that have or have not resulted in liquefaction during previous earthquakes (see Chapter 3). The consequences associated with liquefaction triggering are assessed separately (see Chapters 6 and 7).
The method known as the simplified stress-based procedure (Whitman, 1971; Seed and Idriss, 1971; Seed et al., 1985) is the one most commonly used in practice to predict liquefaction triggering (see Chapter 1, Box 1.3) and is the subject of this chapter. A factor of safety (FS) against liquefaction triggering, defined as the ratio between the seismic loading required to trigger liquefaction (i.e., the liquefaction resistance) and the seismic loading expected from the earthquake (i.e., the seismic demand), is computed. Both the seismic demand and the liquefaction resistance are characterized as cyclic stress ratios, defined as the ratio of the cyclic shear stress (τcyc) to the initial vertical effective stress (σ′vo). The seismic demand is the earthquake-induced cyclic stress
ratio (CSR), and the liquefaction resistance is the cyclic resistance ratio (CRR): that is, the cyclic stress ratio required to trigger liquefaction. The most common approaches used in practice to compute the seismic demand (CSR) and liquefaction resistance (CRR) are described in the next sections. Issues related to the collection of appropriate geotechnical field data for a stress-based liquefaction triggering assessment are discussed. The chapter ends with a discussion of the interpretation of simplified stress-based liquefaction triggering analyses, including a discussion on the use of probabilistic methods.
SEISMIC DEMAND
The CSR represents the cyclic shear stress at a given depth due to earthquake shaking. At sites where the ground slope is less than 6% (per Youd et al., 2001), the earthquake-induced shear stresses are assumed to be due solely to the vertical propagation of shear waves and can be computed by one-dimensional dynamic response analysis of the soil deposit (Seed and Idriss, 1971). Because dynamic response analyses were difficult and time-consuming to perform when the method was developed, however, and because it was challenging to obtain the required site characterization and to identify appropriate input ground motions, Seed and Idriss (1971) proposed the following simplified equation (see Equation 4.1 below), based on Newton’s second law, to compute a representative CSR for an earthquake magnitude M = m:
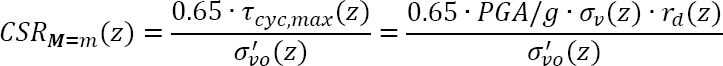 |
(4.1) |
where τcyc,max is the maximum cyclic shear stress at depth z, σ′vo is the initial vertical effective stress at depth z, PGA is the horizontal peak ground acceleration at the ground surface, g is the acceleration of gravity, σv is the total vertical stress, and rd is a depth-dependent shear stress reduction coefficient that accounts for the nonrigid response of the soil deposit. The 0.65 factor was introduced to reduce the CSR from the peak value of the earthquake-induced shear stress, which occurs only once during the earthquake, to a more representative value that occurs multiple times during strong shaking. The value of rd is equal to 1.0 at the ground surface and decreases with depth below the surface to account for the nonrigid response of the soil column subjected to the vertically propagating shear wave.
The cyclic stress ratio required to initiate liquefaction (i.e., the liquefaction resistance, CRR) decreases with increasing number of cycles of loading (see Chapter 2); therefore, the seismic loading must be associated with a number of loading cycles. Earthquake magnitude is used as a proxy for the number of loading cycles because the duration of shaking and the associated number of loading cycles correlate with earthquake magnitude. The CSR is adjusted using a magnitude scaling factor (MSF) to compute an equivalent CSR for a reference M = 7.5 (see Equation 4.2 below):
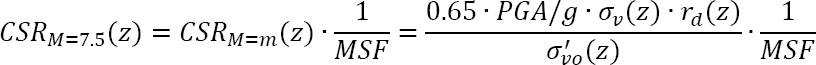 |
(4.2) |
MSFs were first developed by Seed and Idriss (1982) from estimates of the typical number of cycles of loading for different earthquake magnitudes and laboratory test results. Multiple
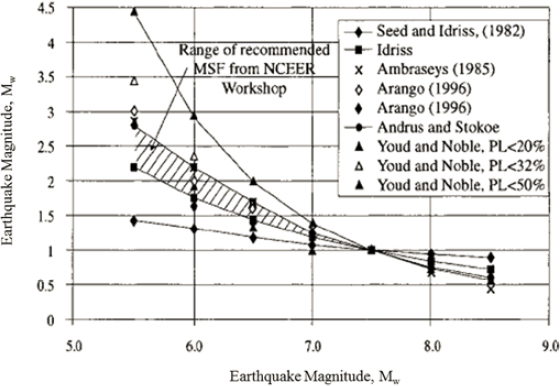
alternative MSFs, some of which are shown in Figure 4.1, have been proposed since then by researchers using various techniques. The 1996/1998 National Center for Earthquake Engineering Research (NCEER)/National Science Foundation (NSF) Workshops on liquefaction evaluation (Youd et al., 2001) recommended a range of MSFs for use in practice (Youd et al., 2001). More recently, Cetin and colleagues (2004), Cetin and Bilge (2012), and Boulanger and Idriss (2014) provided revised recommendations for MSFs. Cetin and colleagues (2004) derived their MSFs directly from the liquefaction case history database by including earthquake magnitude in the regression analysis they used to establish the triggering relationship for liquefaction resistance (described in the next section). But, because a large percentage of data in current liquefaction databases comes from earthquakes of M between about 6.9 and 7.6 (see Chapter 3 and Appendix C), where the MSF is relatively close to 1.0, statistical derivation of MSFs outside of this magnitude range can be questionable. Cetin and Bilge (2012) developed an MSF that depends on relative density and overburden stress. Boulanger and Idriss (2014) applied a cap to the MSF for small magnitude earthquakes (M < 5.25) to account for the dominance of a single large acceleration pulse in these small magnitude events and, based on work by Kishida and Tsai (2014), they made the MSF dependent on a soil type parameter that described the slope of the curve relating the CRR to the number of cycles to liquefaction. Thus, the MSF for dense cohesionless soil is close to the “Idriss” curve shown in Figure 4.1. As the density (or penetration resistance) decreases, however, the MSF curve flattens; this results in smaller values than Youd and colleagues’ (2001) recommended range for M < 7.5 (thereby increasing the liquefaction potential) and larger values for M > 7.5 (thereby decreasing the liquefaction potential).
Prior to 2001, the MSF depended only on earthquake magnitude. Revisions to MSFs since then represent a major departure from this practice, but there is no consensus on which of the more recent recommendations, if any, are appropriate for practical application. Furthermore, the impacts of case history data on MSF from recent large magnitude earthquakes in Chile and Japan have yet to be considered. MSF values also impact recommendations for the number of uniform cycles of loading to use in laboratory-based evaluations of liquefaction triggering. MSFs and the number of uniform cycles of loading for laboratory evaluation of liquefaction triggering, Neq, are intimately related, as discussed in Chapter 5. As is also noted in Chapter 5, recent studies suggest that Neq is negatively correlated with the peak ground acceleration (see, e.g., Biondi et al., 2004), that Neq is a function of site-to-source distance (see, e.g., Liu et al., 2001; Green and Terri, 2005; Stafford and Bommer, 2009), and that Neq may vary with depth in the soil profile (see, e.g., Green and Terri, 2005). If Neq is dependent on these factors, then the MSF should also be dependent on these same factors. Given the importance of the MSF when evaluating liquefaction triggering for both small (e.g., M < 6.5) and large (e.g., M > 8.0) earthquakes, as well as its importance to laboratory evaluation of liquefaction triggering, research to identify and resolve inconsistencies related to the various MSF and Neq recommendations made since 2001 is warranted. New case history data from recent large magnitude earthquakes need to be incorporated into these recommendations.
The 0.65 factor found in Equations 4.1 and 4.2 was originally proposed as a way to relate the number of loading cycles from an irregular earthquake loading to the number of loading cycles from uniform cyclic loading. Although this value is somewhat arbitrary and was unnecessary once MSFs were introduced, 0.65 is still the standard due to historical precedent.
Equations 4.1 and 4.2 require estimates of PGA, M, and rd to compute the CSR. Because the required PGA is at the ground surface of a soil site, the PGA used in a liquefaction triggering analysis must account for the effects of the near-surface soil conditions on ground shaking. Traditionally, ground motion hazards were expressed as scenario events, so the PGA and M values
used in a liquefaction triggering assessment were established deterministically. Probabilistic seismic hazard analysis (PSHA), however, has become the standard for defining ground motions for seismic design for some applications. One challenge using a PSHA-derived PGA is that there is no single earthquake magnitude associated with it from which to compute the MSF. If the magnitude deaggregation1 data associated with the PSHA-derived PGA are available, the associated FS against liquefaction triggering may be calculated by parsing the deaggregated magnitude-distance pairs into magnitude bins; calculating the FS associated with each magnitude bin using the associated MSF; calculating the contribution from each magnitude bin to the design FS by multiplying the FS associated with the magnitude bin by the sum of the relative contributions of each magnitude-distance pair in the bin; and summing up the contribution to the design safety factors from all of the magnitude bins (Idriss, 1985; Finn, 2007). If the deaggregation data are not available, engineering judgment may be required to select a representative magnitude from the earthquake sources (e.g., active faults) associated with the probabilistic PGA. This can be a relatively straightforward process if the seismic environment is dominated by a single large magnitude earthquake source. When the seismic environment is characterized by a number of sources of different magnitude, however, or by a fault capable of generating earthquakes of varying magnitudes, identifying a single representative magnitude is a challenging task that should be delegated to an experienced professional (e.g., an experienced geotechnical earthquake engineer or engineering seismologist).
Different options are available for conducting a probabilistic liquefaction triggering assessment using the stress-based method: these include a single-scenario option in which the user can manually enter PGA and M; a multiple-scenario approach in which the deaggregation data are integrated to obtain a marginal magnitude distribution, for each value of which the FS is computed and then combined using the magnitude probabilities as weighting factors; and a complete probabilistic liquefaction hazard assessment (PLHA) that considers the magnitude distributions at all return periods. Other approaches have also been proposed, but it is essential to recognize that the simplified, stress-based triggering assessment methods are empirical and cannot be manipulated excessively without losing their reliability. A more comprehensive probabilistic liquefaction assessment based on a PSHA takes into account the relative contributions to the liquefaction hazard from the full range of ground motion intensities associated with each magnitude-distance pair. This type of liquefaction assessment is discussed in Chapter 9 within the context of an integrated reliability assessment and performance-based seismic design.
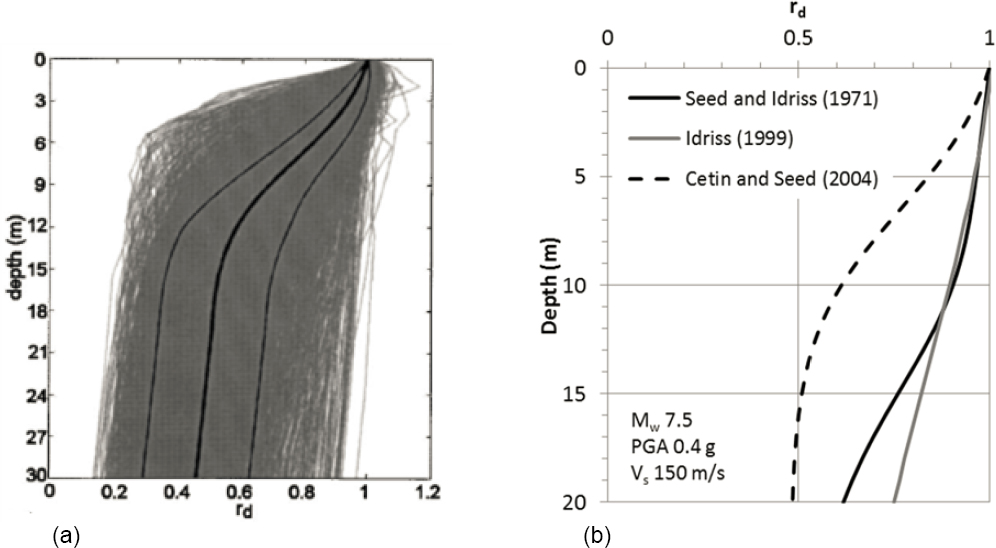
The depth-dependent shear stress reduction coefficient, rd, is a function of the nonrigid response of the soil deposit (characterized in the small strain regime by the shear wave velocity [Vs] profile at the site) as well as the characteristics of the earthquake waves traveling through the soil. As a result, the range of possible rd values is large. Figure 4.2a illustrates the variability in rd values computed for a range of site conditions. Seed and Idriss (1971) initially proposed a relationship between rd and depth that they developed from a limited number of dynamic response analyses for a range of generic site conditions. Using additional site response analyses, Idriss (1999) modified the Seed and Idriss (1971) rd relationship to make rd depth and magnitude dependent. The Idriss (1999) relationship is used to develop the triggering relationships of Idriss and Boulanger (2008) and Boulanger and Idriss (2014).
___________________
1 Magnitude deaggregation refers to the process of dividing the family of earthquakes that contribute to the probabilistic design ground motion into magnitude-distance pairs and calculating the relative contribution of each pair to the design ground motion.
More recently developed rd relationships (see, e.g., Cetin and Seed, 2004; Kishida et al., 2009) take into account additional factors, including the average Vs. Incorporating additional factors may produce more accurate estimates of rd, but the variability remains large. Figure 4.2b shows the depth-dependent rd factors from Seed and Idriss (1971), Idriss (1999), and Cetin and Seed (2004) for an average Vs of 150 m/s over the top 12 m, PGA = 0.4 g, and M = 7.5. The Cetin and Seed (2004) relationship predicts significantly smaller values of rd than either of the other relationships, though the differences between the relationships are smaller for stiffer soil profiles. Differences in the Vs profiles analyzed by Cetin and Seed (2004) compared with those used by either Seed and Idriss (1971) or Idriss (1999) are the main reasons for the differences in rd, although the different modulus reduction and damping curves used by these investigators also influenced their rd values. Cetin and Seed (2004) performed site response analyses for 50 well-characterized sites that previously liquefied in an earthquake, while the other studies analyzed mostly hypothetical sites. As a result, the median values of rd predicted by the Cetin and Seed (2004) relationship are considered more representative of the induced cyclic shear stress at liquefaction sites than are other rd relationships. Because the position of data points on a liquefaction triggering plot—and thus the position of the triggering curve itself—are intimately related to the evaluation of rd, however, the rd relationship developed by Cetin and Seed (2004) may not be appropriate for use with triggering relationships developed using the other rd relationships.
In place of the simplified expressions in Equations 4.1 and 4.2, the earthquake-induced shear stress can be computed directly from site-specific dynamic response analyses (Kramer, 1996). The most common method used to conduct a site-specific dynamic response analysis is a one-dimensional, total stress, equivalent-linear analysis. A one-dimensional nonlinear analysis, a two-dimensional equivalent linear analysis, and two-dimensional nonlinear analysis are sometimes used as well (Kramer, 1996). Many engineers prefer to use dynamic response analysis to evaluate the CSR because the site-specific Vs profile and expected ground shaking at the site are considered in the analysis. Note, however, that the use of site-specific dynamic response analysis to assess the CSR for a simplified liquefaction analysis may not be consistent with the empirical liquefaction curves used to establish liquefaction resistance if those curves are developed using rd relationships that are biased relative to site response analysis (as discussed later in this chapter). If the empirical rd relationship associated with the particular liquefaction method is not an unbiased estimator of rd (e.g., for the triggering relationships developed by Idriss and Boulanger [2008] and Boulanger and Idriss [2014]), the empirical rd relationship associated with the particular liquefaction method should be used to compute induced shear stresses at depth, and the results of site response analyses should be used only to refine the estimate of the PGA at the ground surface. Furthermore, effective stress dynamic response analysis with pore-pressure generation should never be used to estimate the seismic loading, because the seismic loading for the simplified, stress-based procedure ignores the effects of pore-pressure generation.
Estimating the shear stress from dynamic response analysis requires more information than does the simplified equation: it requires the Vs distribution for the entire soil profile and the underlying bedrock; the strain-dependent nonlinear soil properties (e.g., variation of shear modulus and damping ratio with shear strain); and a suite of appropriate input earthquake motions. The selected input motions must match the intensity and frequency content of shaking expected at a site, and multiple time histories must be used to capture the variability inherent to earthquake ground motions. For instance, the International Building Code (ICC, 2011), through incorporation
by reference of ASCE 7 (Chapter 21),2 recommends that at least five different ground motions be used in site response analysis (ASCE, 2010). Alternatively, a random vibration theory (RVT) approach to equivalent-linear site response analysis can be used (see, e.g., Rathje and Ozbey, 2006; Kottke and Rathje, 2008). The RVT approach has the advantage of not requiring the selection of input time series.
There is considerable uncertainty in the CSR expected at a site due to uncertainty and variability in the site characterization, variability in the rd expressions (see, e.g., Figure 4.2), and uncertainty in the ground motion PGA and associated earthquake magnitude. The uncertainty in PGA is somewhat taken into account through the use of a PSHA to estimate the ground motion. Accounting for the other sources of uncertainty may require a more complete PLHA (described later in this chapter).
LIQUEFACTION RESISTANCE
As already described, the resistance to liquefaction for a soil is expressed as the CRR, which is the CSR required to trigger liquefaction. As discussed in Chapter 2, the in situ CRR cannot be measured reliably in the laboratory for most liquefiable soils. Therefore, the simplified method makes use of field observations to develop relationships between measured in situ parameters and CRR. These relationships are derived from case histories of liquefaction and no liquefaction from many sites and many earthquakes (see Chapter 3). The most common in situ parameters used for this purpose (see Chapter 2) are the standard penetration test (SPT) blow count (N), the cone penetration test (CPT) tip resistance (qc), and small strain Vs. SPT and CPT profiles are used more often than Vs profiles to evaluate liquefaction triggering (Siegel, 2013).
___________________
2 See http://ascelibrary.org/doi/book/10.1061/9780784412916.
CRR Relationships
The many relationships available that correlate CRR with measured SPT blow count, CPT tip resistance, or Vs typically predict the cyclic resistance of the soil for a set of reference conditions: an initial vertical effective stress of 1 atmosphere, an M 7.5 earthquake, clean sand (i.e., less than 5% soil grains finer than 0.075 mm), and an area where there is no initial static shear stress on a horizontal surface (i.e., ground slope is less than 6%). For situations that do not satisfy these conditions, adjustment factors are required. Differences among the developed CRR relationships are due predominantly to the data sets from which they are derived, the adjustment factors used, and the regression procedure used to develop the CRR curve.
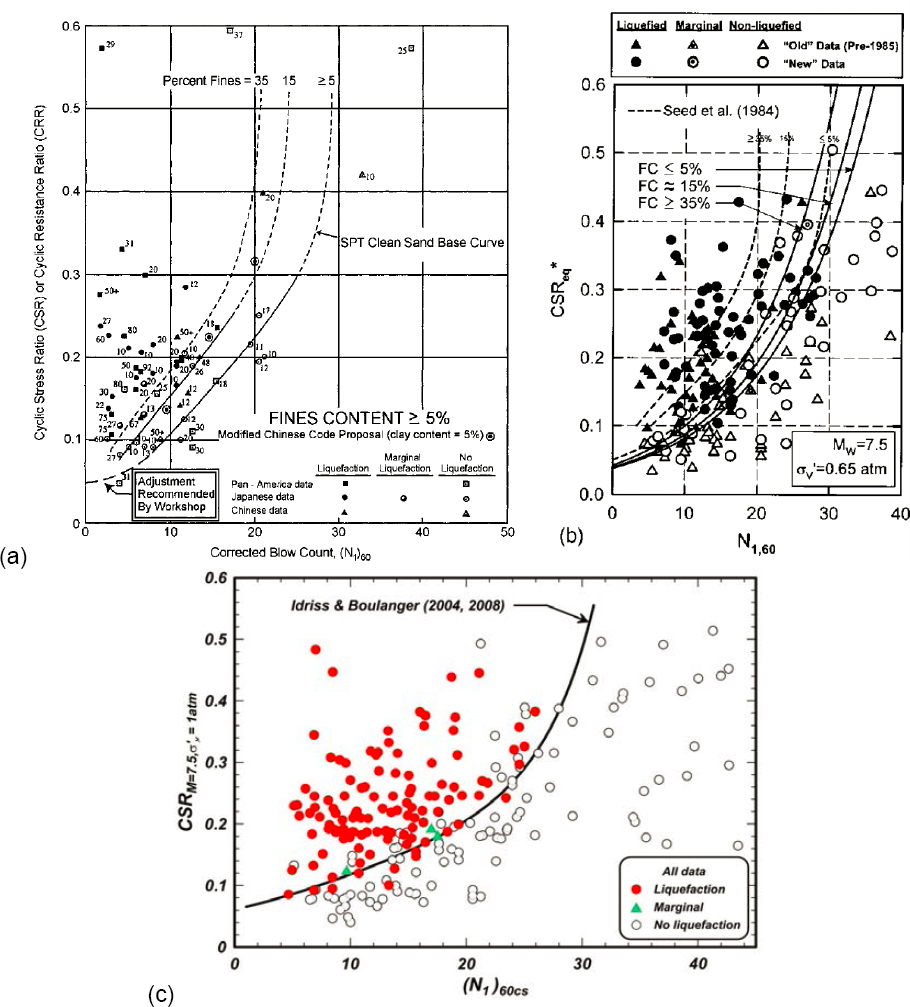
The most commonly used relationships to predict CRR from SPT blow count are those proposed by Youd and colleagues (2001), Cetin and colleagues (2004), Idriss and Boulanger (2008), and Boulanger and Idriss (2014). The Youd and colleagues (2001) relationship was agreed to by consensus at NCEER/NSF workshops in 1996 and 1998, and the others were published since that time. These CRR relationships were developed from different databases of case histories, although many of the case histories are common to each database. For each of these data sets the percentage of cases where liquefaction occurred is between 50% and 55%, which represents a relatively balanced distribution between “yes” (where liquefaction is believed to have occurred) and “no” (where liquefaction is believed not to have occurred) cases. The data for the liquefied and non-liquefied case histories used to develop the Youd and colleagues (2001), Cetin and colleagues (2004), and Idriss and Boulanger (2008) relationships are shown in Figure 4.3 along
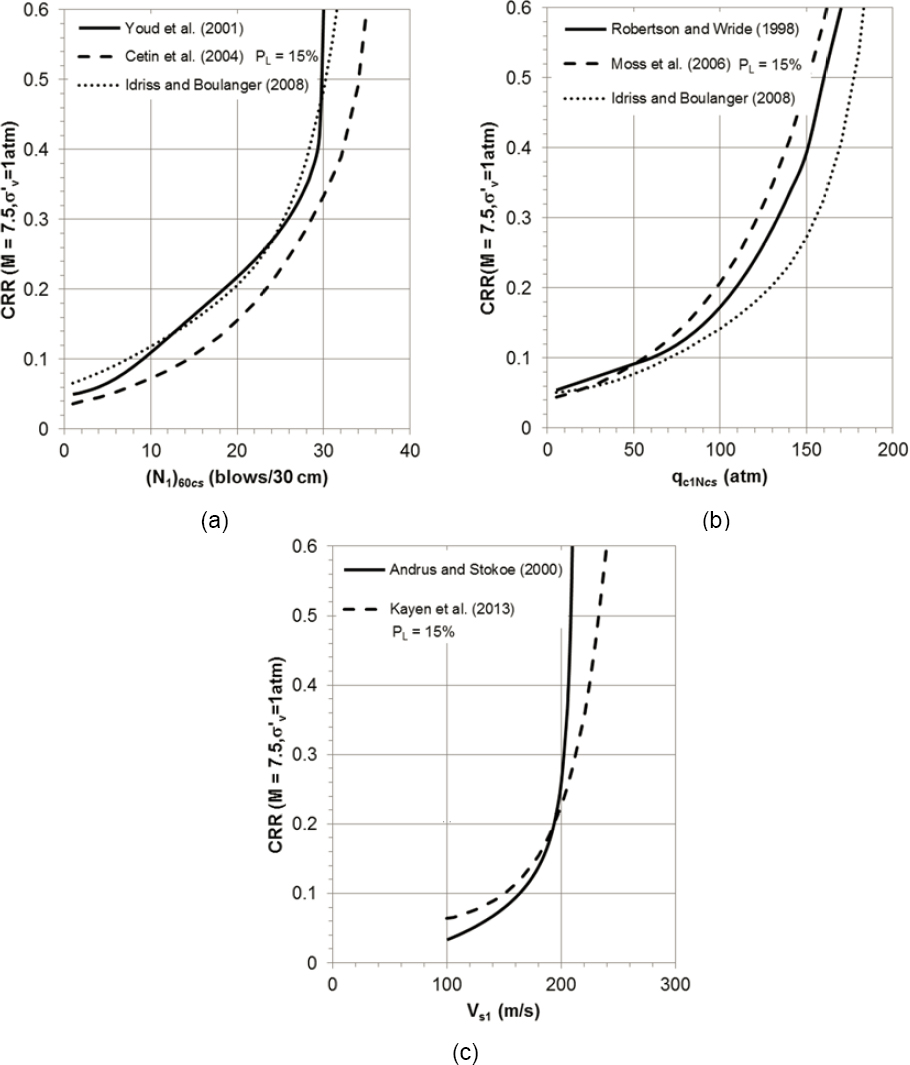
with each proposed CRR relationship. Figure 4.4a shows these three commonly used CRR relationships on the same graph. The relationships developed by Youd and colleagues (2001) and Idriss and Boulanger (2008) are similar, while the relationship developed by Cetin and colleagues (2004) is located below the others, which indicates that for a given SPT blow count, the Cetin and colleagues (2004) relationship will predict a smaller CRR. Directly comparing the CRR relationships is misleading, however, because they incorporate different adjustment factors and use different rd relationships. Comparison of the relationships using their recommended adjustment factors is considered in Box 4.1.
The most commonly used relationships to predict CRR from the CPT tip resistance (qc) are those developed by Robertson and Wride (1998), Moss and colleagues (2006), and Idriss and Boulanger (2008). Robertson and Wride (1998) is a slightly modified version of the relationship recommended by NCEER/NSF workshops in 1996 and 1998 and reported in Youd and colleagues (2001). The Robertson and Wride (1998) relationship is based on the CRR curve from Robertson and Campanella (1985), and this curve was derived from the Seed and colleagues (1985) CRR-SPT relationship by converting SPT blow count into an equivalent CPT tip resistance. This curve subsequently was compared with CPT data from liquefaction and no liquefaction case histories and shown to be consistent with the field data. The Moss and colleagues (2006) and Idriss and Boulanger (2008) relationships were developed directly from databases of about 200 case histories with measured CPT data. The Moss and colleagues (2006) relationship is a probabilistic relationship; for deterministic purposes, they recommend use of the 15% probability curve (PL = 15%). Compared with the liquefaction data sets for SPT, the data sets for the CPT are more heavily weighted toward “yes” cases, with about 70% to 75% of the cases associated with liquefaction (see Chapter 3). Figure 4.4b plots the predicted CRR as a function of CPT tip resistance from Robertson and Wride (1998), Idriss and Boulanger (2008), and Moss and colleagues (2006) for an M 7.5 earthquake and a vertical effective stress of 1 atmosphere. The relationships are similar for CPT tip resistances less than about 50 atmospheres, but they deviate more substantially at larger values, with the Idriss and Boulanger (2008) relationship predicting smaller CRR at CPT tip resistances greater than about 100 atmospheres. Once again, however, this direct comparison may be misleading due to differences in the adjustment factors used in the different relationships. (See Box 4.1 for a comparison of the models using their recommended adjustment factors.)
A commonly used relationship to predict CRR from Vs is the relationship developed by Andrus and Stokoe (2000), which was recommended for use by the NCEER/NSF workshops reported in Youd and colleagues (2001). The Andrus and Stokoe (2000) relationship was developed from a database of 225 case histories, of which about 55% represented liquefaction cases. More recently, Kayen and colleagues (2013) developed a CRR-Vs relationship based on a database of 422 case histories; this data set is more heavily weighted to liquefaction cases (about 70%). The Kayen and colleagues (2013) relationship is a probabilistic relationship; for deterministic purposes, they recommend the use of the 15% probability curve (PL = 15%). Figure 4.3c plots the predicted CRR for an M 7.5 earthquake and a vertical effective stress of 1 atmosphere as a function of Vs from the Andrus and Stokoe (2000) and Kayen and colleagues (2013) relationships. The Kayen and colleagues (2013) relationship predicts larger CRR than Andrus and Stokoe (2000) at shear wave velocities less than about 180 m/s and predicts smaller CRR at larger values of Vs. But again, this comparison may be misleading due to the different adjustment factors used. (See Box 4.1.)
Adjustment Factors Applied to CRR
Adjustments to the measured in situ resistance parameter and CRR are required for situations that do not satisfy the standard reference conditions. The situations typically adjusted in simplified stress-based liquefaction triggering assessment are summarized in Table 4.1. The fines content adjustment is applied to the measured in situ parameter to modify it to an equivalent clean sand value. Effective stress adjustments are applied to both the in situ parameter and the CRR. The stress adjustment to the in situ parameter attempts to remove the effects of vertical effective stress so that the adjusted in situ parameter predominantly reflects the relative density of the soil. The
effective overburden stress factor (Kσ) modifies the CRR to account for the suppression of dilatancy with increasing effective stress. The shear stress adjustment (Kα) is a factor that modifies the CRR to account for the effects of a static shear stress on the horizontal plane (i.e., non-level ground conditions) on the liquefaction resistance of the soil.
Each developed CRR relationship incorporates its own set of adjustment factors. The equations for these adjustment factors have become increasingly complex as a consequence of efforts to incorporate the effects of different potential conditions that may influence them. This extensive fine-tuning of the adjustment factors—in particular, for conditions not constrained by field case history data—has complicated the “simplified” method of liquefaction evaluation. Adjustment factors need to be carefully evaluated as additional case history data become available, and modifications to the adjustment factors that increase their complexity should result in decreasing uncertainty.
There are two basic approaches to developing adjustment factors: one, they can be developed using theoretical constraints from soil mechanics principles and experimental data, or two, they can be derived directly in the regression for the CRR relationship. The liquefaction case history databases generally do not include enough data either at effective stresses corresponding to depths less than 1.5 meters or in excess of 15 meters or at small (e.g., M < 6.0) and very large (e.g., M > 8.0) earthquake magnitudes to constrain the adjustment factors adequately within a regression analysis. Additionally, using regression analysis alone may result in unintended trends in the relationship: for example, the MSF within the Moss and colleagues (2006) regression equation results in a weak magnitude dependence for CRR. Using soil mechanics principles and experimental data to constrain adjustment factors beyond the range over which they are constrained by case history data is a fundamentally more sound approach than is simple extrapolation of regression equations. Documenting field case histories that can constrain adjustment factors outside the current bounds is a priority.
TABLE 4.1 Situations Typically Requiring Adjustment Factors in CRR Calculation
| Adjustment | Applied to In Situ Parameter? | Applied to CRR? |
|---|---|---|
| Fines Content | Yesa | Noa |
| Effective Stress | Yes | Yes |
| Static Shear Stress | No | Yes |
aThe adjustment for fines content may be applied to either the in situ parameter (i.e., SPT N value, CPT qc, shear wave velocity) or the CRR.
Adjustment for Fines Content
The fines content influences both the measured in situ parameter and the CRR, but it is difficult to separate the two effects. Early CRR relationships (see, e.g., Seed et al., 1985) included curves for different fines contents. Most current CRR relationships only provide a clean sand curve to be used with an equivalent clean sand in situ parameter: for example, (N1)60cs, qc1Ncs. The shear wave velocity CRR relationships do not show a strong influence of fines content. The developers of each CRR relationship recommend their own method to adjust for fines content. Most fines content adjustments have been developed directly from the case history databases, and they use
the measured fines content from soil samples as input. Traditional CPT soundings and Vs measurements, however, do not provide soil samples for the direct measurement of fines content. The adjustment factors for CPT use measurements of tip resistance and skin friction directly to adjust the CPT tip resistance (Robertson and Wride, 1998; Moss et al., 2006), often using the soil behavior type index (Robertson, 1990).
The different approaches to correct for fines content could result in discrepancies among different liquefaction triggering relationships. Research is needed to better evaluate these different approaches. The consistency between the methods that use direct measurement of fines content and those that infer fines content from CPT measurements needs to be investigated. Until the indirect methods are fully vetted, it is good practice to measure fines content at a site directly and to develop site-specific relationships between fines content and the soil behavior type index.
Adjustments for Effective Stress
The stress adjustment factors applied to correct in situ penetration test parameters to a vertical effective stress of 1 atmosphere were developed from data from large-scale calibration chamber tests (see, e.g., Marcuson and Bieganousky, 1977), field tests (see, e.g., Skempton, 1986), and theoretical solutions (see, e.g., Salgado et al., 1997). In the stress ranges where little to no experimental or field data exist, the relationships for the adjustment factors were either extrapolated from stress ranges where more data existed and/or extrapolated based on soil mechanics principles. The relationships for the adjustment factors associated with the different variants of the simplified procedure can have a considerable influence on the predicted liquefaction potential, particularly at higher effective overburden stresses (e.g., depths greater than approximately 20 meters).
The stress adjustment factor applied to the CRR (i.e., Kσ, defined as the ratio of the CRR for a given vertical effective stress to the CRR for a vertical effective stress of 1 atmosphere for the same soil) was first proposed by Seed (1983). Values of Kσ have been derived from either laboratory data and soil mechanics principles (see, e.g., Hynes and Olsen, 1999; Youd et al., 2001; Idriss and Boulanger, 2008, 2010; Dobry and Abdoun, 2015) or directly from regression of the liquefaction database (see, e.g., Cetin et al., 2004; Moss et al., 2006; Kayen et al., 2013). It is important to note that none of the liquefaction case histories include critical layers in which the vertical effective stress was greater than 2 atmospheres, which corresponds to a depth below ground level of approximately 20 meters. Most cases correspond to vertical effective stresses less than 1 atmosphere (see Chapter 3, Table 3.2). The values of Kσ developed by different researchers generally agree over effective stresses ranging 0.5 to 1.2 atmospheres—the range well represented in the case history database. Recommended values for Kσ begin to deviate beyond that range.
The depth of the water table below the ground surface can be important in liquefaction potential assessments. Fluctuations in the water table depth may occur on timescales of years (e.g., in areas of groundwater injection or withdrawal or during periods of drought), seasonally, or daily (e.g., in a port and harbor environment). The water table depth may influence both the extent of the saturated zone that is susceptible to liquefaction and the value of the effective stress at any particular point below its surface. Observations made following the 2011 earthquake in Christchurch, New Zealand, suggest unsaturated zones of sandy soil are likely below the water table where short-term (e.g., daily) fluctuations in the water table occur (Stokoe et al., 2014a). In such zones, the potential for liquefaction triggering is mitigated, but this may not be true in high-permeability soils such as gravel and rockfill.
The change in effective stress due to water table fluctuations can impact the cyclic resistance of the soil, particularly at shallow depths where small changes in the water table can result in relatively large changes in the effective stress used to calculate the cyclic stress ratio. For example, if the water table changes from four to two meters beneath the ground surface, the effective stress at a depth of five meters can decrease from approximately 88 kPa to 64 kPa, a decrease of more than 25%. At present, there is no consensus and little guidance on what values for water table level to use when the water table is known to fluctuate. The absence of such guidance may lead the geotechnical engineer to use historic high water tables (if such data are available) or the mean high water level (e.g., for port and harbor projects, because the higher the water table the greater the potential for triggering liquefaction). In a true probabilistic assessment of liquefaction potential, the depth of the water table could be treated as a random variable and assigned a mean and standard deviation to capture the fluctuations. Results from such analyses could be used to establish guidance on how to appropriately account for the water table level in a deterministic analysis. In the absence of such guidance, professional judgment is necessary.
The Kσ relationships deviate at small effective stresses because there is a debate about whether it is advisable to cap the maximum value of Kσ and, if so, at what value to cap it. At effective stresses significantly larger than 1 atmosphere, recommended values of Kσ represent significant extrapolations from the liquefaction case history databases, and the values recommended by different researchers deviate significantly from each other. Given the uncertainty involved in any extrapolation, it is important that experimental data, soil mechanics principles, or both be used to constrain Kσ outside of the range represented in the database. As an example of the problems associated with using only field case histories to constrain Kσ within the regression, some CRR relationships show almost no stress dependency because the case history data they employ do not extend across a large enough stress range to constrain the influence of effective stress on CRR: this was shown by Moss and colleagues (2006) and Kayen and colleagues (2013). Nevertheless, experimental data and soil mechanics principles do indicate that effective stress influences CRR. Consequently, Kayen and colleagues (2013) do recommend that stress adjustment factors from other studies be applied to the computed CRR from their relationships.
One possible reason why the existing liquefaction databases do not include enough data at large effective stresses to constrain the stress corrections is that liquefaction at depth may not produce a surface manifestation of liquefaction, and surface manifestation of liquefaction is the primary means of identifying sites where liquefaction has occurred. In engineering practice, however, liquefaction triggering analysis is performed routinely for soil at significant depth under large effective stress. Although the measured in situ test parameters for these deep soils may be far in excess of any uncorrected values in the liquefaction databases, a liquefaction triggering analysis may show such soils to be highly liquefiable after application of the various stress adjustment factors. Data from laboratory experiments performed at large effective stresses have been used by some investigators to constrain the stress adjustment factors (see, e.g., Seed and Harder, 1990) at vertical effective stresses larger than 1 atmosphere, and some investigators have also incorporated soil mechanics principles (e.g., principles from critical state soil mechanics) to constrain these adjustment factors (see, e.g., Boulanger, 2003b). More recently, Montgomery and colleagues (2012) compiled an expanded database of experimental results at large effective stress and evaluated the Kσ relationships of Youd and colleagues (2001) and Idriss and Boulanger (2008). They concluded that the Youd and colleagues (2001) relationship predicted values of Kσ that were 10% to 15% smaller than the data and that the Idriss and Boulanger (2008) relationship predicted values of Kσ that were 0% to 10% larger. A thorough examination of all of the available
experimental data from laboratory and centrifuge tests regarding stress adjustment factors at both small and large effective stresses is warranted in an effort to provide more insight about the values of Kσ at large effective stresses.
Adjustment for Initial Static Shear Stress
The initial static shear stress on the horizontal plane present in the soil before earthquake shaking also influences the CRR and is taken into account through the multiplicative shear stress adjustment factor, Kα, introduced by Seed (1983). A parameter α is defined as the ratio of the initial static shear stress to the normal effective stress on the horizontal plane, and Kα represents the ratio of the CRR for a given value of α to the CRR for α = 0. As the CRR relationships represent level or gently sloping ground (e.g., ground slope less than 6%), the CRR obtained from a CRR relationship represents α = 0 (i.e., level ground) conditions and must be adjusted if the in situ α is larger than zero (e.g., slopes and in and under earth dams).
Insights into the effects of an initial static shear stress on the CRR have been obtained predominantly from laboratory tests. These experimental data show that Kα is influenced not only by α but also by the state of the soil as expressed both by its relative density and the effective confining pressure and by the criterion used to define liquefaction in the experiments. Importantly, the presence of an initial static shear stress appears to increase the CRR for denser soils and to decrease it for looser soils. Seed and Harder (1990) compiled a wide range of laboratory test data from the 1970s and 1980s and used a strain-based definition of liquefaction to develop recommended values for Kα that vary with α and relative density. Harder and Boulanger (1997) revised those recommended values in light of new experimental data (Boulanger et al., 1991; Boulanger and Seed, 1995), including data on the effect of multidirectional shaking and the use of a smaller strain criterion to define liquefaction triggering. Nevertheless, the consensus from the NCEER/NSF liquefaction workshops (Youd et al., 2001) was not to recommend values of Kα because of the large scatter in the experimental data and to recommend that additional research on this subject was needed.
Since the NCEER/NSF workshops, the theoretical framework of critical state soil mechanics has been applied to the experimental data to explain the combined effects of relative density and effective stress on the Kα relationships (Boulanger, 2003a). Additionally, new experimental data have been generated (see, e.g., Kammerer, 2002; Wu et al., 2003; Cetin and Bilge, 2014), much of it focused on multidirectional shaking using a wide variety of stress paths. But there is still no consensus on recommended Kα factors for use in engineering practice. For projects that require the effects of an initial static shear stress to be considered (e.g., large dams), the most commonly used Kα factors are those from Boulanger (2003a). These empirical factors were developed with guidance from soil mechanics principles and were compared with a small set of experimental data for three different sands. A favorable comparison was observed, but only a limited amount of data was considered. Therefore, additional research is needed for clear resolution of this topic. This research needs to take advantage of centrifuge testing, for example, as well as physics-based numerical modeling (e.g., discrete element analysis) to improve understanding of this effect.
Use of Consistent Adjustment Factors in Engineering Practice
It is critical to note that the liquefaction triggering adjustment factors, including the magnitude scaling factor (MSF) and rd factors discussed earlier, are used in the development of the CRR triggering relationships. These factors are used to adjust the CSR (i.e., demand) for each case history to the reference conditions (i.e., σ′v = 1 atmosphere, M = 7.5, clean sand conditions) before plotting it on graphs such as those shown in Figure 4.3. Therefore, the adjustment factors directly influence the location of the derived CRR relationship. To use a CRR relationship in engineering practice appropriately, adjustment factors consistent with those used in the development of the CRR relationship must be employed. Engineers should not mix and match adjustment factors from different CRR relationships. This was not commented on during previous efforts to develop consensus (i.e., Youd et al., 2001). Thus, the use of site response analysis to estimate the earthquake-induced CSR is appropriate if, and only if, the rd factors used in the development of the CRR curve are unbiased relative to the values expected at liquefaction sites. The rd factors developed by Cetin and Seed (2004) are considered by the present study committee to be unbiased because they analyzed about 50 well-characterized liquefaction sites and used a large number of earthquake motions. Therefore, site response analysis may be employed for the computation of the earthquake-induced CSR in conjunction with the CRR relationships developed using the Cetin and Seed (2004) rd factors (i.e., Cetin et al., 2004; Moss et al., 2004; and Kayen et al., 2013).
To avoid compounding uncertainties in CRR relationships developed in the future, unbiased estimates of all parameters need to be used. This includes using site response analysis to estimate the earthquake-induced CSR for all of the liquefaction case histories employed in development of a new CRR relationship.
Comparisons Between CRR Relationships
There are controversies related to the differences among various CRR relationships. Idriss and Boulanger (2012) state that certain misinterpretations and inconsistencies in the Cetin and colleagues (2004) database are responsible for the differences between the CRR relationships for the SPT shown in Figure 4.4a. Preliminary results provided to the committee by Cetin (written communication, June 29, 2014),3 however, indicate that the inconsistencies identified by Idriss and Boulanger (2012) do not noticeably alter the location of the Cetin and colleagues (2004) CRR curve. The information provided to the committee by Cetin suggests that the differences in the Cetin and colleagues (2004) and Idriss and Boulanger (2008) CRR relationships are due primarily to differences in rd and Kσ. The results shared with the committee by Cetin need to be evaluated carefully by the technical community once published in the peer-reviewed literature. Additionally, when using adjustment factors consistent with the development of each relationship under conditions where both relationships are well constrained by data (e.g., depths less than 20 meters), the differences between the Cetin and colleagues (2004) and Idriss and Boulanger (2008) triggering approaches are not as significant as suggested by the CRR relationships alone, as illustrated in Box 4.1. At depths greater than 20 meters, however, the FS evaluated using these methods diverges (Griffiths and Cox, 2012).
___________________
3 Available by request from https://www8.nationalacademies.org/cp/ManageRequest.aspx?key=49573.
Comparison of Triggering Evaluation Methods
Several liquefaction triggering evaluation procedures are commonly used in practice (see, e.g., Robertson and Wride, 1998; Andrus and Stokoe, 2000; Youd et al., 2001; Cetin et al., 2004; Moss et al. 2006; Idriss and Boulanger, 2008; Kayen et al., 2013; Boulanger and Idriss, 2014). As discussed throughout this chapter, each procedure has advantages and disadvantages. For example, a notable strength of the approach developed by Idriss and Boulanger (2008) is the use of laboratory and soil mechanics principles to extrapolate the applicable range of the procedure beyond that constrained by case study data. And, a notable strength of the Cetin and colleagues (2004) procedure is the use of the unbiased estimator for rd (i.e., for adjusting the earthquake-induced shear stress computed using equation 4.1 to account for the nonrigid response of the soil column). Differences between various methods that are soundly based may be considered to be epistemic uncertainty. As such, the engineer may apply various methods and weight the results, wherein the weighting factors are developed based on professional judgment on a case-by-case basis depending on the specifics of the problem. The sum of all weights should be 1.0.
Probabilistic CRR Relationships
Various CRR relationships have been developed within a probabilistic framework. Most of these use well-known statistical methods like logistic regression or discriminant analysis (see, e.g., Liao et al., 1988; Youd and Noble, 1997a) to distinguish between liquefaction and no-liquefaction categories. It is not widely appreciated, however, that these regression techniques provide the probability of observing the collected liquefaction data set given that liquefaction has occurred. These techniques do not provide the probability of liquefaction given the observed in situ parameters at a site. Some researchers have used Bayesian techniques to avoid this problem (see, e.g., Cetin et al., 2004; Moss et al., 2006), usually assuming a non-informative prior probability that indicates liquefaction and non-liquefaction are equally probable at the site being evaluated, or employing non-informative prior probabilities in developing the model coefficients themselves. This assumption may not be reasonable for some sites because information is available that makes liquefaction more or less likely (e.g., geologic age, depositional environment, evidence of prior liquefaction), and this prior probability information could be used to enhance a liquefaction analysis. Plotting the CRR curves associated with the likelihood ratio rather than probability would enable the user to deal with prior and posterior probabilities directly within a Bayesian framework (see Box 4.2).
Effect of Geologic Age
Chapter 3 (“Influence of Soil Age on Liquefaction Potential”) provided a description of the effects of geologic age on soils. The effects of age often manifest themselves as an increase in CRR with time under confinement (e.g., Seed, 1979). Ideally, any increase in liquefaction resistance with age would manifest itself in larger values of the in situ parameters used to evaluate CRR (e.g., SPT blow count, CPT tip resistance, or Vs). Penetration resistance measured by the SPT and the CPT, however, may not be very sensitive to the effects of aging
(Andrus et al., 2009) because these tests induce large strains in the soil that may destroy the beneficial effects of aging. Andrus and colleagues (2009) have suggested that Vs, which reflects the small-strain stiffness of the soil, is more sensitive to the effects of aging and therefore can be used to account for aging effects.
Significant uncertainty remains regarding the physical mechanisms that increase the liquefaction resistance with time, although secondary compression and biogeochemical processes may be involved. Additionally, the effect of aging on the liquefaction resistance of field deposits has been studied in only a few geographic areas (e.g., Charleston, South Carolina, and Christchurch, New Zealand). Further research is needed to understand fully the effects of aging on liquefaction resistance and to develop rational and defensible methods for taking it into account.
Fine-Grained Soils
In the past, if more than 50% of a soil’s constituents (by weight) passed the #200 (0.075 mm) sieve (i.e., fine-grained soils), the soils were considered non-liquefiable. It is now commonly recognized that low plasticity fine-grained soils are susceptible to liquefaction. It is also recognized that soils with less than 50% passing the #200 sieve may not be susceptible to liquefaction if the percentage passing through the #200 sieve and the plasticity index (PI) of the soil that passes through are above certain threshold values. This may be true even if those soils are classified as a sand, or possibly a gravel, under the Unified Soil Classification System. Various criteria for liquefaction susceptibility of soils have been proposed involving grain size distribution, water content, Atterberg limits (e.g., liquid limit [LL] and PI), and CPT indices (see, e.g., Wang, 1979; Seed and Idriss, 1982; Iai et al., 1986, 1989; Robertson and Wride, 1998; Andrews and Martin, 2000; Youd et al., 2001; Seed et al., 2003; Boulanger and Idriss, 2006; Bray and Sancio, 2006).
As discussed in Chapter 3, many practicing engineers still use the “Chinese criteria” when assessing the potential for liquefaction triggering in soils containing fine-grained (silt and clay-sized) particles. Seed and Idriss (1982) stated that if clay size soils meeting the criteria (see Chapter 3) plotted above the A-line on a Casagrande plasticity chart, liquefaction characteristics should be determined through testing; otherwise, the soils were not considered vulnerable to liquefaction.
Based on differences in index tests in the United States and China (Koester, 1992), Andrews and Martin (2000) proposed the modification to the Chinese criteria presented in Table 4.2. Also, Moss and Chen (2008) state that the 2001 Chinese Building Code (CNS, 2001) used a slight variation of the original Chinese criteria, specifying the clay fraction limit (i.e., the maximum percent by weight finer than 0.005 mm) above which the soil is considered not susceptible to liquefaction as a function of the intensity of ground shaking. The CNS (2001) specifies the clay fraction as 10%, 13%, and 16% for Chinese Intensity 7, 8, and 9, respectively, and Moss and Chen (2008) note that Chinese Intensity 7 through 9 is approximately equal to Modified Mercalli Intensity VI through X.
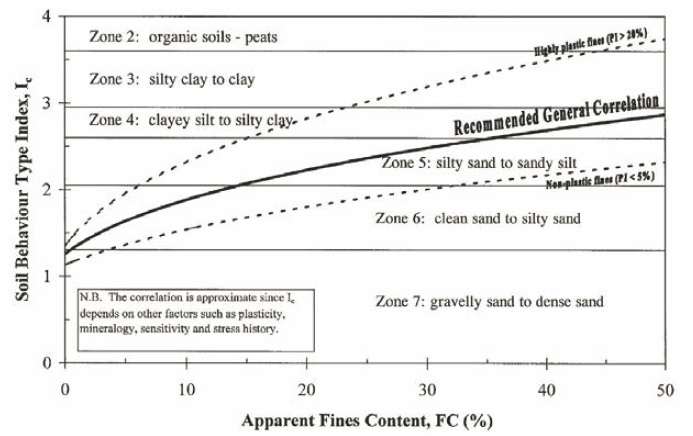
Although the Chinese criteria are still used, more recent investigators have dismissed them as insufficient or simply incorrect. Alternative criteria commonly used in practice in the United States are those developed by Robertson and Wride (1998), Seed and colleagues (2003), Bray and Sancio (2006), and Boulanger and Idriss (2006). The first three criteria are based on index properties determined from laboratory tests. Robertson and Wride (1998) define a soil behavior type index, Ic, in terms of normalized values of CPT tip resistance and friction ratio.
The liquefaction susceptibility criterion proposed by Robertson and Wride (1998) is based on the empirical classification of soils with Ic ≤ 2.6 as sand and sand mixtures (see Figure 4.5) and thus are assumed to be susceptible to liquefaction. Robertson and Wride (1998) suggest that the CPT version of the simplified stress-based liquefaction procedure can be used to evaluate the liquefaction potential of these soils. Soils with Ic > 2.6 are classified empirically as clayey silt, silty clay, clay, or organic soils (see Figure 4.5). Robertson and Wride (1998) state that soils with Ic > 2.6 should be sampled and evaluated for liquefaction susceptibility based on laboratory measured index properties and cyclic shear testing. Youd and colleagues (2001) lowered the threshold for sampling and testing to evaluate liquefaction potential to Ic > 2.4. The original Robertson and Wride (1998) criterion (i.e., soils with Ic ≤ 2.6 are assumed to be liquefiable and can be evaluated using the simplified procedure) was adopted by the Earthquake Commission (EQC) in New Zealand as the criterion for determining susceptibility to liquefaction triggering for sites in Christchurch (Tonkin and Taylor, 2013).
Based on a combination of post-earthquake observational data and laboratory tests, Seed and colleagues (2003), Bray and Sancio (2006), and Boulanger and Idriss (2006) proposed liquefaction susceptibility criteria and liquefaction potential assessment procedures based upon the percent fines and Atterberg limits of the soil. The case history data supporting the development of these criteria are discussed in Chapter 3 in the section on liquefaction of fine-grained soils.
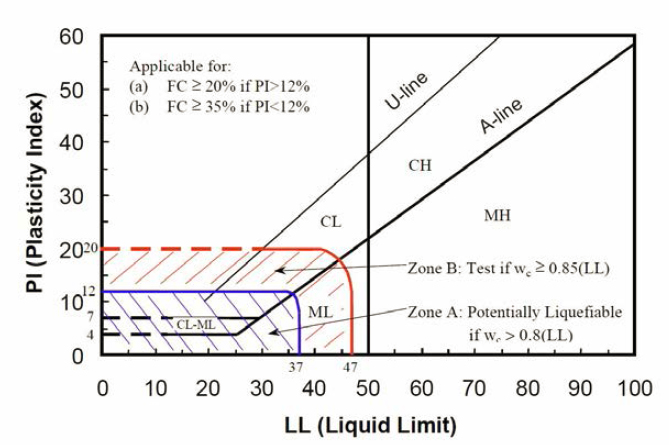
Seed and colleagues (2003) proposed the screening criteria shown in Figure 4.6 which defines three zones of susceptibility to what they describe as “classic cyclic liquefaction”—the loss of strength and stiffness due to cyclic pore-pressure generation. These zones include soils that are potentially liquefiable (Zone A in Figure 4.6); soils that may be potentially liquefiable (Zone B of the figure); and soils not susceptible to “classic cyclic liquefaction.” Seed and colleagues (2003) explain that soils classifying as not susceptible to “classic cyclic liquefaction” could exhibit what they called “sensitivity” to liquefaction: strength loss resulting from monotonic shearing or remolding due to large, monotonic (unidirectional) shear displacements. PI is used in place of percent clay fines in the Seed and colleagues (2003) criteria, as is done in the Chinese criteria. Water content (wc) and LL are still part of the Seed and colleagues (2003) criteria. Those criteria apply to fine-grained soils with either a fines content (FC) equal to or greater than 20% if the PI is equal to or greater than 12, or an FC equal to or greater than 35% and a PI less than or equal to 12. Soils considered potentially susceptible to “classic cyclic liquefaction” (Zone A in Figure 4.6) can be evaluated using the simplified procedure. Soils falling in Zone B and thus possibly susceptible to “classic cyclic liquefaction” need verification of their liquefaction susceptibility—beyond evaluation through the simplified procedure—through sampling and laboratory testing. Zone C soils, although generally not considered to be susceptible to “classic cyclic liquefaction,” may be sensitive to liquefaction.
TABLE 4.2 Modified Chinese Criteria Proposed by Andrews and Martin (2000)
| Liquid Limit < 32 (1) | Liquid Limit ≥ 32 | |
|---|---|---|
| Clay Content < 10% (2) | Susceptible | Further Studies Required (Considering plastic non-clay-sized grains such as mica) |
| Clay Content ≥ 10% | Further Studies Required (Considering non-plastic clay-sized grains such as mine and quarry tailings) |
Not Susceptible |
(1) Liquid Limit determined by Casagrande-type percussion apparatus.
(2) Clay defined byas grains finer than 0.002 mm.
Bray and Sancio (2006) also identified three zones of susceptibility for soils containing fine-grained particles, shown graphically in Figure 4.7: susceptible, moderately susceptible, and not susceptible. Soils that fall in their “not susceptible” zone are not considered to be susceptible to liquefaction triggering but may be sensitive. According to Bray and Sancio (2006), the cyclic behavior of fine-grained soils is controlled by numerous factors. They recommend that soils that soils categorized as “susceptible” and “moderately susceptible” be sampled and tested to ascertain their susceptibility to liquefaction and their strain potential. This recommendation assumes that soils in the susceptible zone have enough fines such that they can be sampled and tested without excessive disturbance, which is not unreasonable given that the data on which Bray and Sancio (2006) based their criteria included mostly soils with an FC ≥ 35%. Their recommendation to sample and test all soils with FC ≥ 35% differs from the finding of Seed and colleagues (2003)—that the liquefaction potential of soils in Zone A may be evaluated using the simplified procedure.
The criterion proposed by Boulanger and Idriss (2006) is solely a function of the PI. As discussed in Chapter 3, they use their criteria to distinguish between soils that are susceptible to liquefaction triggering (i.e., they exhibit “sand-like” behavior) and those that are susceptible to some strength loss due to cyclic loading but are not susceptible to the loss of stiffness and strength and cyclic pore-pressure generation characteristic of what Seed and colleagues (2003) referred to as “classic cyclic liquefaction” (i.e., they exhibit “clay-like” behavior). Boulanger and Idriss (2006) state that soil behavior transitions from sand-like to clay-like over the PI range of approximately 3 to 8, but they recommend PI = 7 as a conservative boundary between the two behaviors (see Figure 4.8). The distinction between the two types of behavior defined by Boulanger and Idriss (2006) relates not only to differences in the cyclic response of these soils but also to differences in the appropriate testing and analysis procedures used to evaluate the dynamic response characteristics of these soils (Armstrong and Malvick, 2014, 2015). The simplified stress-based liquefaction evaluation procedure is appropriate only for soils having PI < 7 (i.e., sand-like behavior). On the contrary, soils having PI ≥ 7 (i.e., clay-like behavior) may be susceptible to cyclic softening or may be sensitive and should be evaluated accordingly, but the simplified stress-based liquefaction evaluation procedure should not be used to evaluate the dynamic response characteristics of these soils.
When comparing the Seed and colleagues (2003), the Bray and Sancio (2006), and the Boulanger and Idriss (2006) criteria, note that Seed and colleagues (2003) use a combination of FC and PI to define the boundary between susceptible and not susceptible soils (i.e., fines-controlled soils are those having FC > 20% and PI > 12 or FC > 35% and PI < 12). In contrast, Bray and Sancio (2006) apply their criteria to all soils having FC > 35%, and Boulanger and Idriss (2006) state that their criterion can be used for soils having FC less than 50% if it can be shown that the soil behavior is controlled by fine-grained fraction. These three sets of criteria also differ in the required input properties and their intended use. The criteria proposed by Seed and colleagues (2003) and Bray and Sancio (2006) require PI, LL, and water content (wc), while the criterion proposed by Boulanger and Idriss (2006) requires only PI. Laboratory testing of undisturbed samples in all three criteria for a class of soils that fall between susceptible and not susceptible, though the criteria for these intermediate soil classes vary among the three sets of criteria. Laboratory testing to evaluate the liquefaction triggering of undisturbed soil specimens is discussed in Chapter 5.

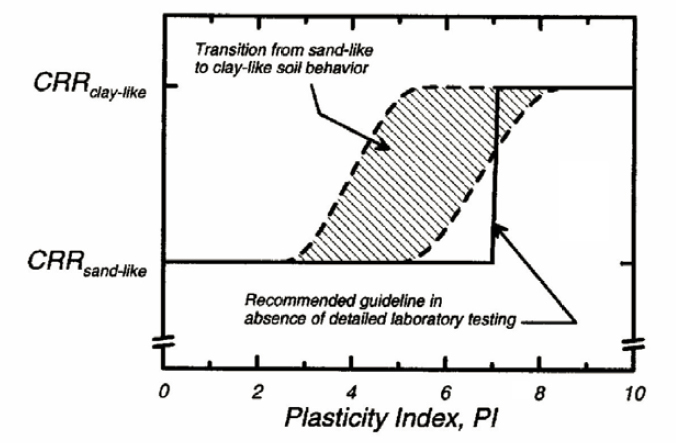
Seed and colleagues (2003) and Boulanger and Idriss (2006) state that the simplified method (with appropriate fines content corrections) can be used for the soils they identify as susceptible to liquefaction. Bray and Sancio (2006) make no statements about the applicability of the simplified stress-based liquefaction evaluation procedure for soils that fall into their susceptible (to liquefaction) zone. For establishing whether or not laboratory testing is needed to assess if a soil is liquefiable, however, their recommendations apply only to soils with FC greater than 35%, suggesting that the simplified method not be used and that laboratory testing is required when the FC is greater than 35%.
While similar conclusions regarding liquefaction susceptibility may be reached from these three sets of criteria for most soils, the varying criteria inevitably will yield different conclusions about the liquefaction susceptibility for some fine-grained soils. This potential for conflicting conclusions is exacerbated by the relatively poor accuracy and precision associated with measurements of Atterberg limits (e.g., LL and PI) in low-plasticity soils. As a result, all criteria should be applied with caution in any liquefaction assessment. Furthermore, additional field data on fine-grained soils, including soils with an FC between 35% and 50%, are necessary to resolve the conflicts between these sets of recommendations. As noted in Chapter 3, data need to include those for fine-grained. Additionally, because these soils generally are amenable to undisturbed sampling, field data need to be supplemented with laboratory testing of intact samples to refine and/or validate the criteria limits.
Gravelly Soils
Loose gravelly soils have liquefied in earthquakes (see, e.g., Youd et al., 1985). Gravelly soils may consist of gravel-sized particles floating in a matrix of finer particles (e.g., sands, silts, and clays) or may consist of a gravel matrix in which the gravel particles are in contact and finer particles may fill in part of the pore space. Gravel soils that do not contain a significant finer-grained component are believed to be less susceptible to liquefaction due to their large hydraulic conductivity, which allows porewater pressures to dissipate quickly during earthquake shaking (Kramer, 1996). Nevertheless, layers of gravel with few fines confined between low-permeability layers can liquefy in an earthquake because the low-permeability layers impede drainage (Stokoe et al., 1988).
It is difficult to characterize the liquefaction resistance of gravelly soils using the SPT or the CPT because the large size of the particles relative to the SPT sampler or the CPT cone tip can increase the measured penetration resistance in a nonrepresentative manner. Different types of in situ tests, such as the Becker penetration test (BPT; Harder and Seed, 1986), various large penetration tests (LPTs; Daniel et al., 2003), and large dynamic penetration tests (DPTs; Cao et al., 2013), have been developed to circumvent these problems. To minimize the effects of large particles, the BPT uses a diesel hammer to drive a 17-cm diameter closed-end pipe, while LPTs drive large samplers (7 to 14 cm diameter) using larger hammers than the SPT hammer. A DPT developed in China (Cao et al., 2013) drives a 7.4-cm diameter cone tip with a large hammer and reports the number of blows to advance 10 cm. Both the BPT and the LPTs measure the number of blows to advance 30 cm and attempt to convert that number to an equivalent SPT blow count (see, e.g., Harder and Seed, 1986).
Research has shown that the BPT is influenced by variable hammer energy and efficiency (Sy and Campanella, 1994) as well as shaft friction (Ghafghazi et al., 2014). Details of the test setup influence the LPT (Daniel et al., 2003). As a result, there is significant scatter in the conversions
of BPT and LPT penetration resistances to the SPT (see, e.g., Youd et al., 2001), which increases the uncertainty in their use in liquefaction evaluations. An instrumented BPT is being developed (DeJong et al., 2014; Ghafghazi et al., 2014) that measures the energy at the tip of the BPT penetrometer, which can be used to improve the BPT-SPT conversion.
Further improvements to the LPT and BPT test procedures and their conversion to equivalent SPT blow counts are still needed for these methods to be considered reliable means of assessing liquefaction resistance. Direct evaluation of the liquefaction resistance of gravels using these test methods is preferable to converting the measurements to SPT blow count, but the case history data required to do this are not available at the present time. This direct approach has been applied on a limited scale to the Chinese DPT (Cao et al., 2013). Consideration should also be given to developing a large-scale CPT for gravelly materials. The theoretical and fundamental understanding of the static push of a CPT is well developed through cavity expansion theory (see, e.g., Salgado et al., 1997), which can make any required corrections more robust. Nonetheless, penetration of a large-diameter cone into a gravel stratum may be difficult and impractical.
Shear wave velocity (Vs) represents an alternative to using large-scale penetration tests to characterize the liquefaction resistance of gravelly soils. Vs can be measured easily in gravelly soils, especially when using non-invasive surface wave methods. As Vs is directly correlated to liquefaction triggering potential, conversion to an equivalent SPT blow count is not required. Limited measurements of Vs at gravelly sites that liquefied in previous earthquakes have shown that the Vs of these materials was consistent with existing CRR-Vs relationships developed for sandy sites (Andrus et al., 1992; Andrus and Stokoe, 2000). More research is needed to confirm this observation because prior research (Seed and Idriss, 1970; Seed et al., 1986) indicates that the Vs of gravels is significantly higher than that of sands at the same relative density. Through further research, however, Vs may be developed as a practical basis to assess the liquefaction of gravelly materials.
GEOTECHNICAL FIELD DATA FOR LIQUEFACTION TRIGGERING ANALYSES
Site characterization for an analysis of liquefaction triggering includes collection of information to accurately estimate the values of CRR and earthquake-induced CSR at the site. Calculation of the CRR requires in situ measurement of the profile of SPT blow count, CPT tip resistance, or Vs as a function of depth and at multiple locations across the site. Various correction factors are applied to the measured SPT blow count to define a stress- and energy-corrected SPT resistance (N1)60 based on the test setup. The energy transferred to the SPT rod needs to be measured (ASTM D4633) for accurate energy corrections to be applied. Note that the use of the automatic hammer does not negate the need for energy measurements or the use of a correction factor. The use of SPT setups that require other adjustments—such as the use of a non-standard borehole diameter or of samplers configured for liners but used without liners (even though the setups may be allowed by the ASTM D1586)—need to be avoided. Furthermore, SPT blow counts recorded in hollow stem auger borings below the water table are particularly susceptible to error due to soil disturbance and may result in abnormally low blow count values.
It is important to identify and characterize the detailed variations in the in situ resistance within a soil profile. The SPT provides measurements at widely spaced intervals (often 1.5 m, but never less than the length of the split spoon sampler, 0.45 m), which limits the ability to use SPT measurements to identify thinner layers or detailed variations within a soil profile. Because the CPT provides almost continuous measurements, it is ideal for characterizing thinner layers and
detailed variations within strata. Depending on the method of measurement, Vs may be used to identify thin layers and variations within strata, but it does not provide the detail and the resolution of the CPT. A seismic CPT provides a cost-effective means of measuring Vs while also providing a detailed profile of in situ tip resistance. Pore-pressure data from piezocone penetration testing (CPTu) can provide additional information, both qualitative (e.g., whether soil is dilatant or not) and quantitative (e.g., the steady-state porewater pressure). Characterization of soil type is also important to a liquefaction triggering analysis, and CPT and Vs methods do not provide a direct measure of soil type. In these cases, additional boring and sampling, or sampling using a special sampler adapted for use with CPT rigs, is needed to determine soil type directly.
When using liquefaction triggering methods that require Vs values to calculate the earthquake-induced CSR from site response analysis (see, e.g., Cetin and Seed, 2004), Vs should be measured directly and not estimated by correlations with the SPT or the CPT. A comprehensive site investigation for liquefaction triggering on an important project could include all three characterization techniques: borings with SPT sampling (with hammer energy measurements—a stricter requirement than use of the automatic hammer) to obtain blow counts and soil type; CPT soundings to obtain detailed profiles of in situ resistance; and Vs profiles to accurately assess the earthquake-induced CSR and to provide additional insights into the CRR.
INTERPRETING THE RESULTS OF STRESS-BASED TRIGGERING ANALYSIS
Assessments of liquefaction triggering may not match observed field behavior for many reasons, including the presence of unsaturated zones beneath the water table, horizontal stresses due to over-consolidation, or artesian conditions and inadequacies in the simplified methods. The goal of a liquefaction triggering analysis is to evaluate whether liquefaction is expected to occur at a site under a given seismic load. Traditionally, this evaluation has been based on computing the FS, defined as the ratio of CRR to CSR, at different depths within the soil profile. An FS less than 1.0 is generally assumed to indicate that liquefaction is expected to trigger at that depth. The FS against liquefaction, however, does not give insights into the associated uncertainties and variability related to the calculation of CRR and CSR. In practice, a minimum required FS for design as low as 1.0 has been required when coupled with an extreme ground motion level (Kavazanjian et al., 2011). Typical minimum values used in practice are between 1.1 and 1.3, but one part the California Code of Regulations calls for an FS of 1.5 under dynamic conditions, including liquefaction.4
As noted in Box 4.1, different CRR relationships and associated adjustment factors will produce different values for the FS against liquefaction. These differences may be regarded as a result of epistemic uncertainty in the liquefaction triggering models due to imperfect data and imperfect models, which is analogous to the epistemic uncertainty observed in earthquake ground motion prediction (Douglas, 2010), where different ground motion prediction equations predict different levels of earthquake shaking for the same magnitude, distance, site conditions, and other factors. In seismic hazard analysis, it has become standard practice to include this epistemic uncertainty through the use of a logic tree (Bommer and Scherbaum, 2008; Atkinson et al., 2014), where each branch of the logic tree represents an alternative model, and weights assigned to each branch represent the relative degree of belief regarding the accuracy of the model. This approach has not been widely used to date for liquefaction hazard assessment but could be used to
___________________
4 See http://www.calrecycle.ca.gov/laws/regulations/title27/ch4sb3c.htm#21750.
incorporate the results from the different liquefaction triggering relationships to account for the epistemic uncertainty. Different liquefaction triggering models can be assigned to each logic tree branch with weights assigned based on the judgment of the engineer. The FS against liquefaction is then computed for each model in the logic tree and these values are used to compute a weighted mean FS using the assigned weights.
Populating a logic tree involves critical evaluation of the available liquefaction models combined with professional judgment to assign the weights to the logic tree branches. The critical evaluation includes an assessment of the data used in model development, the techniques used to derive the applicable adjustment factors and their extrapolation outside the limits of the data, and the statistical procedures used. All available liquefaction models need not be included in a logic tree, but clear descriptions and justifications of the developed logic tree are required. Details regarding the incorporation of uncertainties and expert judgment in probabilistic analyses can be found in Budnitz and colleagues (1997). Additional research is needed in applying these approaches to liquefaction analysis, particularly regarding the appropriate logic tree implementation that will accurately model the epistemic uncertainty across all scenarios of interest (e.g., fines contents, penetration resistances, depths) considering what is known and unknown about liquefaction triggering.
The probability of liquefaction is an alternative to the FS. For example, Juang and colleagues (2002) developed mappings between FS and probability of liquefaction triggering. Cetin and colleagues (2004) and Idriss and Boulanger (2014) both suggest that the deterministic triggering curve is associated with a probability of liquefaction of approximately 15%. The probability of liquefaction has three components: the probability of the earthquake motion used to compute the CSR, the uncertainty in the relationship between the CRR and in situ test parameters, and the uncertainty in the parameters that enter into the calculation of CRR and CSR. Box 4.3 presents a simple analysis that demonstrates that the uncertainty in the adjustment factors and parameters used in a liquefaction analysis can be larger than the uncertainty in the location of the CRR curve.
The FS or probability of liquefaction is often computed for a single level of ground shaking and its associated earthquake magnitude. Over time, though, a given site may experience a wide range of ground shaking, from frequent weak motions to strong motions that occur only rarely. Furthermore, each level of ground shaking is associated with a distribution of contributing earthquake magnitudes, and those distributions vary with the level of shaking. An alternative to the characterization of liquefaction triggering is a PLHA, in which the seismic hazard curve from a PSHA is convolved with a probabilistic liquefaction triggering model to compute the mean annual rate of non-exceedance for different FSs against liquefaction (see, e.g., Kramer and Mayfield, 2007). Epistemic uncertainty can also be included in a PLHA through a logic tree. The reciprocal of the mean annual rate of non-exceedance for FS = 1.0 from a PLHA is the return period of liquefaction (i.e., the average time between occurrences of liquefaction at a site). Computed in this manner the return period of liquefaction accounts for uncertainties in the local seismicity, earthquake magnitude, source-to-site distance, and ground shaking as well as the prediction of liquefaction triggering. It therefore provides a more complete and objective indication of liquefaction triggering than the FS or probability of liquefaction do based on a single ground motion value and magnitude. Publicly available computer programs exist that perform these calculations (see, e.g., Kramer, 2008; Franke et al., 2014), and the calculations can be incorporated relatively easily within a spreadsheet if the model components are available. PLHA for liquefaction triggering, as well as its application to the evaluation of liquefaction consequences, is discussed further in Chapter 9.
The empirical stress-based simplified methods have served the profession well, but they all are flawed to various degrees. Although a variety of issues associated with their use remains, the technical community will rely heavily on these stress-based methods until reliable and readily usable mechanics-based approaches are available to evaluate liquefaction and related phenomena (see Chapter 8). Better results are likely if the practicing engineer employs multiple empirical methods, the sources of discrepancies between results of the various methods are assessed, and engineering judgment is applied to resolve those differences. The concepts expressed herein are reinforced with recommendations provided in Chapter 10.





























