Are There “Laws” of Manufacturing?
JOHN D. C. LITTLE
If we are to have a meaningful discipline of manufacturing, it is argued, then we should have intellectual foundations to include what might be called “laws of manufacturing.” What are the prospects for identifying and creating such?
It may be useful to distinguish between three types of potential “laws”: mathematical tautologies, physical laws and their analogs, and empirical models. Then we can ask separately whether we are likely to develop further along each line.
TAUTOLOGIES VERSUS LAWS
L = λW (“Little's Law”) is a mathematical tautology with useful mappings onto the real world. L = λW relates the average number of items present in a queuing system to the average waiting time per item. Specifically, suppose we have a queuing system in steady state and let
L = the average number of items present in the system,
λ = the average arrival rate, items per unit time, and
W = the average time spent by an item in the system, then, under remarkably general conditions,
L = λW. (1)
This formula turns out to be particularly useful because many ways of
analyzing queuing systems produce either L or W but not both. Then equation 1 permits an easy conversion from one to the other of these performance measures. Queues and waiting are ubiquitous in manufacturing: jobs to be done, inventory in process, orders, machines down for repair, and so forth. Therefore, equation 1 finds many uses.
As a mathematical theorem, L = λW has no necessary relationship to the world. Given the appropriate set of mathematical assumptions, L = λW is true. There is no sense going out on the factory floor and collecting data to test it. If the real world application satisfies the assumptions, the result will hold.
The basic tautological nature of the proof can be illustrated by drawing a plot of the number of items in the system versus time, as in Figure 1 . The area, A, under the curve represents the total waiting done by the items passing through the system in the time period T. Since the average number of items arriving in a time period T is λT, we have as the average wait per item (at least to first order, with an accuracy that increases as T becomes larger): W = A/λT. However, the same area, if divided by the time, also represents the average number of items in the system during the period: L=A/T. Eliminating A from these two expressions gives equation 1. Thus, the two sides of equation 1 are really two views of the same thing and, with appropriate treatment of end effects and the taking of mathematical limits, become equal.
Physical laws are different. For example, the equality of the two sides of Newton 's law, F = ma, cannot be taken for granted. Each must be
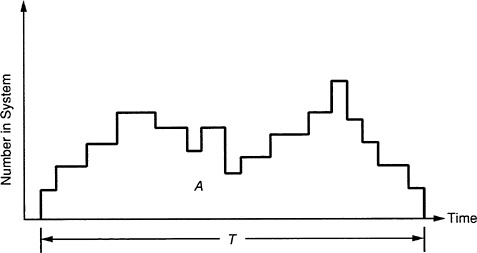
FIGURE 1 The area, A, under the curve represents the total waiting done by the items passing through the system in the time period T.
measured separately and the equivalence verified experimentally. In fact, as is well known, F = ma is only approximate and breaks down at velocities approaching the speed of light. Thus, physical laws require observation of the world and induction about the relationships among observable variables.
LAWS VERSUS EMPIRICAL MODELS
Nineteenth-century physics produced many “laws of nature”: Hooke's law, Ohm's law, Newton's laws, the laws of thermodynamics. By the mid-twentieth century, however, many of these laws had been found to be only approximate, and many new, messy phenomena were being examined. As a result, scientists became more cautious in their terminology and started speaking of models of phenomena. This continues to be the popular terminology today. Such is particularly the case in the study of complex systems, social science phenomena, and the management of operations. The word model conveys a tentativeness and incompleteness that are often appropriate. We enter a class of descriptions of the world in which there are fewer simple formulas, fewer universal constants, and narrower ranges of application than were achieved in many of the classical “laws of nature.”
The incompleteness of models, however, has a virtue in engineering and in applications to managerial decision making. We should include in our models that which is important to the task at hand and leave out that which is not (Little, 1970). This objective is different from the traditional scientific one of describing the world with fidelity and parsimony. For decision-making purposes, we want to restrict ourselves only to the detail required for the job to be done.
Much valuable knowledge can be packaged into empirical models. Their accumulation into organized bodies of learning represents scientific advance and provides a basis for engineering and managerial practice. Here are a couple of examples.
If you examine communications between pairs of individuals in R&D groups versus the physical distance between them, you find a curve like Figure 2 (Allen, 1977, pp. 238-239). Although there is no strictly prescribed functional form or universal constant here, there is definitely a general shape and an experimentally determined range of parameter values. The regularity of the curves can be distorted by a variety of special circumstances, such as electronic mail, location of people on different floors, and the presence of a coffee machine, but the basic phenomenon is strong and its understanding is vital for designing buildings and organizing work teams effectively.
Another example is the experience curve, which is illustrated in Figure 3 . It is well known that manufacturing costs per unit tend to decrease with cumulative production. This has been documented in a variety of cases
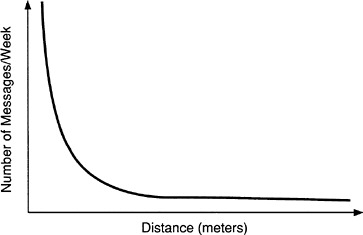
FIGURE 2 Communications between R&D groups as a function of their physical distance from each other.
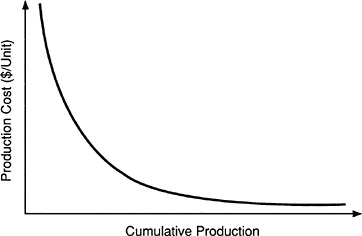
FIGURE 3 Experience curve illustrates the decreasing unit costs for manufacture with accumulated production.
(see, for example, Hax and Majluf, 1984, p. 111). However, the experience curve is a somewhat different kind of relationship than the communications example, because the decreasing cost does not happen automatically. Rather it is the result of much purposeful activity in managing the manufacturing process. In a sense, this seems less satisfying than, say, Newton's law, which predicts unequivocally the trajectory of a ball after it has been struck by a bat.
As another example, even further away from the well-calibrated formulas of nineteenth-century physics, consider prospect theory (Tversky and Kahneman, 1981). This describes how people make decisions under uncertainty. As a result of many experiments in which people make choices in different situations with uncertainties, Tversky and Kahneman have produced a descriptive theory of how people make such decisions. They illustrate it with Figure 4 , which shows a hypothetical value function for an individual, expressing the person's utility for the outcome of some decision. The curve displays three interesting characteristics of people's behavior. First, people tend to make decisions based on potential gains or losses relative to some reference point. If you change the reference point you are likely to change how they value the possible outcomes of a choice and may therefore affect the choice itself.
For example, if a person has, as a reference point, the catalog price of a particular product and then finds the item in a store at a lower price, he or she is likely to treat the difference as a potential gain. Subsequently, if the person buys the product, the purchase is likely to be considered especially satisfactory, and, in fact, the price “gain” may have helped stimulate the transaction. This is why stores that are running sales usually display the original price prominently. This sets the reference point and makes the discount a net gain for the customer.
A second characteristic of Figure 4 is that the slopes of the curves describing gains and losses are different near the origin. The steeper slope for losses indicates that most people dislike a loss more than they like a corresponding gain. This helps explain the current unfortunate tendency
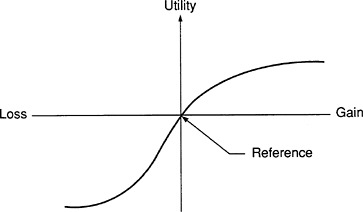
FIGURE 4 Prospect theory illustrates the tendency of people to treat gains and losses differently.
toward negative political advertising. A quantity of negative information suggesting that a candidate might do something harmful if elected may have more influence on the voters than a similar quantity of positive information.
As a third property, Figure 4 indicates that people treat gains and losses differently by showing a concave curve for gains and a convex one for losses. The concavity for gains says, for example, that two separate small rewards to an employee are likely to be appreciated more than a single reward with the same total value. The convexity of losses means that people find it desirable to combine a number of small losses into a large one, as we do when we charge by credit card and pay a monthly total bill instead of several individual ones.
Thus, the shape of the curve in Figure 4 sheds light on a whole variety of phenomena, even though prospect theory does not have the specificity and precision of an F = ma. Contemporary psychology is making impressive strides in understanding human behavior, but it often does so more by identifying phenomena and indicating the direction of effects than by producing calibrated models analogous to physical laws.
OUTLOOK FOR LAWS OF MANUFACTURING
What can we anticipate, then, in terms of laws of manufacturing? Are there more laws like L = λW? Probably so, in the sense that we should be able to find other useful mathematical relationships that map well onto the world and provide valuable insights about operations.
One example might be duality in linear programming. To any linear program (say, a minimization) there corresponds another linear program (a maximization) that uses the same set of constants but involves a new set of variables. The variables in the new problem have an important operational interpretation in the original one, namely, as prices for changing the constraints. The new linear program also has the fascinating property that the optimal value of its objective function is the same as that of the original problem. Familiarity with linear programming and duality provides a powerful framework for thinking qualitatively about many scheduling and resource allocation problems and for building specific manufacturing models.
Another candidate could be the economic lot size model. Faced with a fixed setup cost, a linear carrying cost of items produced, and a constant sales rate, how many items should be produced? A simple formula provides the answer. In turn, the formula produces insights, such as the result that total costs vary with square root of sales rate.
I am less optimistic about finding many analogs of laws like F = ma, because our systems are quite complicated and messy. (Of course, we use the laws of physics directly in the engineering of manufacturing systems.)
On the other hand, I expect much valuable new knowledge to be devel-
oped about manufacturing in the form of empirical models like the experience curve. These models follow the spirit of classical physical laws without the three-decimal-place accuracy. Manufacturing is characterized by large, interactive complexes of people and equipment in specific spatial and organizational structures. It seems likely that researchers will find useful macro- and micro-models of many new aspects of these systems. Such models may not often have the cleanness and precision of an L = λW or an F = ma, but they can generate important knowledge that designers and managers of manufacturing systems will use in problem solving.
ON COMPLEX SYSTEMS AND THEIR MODELING
Manufacturing systems are often remarkably complicated, involving not only machines and organizations of people, but many and varied information flows and control processes.
Since humans have finite intellectual capacity or “bounded rationality” (Simon, 1957), they like to break systems down into more manageable pieces for analysis, design, and management. This approach is effective, but, of course, the pieces sometimes interact in unexpected ways. Once we have decomposed a system into pieces, we then have a desire to resynthesize the small entities into big ones and work with the large entities as new units. Such hierarchical modeling is certainly a useful approach, if not without its pitfalls.
Large-scale simulations run in computer languages designed for the purpose are now quite common (Pritsker, in this volume). We have outstanding computer capabilities and increasing experience in modeling of complex systems. However, care must always be exercised in order not to lose sight of the forest for the trees. I would argue for having simple models both before and after a large-scale simulation. Before one begins, it is important to ask what are the critical phenomena relevant to the decision or at hand. It can be helpful to build an informal model to represent these phenomena. It is likely that such a model will make too many assumptions to be accepted for the decision at hand, so a more complex and detailed model may be desirable. However, if the results of running a complex model suggest a particular course of action, it is imperative to know why the model produced those results, that is, what were the key assumptions and parameter values that made things come out as they did. We should have a simple model that uses a few key variables to boil down the essence of why the recommendations make sense.
Another approach to thinking about complex systems has been advanced by system dynamics. Two separate streams of development can be identified here. One might be called “qualitative thinking through quantitative models.” This involves representing by computer variables a variety of
interacting quantities, some of which may be quite abstract and not directly measured; examples might be product quality or service level. Other entities could be more concrete, such as production rates and inventories. The goal is to construct a dynamic model in which key variables interact with each other such that the model exhibits the major characteristics of the system's observed behavior in the external world. The results sought from such an analysis are often qualitative, the goal being to understand system behavior: Are there instabilities? What is the system's sensitivity or insensitivity to changes in parameter values?
Other system dynamics models are calibrated on large data bases to represent specific operational systems with statistical fidelity. Some of these models applied to large project management have been very successful, for example, in shipbuilding (Cooper, 1980).
The Need for Multiple Views
The building of more and more complicated models of systems using the same methodologies is likely to yield diminishing returns. Managers face dozens of different problems each day; not just late schedules and excess inventories but also issues such as key people being hired away, roofs that leak, customer dissatisfaction with products, and employee absenteeism. Thus, a hundred different models are often needed, not one big model.
Modeling Myopia
People trained in operations research and management science or in engineering tend to think top-down, that is, in terms of objective functions, control or design variables, models, synthesis of systems from subsystems and the like, with the goal of using the entities under their control to maximize system performance. Consider, however, the following observation by Konosuke Matsushita of Matsushita Electric Industrial company (Stevens, 1989).
We are going to win and the industrial west is going to lose; there 's nothing much you can do about it because the reasons for your failure are within yourselves. Your firms are built on the Taylor model; even worse, so are your heads. With your bosses doing the thinking while the workers wield the screwdrivers, you're convinced deep down that this is the right way to run a business. For you, the essence of management is getting the ideas out of the heads of the bosses and into the hands of labor. We are beyond the Taylor model; business, we know, is now so complex and difficult, the survival of firms so hazardous in an environment increasingly competitive and fraught with danger, that their continued existence depends on the day-to-day mobilization of every ounce of intelligence.
Whether or not Mr. Matsushita's forecast is correct, he forcefully articulates a critical idea—the need for empowering and enhancing the effectiveness of people at all levels of an organization.
We indulge in modeling myopia if we believe as system analysts that we can (or should) be building complete models of our systems and setting all the control variables. Doing so misses the major opportunities for system improvement that are possible by finding new ways to empower the people on the front lines of the organization by giving them information, training, and tools with which to improve their own performance.
Another theme implicit here is that organizational coordination is something much more than top-down control. Interesting new ideas are evolving in this area, for example, developments in computer-assisted collaborative work and coordination theory (Malone, 1988). As information technology has decreased the cost of communication, there has been a growth of lateral communication and coordination and a shift from vertically hierarchical organizations to more lateral and marketlike structures. Lateral coordination is valuable in speeding new product development, finding process improvements, implementing new ideas, and generally facilitating parallel operations in different physical locations.
Thus, in analyzing and designing manufacturing systems, we need to combine new organizational and managerial knowledge with that from physical and operational systems. Many of the issues involved are ill understood today and create fruitful research agendas.









