1
Progress in Computing
Recently, stories about the development of small-scale quantum computers and their potential capabilities have regularly appeared in the popular press, driven largely by the rapid advance of ongoing public research in the field, the beginning of corporate investment, and concern about the future of performance scaling of traditional computers [1]. While progress in the field of quantum computing has been impressive, many open questions exist about the potential applications of such a system, how these types of computers could be built, and when—or whether—this technology will disrupt today’s computing paradigm.
The goal of this report is to assess the feasibility, time frame, and implications of building a general-purpose quantum computer. Before examining the capabilities of this emerging technology, it is instructive to review the origin and capabilities of current commercial computing technologies, the economic forces that drove their development, and the limitations that are beginning to confront them. This information will provide context for understanding the unique potential of quantum computing along with potential challenges to development of any new and competitive computing technology and will serve as a comparative framework for understanding progress toward a practical quantum computer.
1.1 ORIGINS OF CONTEMPORARY COMPUTING
Progress in one area of science and engineering often catalyzes or accelerates discovery in another, creating new pathways forward for both
new science and the design and deployment of new technologies. Such interconnections are particularly visible in the development of computing technologies, which emerged from millennia of progress in mathematical and physical sciences to launch a transformative industry in the mid-20th century. In less than one hundred years, research, development, and deployment of practical computing technologies have transformed science, engineering, and society at large.
Before the mid-20th century, practical “computers” were not machines, but people who performed mathematical computations with the aid of simple tools, such as the abacus or the slide rule. Today, we generally define a computer as a complex machine that can solve many problems more rapidly, precisely, or accurately than a human, by manipulating abstract representations of data embodied within some physical system using a set of well-defined rules. Given the appropriate input and the right set of instructions, a computer can output the answers to a host of problems. In the early 1800s, Charles Babbage designed a mechanical computer, the “difference engine,” to print astronomical tables, and later proposed a more complex mechanical computing machine, the “analytical engine.” Due to the absence of practical manufacturing technologies, neither was built at that time, but this engine was the first conception of a general-purpose programmable computer. The contemporary concept of a computer further coalesced in the 1930s with the work of Alan Turing. His abstract, mathematical model of a simple computer capable of simulating any other computing device, “the Turing machine,” described the foundational capabilities of all digital computers.
While computing is predicated by millennia of exploration of mathematical principles, practical devices require a concrete, physical implementation of abstract and theoretical ideas. The first successful realizations of such devices emerged during World War II. Alan Turing built a special-purpose electromechanical computer for cryptanalysis, the “Bombe,” and developed a detailed specification for an “automatic computing engine,” a real general-purpose stored-program computer. In Germany, in a separate development, Konrad Zuse created the Z1, the first programmable computer, using electromechanical relays. Subsequent to the war, the so-called von Neumann architecture1 — a reformulation of the universal Turing machine in terms of the stored program model of computing—became the dominant architecture for most computer systems.
In subsequent decades, driven mostly by military funding, computers continued to improve in performance and capabilities. The physical components used to create computers also improved with time. Since the nascent computer industry was too small to drive technology
___________________
1 So-named for John von Neumann, the first to propose the stored-program model.
development, its designers leveraged the technology (vacuum tubes, then transistors, and finally integrated circuits) that was developed to support radio, television, and telephony, which were the driving commercial applications of the day. Over time, the computing industry grew much larger than the military sector that started it, and large enough to support customized technology development. Today, computing is one of the largest commercial drivers of integrated circuit development, and many other areas leverage integrated circuits designed for the computing industry for their needs. As a result, today’s electronic computers—from mobile devices and laptops to supercomputers—are the fruits of tremendous progress in human understanding of and control over physical materials and systems.
1.2 QUANTUM COMPUTING
While today’s computing machines leverage exquisite control over nature to create designs of immense complexity, the representation and logical processing of information in these machines can be explained using the laws of classical physics.2 These classical descriptions of electromagnetism and Newtonian physics provide an intuitive and deterministic explanation of the physical universe, but they fail to predict all observable phenomena. This realization, made around the turn of the 20th century, led to the most important transformation in physics: the discovery of the principles of quantum mechanics. Quantum mechanics (or quantum physics) is a theory of the physical world that is not deterministic, but probabilistic, with inherent uncertainty. While the dynamics it describes at a small scale are exotic and counterintuitive, it accurately predicts a wide range of observable phenomena that classical physics could not, and replicates correct classical results for larger systems. The development of this field has transformed the way scientists understand nature. Very small systems whose behavior cannot be adequately approximated by the equations of classical physics are often referred to as “quantum systems.”
While classical physics is often a good approximation for observable phenomena, all matter is fundamentally quantum mechanical—including the materials from which today’s computers are built. However, even as the design of their hardware components is increasingly informed by the quantum properties of materials, and as the ever-shrinking size of these components means that quantum phenomena introduce more constraints
___________________
2 While the laws of quantum mechanics must be invoked to design or explain the operation of semiconductor materials whose bandgaps enable the implementation of today’s widely deployed conventional computer logic gates, the nature of the logical information processing itself is based upon the flow of a classical model of a charged particle.
on their design, the principles and operations that these computers implement have remained classical.
Despite the extraordinary power of today’s computers, there are applications that are difficult for them to compute but seem to be easily “computed” by the quantum world: estimating the properties and behavior of quantum systems. While today’s classical computers can simulate simple quantum systems, and often find useful approximate solutions for more complicated ones, for many such problems the amount of memory needed for the simulation grows exponentially with the size of the system simulated.
In 1982, physicist Richard Feynman suggested that quantum mechanical phenomena could themselves be used to simulate a quantum system more efficiently than a naïve simulation on a classical computer [2,3]. In 1993, Bernstein and Vazirani showed [4] that quantum computers could violate the extended Church-Turing thesis—a foundational principle of computer science that said that the performance of all computers was only polynomially faster than a probabilistic Turing machine [5,6]. Their quantum algorithm offered an exponential speedup over any classical algorithm for a certain computational task called recursive Fourier sampling. Another example of a quantum algorithm demonstrating exponential speedup for a different computational problem was provided in 1994 by Dan Simon [7]. Quantum computation is the only model of computation to date to violate the extended Church-Turing thesis, and therefore only quantum computers are capable of exponential speedups over classical computers.
In 1994, Peter Shor showed that several important computational problems could, in principle, be solved significantly more efficiently using a quantum computer—if such a machine could be built. Specifically, he derived algorithms for factoring large integers and solving discrete logarithms rapidly—problems that could take even the largest computer today thousands or millions of years—or even the lifetime of the universe—to compute. This was a striking discovery because it also suggested that anyone with a real-world quantum computer could break the cryptographic codes that make use of these problems, compromising the security of encrypted communications and encrypted stored data, and potentially uncovering protected secrets or private information. These results catalyzed interest among researchers in developing other quantum algorithms with exponentially better performance than classical algorithms, and trying to create the basic quantum building blocks from which a quantum computer could be built.
During the past few decades, this research has progressed to the point where very simple quantum computers have been built, and a positive outlook is emerging based upon the assumption that the complexity
of these machines will grow exponentially with time, analogous to the growth that has been achieved in performance of classical computers. Given the importance of this scaling assumption to the future of quantum computing, understanding the factors that drive scaling is critical.
1.3 HISTORICAL PROGRESS IN COMPUTING: MOORE’S LAW
While the early computers were huge, expensive, and power-hungry devices often funded by the government, today’s computers are dramatically smaller, cheaper, more efficient, and more powerful as a result of improvements in hardware, software, and architecture. Today’s smart-phones, computers that fit in one’s pocket, have as much computational power as the fastest supercomputers of 20 years ago. The low cost of computer hardware has led to the permeation of computers throughout various environments and has enabled the aggregation of tens to hundreds of thousands of computers that provide the Web computing services that many have come to depend on. Computers are now commonly embedded in increasing numbers of manufactured goods, from washing machines to singing greeting cards. This section describes how this happened, which reveals a number of lessons and challenges for any new computing technology.
The process used to create integrated circuits, the key components of today’s computers, emerged as an unplanned advance amid efforts in the 1960s to improve the industrial manufacturing process for transistors. Transistors are small electrical devices that can be used as electronic switches or amplifiers, and were used at the time in a variety of electronic devices, including radios, TVs, audio amplifiers, and early computers. Efforts to increase transistor quality and manufacturing yield (which lower costs) led to several inventions at Fairchild Semiconductor, a transistor startup company. The first was a method of fabricating transistors called the “planar process,” which enabled transistors to operate after being fabricated on the surface of a flat piece of silicon. Previously, the material outside of the transistor needed to be etched away, creating a silicon transistor “mesa.” The planar processes enabled the fabrication of many transistors on a given piece of silicon, which could then be cut to separate them. The second invention was a means for connecting a few of these transistors together via a metal layer on the silicon surface to create a complete circuit. Since this transistor circuit was integrated on one piece of silicon, the result was called an “integrated circuit,” or IC. This concept of connecting multiple devices on one substrate had been demonstrated a year earlier in a crude germanium prototype by Jack Kilby at Texas Instruments, also with the intent of lowering the cost and improving the reliability of transistor circuits.
The manufacturing process for creating an integrated circuit, which has become increasingly complex over time, can be viewed as a type of layered printing process. A transistor can be created by successive “printing” of different shapes in a series of layers. For an integrated circuit, the shapes for all of the circuit’s transistors are “printed” at the same time, layer by layer, onto a piece of silicon. The process takes the same amount of time regardless of the number of transistors in the circuit; further reduction of costs can be achieved by making multiple copies of the circuit at the same time on a large piece of silicon, called a wafer. As a result, an IC’s production cost is set by the size of the silicon that it occupies (which determines how many circuits can be manufactured in the processing of a single wafer), rather than the number of transistors in the circuit.
In 1964, Gordon Moore, also at Fairchild, examined the costs of creating integrated circuits. He noticed that, as a result of design and processing improvements, the number of transistors that could be economically printed on each circuit had been increasing exponentially over time—doubling roughly every year. Moore conjectured that IC fabrication technology would continue to improve with exponential growth in number of transistors per integrated circuit, and he pondered in a 1964 paper how the world would use all of these devices. In the many decades that followed, his conjecture of exponential growth has borne out as an accurate one, and is now commonly referred to as “Moore’s law.”
Moore’s law is not a physical law; it is simply the empirical production trend for the integrated circuit industry as a result of its business cycle. While the exponential growth in the capability of integrated circuits is commonly touted, the costs that support this growth are often overlooked. During the past 50 years, the revenue of the computer hardware industry also grew exponentially, increasing by more than one thousandfold, to just under half a trillion U.S. dollars annually today. Over this same period, the share of this revenue reinvested into the industry’s research and development (R&D) operations remained roughly constant, meaning that the financial cost of the technology improvements underlying Moore’s law also increased exponentially. Interestingly, in addition to this exponential growth, both the cost of building an IC manufacturing plant and the cost of creating a design to be manufactured also displayed exponential growth.
This illustrates a critical point: Moore’s law is the result of a virtuous cycle, where improvements in integrated circuit manufacturing allow the manufacturer to reduce the price of their product, which in turn causes them to sell more products and increase their sales and profits. This increased revenue then enables them to improve the manufacturing process again, which is harder this time, since the easier changes have already
been made.3 The key to this cycle is to create a growing market for one’s product. For integrated circuits, the new affordability causes designers of many general products to replace some existing mechanism with an IC because it makes the product better or cheaper (e.g., changing a key lock to an electronic lock), which grows the market for ICs, creating the growing revenue needed to continue scaling their complexity.
It is hard to achieve this type of exponential scaling without such a virtuous cycle. This is apparent from the historical example of efforts to make transistors out of a material other than silicon. Because transistors made from gallium arsenide (GaAs) are capable of higher performance than silicon transistors, researchers believed that computers built from GaAs ICs would have higher performance than those built using silicon ICs. Given this promise, by the mid-1970s many research groups—and, later, companies—worked toward making ICs using GaAs transistors. However, by the time this effort started, the silicon IC industry was large, and companies had already begun reinvesting part of their revenue in improvements to their manufacturing process. The manufacturing process for GaAs was sufficiently different from silicon that developers needed to develop new GaAs-specific fabrication steps. This development put GaAs manufacturers in a Catch-22 situation: to fund their manufacturing R&D, they needed robust sales; to get robust sales, they needed state-of-the-art manufacturing techniques to compete against the silicon alternatives, which were constantly improving. The industry was never able to break this cycle, and the efforts to build commercially successful GaAs ICs ultimately failed; general-purpose digital GaAs ICs never became competitive.
The virtuous cycle underlying Moore’s law is not just financial. It also depends on the existence of a vibrant ecosystem to support the growth of the market. In many ways, the integrated circuit industry created—and then grew to depend upon—Silicon Valley, which later globalized to its position today. The growing capabilities of, and market for, computer hardware attracted venture funding, support industries, and, most importantly, talent into the field. This growing community was then able to solve previously unsolvable problems, further contributing to advances and growth in the industry, which in turn brought even more people to the area. The result of this virtuous cycle is amazing. In today’s technologies, a digital gate, the simple building block of a computer, costs around a few millionths of a penny (100,000,000 gates per dollar), and each gate can compute its result in under 10 picoseconds (that is, one hundredth of a billionth of a second) at low-enough power levels to work in a cell phone.
___________________
3 This is one of the reasons behind the so-called Rock’s law, which states that the cost of building a new semiconductor fabrication facility doubles every 4 years.
Finding: Moore’s law for integrated circuits resulted from a virtuous cycle, where improved technology generated exponentially increasing revenue, enabling reinvestment in R&D and attracting new talent and industries to help innovate and scale the technology to the next level.
1.4 CONVERTING TRANSISTORS TO CHEAP COMPUTERS
Moore’s law of technology scaling has roughly halved the cost of building a transistor every two years. Over the past half-century, this has translated to a cost decrease by a factor of more than 30 million. While this decrease in transistor cost made it cost effective to manufacture ICs with increasing transistor complexity, designing these complex ICs becomes increasingly difficult. Designing a circuit with 8 transistors is not hard; designing a circuit with 100 million transistors is a different story. To deal with this increasing complexity, designers of computing hardware created new ways of thinking about transistor circuits that allowed them to reason about a smaller number of objects. While initially they thought in terms of connecting individual transistors, soon they began thinking in terms of “logic gates”—collections of transistors that could be represented and modeled using Boolean logic (rules that combine signals that can be either false [represented as 0] or true [represented as 1], via operations that yield defined outputs). As complexity continued to increase, logic gates were grouped into a larger circuit such as an adder or a memory block, again reducing the complexity that the designer needed to work with. These different levels of thinking about design, which allow people to build systems without thinking about every detail all at once, are called “abstractions.” Abstractions enable the essential components of a computer to be grouped conceptually by form or function.
A computer is another design abstraction. It represents a transistor circuit whose function is controlled by a set of instructions read from an attached memory. Once it became possible to build complex integrated circuits, it became possible to integrate a small computer onto a single IC, creating a “micro-computer,” or “microprocessor.” This design made it much easier to leverage cheap transistors; new applications no longer required the design and fabrication of an application-specific IC but could instead be implemented by changing the instructions provided to an existing microprocessor to create the desired solution. The ease of developing and deploying computer-based solutions, coupled with the decreasing cost of computing, greatly increased the demand for this type of device. Thus, the ubiquity of computing is both enabled by (via cheaper computing) and enabling to (via higher revenue) Moore’s law. Computing is one way that the industry creates products people want to buy out of increasingly cheap transistors.
Continued benefits from the exponentially falling cost of transistors required the creation of many abstraction layers like those described above, and new software (computer programs) and design frameworks. While these software and design frameworks were expensive to develop, their cost was supported by the revenue streams of previous products, and the projected revenue of the future products that they would enable. Yet, even with this additional support, design of a state-of-the-art chip is still expensive, costing over $100 million. Since the cost of each device is the manufacturing cost plus the amortized design cost, IC-based computing is cheap only if it is sold in high enough volume (typically 10 million units or more), ensuring that the amortized design cost does not dominate the manufacturing cost. It is the amortization of design costs that makes commodity computing devices so much cheaper than specialized computers.
New computing approaches, such as quantum computing, that change the fundamental building blocks of a computer will require creation of not only a new type of hardware building blocks but also new abstraction layers, software, and design frameworks to enable designers to build and use these systems if their complexity will need to scale over time. The costs of creating these new hardware and software tools are important for new technologies, since the price of early machines will need to be high enough to start recovering some of the costs. This premium always penalizes new approaches when competing against an established player.
1.5 A SLOWDOWN IN SCALING
Although Moore’s law reflects great progress in classical computing over several decades, it is clear that the exponential trend cannot be sustained indefinitely, due to both physical limitations and the finite size of the world market. While there is much debate over when exactly this scaling will cease, signs of the end of scaling have come into clearer view over the past decade. Since Moore’s law is really about transistor cost, one indication of scaling issues is the fact that transistor costs are not dropping at their historical rate in the most advanced technologies., It is also interesting to note that the International Technology Roadmap for Semiconductors, an international consortium that was formed to help keep technology scaling in line with Moore’s law and address possible roadblocks to doing so, decided to stop its scaling projections with the 5-7 nanometer feature sizes expected around 2021.
Decreased growth is also apparent in net revenue trends for the integrated circuit industry, illustrated in Figure 1.1. This semi-log plot of revenue over time shows a straight line when revenue growth is exponential. The data shows a strong exponential growth in revenue through 2000,
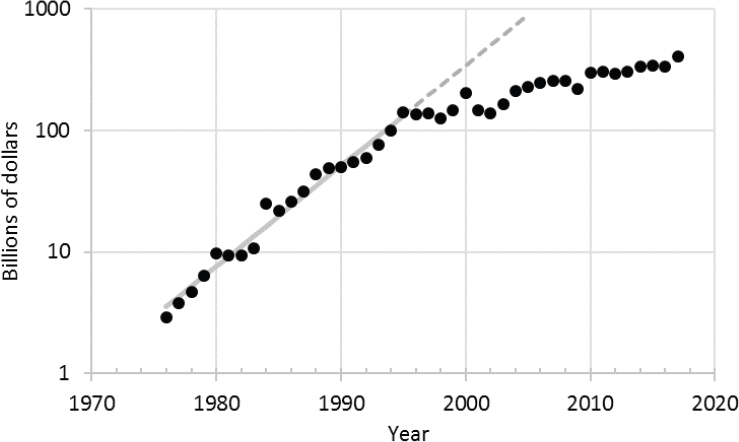
followed by a decrease in growth rate. This plot indicates that the virtuous cycle, where each improvement in technology brought more money to the industry, has begun to slow down. This slowdown in revenue growth is likely to affect technology development cycles, which will affect technology scaling. The slowing of growth is not surprising: at $300-$400 billion in revenue, this industry represents a few percent of the manufacturing sector’s contribution to the world’s entire GDP. It cannot continue to increase forever at a rate faster than the world’s GDP.
1.6 QUANTUM: A NEW APPROACH TO COMPUTING
It is against this backdrop that the theory and prototypes for quantum computing have emerged. As noted in Section 1.2, quantum computing uses a very different approach to computation by leveraging some of the unusual properties of the quantum world. When the idea was formally proposed in the 1980s, and new algorithms were discovered in the 1990s, no one knew how to actually build this type of machine. Over the past two decades, efforts to create a working quantum computer have made
noteworthy progress, reviving interest in the potential of this technology. It remains to be seen whether practical quantum computers can or will be developed in a way that will sustain Moore’s law-type growth in computational capabilities. The failed GaAs IC experiment illustrates the difficulty of trying to enter an established market with an existing dominant player. Nonetheless, quantum computing is the only truly new model of computing that has been proposed, in the sense that it is not bound by the extended Church-Turing thesis. As a more general model of computing—in much the same way in which quantum mechanics is a more general model of physics than classical mechanics—quantum computing has the theoretical potential to solve some problems that no classical computer could realistically attack. This “quantum advantage,” which could manifest as a disruptive rather than an incremental innovation, is what makes quantum computing so interesting, and motivates both the commercial interest in quantum computing and the rest of this report.
The next chapter describes the physical phenomena that underlie quantum computing, comparing the associated operation principles to those of conventional computers. Subsequent chapters then describe tasks at which quantum computers could potentially outperform classical computers, their implications for cryptography, the hardware and software needed to create a working quantum computer, and the strengths and weaknesses of the underlying physical technologies for creating quantum computers. The report closes by assessing the feasibility of implementing a practical quantum computer, the associated timelines and resources required, and milestones and metrics that can be used to track future progress.
1.7 NOTES
[1] See, for example, J. Dongarra, 2018, “The U.S. Once Again Has the World’s Fastest Supercomputer. Keep Up the Hustle,” The Washington Post, June 25, https://www.washingtonpost.com/opinions/united-states-wins-top-honors-in-supercomputer-race/2018/06/25/82798c2c-78b1-11e8-aeee-4d04c8ac6158_story.html;
J. Nicas, 2017, “How Google’s Quantum Computer Could Change the World,” Wall Street Journal, October 16, https://www.wsj.com/articles/how-googles-quantum-computer-could-change-the-world-1508158847;
J. Asmundsson, 2017, “Quantum Computing Might Be Here Sooner than You Think,” Bloomberg, June 14, https://www.bloomberg.com/news/features/2017-06-14/the-machine-of-tomorrow-today-quantum-computing-on-the-verge; D. Castevecchi, 2017, Quantum computers ready to leap out of the lab in 2017, Nature 541(7635):9-10.
[2] R.P. Feynman, 1982, Simulating physics with computers, International Journal of Theoretical Physics 21(6-7):467-488.
[3] S. Lloyd, 1996, Universal quantum simulators, Science 273(5278):1073-1078.
[4] E. Bernstein and U. Vazirani, 1993, “Quantum Complexity Theory,” pp. 11-20 in Proceedings of the Twenty-Fifth Annual ACM Symposium on Theory of Computing (STOC ‘93), Association of Computing Machinery, New York, https://dl.acm.org/citation.cfm?id=167097.
[5] P. Kaye, R. Laflamme, and M. Mosca, 2007, An Introduction to Quantum Computing, Oxford University Press, Oxford, U.K.
[6] M.A. Nielsen and I. Chuang, 2002, Quantum Computation and Quantum Information, Cambridge University Press, Cambridge, U.K.
[7] D. Simon, 1997, On the power of quantum computation, SIAM Journal on Computing 26(5):1474-1483.












