4
Quantum Computing’s Implications for Cryptography
Increases in computational power are desirable, except for applications that rely upon the computational complexity of certain operations in order to function, which is the case in cryptography. Cryptography is an indispensable tool used to protect information in computer systems and it is used widely to protect communications on the Internet. Practical quantum computing at scale would have a significant impact on several cryptographic algorithms currently in wide use. This section explains what these algorithms are for and how they will be affected by the advent of large-scale quantum computers. Given the computing power that such a quantum computer is expected to have, the cryptography research community has developed and is continuing to develop post-quantum (or “quantum-safe”) cryptographic algorithms. These are candidate cryptographic algorithms that run on a classical computer and are designed to remain secure even against an adversary who has access to a scalable, fault-tolerant quantum computer.
While it may not be obvious to the general public, cryptography underlies many interactions and transactions on the World Wide Web. As one example, most connections to websites use “https,” a Web protocol that encrypts both the information a user sends to a website, and the information that the website sends back—for example, credit card information, bank statements, and e-mail. Another example is protecting stored passwords in a computer system. Passwords are stored in a form that allows the computer system to check that a user-entered password is correct, without storing the actual password. Protecting stored passwords
in this way prevents passwords from being “stolen” from the computer system in case of a security breach.
In today’s Web-based world, it is relatively easy for a large company like Google to experiment with new types of cryptography. A company like Google can make changes to its browser and its servers to add support for a new protocol: when a Google browser connects to a Google server, it can elect to use the new protocol. However, removing an existing protocol is much harder, since before this can be done, all of the machines in the world that rely upon the old protocol must be updated to use the alternative protocol. This type of replacement has already had to be done when a widely deployed hash function, called MD5, was found to be vulnerable to attack. While alternatives were deployed rapidly, it took over a decade for the vulnerable hash function to be completely removed from use.1
This chapter explains the key cryptographic tools deployed throughout today’s conventional computing systems, what is known about their susceptibility to attack via a quantum computer, alternative classical cryptographic ciphers expected to be resilient against quantum attack, and the challenges and constraints at play in changing a widely deployed cryptographic regime.
4.1 CRYPTOGRAPHIC ALGORITHMS IN CURRENT USE
Creating a secure communication channel between two people is usually done as a two-step process: two people are given a shared secret key in a process called key exchange, and then this shared secret key is used to encrypt their communication so it cannot be understood (decrypted) by anyone without the secret key. The message encryption is called symmetric encryption, since both parties used the same shared secret key to encrypt and decrypt the communications traffic.
4.1.1 Key Exchange and Asymmetric Encryption
The first step in encrypting communications between two parties—in this example, called Alice and Bob—is for them to obtain a shared (symmetric) key that is known to them but to no one else. To establish this shared key, the two parties engage in a key exchange protocol. The most widely used key exchange protocol, called the Transport Layer Security
___________________
1 The attack on MD5 was discovered by Wang in 2005. Only in 2014 did Microsoft release a patch to disable MD5; see Microsoft, “Update for Deprecation of MD5 Hashing Algorithm for Microsoft Root Certificate Program,” Microsoft Security Advisory 2862973, updated June 10, 2014, Version 3.0, https://docs.microsoft.com/en-us/security-updates/SecurityAdvisories/2014/2862973.
(TLS) handshake, is used to protect Internet traffic. During a key exchange protocol, the parties send a sequence of messages to each other. At the end of the protocol, they obtain a shared secret key that both of them know, but that no one else knows, including any adversary. This key can then be used for exchanging data securely using a symmetric encryption algorithm, which is discussed in Section 4.1.2.
Key exchange protocols rely upon the assumption that certain algebraic problems are intractable. One such problem that is widely used in practice is called the “discrete-log problem on elliptic curves.” For the purpose of this discussion, it suffices to say that an instance of this problem of size n bits can be solved classically in exponential time in n, or more precisely in time 2n/2. No better classical algorithm is known (although it has not been proven that none exists). In practice, one typically sets the key size as 256, meaning that the best-known classical attack on the key exchange protocol runs in time 2256/2 = 2128—the same as the time required to attack 128-bit AES-GCM. This way, security of key exchange and security of symmetric encryption are comparable.
The impact of a quantum computer: Asymmetric cryptographic algorithms used in key exchange protocols appear to be the most vulnerable to compromise by known quantum algorithms, specifically by Shor’s algorithm. Because Shor’s algorithm provides an exponentially faster method for solving the discrete-log problem and for the problem of factoring large integers, an adversary able to deploy it on a quantum computer could break all the key exchange methods currently used in practice. Specifically, key exchange protocols based on variants of the Diffie-Hellman and the RSA protocols would be insecure. To break RSA 1024 would require a quantum computer that has around 2,300 logical qubits, and even with the overhead associated with logical qubits, this algorithm could likely be carried out in under a day (see Table 4.1). Because of the seriousness of this potential compromise, the National Institute of Standards and Technology (NIST) in 2016 began a process that is expected to last six to eight years [1] to select and standardize replacement asymmetric cryptographic algorithms that are quantum secure. Potential replacements to currently deployed key exchange systems are discussed later in this chapter.
4.1.2 Symmetric Encryption
Once Alice and Bob have established their shared secret key, they can use it in a symmetric cipher to ensure that their communication stays private. A widely used encryption method called the Advanced Encryption Standard-Galois Counter Mode (AES-GCM) has been standardized for this purpose by NIST. In its simplest form, this encryption method is based on a pair of algorithms: an encryption algorithm and a decryption
TABLE 4.1 Literature-Reported Estimates of Quantum Resilience for Current Cryptosystems, under Various Assumptions of Error Rates and Error-Correcting Codes
| Cryptosystem | Category | Key Size | Security Parameter | Quantum Algorithm Expected to Defeat Cryptosystem | # Logical Qubits Required | # Physical Qubits Requireda | Time Required to Break Systemb | Quantum-Resilient Replacement Strategies |
|---|---|---|---|---|---|---|---|---|
| AES-GCMc | Symmetric encryption | 128 192 256 |
128 192 256 |
Grover’s algorithm | 2,953 4,449 6,681 |
4.61 × 106 1.68 × 107 3.36 × 107 |
2.61 × 1012 years 1.97 × 1022 years 2.29 × 1032 years |
|
| RSAd | Asymmetric encryption | 1024 2048 4096 |
80 112 128 |
Shor’s algorithm | 2,050 4,098 8,194 |
8.05 × 106 8.56 × 106 1.12 × 107 |
3.58 hours 28.63 hours 229 hours |
Move to NIST-selected PQC algorithm when available |
| ECC Discrete-log probleme-g | Asymmetric encryption | 256 384 521 |
128 192 256 |
Shor’s algorithm | 2,330 3,484 4,719 |
8.56 × 106 9.05 × 106 1.13 × 106 |
10.5 hours 37.67 hours 55 hours |
Move to NIST-selected PQC algorithm when available |
| SHA256h | Bitcoin mining | N/A | 72 | Grover’s Algorithm | 2,403 | 2.23 × 106 | 1.8 × 104 years | |
| PBKDF2 with 10,000 iterationsi | Password hashing | N/A | 66 | Grover’s algorithm | 2,403 | 2.23 × 106 | 2.3 × 107 years | Move away from password-based authentication |
a These are rough estimates. The number of physical qubits required depends on several assumptions, including the underlying architecture and error rates. For these calculations, assumptions include a two-dimensional (2D) lattice of qubits with nearest neighbour interactions, an effective error rate of 10–5, and implementing the surface code.
b These are rough estimates. In addition to the assumptions associated with estimation of the number of physical qubits required, a quantum computer with gates operating at a 5 MHz frequency was assumed.
c M. Grassl, B. Langenberg, M. Roetteler, and R. Steinwandt, 2015, “Applying Grover’s Algorithm to AES: Quantum Resource Estimates,” Proceedings of Post-Quantum Cryptography 2016, vol. 9606 of Lecture Notes in Computer Science, pp. 29-43, Springer; M. Mosca and V. Gheorghiu, 2018, “A Resource Estimation Framework for Quantum Attacks Against Cryptographic Functions,” Global Risk Institute, http://globalriskinstitute.org/publications/resource-estimation-framework-quantum-attacks-cryptographic-functions/.
d T. Häner, M. Roetteler, and K.M. Svore, 2017, “Factoring using 2n+2 qubits with Toffoli based modular multiplication,” Quantum Information and Computation, 18(7and8):673-684.; M. Mosca and V. Gheorghiu, 2018, “A Resource Estimation Framework for Quantum Attacks Against Cryptographic Functions,” Global Risk Institute, http://globalriskinstitute.org/publications/resource-estimation-framework-quantum-attacks-cryptographic-functions/.
e The values given are for the NIST P-256, NIST P-386, and NIST P-521 curves.
f M. Roetteler, M. Naehrig, K.M. Svore, and K. Lauter, 2017, “Quantum Resource Estimates for Computing Elliptic Curve Discrete Logarithms,” Advances in Cryptology –— ASIACRYPT 2017, Lecture Notes in Computer Science 10625, Springer-Verlag, pp. 241-272.
g M. Mosca and V. Gheorghiu, 2018, “A Resource Estimation Framework for Quantum Attacks Against Cryptographic Functions—Part 2 (RSA and ECC),” Global Risk Institute, https://globalriskinstitute.org/publications/resource-estimation-framework-quantum-attacks-cryptographicfunctions-part-2-rsa-ecc/.
h M. Mosca and V. Gheorghiu, 2018, “A Resource Estimation Framework for Quantum Attacks Against Cryptographic Functions—Improvements,” Global Risk Institute, https://globalriskinstitute.org.
i The time estimate for password hashing is based upon the time estimate (as it appears in the preceding row of the table) for SHA256, which is often used iteratively in PBKDF2, a password hashing algorithm. Assuming 10,000 iterations of SHA256 (a common deployment practice) would take 10,000 times as long as a single iteration. The classical search space of one cycle is 266, which implies a running time for Grover of 233, or one-eighth that required for breaking SHA256 in Bitcoin. Thus, the current estimate of 2.3 × 107 years is obtained by multiplying the value obtained for SHA256 by 10,000 and dividing by 8.
NOTE: These estimates are highly dependent on the underlying assumptions and are subject to update in the final report.
algorithm that encode and decode a message. The encryption algorithm takes as input a key and a message, scrambles the bits of the message in a very precise way, and outputs a ciphertext, an encoded form of the message that looks like random bits. The decryption algorithm takes as input a key and a ciphertext, uses the key to reverse the scrambling and output a message. AES-GCM is designed so that analysis of the ciphertext provides no information about the message.
AES-GCM supports three key sizes: 128 bits, 192 bits, and 256 bits. Suppose that an adversary, Eve, intercepts a ciphertext that she wants to decrypt. Furthermore, suppose Eve knows the first few characters in the decrypted message, as is common in Internet protocols where the first few characters are a fixed message header. When using a 128-bit key in AES-GCM, Eve can try all 2128 possible keys by exhaustive search until she finds a key that maps the first bytes of the given ciphertext to the known message prefix. Eve can then use this key to decrypt the remainder of the intercepted ciphertext. For a 128-bit key, this attack takes 2128 trials, which even at a rate of a 1018 (1 quintillion) trials per second—which is faster than even a very large custom-built AES computer would run—will still take 1013 (10 trillion) years. For this reason, AES-GCM is frequently used with a 128-bit key. Longer keys, 192-bits and 256-bits, are primarily used for high-security applications where users are concerned about preprocessing attacks or potential undiscovered weaknesses in the AES-GCM algorithm that would enable a faster attack.
The impact of a quantum computer: AES is a perfect fit for Grover’s algorithm, which was discussed in the previous chapter. The algorithm can identify the secret key over the entire 128-bit key space of AES-GCM in time proportional to the square root of 2128—namely, time 264. Running the algorithm on a quantum computer is likely to require around 3,000 logical qubits and extremely long decoherence times.
How long would a quantum computer take to run the 264 steps of Grover’s algorithm, called Grover steps, to break AES-GCM? That is hard to answer today, since it depends on how long a quantum computer takes to execute each Grover step. Each Grover step must be decomposed into a number of primitive operations to be implemented reversibly. The actual construction of the quantum circuit for each Grover step can substantially increase the number of qubits and coherence times required for physical implementation. Using classical hardware, one can build a special purpose circuit that tries 109 keys per second. Assuming a quantum computer can operate at the same speed, it would need about 600 years to run Grover’s algorithm for the necessary 264 steps. It would therefore take a large cluster of such quantum computers to crack a 128-bit key in a month. In fact, this is an overly optimistic estimate, because this type of quantum computer requires logical qubits; this not only greatly increases the number
of physical qubits required, but, as described in Section 3.2, operations on logical qubits require many physical qubit operations to complete. This overhead is high for “non-Clifford” quantum gates, which are common in this algorithm. As Table 4.1 shows, assuming 200-nanosecond gate times and current algorithms for error correction, a single quantum computer would require more than 1012 years to crack AES-GCM.
Even if a computer existed that could run Grover’s algorithm to attack AES-GCM, the solution is quite simple: increase the key size of AES-GCM from 128-bit to 256-bit keys. Running Grover’s attack on a 256-bit key is effectively impossible, since it requires as many steps as a classical attack on a 128-bit key. Transitioning to a 256-bit key is very practical and can be put to use at any time. Hence, AES-GCM can be easily made secure against an attack based on Grover’s algorithm.
However, AES-GCM was designed to withstand known sophisticated classical attacks, such as linear and differential cryptanalysis. It was not designed to withstand a sophisticated quantum attack. More precisely, it is possible that there is some currently unknown clever quantum attack on AES-GEM that that is far more efficient than Grover’s algorithm. Whether such an attack exists is currently an open problem, and further research is needed on this important question. If a sophisticated quantum attack exists—one that is faster than exhaustive search using Grover’s algorithm—then increasing the AES-GCM key size to 256 bits will not ensure post-quantum security and a replacement algorithm for AES-GCM will need to be designed.
4.1.3 Certificates and Digital Signatures
Digital signatures are an important cryptographic mechanism used to verify data integrity. In a digital signature system, the signer has a secret signing key, and the signature verifier has a corresponding public key, another example of asymmetric encryption. The signer signs a message using its secret key. Anyone can verify the signature using the corresponding public key. If a message-signature pair is valid, then the verifier has some confidence that the message was authorized by the signer. Digital signatures are used widely, as illustrated in the following three examples.
First, digital signatures are necessary for establishing identity on the Internet using a digital certificate. Here, a certificate authority (CA) uses its secret signing key to issue an identity certificate to an individual or an organization. A certificate is a statement that binds an identity, such as nas.edu, to a cryptographic key. Anyone can verify a certificate, but only the CA can issue a certificate, by digitally signing it using a secret signing key. An adversary who can forge the CA’s signature can, in principle, masquerade as any entity.
A second application for digital signatures is in payment systems, such as credit card payments or a cryptocurrency such as Bitcoin. With these systems, a payer who wants to make payments holds a secret signing key. When making a payment, the payer signs the transaction details. The signature can be verified by anyone, including the payee and all relevant financial institutions. An attacker who can forge signatures can effectively spend other people’s funds.
For a third example, consider the verification of software authenticity. Here, a software vendor uses its secret signing key to sign software and software updates that it ships. Every client verifies these signatures before installing the software, as they do with subsequent software updates. This ensures that clients know the software provenance and do not install software that has been tampered with or malware created and distributed by malicious actors. An attacker who could forge signatures could distribute malicious software to unsuspecting clients, who might install it thinking that it is authentic.
The two most widely used signature algorithms are called RSA and ECDSA.2 Roughly speaking, one algorithm is based on the difficulty of factoring large integers, and the other is based on the same discrete log problem used for key exchange. The parameters for both systems are chosen so that the best-known classical attacks run in time 2128.
The impact of a quantum computer: An adversary who has access to a quantum computer capable of executing Shor’s algorithm would have the ability to forge both RSA and ECDSA signatures. This adversary would be able to issue fake certificates, properly sign malicious software, and potentially spend funds on behalf of others. The attack is worse than just forging signatures; Shor’s algorithm allows attackers to recover private keys, which facilitates forging signatures but also eliminates the security of all other uses of the keys. Fortunately, there are several good candidate signature schemes that are currently believed to be post-quantum secure, as discussed at the end of this chapter.
4.1.4 Cryptographic Hash Functions and Password Hashing
The final cryptographic primitive discussed here enables one to compute a short message digest, called a hash, from an arbitrarily long message. The hash function can take gigabytes of data as input and output a short 256-bit hash value. There are many desirable properties that we might want hash functions to satisfy. The simplest is called “one-wayness,” or “collision-resistance,” which means that for any given hash
___________________
2 The former is named after its inventors, Rivest, Shamir, and Adelman. The latter stands for “elliptic curve digital signature algorithm.”
output value T, it should be difficult to find an input message that would yield that hash.
Hash functions are used in many contexts; a simple example is their use in password management systems. A server that authenticates user passwords usually stores in its database a one-way hash of those user passwords. This way, if an attacker steals the database, it may be difficult for the attacker to recover the cleartext passwords. Currently, the most commonly used hash function is called SHA256. It outputs a 256-bit hash value no matter how large the input is. This hash function is the basis of many password authentication systems. To be precise, the actual hash function used to hash passwords is derived from SHA256 via a construction called PBKDF2 [2].
The impact of a quantum computer: A hash function that produces 256-bit outputs is not expected to be threatened by quantum computing. Even using Grover’s algorithm, it is currently believed to be essentially impossible (with a depth on the order of 2144 T gates on 2400 logical qubits) to break a hash function like SHA256. However, password hashing is at a higher risk because the space of user passwords is not very large. The set of all 10-character passwords is only about 266 passwords. An exhaustive search over a space of this size using a cluster of classical processors is possible, but very costly. Using Grover’s algorithm, the running time shrinks to only 233 (about 10 billion) steps, which at the speed of a modern classical processor takes only a few seconds. However, the need for QEC for deploying Grover’s algorithm again suggests that, with current error correction algorithms (and reasonable assumptions about error rates and architectures), the time required for this attack is still too long to be practical, at more than 107 years, although the time frame could be reduced through reduction of QEC overheads.
If QEC is improved to the point where Grover’s algorithm becomes a threat to password systems, then there will be a need to move away from password authentication. Other authentication methods, which do not rely on passwords or other static values that need to be stored in hashed form, have been developed and are being adopted in some applications. These methods include biometric authentication, cryptographic one-time values, device identification, and others. The development of quantum computers may further motivate the deployment of such systems. Another defense is to harden password management systems using secure hardware [3], as already implemented by major websites.
Another popular application of hash functions is called proof-of-work, used in many crypto currencies such as Bitcoin and Ethereum. Blocks of Bitcoin transactions are validated every 10 minutes by a process in which “miners” solve a certain computation challenge; the first miner to solve the problem is paid by the cryptocurrency system. Grover’s
algorithm would be suited to solving a Bitcoin challenge. However, as the second to last row in Table 4.1 shows, the overhead of implementing Grover’s algorithm using physical qubits to solve the proof-of-work challenge is currently estimated to require well over 10 minutes, which would make the attack a nonthreat to the current Bitcoin ecosystem. If the overheads required for this implementation were significantly reduced, there could be some risk if or when fault-tolerant quantum computers become available; Bitcoin would thus also need to transition to a post-quantum secure digital signature system to avoid bitcoin theft.
4.2 SIZING ESTIMATES
A critical question for understanding the vulnerability of cryptographic tools is: What scale of a quantum computer would be required to defeat the cipher? The answer to this question is expected to vary with the details of how the quantum algorithm is deployed. Nonetheless, a rough approximation of the number of qubits required for defeating various protocols for a given key size is provided in Table 4.1. This table also estimates the number of physical qubits required (assuming an effective error rate of 10–5), and the time required for the algorithm’s execution, using a surface code for quantum error correction and a surface code measurement cycle time of 200 nanoseconds. These assumptions for gate fidelity and gate speed are well beyond the capabilities of multiqubit systems in 2018. The table clearly shows that the major threats posed by a sophisticated quantum computer are breaking key exchange and digital signatures. While these figures reflect the current state of knowledge, the committee cautions the reader that these assessments are based upon quantum algorithms that are currently known, as well as implicit assumptions about the architecture and error rates of a quantum computer. Advances in either area have the potential to change timings by orders of magnitude. For example, if physical gate error rates of 10–6 were to be achieved (e.g., by topological qubits), and the other assumptions remain the same, then the number of physical qubits required to break RSA-4096 would drop to 6.7 × 106, and the time would drop to 190 hours. Similarly, if the assumptions are not achieved, then implementing these algorithms might not be possible or might come at a greater cost—for example, if physical gate error rates of only 10–4 are achieved, then the number of physical qubits required to break RSA-4096 would increase to 1.58 × 108 and the time required would increase to 280 hours [4]. It is also possible that new algorithms could be developed (or could already have been developed outside of the public sphere) that would present different attack vectors—for that matter, the same can also be said about potential alternative classical attacks.
4.3 POST-QUANTUM CRYPTOGRAPHY
The cryptographic research community has been working to develop replacement algorithms that are expected to be secure against an adversary with access to a large-scale quantum computer. These replacement algorithms, when standardized, will be executable on off-the-shelf classical processors. Their security relies on mathematical problems that are believed to be intractable even for a large-scale quantum computer. These algorithms, currently being evaluated by NIST, are thus expected to remain secure even after large-scale quantum computers are widely available. Like all cryptography, the hardness of these problem cannot be proved, and must continue to be evaluated over time to ensure that new algorithmic approaches do not weaken the cypher.
4.3.1 Symmetric Encryption and Hashing
Post-quantum secure symmetric encryption and hash functions are obtained by simply increasing the encryption key size or hash output size. Adequate solutions already exist, and the primary remaining challenge is to verify, through additional research to identify possible quantum attacks, that the standardized schemes, such as 256-bit AES-GCM and SHA256, are indeed secure against an adversary who has access to a quantum computer.
Problems where an increase in the size of the hashed data is not possible (or where the hashed data’s entropy does not increase much even if its size is increased), like password systems, would be difficult to secure in a world with fast quantum computers. If a quantum computer was as fast as a modern classical processor in logical operations per second, thanks to Grover’s algorithm, a quantum computer would likely be able to identify the 10-character password in a few seconds. While the need for extensive error correction would make this attack much slower in practice, the availability of low-overhead approaches would place passwords at risk. Defending against this threat requires either moving away from password authentication or using a hardware-based password hardening scheme, as mentioned earlier.
4.3.2 Key Exchange and Signatures
The most significant challenges are post-quantum key-exchange and post-quantum digital signatures. For quantum resilience, existing schemes such as RSA and ECDSA will need to be abandoned and new systems will need to be designed. NIST has already initiated a Post-Quantum Cryptography project to facilitate this process, seeking proposals for new cryptographic algorithms [5]. In the first round of submissions, which
ended in November 2017, NIST received over 70 submissions. The NIST process is scheduled to conclude by 2022-2024; its selections are likely to become frontrunners for broader standardization—for example, through the Internet Engineering Task Force (IETF), the International Organization for Standardization (ISO), and the International Telecommunication Union (ITU). Internet systems will likely begin incorporating post-quantum resistant cryptography once the NIST process concludes, if not sooner. Boxes 4.1 to 4.4 provide brief descriptions of a few candidate post-quantum key-exchange and signature systems, as well as pointing out some early experiments done with some of these systems.
Finding: While the potential utility of Shor’s algorithm for cracking deployed cryptography was a major driver of early enthusiasm in quantum computing research, the existence of cryptographic algorithms that are believed to be quantum-resistant will reduce the usefulness of a quantum computer for cryptanalysis and thus will reduce the extent to which this application will drive quantum computing R&D in the long term.
4.4 PRACTICAL DEPLOYMENT CHALLENGES
It is important to remember that today’s encrypted Internet traffic is vulnerable to an adversary who has a sufficiently large quantum computer running quantum error correction. In particular, all encrypted data that is recorded today and stored for future use, will be cracked once a large-scale quantum computer is developed.
Finding: There is strong commercial interest in deploying post-quantum cryptography even before such a quantum computer has been built. Companies and governments cannot afford to have their private communications decrypted in the future, even if that future is 30 years away. For this reason, there is a need to begin the transition to post-quantum cryptography as soon as possible.
Realistically, completing the transition to Internet-wide post-quantum cryptography will be a long and difficult process. Some computer systems remain operational for a very long time. For example, computer systems in cars sold today will still be on the road in 15, and perhaps even 20 years. A quantum-vulnerable algorithm can be deprecated only once the vast majority of Internet systems are updated to support new algorithms. Once a major site like Google deprecates an algorithm, old devices that support only that algorithm can no longer connect to Google. A good example of this timeline is the long process of deprecating the SHA1 hash function and the transition to SHA256. The SHA1 function was considered to be insecure since 2004. However, it took many years to disable it. Even as of 2018, it is still not universally decommissioned—some old browsers and servers still do not support SHA256.
The transition from SHA1 to SHA256 provides a map for the steps required to transition to post-quantum cryptography. First, post-quantum cryptographic algorithm standards for key-exchange and signatures will need to be developed and ratified. After adoption as an official standard, the new standard algorithms must be implemented in a wide variety of computer languages, popular programming libraries, and hardware cryptographic chips and modules. Then the new standard algorithms will need to be incorporated into encryption format and protocol standards such as PKCS#1, TLS, and IPSEC. These revised format and protocol standards will need to be reviewed and adopted by their respective standards committees. Then vendors will need to implement the new standards in hardware and software product updates. From there, it will likely take many years until the majority of Internet systems are upgraded to support the new standards—and quantum-vulnerable algorithms cannot be disabled until their replacements are widely deployed. After this is done, sensitive data in corporate and government repositories must be reencrypted, and any copies encrypted under the previous paradigm need to be destroyed—especially given that some organizations rely upon merely deleting encryption keys as a substitute for destroying files, which will not help against an attack by a quantum computer. Vulnerable public-key certificates must be reissued and redistributed, and any documents that must be certified from official sources must be re-signed. Last, the signing and verification processes for all software code must be updated, and the new code must be re-signed and redistributed. This process probably cannot be completed in less than 20 years; the sooner it is begun, the sooner it will conclude [6].
Since the invention of a scalable general-purpose quantum computer would constitute a total, simultaneous, instantaneous, worldwide compromise of all of today’s public-key cryptographic algorithms, quantum-resistant cryptographic algorithms would need to be designed,
standardized, implemented, and deployed before the first quantum computer goes online. But in fact, the quantum-resistant infrastructure must be in place even before a quantum computer goes live, because encrypted (or signed) data needs to be protected for longer than an instant.
For example, consider a company’s 10Q filing. This quarterly tax document contains information that is sensitive until it is published; people who come into possession of a 10Q before it is public information know things about the company’s financial condition that they could use to profit from insider trading (because the stock value will change once the 10Q information becomes public, and people who know the information in advance can predict the magnitude and direction of the change and buy or sell shares accordingly). A 10Q filing needs to stay secret for no more than three months; after the end of the quarter, it is filed and published, and the information is no longer sensitive—so it does not need to be secret. So for a 10Q filing, the required “protection interval” is three months.
Now, consider a government classified document. Under the 50-year rule, the contents should not be made public for at least 50 years. Hence, the document must be encrypted with an encryption scheme that is expected to remain secure for at least 50 years. The required “protection interval” is 50 years.
Three pieces of information are necessary to determine when a quantum-resistant cryptographic infrastructure should be put in place:
- When will the current cryptographic infrastructure fail? (That is, when would a quantum computer of sufficient sophistication to deploy Shor’s or Grover’s algorithms go live?)
- How long does it take to design, build, and deploy the new quantum-resistant infrastructure?
- What’s the longest protection interval of concern?
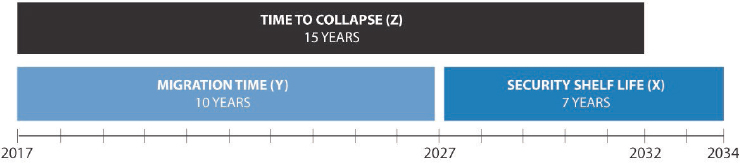
Once these three things have been identified, the required timing can be computed using a simple formula3 illustrated in Figures 4.1 and 4.2, where:
- X is the “security shelf life” (the longest protection interval we care about, assuming that the data is protected starting today)
- Y is the “migration time” (the time it takes to design build, and deploy the new infrastructure)
- Z is the “collapse time” (the time it takes for a sufficiently large quantum computer to become operational, starting from today)
___________________
3 This formula was introduced by committee member Michele Mosca: M. Mosca, 2015, Cybersecurity in an era with quantum computers: Will we be ready? IACR Cryptology ePrint Archive 2015:1075.

The example in Figure 4.1 assumes that no quantum computer will exist for 15 years, that a quantum-resistant infrastructure can be designed, built, and deployed in only 3 years, and that the longest security shelf-life of concern is only 5 years. This optimistic scenario yields a safety margin of 7 years, suggesting that the start of earnest working on replacing our public-key cryptographic infrastructure could be delayed for several years.
A less optimistic scenario would set migration time at 10 years (the pessimistic estimate for completion of NIST’s planned standardization interval of 2022-2024 plus up to 3 years for implementation and deployment), and security shelf life at 7 years (a common legally required retention interval for many kinds of business records). In this gloomier scenario, illustrated in Figure 4.2, there is no safety margin; if a large quantum computer goes online 15 years from today, sensitive data will remain at risk of compromise, with no effective protection technology available, for 3 years—even if the work to replace our public-key cryptographic infrastructure begins today.
The most realistic scenario is even more pessimistic. As noted in the preceding section, NIST’s current schedule will result in the selection of
a quantum-safe cryptographic algorithm suite around 2022-2024. Past experience with replacing the data encryption standard (DES) symmetric cryptosystem and various hash functions (SHA-1, MD5) suggests that the minimum time required to replace a widely deployed cryptographic algorithm, including retiring most consequential implementations of the broken algorithm, is about 10 years after design and standardization of the new algorithms are complete. Assuming a security shelf life of 7 years as in the previous scenario, the earliest safe date for the introduction of a quantum computer capable of breaking RSA 2048 is about 2040—if the work of replacing today’s cryptographic libraries and crypto-dependent applications is begun as soon as NIST finishes its selection process. To put this another way, if a fault-tolerant quantum computer with 2,500 logical qubits is built any time in the next 25 years, some data will likely be compromised—even if work on the cryptographic fallout is begun today and continued diligently during the entire interval.
Much depends upon when such a device will come on the scene. The following two chapters provide a closer view of the current status of efforts to build a large-scale, fault-tolerant quantum computer. Chapter 5 describes progress in constructing quantum computing hardware and control systems, and Chapter 6 examines the software and architecture—including the classical co-processing—that will be required to implement algorithms on a mature device.
4.5 NOTES
[1] National Institute of Standards and Technology, 2018, “Post-Quantum Cryptography: Workshops and Timeline,” last updated May 29, 2018, https://csrc.nist.gov/projects/post-quantum-cryptography/workshops-and-timeline.
[2] D. Martin, 2015, “Real World Crypto 2015: Password Hashing According to Facebook,” Bristol Cryptography Blog, http://bristolcrypto.blogspot.com/2015/01/password-hashing-according-to-facebook.html.
[3] Ibid.
[4] V. Gheorghiu and M. Mosca, in preparation.
[5] National Institute of Standards and Technology, 2018, “Post-Quantum Cryptography,” last modified May 29, 2018, http://csrc.nist.gov/groups/ST/post-quantum-crypto/.
[6] For additional discussion of the process and challenges associated with transitioning between cryptosystems, see National Academies of Sciences, Engineering, and Medicine, 2017, Cryptographic Agility and Interoperability: Proceedings of a Workshop, The National Academies Press, Washington, DC, https://doi.org/10.17226/24636.


















