6
Essential Software Components of a Scalable Quantum Computer
In addition to creating the hardware functionality to support quantum computing, a functional QC will also require extensive software components. This is analogous to the operation of classical computers, but new and different tools are required to support quantum operations, including programming languages that enable programmers to describe QC algorithms, compilers to analyze them and map them onto quantum hardware, and additional support to analyze, optimize, debug, and test programs for implementation on specific quantum hardware. Preliminary versions of some of these tools have been developed to support the QCs currently available on the web [1]. Ideally, these tools should be accessible to software developers without a background in quantum mechanics. They should offer abstractions that allow programmers to think at an algorithmic level with less concern for details like control pulse generation. Last, they should ideally enable programming of any quantum algorithm in a code that can translate to any target quantum architecture.
For the results described in Chapter 5, hardware controls and software implementation routines were deployed in an implementation-specific manner, with significant manual optimization. These approaches will not scale efficiently to large devices. Given the different, and emerging, approaches to building a quantum data plane, early-stage high-level software tools must be particularly flexible if they are to remain useful in the event of changes in hardware and algorithms. This requirement complicates the task of developing a complete software architecture for quantum computing. The rest of this chapter explores these issues in more
detail, providing a look at the current state of progress in development of software tools for QC, and what needs to be accomplished to create a scalable QC.
The software ecosystem for any computer—classical or quantum—includes the programming languages and compilers used to map algorithms onto the machine, but also much more than that. Simulation and debugging tools are needed to debug the hardware and software (especially in situations where the hardware and software are being co-developed); optimization tools are required to help implement algorithms efficiently; and verification tools are needed to help work toward both software and hardware correctness.
For quantum computers, simulation tools, such as a so-called universal simulator, can provide a programmer with the ability to model each quantum operation and to track the quantum state that would results, along with its evolution in time. This capability is essential for debugging both programs and newly developed hardware. Optimization tools such as resource estimators would enable rapid estimation of the performance and qubit resources needed to perform different quantum algorithms. This enables a compiler to transform the desired computation into an efficient form, minimizing the number of qubits or qubit operations required for the hardware in question.
6.1 CHALLENGES AND OPPORTUNITIES
The QC software ecosystem is fundamental to QC systems design for several reasons. First, and most fundamentally, the compiler tool flows that map algorithms down to a QC hardware system are crucial for enabling its design and use. Even before the QC hardware is available, a compiler system coupled with resource estimators and simulation tools can be developed; these are critical for algorithm design and optimization. A good example of the power of this type of tool set can be found in the work by Reiher et al. on optimizing QC operations required to computationally model the biochemical process of nitrogen fixation [2]. By using feedback from resource estimators, and improved compiler optimizations, they were able to reduce the estimated run time of their quantum algorithm from a high-degree polynomial to a low-degree polynomial, bringing the expected time to solution using a quantum computer from billions of years down to hours or days.
This example shows how languages and compilers (the software “toolchain”) can have a dramatic effect on the resources required to execute a quantum computation. Compilers—for both classical and quantum computing—perform many resource optimizations as they analyze and translate the algorithms to machine-executable code. Successful QC
toolchain resource optimizations offer significant savings in terms of the number of qubits and the amount of time required to execute an algorithm, in turn helping accelerate the arrival of the QC versus classical “tipping point.” In essence, high-performing synthesis and optimization offers the potential for implementing an algorithm in a much smaller QC system than would be required for an unoptimized version; while software development traditionally tends to come after hardware development, making good on the potential for concurrent hardware and software development could move forward the time quantum computing is practical by years.
Finally, digital noisy intermediate-scale quantum (NISQ) systems under current development are particularly sensitive to the quality and efficacy of the software ecosystem. By definition, NISQ systems are very resource constrained, with limited numbers of qubits and low gate fidelities. Therefore, making effective use of NISQ machines will require careful algorithm optimization, probably requiring nearly full stack information flow to identify tractable mappings from algorithms designed for these size devices to the specific NISQ implementation. In particular, information such as noise or error characteristics can usefully percolate up the stack to influence algorithm and mapping choices. Likewise, information about algorithm characteristics (e.g., parallelism) can usefully flow down the stack to inform mapping choices. Put another way, a digital NISQ may require communications between nearly every layer of the stack, meaning that there are fewer opportunities simplify the system design. These challenges will drive specific aspects of toolchain design—for example, limiting cross-layer abstraction or encouraging the use of libraries of “hand-tuned” modules.
Finding: To create a useful quantum computer, research and development on the software toolchain must be done concurrently with the hardware and algorithm development. In fact, insight gained from these tools will help drive research in algorithms, device technologies, and other areas, toward designs with the best chance for overall success.
Several challenges must be solved to create a complete QC software tool flow. Simulation, debugging, and validation are particularly problematic. The following sections describe these issues in more detail.
6.2 QUANTUM PROGRAMMING LANGUAGES
Algorithm design, including for QC algorithms, usually starts with a mathematical formulation of an approach for solving a problem. Programming and compilation are the nontrivial tasks of converting an
algorithm’s abstract mathematical description to an implementation that is executable on a physical computer. Programming languages support this process by offering syntax to support the natural expression of key concepts and operations. Programming QC systems requires very different concepts and operations than programming for classical computers, and as such requires new languages and a distinct set of tools. For example, designing a language that enables a programmer to exploit quantum interference in a quantum algorithm is a unique and nontrivial challenge.
There are several levels of abstraction in software and algorithms, so several layers of languages are required. At the highest level, a programming language should enable a user to easily and rapidly program an algorithm, while ideally shielding the programmer from detailed underlying hardware specifications. This abstraction of detail is helpful both because it can help mitigate the massive complexity of these systems and also because it can lead to more device-independent and portable software. This device independence can allow the same QC program to be recompiled to target different QC hardware implementations. Current prototype languages enable developers and programmers to interact with quantum hardware through a high-level language that is at least somewhat device independent.
At the lowest level, a language must be able to interact seamlessly with the hardware components and give a complete specification of the physical instructions necessary to execute a program at speed. While some low-level languages are used at present to program devices directly, the long-term vision and goal for quantum computing is to absorb such languages into automated tool flows; as in classical computers, the goal is to have lower-level QC device orchestration be automatically generated, and to abstract such low-level information away from the programmer.
Similar to early stages of a classical computing ecosystem, the current state of play in QC software includes many languages and tools, a number of them open-source efforts,1 in development both commercially and academically. With the recent industry push toward larger quantum hardware prototypes (including availability on public clouds for broad use), there is an increased awareness of the need for full-stack QC software and hardware in order to encourage usage and nurture a developer community around quantum software and hardware. Thus, it is reasonable to expect that quantum programming languages and software ecosystems will receive considerable attention and may see significant changes in coming years.
___________________
1 See, for example, https://github.com/markf94/os_quantum_software.
6.2.1 Programmer-Facing (High-Level) Programming Languages
An initial generation of QC programming languages has been developed, and continued attention is leading to the evolution of new languages and language constructs over time. From the nascent experiences so far, several programming language attributes seem likely to offer useful leverage in overall system design and success.
First, a high-level quantum programming language should strike a balance between abstraction and detail. On one hand, it should be capable of concisely expressing quantum algorithms and applications. On the other hand, it must allow the programmer to specify sufficient algorithmic detail to be used within the software tool flow that maps the quantum algorithm to the hardware-level primitive operations. High-level quantum programming languages are themselves domain-specific languages (DSLs), and in some cases there have been proposals for further specialization for given QC subdomains such as the variational quantum eigensolver, quantum approximate optimization algorithm, and others.
In some quantum programming languages, the approach is to describe an algorithm as a quantum circuit. Software toolchain systems then analyze this circuit in terms of both circuit width and circuit depth to optimize it for a particular quantum data plane. Somewhat in contrast to these approaches, other languages emphasize higher-level algorithm definition over circuit definition. To support good mappings to hardware despite this higher-level approach, some languages support extensive use of function libraries; these contain subroutines and high-level functions implemented as module mappings hand-tuned for particular hardware and are discussed in Section 6.2.3.
Programming languages fall generally into two categories: functional and imperative. QC programming languages of both types have been developed, and there is no consensus yet on whether one is better suited than the other for programming QC applications. Functional languages align well with more abstract or mathematical implementation of algorithms. This approach tends to lead to more compact—and, some programming language researchers argue, less error prone—codes. Examples of QC functional programming languages include Q#, Quipper, Quafl, and LIQuI | > (“Liquid”). Imperative languages, in contrast, allow direct modification of variables and are often viewed as supportive of the resource-efficient system design that QC systems, particularly NISQ systems, will need to be practical [3]. Examples of imperative QC languages are Scaffold [4] and ProjectQ [5].
Another design decision pertains to whether the language is “embedded” off a base language. Embedded languages are formally defined extensions of a base language, an approach that allows the language developer to use the base language’s software stack to speed initial
implementation. These languages are practically constructed through modest additions to the base language’s compiler and related software, as opposed to writing an entire software ecosystem from scratch. To exploit commonality in this way, some current QC programming languages are embedded in widely used non-QC languages.2 Others are not formally embedded but instead are very close in style to a non-QC base language.3 Given the fast rate of change in QC hardware and systems design at present, a language that is either formally embedded or at least stylistically related to a widely used base language can allow compilers and other tools to be built quickly and modified more easily than “from-scratch” language design.
Another important design issue for QC programming languages is the language’s approach to data typing. “Data typing” refers to programming language constructs that label the kind (or type) of data that a program or function expects, and allows the function to use the type of the data to determine how to perform a specific operation. All languages use some forms of data types. For example, in most programming languages, base data types are provided for integers, floating point numbers, characters, and other commonly used entities; the definition of addition is different for integers than it is for floating point numbers. Some more recent QC languages support a much richer data type system and have stronger type checking rules. These “strongly typed” languages yield even stricter guarantees on type safety that can be helpful in generating reliable software. In particular, compilers can perform type checking regarding whether the program being compiled manipulates variables of a particular data type correctly and abides by the corresponding rules when variables of one type are assigned to another variable. (By analogy, integer values may be assigned to a floating point variable without loss of precision, but an assignment of a floating point value to an integer variable would either be illegal or would result in a loss of precision depending on the language.) Last, a discussion of programmer-facing software would not be complete without some mention of the user “command-line” interface. Because quantum computers are expected to be large, expensive, custom-built pieces of instrumentation in the near term, it is likely that such systems will be housed at a few designated locations, such as major data centers or manufacturers’ facilities, and accessed by users through the Web over a cloud service.4 Under these circumstances, various levels of
___________________
2 This includes Quipper, Quafl, Quil, ProjectQ, and LIQuI | >.
3 For example, the Scaffold language and ScaffCC toolchain are based on the C programming language. Scaffold uses a very widely used classical compiler infrastructure, LLVM (https://llvm.org/).
4 Indeed, this is currently the case for D-Wave pilot systems installed at National Labs and with IBM’s open superconducting qubit-based processors.
service can be provided to the users—for example, at an application level, as a programming environment, or at an application programming interface (API) level. The future user interface to QCs will continue to evolve, as the physical hardware, relevant applications, and the manufacturer, service provider, and user community all develop.
6.2.2 Control Processing (Low-Level) Languages
In addition to high-level programmer-facing languages for algorithm development, lower-level languages are also necessary in order to generate instructions for the control processor (Section 5.1.3) of a specific quantum data plane (Section 5.1.1). These languages correspond to the assembly language programming or “instruction set architecture” of classical computers. As such, they must be designed to express central aspects of QC execution, such as the fundamental low-level operations or “gates.” They can also have constructs to express operation parallelism, qubit state motion, and control sequencing. They are sometimes referred to as a quantum intermediate representation (QIR).
For efficiency reasons, in the foreseeable future, lower-level QC programs and tools likely will need to be more hardware specific than the tools used with classical computers. Given the severe resource constraints facing quantum computers, compilation of quantum programs is likely to be tightly specialized to a particular program input—that is, compilation will likely need to be conducted before every task. For example, a QC running Shor’s factoring algorithm would have a program compiled to factor a specific large number provided as a constant. Or a QC for chemistry simulations would have a program compiled to model a specific molecular structure. This is in contrast to classical computers where ample resources allow more generality. Classical computers compile programs such that they can be run with many different inputs: for example, a spreadsheet program accepts and calculates any numbers typed in by a user, rather than compiling a unique program for each new input. Until QC resource constraints relax considerably, a QC program compilation will much more closely resemble the tight optimization processes used in designing computer hardware (i.e., “hardware synthesis”) than classical software compilation.
An early low-level language called QASM [6] provided very basic operational constructs, but was tied to the early QC practices of simple circuits expressed as linear sequences of gates. Subsequent variations of QASM have provided additional features to improve expressive power and scalability. For example, in conventional classical assembly code for classical computers, it would be common to have constructs for iteration (repeatedly executing a portion of code) and for subroutine calls (jumping
to another module of code). Currently, some convergence is being seen on the OpenQASM [7] quantum assembly-level language, which combines elements of assembly languages and C with the original QASM constructs.
In the final phases of compilation, a program represented in a QIR like OpenQASM is translated into appropriate control instructions, producing code for the control processor. The control processor drives signals to the control and measurement plane. Languages and frameworks can help support the creation of the software for control generation and measurement equipment used in this plane. One example of this type of system is QcoDeS [8], a Python-based data acquisition framework and toolset to interact with physical devices. Other examples often correspond with particular hardware implementations; these include the OpenQASM backend for IBM Q, an open-source system called ARTIQ driven by the ion trap research community [9], and others.
Current NISQ systems are tightly resource constrained both in terms of circuit width (qubits) and depth (time steps or operation counts). This has placed a challenge on QC languages and compilers: mapping algorithms onto NISQ systems requires extensive, aggressive resource optimizations. This includes both algorithm-level resource reductions that are relatively hardware independent, and also lower-level optimizations that are more specific to a particular hardware instance or technology category. Some of the higher-level optimizations are applied using widely known transformations first developed for software compilers for classical computers, such as loop unrolling and constant propagation. Other high-level optimizations might be specific to QC, such as the QC gate operator selection discussed in Section 6.5.1.
Lower-level hardware-dependent optimizations more naturally focus on device specifics. These include optimizations to account for qubit layout and optimize for data communication. There are also approaches that optimize for very specific device characteristics including observed coherence intervals or device error rates [10]. As NISQ systems become more broadly available for public use, toolchains that are tightly tailored to real-machine characteristics are likely to be more widely used. Such tight tailoring in compiler tool flows can allow algorithms to most efficiently use the limited qubit counts available in the NISQ era.
6.2.3 Software Library Support
In classical computers, function libraries help programmers mitigate complexity by using prewritten subroutines for programs. In some cases, the library provides implementations for basic functions like fast Fourier transforms (FFTs) in order to ease programming and enable code
reuse. In other cases, the library functions have been specifically tuned for a particular implementation, and thereby help programmers arrive at a more resource-efficient program than they otherwise would. Library approaches are similarly expected to be essential for efficient quantum computing.
One critical set of libraries arises from the need to evaluate commonly used functions within a quantum algorithm. Some quantum algorithms will require simple mathematical functions such as addition, or other, more complex functions such as modular arithmetic, implementation of block ciphers, and hash functions. A comprehensive set of library functions can save programmers time and help to reduce the likelihood of program errors. In addition, library functions can also be heavily tuned for specific implementations. This shields algorithm-level programmers from the burden of fully familiarizing themselves with hardware details while optimizing for circuit width or depth.
While optimized library functions are often a useful resource, it may be difficult for them to be fully optimized to each of the range of possible underlying hardware implementations. Programmers may find that their algorithm-level expression is—when compiled—more efficient than the library option. To address these trade-offs, there are QC libraries [11-13] that contain a number of options for how to construct the desired functionality—some hardware independent and others tailored for a particular implementation. The compiler tool flow can then use a resource estimate tool to choose the best option for the targeted hardware. Furthermore, if a given user’s implementation remains superior to the library options, then in some cases (e.g., open-source scenarios) it too can be incorporated into the library for future use.
Creation and use of QC function libraries is a practical and effective approach to offering well-optimized solutions for commonly used functions, but their interplay with higher-level programming and compiling remains an area where further research and development are needed. Library development would benefit from further improvements in high-level compiler optimizations, to further support the compiler’s ability to optimize the tradeoff between circuit depth and circuit width. Specific areas of need include better ways to perform ancilla management, and techniques to manage both “dirty” and “clean” ancilla qubits.5 Another area of future research lies in being able to express and analyze what level of numerical precision is required in a quantum algorithm, and
___________________
5 An “ancilla qubit” is a qubit used for scratch space during a quantum computation or circuit implementation. It is allocated temporarily and must be returned to either its identical starting state (if allocated in a nonzero state) or the clean zero state (if allocated in the zero state) when returned.
how to automatically determine such precisions within a compiler. Such precision analysis can be supportive of aggressive resource optimizations that reduce qubit or operator counts by doing the calculation only to the minimally required precision [14].
6.2.4 Algorithm Resource Analysis
A key to developing commercially or practically useful quantum applications and programs will be the ability to understand the cost and performance of that algorithm. Given the challenges of executing on real QC hardware or simulating QC systems at scale, other forms of early-stage resource estimation become especially critical. Fortunately, resource analysis is more tractable than QC simulation or real-machine execution because it needs to determine only the time and resources that would be required to compute the answer; it does not compute the answer itself. As such, it does not need to compute the full quantum state information, which is the intractable challenge in other approaches. Thus, resource estimation can be made efficient and scalable to very large qubit input sizes, and this allows one to analyze the performance of algorithms that are too large to simulate on a classical computer or run on current quantum computers. Resource estimators have been run for Shor’s algorithm and other similarly scaled benchmarks, for up to hundreds of thousands of qubits and millions of quantum operations or execution timesteps [15].
The results of resource estimation analysis can be used by other software tools to guide optimization e orts, especially when mapping to the quantum data plane, and by programmers to identify realistic applications of quantum computers. This detailed analysis of the application is needed since the theoretical analysis gives only the asymptotic scaling of a quantum algorithm. On a particular QC system, the actual resource usage trade-offs may be heavily influenced by implementation choices such as qubit connectivity or communication approaches. Such implementation specifics can be accounted for by resource estimators, in order to get better understanding of what are promising design choices, rather than relying solely on asymptotic scaling estimates.
Resource analysis can be done at various abstraction levels in the compilation of the algorithm to the hardware, with varying trade-offs of detail versus accuracy. Each stage uses a model of the quantum hardware appropriate to the optimization issues at that stage. For example, one can analyze circuit width and depth after the algorithm has been mapped to a discrete set of single- and two-qubit operations to understand how best to minimize the logical resources necessary to run an application. Another level of analysis can be performed again after quantum error correction has been applied and the resulting code has been mapped to the actual
operations the hardware supports. This allows the estimate to account for QEC and communication overheads. Likewise, such estimates allow compiler analyses making use of the estimates to perform optimizations to reduce these overheads.
6.3 SIMULATION
Simulators serve a critical role in the development of quantum computers and their algorithms, and their implementation faces fundamental challenges in scalability and tractability. At the lowest level, a simulator can be used to simulate the operation of the native quantum hardware gates to provide the expected outputs of a quantum computer, and in turn can be used to help check the hardware. At the highest level, a simulator can track the logical algorithmic computation and the state of the logical qubits. Simulators can model the effect of noise for di erent hardware technologies. This helps algorithm designers to predict the e ects of noise on the performance of quantum algorithms before there are machines capable of running them. Such simulation capabilities will be particularly important for NISQ systems whose lack of QEC support means that noise effects will fundamentally impact algorithm performance and success.
The fundamental challenge of QC simulation is how quickly the state space scales. Since a gate operation can be implemented on a classical computer by a sparse matrix-vector multiplication, a simulation of a quantum computer is a sequence of matrix-vector multiplications. However, the size of the complex-valued wave function representing the state of a quantum computer with N qubits grows as 2N. This means that QC hardware with just a single additional qubit has double the state space. Very quickly, the space becomes too large to be simulated tractably on even the largest classical supercomputer. Current supercomputers are capable of simulating on the order of 50-qubit systems.6
To work around the intractability of full-system QC simulation, QC simulators can be built to model subsets of quantum operations. For example, to evaluate the behavior of a particular QEC code, one may want to simulate just the relevant Clifford operations. (They do not constitute a “universal gate set,” but they do comprise the gates of interest for certain
___________________
6 While recent progress toward modeling larger systems has been reported, the exact number is currently up for debate, and depends upon the specifics of the method. See, for example, C. Neill, P. Roushan, K. Kechedzhi, S. Boixo, S.V. Isakov, V. Smelyanskiy, R. Barends, et al., 2018, A blueprint for demonstrating quantum supremacy with superconducting qubits, Science 360(6385):195-199; E. Pednault, J.A. Gunnels, G. Nannicini, L. Horesh, T. Magerlein, E. Solomonik, and R. Wisnieff, 2017, “Breaking the 49-Qubit Barrier in the Simulation of Quantum Circuits,” arXiv:1710.05867; and J. Chen, F. Zhang, C. Huang, M. Newman, and Y. Shi, 2018, “Classical Simulation of Intermediate-Size Quantum Circuits,” arXiv:1805.01450.
QEC approaches.) In this case, QC simulation is tractable [16] and error correction can be studied on upward of thousands of qubits. Simulation of the Toffoli, CNOT, and NOT gates is also efficient and enables studying and debugging large-scale arithmetic quantum circuits, for example. Another example is the simulation of Toffoli circuits, which contain only NOT (Pauli X), controlled-NOT, and doubly controlled-NOT (Toffoli) operations. Such circuits can be efficiently simulated on classical inputs.
For the universal gate scenarios that are most challenging to simulate, simulation speed can be improved by simulating some of the operations in the quantum algorithm at a higher level of abstraction [17]. For example, in a case in which the quantum program wants to execute the quantum Fourier transform, the simulator would invoke the fast Fourier transform on the wave function and evaluate that on the classical computer running the simulation. For a mathematical function such as modular addition, which is used in Shor’s algorithm, the simulator again simply implements modular addition on each of the computational basis states rather than applying the sequence of quantum operations required for reversible modular addition. While creating these higher-level abstract functions is difficult in general, any existing options could be linked into the functional library. This approach is particularly useful for quantum algorithms that use “oracle functions,” functions for which the quantum implementation is not known—in this case, the programmer can provide a classical implementation of the oracle function.
6.4 SPECIFICATION, VERIFICATION, AND DEBUGGING
The specification, verification, and debugging of quantum programs is an extremely difficult problem. First, the complexity of QC software and hardware makes their correct design extremely difficult. Second, the intractability of QC simulation limits the amount of predesign testing and simulation available to developers. Third, the nature of QC systems is that measurement collapses the state; therefore, conventional debugging methods based on measuring program variables during program execution would disrupt execution and so cannot be used.
At its heart, the verification problem asks the question is it possible for a classical client to verify the answer provided by a quantum computer? The difficulties in answering this question stem from fundamental principles of quantum mechanics and may seem inherently insurmountable: (1) direct simulation of quantum devices, even of moderate size, by classical computers is all but impossible, due to the exponential power of quantum systems, and (2) the laws of quantum mechanics severely limit the amount of information about the quantum state that can be accessed via measurement. Three avenues have been explored to answer
this challenge. Each builds on results from the theory of interactive proof systems, exploring further the deep interaction of that theory with classical cryptography that has led to an amazing wealth of results over the past three decades.
In the first, the experimentalist or verifier is “slightly quantum,” has the ability to manipulate a constant number of qubits, and has access to a quantum channel to the quantum computer [18,19]. The use of quantum authentication techniques helps keep the quantum computer honest. Security proofs for such protocols are extremely delicate and have only been obtained in recent years [20,21].
A second model considers a classical verifier interacting with multiple quantum devices sharing entanglement, and describes a scheme for efficiently characterizing the quantum devices, and verifying their answers [22-24]. In the context of quantum cryptography, this model, where the quantum devices are adversarial, has been studied under the name of device independence. Efficient protocols for certified random number generation in this have been obtained [25,26]. These have further led to protocols for fully device independent quantum key distribution [27-29].
A third model considers a classical verifier interacting with a single quantum device, where the verifier uses post-quantum cryptography to keep the device honest. Recent work shows how to carry out efficiently verifiable quantum supremacy based on trapdoor claw-free functions (which can be implemented based on learning with errors [LWE]) [30]. The paper also shows how to generate certifiable random numbers from a single quantum device. Recent work has shown how a classical client can use trapdoor claw-free functions to delegate a computation to a quantum computer in the cloud, without compromising the privacy of its data—a task known as “quantum fully homomorphic encryption” [31]. In a further development, it was shown [32] that an ingenious protocol based on trapdoor claw-free functions can be used to efficiently verify the output of a quantum computer.
As a result of the fact that measurement changes the system state, and provides limited information about that state, measuring the state of a quantum computer to better understand the source of errors is a complex task. Since each measurement returns only a single index of the overall quantum state, reconstructing the state itself requires repeatedly preparing and measuring it a large number of times to generate the probability distribution of quantum state being measured. This measurement method, called “quantum state tomography,” provides an estimate of the underlying quantum state, but requires a large number of repeated preparations and measurements—for n qubits, 22n measurements are used to ensure adequate number of samples in each possible output state. If one is trying to debug a quantum circuit, then one needs to apply quantum process
tomography, where quantum state tomography is performed on a number of different input sets, to characterize how the circuit transforms the quantum state of its input state to its output state. Process tomography represents a complete description of the errors during a circuit’s operation, but it also requires an extremely large number of steps to implement.
Given the difficulty of developing quantum algorithms and tool flows, designers need methods to help validate both the initial algorithm and the low-level output that the compiler generates (to check the optimizations done in the compiler). QC developers will always be implementing some programs for QC machines before they have been built, making this task especially problematic. This situation will lead to programs that cannot be validated by direct execution.
There are several limited options for QC debugging today. For example, one can use classical or hybrid classical-quantum simulation to partially test an application, but this runs into the simulator limitations previously discussed in Section 6.3. Another option is to use programming language constructs such as data types or assertions to make errors easier to find. Assertions are inserted as lines into a program to state (“assert”) some characteristic that should be true at that point in the execution. For example, a QC program might include assertions about the expected eigenstates or correlations at particular points in the algorithm progression. Compiler and run time analysis can then be used to check these types or assertions. However, since measurement of variables collapses their state, these assertion checks must either be limited to measurement of ancillary variables not central to the computation or must otherwise be structured such that their measurement ends the program at useful points.
Since full-state simulation is not practical for all but the smallest systems, users can use tools such as the resource estimators described in Section 6.2.3 to debug aspects of quantum programs. Tools also exist to test branches of the quantum program, subject to programmer specified expectations about branching probabilities or other statistics. In addition, QC tools can be integrated into conventional software development packages, to enable conventional software debugging strategies such as setting program breakpoints.
In general, however, the above techniques represent small and inadequate inroads into a largely unmapped space of challenges. The challenges of debugging QC systems—and more specifically the near-intractability of approaches like simulations or assertions—means that there remains a critical need to continue development of tools to verify and debug quantum software and hardware.
Finding: Development of methods to debug and analyze larger quantum
systems and programs is a critical need in the development of large-scale quantum computers.
6.5 COMPILING FROM A HIGH-LEVEL PROGRAM TO HARDWARE
Classical computers manage the massive complexity of today’s hardware and software systems (comprised of billions of transistors and lines of code, respectively) by layering many abstractions and tools. In contrast, QC systems, particularly near-term NISQ systems, will be too resource constrained to have that luxury. While the prior sections lay out categories of software, the stringent resource constraints have slowed the acceptance of well-defined abstraction layers, because the information-hiding aspect of traditional abstraction layers translates to higher circuit widths or depths in QC systems. Nonetheless, QC program compilation thus far typically follows stages somewhat similar to classical counterparts, as depicted in Figure 6.1 [33].
Figure 6.1 offers a general sketch of a compiler tool flow from high-level applications through compiler optimizations and down to the actual control pulses that create the quantum operations themselves. Given the unique requirements and operations of quantum algorithms, the programmer would use a domain specific language (DSL) created for quantum computing or perhaps even for algorithmic subdomains within QC. DSLs are programming languages designed with features specific to a particular problem domain. Programmers may also have access to libraries of useful routines written by others.
The first stage of the DSL compiler converts the program into a quantum intermediate representation (QIR) that represents the same program but in a lower-level form that is easier for the compiler to analyze and manipulate. This QIR then goes through a number of optimization passes to make it more efficient to run on the control processor and ultimately execute on the quantum computer. The final stages of this compiler map the qubits to physical locations on the quantum data plane, and then generate the sequence of operations that execute the desired quantum circuit on this data plane.
For QC compilers, appropriate layering approaches and abstractions are still being refined. For example, in classical computers, the instruction set architecture (ISA) forms a durable long-term abstraction of possible hardware targets. Namely, software can run on different implementations of the same ISA without recompiling. Current QC systems, in contrast, often expose details of the hardware all the way up to the programmer. The lack of abstractions is partly forced by extreme resource constraints, and partly due to simple conventions from early QC implementations
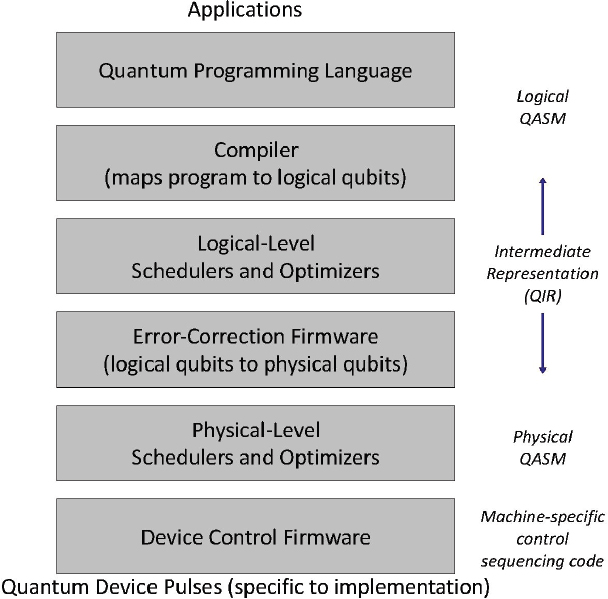
that are expected to mature into more principled abstraction layers as QC implementations become more complex. Nonetheless, it is instructive to consider compilation as occurring in the illustrated phases. Some of the above steps have either already been discussed or are quite similar to compilation for classical computers, and need not be discussed further. The subsections that follow offer more details on two aspects of particular interest: gate synthesis and layout/QEC.
6.5.1 Gate Synthesis
One role of the physical-level (hardware-specific) compilation stage is to select and synthesize the particular gate functions needed for the computation. These gate functions are akin to the instruction set architecture or hardware functional units of a conventional computer. For example, multiqubit gates will be synthesized from one-qubit gates and a two-qubit gate specific to the qubit technology. Further hardware-specific rewriting rules are then applied, which include the decomposition of single-qubit operations into sequences of gates drawn from a technology-dependent set [34].
As mentioned earlier, arbitrary single-qubit rotations cannot be expressed exactly using a Clifford + T gate set; thus, these rotations must be decomposed (also called “synthesized”) into a series of gate operations. Decomposition enables a general circuit expressed in arbitrary unitaries to be synthesized into an approximate circuit composed of a sequence of elementary gates, where the gates are drawn from a given universal, discrete set. The typical universal gate set employed is the Clifford + T gate set; however, other gates are also possible (e.g., Clifford and Toffoli, V basis gate set, etc.). Choice of a particular universal gate set is driven by hardware considerations as well as requirements for fault tolerance and quantum error correction. In general, state-of-the-art synthesis methods [35-40] have been developed that enable a quantum single-qubit rotation to be synthesized in roughly log(1/ɛ) gates, where ɛ is the accuracy of the sequence. This means that the number of required gates grows slowly with increased accuracy.
6.5.2 Quantum Error Correction
Given the high error rates of quantum gates, once quantum error correction can be deployed, one of the key jobs of the tool flow is to map the needed logical qubits into a set of the physical qubits, and the logical qubit operations into operations on the physical qubits. Until qubit gate error probabilities fall precipitously, the fault-tolerant architectures adopted will have complex structures (both in terms of the number of
physical qubits and the sequence of gate operations among them necessary to accomplish fault tolerance). These quantum computers will therefore benefit from being designed with the fault-tolerance architecture for the system in mind. As described in Chapter 3, feasible architectures include surface codes implemented on a two-dimensional (2D) array of qubits with nearest neighbor gates [41,42] and concatenated Calderbank-Shor-Steane (CSS) codes implemented on a densely connected quantum register with modules connected in a network [43,44]. Many alternative fault-tolerant architectures are being actively investigated and developed in order to identify architectures requiring fewer resources and better error correction properties.
Given the large number of qubits and operations required for error correction, it is essential that the error correction operations be accomplished as efficiently as possible. Since these operations will be created by the software tool chain, achieving this efficiency requires that the tool chain be tightly configured for the hardware it is targeting.
6.6 SUMMARY
The software tools needed to create and debug quantum programs are as essential to all scales of quantum computer as the underlying quantum data plane. While good progress has been made in this area, a number of challenging problems remain to be solved before a practical machine could become operational. One challenge is in simulation—both higher-level algorithmic simulation and lower-level physics simulation. A typical computer design cycle often involves simulating designs that have not yet been built using current-generation already-built systems. They allow us to estimate run time performance and hardware resource requirements, and they allow some degree of correctness testing. Both types of simulation are important for planning and debugging next-stage QC hardware and software systems designs, and both represent fundamental challenges. At the algorithm level, the state-space of QC systems is so large that even simulating the QC algorithmic behavior of around 60 or more qubits cannot be done in reasonable time or space on today’s classical machines. The same capability to represent complex state spaces that makes QC compellingly attractive also makes it fundamentally difficult or intractable to simulate on classical hardware.
Lower-level simulations accounting for noise and other environmental and hardware specifications have even more limited performance, because the detail they attempt to account for can be vastly beyond the abilities of classical computers to represent. As a result, the QC community is developing methods in which smaller quantum systems may be used to simulate specific aspects of larger ones, analogous to the so-called “bootstrapping methods” employed in the classical computer hardware
design community where a current-generation machine is used to simulate newly proposed next-generation machines to be built. In addition, approximate simulations of the full system can have value for early design assessments and may be performed on high-end classical machines.
Debugging and verification of quantum programs are also major challenges. Most classical computers provide programmers the ability to stop execution at an arbitrary point in the program, and examine the machine state—that is, the values of program variables and other items stored in memory. Programmers can determine whether the state is correct or not, and if not, find the program bug. In contrast, a QC program has an exponentially large state-space that is collapsed by physical qubit measurements, and QC execution cannot be restarted after a mid-run measurement. Thus, design of debugging and verification techniques for quantum programs is an essential and fundamentally challenging requirement to enable progress in QC development.
While QC simulation and debugging are truly grand challenge research endeavors, other aspects of the software toolchain such as languages and compilers have seen greater progress, but also remain important.
The NISQ era may prove to be one of significant change in software compilation and tools. In particular, the ability to rapidly develop and test quantum programs on real hardware will be critical in developing a deeper understanding of the power of quantum computers for concrete applications, as well as enabling fast feedback and progress in hardware development. Coordinating the advancement of software techniques in addition to hardware ones will help spur progress for the field overall.
6.7 NOTES
[1] For example, QISKit and OpenQASM from IBM (https://www.qiskit.org/) and Forest from Rigetti (https://www.rigetti.com/forest).
[2] M. Reiher, N. Wiebe, K.M. Svore, D. Wecker, and M. Troyer, 2017, Elucidating reaction mechanisms on quantum computers, Proceedings of the National Academy of Sciences of the U.S.A. 201619152.
[3] F.T. Chong, D. Franklin, and M. Martonosi, 2017, Programming languages and compiler design for realistic quantum hardware, Nature 549(7671):180.
[4] A. Javadi-Abhari, S. Patil, D. Kudrow, J. Heckey, Al. Lvov, F.T. Chong, and M. Martonosi, 2014, “ScaffCC: A Framework for Compilation and Analysis of Quantum Computing Programs,” in Proceedings of the 11th ACM Conference on Computing Frontiers, http://dx.doi.org/10.1145/2597917.2597939.
[5] ProjectQ can be found at https://github.com/ProjectQ-Framework/ProjectQ.
[6] A.W. Cross, unpublished, https://www.media.mit.edu/quanta/quanta-web/projects/qasm-tools/.
[7] A.W. Cross, L.S. Bishop, J.A. Smolin, and J.M. Gambetta, 2017, “Open Quantum Assembly Language,” arXiv:1707.03429.
[8] QCoDeS has recently been released and is available at http://qcodes.github.io/
[9] The latest version of the ARTIQ is available at https://github.com/m-labs/artiq.
[10] IBM Q Experience Device, https://quantumexperience.ng.bluemix.net/qx/devices.
[11] M. Soeken, M. Roetteler, N. Wiebe, and G. De Micheli, 2016, “Design Automation and Design Space Exploration for Quantum Computers,” arXiv:1612.00631v1.
[12] A. Parent, M. Roetteler, and K.M. Svore, 2015, “Reversible Circuit Compilation with Space Constraints,” arXiv:1510.00377v1.
[13] P.M. Soeken, T. Häner, and M. Roetteler, 2018, “Programming Quantum Computers Using Design Automation,” arXiv:1803.01022v1.
[14] M. Roetteler and K.M. Svore, 2018, Quantum computing: Codebreaking and Beyond, IEEE Security and Privacy 16(5):22-36.
[15] Microsoft’s Quantum Development Kit found at https://www.microsoft.com/en-us/quantum/development-kit; ScaffCC found at https://github.com/epiqc/ScaffCC.
[16] S. Aaronson and D. Gottesman, 2004, Improved simulation of stabilizer circuits, Physical Review A 70:052328.
[17] T. Häner, D.S. Steiger, K.M. Svore, and M. Troyer, 2018, A software methodology for compiling quantum programs, Quantum Science and Technology 3:020501.
[18] D. Aharonov, M. Ben-Or, E. Eban, and U. Mahadev, 2017, “Interactive Proofs for Quantum Computations,” preprint arXiv:1704.04487.
[19] A. Broadbent, J. Fitzsimons, and E. Kashefi, 2009, “Universal Blind Quantum Computation,” pp. 517-526 in 50th Annual IEEE Symposium on Foundations of Computer Science 2009.
[20] J.F. Fitzsimons, and E. Kashefi, 2017, Unconditionally verifiable blind quantum computation, Physical Review A 96(1):012303.
[21] D. Aharonov, M. Ben-Or, E. Eban, and U. Mahadev, 2017, “Interactive Proofs for Quantum Computations,” preprint arXiv:1704.04487.
[22] B.W. Reichardt, F. Unger, and U. Vazirani, 2012, “A Classical Leash for a Quantum System: Command of Quantum Systems via Rigidity of CHSH Games,” preprint arXiv:1209.0448.
[23] B.W. Reichardt, F. Unger, and U. Vazirani, 2013, Classical command of quantum systems, Nature 496(7446):456.
[24] A. Natarajan and T. Vidick, 2017, “A Quantum Linearity Test for Robustly Verifying Entanglement,” pp. 1003-1015 in Proceedings of the 49th Annual ACM SIGACT Symposium on Theory of Computing.
[25] S. Pironio, A. Acín, S. Massar, A. Boyer de La Giroday, D.N. Matsukevich, P. Maunz, S. Olmschenk, et al., 2010, Random numbers certified by Bell’s theorem, Nature 464(7291):1021.
[26] U. Vazirani and T. Vidick, 2012, “Certifiable Quantum Dice: Or, True Random Number Generation Secure Against Quantum Adversaries,” pp. 61-76 in Proceedings of the Forty-Fourth Annual ACM Symposium on Theory of Computing.
[27] U. Vazirani and T. Vidick, 2014, Fully device-independent quantum key distribution, Physical Review Letters 113(14):140501.
[28] C.A. Miller and Y. Shi, 2016, Robust protocols for securely expanding randomness and distributing keys using untrusted quantum devices, Journal of the ACM (JACM) 63(4):33.
[29] R. Arnon-Friedman, R. Renner, and T. Vidick, 2016, “Simple and Tight Device-Independent Security Proofs,” preprint arXiv:1607.01797.
[30] Z. Brakerski, P. Christiano, U. Mahadev, U. Vazirani, and T. Vidick, 2018, “A Cryptographic Test of Quantumness and Certifiable Randomness from a Single Quantum Device,” in Proceedings of the 59th Annual Symposium on the Foundations of Computer Science.
[31] U. Mahadev, 2018, “Classical Homomorphic Encryption for Quantum Circuits,” Pro
ceedings of the 59th Annual Symposium on the Foundations of Computer Science.
[32] U. Mahadev, 2018, “Classical Verification of Quantum Computations,” Proceedings of the 59th Annual Symposium on the Foundations of Computer Science.
[33] F.T. Chong, D. Franklin, and M. Martonosi, 2017, Programming languages and compiler design for realistic quantum hardware, Nature 549(7671):180.
[34] T. Häner, D.S. Steiger, K.Svore, and M. Troyer, 2018, A software methodology for compiling quantum programs, Quantum Science and Technology 3(2):020501.
[35] V. Kliuchnikov, A. Bocharov, M. Roetteler, and J. Yard, 2015, “A Framework for Approximating Qubit Unitaries,” arXiv:1510.03888v1.
[36] V. Kliuchnikov and J. Yard, 2015, “A Framework for Exact Synthesis,” arXiv:1504.04350v1.
[37] V. Kliuchnikov, D. Maslov, and M. Mosca, 2012, “Practical Approximation of Single-Qubit Unitaries by Single-Qubit Quantum Clifford and T Circuits,” arXiv:1212.6964.
[38] N.J. Ross and P. Selinger, 2014, “Optimal Ancilla-Free Clifford+T Approximation of z-Rotations,” arXiv:1403.2975v3.
[39] A. Bocharov, M. Roetteler, and K.M. Svore, 2014, “Efficient Synthesis of Probabilistic Quantum Circuits with Fallback,” arXiv:1409.3552v2.
[40] A. Bocharov, Y. Gurevich, and K.M. Svore, 2013, “Efficient Decomposition of Single-Qubit Gates into V Basis Circuits,” arXiv:1303.1411v1.
[41] R. Raussendorf and J. Harrington, 2007, Fault-tolerant quantum computation with high threshold in two dimensions, Physical Review Letters 98:190504.
[42] A.G. Fowler, M. Mariantoni, J.M. Martinis, and A.N. Cleland, 2012, Surface codes: Towards practical large-scale quantum computation, Physical Review A 86:032324.
[43] C. Monroe, R. Raussendorf, A. Ruthven, K.R. Brown, P. Maunz, L.-M. Duan, and J. Kim, 2014, Large-scale modular quantum-computer architecture with atomic memory and photonic interconnects, Physical Review A 89:022317.
[44] M. Ahsan, R. Van Meter, and J. Kim, 2015, Designing a million-qubit quantum computer using resource performance simulator, ACM Journal on Emerging Technologies in Computing Systems 12:39.





















