7
Feasibility and Time Frames of Quantum Computing
A large-scale, fault-tolerant, gate-based quantum computer capable of carrying out tasks of practical interest has not yet been achieved in the open science enterprise. While a few researchers [1] have argued that practical quantum computing is fundamentally impossible, the committee did not find any fundamental reason that such a system could not be built—provided the current understanding of quantum physics is accurate. Yet significant work remains, and many open questions need to be tackled to achieve the goal of building a scalable quantum computer, both at the foundational research and device engineering levels. This chapter assesses the progress (as of mid-2018) and possible future pathways toward a universal, fault-tolerant quantum computer, provides a framework for assessing progress in the future, and enumerates key milestones along these paths. It ends by examining some ramifications of research and development in this area.
7.1 THE CURRENT STATE OF PROGRESS
Small demonstration gate-based quantum computing systems (on the order of tens of qubits) have been achieved, with significant variation in qubit quality; however, device size increases are being announced with increasing frequency. Significant efforts are under way to construct noisy intermediate-scale quantum (NISQ) systems—with on the order of hundreds of higher-quality qubits that, while not fault tolerant, are robust enough to conduct some computations before decohering [2].
A scalable, fully error-corrected machine (which can be thought of using the abstraction of logical qubits) capable of a larger number of operations appears to be far off. While researchers have successfully engineered individual qubits with high fidelities, it has been much more challenging to achieve this for all qubits in a large device. The average error rate of qubits in today’s larger devices would need to be reduced by a factor of 10 to 100 before a computation could be robust enough to support error correction at scale, and at this error rate, the number of physical qubits that these devices hold would need to increase by at least a factor of 105 in order to create a useful number of effective logical qubits. The improvements required to enable logical computation are significant, so much so that any predictions of time frames for achieving these requirements based upon extrapolation would exhibit significant uncertainty.
In the course of gathering data for this study, the committee heard from several individuals with experience directing different kinds of large-scale engineering efforts.1 Each described the minimum time frame for funding, developing, building, and demonstrating a complex system as being approximately 8 to 10 years from the time at which a concrete system design plan is finalized [3]. As of mid-2018, there have been no publicly announced design plans for building a large-scale, fault-tolerant quantum computer, although it is possible that such designs exist outside the public domain; the committee had no access to classified or proprietary information.
Key Finding 1: Given the current state of quantum computing and recent rates of progress, it is highly unexpected that a quantum computer that can compromise RSA 2048 or comparable discrete logarithm-based public key cryptosystems will be built within the next decade.
Given the long time horizon for achieving a scalable quantum computer, rather than attempting to predict exactly when a certain kind of system will be built—a task fraught with unknowns—this chapter proposes a framework for assessing progress. It presents a few scaling metrics for
___________________
1 These included the U.S. Department of Energy’s Excascale Computing project, the commercial development of DRAM and 3DNAND technologies, and current efforts to build the world’s largest Tokamak (fusion reactor) at the International Thermonuclear Experimental Reactor site in France. While very different projects, all project directors noted their empirical observations of similar time frames for completing very large engineering projects. To provide context for this estimate of 8 to 10 years, the committee notes that even the Manhattan Project, arguably one of history’s most ambitious and resource-intensive science and engineering projects (with an estimated cost of $22 billion, adjusted to 2016 inflation levels, and an all-hands-on-deck approach to manpower, with 130,000 dedicated staff) took 6 years from its inception in 1939 to successful demonstration in the Trinity Test of 1945.
tracking growth of quantum computers—which could be extrapolated to predict near-term trends—and a collection of key milestones and known challenges that must be overcome along the path to a scalable, fault-tolerant quantum computer.
7.1.1 Creating a Virtuous Cycle
As pointed out in Chapter 1, progress in any field that requires significant engineering effort is very strongly related to the strength of the research and development effort on which it depends, which, in turn, depends on available funding. This is clearly the case in quantum computing, where increased public and private sector investment have enabled much of the recent progress. Recently, the private sector has demonstrated significant engagement in quantum computing (QC) research and development (R&D), as has been broadly reported in various media [4]. However, the current investments in quantum computing are largely speculative—while there are potentially marketable near-term applications of qubits for quantum sensing and metrology, the objective of R&D on quantum computing systems is to build technology that will create a new market. A virtuous cycle, similar to that of the semiconductor industry, has not yet begun for quantum computing technologies. As a technology, quantum computing is still in early stages.2
The current enthusiasm for quantum computing could lead to a virtuous cycle of progress, but only if a near-term application emerges for the technologies under development—or if a major, disruptive breakthrough is made which enables the development of more sophisticated machines. Reaching these milestones would likely yield financial returns and stimulate companies to dedicate even more resources to their R&D in quantum computing, which would further increase the likelihood that the technology will scale to larger machines. In this scenario, one is likely to see sustained growth in the capacity of quantum processors over time.
However, it is also possible that even with steady progress in QC R&D, the first commercially useful application of a quantum computer will require a very large number of physical qubits—orders of magnitude larger than currently demonstrated or expected in the near term. In this case, government or other organizations with long time horizons can continue to fund this area, but this funding is less likely to grow rapidly, leading to a Moore’s law-type of development curve. It is also possible
___________________
2 In fact, QC has been on Gartner’s list of emerging technologies 11 times between 2000 and 2017, each time listed in the earliest stage in the hype cycle, and each time with the categorization that commercialization is more than 10 years away; see https://www.gartner.com/smarterwithgartner/the-cios-guide-to-quantum-computing/.
that in the absence of near-term commercial applications, funding levels could potentially flatten or decline. This situation is common for startup technologies; surviving this phenomenon is referred to as crossing the “valley of death” [5,6]. In severe cases, funding dries up, leading to the departure of talent from industry and academia, and leaves behind a field where little progress can be made in an area for a long time in the future, since the field has a bad reputation. Avoiding this scenario requires some funding to continue even if commercial interest wanes.
Key Finding 2: If near-term quantum computers are not commercially successful, government funding may be essential to prevent a significant decline in quantum computing research and development.
As the virtuous cycle that fueled Moore’s law shows, successful outcomes are critical, not only to fund future development but also to bring in the talent needed to make future development successful. Of course, the definition of a successful outcome varies among stakeholders. There is a core group of people for whom advances in the theory and practice of quantum science is all the success they need. Others, including those groups funded through companies or the venture capital (VC) community, are interested in some combination of scientific progress, changing the world, and financial rewards. For the latter group, commercial success will be required. Given the large number of technical challenges that need to be resolved before a large, error-corrected quantum computer can be built, a vibrant ecosystem that can be sustained over a long period of time will be critical to support quantum computing and enable it to reach its full potential.
7.1.2 Criticality of Applications for a Near-Term Quantum Computer
In the committee’s assessment, the most critical period for the development of quantum computing will begin around the early 2020s, when current and planned funding efforts are likely to require renewal. The best machines that are likely to have been achieved by that time are NISQ computers. If commercially attractive applications for these machines emerge within a reasonable period of time after their introduction, private-market investors might begin to see revenues from the companies they have invested in, and government program managers will begin to see results with important scientific, commercial, and mission applications emerging from their programs. This utility would support arguments in favor of further investments in quantum computing, including reinvestment of the capital these early successes bring in. In addition, the ability of working
quantum computers to solve problems of real-world interest will create demand for expert staff capable of deploying them for that purpose, and training staff in academic and other programs who can drive progress in the future. This training will be facilitated by the availability of NISQ computers to program and improve. Commercial applications for a NISQ computer—that is, some application that will create sufficient market interest to generate a return on investment—will thus be a major step in starting a virtuous cycle, where success leads to increased funding and talent, which enables improvements in quantum computing capacity, which in turn enables further success.
NISQ computers are likely to have up to hundreds of physical (not error-corrected) qubits, and, as described in Chapter 3, while there are promising research directions, there are at present no known algorithms or applications that could make effective use of this class of machine. Thus, formulating an R&D program with the aim of developing commercial applications for near-term quantum computing is critical to the health of the field. Such a program would include the following:
- Identification of algorithms with modest problem size and limited gate depth that show quantum speedup, in application domains where algorithms for classical computers are unlikely to improve much.
- Identification of algorithms for which hybrid classical-quantum techniques using modest-size quantum subsystems can provide significant speedup.
- Identification of problem domains in which the best algorithms on classical computers are currently running up against inherent scale limits of classical computation, and for which modest increases in problem size can bring economically significant increases in solution impact.
Key Finding 3: Research and development into practical commercial applications of noisy intermediate-scale quantum (NISQ) computers is an issue of immediate urgency for the field. The results of this work will have a profound impact on the rate of development of large-scale quantum computers and on the size and robustness of a commercial market for quantum computers.
Even in the case where near-term quantum computers have sufficient economic impact to bootstrap a virtuous cycle of investment, there are many steps between a machine with hundreds of physical qubits and a large-scale, error-corrected quantum computer, and these steps will likely require significant time and effort. To provide insights into how to
monitor the transition between these types of machine, the next section proposes two strategies for tracking and assessing progress.
7.2 A FRAMEWORK FOR ASSESSING PROGRESS IN QUANTUM COMPUTING
Given the difficulty of predicting future inventions or unforeseen problems, long-term technology forecasting is usually inaccurate. Typically, technological progress is predicted by extrapolating future trends from past performance data using some quantifiable metric of progress. Existing data on past trends can be used to create short-term forecasts, which can be adjusted as new advances are documented to update future predictions. This method works when there are stable metrics that are good surrogates for progress in a technology. While this method does not work well for all fields, it has been successful in several areas, including silicon computer chips (for which the metric is either the number of transistors per computer chip, or the cost per transistor) and gene sequencing (for which the metric is cost per base pair sequenced), for which progress proceeded at an exponential rate for many years.
For quantum computing, an obvious metric to track is the number of physical qubits operating in a system. Since creating a scalable quantum computer that can implement Shor’s algorithm requires improvements by many orders of magnitude in both qubit error rates and number of physical qubits, reaching this number in any reasonable time period requires a collective ability of the R&D community to improve qubit quantity per device exponentially over time. However, simply scaling the number of qubits is not enough, as they must also be capable of gate operations with very low error rates. Ultimately, error-corrected logical qubits will be required, and the number of physical qubits needed to create one logical qubit for a given QECC depends strongly on the error rate of basic qubit operations, as discussed in Chapter 3.
7.2.1 How to Track Physical and Logical Qubit Scaling
One can separate progress in quantum computing hardware into two regimes, each with its own metric: the first tracks progress of machines in which physical qubits are used directly without quantum error correction, and the second tracks progress toward systems where quantum error correction is effective.3 The first metric (referred to as “Metric 1”) is the time
___________________
3 As previously mentioned, qubit connectivity is also an important parameter that changes the overhead for carrying out a computation on a device; however, it is not as important as qubit number and error rate, and its importance depends upon the specific context of a given system’s overall design. Connectivity is thus not included in the metric proposed here.
required to double the number of physical qubits in a system, where the average fidelity of all the qubits (and single and two-qubit gates) is held constant. Tracking the size and doubling times for systems at different average physical qubit gate error rates, for example, 5 percent, 1 percent, and 0.1 percent, provides a method to extrapolate progress in both qubit quality and quantity.4 Since the committee is interested in the error rates that will occur when the operations are used in a computation carried out in a real device, it notes that randomized benchmark testing (RBM), is an effective method of determining this error rate. This method will ensure that the reported error rates account for all system-level errors, including crosstalk.5
Even though several companies have announced superconducting chips comprised of more than 50 qubits [7], as of mid-2018, no concrete numbers on error rates for gate operations have been published for these chips; the largest superconducting QC with a reported error rate is IBM’s 20 qubit system. Their system’s average two-qubit gate error rate is around 5 percent [8]. During the early stages of QC, growth will initially be seen at the higher gate error-rate levels that will preclude achieving error-free operations using QEC; however, over time, this growth will move into higher quality qubit systems with lower error rates such that fully error corrected operation is possible. Tracking the growth of physical qubits at constant average gate error rate will provide a way to estimate the arrival time of future machines, which is useful, especially if NISQ computers become commercially viable.
The second metric (referred to as “Metric 2”) comes into play once QC technology has improved to the point where early quantum computers can run error-correcting codes and improve the fidelity of qubit operations. At this point, it makes sense to start tracking the effective number of logical qubits6 on a given machine, and the time needed to
___________________
4 Other metrics have been proposed—and new metrics may be proposed in the future—but most are based on these parameters. For example, the metric of quantum volume (https://ibm.biz/BdYjtN) combines qubit number and effective error rate to create a single number. Quantum computer performance metrics are an active area of research. The committee has chosen metric 1 for a simple and informative approach now.
5 Unfortunately, this metric has not been published for many of the current machines. Thus, while the committee recommends that RBM be used in determining metric 1, the examples used to illustrate determination of metric 1 in this chapter often use the average two-qubit error rate of the machine as a placeholder. This data should be updated when RBM data is available.
6 The number of physical qubits needed to create a logical qubit depends on the error rate of the physical qubits, and the required error rate of the logical qubits, as was described in Section 3.2. This required error rate of the logical qubits depends on the logical depth of the computation. For this metric, one would choose a large but constant logical depth—for example, 1012—and use that to track technology scaling.
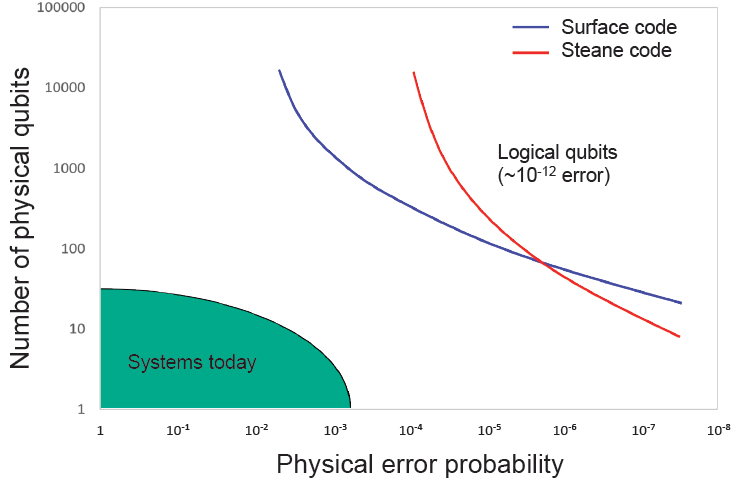
double this number. To estimate the effective number of logical qubits in a small machine with error correction, one can extrapolate the number of physical qubits required to reach a target logical gate error rate (e.g., <10–12) from the measured error rates using different numbers of physical qubits. For concatenated codes, this comes from the number of levels of concatenation needed, and for surface codes, it is the size (distance) of required code, as described in Chapter 3. The number of logical qubits is simply the size (that is, the number of physical qubits) of the QC that was fabricated divided by the calculated number required to create a logical qubit; in the near-term, the value of this metric will be less than one.7 One way to envision this metric is shown in Figure 7.1, which plots the effective error probability (or infidelity) of the two-qubit gate operation (which is in practice typically worse than that of the single-qubit operation) for physical qubits along the x-axis and the number of physical qubits along
___________________
7 It should be noted that this calculation does not account for the cost of implementing a universal gate set; it only tracks the number of physical qubits needed to hold the logical qubit state. For example, performing T gates on logical qubits under the surface code requires many more physical qubits than other operations.
the y-axis, with the goal of achieving a high-performance logical qubit protected by QECC. The different lines show the requirements for achieving logical error probabilities of 10–12 for two different QEC codes. The results of running QEC will allow one to extract the overall qubit quality for this machine. The number of logical qubits is the ratio between the fabricated number of qubits and the smallest size shown in Figure 7.1 for a logical qubit using qubits with the measured physical error rate.
Tracking the number of logical qubits has clear advantages over tracking the number of physical qubits in predicting timing of future error-corrected quantum computers. This metric assumes the construction of error-corrected logical qubits with a target gate error rate, and naturally reflects progress resulting from improvements in the physical qubit quality or QEC schemes which decrease the physical qubit overhead and lead to more logical qubits for a given number of physical qubits. Thus, the number of logical qubits can serve as a single representative metric to track scaling of quantum computers. This also means that the scaling rates for physical and logical qubits are likely to be different; the doubling time for logical qubits should be faster than physical qubits if qubit quality and QEC performance continue to improve with time. While physical qubit scaling is important for near term applications, it is the scaling trend for logical qubits that will determine when a large-scale, fault-tolerant quantum computer will be built.
Key Finding 4: Given the information available to the committee, it is still too early to be able to predict the time horizon for a scalable quantum computer. Instead, progress can be tracked in the near term by monitoring the scaling rate of physical qubits at constant average gate error rate, as evaluated using randomized benchmarking, and in the long term by monitoring the effective number of logical (error-corrected) qubits that a system represents.
As Chapter 5 discusses, while superconducting and trapped-ion qubits are at present the most promising approaches for creating the quantum data plane, other technologies such as topological qubits have advantages that might in the future allow them to scale at a faster rate and overtake the current leaders. As a result, it makes sense to track both the scaling rate of the best QC of any technology and the scaling rates of the different approaches to better predict future technology crossover points.
7.2.2 Current Status of Qubit Technologies
The characteristics of the various technologies that can be used to implement qubits have already been discussed in detail in the body of this report.
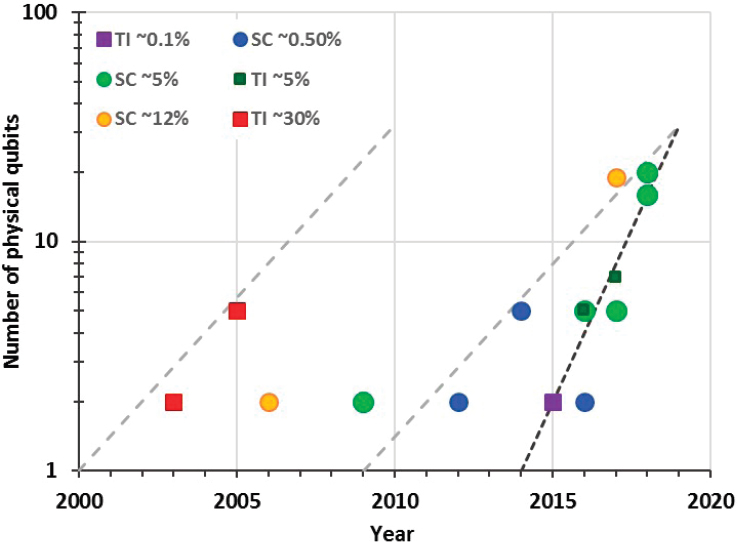
Of the technologies that the report discusses, only two, superconducting and trapped ion qubits, have achieved sufficient quality and integration to try to extract preliminary qubit scaling laws, but even for these, the historical data is limited. Figure 7.2 plots the number of qubits versus time, using rainbow colors to group machines with different error rates, with red points having highest and purple points the lowest error rate. Historically, it has taken more than 2 years for the number of qubits to double, if one holds the error rate constant. After 2016, superconducting qubit systems might have started a faster scaling path, doubling the number of qubits every year. If this scaling continues, one should see a 40-50 qubit system with average error rates of less than 5 percent in 2019. The ability to extract trends with which to make future predictions will improve as the number of data points increases, most likely within the next few years.
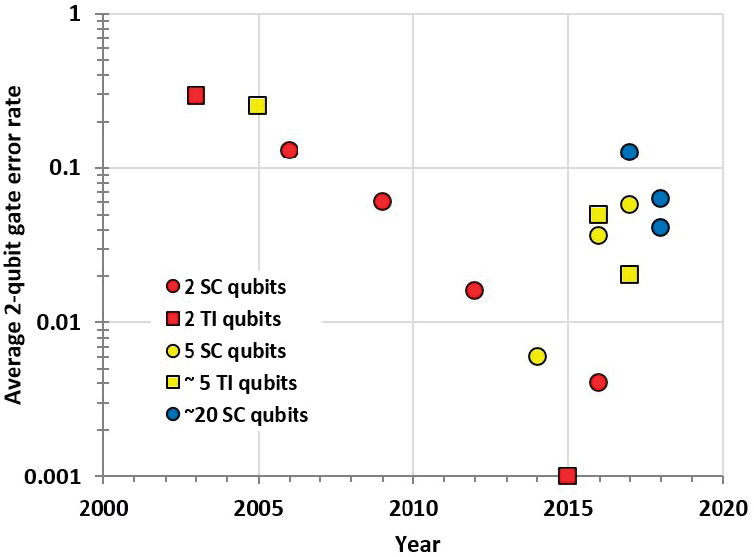
Figure 7.3 plots these same data points, but now with error rate on the y-axis, and representing the machine size by color. This data clearly shows the steady decrease in error rate for two-qubit systems, halving roughly every 1.5 to 2 years. Larger qubit systems have higher error rates, with the current 20-qubit systems at error rates that are 10 times higher than two-qubit systems (a shift of 7 years).
It is again worth noting the limited number of data points that can be plotted in this way, in part because those building prototypical QC devices do not necessarily report comparable data. More data points—and, more importantly for Metric 1, consistent reporting on the effective error rate using RBM on one-qubit and two-qubit gates within a device—would make it easier to examine these trends and compare devices.
For the rest of this chapter, machine milestones mapping progress in QC will be measured in the number of doublings in qubit number, or halving of the error rate required from the current state-of-the-art functioning QC system, which is assumed to be the order of 24 physical qubits in mid-2018, with 5 percent error rates.
The performance of a quantum computer depends on the number and quality of its qubits, which can be tracked by the metrics defined in this section, and the speed and connectivity of its gates. As with classical computers, different quantum computers will operate at different clock rates, exploit different levels of quantum gate parallelism, and support different primitive gate operations. Machines that can run any application will support a universal set of primitive operations, of which there are many different possible sets. The efficiency of an application’s execution will depend on the set of operations that the quantum data plane supports, and the ability of the software compilation system to optimize the application for that quantum machine.
To help track the quality of the software system and the underlying operations provided by the quantum data layer, it will be useful to
standardize a set of simple benchmark applications8 that can be used to measure both the performance and the fidelity of computers of any size. However, because many primitive operations may be required to complete a particular task,9 the speed or quality of a single primitive may not be a reasonable measure of the system’s overall performance. Instead, benchmarking of application performance will enable a more useful comparison between machines with different fundamental operations.
The benchmark applications would need to be periodically updated as the power and complexity of quantum computers improves. Such a set of evolving benchmarks is analogous to the Standard Performance Evaluation Corporation benchmark application suite [9] that has been used to compare classical computer performance for many decades. This
___________________
8 These applications could include different quantum error-correcting codes, variational eigensolvers, and “classic” quantum algorithms, and should be able to run on different-size “data sets” to enable then to be able to measure different-size quantum computers.
9 For example, many of the superconducting data planes support only nearest neighbor communication, which means that two-input gates must use adjacent qubits. Thus, a two-input gate requiring distant qubits would need to be broken into a number of steps to move information to two adjacent qubits before the operation can be completed. Similarly, some qubit rotations need to be decomposed into a number of operations to approximate a desired rotation.
was originally a simple set of commonly used programs and has changed over time to more accurately represent the compute loads of current applications. Given the modest computing ability of near-term quantum computers, it seems clear that at first these applications would be relatively simple, containing a set of common primitive routines, including quantum error correction, which can be scaled for different-size machines.
Key Finding 5: The state of the field would be much easier to monitor if the research community adopted clear reporting conventions to enable comparison between devices and translation into metrics such as those proposed in this report. A set of benchmarking applications that enable comparison between different machines would help drive improvements
in the efficiency of quantum software and the architecture of the underlying quantum hardware.
7.3 MILESTONES AND TIME ESTIMATES
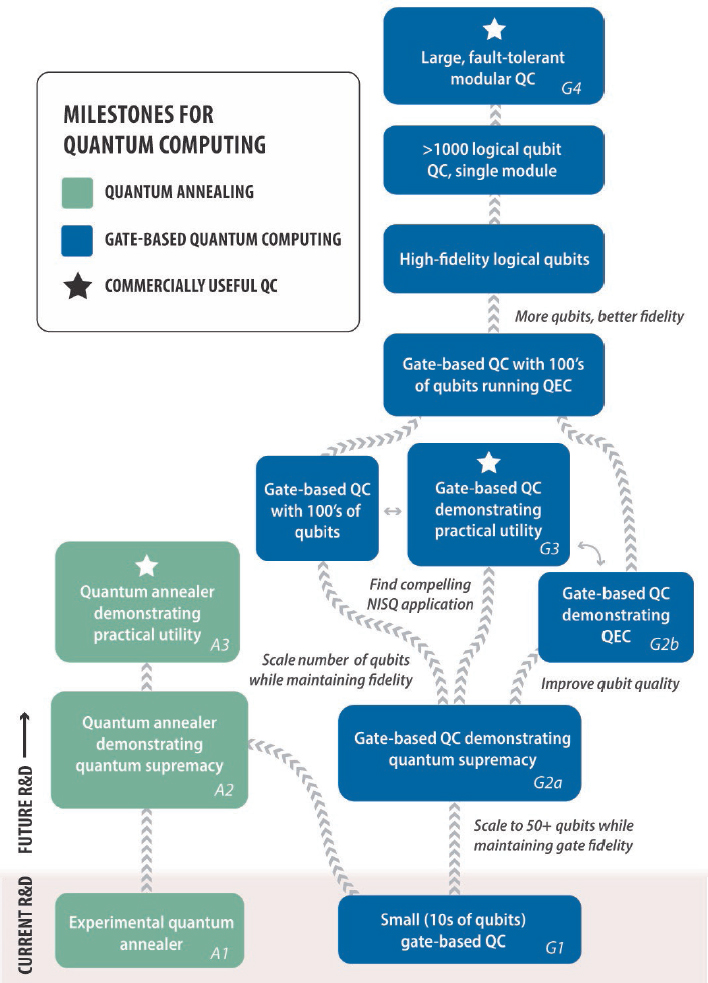
A large-scale, fully error corrected quantum computer is expected to require logical (error corrected) qubits in a design that can scale to many thousands, and a software infrastructure that can efficiently help programmers use this machine to solve their problems. This capability will likely be reached incrementally via a series of progressively more complex computers. These systems comprise a set of milestones that can be used to track progress in quantum computing, and in turn depend on progress in hardware, software and algorithms. As the previous section made clear, early work on algorithms is essential to help drive a growing quantum ecosystem, and work on hardware is needed to increase the number of physical qubits and improve qubit fidelity. Software and QEC improvements will also help by reducing the number of physical qubits needed for each application. These milestone computers are illustrated in Figure 7.4, and the main technical challenges that must be overcome to create them are described in the following sections.
7.3.1 Small (Tens of Qubits) Computer (Milestone G1)
The first benchmark machine is the class of digital (gate-based) quantum computers containing around 24 qubits with average gate error rate better than 5 percent, which first became available in 2017. At the time of this writing, the largest operational gate-based quantum computer is a 20-qubit system from IBM Q [10] with an average two-qubit gate error rate of about 5 percent. Systems with similar approach are also available from other university groups and commercial vendors [11]. In these systems, the control plane and control processor are all placed at room temperature with the control signals flowing through a cryostat to the quantum plane. Ion-trap QCs exist at a similar scale. Papers on a 7-qubit system from the University of Maryland with two-qubit error rate of 1-2 percent [12], and a 20-qubit system from Innsbruck [13] were published in 2017. The results from Innsbruck are not based on a conventional quantum gate-based approach,10 so it is hard to extract gate error rates, but the results do indicate scaling progress in trapped ion machines.
___________________
10 Instead of two-qubit gates, they use a “global” gate that entangles all the qubits in the chain, with the option of pulling some qubits out of the gate (any qubit combination can be “pulled” from this gate). They also have individually addressed single-qubit gates. While in principle these operations provide a complete gate set, characterizing an error rate is problematic.
7.3.2 Gate-Based Quantum Supremacy (Milestone G2a)
The next benchmark system is a quantum computer that demonstrates quantum supremacy—that is, one that can complete some task (which may or may not be of practical interest) that no existing classical computer can. Current projections from the literature indicate that this would require a machine with more than 50 qubits, and average gate error rate around 0.1 percent. However, this is necessarily a moving target, as improvements continue to be made in the approaches for classical computers that the quantum computers are trying to outperform. For a rough estimate of the limit of a classical computer, researchers have benchmarked the size of the largest quantum computer that a classical computer can simulate. Improvements in classical algorithms for simulating a quantum computer have recently been reported, and such progress may raise the bar somewhat, but not by orders of magnitude [14].11
This class of machine represents two generations (about a factor of 4) of scaling from machines available in 2017, and a decrease in average gate error rate of at least an order of magnitude. Several companies are actively trying to design and demonstrate quantum processors that achieve this goal, and some have already announced superconducting chips that surpass the threshold number of qubits identified. However, as of the time of this writing, none have demonstrated quantum supremacy or even published results from a working system using these quantum data planes [15].
Growing the number of qubits to meet this milestone does not require any new fabrication technology. The manufacturing process for both superconducting and trapped ion qubit arrays can easily accommodate the incorporation of additional qubits into the quantum data plane of a device. The challenge is to maintain or improve the quality of the qubits and qubit operations as the number of qubits and associated control signals scale. This challenge arises from two factors. First, since each manufactured qubit (or, in the case of trapped ions, the electrodes and optical coupling that contain or drive the qubits) is a little different than its neighbors, as the number of qubits increases, the expected variance in qubits also increases. Second, these additional qubits require additional control signals, increasing the potential for crosstalk noise. Thus, the main challenge is to mitigate these added “noise” sources through careful design and calibration. This problem will get harder as the system size increases, and the quality of calibration will likely define the qubit
___________________
11 For example, researchers have taken advantage of the limitations of the machines being simulated to reduce the problem space for the classical algorithm. See E. Pednault, J.A. Gunnels, G. Nannicini, L. Horesh, T. Magerlein, E. Solomonik, and R. Wisnieff, 2017, “Breaking the 49-Qubit Barrier in the Simulation of Quantum Circuits,” arXiv: 1710.05867v1.
fidelity of the resulting system and determine when quantum supremacy will be achieved. As noted in Chapter 3, several companies are trying to demonstrate quantum supremacy in 2018.
Achieving quantum supremacy requires a task which is difficult to perform on a classical computer but easy to compute on the quantum data plane. Since there is no need for this task to be useful, the number of possible tasks is quite large. Candidate applications have already been identified, as discussed in Chapter 3, so the development of benchmark applications for this specific purpose are unlikely to delay the time frame for achieving this milestone.
7.3.3 Annealer-Based Quantum Supremacy (Milestone A2)
While Chapters 5 and 6 focused on gate-based quantum computing, as Chapter 3 showed, quantum computing need not be gate based. D-Wave has been producing and selling superconducting qubit-based quantum annealers since 2011. While this family of systems has generated much interest and produced papers that show performance gains for specific applications, recent results [16] have shown that algorithms for classical computers can usually be optimized to the specifics of the given problem, enabling classical systems to outperform the quantum annealer. It is unclear whether these results are indicative of limitations in the current D-Wave architecture (how the qubits are connected) and qubit fidelity, or are more fundamental to quantum annealing. It follows that a key benchmark of progress is a quantum annealer that can demonstrate quantum supremacy.
Reaching this milestone is more challenging than simply scaling the number and improving the fidelity of qubits: the desired problems to be solved must be matched to the annealer’s architecture. This makes it challenging to estimate the time frame within which this milestone will likely be met. Since theoretical analysis of these problems is difficult, designers must test different problems and architectures in order to find an appropriate problem to attack. Even if a problem is found for which a quantum speedup is apparent, there is no way to rule out the possibility that a better classical computing approach will be found for the same class of problem. All initial D-Wave speedups were negated by demonstration of a better classical approach. In one instance of a specific synthetic benchmark problem, D-Wave’s performance roughly matched that of the best classical approach [17], but the use of faster classical CPUs or GPUs leads to outperformance of the annealer. Given the challenge associated with formally demonstrating supremacy on a quantum annealer, if this milestone is not met by the early 2020s, researchers may choose instead to direct their efforts toward the better-defined problem of building a
quantum annealer that can perform a useful task—an attribute that is more straightforward to identify, and may nonetheless lead to quantum supremacy.
7.3.4 Running QEC Successfully at Scale (Milestone G2b)
While both trapped ion and superconducting qubits have demonstrated qubit gate error rates below the threshold required for error correction, these gate error-rate performances have not yet been demonstrated in systems with tens of qubits, nor are these early machines able to measure individual qubits in the middle of a computation. Thus, creation of a machine that successfully runs QEC, yielding one or more logical qubits of better error rates than possible with physical qubits, is an important milestone. It will demonstrate not only one’s ability to create a system where the worst gate of the system still has an error rate below the threshold for error correction, but also that QEC codes are effective at correcting the types of errors that occur on the quantum data plane used in that machine. These machines will also provide opportunities for software and algorithm designers to further optimize the codes for the types of errors that occur.
This milestone may occur around the time gate-based quantum supremacy is demonstrated, since machines of that scale are expected to be large enough, and have low enough error rates, to employ QEC. The time order of these events will depend on the exact error rates needed to achieve quantum supremacy, compared to the QEC requirement that the effective error rate determined by RBM testing is much less than 1 percent [18].
As discussed at the beginning of this chapter, this milestone is also important because, once it is surpassed, the scaling rate for subsequent machines can be tracked in terms of the number of logical qubits, rather than the number of physical qubits and their error rates. In the committee’s assessment, machines of this scale are likely to be produced in academia or the private sector by the early 2020s.
The engineering process for scaling the number of logical qubits will likely proceed via two related efforts. The first will take the current best qubit design and focus on scaling the number of physical qubits in the system while maintaining or decreasing qubit error rates. The challenging aspect of this task is to scale the control layer to provide sufficient control bandwidth and isolation between the growing number of control signals and the quantum data plane, and to create the methodology for calibrating these increasingly complex systems. Addressing these challenges will drive learning about system design and scaling issues.
The other effort will explore ways of changing the qubit or system design to decrease its error rates, and will focus on smaller systems to
ease analysis. Successful approaches for decreasing error rates can then be transferred to the larger system designs. For example, decoherence-free subspaces and noiseless subsystem-based approaches to error mitigation could help to improve on qubit and gate error rates. Another promising approach may be to consider systems with inherent error correction as these technologies emerge or improve, such as topological qubits based on non-Abelian anyons, described in Chapter 5. While achieving quality improvement through QEC shows that building a logical qubit is possible, the overhead of QEC is strongly dependent on the error rates of the physical system, as shown earlier in Figure 7.1. Improvement in both areas is required in order to achieve an error-corrected quantum computer that can scale to thousands of logical qubits.
7.3.5 Commercially Useful Quantum Computer (Milestones A3 and G3)
As mentioned earlier in this chapter, recent progress and the likelihood of demonstrating quantum supremacy in the next few years will probably create enough interest to drive quantum computing investment and scaling into the early 2020s. Further investment will be required for improvements to continue through the end of the 2020s, and this investment will likely depend upon some demonstration of commercial utility—that is, upon demonstration that quantum computers can perform some tasks of commercial interest significantly more efficiently than classical computers. Thus, the next major milestone is creation of a quantum computer that generates a commercial demand, to help launch a virtuous cycle for quantum computation.
This successful machine could be either gate based or an analog quantum computer. As Chapter 3 described, both machines use the same basic quantum components—qubits and methods for these qubits to interact—so increasing resources toward building any type of computer would likely have spillover effects for the entire quantum computing ecosystem.
Many groups are working hard to address this issue, by providing Web-based access to existing quantum computers to enable a larger group of people to explore different applications, creating better software development environments, and exploring physics and chemistry problems that seem well matched to these early machines. If digital quantum computers advance at an aggressive rate of doubling qubits every year, they will likely have hundreds of physical qubits in roughly five years, which still may be not be enough to support one full logical qubit. Therefore, a useful application would most likely need to be found for a NISQ computer in order to stimulate a virtuous cycle. The timing of this milestone again depends not only on device scaling but also on finding
an application that can run on a NISQ computer; thus, the time frame is more difficult to project.
7.3.6 Large Modular Quantum Computer (Milestone G4)
At some point, the current approaches to scaling the number of qubits, discussed in Chapter 5, will reach practical limits. For superconducting qubits in gate-based machines, this will likely manifest as a practical inability to manage the control lines required to operate a device above a certain size threshold—in particular, to pass them through the cryostat within which the device is contained. Superconducting qubit-based annealers have already addressed this issue through the integration of the control and qubit planes, albeit with a trade-off in qubit fidelity; some of these engineering strategies could potentially inform those for gate-based systems. For trapped ions, this is likely to manifest as the complexity in the optical systems used to deliver the control signals, or the practical challenge to control the motional degree of freedom for the ions as the size of the ion crystal grows. These limits are likely to be reached for both superconducting and trapped-ion gate-based technologies when the number of physical qubits grows to around 1,000, or six doublings from now. Similar limitations arise for all large engineered systems. As a result, many complex systems use a modular design approach: the final system is created by connecting a number of separate, often identical modules, each in turn often built by assembling a set of even smaller modules. This approach, which is shown in Figure 7.5, enables the number of qubits in a computer to scale by increasing the number of quantum data plane modules it contains.
There are a large number of system issues that would need to be solved before these large-scale machines could be realized. First, owing
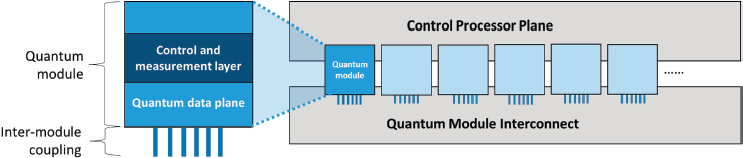
to space constraints, it is likely that the control and measurement layer will need to be integrated into a quantum module, as has been done in large quantum annealers to achieve cold control electronics (at the cost of increased noise). Thought must also be given to strategies for debugging and repairing individual modules, since in a large machine some modules are likely to break; for systems that run at very cold temperatures, a faulty module would require warming, repair, and recooling—a time- and energy-intensive process that would disrupt the entire machine. In addition to these module- and system-level challenges, two key interconnection challenges must be addressed to enable this type of modular design. The first is creating a robust mechanism for coupling quantum states contained in different modules at low error rates, since gate operations must be supported between qubits in different modules. The second is to create an interconnection architecture and module size that maximizes the overall performance while minimizing the cost of building the machine, since these module connections are difficult to create with sufficiently low error rates. Since the dominant algorithm that will be run on any error-corrected quantum computer is QEC, efficient execution of QEC is expected to drive many of these design trade-offs. Last, it is highly likely that such systems will be large and energy intensive. Needless to say, it is too early to anticipate how these challenges might be overcome, as other near-term challenges remain the immediate bottleneck to progress.
7.3.7 Milestone Summary
The time to create a large fault-tolerant quantum computer that can run Shor’s algorithm to break RSA 2048, run advanced quantum chemistry computations, or carry out other practical applications likely is more than a decade away. These machines require roughly 16 doublings of the number of physical qubits, and 9 halvings of qubit error rates. The qubit metrics and quantum computing milestones introduced in this chapter can be used to help track progress toward this goal. As more experimental data becomes available, the extracted metrics will allow for short-term predictions about the number and error rates of future machines, and later, the number of logical qubits they will contain. The milestones are useful for tracking some of the larger issues that affect this rate of progress, since they represent some of the larger hurdles that need to be crossed to create a large fault tolerant quantum computer. Table 7.1 summarizes the milestone machines, the advances they required, and information on timing.
TABLE 7.1 Key Milestones along the Path to a Large-Scale, Universal, Fault-Tolerant Quantum Computer
| Milestone | Technical Advances Required | Expected Time Frames |
|---|---|---|
| A1—Experimental quantum annealer | N/A | Systems of this type already exist. |
| G1—Small (tens of qubits) computer | N/A | Systems of this scale already exist. |
| G2a—Gate-based quantum computer that demonstrates quantum supremacy |
|
There are active efforts to create these machines in 2018. The community expects these machines to exist by the early 2020s, but their exact timing is uncertain. The timing depends on both hardware progress and the ability of classic hardware to simulate these machines. |
| A2—Quantum annealer that demonstrates quantum supremacy |
|
Unknown. |
| Milestone | Technical Advances Required | Expected Time Frames |
|---|---|---|
| G2b—Implementation of QEC for improved qubit quality |
|
Similar timing to G2a machines. Might be available earlier, if simulation techniques on classical machines continue to improve. |
| A3/G3—Commercially useful quantum computer |
|
Funding of QC will likely be impacted if this milestone is not available in mid- to late 2020s. The actual timing depends on the application, which is currently unknown. |
| G4—Large (>1,000 qubits), fault-tolerant, modular quantum computer |
|
Timing unknown, since current research is focused on achieving robust internal logic rather than on linking modules. |
7.4 QUANTUM COMPUTING R&D
Regardless of the exact time frame or prospects of a scalable QC, there are many compelling reasons to invest in quantum computing R&D, and this investment is becoming increasingly global. QC is one element (perhaps the most complex) of a larger field of quantum technology. Since the different areas in quantum technology share common hardware components, analysis methods, and algorithms, and advances in one field may often be leveraged in another, funding for all quantum technology is often lumped together. Quantum technology generally includes quantum sensing, quantum communication, and quantum computing. This section examines the funding for research in this area, and the benefits from this research.
7.4.1 The Global Research Landscape
Publicly funded U.S. R&D efforts in quantum information science and technology are largely comprised of basic research programs and proof-of-concept demonstrations of engineered quantum devices.12 Recent initiatives launched by the National Science Foundation (NSF) and the Department of Energy (DOE) add to the growing framework of research funded by the National Institute of Standards and Technology (NIST), the Intelligence Advanced Research Projects Activity (IARPA), and the Department of Defense (DOD). The latter agency’s efforts include the Air Force Office of Scientific Research (AFOSR), the Office of Naval Research (ONR), the Army Research Office (ARO), and the Defense Advanced Research Projects Agency (DARPA). There are now major efforts in quantum computing at several national laboratories and nonprofit organizations in the United States [19]. These publicly funded efforts are being amplified by growing interest from industry in quantum engineering and technology, including significant efforts at major publicly traded companies [20]. A number of startup companies, funded by private capital, have been created and are growing in this space [21].
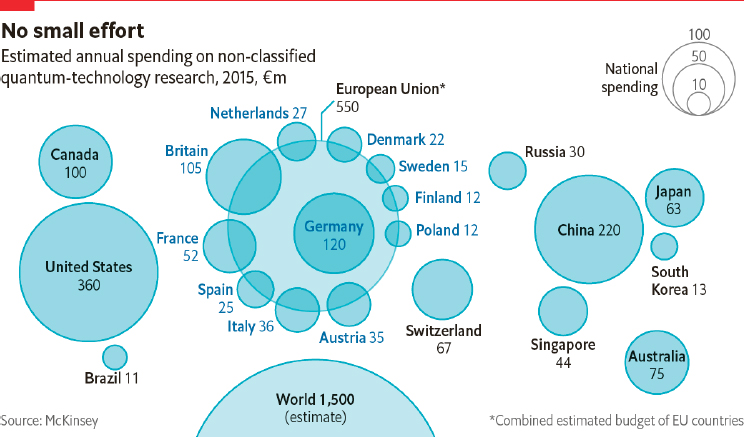
While U.S. R&D in quantum science and technology are substantial, the true scale of such efforts is global. A 2015 report from McKinsey corporation placed global nonclassified investment in R&D in quantum technology at €1.5 billion ($US1.8 billion), distributed as indicated in Figure 7.6.
This large international funding is likely to grow as a result of a number of several noteworthy non-U.S. national-level programs and
___________________
12 The funding efforts described in this section are for quantum information science and technology, which is broader than QC; the data is aggregated such that levels for QC in particular cannot be extracted.
initiatives in quantum information science and technology (QIST) that have been announced recently, which may reshape the research landscape in years to come. These initiatives, summarized in Table 7.2, and described in Appendix E, illustrate the commitment of the corresponding governments to leadership in QIST writ large. In general, they span a range of subfields, and are not focused on quantum computing exclusively. As of the time of this writing, the United States had released a National Strategic Overview for Quantum Information Science, emphasizing a science-first approach to R&D, building a future workforce, deepening engagement with industry, providing critical infrastructure, maintaining national security and economic growth, and advancing international cooperation [22]. Several pieces of legislation for a national quantum initiative have been introduced and advanced in the U.S. Senate and House of Representatives.
TABLE 7.2 Publicly Announced National and International Initiatives in Quantum Science and Technology Research and Development, as of Mid-2018
| Nation(s) | Initiative | Year Announced | Investment, Time Frame | Scope |
|---|---|---|---|---|
| United Kingdom | UK National Quantum Technologies Program | 2013 | £270 million (US$358 million) over 5 years, beginning in 2014 | Sensors and metrology, quantum enhanced imaging (QuantIC), networked quantum information technologies (NQIT), quantum communications technologies |
| European Union | Quantum Technologies Flagship | 2016 | €1 billion (US$1.1 billion) over 10 years; preparations under way; launch expected 2018 | Quantum communication, metrology and sensing, simulation, computing, and fundamental science |
| Australia | Australian Centre for Quantum Computation and Communication Technology | 2017 | $33.7 million (US$25.11 million) over seven years | Quantum communication, optical quantum computation, silicon quantum computation, and quantum resources and integration |
| Sweden | Wallenberg Center for Quantum Technology | 2017 | SEK 1 billion (US$110 million) | Quantum computers, quantum simulators, quantum communication, quantum sensors; sponsored by industry and private foundation |
| China | National Laboratory for Quantum Information Science | 2017 | 76 billion Yuan (US$11.4 billion); construction over 2.5 years | Centralized quantum research facility |
7.4.2 Importance of Quantum Computing R&D
The potential for building a quantum computer that could efficiently perform tasks that would take lifetimes on a classical computer—even if far off, and even though not certain to be possible—is a highly compelling prospect. Beyond potential practical applications, the pursuit of quantum computing requires harnessing and controlling the quantum world to an as yet unprecedented degree to create state spaces that humans have never had access to before, the so-called “entanglement frontier.” This work requires extensive engineering to create, control, and operate low-noise entangled quantum systems, but it also pushes at the boundaries of what we have known to be possible.
As QCs mature, they will be a direct test of the theoretical predictions of how they work, and of what kind of quantum control is fundamentally possible. For example, the quantum supremacy experiment is a fundamental test of the theory of quantum mechanics in the limit of highly complex systems. It is likely that observations and experiments on the performance of quantum computers throughout the course of QC R&D will help to elucidate the profound underpinnings of quantum theory and feed back into development and refinement of quantum theory writ large, potentially leading to unexpected discoveries.
More fundamentally, development of elements of the theories of quantum information and quantum computation have already begun to affect other areas of physics. For example, the theory of quantum error correction, which must be implemented in order to achieve fault-tolerant QCs, has proven essential to the study of quantum gravity and black holes [23]. Furthermore, quantum information theory and quantum complexity theory are directly applicable to—and have become essential for—quantum many-body physics, the study of the dynamics of systems of a large-number of quantum particles [24]. Advances in this field are critical for a precise understanding of most physical systems.
Advances in QC theory and devices will require contributions from many fields beyond physics, including mathematics, computer science, materials science, chemistry, and multiple areas of engineering. Integrating the knowledge required to build and make use of QCs will require collaboration across traditional disciplinary boundaries; this cross-fertilization of ideas and perspectives could generate new ideas and reveal additional open questions, stimulating new areas of research.
In particular, work on the design of quantum algorithms (required to make use of a quantum computer) can help to advance foundational theories of computation. To date, there are numerous examples of quantum computing research results leading directly to advances in classical computing via several mechanisms. First, approaches used for developing quantum algorithms have in some cases turned out to be translatable
to classical algorithms, yielding improved classical methods [25-27].13 Second, quantum algorithms research has yielded new fundamental proofs, answering previously open questions in computer science [28-31].14 Last, progress in quantum computing can be a unique source of motivation for classical algorithm researchers; discovery of efficient quantum algorithms has spurred the development of new classical approaches that are even more efficient and would not otherwise have been pursued [32-35].15 Fundamental research in quantum computing is thus expected to continue to spur progress and inform strategies in classical computing, such as for assessing the safety of cryptosystems, elucidating the boundaries of physical computation, or advancing methods for computational science.
Progress in technology has always gone hand-in-hand with foundational research, as the creation of new cutting-edge tools and methods provides scientists access to regimes previously not accessible, leading to new discoveries. For example, consider how advances in cooling technologies led to the discovery of superconductivity; the engineering of high-end optical interferometers at LIGO enabled the observation of gravitational waves; the engineering of higher-performance particle accelerators enabled the discovery of quarks and leptons. Thus, QC R&D could lead to technologies—whether component technologies or QCs themselves—that similarly enable new discoveries or advances in a host of scientific disciplines, such as physics, chemistry, biochemistry, and materials science. These in turn enable future advances in technology. As with all foundational science and engineering, the future impacts of this work are not easily predictable, but they could potentially offer transformational change and significant economic benefits.
___________________
13 See, for example, quantum-inspired improvements in classical machine learning (Wiebe et al., 2015) and optimization algorithms (Zintchenko et al., 2015).
14 For example, the quantum approximate optimization algorithm (QAOA), while no more efficient than classical approaches, has a performance guarantee for a certain type of problem that researchers were able to prove formally—something never achieved previously for any approach to this type of problem (Farhi et al., 2014). In another instance, properties of quantum computers were critical to proving the power of certain types of classical computers (Aaronson, 2005). In a third example, an argument based upon quantum computing was used to prove for the first time that a classical coding algorithm called a “two-query locally decodable code” cannot be carried out efficiently (Kerenidis et al., 2004).
15 For example, the discovery of an efficient quantum algorithm for a linear algebra problem called MaxE3Lin2 (Farhi et al., 2014) spurred computer scientists to develop multiple new, more efficient classical approaches to the same problem (Barak et al., 2015; Hastad, 2015). These results in turn spurred improvement of the quantum approach, although the classical approaches remain more efficient. In another example, an undergraduate student discovered a classical algorithm whose performance matched that of an important quantum algorithm, providing exponential speedup over all previous classical approaches. (Hartnett, 2018).
Key Finding 6: Quantum computing is valuable for driving foundational research that will help advance humanity’s understanding of the universe. As with all foundational scientific research, discoveries in this field could lead to transformative new knowledge and applications.
In addition to its strength as a foundational research area, quantum computing R&D is a key driver of progress in the field of quantum information science (QIS) more broadly, and closely related to progress in other areas of quantum technology. The same types of qubits currently being explored for applications in quantum computing are being used to build precision clocks, magnetometers, and inertial sensors—applications that are likely to be achievable in the near term. Quantum communication, important both for intra- and intermodule communication in a quantum computer, is also a vibrant research field of its own; recent advances include entanglement distribution between remote qubit nodes mediated by photons, some over macroscopic distances for fundamental scientific tests, and others for establishing quantum connections between multiple quantum computers.
Work toward larger-scale quantum computers will require improvements in methods for quantum control and measurement, which will also likely have benefits for other quantum technologies. For example, advanced quantum-limited parametric amplifiers in the microwave domain, developed recently for measuring superconducting qubits in QC systems, are used to achieve unprecedented levels of sensitivity for measuring nonclassical states of microwave fields (such as squeezed states), which have been explored extensively for achieving sensitivities beyond the standard limit in sensing and metrology [36,37]. In fact, results from quantum computing and quantum information science have already led to techniques of value for other quantum technologies, such as quantum logic spectroscopy [38] and magnetometry [39].
Key Finding 7: Although the feasibility of a large-scale quantum computer is not yet certain, the benefits of the effort to develop a practical QC are likely to be large, and they may continue to spill over to other nearer-term applications of quantum information technology, such as qubit-based sensing.
Quantum computing research has clear implications for national security. Even if the probability of creating a working quantum computer was low, given the interest and progress in this area, it seems likely this technology will be developed further by some nation-states. Thus, all nations must plan for a future of increased QC capability. The threat to current asymmetric cryptography is obvious and is driving
efforts toward transitioning to post-quantum cryptography as described in Chapter 4.
Any entity in possession of a large-scale, practical quantum computer could break today’s asymmetric cryptosystems and obtain a significant signals intelligence advantage. While deploying post-quantum cryptography in government and civilian systems may help protect subsequent communications, it will not protect communications or data that have already been intercepted or exfiltrated by an adversary. Access to prequantum encrypted data in the post-quantum world could be of significant benefit to intelligence operations, although its value would very likely decrease as the time horizon to building a large-scale QC increases. Furthermore, new quantum algorithms or implementations could lead to new cryptanalytic techniques; as with cybersecurity in general, post-quantum resilience will require ongoing security research.
But the national security implications transcend these issues. A larger, strategic question is about future economic and technological leadership. Quantum computing, like few other foundational research areas, has a chance of causing dramatic changes in a number of different industries. The reason is simple: advances in classical computers have made computation an essential part of almost every industry. This dependence means that any advances in computing could have widespread impact that is hard to match. While it is not certain when or whether such changes will be enabled, it is nonetheless of strategic importance for the United States to be prepared to take advantage of these advances when they occur and use them to drive the future in a responsible way. This capability requires strong local research communities at the cutting edge of the field, to engage across disciplinary and institutional boundaries and to capitalize on advances in the field, regardless of where they originate. Thus, building and maintaining strong QC research groups is essential for this goal.
Key Finding 8: While the United States has historically played a leading role in developing quantum technologies, quantum information science and technology is now a global field. Given the large resource commitment several non-U.S. nations have recently made, continued U.S. support is critical if the United States wants to maintain its leadership position.
7.4.3 An Open Ecosystem
Historically, the unclassified quantum computing community has been collaborative, with results openly shared. Recently, several user communities have formed to share prototypical gate-based and annealing machines, including through remote or cloud access. For example, the USC-Lockheed-Martin Quantum Computing Center was the first shared
user facility, established in 2011 with a 128-qubit D-Wave One System, which currently operates a D-Wave 2X system. Another shared user facility, for a 512-qubit D-Wave Two quantum annealing system, was established at the Ames Research Center in 2013,16 and another was formed by the Quantum Institute at Los Alamos National Laboratory for a D-Wave 2X quantum annealing system.17 On the digital QC front, both Rigetti and IBM provide Web access to their gate-based computers. Anyone (e.g., students, researchers, members of the public) interested in implementing quantum logic on an actual device may create an account and remotely experiment with one of these systems, under the condition that the results of their experimentation also be made available to others to help advance the state of knowledge about and strategies for programming this hardware. Dozens of research papers have already emerged as a result of these collaborations [40].
Open research and development in quantum computing is not limited to hardware. Many software systems to support quantum computing are being developed and licensed using an open source model, where users are free to use and help improve the code [41]. There are a number of emerging quantum software development platforms pursuing an open source environment.18 Support for open quantum computing R&D has helped to build a community and ecosystem of collaborators worldwide, the results and advances of which can build upon each other. If this continues, this ecosystem will enable discoveries in quantum science and engineering—and potentially in other areas of physics, mathematics, and computation—advancing progress in foundational science and expanding humanity’s understanding of the building blocks of the physical world.
At the same time, the field of quantum computing is becoming increasingly globally competitive. As described in the previous section, several countries have announced large research initiatives or programs to support this work, including China, the UK, the EU, and Australia, and many are aiming to become leaders in this technology. This increased competition among nation-states or private sector entities for leadership in quantum computing could drive the field to be less open in publishing
___________________
16 This is a collaboration between Google, the USRA, and NASA Advanced Computing Division, currently in use to study machine learning applications.
17 The machine is called “Ising.” One of the aims of the facility is to develop an open network for the exchange of ideas, connecting users to enable collaboration and exploration of a range of applications of the system.
18 For example, Microsoft released the Quantum Development Kit and corresponding language Q# under an open source license to encourage broad developer usage and advancement in quantum algorithms and libraries. Other open source quantum software packages include ProjectQ developed at ETH Zurich, Quipper at Dalhousie University, and QISKit developed at IBM.
and sharing research results. While it is reasonable for companies to desire to retain some intellectual property, and thus not publish all results openly, reducing the open flow of ideas can have a dampening effect on progress in development of practical technologies and human capital.19
Key Finding 9: An open ecosystem that enables cross-pollination of ideas and groups will accelerate rapid technology advancement.
7.5 TARGETING A SUCCESSFUL FUTURE
Quantum computing provides an exciting potential future, but to make this future happen, a number of challenges will need to be addressed. This section looks at the most important ramifications of the potential ability to create a large fault-tolerant quantum computer and will end with a list of the key challenges to achieve this goal.
7.5.1 Cybersecurity Implications of Building a Quantum Computer
The main risk arising from the construction of a large general-purpose quantum computer is the collapse of the public-key cryptographic infrastructure that underpins much of the security of today’s electronic and information infrastructure. Defeating 2048-bit RSA encryption using the best known classical computing techniques on the best available hardware is utterly infeasible, as the task would require quadrillions of years [42]. On the other hand, a general-purpose quantum computer with around 2,500 logical qubits could potentially perform this task in no more than a few hours.20 As mentioned in Chapter 4, there are protocols for classical machines currently believed to be resistant to such attack—however, they are not widely deployed; and any stored data or communications encrypted with nonresilient protocols will be subject to compromise by any adversary with a sufficiently large quantum computer. As Chapter 4 explained, deploying a new protocol is relatively easy but replacing an old one is very hard, since it can be embedded in every computer, tablet, cell phone, automobile, Wi-Fi access point, TV cable box, and DVD player (as well as hundreds of other kinds of devices, some quite small and
___________________
19 While it is difficult to provide evidence of cases where the lack of dissemination of research results caused a technology to fail, there are cases that illustrate the contrapositive. For example, consider the wealth of applications developed by the thriving open-source software community, or the rapid development of the Internet after the launch of NSFNet (the original backbone of the civilian Internet) and subsequent commercial investments.
inexpensive). Since this process can take decades, it needs to be started well before the threat becomes available.
Key Finding 10: Even if a quantum computer that can decrypt current cryptographic ciphers is more than a decade off, the hazard of such a machine is high enough—and the time frame for transitioning to a new security protocol is sufficiently long and uncertain—that prioritization of the development, standardization, and deployment of post-quantum cryptography is critical for minimizing the chance of a potential security and privacy disaster.
7.5.2 Future Outlook for Quantum Computing
Our understanding of the science and engineering of quantum systems has improved dramatically over the past two decades, and with this understanding has come an improved ability to control the quantum phenomena that underlie quantum computing. However, significant work remains before a quantum computer with practical utility can be built. In the committee’s assessment, the key technical advances needed are:
- Decreased qubit error rates to better than 10–3 in many-qubit systems to enable QEC.
- Interleaved qubit measurements and operations.
- Scaling the number of qubits per processor while maintaining/improving qubit error rate.
- Development of methods to simulate, verify, and debug quantum programs.
- Creating more algorithms that can solve problems of interest, particularly at lower qubit counts or shallow circuit depths to make use of NISQ computers.
- Refining or developing QECCs that require low overhead; the problem is not just the number of physical qubits per logical qubit, but to find approaches that reduce the large overheads involved with implementing some operations on logical qubits (for example, T-gates or other non-Clifford gates in a surface code) take a very large number of qubits and steps to implement.
- Identifying additional foundational algorithms that provide algorithmic speedup compared to classical approaches.
- Establishing intermodule quantum processor input and output (I/O).
While the committee expects that progress will be made, it is difficult to predict how and how soon this future will unfold: it might grow slowly
and incrementally, or in bursts from unexpected innovation, analogous to the rapid improvement in gene sequencing that resulted from building “short read” machines. The research community’s ability to do this work in turn depends on the state of the overall quantum computing ecosystem, which will depend upon the following factors:
- Interest and funding levels in the private sector, which may in turn depend on
- Achievement of commercial benchmarks, especially the development of a useful near-term application for noisy intermediate-scale quantum computers that sustain private-sector investments in the field; and
- Progress in the field of quantum computing algorithms and the presence of marketable applications for QC devices of any scale.
- Availability of a sufficient level of government investment in quantum technology and quantum computing R&D, especially under the scenario that private-sector funding collapses.
- Availability of a multidisciplinary pipeline of scientists and engineers with exposure to systems thinking to drive the R&D enterprise.
- The openness of collaboration and exchange of ideas within the research community.
Over time, the state of progress in meeting the open technical challenges and the above nontechnical factors may be assessed while monitoring the status of the two doubling metrics defined earlier in this chapter. Regardless of when—or whether—the milestones identified in this chapter are achieved, continued R&D in quantum computing and quantum technologies promise to expand the boundaries of humanity’s scientific knowledge and will almost certainly lead to interesting new scientific discoveries. Even a negative result—such as proof that quantum supremacy cannot be achieved or that today’s description of quantum mechanics is incomplete or inaccurate—would help elucidate the limitations of quantum information technology and computing more generally, and would in itself be a groundbreaking discovery. As with all foundational scientific research, the results yet to be gleaned could transform our understanding of the universe.
7.6 NOTES
[1] See, for example, G. Kalai, 2011, “How Quantum Computers Fail: Quantum Codes, Correlations in Physical Systems, and Noise Accumulation,” preprint arXiv:1106.0485.
[2] J. Preskill, 2018, “Quantum Computing in the NISQ Era and Beyond,” preprint arXiv:1801.00862.
[3] Remarks from John Shalf, Gary Bronner, and Norbert Holtkamp, respectively, at the third open meeting of the Committee on Technical Assessment of the Feasibility and Implications of Quantum Computing.
[4] See, for example, A. Gregg, 2018, “Lockheed Martin Adds $100 Million to Its Technology Investment Fund,” The Washington Post, https://www.washingtonpost.com/business/economy/lockheed-martin-adds-100-million-to-its-technology-investmentfund/2018/06/10/0955e4ec-6a9e-11e8-bea7-c8eb28bc52b1_story.html;
M. Dery, 2018, “IBM Backs Australian Startup to Boost Quantum Computing Network,” Create Digital, https://www.createdigital.org.au/ibm-startup-quantumcomputing-network/;
J. Tan, 2018, “IBM Sees Quantum Computing Going Mainstream Within Five Years,” CNBC, https://www.cnbc.com/2018/03/30/ibm-sees-quantum-computing-goingmainstream-within-five-years.html;
R. Waters, 2018, “Microsoft and Google Prepare for Big Leaps in Quantum Computing,” Financial Times, https://www.ft.com/content/4b40be6c-0181-11e8-9650-9c0ad-2d7c5b5;
R. Chirgwin, 2017, “Google, Volkswagen Spin Up Quantum Computing Partnership,” The Register, https://www.theregister.co.uk/2017/11/08/google_vw_spin_up_quantum_computing_partnership/;
G. Nott, 2017, “Microsoft Forges Multi-Year, Multi-Million Dollar Quantum Deal with University of Sydney,” CIO, https://www.cio.com.au/article/625233/microsoftforges-multi-year-multi-million-dollar-quantum-computing-partnership-sydney-university/;
J. Vanian, 2017, “IBM Adds JPMorgan Chase, Barclays, Samsung to Quantum Computing Project,” Fortune, http://fortune.com/2017/12/14/ibm-jpmorgan-chase-barclaysothers-quantum-computing/;
J. Nicas, 2017, “How Google’s Quantum Computer Could Change the World,” Wall Street Journal, https://www.wsj.com/articles/how-googles-quantum-computer-could-change-the-world-1508158847;
Z. Thomas, 2016, “Quantum Computing: Game Changer or Security Threat?,” BBC News, https://www.bbc.com/news/business-35886456;
N. Ungerleider, 2014, “IBM’s $3 Billion Investment in Synthetic Brains and Quantum Computing, Fast Company, https://www.fastcompany.com/3032872/ibms-3-billioninvestment-in-synthetic-brains-and-quantum-computing.
[5] Committee on Science, U.S. House of Representatives, 105th Congress, 1998, “Unlocking Our Future: Toward a New National Science Policy,” Committee Print 105, http://www.gpo.gov/fdsys/pkg/GPO-CPRT-105hprt105-b/content-detail.html.
[6] L.M. Branscomb and P.E. Auerswald, 2002, “Between Invention and Innovation—An Analysis of Funding for Early-Stage Technology Development,” NIST GCR 02-841, prepared for Economic Assessment Office Advanced Technology Program, National Institute of Standards and Technology, Gaithersburg, Md.
[7] See, for example, Intel Corporation, 2018, “2018 CES: Intel Advances Quantum and Neuromorphic Computing Research,” Intel Newsroom, https://newsroom.intel.com/news/intel-advances-quantum-neuromorphic-computing-research/;
Intel Corporation, 2017, “IBM Announces Advances to IBM Quantum Systems and Ecosystems,” IBM, https://www-03.ibm.com/press/us/en/pressrelease/53374.wss;
J. Kelly, 2018, “A Preview of Bristlecone, Google’s New Quantum Processor,” Google AI Blog, https://ai.googleblog.com/2018/03/a-preview-of-bristlecone-googles-new.html.
[8] Current performance profiles for IBM’s two cloud-accessible 20-qubit devices are published online: https://quantumexperience.ng.bluemix.net/qx/devices.
[9] See Standard Performance Evaluation Corporation, https://www.spec.org/.
[10] See, for example, B. Jones, 2017, “20-Qubit IBM Q Quantum Computer Could Double Its Predecessor’s Processing Power,” Digital Trends, https://www.digitaltrends.com/computing/ibm-q-20-qubits-quantum-computing/;
S.K. Moore, 2017, “Intel Accelerates Its Quantum Computing Efforts With 17-Qubit Chip,” IEEE Spectrum, https://spectrum.ieee.org/tech-talk/computing/hardware/intel-accelerates-its-quantum-computing-efforts-with-17qubit-chip.
[11] See, for example, Rigetti, “Forest SDK,” http://www.rigetti.com/forest.
[12] N.M. Linke, S. Johri, C. Figgatt, K.A. Landsman, A.Y. Matsuura, and C. Monroe, 2017, “Measuring the Renyi Entropy of a Two-Site Fermi-Hubbard Model on a Trapped Ion Quantum Computer,” arXiv:1712.08581.
[13] N. Friis, O. Marty, C. Maier, C. Hempel, M. Holzapfel, P. Jurcevic, M.B. Plenio, M. Huber, C. Roos, R. Blatt, and B. Lanyon, 2018, “Observation of Entangled States of a Fully Controlled 20-Qubit System,” https://arxiv.org/pdf/1711.11092.pdf.
[14] T. Simonite, 2018, “Google, Alibaba Spar Over Timeline For ‘Quantum Supremacy,’” Wired, https://www.wired.com/story/google-alibaba-spar-over-timeline-forquantum-supremacy/.
[15] See, for example, J. Kahn, 2017, “Google’s ‘Quantum Supremacy’ Moment May Not Mean What You Think,” Bloomberg, https://www.bloomberg.com/news/articles/2017-10-26/google-s-quantum-supremacy-moment-may-not-mean-whatyou-think;
P. Ball, 2018, “The Era of Quantum Computing Is Here. Outlook: Cloudy,” Quanta Magazine, https://www.quantamagazine.org/the-era-of-quantum-computing-is-hereoutlook-cloudy-20180124/.
[16] T.F. Rønnow, Z. Wang, J. Job, S. Boixo, S.V. Isakov, D. Wecker, J.M. Martinis, D.A. Lidar, and M. Troyer, 2014, Defining and detecting quantum speedup, Science 345(6195):420-424.
[17] In this case, D-Wave demonstrated a constant speedup for an abstract problem optimized to the machine. See S. Mandrà and H.G. Katzgraber, 2017, “A Deceptive Step Towards Quantum Speedup Detection,” arXiv:1711.01368.
[18] A.G. Fowler, M. Mariantoni, J.M. Martinis, and A.N. Cleland, 2012, “Surface Codes: Towards Partical Large-Scale Quantum Computation,” https://arxiv.org/ftp/arxiv/papers/1208/1208.0928.pdf.
[19] Quantum Computing Report, “Government/Non-Profit,” https://quantumcomputingreport.com/players/governmentnon-profit/.
[20] Quantum Computing Report, “Public Companies,” https://quantumcomputingreport.com/players/public-companies/.
[21] Quantum Computing Report, “Private/Startup Companies,” https://quantumcomputingreport.com/players/privatestartup/.
[22] Office of Science and Technology Policy, 2018, National Strategic Overview for Quantum Information Science, https://www.whitehouse.gov/wp-content/uploads/2018/09/National-Strategic-Overview-for-Quantum-Information-Science.pdf.
[23] D. Harlow, 2018, “TASI Lectures on the Emergence of Bulk Physics in AdS/CFT,” arXiv:1802.01040.
[24] G.K.L. Chan, A. Keselman, N. Nakatani, Z. Li, and S.R. White, 2016, Matrix product operators, matrix product states, and ab initio density matrix renormalization group algorithms, Journal of Chemical Physics 145(1):014102.
[25] N. Wiebe, A. Kapoor, C. Granade, and K.M. Svore, 2015, “Quantum Inspired Training for Boltzmann Machines,” preprint arXiv:1507.02642.
[26] I. Zintchenko, M.B. Hastings, and M.Troyer, 2015, From local to global ground states in Ising spin glasses, Physical Review B 91(2):024201.
[27] G.K.L. Chan, A. Keselman, N. Nakatani, Z. Li, and S.R. White, 2016, Matrix product operators, matrix product states, and ab initio density matrix renormalization group algorithms, Journal of Chemical Physics 145(1):014102.
[28] E. Farhi, J. Goldstone, and S. Gutmann, 2014, “A Quantum Approximate Optimization Algorithm,” preprint arXiv:1411.4028.
[29] S. Aaronson, 2005, Quantum computing, postselection, and probabilistic polynomial-time, Proceedings of the Royal Society of London A 461(2063):3473-3482.
[30] I. Kerenidis and R. De Wolf, 2004, Exponential lower bound for 2-query locally decodable codes via a quantum argument, Journal of Computer and System Sciences 69(3):395-420.
[31] S. Aaronson, 2006, Lower bounds for local search by quantum arguments, SIAM Journal on Computing 35(4):804-824.
[32] E. Farhi, J. Goldstone, and S. Gutmann, 2014, “A Quantum Approximate Optimization Algorithm Applied to a Bounded Occurrence Constraint Problem,” preprint arXiv:1412.6062.
[33] B. Barak, A. Moitra, R. O’Donnell, P. Raghavendra, O. Regev, D. Steurer, L. Trevisan, A. Vijayaraghavan, D. Witmer, and J. Wright, 2015, “Beating the Random Assignment on Constraint Satisfaction Problems of Bounded Degree,” preprint arXiv:1505.03424.
[34] J. Hastad, 2015, Improved Bounds for Bounded Occurrence Constraint Satisfaction, Royal Institute of Technology, Stockholm, Sweden.
[35] K. Hartnett, 2018, “Major Quantum Computing Advance Made Obsolete By Teenager,” Quanta Magazine, https://www.quantamagazine.org/teenager-finds-classicalalternative-to-quantum-recommendation-algorithm-20180731/.
[36] C. Macklin, K. O’Brien, D. Hover, M.E. Schwartz, V. Bolkhovsky, X. Zhang, W.D. Oliver, and I. Siddiqi, 2015, A near-quantum-limited Josephson traveling-wave parametric amplifier, Science 350(6258):307-310.
[37] A. Roy and M. Devoret, 2018, Quantum-limited parametric amplification with Josephson circuits in the regime of pump depletion, Physical Review B 98(4):045405.
[38] P.O. Schmidt, T. Rosenband, C. Langer, W.M. Itano, J.C. Bergquist, and D.J. Wineland, 2005, Spectroscopy using quantum logic, Science 309:749-752.
[39] J.R. Maze, P.L. Stanwix, J.S. Hodges, S. Hong, J.M. Taylor, P. Cappellaro, L. Jiang, et al., 2008, Nanoscale magnetic sensing with an individual electronic spin in diamond, Nature 455(7213):644.
[40] B. Sutor, 2018, “First IBM Q Hub in Asia to Spur Academic, Commercial Quantum Ecosystem,” IBM News Room, http://newsroom.ibm.com/IBM-research?item=30486.
[41] Quantum Computing Report, “Tools,” https://quantumcomputingreport.com/resources/tools/.
[42] digicert, “Check our Numbers,” https://www.digicert.com/TimeTravel/math.htm.





































