2
Quantum Computing: A New Paradigm
Computers today work by converting information to a series of binary digits, or bits, and operating on these bits using integrated circuits (ICs) containing billions of transistors. Each bit has only two possible values, 0 or 1. Through manipulations of these so-called binary representations, computers process text documents and spreadsheets, create amazing visual worlds in games and movies, and provide the Web-based services on which many have come to depend.
A quantum computer also represents information as a series of bits, called quantum bits, or qubits. Like a normal bit, a qubit can be either 0 or 1, but unlike a normal bit, which can only be 0 or 1, a qubit can also be in a state where it is both at the same time. When extended to systems of many qubits, this ability to be in all possible binary states at the same time gives rise to the potential computational power of quantum computing. However, the rules that govern quantum systems also make it difficult to take advantage of this power. How best to make use of quantum properties—and the nature of the improvements these properties make possible—is neither trivial nor obvious.
This chapter provides an introduction to some of the unique properties of the quantum world, showing how some provide computational advantages while others constrain the ability to use these advantages. The mechanisms for manipulating classical and quantum bits are compared and contrasted to illustrate the unique challenges and benefits of quantum computing. The chapter concludes by describing the types of quantum computers currently being pursued by researchers, providing a first look at the progress that will be assessed in the chapters to follow.
2.1 THE NONINTUITIVE PHYSICS OF THE QUANTUM WORLD
Originally introduced in the early 20th century, quantum mechanics is one of the most well-tested models for explaining the physical world. The theory—that is, the underlying abstract rules and their mathematical representations—describes the behavior of particles at very small distances and energy scales. These properties are the basis for understanding the physical and chemical properties of all matter. Quantum mechanics provides the same observable and intuitive results we expect for large objects, but its descriptions of the small-scale behavior of subatomic particles, although accurate, are exotic and nonintuitive.1
According to the theory, a quantum object does not generally exist in a completely determined and knowable state. In fact, each time one observes a quantum object it looks like a particle, but when it is not being observed it behaves like a wave. This so-called wave-particle duality leads to many interesting physical phenomena.
For example, quantum objects can exist in multiple states all at once, with each of the states adding together and interfering like waves to define the overall quantum state. In general, the state of any quantum system is described in terms of “wave functions.” In many cases, the state of a system can be expressed mathematically as a sum of the possible contributing states,2 each scaled by a complex number3 coefficient that reflects the relative weight of the state. Such states are said to be “coherent,” because the contributing states can interfere with each other constructively and destructively, much like wavefronts.4
However, when one attempts to observe a quantum system, only one of its components is observed, with a probability proportional to the square of the absolute value of its coefficient. To an observer, the system
___________________
1 This simple overview of quantum phenomena is intended to provide context for discussion of quantum computing. The foundational theory and scientific history of the field are fascinating and extensive, and beyond the ability of this report to fully convey. The committee refers the interested reader to the following reference for additional explanation and discussion of quantum mechanical phenomena: N.D. Mermin, 1981, “Quantum Mysteries for Anyone,” Journal of Philosophy 78(7):397-408.
2 Strictly speaking, each of the contributing states is also called a “wave function”; the state of any coherent quantum system is defined by a wave function.
3 The wave-like nature of the wave function means that the coefficients can describe both the amplitude and phase of this state. In this usage, “complex” means a number that is represented by two real numbers, one defining the amplitude, and the other the phase. This is often represented as Aei θ, where A is the amplitude, and θ is the phase shift. A phase shift of π/2 or 90 degrees is written as i and a phase shift of π or 180 degrees is −1.
4 Quantum systems that are not fully coherent must be represented using a “density matrix,” which defines the classical probability that a system is in any particular quantum state—in this case, the possible contributing states do not interfere with each other.
will always look classical when measured. Observation of a quantum object (or quantum system—that is, a system of quantum objects), formally called “measurement,” occurs when the object interacts with some larger physical system that extracts information from it. Measurement fundamentally disrupts a quantum state: it “collapses” the aspect of wave function that was measured into a single observable state, resulting in a loss of information. After the measurement, the quantum object’s wave function is that of the state that was detected, rather than that of its premeasurement state.
To visualize this, consider an ordinary coin on a table-top. In the classical world that we experience daily, its state is either heads-up (U) or heads-down (D). A quantum version of a coin would exist in a combination, or “superposition,” of both states at the same time. The wave function of a quantum coin could be written as a weighted sum of both states, scaled by coefficients CU and CD. However, an attempt to observe the state of a quantum coin will result in finding it to be only heads up or heads down—upon measurement, it will be in only one of the two states, with a probability proportional to the square of the corresponding coefficient.
Because a pair of conventional coins has four possible states (UU, UD, DU, and DD), a pair of quantum coins could exist as a superposition of these four conventional states, each weighted by its own coefficient, CUU, CUD, CDU, CDD—and so on for larger collections of quantum coins.
Upon measurement, a pair of quantum coins will appear like a pair of classical coins—in only one of the four possible configurations on the table-top. Similarly, a system of n quantum coins will only ever be observed to be in one of its 2n possible states.
Under some circumstances, two or more quantum objects in a system can be intrinsically linked such that measurement of one dictates the possible measurement outcomes for another, regardless of how far apart the two objects are. The property underlying this phenomenon, known as “entanglement,” is key to the potential power of quantum computing.
The evolution of any quantum system is governed by the Schrödinger equation, which relates how the wave function of the system changes given the energy environment that it experiences. This environment is defined by the so-called Hamiltonian of the system, a mathematical representation of the energies resulting from all forces felt by all elements of the system.5 In order to control a quantum system, one must therefore carefully control its energy environment, both by isolating the system from
___________________
5 Strictly speaking, the Hamiltonian is the mathematical description of the environment, which, for a quantum-mechanical system, takes the form of an operator. However, the term is often also used to refer to the environment itself; this convention may also be used in this report.
the rest of the universe (which contains forces not easily controlled), and by deliberately applying energy fields within the isolation region to elicit a desired behavior. In practice, complete isolation is impossible, although interactions with the environment can be minimized; the quantum system will ultimately exchange some energy and information with the broader environment over time, a process known as “decoherence.” This can be thought of as the environment continually making small random measurements on the system, each of which causes a partial collapse of the wave function.
The unique properties described above, and summarized in Box 2.1, were revealed through foundational scientific discovery. When carefully controlled, these intrinsic characteristics of matter also present new potential paradigms for engineering—in particular, for encoding, manipulating, and transferring information.
2.2 THE LANDSCAPE OF QUANTUM TECHNOLOGY
Over the past several decades, significant progress has been made in R&D for controlling and harnessing the power of quantum systems, revealing the potential for transformative quantum technologies. While the field of quantum computing has been perhaps most visible in the public eye, it is important to recognize that the range of applications of quantum phenomena is broader than quantum computing alone. Under the general heading of quantum information science, the fields of quantum communication and networking, and quantum sensing and metrology are also thriving areas of foundational scientific research with distinct technological objectives. While these fields are at differing levels of technological maturity, the boundaries between them are not always easily defined, because all of the fields are based upon the same underlying phenomena and face many of the same challenges [1]. They all make use of the unique properties of quantum systems, are based upon the same underlying physical theory, and share many common hardware and laboratory techniques. As a result, their progress is mutually dependent. For a rough sense of research output in each of these areas, one may examine the number of published research papers produced over time. Research trends for quantum computing and algorithms, quantum communications, and quantum sensing and metrology are illustrated in Figure 2.1.6
The field of quantum information science generally explores how information can be encoded in a quantum system, including the associated statistics, limitations, and unique affordances of quantum mechanics.
___________________
6 See Appendix E for a discussion of research efforts by nation of origin.
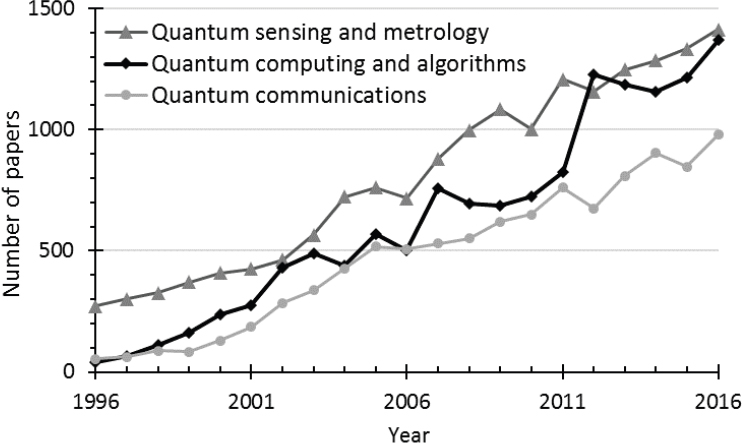
This area provides much of the foundation for quantum computing, communications, and sensing.
R&D in quantum communication focuses on the transport or exchange of information by encoding it into a quantum system. Quantum communication protocols are likely to be necessary for quantum computing—whether to transport information from one part of quantum computer hardware to another, or to enable communication between quantum computers. A subfield of quantum communication is quantum cryptography, in which quantum properties are used to design communication systems that may not be eavesdropped upon by an observer.7
___________________
7 The most prominent example is quantum key distribution (QKD), a quantum measurement-based method of distributing cryptographic keys to use for standard (classical) encryption of data sent over classical communication channels. The best-known protocol, called BB84, was developed by Charlie Bennett and Gilles Brassard in 1984. This protocol has been experimentally deployed both via fiber optic cables and via satellite. It has even led to several companies and commercial products. While QKD and quantum cryptography in general do not remove the risk of side channel attacks and are currently more expensive than classical methods to deploy, theoretical and experimental research continues to advance.
Quantum sensing and metrology involve the study and development of quantum systems whose extreme sensitivity to environmental disturbances can be exploited in order to measure important physical properties (such as magnetic fields, electric fields, gravity, and temperature) with more precision than is possible with classical technologies. Quantum sensors are commonly based upon qubits and are implemented using many of the same physical systems8 used in experimental quantum computers.
Quantum computing, the primary focus of this report, leverages the quantum mechanical properties of interference, superposition, and entanglement to perform computations that are roughly analogous to (although they operate quite differently from) those performed on a classical computer. In general, a quantum computer is defined as a physical system that comprises a collection of coupled qubits that may be controlled and manipulated in order to implement an algorithm such that measurement of the system’s final state yields the answer to a problem of interest with a high probability. The qubits of a quantum computer themselves must be sufficiently isolated from the environment for their quantum state to remain coherent for the duration of a computation.
Finding: Research in quantum mechanics has already led to fundamental advances in physics and to promising new technologies—for example, in quantum sensing. Such advances and applications are likely to drive further work that will help to deepen human knowledge of quantum phenomena and lead to improved methods for quantum engineering.
The foundations of classical and quantum computing are compared in the remainder of this chapter, in order to illustrate the fundamental differences between their components, and to provide a basic overview of the properties of quantum computation.
2.3 BITS AND QUBITS
In order to provide insight into how quantum properties enable a new computing paradigm, and how to meet the ensuing challenges, this section provides a brief overview of the foundations of classical computing, including how machines process information, which is represented by bits. The analogous quantum systems are then presented, and their properties compared and contrasted.
___________________
8 For example, trapped ions, superconducting circuits, neutral atoms, nitrogen vacancies in diamond; these technologies are discussed in more detail later in this chapter and in Chapter 5.
2.3.1 Classical Computing: From Analog Signals to Bits and Digital Gates
The powerful classical computing systems that exist today are based upon a robust foundation of reliable physical components. Transistors, the basic building blocks for integrated circuits (ICs) in classical computers, communicate with each other through the use of electrical “signals.” These signals are “analog” in nature, which means that their values can change smoothly, as with temperature, or speed.9 In a circuit, transistors are connected via wires, which conduct the electrical signals from one device to the other. Unfortunately, these electrical signals also interact with their environment, and this interaction can disrupt or “perturb” their value. Such perturbation is called “noise,” and it can be broken down into two components. The first, “fundamental noise,” results from energy fluctuations arising spontaneously within any object that is above absolute zero in temperature. The second, “systematic noise,” results from signal interactions that in theory could have been modeled and corrected, but either were not modeled at all, were not modeled correctly, or were left deliberately uncorrected at the hardware level. This systematic noise arises from many sources. For example, abstractions are used to reduce design complexity, which is essential when creating complex systems. Yet these abstractions often introduce systematic noise, since by hiding implementation details, the designers do not know the precise details of the implementation they are using. Even when information hiding is not a problem, systematic noise still arises from manufacturing variations. While a designer can consider the nominal signal interactions, variations in the manufacturing process—which, as a matter of practice, is not perfectly precise—would create a system slightly different from the one designed. These residual differences also give rise to systematic noise. In order to work properly, a circuit must be robust to the noise these variations cause.
When a circuit is analog (that is, when small changes in its input or parameters cause small changes in its output) the effects of noise are usually additive, accumulating as a signal passes through each successive circuit. While the noise added at each stage may be small enough that it does not disrupt a given process, the cumulative noise can ultimately become large enough to affect the accuracy (or fidelity) of the result. Consequently, electronic analog computers were never very popular or very complex, and they fell out of use after the 1950s and 1960s.
To get around the noise problem with analog circuits, most ICs use transistors to create circuits which operate on digital, binary signals (called
___________________
9 By analogy, to get to 60 miles per hour in a car from a stop, the car’s speed continuously increases from 0 to 60 miles per hour and hits all speeds between those limits.
“bits”), rather than analog signals. These circuits, called “digital gates” or simply “gates,” view the electrical signal as a binary value, as either 0 or 1, rather than viewing it as a real number that changes smoothly from 0 to 1. Some gates, called “registers” or “memories,” store the value of a bit, while others process a number of input bit values to create a new output value. By restricting the set of values a signal can carry, gates can reject noise that was added to the signal, providing what is called “noise immunity.” This is achieved by treating all signals that have electrical values close to the nominal 0 level as a zero, and signals around the 1 level as a one, and provide an output value that doesn’t depend on the exact input voltage. Figure 2.2 shows the input/output relationship for an analog amplifier, and a digital logic gate (an inverter), which shows how the inverter is able to reject noise that is a third the size of the output swing.
Building ICs entirely out of digital gates simplifies the design process for digital systems significantly by creating a robust circuit framework that is insensitive to most fabrication or design variation. Thus, the designers can ignore all the circuit issues and think about gates simply as functions (known as Boolean functions) that take in binary values and output binary values. The kinds of functions that operate this way are completely
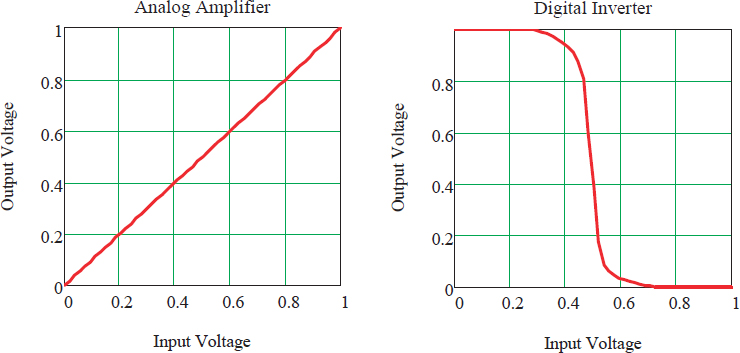
TABLE 2.1 Primitive Boolean Operations
| Boolean Operation | Inputs | Output | S mbolic Notation | |
|---|---|---|---|---|
| x | y | |||
| AND | 0 | 0 | 0 | x ∧ y |
| 0 | 1 | 0 | ||
| 1 | 0 | 0 | ||
| 1 | 1 | 1 | ||
| OR | 0 | 0 | 0 | x ∨ y |
| 0 | 1 | 1 | ||
| 1 | 0 | 1 | ||
| 1 | 1 | 1 | ||
| XOR | 0 | 0 | 0 | x ⊕ y |
| 0 | 1 | 1 | ||
| 1 | 0 | 1 | ||
| 1 | 1 | 0 | ||
| NOT | 0 | 1 | ~x | |
| 1 | 0 | |||
NOTE: Primitive Boolean operations, implemented through digital logic gates, are the building blocks of contemporary computation. A universal set of basis operations can be constructed from just two of these operations: NOT and one of either AND or OR.
described by the well-established rules of Boolean algebra. These rules describe how any complicated Boolean function can be decomposed into a small series of simpler operations, such as those listed in Table 2.1. This translation allows today’s hardware designers to describe their designs at a relatively high abstraction level and to use an automated design tool to map them to the required logic gates, a process called “logic synthesis.” Since the number of basic building blocks is limited, all IC manufacturers provide a set of predesigned and tested logic gates, their “standard cell library,” that may be incorporated into a chip’s design and built in silicon using their manufacturing technology.
Using both digital logic and standard libraries for these logic gates also makes designs robust—that is, they have negligible error rates. IC manufacturers provide checking tools that analyze a design to ensure that its systematic noise is smaller than the noise margin of their gates, ensuring that the logical abstraction can be implemented by the underlying components.
Even with the large noise margin in digital gates, noise can sometimes be large enough to disrupt the Boolean values stored in memories. To get
high density and high performance, these structures typically have larger device variations and smaller noise margins, so occasionally the noise is large enough to corrupt a digital output. To correct for this, a layer of error protection is added. The data is “encoded,” using an error correction code (ECC), adding some bits that add redundancy to the values stored in the memory. This code is checked on each read, making it possible to detect memory errors. Efficient ECCs have been developed that, with small overheads (adding 8 bits to a 64-bit value, which is <15 percent overhead), can detect and correct any single-bit error in a memory operation and detect double-bit errors. Efficient error correction schemes are critical to the success and reliability of today’s classical computing systems. This type of algorithmic error correction is even more important in quantum computing, since quantum gates have little intrinsic noise immunity, as the next section will show.
The digital design flow also helps with other aspects of the design, such as testing and removing errors from the design, a process generally called “debugging.” In ICs, there are two types of errors that need to be dealt with: design errors and manufacturing defects. Given the complexity of modern systems, errors (bugs) inevitably occur in the design, so methods to find these errors and correct them is a key aspect of any design strategy. When the circuit is integrated on a small piece of silicon, it is hard or impossible to look at internal signals to try to track the error. To mitigate this, the synthesis tools that map the high-level design description into gates add additional hardware to the design to provide internal test points that enable this type of design debugging. These internal test points also enable tools to automatically generate tests that can confirm that the manufactured chip performs the exact same Boolean function as specified in the design, greatly simplifying manufacturing tests.
As the next sections will show, while quantum computers have bit-like structures (called “qubits”) and gates, they behave very differently from classical bits and digital gates. The qubits possess both digital and analog character that provide their potential computational power. Their analog nature implies that unlike classical gates, the quantum gates have no noise margin (input errors are passed directly to output of the gate), but their digital nature provides a means to recover from this critical drawback. Thus, the digital design approach and abstractions developed for classical computing cannot be used directly for quantum computing. Quantum computing may borrow ideas from conventional computing; however, it will ultimately need its own method to mitigate the effects of processing variations and noise, and it will have to develop its own approach to debug design errors and manufacturing defects.
2.3.2 The Quantum Bit, or “Qubit”
When creating conventional ICs, designers take great pains to minimize the effect of quantum phenomena, which typically manifest as noise or other errors that affect transistor performance, especially as devices get smaller and smaller. Quantum computing in all its forms takes a very different approach by embracing rather than trying to minimize quantum phenomena, using quantum rather than classical bits.
A quantum bit, or qubit, has two quantum states, analogous to the classical binary states. While the qubit can be in either state, it can also exist in a “superposition” of the two (as described earlier in the example of a quantum coin). These states are often represented in so-called Dirac notation, where the state’s label is written between a | and a ⟩. Thus, a qubit’s two component, or “basis,” states are generally written as | 0 ⟩ and | 1 ⟩. Any given qubit wave function may be written as a linear combination of the two states, each with its own complex coefficient ai: | ψ⟩ = a0 | 0 ⟩+ a1 | 1 ⟩. Since the probability of reading a state is proportional to the square of its coefficient’s magnitude, | a0 | 2 corresponds to the probability of detecting the state | 0 ⟩, and | a1 | 2 to the probability of detecting | 1 ⟩. The sum of the probabilities of each possible output state must be one hundred percent, mathematically expressed in this case as | a0 | 2 + | a1 | 2 = 1.
While a classical bit is entirely specified either as 1 or 0, a qubit is specified by the continuum of the values a0 and a1, which are actually analog—that is, the relative contribution from each possible state can be any value between zero and one, provided the total probability is one. Of course, this richness exists before the qubit’s state is measured, or “read out.” The result of a measurement looks just like a classical bit, a 0 or a 1, with the associated probability of getting each value proportional to the square of the absolute value of the coefficient of the corresponding state, | a0| 2 or | a1| 2. Furthermore, upon measurement, the qubit’s coefficient (or amplitude) becomes one in the state that is read and zero in the other; all information about the amplitudes is destroyed upon measurement.10 Measurement outcomes for a single qubit are listed in Table 2.2 and explained in more detail in Box 2.2.
___________________
10 However, if one were to initialize a qubit in a specific state an arbitrary number of times, and measure it each time, one would be able to create a histogram of the number of times that a measurement yields each output, which would enable one to statistically approximate the relative probabilities associated with each state, and so infer the absolute value of the coefficient (equivalent to the square root of the calculated probability).
TABLE 2.2 Measurement Outcomes and Probabilities for a Single Qubit Given Its Initial State for Several Examples
| Premeasurement State (Wave function) of Qubit | Measurement Outcome | Probability of Outcome | Postmeasurement State of Qubit |
| | ψ⟩= | 0⟩ | 0 | 100% | | ψ⟩= | 0⟩ |
| | ψ⟩= | 1⟩ | 1 | 100% | | ψ⟩= | 1⟩ |
| 0 | 50% | | ψ⟩= | 0⟩ | |
| 1 | 50% | | ψ⟩= | 1⟩ | |
| 0 | 25% | | ψ⟩= | 0⟩ | |
| 1 | 75% | | ψ⟩= | 1⟩ | |
| 0 | 25% | | ψ⟩= | 0⟩ | |
| 1 | 75% | | ψ⟩= | 1⟩ |
2.3.3 Multiqubit Systems
Consider a system of two bits. Classically, two bits can exist in four possible configurations, 00, 01, 10, and 11. In order to compute the output of a two-bit Boolean function for each of these possible inputs using a classical circuit, one would need to generate each corresponding pair of signals, and either send each in turn into a gate corresponding to the function, or direct each signal into its own copy of four identical gates corresponding to the function of interest.
On the other hand, if one used a quantum computer, all four possibilities could be encoded into the state of the two qubits via superposition of the four quantum basis states | 00 ⟩, | 01 ⟩, | 10 ⟩, and | 11 ⟩. The computation could be executed using a single quantum gate, which would operate on all of the states in parallel, at the same time. It is easy to see why a multiqubit system might be powerful. However, as alluded to previously—and as the next two sections will show—extracting any corresponding value out of the quantum system is hard.
Another way to think about the potential power of a collection of qubits is to look at the amount of information needed to fully specify the state of the system of qubits. A conventional digital two-bit system requires two bits of information to represent its state. In contrast, a two-qubit system exists in a superposition of four states (| 00 ⟩, | 01 ⟩, | 10 ⟩, and | 11 ⟩), requiring four complex constants, (a00, a01, a10, and a11) to fully describe the quantum state, rather than two bits. Different values of the four coefficients encode the results of all possible types of previous operations done on these two qubits, as well as the probability of ending up in each state if the system is measured. For a three-qubit system, eight coefficients are required to specify to contributions from the basis states (| 000 ⟩, | 100 ⟩, | 010 ⟩, | 001 ⟩, | 110 ⟩, | 101 ⟩, | 011 ⟩, and | 111 ⟩) to the three-qubit wave function. Following this logic, an n-qubit system requires 2n coefficients, ai, to be specified, rather than n bits as in a classical computer. This exponential scaling of the quantum state is what allows 32 qubits to represent all 232 possible outputs of a 32-bit function and illustrates the richness of a quantum computer, and the difficulties in modeling these machines classically as they increase in size.
This view also points out that, while qubits have “bit” in their name, they are neither digital nor purely binary. The state of a qubit system is encoded in the ai coefficient values, a set of analog signals (actually complex numbers), which are not robust to noise. In a digital system with only two legitimate levels, say 0 and 1, it is easy to remove noise in the system, as the values will all be close to 0 or 1, with minor deviations. For example, an input signal value of 0.9 is almost certainly a 1, so a gate can “remove” the noise by treating this input value as a 1 before computing its output. In an analog signal, for which any value between 0 and 1 might
be meaningful and allowed, there is no way to know whether the signal is correct or if it has been corrupted by noise. For example, 0.9 could mean 1 with some error, or it could mean 0.9 with no error. In this situation, the best guess (that results in the smallest net error) is always to assume the error is zero and to treat the noisy value as the actual signal. This means that noise in a physical implementation of a qubit system perturbs the actual ai values and affects the “fidelity” of the resulting quantum computation. Quantum gates have no noise margins, since their inputs (the initial ai values) and their outputs (the final ai values) are analog values. Since no analog gate perfectly matches its specifications (it is impossible to be perfectly precise), each gate operation will also add noise to the overall system, in a quantity that depends on the precision of the gate operations.
Normally, this lack of noise immunity would mean that the “compute depth”—the number of sequential operations that can be performed accurately—of a quantum computer would be limited, as with any analog computer. However, quantum gates are not completely analog: measurement of a qubit always returns a binary value. This digital relationship between inputs and outputs means that logical error correction can be applied to quantum machines that use quantum gates as their basic operations. These algorithms are called quantum error correction (QEC) and can be run on a noisy, gate-based quantum computer to reduce errors and emulate a noiseless system. As with classical error correcting codes mentioned in Section 2.3.1, QEC must add redundancy, and in the quantum case this redundancy must be entangled with the rest of the system state, in order to recover from error. Unlike classical codes, which have small overheads, QEC codes tend to have very high overheads, and can increase the number of qubits required to execute an error-free computation by many orders of magnitude. QEC algorithms are described in more detail in Section 3.2.
2.4 COMPUTING WITH QUBITS
The analog nature of qubit states and quantum gates dramatically changes the necessary design approaches and circuit architectures for quantum computers. (See Figure 2.3.) In conventional computer design, the robustness of the digital signal and gates to noise make it easy to optimize the design for performance—that is, to maximize the number of operations that can be performed in parallel (at the same time). A single IC can contain hundreds of millions of gates placed in different locations. Each wire connects the output of a gate (a 1 or a 0) to the gates that use that electrical signal as an input. While manufacturing variations make each gate a little different, and the electrical signals on the wires can interact with and introduce systematic noise in each other, the noise immunity
of the digital gates used is sufficient to negate the effect of all these noise sources. Thus, even with the parallel operation of millions of gates, the resulting system behaves as intended, producing the same output as the Boolean model of the design.
Because quantum signals are analog and sensitive to noise, an entirely different approach is used in the design of quantum systems. Here, the key design goal is to minimize the introduction of noise into the qubit, which precludes sending the qubit state through noisy channels, such as a long wire.11 Thus, these systems generally focus on building qubits, or containers for the qubits, along with the associated support circuitry required to do various operations on the qubits’ states, including entangling qubits with other qubits in the same vicinity. In quantum systems, the operations (gates) tend to come to the qubits, while in classical machines, the bits go to the gates.
In addition to this difference in architecture, since quantum computers operate on different types of values than classical computers, they cannot use the same logical gate abstractions that were developed to manipulate classical bits. New abstractions for computations using qubits are required, providing a way to implement specified changes in quantum states. As with all quantum systems, the state of a qubit can be changed by changing its energy environment, which is the physical manifestation of its Hamiltonian.
There are two main approaches to quantum computing. The first generates the desired result by initializing the state of a quantum system and then using direct control of the Hamiltonian to evolve the quantum state in a way that has a high probability of answering the question of interest. In these systems, the Hamiltonian is often smoothly changed, so the quantum operations are truly analog in nature and cannot be fully error corrected,12 and will be referred to as “analog quantum computing.” This approach includes adiabatic quantum computing (AQC), quantum annealing (QA), and direct quantum simulation. The second approach, called “gate-based quantum computing,” is similar to today’s classical approaches, in that the problem is broken down into a sequence of a few very basic “primitive operations,” or gates, which have well-defined “digital” measurement outcomes for certain input states. This digital property means that these type of designs can in principle use system-level error
___________________
11 Qubits also must obey a no-cloning rule, which also precludes sending a qubit state to two different gates at the same time. This will be discussed further in Section 2.5.
12 While methods for reducing the effects of noise have been developed and deployed for analog QCs, a theory for analog QC QEC has been proposed only for AQC; this is not expected to be easily achieved, and full error correction would require boundless resources. Thus, no practical method of achieving an error-free machine has been established for analog QCs. These issues are addressed further in Section 3.2.
correction to achieve fault tolerance. However, as noted above, the set of primitive quantum operations are distinct from classical primitives.
2.4.1 Quantum Simulation, Quantum Annealing, and Adiabatic Quantum Computation
Analog quantum computing involves a system of qubits in an initial quantum state, and changes to the Hamiltonian such that the problem is encoded in the final Hamiltonian and the final state corresponds to the answer. If the system remains in the ground state of the changing Hamiltonian, this approach is referred to as adiabatic quantum computing (AQC). When this requirement is relaxed—for example, if the quantum computer is also allowed to interact with a thermal environment, or if it is allowed to evolve too quickly—this protocol is called “quantum annealing.” For a sufficiently complex choice of Hamiltonians, AQC is formally equivalent in computational power to the gate-based quantum computing model. For existing quantum annealing devices, the choice of Hamiltonians is limited, and these devices are not formally equivalent to universal quantum computers. Direct quantum simulation is where the Hamiltonian between qubits is set to model a quantum system of interest, so its evolution simulates that system.
As mentioned above, in these analog quantum computing approaches, not only are the values of the qubits analog but also the quantum operations are done by smoothly changing the Hamiltonian. This nondiscrete set of quantum operators confounds conventional approaches to system level error correction. While a model for QEC has been proposed for AQCs in particular [2], it would be challenging to implement in practice, since removing all errors would require unbounded resources. As a result, one tries to minimize the effect of noise in such systems via quantum error and noise suppression [3].
Decoherence plays a very different role in digital quantum computers and analog quantum computers. In digital quantum computers, decoherence is rarely desirable.13 In the case of an analog quantum computer—and, in particular, a quantum annealer—decoherence plays a more subtle role. On the one hand, energy relaxation (dissipation) is desirable, because it enables the system to find the ground state, as required for the method to yield correct outputs. For larger-scale problems, an annealer will almost certainly leave its ground state during the annealing protocol, either as a result of changing the Hamiltonian too quickly, or due to thermal excitation from the environment. In these cases, dissipation to the environment is clearly advantageous, as it tends to bring the annealer back to its
___________________
13 Except possibly during state preparation and projective measurement.
ground state. However, if there is too much dissipation, the system will no longer behave quantum mechanically and thus cease to be a quantum computer. Furthermore, phase coherence is also required for “coherent co-tunneling,” a quantum process that enables more efficient relaxation to the ground state through coordinated flipping of qubits. In practice, a balance must be achieved in order for annealers to be effective. Analog quantum computing is discussed in more detail in Chapters 3 and 5.
2.4.2 Gate-Based Quantum Computing
In a gate-based approach to quantum computing, each primitive operation (gate) is performed by precisely changing the Hamiltonian of one or more qubits for the specific amount of time required to achieve the desired transformation. This is done by changing the physical environment, for example, via a laser pulse or application of some other electromagnetic field, depending on the way in which the qubits are built.14 Since these primitive operations are analogous to logic gates in classical computing, systems built using this approach are called “digital quantum computers.”
The rules of quantum mechanics constrain the set of possible quantum gate operations in a few interesting ways. First, the operations must be “lossless”—that is, they must not dissipate any energy, since energy dissipation means that the system is connected to the environment to allow heat to flow out, which would result in unacceptable decoherence. Since losing information dissipates energy [4], quantum gates must be reversible, which means that not only can you compute the gate’s outputs from its inputs, you can also compute the gate’s inputs from its outputs (the gate’s computation can be run backward, or reversed). To be reversible, a function must always have as many outputs as it had inputs.
Second, while the operations will change the coefficients, or “amplitude distribution,” of the different possible states, the sum of the squares of their absolute values (the sum of their probabilities) always remains one. One mathematical way to visualize the operations of quantum gates is to represent the state of ‘n’ qubits as a vector in a high dimensional space (2n complex dimensions), where the value of the vector in each dimension is given by the complex coefficients ai. Conserving probability forces the length of the vector to be constant and equal to 1, so the state of the system can be any place on the unit hypersphere (the extension of a sphere to higher dimensions). All quantum gates are simple rotations of the state vector to a new position on the hypersphere. As the number
___________________
14 See Chapter 5 for further discussion of current approaches to physical implementations of qubits.
of qubits increases, the dimension of the space grows exponentially, but the state vector remains unit length, and the operations remain the different rotations possible on the hypersphere (which are all reversible). Operations that preserve the vector length are said to be “unitary.” Box 2.3 shows the sphere generated by a single qubit.
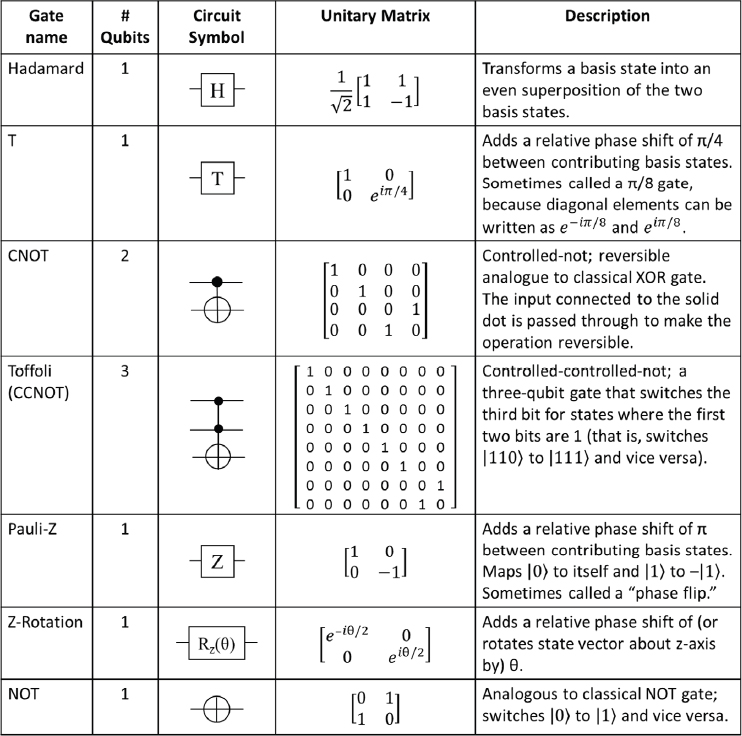
As with classical logic, gates with a large number of inputs are hard to create, but can be constructed, or “synthesized,” using a series of simpler gates, each of which takes a smaller number of inputs. In practice, quantum gates typically designed to operate on inputs of one, two, or three qubits. Also like classical logic, a small number of base quantum gates can be used to create all possible quantum gate functions. A common set of basic quantum gates and their representations is shown in Figure 2.4. Of particular significance is the Hadamard gate for superposition, which evolves a qubit in the | 0 ⟩ state to an equal superposition of | 0 ⟩ and | 1 ⟩, where both have the same relative phase ![]() and evolves the | 1 ⟩ state to an even superposition of | 0⟩ and | 1⟩, but with opposite phases
and evolves the | 1 ⟩ state to an even superposition of | 0⟩ and | 1⟩, but with opposite phases ![]() The two-qubit CNOT gate performs an XOR logic operation, but it must pass one of the inputs to the output to make the computation reversible.
The two-qubit CNOT gate performs an XOR logic operation, but it must pass one of the inputs to the output to make the computation reversible.
Because quantum gates map initial ais of a set of input qubits into a new set of ais, these gates are often written mathematically in the form of a matrix. In this representation, the ai for each of the input states are stacked on top of each other to form a vector, and the result of the matrix vector multiplication results in a vector which represents the ais of the output state. An n-input logic operation, or “gate,” can be described mathematically as a 2n × 2n unitary matrix that operates on n input qubits (encoding the initial 2n ais) producing n output qubits (encoding the 2n new ais).
It is known that the gates T, Hadamard, and CNOT, where T is a rotation by π/4 (90 degrees), forms a universal gate set [5] (that is, any unitary function can be approximated to arbitrary precision using a computer built from only gates in this set) [6].15
Unlike unitary operations that are the basis for implementing a quantum algorithm, the measurement operation strongly couples the quantum state to the measurement device, which produces a binary output and is
___________________
15 For rotation of a general angle θ, single-qubit rotations cannot be expressed exactly in this gate set; thus, it is necessary to decompose the desired operation into a sequence of operations. Such “decomposition” of a given operation into a sequence of simple gates also enables a general circuit to be compiled as a sequence of simpler primitive gates that can more easily be implemented in hardware. It is worth noting that known algorithms for some applications, for example in computational chemistry, rely heavily upon general angle rotations; for these cases in particular, it is thus very important to have methods which can create, or synthesize, these operations using a small number of primitive gate operations. Better synthesis algorithms generate the target gates from fewer primitive gates.
not reversible. Measurement is necessary in order to extract information from the quantum computer; however, measurement collapses the system wave function and returns only n bits of information from the n-qubit quantum register, that is, it returns one classical result. The information that was held in the ais of the 2n states that the register encoded up until the instant of measurement is lost. The outputs of measurement of a two-qubit system are illustrated in Table 2.3 and discussed in Box 2.4 [7].
2.5 QUANTUM COMPUTER DESIGN CONSTRAINTS
As alluded to in previous sections, the large potential power of a quantum computer comes with four major constraints. The first major constraint is that the number of coefficients required to describe a state of a quantum computer increases exponentially with the number of qubits only when the qubits all become entangled with each other. While adding a qubit to a system does double the number of quantum states, if this qubit has not interacted with the rest of the system, the description of the quantum state can be factored and represented as the product of the added qubit’s state, times the state of the rest of the system. This factored state requires only two additional coefficients (the state of the added qubit) compared to the original quantum system. To get the power of quantum computing, qubits must be entangled—that is, the state of any qubit must be correlated with the states of the other qubits. To form such a dependence between two qubits, they need to interact either directly or indirectly via an intermediate quantum system—whether a photon, phonon, or another qubit—which at some point interacts with each qubit to be entangled.16
Even though the generation of direct interaction between qubits that are physically separated (that is, nonadjacent) inside the quantum processor, like complex gates, can be hard to achieve,17 it can be decomposed into a number of simpler primitive gate operations directly supported by the hardware. This indirect coupling can be performed through a chain
___________________
16 If qubit A is entangled with qubit B, and at some later time qubit B becomes entangled with qubit C, it is likely that qubit A is now also entangled with qubit C. To see this, assume all qubits start in the | 0> state, and qubit A is then operated on by a Hadamard gate. It is the control input to a CNOT gate for qubit B, and qubit B is then the control terminal for qubit C. Measurement of A, B, or C will give zero 50 percent of the time, and one 50 percent of the time. But once one of the qubits is measured, the state of the other qubits will be known with 100 percent probability.
17 To prevent the qubit energy from coupling with the environment, it is held in localized, well-isolated spots. Distributing the energy over a wide area for two qubits to interact would also expose those qubits to a lot of environment, which in today’s technologies greatly shortens the coherence time.
TABLE 2.3 Measurement Outcomes and Probabilities for Some Possible States of a Two-Qubit System, Given Its Initial State
| Premeasurement State (Wave Function) of System | Measurement Outcome | Probability of Outcome | Postmeasurement State of System |
|---|---|---|---|
| | ψ〉 = | 00〉 | 00 | 100% | | ψ〉 = | 00〉 |
| | ψ〉 = | 01〉 | 01 | 100% | | ψ〉 = | 01〉 |
| 00 | 50% | | ψ〉 = | 00〉 | |
| 11 | 50% | | ψ〉 = | 11〉 | |
| 00 | 25% | | ψ〉 = | 00〉 | |
| 10 | 25% | | ψ〉 = | 10〉 | |
| 01 | 25% | | ψ〉 = | 01〉 | |
| 11 | 25% | | ψ〉 = | 11〉 | |
| 01 | 25% | | ψ〉 = | 01〉 | |
| 10 | 75% | | ψ〉 = | 10〉 |
of operations, using intermediate qubits or other quantum systems to facilitate the interaction. However, as in classical computing this indirect coupling creates an overhead in the machine, the first major design constraint. This cost of communication is well understood in classical computing and contributes to the very high gate counts in modern machines. In many quantum computing implementations, generating this long-range interaction will consume some of the qubits in the machine, and the number of useful qubits will be less than the number of physical qubits in the machine. This need to break down long-range interactions also means that some of the two-qubit operations taken from the universal gate set
will take multiple primitive gate operations to perform. These overheads are most significant in the early stages of a technology’s development when qubits and gate operations are limited.
A second constraint comes from the fact that it is impossible to make a copy of a quantum system, because of the so-called no-cloning principle [8,9]. While the state of a set of qubits can be moved to another set of qubits, this has the effect of deleting that information from the original qubits; arbitrary quantum information may be moved but not copied. Since making and storing copies of intermediate states or partial results in memory is an essential part of classical computing and the way we think about programming, quantum computers require a different approach to algorithm design. Also, computing tasks often require the ability to access stored data, and many quantum algorithms require a means to access stored classical bits in a way that reveals which bits are being queried and loaded into quantum memory.
The third main constraint comes from the lack of noise immunity of quantum operations. Since small imperfections in the input signals or gate operations are not removed by the basic gate operations, as they are in classical logic gates, these small errors will accumulate over time, perturbing the system’s state. These errors affect the accuracy of the calculation, and, when large enough, can lead to measurement errors, or even a loss of quantum coherence (and thus loss of any quantum advantage). This noise comes from imperfect isolation from the environment, uncorrected variations in physical preparation or manufacture of the qubits themselves (or the devices that contain or maintain them), and imperfections in the signals used to perform the desired qubit operations. Taken together, these imperfections generally degrade the quality of a qubit operation. These effects are still significant even when using strategies to minimize and avoid noise that leads to errors.
The quality of a gate operation is measured either by the error rate, defined by the probability that the gate operation yields an incorrect outcome, or by the fidelity, the probability that the operation yields the correct outcome (Box 2.5). For state-of-the-art systems in 2018, the best error rates are in the 10–3 to 10–6 range for single qubit gates [10-13] and in the 10–2 to 10–3 range for two qubit (entangling) gates [14-17] in superconducting and trapped ion qubits. In current machines, this quality degrades as the number of qubits in the machine increases; the capabilities of today’s systems are discussed in more detail in Chapter 5.
The final constraint is the inability to actually observe the full state of the machine after it has completed its operation. For example, if the quantum computer initializes a set of qubits into a superposition of all qubit-state combinations, and then applies a function to this input state, the resulting quantum state will have information about the value of
the function for each possible input value. Yet measuring this quantum system directly will not yield this information. Instead, since all the input cases were equally likely, the measurement will return only one of the 2n possible outputs. The key to a successful quantum algorithm is to manipulate the system so the states that correspond to the sought-after solution have much higher probability of being measured than any other possible output. This condition is intrinsic to quantum algorithm primitives such as the quantum Fourier transform and amplitude amplification, which are described in more detail in Chapter 3. These operations amplify the coefficient of the state whose index indicates the answer sought, such that the meaningful answer is highly likely to be observed in the readout measurement; however, they can require a nontrivial amount of time, reducing the overall speedup of the quantum algorithm.
The characteristics of quantum phenomena both provide a QC’s computational power, and greatly constrain how it can be used.
2.6 THE POTENTIAL FOR FUNCTIONAL QUANTUM COMPUTERS
As previously noted, computation built upon quantum rather than classical interactions presents the opportunity for a new type of computing machine. It has the potential to address some computational problems that are currently intractable on even the most powerful supercomputers today, and on any future classical computer. For example, in addition to excitement for potential cryptanalytic applications, there is much interest in applications involving the simulation of quantum systems of relevance for chemistry, materials science, and biology, in particular with potential applications to new materials development.
Experimentalists around the world are working to develop both gate-based and analog computers that could carry out useful computations, using a range of underlying qubit technologies. The rest of this report will
discuss progress that has been made to devise useful applications for these machines, and to create the hardware and software platforms needed to create a quantum computer. Because quantum computing devices are generally at early stages, and because the capabilities of devices will depend upon their type and maturity levels, it is useful to define several different categories of quantum computers for easy reference and comparison, as outlined below:
- Analog quantum computer (quantum annealer, adiabatic QC, direct quantum simulation). Such a system would operate through coherent manipulation of qubits, by changing the analog values of the system’s Hamiltonian, without using quantum gates. For example, computation on a “quantum annealer” is conducted by preparing a set of qubits in some initial state, and slowly changing the energy they experience until the Hamiltonian defines the parameters of a given problem, so that the final state of the qubits corresponds, with a high probability, to the answer of the problem. An “adiabatic quantum computer” (AQC) operates by initializing the qubits into the ground state of the starting Hamiltonian, and then changing the Hamiltonian slowly enough that the system remains in its lowest-energy, or ground state throughout the process. An AQC, although not gate-based, has the same theoretical processing power as a gate-based quantum computer, but does not have a practical means for full error correction.
- Noisy intermediate-scale quantum (NISQ) gate-based computer [18]. Such a system would operate through gate-based operations on a coherent collection of qubits without the full quantum error correction required to suppress all errors; calculations would need to be designed to be feasible on quantum systems with some noise, and be completed in few enough steps (a shallow enough logical depth) such that gate errors and decoherence of the qubits don’t obscure the results. The report will also refer to these systems as “digital NISQ” computers.
- Fully error-corrected gate-based quantum computers. Such a system would operate through gate-based operations on qubits, implementing quantum error correction to correct any system noise (including errors introduced by imperfect control signals or device fabrication, or unintended coupling of qubits to each other or to the environment) that occurs during the time frame of the calculation. In such systems, the error probability rates are reduced so significantly that the machine appears reliable for all computations. The design of these machines should allow them
to scale to hold thousands of these fully error corrected or logical qubits.
Gate-based quantum computers can have many physical realizations. However, any realizations must satisfy the celebrated DiVincenzo criteria, which stipulate that they have the following [19]:
- Well-characterized quantum two-level systems that can be employed as qubits.
- An ability to initialize the qubits.
- Decoherence times that are long enough to be able to carry out the computation or error correction.
- A set of quantum operations on the qubits, known as “quantum gates,” that is universal for quantum computation.
- An ability to measure quantum bits one by one, without disturbing the others.
Quantum annealers need all of the above except for item 4, since they do not use gates to express their algorithms. However, decoherence (item 3) plays a very different role in quantum annealing than in the gate model—in particular, some decoherence is tolerable in quantum annealing [20,21], and some amount of energy relaxation is necessary for quantum annealing to succeed [22,23]. To date, progress has been made toward building analog quantum and digital NISQ computer systems, while fully error-corrected systems are much more challenging.
In order to build a functional quantum computer, one must create a physical system that encodes qubits and control and manipulate these qubits precisely in order to carry out computations. Today, experimentalists are building and operating these systems in carefully controlled environments in laboratories. Two leading technologies for quantum computing—trapped ions and superconducting qubits—use very different strategies for embodying and operating on qubits. Trapped ion systems use two internal states of an atom as their fundamental quantum element. The atoms are each stripped of an outer electron, leaving them positively charged so that their positions can be controlled with electric fields in devices called “ion traps.” Both the ions and the traps are contained in ultra-high vacuum chambers to minimize interaction with the environment, and lasers are used to cool the motion of the ions down to very low temperatures (0.1-1 mK). Although the ion traps typically operate at room temperature, they can also be cooled to cryogenic temperatures (4-10 K) to improve the vacuum environment or reduce the impact of intrinsic electrical noise on the ion’s motion. The state of each ion can be changed by using precisely controlled laser pulses or microwave radiation. These
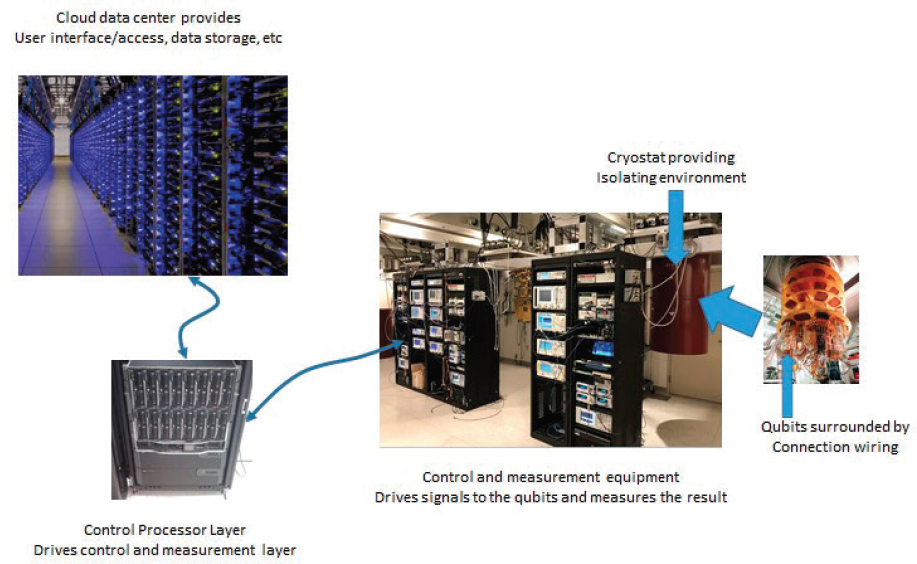
pulses can be arranged to couple the states of two or more ions together to create entanglement between the ions. An example of a laboratory apparatus containing an ion trap system and control units is provided in Figure 2.5.
Superconducting systems are built using a very different approach. Instead of using a natural quantum system, this approach uses the unique properties of superconducting materials to create a circuit that acts as an artificial atom.18 Since this circuit can be defined lithographically like an integrated circuit, it is possible to build arrays of these artificial atoms using a process similar to that used for manufacturing ICs. Microwave radiation is again used to manipulate the state of these “atoms,” and adjacent “atoms” can be electronically coupled together to create entangled

___________________
18 This circuit essentially is a nonlinear oscillator, which means that, like an atom, it supports different energy states, and the separation between the energy states changes with energy level, so that the gap between the states of interest is unique, and the states of interest can be interrogated exclusively.

states. Unfortunately, the energy levels in these circuits are still very small, and these circuits are always in contact with the material that they are built on. Isolating these circuits therefore requires cooling them to approximately 10 mK. Figure 2.6 provides a snapshot of an experimental superconducting quantum computer in a laboratory, including some of the apparatus required to maintain the temperature of the qubit environment and control the quantum system.
Interest in quantum computing has increased as the coherence times and fidelity of quantum operations have improved for the underlying quantum systems. Chapters 3 and 4 describe the potential capabilities of a quantum computer. Chapters 5 and 6 explore in greater depth the hardware and software technologies for building quantum computers, along with the coherence and fidelity levels that have so far been achieved.
2.7 NOTES
[1] J. Preskill, 2018, “Quantum Computing in the NISQ Era and Beyond,” arXiv:1801.00862.
[2] See, for example, K.C. Young, M. Sarovar, and R. Blume-Kohout, 2013, Error suppression and error correction in adiabatic quantum computation: Techniques and challenges, Physical Review X 3:041013;
A. Mizel, 2014, “Fault-Tolerant, Universal Adiabatic Quantum Computation,” https://arxiv.org/abs/1403.7694;
S.P. Jordan, E. Farhi, and P.W. Shor, 2006, Error-correcting codes for adiabatic quantum computation, Physical Review A 74:052322; K.L. Pudenz, T. Albash and D.A. Lidar, 2014, Error-corrected quantum annealing with hundreds of qubits, Nature Communications 5:324;
W. Vinci, T. Albash and D.A. Lidar, Nested quantum annealing correction, 2016, npj Quantum Information 2:16017.
[3] See, for example, A.D. Bookatz, E. Farhi, and L. Zhou, 2015, Error suppression in Hamiltonian-based quantum computation using energy penalties, Physical Review A 92:022317;
M. Marvian and D.A. Lidar, 2017, Error suppression for Hamiltonian-based quantum computation using subsystem codes, Physical Review Letters 118:030504.
[4] R. Landauer, 1961, Irreversibility and heat generation in the computing process, IBM Journal of Research and Development 5(3):183-191.
[5] M. Nielsen and I. Chuang, 2016, Quantum Computation and Quantum Information, Cambridge University Press, p. 189.
[6] M. Roetteler and K.M. Svore, 2018, Quantum computing: Codebreaking and beyond, IEEE Security and Privacy 16:(5):22-36.
[7] Ibid.
[8] W.K. Wootters and W.H. Zurek, 1982, A single quantum cannot be cloned, Nature 299(5886):802-803.
[9] D. Dieks, 1982, Communication by EPR devices, Physics Letters 92A(6):271-272.
[10] T.P. Harty, D.T.C. Allcock, C.J. Ballance, L. Guidoni, H.A. Janacek, N.M. Linke, D.N. Stacey, and D.M. Lucas, 2014, High-fidelity preparation, gates, memory, and readout of a trapped-ion quantum bit, Physical Review Letters 113:220501.
[11] R. Blume-Kohout, J.K. Gamble, E. Nielsen, K. Rudinger, J. Mizrahi, K. Fortier, and P. Maunz, 2017, Demonstration of qubit operations below a rigorous fault tolerance threshold with gate set tomography, Nature Communications 8:4485.
[12] E. Mount, C. Kabytayev, S. Crain, R. Harper, S.-Y. Baek, G. Vrijsen, S.T. Flammia, K.R. Brown, P. Maunz, and J. Kim, 2015, Error compensation of single-qubit gates in a surface-electrode ion trap using composite pulses, Physical Review A 92:060301.
[13] S. Gustavsson, O. Zwier, J. Bylander, F. Yan, F. Yoshihara, Y. Nakamura, T.P. Orlando, and W.D. Oliver, 2013, Improving quantum gate fidelities by using a qubit to measure microwave pulse distortions, Physical Review Letters 110:0405012.
[14] J.P. Gaebler, T.R. Tan, Y. Lin, Y. Wan, R. Bowler, A.C. Keith, S. Glancy, K. Coakley, E. Knill, D. Leibfried, and D.J. Wineland, 2016, High-fidelity universal gate set for 9Be+ ion qubits, Physical Review Letters 117:060505.
[15] C.J. Ballance, T.P. Harty, N.M. Linke, M.A. Sepiol, and D.M. Lucas, 2016, High-fidelity quantum logic gates using trapped-ion hyperfine qubits, Physical Review Letters 117:060504.
[16] R. Barends, J. Kelly, A. Megrant, A. Veitia, D. Sank, E. Jeffrey, T.C. White, et al., 2014, Logic gates at the surface code threshold: Supercomputing qubits poised for fault-tolerant quantum computing, Nature 508:500-503.
[17] S. Sheldon, E. Magesan, J. Chow, and J.M. Gambetta, 2016, Procedures for systematically turning up cross-talk in the cross-resonance gate, Physical Review A 93:060302.
[18] J. Preskill, 2018, “Quantum Computing in the NISQ Era and Beyond,” arXiv:1801.00862.
[19] D.P. DiVincenzo, 2000, The physical implementation of quantum computation, Fortschritte der Physik 48:771-783.
[20] M.H.S. Amin, D.V. Averin, and J.A. Nesteroff, 2009, Decoherence in adiabatic quantum computation, Physical Review A 79(2):022107.
[21] A.M. Childs, E. Farhi, and J. Preskill, 2001, Robustness of adiabatic quantum computation, Physical Review A 65(1):012322.
[22] M.H.S. Amin, P.J. Love, and C.J.S. Truncik, 2008, Thermally assisted adiabatic quantum computation, Physical Review Letters 100(6):060503.
[23] N.G. Dickson, M.W. Johnson, M.H. Amin, R. Harris, F. Altomare, A.J. Berkley, P. Bunyk, et al., 2013, Thermally assisted quantum annealing of a 16-qubit problem, Nature Communications 4:1903.

































