3
Quantum Algorithms and Applications
A bedrock of the field of algorithms lies in the principle that the total number of computational steps required to solve a problem is (roughly) independent of the underlying design of the computer—remarkably, to a first approximation what is designated a single step of computation is a matter of convenience and does not change the total time to solution. This basic principle, called the extended Church-Turing thesis, implies that to solve a computational problem faster, one may (1) reduce the time to implement a single step, (2) perform many steps in parallel, or (3) reduce the total number of steps to completion via the design of a clever algorithm.
The discovery that quantum computers violate the extended Church-Turing thesis [1,2]—by solving certain computational tasks with exponentially fewer steps than the best classical algorithm for the same task—shook up the foundations of computer science, and opened the possibility of an entirely new way of solving computational problems quickly.1 The practical potential of quantum computers was illustrated soon thereafter when Peter Shor created quantum algorithms for factoring large numbers and computing discrete logarithms that were exponentially faster than
___________________
1 Note that quantum computers do not violate the original Church-Turing thesis, which defines the limits of what it is possible to compute at all (independent of time required to perform the computation). See D. Deutsch, 1985, Quantum theory, the Church-Turing Principle and the universal quantum computer, Proceedings of the Royal Society of London A 400(1818):97-117. The extended Church-Turing thesis is sometimes referred to as “the feasibility thesis” or the “computational complexity-theoretic Church-Turing thesis.”
any developed for a classical computer [3-4].2 These quantum algorithms generated serious concern in the security community, since the classical hardness of these two problems lie at the core of the public key “cryptosystems” that protect the vast majority of society’s digital data.
Indeed, algorithms for factoring large numbers have been studied over the centuries by mathematicians and very intensely over the last few decades by computer scientists. The main issue in these, and most other computational problems, is combinatorial explosion: the exponential number of potential solutions that the algorithm must choose between. In the case of factoring an n bit number N, the possible prime divisors of N include all prime numbers less than N, and there are exp(n) many such primes. Indeed, the fastest classical algorithm for actually finding the prime divisors of N takes exp(O(n1/3)) steps, while Shor’s quantum algorithm took only O(n3) steps, later improved to O(n2log[n]).
A very general goal of the field of algorithms is to solve a computational task by an algorithm whose number of steps (colloquially called its “running time”) scales polynomially in the size, n, of the input, thereby bypassing the combinatorial explosion. Computational tasks for which such polynomial time (classical) algorithms exist are referred to as belonging to the complexity class P. The corresponding complexity class, bounded-error quantum polynomial time (BQP), contains all those computational tasks that a quantum computer would be able to solve in polynomial time. By contrast, algorithms whose running time scales exponentially in the size of the input very quickly become prohibitively expensive as the input size is scaled.
It is important to realize that quantum computers do not uniformly speed up all computational problems. One of the most important classes of computational problems, the NP-complete problems [5], have been described as looking for a needle in an exponentially large haystack. About the same time as Shor’s announcement, Bennett et al. [6] proved that quantum algorithms require exponential time to solve NP-complete problems in the black box model—that is, if the algorithm ignores the detailed problem structure—and are therefore unlikely to provide exponential speedups for such problems. More precisely, if N denotes the size of the haystack, Bennett et al. showed that any quantum algorithm to find the needle must take at least N1/2 steps. A few years later, Grover showed that there is a quantum algorithm that can find the needle in O(N1/2) steps [7]. The class NP is characterized by the requirement that a classical computer should be able to check the correctness of a solution in polynomial time (no matter how hard it is to actually find the solution). NP-complete
___________________
2 Shor’s algorithm for factorization scales asymptotically as O(n3), compared to O(exp[n1/3]) for the best classical approach, the general number field sieve algorithm.
problems are the hardest problems in NP, and include the famous Traveling Salesman Problem, as well as thousands of problems from every field in science. It is widely conjectured that P ≠ NP (this is one of the famous seven Clay Millennium Problems), and that any classical algorithm must require exp(n) steps to solve NP-complete problems [8].
The design of quantum algorithms follows completely different principles from those of classical algorithms. To begin with, even classical algorithms have to be cast in a special form—as reversible algorithms—before they can be run on a quantum computer. Algorithms that achieve quantum speedups use certain quantum algorithmic paradigms or building blocks that have no classical counterparts.
There is an extensive literature on quantum algorithms that has been developed in the quarter century since the first algorithms discussed above. All of these algorithms rely on a handful of quantum building blocks that are described in the next section and are designed to run on an idealized quantum computer. Real quantum devices are noisy, so an elaborate theory of quantum error correcting codes and fault-tolerant quantum computing has been developed to convert noisy quantum computers to ideal quantum computers. However, this conversion incurs an overhead both in number of qubits as well as running time.
The field is now entering the era of noisy intermediate-scale quantum (NISQ) devices [9]—the race to build quantum computers that are sufficiently large (tens to hundreds or a few thousand qubits) that they cannot be efficiently simulated by a classical computer, but are not fault tolerant and so cannot directly implement the algorithms developed for ideal quantum computers. While the enormous interest and funding for building NISQ computers has undoubtedly moved up the calendar for scalable, fault-tolerant quantum computers, significant work remains before each milestone is met.
The biggest upcoming challenges are algorithmic; in the near-term, this includes the search for computational tasks that such computers can speed up. Developing algorithms that run on NISQ computers are as important as creating the physical devices, since without both, the machine is not useful. In the longer term, much work remains to be done in the field of quantum algorithms for ideal (scalable, fault-tolerant) quantum computers. The next section describes major building blocks for quantum algorithms, as well as known algorithms for idealized quantum computers that provide speedups over the best classical algorithms for the same computational tasks. The subsequent section describes quantum error-correction and fault-tolerance techniques for converting a noisy quantum computer to an idealized quantum computer. The chapter concludes with a discussion of the major algorithmic challenge presented by NISQ computers, and the most promising leads in the search for such algorithms.
Finding: Progress in quantum algorithms is essential for quantum computing success. In the near term, developing algorithms that work on NISQ machines is critical.
3.1 QUANTUM ALGORITHMS FOR AN IDEAL GATE-BASED QUANTUM COMPUTER
The power of quantum algorithms ultimately derives from the exponential complexity of quantum systems—the state of a system of n entangled qubits is described by (and can thus encode) N = 2n complex coefficients, as discussed in the previous chapter. Moreover, the application of each elementary gate on, say, two qubits updates the 2n complex numbers describing the state, thereby seeming to perform 2n computations in a single step. On the other hand, at the end of the computation, when the n qubits are measured, the result is just n classical bits. The challenge of designing useful and advantageous quantum algorithms derives from the tension between these two phenomena—one must find tasks whose operational solutions both make use of this parallelism and yield a final quantum state that has a high probability of returning valuable information upon measurement. Successful approaches take advantage of the phenomenon of quantum interference for generating useful results. In the following, some of the major building blocks for quantum algorithms are described, as well as several foundational quantum algorithms and how they can be used to solve different kinds of abstract problems.
3.1.1 The Quantum Fourier Transform and Quantum Fourier Sampling
One of the most basic building blocks for quantum algorithms is the quantum Fourier transform (QFT) algorithm. The Fourier transform, a critical step in many classical calculations and computations, is an operation that transforms one representation of a signal of interest into a different representational form. The classical Fourier transform turns a signal represented as a function of time into its corresponding signal represented as a function of frequency. For example, this could mean transforming a mathematical description of a musical chord in terms of air pressure as a function of time into the amplitudes of the set of musical tones (or notes) that combine to form the chord. This transformation is reversible via the inverse Fourier transform, so involves no information loss—a key requirement for any operation on a quantum computer. Concretely, the input is an N-dimensional vector with complex entries (a1, a2, …, aN), and the output is an N-dimensional vector with complex entries (b1, b2, …, bN) which is obtained by multiplying the input vector with the N × N Fourier transform matrix.
Given the utility of the Fourier transform, many clever algorithms have been developed to implement it on classical computers. The best, the fast Fourier transform (FFT), takes O(NlogN) time, which is only slightly longer than it takes to read the input data [O(N)]. While the classical FFT is quite efficient, quantum Fourier transform (QFT) is exponentially faster, requiring only O(log2N) = O(n2) time (where N = 2n) in its original formulation, later improved to O(nlogn) [10].
Before describing the QFT, it is important to understand how the input and output are represented as quantum states. The input (a1, a2, … aN) is represented as the quantum state Σiai | i ⟩, and the output (b1, b2, … bN) is represented as the quantum state Σibi | i ⟩. Thus, the input and output are represented as states of just n qubits, where n = log N. This is shown in Figure 3.1. Exponential speedup is possible only if the input data has already be encoded into a compact quantum state, or can be encoded into this state in O(log N) steps. The quantum circuit that carries out this transformation has total number of gates that scales as O(n log n). Another caveat is that one of course cannot access the amplitudes bi through measurement. Indeed, if the output of the QFT is measured, it yields the index i with probability | bi| 2. Thus, measuring this algorithm’s output only yields the index of a probable output, which is called quantum Fourier sampling (QFS). QFS is an important primitive in quantum algorithms, and entails applying the QFT and measuring the output state, resulting in the sampling of an index i from a certain probability distribution.
First, since O(N) time is required to read the input data, the quantum algorithm can be completed only in O(log2N)—that is, it can yield speedup only compared to its classical analogue—if the input data is preencoded into logN qubits and not read in directly from a file of data. These logN qubits are in a superposition of N quantum states, and the coefficient on each state represents the data sequence to be transformed. This is shown in Figure 3.1. Applying the QFT algorithm to this input changes the state of the log N qubits such that the new coefficients are the Fourier Transform of the input coefficients. Of course, since the output is a quantum state, there is no way to directly read these values. When the output is measured, only one of the N possible classical output states is observed. The probability that any of the N states will be observed is the square of the absolute value of the coefficient of that state, which is also the square of its Fourier transform value. Performing a QFT on a set of qubits and then measuring their final state accomplishes the same task as what is referred to classically as Fourier sampling.
It turns out that sampling the output of the Fourier transform is useful in some cases for finding structure in a sequence of numbers, as illustrated in Figure 3.1. Notice that the coefficients of the input data are periodic, with four periods in this sequence. This periodicity causes the amplitude of state | 100 ⟩ to be much larger than all the others, so with high
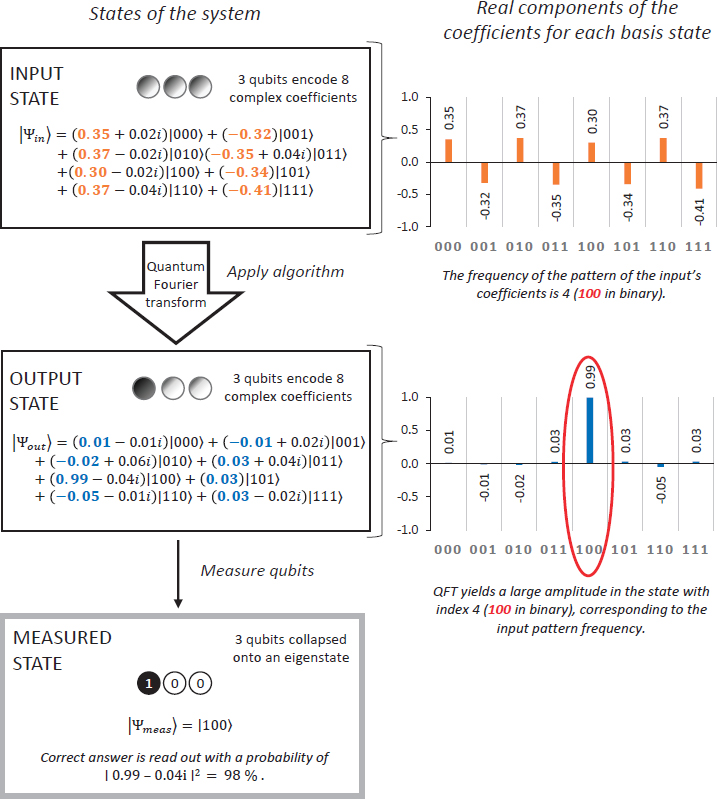
probability, measuring the final system state will return 100 (binary for 4), revealing the input sequence repeated 4 times, or had a repeat distance of 2. This example illustrates the power and pitfalls of quantum computing. If the initial input superposition already exists, the Fourier transform can be performed on the superposition coefficients exponentially faster than would be possible classically. However, at the end of this operation, one samples only one of the N states, rather than obtaining the entire set of output coefficients. Furthermore, it is not clear in general how to create the input superposition without taking O(N) time—although this becomes less of a problem if QFT is performed on a preloaded input quantum state as one step in a longer algorithm.
The QFT, which cleverly leverages the characteristics of quantum computation, is useful in constructing a host of quantum algorithms. Examples include quantum factoring, finding hidden structure, and quantum phase estimation.
3.1.2 Quantum Factoring and Finding Hidden Structures
Shor’s discovery of polynomial time algorithms for factoring and calculating discrete logarithms [11] was a major breakthrough for the field of quantum algorithms, both because of the apparent speedup compared to the classical algorithms and because of the implications of this speedup for known applications. At their heart, both algorithms may be seen as an ingenious way of exploiting the exponential speedup in the QFT, even given the input and output limitations of Fourier sampling.
To be able to use the power of the QFT, Shor first converted the problem of finding the factors of a number to a problem that involves finding a repeating pattern—exactly what the FT detects. Shor was able to show that the factoring problem was equivalent to the problem of finding the period in a sequence of numbers, albeit a sequence of numbers that is exponentially longer than the number of bits of the corresponding number to be factored. Thus, while this equivalency does not provide any help in solving the problem on a classical computer (since it would need to generate this sequence of 2n numbers for an n-bit number to factor, which would take an exponential amount of time), it is a perfect problem for a quantum computer. In a quantum computer, the exponentially long sequence can be encoded into merely n qubits, and generated in a time that is polynomial in n. Once that sequence is generated, the QFT can be used to find the period. The fact that the returned result is only a sample of the output FT amplitudes is not limiting, since the desired information is highly likely to be what a measurement would sample.
Shor’s algorithm, if deployed on a perfect quantum computer, would make it possible to compute the secret key of the most widely used public key cryptosystems, RSA. In addition, it would be able to compute the
secret key of other widely used public-key cryptosystems, such as Diffie-Hellman and elliptic curve cryptography. The implications of quantum computing for cryptography are discussed in more detail in Chapter 4.
Shor’s quantum algorithm for factoring and discrete log can both be regarded as examples of finding hidden algebraic structure, related to a well-known mathematical problem called the “hidden subgroup problem” [12,13]. Currently, there are quantum approaches for solving some cases of this problem efficiently, specifically for so-called Abelian and closely related groups (characterized by their symmetry properties). On the other hand, the problem is expected to be hard for the so-called dihedral symmetry group. This hard problem is closely related to another, called the shortest vector problem—the basis of the learning with errors (LWE) cryptosystem, one of the proposed post-quantum (that, is, quantum-resistant) cyphers described in Chapter 4.
3.1.3 Grover’s Algorithm and Quantum Random Walks
While the QFT underlies many quantum algorithms, another class of algorithms take advantage of a different method, called the “quantum random walk.” This method is analogous to classical random walk methods, which probabilistically simulate progress in traversing some terrain.
Grover’s algorithm addresses the specific problem of finding the unique inputs to a given function that will yield a certain output [14].3 Classically, this is a basic NP-hard search problem—that is, there are no known polynomial time solutions. In the absence of information about the nature of the function, the fastest known classical algorithm for this problem is exhaustive search, or exploration of all possible inputs to find the answer—a process that takes O(N) = O(2n) steps, where n is the number of bits required to represent the input. Grover’s algorithm solves this problem in ![]() steps. While this is only a polynomial speedup over the best classical approach, it could nonetheless be significant in practice. As will be discussed in the next chapter, this could be sufficient to compromise additional cryptographic operations. Moreover, this is the optimal quantum algorithm for this problem, in light of the result of Bennett et al. [15] showing that any quantum algorithm must take at least
steps. While this is only a polynomial speedup over the best classical approach, it could nonetheless be significant in practice. As will be discussed in the next chapter, this could be sufficient to compromise additional cryptographic operations. Moreover, this is the optimal quantum algorithm for this problem, in light of the result of Bennett et al. [15] showing that any quantum algorithm must take at least ![]() steps to solve this problem in the black box model.
steps to solve this problem in the black box model.
The problem with the classical exhaustive search approach is that the systematic testing of each possible answer is a blind guess-and-check: each query provides no information about the answer until it is actually found. To get around this problem, Grover’s algorithm proceeds by
___________________
3 The problem can be more formally phrased as follows: If f is an efficiently computable binary function that operates on strings of length n, find x such that f(x) = 1.
iterating a set of two operations on the qubits. The first effectively flags the state corresponding to the correct answer by changing the sign of its coefficient. The second, called the Grover diffusion operator, is then able to slightly increase the magnitude of this coefficient. Together, the two steps comprise a so-called Grover iteration, each application of which increases the probability that the correct answer will be read-out upon measurement. This procedure to increase the amplitude of the state(s) containing the correct answer is an example of a general algorithmic approach called amplitude amplification [16], which is useful in a number of quantum algorithms.
The sequence of amplitude amplification operations can be viewed as a sort of quantum random walk; however, Grover’s algorithm does the “walk” backward, from a distributed state (analogous to all possible endpoints of a random walk from a given starting point) back to a state focused around the single correct component (analogous to the starting point of the walk). A classical random walk approach can explore an area proportional to the square root of the number of steps; the quantum random walk can explore an area proportional to the number of steps. Hence, the quantum algorithm provides quadratic speedup.
This technique is very versatile and has led to a number of quantum algorithms providing polynomial speedups for specific computational tasks. For example, there is a quantum walk-based algorithm for solving the basic problem of determining whether the player making the first move has a winning strategy in a combinatorial game (such as chess). The naïve classical algorithm involves an exponential search of the possible moves and outcomes, called the “game tree,” while the quantum algorithm provides the quadratic speedup described above. More generally, the quantum algorithm provides a quadratic speedup for evaluating any AND-OR formula [17,18].
While Grover’s algorithm is often referred to as quantum “search,” this is not really a valid application of the technique. To perform a true quantum search, the set of data to be searched must first be represented as a superposition of quantum states and for a quantum algorithm to provide any speedup, this representation would need to be created in a time much less than the number of data points, N—somewhere between O(1) to O(logN). In the classical case, this data would simply be stored in random access memory (RAM) and called when needed. However, while RAM is a key element of classical computing, there is currently no robust practical RAM equivalent that generates the needed quantum superposition state for a quantum computer.
It has been proposed that a quantum version of random access memory (RAM), or QRAM, could generate this data in O(log N) time [19], although this has not been practically demonstrated. To achieve this, a classical data storage unit would be supplemented with quantum logic
around the memory cells. A classical analogue to this structure, called a content addressable memory, or CAM, exists, and solves this search problem in O(log N) time. However, with CAM and with QRAM, getting the data into the device in the first place still takes O(N) time, so either approach will only be useful when multiple queries are performed on the same data set—that is, the utility of CAM and QRAM, if it can be built, grows in direct proportion to the number of times the input can be reused.
3.1.4 Hamiltonian Simulation Algorithms
Simulating the dynamics of quantum systems is the most natural and obvious application of quantum computers and was the motivation for Richard Feynman’s pioneering exploration of quantum computing [20]. Quantum algorithms can exponentially outperform classical ones when simulating a system with many quantum degrees of freedom, with applications including problems in chemistry, materials science, condensed matter, nuclear physics, and high-energy physics.
The general objective in simulating a quantum system is to determine its structure or behavior, given knowledge of its components and the environment in which it exists. For example, a simulation could be used to elucidate the structure of a substance, or the behavior over time of a collection of interacting particles. These problems can have a variety of applications, from informing the development of new industrial materials to solving important physics problems. In general, these simulations require knowledge of the Hamiltonian (energy operator) describing all elements and interactions of the system. From there, one can either solve for the ground-state wave function for that system (in the time-independent picture), or, given some initial state of the system at a time t0, compute a close approximation to the quantum state at a future time t. Scientists have been performing classical simulations of quantum systems for decades, either restricting attention to small systems or relying upon approximate methods that can trade accuracy for computational efficiency. Accurate models are so compute-intensive (given the intrinsic high dimensionality of quantum systems) as to be inadequate for all but small systems.
A quantum, rather than classical, simulation is naturally better equipped to explore the state space spanned by quantum systems. In principle, quantum simulation can proceed via at least three general approaches, each of which promises more efficient solutions in certain scenarios. The first approach involves implementation of time-evolution algorithms on a gate-based quantum computer, commonly referred to as “Hamiltonian simulation.” The second is a variational approach for obtaining approximations to quantum states using quantum computers and will be discussed later in this chapter. Last, in the field of analog quantum simulation, dedicated quantum systems, although not full-blown
quantum computers, are built to emulate specific Hamiltonians. While this hardware is likely to be much simpler than gate-based machine solving the same problem, the downside of the analog simulation approach is that the hardware has limitations on the Hamiltonians it can create, so the resulting system is special-purpose and the application and simulator need to be co-designed. In addition, unlike digital quantum computations that can be protected using fault-tolerant protocols, the ability to perform analog quantum simulation in realistic, noisy environments is less well understood.
In the time-evolution Hamiltonian simulation algorithms, the form of the Hamiltonian, and potentially its own dependence on time, as well as the initial state of the system must be provided as inputs. The algorithm begins by initializing the qubits into the initial system state or an approximation to it. Then, the system is advanced through time, or “propagated,” according to its Hamiltonian, in discrete intervals, ∆t, for the number of iterations required to arrive at the time of interest, tf. In practice, the overall Hamiltonian is usually represented as a sum of smaller, so-called local Hamiltonians, each of which act on only a component of the larger system, which provides a useful decomposition (more generally, the Hamiltonian can be simulated efficiently provided it is sparse and the nonzero entries in any given row can be efficiently located and computed). For the process to proceed efficiently, the method of encoding of the initial state in qubits and of representing the time propagation as a gate sequence must be carefully chosen for the system in question. The first concrete quantum algorithms for gate-based Hamiltonian simulation were developed in the mid-1990s [21], and additional methods for different kinds of quantum systems has followed, along with algorithmic insights that have yielded significant reductions in time [22-28].4
Efficient Hamiltonian simulation on a quantum computer would enable important speedups for problems in quantum chemistry and materials simulation [29,30]. In particular, the electron correlation problem has been one of the most challenging problems for classical methods to tackle [31]. To understand and predict complex reaction mechanisms involved in, for example, a transition-metal catalyzed chemical transformation, requires extremely accurate electronic structure approaches. Classically, even molecules with fewer than one hundred strongly correlated electrons are beyond the scale of classical ab initio methods at chemical accuracy. Quantum computers promise exponential speedups for the simulation of the electronic structure problem and it has been shown that they would enable efficient elucidation of chemical reaction mechanisms [32]. Here,
___________________
4 Specifically, discrete-time random walks; see A.M. Childs, 2010, On the relationship between continuous- and discrete-time quantum walk, Communications in Mathematical Physics 294(2):581-603.
a quantum computer could enable researchers to compute or confirm the energies of chemical intermediates and transition states, and in turn help to determine accurate activation energies for chemical processes, which are important for understanding the kinetics of chemical reactions [33]. Strongly correlated species involved in chemical reactions where classical approaches presently fail include problems such as photochemical processes, nitrogen fixation, C-H bond breaking, carbon dioxide fixation and transformation, hydrogen and oxygen production, and other transition-metal catalysis problems. These applications extend to important industrial applications including fertilizer production, polymerization catalysis and clean energy processes. [34]. Hamiltonian simulation is also used within quantum algorithms for solving complex correlated material problems [35], which may have application in, for example, the search for a high-temperature superconductor. Quantum computers promise an exponential speedup over classical approaches for time evolution of quantum systems. Thus, quantum computers may have the most impact in their application to problems in quantum chemistry, for example as applied in pharmaceutics, and materials science [36].
However, there are many types of Hamiltonians that will require new methods if they are to become efficiently solvable on a quantum computer. For example, to model the electronic structure for applications in quantum chemistry [37], the Hamiltonian of an n-orbital system involves O(n4) terms, which means a low-error quantum computer will be required for its computation. Classical approaches to solving such problems have leveraged an understanding of the system’s physical structure to create tailored techniques [38]. Researchers have recently combined these techniques with the existing framework for quantum Hamiltonian simulation that has led to rapid progress in these quantum algorithms for such problems [39-47].
Hamiltonian simulation has also proven to be a powerful tool for developing quantum algorithms for problems with no immediate connection to quantum mechanics. A prominent example is the recent development of a new class of quantum algorithms that directly perform linear algebra on the quantum state; this is discussed next.
3.1.5 Quantum Algorithms for Linear Algebra
Linear algebra, a foundational area of mathematics, can be useful in a range of contexts, from the science of quantum mechanics to computer graphics design to methods in machine learning. The general task of linear algebra is to find the solution to a system of linear equations, that is, one or more equations of the form where the sum of a set of independent variables, each scaled by some coefficient, is equal to a constant value.
Mathematically speaking, such a problem can be written in matrix form as A x = b, where A is an N × N matrix whose elements are the coefficients on the variables in the equations, x is a column vector whose elements are each of the variables to be solved for, and b is a column vector of the constants.
A quantum algorithm for such applications, termed HHL after its developers Harrow, Hassidim, and Lloyd, makes use of methods from Hamiltonian simulation [48]. It assumes that the input vector b is given as a quantum state of logN qubits | b⟩ = Σibi | i⟩. It also assumes that the matrix A is sparse and its entries are accessible via an easy to compute function. Moreover, it computes the output vector x in the form of a quantum state of logN qubits | x⟩ = Σixi | i⟩. At the heart of the HHL algorithm lies one of the basic quantum algorithmic building blocks: Kitaev’s quantum phase estimation algorithm. This is a procedure for exponentially fast estimation of the eigenvalue (or phase) of an eigenvector of a unitary operator. This is relevant to linear algebra, since inverting the matrix A is easy if its eigenvalues are known. The running time of the HHL algorithm scales as a polynomial in logN and the condition number of A. Of course, the access to the solution x is restricted to information that can be readily accessed from the quantum state | x⟩. For a given A and b, the algorithm would output a quantum state for which the values of the N coefficients are proportional to the N elements of solution x. Although the solution is present in the quantum computer, the rules of quantum mechanics also prevent it from being directly read out. However, if one is interested in only finding certain expectation values of the solution, one can obtain this result with a number of gates that has poly(logN) cost [49].
Linear algebra problems can be solved with a classical computer using memory and running time that scale as poly(N) so a quantum computer would use exponentially fewer resources and time for solving this more restricted problem. Recent related work has shown similar results for solving linear differential equations [50] and performing convex optimization [51], under the assumption that the input matrix A is very sparse—that is, that most of the coefficients are zero—since the algorithm’s running time is polynomial in the number of nonzero elements per row.
As with the preceding algorithms, this exponential speedup comes with a number of important caveats. As previously mentioned, reading the output provides only an index i with probability proportional to | xi | 2. Thus, one major issue in using this algorithm is finding settings where this limited information is useful. One example of such a setting is recommendation systems, where past ratings of several products by a group of users (specified by a matrix) are used to provide personalized recommendations to individual users. The recommendation is a product, which is specified
by an index. A quantum algorithm for this problem was found with an exponential speedup over existing classical algorithms [52]. Recently, this quantum algorithm inspired a new classical algorithm which is only polynomially slower than the quantum algorithm [53].5
Another issue is that this exponential speedup is only true if both the input b and the matrix A are already encoded in logN qubits, or if they can be encoded into qubits in poly(logN) time. This precludes reading in this data, since simply reading the data to create this state would take at least O(N) time. This exponential speedup is only possible if this data was already prepared as a quantum state before the start of the algorithm, or if some method is found to prepare it efficiently.
As previously mentioned, for exponential speedup the current ability for a quantum processor to read-in large amounts of data efficiently is a common challenge in quantum algorithm development; an efficient solution to this problem will likely be required for many algorithms to be useful in practice. Of course, even if this issue is not resolved, quantum algorithms can still provide polynomial speedup where classical algorithms require O(N2) or higher steps to process the input, since a quantum computer can read the data in O(N) steps.
3.1.6 Required Machine Quality
The algorithms described in this section illustrate the types of tasks which when executed on a quantum computer would lead to an enormous computational advantage. For interesting problem sizes, they mostly require thousands of qubits, a few orders of magnitude larger than current machines. Unfortunately, these algorithms need to do a very large number of qubit gate operations, requiring order 1012 or even as high as 1018 operations.6 In order for these results to be correct in the end, the gate error rate must be very small (on the order of 10−12 to 10−18). As explained in Chapter 2, unlike today’s classical computers, whose gates can achieve these low error rates by directly rejecting noise and producing outputs with less noise than contained in their inputs, quantum gates have much higher error rates. As shown in Chapter 5, current quantum computers have error rates in the 10−2-10−3 range, and are unlikely to reach the required error needed to run these quantum algorithms natively. Quantum error correction is one way to overcome this limitation, and is described next.
___________________
5 In this manner, progress in quantum algorithms has commonly spurred new advances in classical algorithms. This is discussed further in Chapter 7.
6 See, for example, Figure 3.2 and Table 4.1 for runtime estimates for illustrative problems in chemistry and cryptanalysis.
3.2 QUANTUM ERROR CORRECTION AND MITIGATION
Two general approaches have been developed to reduce errors in quantum systems: correction and mitigation. Of the two, quantum error correction (QEC) is the only way to dramatically lower effective error rates. This approach involves encoding the quantum state using many redundant qubits, and the using a QEC code (QECC) that exploits this redundancy of information to emulate stable qubits with very low error rates, often called “fault-tolerant” or “logical” qubits. The state of some of these additional qubits are periodically measured and a classical computing device “decodes” this information to determine which qubits have errors. Given this information, the errors can be corrected. Each logical qubit requires a large number of physical qubits and many quantum gate operations (and classical computation) to achieve and maintain its state. Gate operations on the more robust logical qubit, which exists only as an abstraction, must be translated into operations on the underlying physical qubits. Thus, QEC incurs costs, or “resource overheads,” of both additional qubits for each logical qubit, and additional quantum gates for each logical operation.
Quantum error correction is an active area of quantum algorithm research, with the goal of dramatically lower the overheads in qubits and time to achieve fully error free operation. Much of this research has focused on studying surface codes and the larger class of topological codes of which they are a part. Current codes for gates with error rates of 0.1 percent still have high overheads (15,000 times) to create a logical qubit. Until a breakthrough in either gate error rate or QEC code overhead, near-term machines will not be able to achieve logical qubits, leading to machines that must deal with noise and errors (NISQ computers). In the shorter term, researchers have turned to approaches for quantum error mitigation (QEM) and may use QEC to lower, but not eliminate errors, as error rates fall.
3.2.1 Quantum Error Mitigation Strategies
Compared to QEC, QEM has the more modest goal of reducing the effective error rate of the quantum calculation to support simple computations, or for non-gate-based quantum approaches to extend the coherence of imperfect qubits [54,55] for durations long enough to complete short algorithms. Since a lower error rate lowers the overhead when using QEC, many of these mitigation strategies would also be used with error correction.
Two useful error-mitigation approaches that are widely used today include the application of composite pulses and dynamical decoupling methods. Although such techniques do not suppress all types of errors,
they can be designed to mitigate known systematic errors (composite pulses) or coherent dephasing errors (dynamical decoupling sequences).
For both analog and digital quantum computers, error suppression techniques are being developed based on “energy penalties” to suppress specific types of errors. These approaches work by encoding the qubits strategically in ways for which these errors are less energetically favorable and therefore less likely. In addition, both types of computers may take advantage of “decoherence-free subspaces,” where multiqubit architectures are designed in ways that make the qubit system insensitive to certain channels of noise. Since these techniques suppress only certain types of errors, the error-rate improvement will depend on the system and may be modest.
QEM is expected to be particularly important for analog QCs, as full QEC is not currently understood to be practically achievable on these systems. While QEC is corrective—that is, it measures errors and then fixes them—QEM methods are preventative and attempt to reduce the adverse impacts of noise and the probability of errors.
3.2.2 Quantum Error Correction Codes
The first quantum error correction codes were developed in the mid-1990s [56,57]. Further work has provided practical insights into the error threshold—that is, the maximum allowable error rate of every physical gate in an actual device for which QEC will correct more errors than it introduces [58,59]. However, achieving both the number and fidelity of qubits required to successfully implement QEC and enable fault-tolerant computing has proven challenging.
In classical computing, one of the simplest types of error correction codes, called a “repetition code,” copies each bit of information into several bits to preserve the information through redundancy. All gate operations are also replicated to maintain this redundancy. These bits all have the same value, unless an error occurs, which would result in one of the bits being set to the wrong value. Since the likelihood of any error arising is small, the correct value can be identified as that held by the majority of the copies. The “distance” of an error correcting code is the minimum number of errors that are needed to convert one valid representation of data to another valid data representation. A repetition by 3 code (each bit is either 000, or 111) is a distance 3 code, since one need change all three bits to go from one valid representation, 111, to another valid representation, 000. In general, a distance D code can correct (D–1)/2 errors, so the replication 3 code can correct one error. This makes sense, since if only a single error occurred, the majority of the bits will still represent the right value.
Approaches to QEC are similar to this classical approach. However, the precise implementation of QEC requires vastly different techniques than the classical repetition code because quantum information cannot be directly copied, as described in the no cloning theorem [60], and owing to the additional types of errors that can occur in quantum gates. Nonetheless, QEC protocols have been developed that enable the encoding of a logical qubit into a distributed fabric of physical qubits. Since these qubits hold the quantum state, none of them can be directly measured: any measurement would cause the quantum state to collapse and destroy the computation. Instead, two qubits, which should have the same value, are compared to each other, and all one reads out is whether these two qubits agree or disagree. This measurement does not reveal the value of the qubit, so it does not cause the quantum state to collapse. The qubits that are measured are sometimes called the “syndrome” or “ancilla” qubits (Box 3.1). From all these comparison measurements and knowledge about the QECC used, a classical computer can compute which qubits have errors, and what type of error a qubit has. Thus, it can provide the quantum operation that need to be applied to remove the errors in the quantum state. While these operations can be directly applied to the physical qubits, it is often more efficient for the software to “virtually” apply these corrections, modifying future operations to account for these errors rather than adding a separate step just to correct them. The classical algorithm, also called a “decoding algorithm” or “decoder,” which takes syndrome measurements as its input and computes which qubits have errors grows
in complexity as the distance increases to handle higher error rates. If the error rate is close to the error threshold, not only are the overheads very high but the decoding algorithm is more complex as well. If the error rates are low or there are very few logical qubits required to run the algorithm, then a small lookup table can be used as the decoder.
The computational complexity of the error decoder might be an issue, since running QEC tightly couples the qubits of a quantum computer and the classical control processor that decodes the errors and selects the next quantum gate operations to be performed. At a high level, the following operations are needed. First, the control processor sends a quantum operation to the qubits, and some time is needed to perform the operations. Second, the syndrome qubit must be measured and sent back to the control processor. Third, the control processor must then use these measurements to decode which errors are present, and, fourth, update its future operations to account for these errors. It is simplest for the quantum computer if the classical computer can decode the error state without slowing down the next quantum operation. For a superconducting QC, this means the classical computer has only a few hundred nanoseconds (on the order of a thousand instructions on a modern processor) to decode the errors. If this is not possible, either custom hardware, to speed up the computation, or changing the QEC algorithm to allow additional quantum operations to occur before the error information is decoded, could be used to address the issue. If these techniques are not done, the added time will slow down the effective speed of a quantum computer, with delays between gates leading to additional decoherence and higher error rates.
3.2.3 Quantum Error Correction Overhead
The number of physical qubits required to encode a fault-tolerant, logical qubit depends on the error rates of the physical quantum device and the required distance, or the protection capacity, of the quantum error-correcting code chosen. As a simple example, consider the so-called Steane quantum error correction code. This approach encodes a single logical qubit into seven physical qubits, and is has a distance of three,7 which means that it can correct a single error. To achieve a higher-distance protocol (one which can correct additional errors) using the Steane code, one can use a recursive approach called “concatenation.” This essentially entails applying the Steane code to a set of physical qubits, and then applying it again to the corrected qubits, using the output of the first
___________________
7 One needs more than 3 qubits for a distance 3 code since the syndrome measurements cannot reveal any information about the actual quantum state (which would force it to collapse).
level of corrections as the better qubits to be used in a subsequent level. Multiple levels can be stacked until the desired degree of error protection is achieved. In general, concatenating a QECC that encodes k qubits into n physical qubits and has distance d, written as [[n, k, d]], scales to a [[nr, k, d*]] code for r levels of concatenation, where d* ≥ dr. That is, nr it requires physical qubits per logical qubit. For example, three levels of concatenation of the Steane code would require 343 physical qubits to encode a single logical qubit and achieve a distance of at least 27. This qubit overhead is smaller than many other QEC approaches. However, a Steane code requires error rates lower than 10−5, which is much lower than current machines. Other concatenation codes have higher qubit overheads but can accommodate higher error rates. Finding better codes is an active area of research.
Another approach to a QECC, the so-called surface code, is less sensitive to physical qubit error rate, with the potential to protect against errors even for quantum device error rates as high as 10−2 (1 percent), meaning it corrects more errors than it adds if all gates and measurements fail at most 1 in 100 times on average. The surface code’s error threshold of one percent applies for a device architecture where each physical qubit interacts only with its four nearest-neighboring qubits, which—as Chapter 5 will show—is common in some current quantum computer designs.
However, a high error threshold comes at the price of high overhead. A distance d surface code requires a lattice of (2d – 1) × (2d – 1) physical qubits in order to encode a single logical qubit. As apparent from the formula, a surface code with a distance of three—the smallest possible code—requires 25 physical qubits to encode a logical qubit.8 While a distance three code will not fully correct all errors, since two errors generate an incorrect output, this code reduces the effective error rate. As QCs grow in size and decrease in error rates, these smaller codes can be used to improve the effective error rate of the machine, but with a significant reduction in the number of effective qubits.
Of course, to completely remove errors, most quantum algorithms are extensive enough to require a distance of greater than three. For example, to fault-tolerantly perform Shor’s algorithm or Hamiltonian simulation for quantum chemistry, the required distance is closer to 35, meaning that approximately 15,000 physical qubits are required to encode a logical qubit, assuming a starting error rate of 10−3 [61,62]. Beyond the Steane and surface codes, other more resource-efficient QECCs have been developed;
___________________
8 There are some improvements to the encoding cost; however, they are minimal, enabling a distance 3 surface code to use only 13 or 17 qubits. See, for example, Y. Tomita and K.M. Svore, 2014, Low-distance surface codes under realistic quantum noise, Physical Review A 90:062320.
however, in 2018 such codes either lack efficient decoding algorithms or require error rates that are too low for the NISQ era. Work in this area is essential to reach the goal of creating a fully error corrected quantum computer.
In addition to the physical qubit overhead of QEC, in order to operate on fault-tolerant, logical qubits, there must be software available at compile time to convert the desired gate on the logical qubits to gates on the actual physical qubits that encode them. This translation would occur directly in the compilation of a quantum algorithm, with each logical qubit and each logical operation replaced according to a QECC and a distance-specific fault-tolerant replacement rule. The replacement rule accounts for the implementation of both the logical gate and the error correction algorithm, including the syndrome measurements and the corresponding classical decoding algorithm. The number of gates and time-steps required to implement each logical gate depends on the logical gate and the QEC algorithm; details of such calculations may be found elsewhere [63].
Finding: Quantum error correction (QEC) algorithms would enable the emulation of a perfect quantum computer using noisy physical qubits in order to deploy practical algorithms. However, QEC incurs significant overheads in terms of both the number of physical qubits required to emulate a logical qubit and the number of primitive qubit operations required to emulate a logical quantum operation.
Arguably the most daunting and costly challenge in quantum error correction is that of achieving a fault-tolerant “universal” set of operations. Existing QEC schemes have developed very cost efficient replacement rules and other methods for achieving fault-tolerant logical gate operations in the so-called Clifford group (consisting of the Pauli operations, controlled-NOT [CNOT], Hadamard [H], the phase gate S, and their products), as well as measurement in the computational basis. However, achieving universality also requires fault-tolerant implementation of non-Clifford gates (such as the Toffoli gate, or the π/8 gate also known as T). To do so, one can invoke a variety of techniques. For example, so-called magic state distillation enables improvement of the error rate of a logical non-Clifford operation such as the logical T gate. Another more newly developed technique, “code switching,” switches back and forth between a code that is efficient for Clifford gates and a code that is optimized for non-Clifford gates to achieve universality. Both approaches incur overhead in the form of additional physical qubits, quantum gates, and classical decoding complexity. The substantial overhead introduced going from fault-tolerant Clifford gates to a universal set of fault-tolerant gates
has been a major driver of research in quantum error correction codes and fault-tolerance schemes.
In the case of magic state distillation, several methods have been developed to lower the overhead cost [64]. In its simplest form, albeit not the optimal form in terms of resource overhead, magic state distillation for the T gate can transform a physical T gate with error rate to a logical T gate with an error rate of roughly 35p3. If this is still too high to be able to implement an algorithm of interest, then the procedure can be recursed, achieving 35(35p3)3, and so on for r rounds resulting in 35rp3r. In turn, each round requires 15 qubits to perform one improved T gate; thus, r rounds require 15r qubits (physical or logical qubits may be used, depending on the desired output error rate on the T gate). Thus, while the QEC protocol is costly for Clifford operations and logical qubit encoding, the most costly procedure by far is the fault-tolerant implementation of the non-Clifford gate required for universality [65]. To convey a sense of the resource requirements of Clifford- and non-Clifford gates, Table 3.1 provides estimates of the requirements for carrying out an error-corrected quantum simulation of the molecular system FeMoco. This example should be seen as a snapshot of capabilities as of 2017. Progress
TABLE 3.1 Estimates of the Resource Requirements for Carrying Out Error-Corrected Simulations of a Chemical Structure (FeMoco in Nitrogenase) Using a Serial Algorithmic Approach for Hamiltonian Simulation and the Surface Code for Error Correction
| Physical qubit error rate | 10−3 | 10−6 | 10−9 |
| Physical qubits per logical qubit | 15,313 | 1,103 | 313 |
| Total physical qubits in processor | 1.7 × 106 | 1.1 × 105 | 3.5 × 104 |
| Number of T state factories | 202 | 68 | 38 |
| Number of physical qubits per factory | 8.7 × 105 | 1.7 × 104 | 5.0 × 103 |
| Total number of physical qubits including T state factories | 1.8 × 108 | 1.3 × 106 | 2.3 × 105 |
NOTE: The table illustrates the trade-offs, for three specific physical qubit error rates, between the number and quality of the physical qubits required to achieve a fault-tolerant implementation of the algorithm. Estimates are based on a requirement of 111 logical qubits for the algorithm instance and physical gate frequencies of 100 MHz. Note that the requirements for distillation (T factories) are far greater than those for the rest of the error corrections. The cost of achieving an error-free, non-Clifford gate is orders of magnitude higher than encoding the qubits and their other Clifford operations with this particular QECC (surface code and magic state distillation).
SOURCE: Adapted from M. Reiher, N. Wiebe, K.M. Svore, D. Wecker, and M. Troyer, 2017, Elucidating reaction mechanisms on quantum computers, Proceedings of the National Academy of Sciences of the U.S.A. 114:7555-7560.
in quantum chemistry and simulation algorithms is ongoing, and these numbers will likely be improved.9
Finding: The performance of an error-corrected quantum algorithm will be limited by the number of operations which are the most expensive to error correct required for its implementation—for example, in the case of surface code QECC, the “non-Clifford Group” operations require many primitive gate operations to error correct and dominates the overall time (number of operations) that an algorithm requires.
Research continues on developing new quantum error-correcting codes and new quantum fault-tolerance schemes with the aim of dramatically lowering the resource overheads required to achieve fault-tolerant quantum computation. Much of this work has coalesced on studying surface codes and variants thereof, a class of code called topological codes [66].10 Owing to the numerous unresolved questions about surface codes, researchers continue to find better ways of using these codes [67], and better ways of evaluating and decoding these codes [68]. When experimental systems reach the size at which interesting fault-tolerance experiments can be run, and these machines can interleave quantum operations and measurement, QEC schemes can be tested in order to verify the theory and analyses. The real benefit of these experiments will be that researchers working on QEC will see the effects and sources of “real” system errors, rather than using theoretical noise models. Insights about the actual errors could enable the development of more efficient QEC codes tailored for the error statistics of the actual machine. Again, minimizing the overhead is critical for deploying fault-tolerance schemes, especially on early quantum devices which will have a limited number of high-quality qubits.
Early demonstration of limited QEC operation on devices dates to as early as 2005, and the basic features of such protocols have been implemented on both superconducting qubit and trapped ion qubit devices. Such experiments have not yet yielded fault-tolerant logical qubits, given the generally poor gate fidelity of physical qubit operations [69-71]. Recently, quantum error detection codes—smaller precursors to QECs—have been implemented in available quantum processors, with some evidence of success [72,73]. As will be discussed in Chapter 7, successful
___________________
9 For a recent review of progress in the field, see S. McArdle, S. Endo, A. Aspuru-Guzik, S. Benjamin, and X. Yuan, 2018, “Quantum Computational Chemistry,” preprint arXiv:1808.10402.
10 Topological codes are relatively good performers in terms of noise tolerance and qubit overhead, and they have the advantage of being naturally geometrically local in two dimensions, making them a promising class of codes for physical implementation—although some of the important variants live naturally in three or more dimensions.
demonstration of QEC to emulate practical, fault-tolerant logical qubits remains a significant milestone yet to be reached.
3.3 QUANTUM APPROXIMATION ALGORITHMS
Given that the high cost of error correction will preclude its use in early quantum computers, researchers have looked for other approaches for taking advantage of early quantum computers. A promising approach is to forgo the desire to obtain an exact solution for the computational problem and instead use an approximate, or heuristic approach to solve the problem. This approach has given rise to a number of quantum and hybrid quantum-classical algorithms for tasks that range from the simulation of many-body systems such as molecules and materials [74-82] to optimization [83] and machine learning applications [84-86]. The goal of these methods is to provide approximate but useful solutions to the problem at hand, with lower resource requirements than other approaches.
3.3.1 Variational Quantum Algorithms
Many problems of interest, in particular, problems in quantum chemistry, can be framed as so-called eigenvalue problems. According to the variational principle of quantum mechanics, the computed energy of the ground (lowest-energy) state of a quantum chemical system decreases as the approximations to the solution improve, asymptotically approaching the true value from above. This principle has given rise to iterative classical algorithms for solving these problems, where a crude guess of the solution is the input, and a somewhat-improved approximation is the output. This output is then used as the guess for the next iteration, and, with each cycle, the output gets closer and closer to the true solution, but never overshooting.
This approach can be split between a classical and a quantum algorithm, with the optimization step performed by the quantum processor, and subsequently read out, with a classical control unit deciding whether to perform another iteration. The ability to separate the quantum processing among many small, independent steps—with coherence required only over the course of a single step—makes these approaches a clever way to minimize the qubit fidelity requirements and obtain a useful result. For this reason, quantum variational algorithms have been suggested as applications for digital NISQ computers. It is worth noting that, of course, these algorithms are readily carried out using fully error-corrected quantum computers as well.
One specific example is the variational quantum eigensolver (VQE) [87-95], where the problem is broken into the sum of set of smaller
problems that can each be approximated independently, with the sum of all outputs corresponding to the approximate solution of interest. The process is repeated until a heuristic stopping criteria is reached, usually corresponding to the achievement of an energy threshold. The computational power of VQE depends on the form of the assumed quantum state, or ansatz, employed. Some ansatz are purely defined by convenient circuit forms that can be readily accessible by hardware, whereas others are designed to capture specific types of quantum correlations. The VQE algorithm is believed to become competitive with a classical computer at the similar task of approximating the wave function and properties of a many-body system of interest when the number of qubits in the quantum register and the depth of the quantum circuit employed generate states that are intractable to prepare in a classical computer. The specific number of gates and qubits where this occurs is heavily dependent on the type of algorithm, but a very rough estimate for quantum simulation applications could consist of hundreds of qubits and tens of thousands of quantum gates [96].
A related approach is the quantum approximate optimization algorithm (QAOA) [97], an algorithm for preparing a variational guess of a wave function that satisfies an optimization problem, such as the satisfiability problem. The algorithm follows a similar procedure as the VQE algorithm—namely, a series of preparation and measurement experiments followed by optimization by a classical computer. The resulting quantum state, when sampled, provides approximate or exact solutions to the computational problem.
3.3.2 Analog Quantum Algorithms
In addition to algorithms that require a gate-based quantum computer, there are set of approaches that work by directly representing the task in terms of a Hamiltonian, which may or may not vary with time. The desired result is encoded in the system state at the end of the simulation run. “Direct quantum simulation,” where the Hamiltonian created is analogous to that of the quantum system being explored, is one example of this type of approach, and a type of analog quantum computation. Examples of direct quantum simulation include the realization of spin Hamiltonians [98] or the study of quantum phase transitions [99-101].
Quantum annealing and, more specifically, adiabatic quantum optimization, also take this “analog” approach and provide a general-purpose schema for designing quantum algorithms without requiring the abstraction layer of logical operations, or gates. These two approaches are closely related: adiabatic quantum optimization is simply quantum annealing at zero temperature. Adiabatic quantum computation is interesting because
one can in principle convert any gate-based quantum computation to an equivalent adiabatic quantum computation (although it might not be an efficient solution method) [102]. These methods require mapping an optimization problem of interest into a Hamiltonian, Hf, such that finding the lowest energy, or ground state, of a system defined by that Hamiltonian is equivalent to solving the problem.
The algorithm for quantum adiabatic optimization is implemented as follows: a set of qubits begins with a Hamiltonian Hi for which the ground state is known, and Hi is then slowly transformed into Hf. Since a quantum system will remain in its ground state if the Hamiltonian is changed slowly enough (adiabatically), this procedure drags the system from the ground state of Hi to the ground state of Hf. Measurement of the final state provides the answer sought with a high probability [103,104].
There was a great deal of excitement about the prospects of such algorithms following work by Farhi et al. [105], giving evidence suggesting that these algorithms could be fast on random instances of 3SAT, a logic satisfiability problem that is equivalent to many other hard problems. The theoretical analysis of this algorithm was quite challenging, since its running time was governed by the spectral gap (the difference in energy of states near the ground state), of the time evolving Hamiltonian. A sequence of papers analyzed this gap in a number of cases, establishing there are classes of 3SAT formulae and other NP-complete problems for which the spectral gap for an adiabatic algorithm is exponentially small, which means for these problems this approach will take time exponential in the size of the problem [106,107]. As a result, the formal power of this type of computing is still not known. Thus, the approach to establishing the speedup of quantum annealing algorithms is largely empirical; researchers literally compare the time required to complete a given task on a quantum annealer with the best times of optimal classical computer systems for arriving at the same result.
All real quantum computers operate at a finite temperature. When that temperature corresponds to an energy greater than the spectral gap, an analog quantum computer can only implement quantum annealing rather than quantum adiabatic computation. Quantum annealing is particularly attractive from the viewpoint of experimental realization, with the caveat that theoretical analysis of these algorithms is difficult, and there is no clear theory of fault-tolerance for this model. Adiabatic optimization devices, in particular the D-Wave machines, have overcome significant engineering challenges and scaled rapidly to thousands of qubits, albeit with some trade-offs in qubit fidelity. While it initially looked like these devices demonstrated promising speedups for some applications, further work on new classical algorithms for these specific problems have erased these speedups [108]. Recent work suggests that this reflects the
relatively high temperature at which the D-Wave processors operate [109] and the presence of certain analog errors in these devices [110], although this does not rule out the possibility that there could be other fundamental limitations of quantum annealers.
3.4 APPLICATIONS OF A QUANTUM COMPUTER
As is apparent from the preceding discussions, many quantum algorithms have been developed, both for gate-based quantum computers and for quantum annealers. A comprehensive online catalogue of quantum algorithms is maintained by the U.S. National Institute of Standards and Technology (NIST) [111]. While this collection includes a host of algorithms that theoretically offer quantum speedup, this speedup is often the result of a few basic techniques at their core—in particular, quantum Fourier transform, quantum random walks, and Hamiltonian simulation. Furthermore, most algorithms require a large number of high-quality qubits in order to be useful, most likely requiring quantum error correction—far beyond the quantum resources available in known prototypical devices. In addition, the current inability to load large quantities of input data efficiently suggest that many of these would be difficult to implement in practice.
Furthermore, algorithms are generally not in and of themselves applications; rather, they are building blocks that must be combined in order to perform a useful task. As experimental efforts at realizing quantum computers gain momentum, the near-term challenge is to identify or create quantum applications and the algorithms they require—preferably useful ones which provide dramatic speedup over classical approaches—that can be deployed on non-error-corrected devices.
3.4.1 Near-Term Applications of a Quantum Computer
The potential near-term utility of a quantum computer is currently an active area of research. It is expected that such applications are likely to be those that require few qubits, can be implemented with a relatively shallow code (that is, they require relatively short sequences of gates), and can work on NISQ computers. The approximate algorithms discussed in Section 3.3 are considered to be leading prospects for implementation on near-term analog or digital NISQ machines. While there are many potential commercial11 applications for this class of machine, as of the time of publication of this report (2018), none are certain to provide an
___________________
11 A commercial application is one where someone is willing to pay money for the answer it can provide. It is an application that would bring revenue into quantum computing.
advantage over classical approaches when run on a NISQ computer. All of the researchers who spoke to the committee, including those from startups, agreed this was a critical area for research.
Finding: There is no publicly known application of commercial interest based upon quantum algorithms that could be run on a near-term analog or digital NISQ computer that would provide an advantage over classical approaches.
3.4.2 Quantum Supremacy
A necessary milestone on the path to useful quantum computers is quantum supremacy—a demonstration of any quantum computation that is prohibitively hard for classical computers, whether or not the computation is useful. In essence, quantum supremacy is an experimental demonstration that quantum computers violate the extended Church-Turing thesis. Quantum supremacy would also address skepticism about the viability of quantum computers, as well as provide a test of quantum theory in the realm of high complexity. To achieve this, one would need both to create a quantum computer large enough to demonstrate supremacy and to find a simple problem that it can perform but that is hard for a classical machine to compute. A common type of such problems is those where operations are performed on qubits to generate an entangled quantum state, and then to sample that state to estimate its probability distribution [112].
The first proposal for a good test problem is owing to Aaronson and Arkhipov in 2010, in their boson sampling proposal [113], building on earlier work on the classical complexity of sampling problems [114,115].12 They were able to prove that computing the output probabilities of a random system of noninteracting bosons was in a complexity class (#P-hard) corresponding to computations thought to be difficult for classical computers to run. Moreover, under the plausible conjecture that these probabilities remain #P-hard to approximate, it would follow that classical computers cannot even sample a random output of a typical linear-optical network. For a quantum computer, providing such a sample (referred to as “qubit sampling”) could amount to demonstration of quantum supremacy. While boson sampling has been popular with experimentalists, and small-scale implementations have already been achieved in a number of labs, including a 6-photon experiment [116], it remains
___________________
12 The term “quantum supremacy” was coined by John Preskill in 2012, although work in this area began earlier.
challenging to push these experiments to the roughly 50 photons necessary to establish quantum supremacy [117].
A different approach for demonstrating quantum supremacy in superconducting qubits was proposed by the Google theory group in 2016 [118]. It was experimentally inspired, with quantum supremacy playing the role of a milestone on the way to building superconducting NISQ computers. Concretely, the proposal—Random Circuit Sampling (RCS)—called for implementing a random quantum circuit and measuring the output of the circuit. They conjectured that sampling from the output distribution of such random circuits is a hard problem classically. Recently, strong complexity-theoretic evidence for the classical hardness of RCS, on par with that for boson sampling, was given by Bouland et al. [119].
There are two main parts to a quantum supremacy proposal: the first is the definition of a computational task that could be experimentally realized in the near term, but which is prohibitively difficult for any algorithm running on a classical computer. The second is an efficient method for verifying that the quantum device actually carried out the computational task. This is particularly complicated, since the proposed algorithms are computing samples from a certain probability distribution (namely, the output distribution of the chosen quantum circuit). The first simplification to get around this validation problem is to choose n, the number of qubits, to be small enough (n ≈ 50) so that a classical supercomputer can actually calculate the output distribution of the chosen quantum circuit. This still leaves the challenge of verifying that the outputs of the quantum device are actually drawn from this (or a close-by) distribution. This too can be difficult to prove.
For this, the RCS supremacy model [120] proposes the computation of a score in the form of the cross-entropy between the distribution sampled from the device and the true output distribution of the chosen quantum circuit. It turns out that the cross-entropy score verifies that the two distributions are close, provided a simple condition is met—namely, that the entropy of the distribution sampled from the device is at least as large as the entropy of the true output distribution of the chosen quantum circuit. [121]. Unfortunately, it is not possible to verify this entropy condition using any reasonable number of samples—although it holds for many noise models, such as local depolarizing noise. A different proposal for verification uses the concept of heavy output generation (or HOG) [122] and can be provably shown to verify supremacy under a (nonstandard) complexity assumption. Last, a third verification proposal, binned output generation (BOG), simultaneously verifies HOG and cross-entropy, and is information theoretically optimal in some formal model [123].
A proof-of-concept test for this quantum supremacy algorithm was performed in 2017 on a 9-qubit device [124]. The error rate was shown to
be proportional to the number of operations multiplied by the number of qubits, with an average error per 2-qubit gate of about 0.3 percent. Simple extrapolation to a qubit device with around 50 qubits indicates that a quantum supremacy result should be possible with this architecture, and the Google hardware team (and others) are working hard to achieve this goal.
The approaches leave two questions unanswered. The first is how to perform verification without the entropy assumption (or a nonstandard complexity assumption). The second is the possibility of establishing quantum supremacy beyond the limit of the computing power of classical supercomputers, currently understood13 to correspond to on the order of about 50 qubits. A recent proposal shows how to provably carry out quantum supremacy based on post-quantum cryptography. Specifically, based on the hardness of the learning with errors (LWE) problem, the proposal gives a way of provably testing quantum supremacy for quantum computers with arbitrarily large numbers of qubits [125].
Finding: While several teams have been working to demonstrate quantum supremacy, this milestone has not yet been demonstrated (as of the time of publication of this report). Its achievement will difficult to establish definitively, and this target may continue to move as improvements are made to classical approaches for solving the chosen benchmark problem.
In summary, the pursuit of quantum supremacy has already achieved an interesting goal: the development of theoretical tools useful for rigorously analyzing the computational hardness of certain quantum problems that may soon be experimentally implementable. However, owing both to the uncertain nature of the hardness results (i.e., the reliance on nonstandard hardness conjectures) and to the restrictive nature of the noise models addressed by these results, there is much work remaining to be done.
3.4.3 Applications for an Ideal Quantum Computer
In the event of development of a robust, large-scale error-corrected quantum computer, the existing algorithms with known speedup are likely to be useful for solving any number of practical problems, or parts
___________________
13 While the exact number depends upon the specifications and approximations of the particular simulation, and this number will increase as classical methods improve, it is expected to remain at this order of magnitude for a significant amount of time. Recently, researchers have used a new classical approach to perform a single instance of the quantum supremacy task that would be achievable by a 70-qubit quantum device; however, this does not correspond to the full 100,000-instance quantum supremacy experiment proposed for a 50-qubit device, which has not yet proven achievable on a classical computer.
of problems. Perhaps the best-understood application of quantum algorithms is in the field of cryptography (specifically, defeating it), an application based directly on mathematics; these applications will be discussed in the next chapter. Quantum simulation, for both foundational and applied science, is also commonly raised as a potential “killer app,” especially in the field of quantum chemistry [126].
The electronic structure problem has received much attention, owing to its centrality to the fields of chemistry and materials science. This problem requires solving for the ground state energies and wave functions of electrons interacting in the presence of some external field, usually arising from atomic nuclei. Electronic structure defines chemical properties and the rates and products of chemical reactions. While classical computing approaches to this problem (such as density functional theory) are quite effective in many contexts (such as predicting molecular geometries), they often fail to reach the level of accuracy required to predict chemical reaction rates or distinguish between competing phases of correlated materials. This is especially true when the system involves transition metal elements (which are present in most catalysts). Quantum computers could enable efficient solutions to this problem in the classically intractable regime. In fact, one early quantum algorithm offers exponential speedup over classical approaches to calculation of chemical reaction rate constants [127]. This and other algorithms could open the door to significant insights about chemical reactions and phases of matter that have long eluded description by a systematic and predictive theory. Such results could also have commercial applications in areas such as energy storage, device displays, industrial catalysts, and pharmaceutical development.
3.5 THE POTENTIAL ROLE OF QUANTUM COMPUTERS IN THE COMPUTING ECOSYSTEM
While quantum chemistry, optimization (including machine learning), and defeating cryptography are the best-understood potential applications of an ideal quantum computer, the field is still in early stages—in terms of both algorithms, as discussed in this chapter, and devices, as will be discussed in Chapter 5. Existing algorithms may be modified or implemented in ways not yet anticipated; new algorithms will likely emerge as research continues. As a result, except for cryptography, it is not possible to predict the implications of quantum computers on various commercial sectors—the field is so young that these changes are not even on the horizon. For cryptography, the potential of a future quantum computer running Shor’s algorithm is sufficient to affect action today. These issues are described in Chapter 4.
As is clear from this chapter’s discussions, the ability to deploy known quantum algorithms could render some previously intractable
problems efficiently solvable. However, even a large error-corrected quantum computer would not be generally superior to a classical computer. In fact, quantum computers do not speed up many classes of problems, and the maturity of the classical computing ecosystem (including hardware, software, and algorithms) means that for these classes of problem, classical computing will remain the dominant computing platform. Even applications accelerated by a quantum computer, the parts accelerated are likely to comprise only a small component of the broader task in question. For the foreseeable future, a quantum processor is thus likely to be useful for performing only certain parts of certain tasks, with the remaining operations more efficiently carried out on a classical computer. Thus, a quantum computer is expected to serve as a co-processor to, rather than a replacement for, a classical computer. Furthermore, as will be discussed in Chapter 5, the physical implementation of any quantum computation will require a host of complex gating operations to be performed upon qubits maintained in a controlled environment, which will require the use of classical computers.
Finding: Quantum computers are unlikely to be useful as a direct replacement for conventional computers, or for all applications; rather, they are currently expected to be special-purpose devices operating in a complementary fashion with conventional processors, analogous to a co-processor or accelerator.
3.6 NOTES
[1] E. Bernstein and U. Vazirani, 1997, Quantum complexity theory, SIAM Journal on Computing 26(5):1411-1473.
[2] D. Simon, 1997, On the power of quantum computation, SIAM Journal on Computing 26(5):1474-1483.
[3] P. Shor, 1994, “Algorithms for Quantum Computation: Discrete Logarithms and Factoring,” pp. 124-134 in 35th Annual Symposium on Foundations of Computer Science, 1994 Proceedings, https://ieeexplore.ieee.org.
[4] R.J. Anderson and H. Wolf, 1997, Algorithms for the certified write-all problem, SIAM Journal on Computing 26(5):1277-1283.
[5] R.M. Karp, 1975, On the computational complexity of combinatorial problems, Networks 5(1):45-68.
[6] C.H. Bennett, E. Bernstein, G. Brassard, and U. Vazirani, 1997, Strengths and weaknesses of quantum computing, SIAM Journal on Computing 26(5):1510-1523.
[7] L.K. Grover, 1996, “A Fast Quantum Mechanical Algorithm for Database Search,” pp. 212-219 in Proceedings of the Twenty-Eighth Annual ACM Symposium on Theory of Computing, https://dl.acm.org/proceedings.cfm.
[8] S. Cook, 2006, “The P versus NP problem,” pp. 87-104 in The Millennium Prize Problems (J. Carlson, A. Jaffe, A. Wiles, eds.), Clay Mathematics Institute/American Mathematical Society, Providence, R.I.
[9] J. Preskill, 2018, “Quantum Computing in the NISQ Era and Beyond,” arXiv:1801.00862.
[10] L. Hales and S. Hallgren, 2000, “An Improved Quantum Fourier Transform Algorithm and Applications,” pp. 515-525 in 41st Annual Symposium on Foundations of Computer Science, 2000 Proceedings, https://ieeexplore.ieee.org.
[11] P.W. Shor, 1994, “Algorithms for Quantum Computation: Discrete Logarithms and Factoring,” pp. 124-134 in 35th Annual Symposium on Foundations of Computer Science, 1994 Proceedings, https://ieeexplore.ieee.org.
[12] R. Jozsa, 2001, Quantum factoring, discrete logarithms, and the hidden subgroup problem, Computing in Science and Engineering 3(2):34-43.
[13] A.Y. Kitaev, 1995, “Quantum Measurements and the Abelian Stabilizer Problem,” preprint arXiv:quant-ph/9511026.
[14] L.K. Grover, 1996, “A Fast Quantum Mechanical Algorithm for Database Search,” pp. 212-219 in Proceedings of the Twenty-Eighth Annual ACM Symposium on Theory of Computing, https://dl.acm.org/proceedings.cfm.
[15] C.H. Bennett, E. Bernstein, G. Brassard, and U. Vazirani, 1997, Strengths and weaknesses of quantum computing, SIAM Journal on Computing 26(5):1510-1523.
[16] G. Brassard, P. Hoyer, M. Mosca, and A. Tapp, 2002, Quantum amplitude amplification and estimation, Contemporary Mathematics 305:53-74.
[17] E. Farhi, J. Goldstone, and S. Gutmann, 2007, “A Quantum Algorithm for the Hamiltonian NAND Tree,” preprint arXiv:quant-ph/0702144.
[18] A. Ambainis, A.M. Childs, B.W. Reichardt, R. Špalek, and S. Zhang, 2010, Any AND-OR formula of size N can be evaluated in time N1/2+O(1) on a quantum computer, SIAM Journal on Computing 39(6):2513-2530.
[19] V. Giovannetti, S. Lloyd, and L. Maccone, 2008, Quantum random access memory, Physical Review Letters 100(16):160501.
[20] R.P. Feynman, 1982, Simulating physics with computers, International Journal of Theoretical Physics 21(6-7):467-488.
[21] D.S. Abrams and S. Lloyd, 1997, Simulation of many-body Fermi systems on a universal quantum computer, Physical Review Letters 79(13):2586.
[22] D. Aharonov and A. Ta-Shma, 2003, “Adiabatic Quantum State Generation and Statistical Zero Knowledge,” pp. 20-29 in Proceedings of the Thirty-Fifth Annual ACM Symposium on Theory of Computing, https://dl.acm.org/proceedings.cfm.
[23] D.W. Berry, A.M. Childs, R. Cleve, R. Kothari, and R.D. Somma, 2015, Simulating Hamiltonian dynamics with a truncated Taylor series, Physical Review Letters 114(9):090502.
[24] R. Babbush, D.W. Berry, I.D. Kivlichan, A. Scherer, A.Y. Wei, P.J. Love, and A. Aspuru-Guzik, 2017, Exponentially more precise quantum simulation of fermions in the configuration interaction representation, Quantum Science and Technology 3:015006.
[25] G.H. Low and I.L. Chuang, 2016, “Hamiltonian Simulation by Qubitization,” preprint arXiv:1610.06546.
[26] See, for example, G.H. Low and I.L. Chuang, 2017, Optimal Hamiltonian simulation by quantum signal processing, Physical Review Letters 118(1):010501.
[27] R. Babbush, D.W. Berry, I.D. Kivlichan, A.Y. Wei, P.J. Love, and A. Aspuru-Guzik, 2016, Exponentially more precise quantum simulation of fermions I: Quantum chemistry in second quantization, New Journal of Physics 18:033032.
[28] D.W. Berry, A.M. Childs, and R. Kothari, 2015, “Hamiltonian Simulation with Nearly Optimal Dependence on All Parameters,” pp. 792-809 in Proceedings of the 56th IEEE Symposium on Foundations of Computer Science, https://ieeexplore.ieee.org.
[29] S. McArdle, S. Endo, A. Aspuru-Guzik, S. Benjamin, and X. Yuan, 2018, “Quantum Computational Chemistry,” preprint arXiv:1808.10402.
[30] D. Wecker, M.B. Hastings, N. Wiebe, B.K. Clark, C. Nayak, and M. Troyer, 2015, Solving strongly correlated electron models on a quantum computer, Physical Review A 92(6):062318.
[31] C. Dykstra, G. Frenking, K.S. Kim, and G.E. Scuseria, 2005, Theory and Applications of Computational Chemistry: The First Forty Years, Elsevier, Amsterdam.
[32] M. Reiher, N. Wiebe, K.M. Svore, D. Wecker, and M. Troyer, 2017, Elucidating reaction mechanisms on quantum computers, Proceedings of the National Academy of the Sciences of the U.S.A. 114:7555-7560.
[33] G. Wendin, 2017, Quantum information processing with superconducting circuits: A review, Reports on Progress in Physics 80(10):106001.
[34] M. Reiher, N. Wiebe, K.M. Svore, D. Wecker, and M. Troyer, 2017, Elucidating reaction mechanisms on quantum computers, Proceedings of the National Academy of Sciences of the U.S.A. 114:7555-7560.
[35] B. Bauer, D. Wecker, A.J. Millis, M.B. Hastings, and M. Troyer, 2016, Hybrid quantum-classical approach to correlated materials, Physical Review X 6:031045.
[36] See J. Olson, Y. Cao, J. Romero, P. Johnson, P.-L. Dallaire-Demers, N. Sawaya, P. Narang, I. Kivlichan, M. Wasielewski, and A. Aspuru-Guzik, 2017, “Quantum Information and Computation for Chemistry,” preprint arXiv:1706.05413, for a good overview.
[37] R. Babbush, D.W. Berry, I.D. Kivlichan, A.Y. Wei, P.J. Love, and A. Aspuru-Guzik, 2017, Exponentially more precise quantum simulation of fermions in the configuration interaction representation, Quantum Science and Technology 3:015006.
[38] J. Olson, Y. Cao, J. Romero, P. Johnson, P.-L. Dallaire-Demers, N. Sawaya, P. Narang, I. Kivlichan, M. Wasielewski, and A. Aspuru-Guzik, 2017, “Quantum Information and Computation for Chemistry,” preprint arXiv:1706.05413.
[39] I.D. Kivlichan, J. McClean, N. Wiebe, C. Gidney, A. Aspuru-Guzik, G. Kin-Lic Chan, and R. Babbush, 2018, Quantum simulation of electronic structure with linear depth and connectivity, Physical Review Letters 120:11501.
[40] R. Babbush, C. Gidney, D.W. Berry, N. Wiebe, J. McClean, A. Paler, A. Fowler, and H. Neven, 2018, “Encoding Electronic Spectra in Quantum Circuits with Linear T Complexity,” preprint arXiv:1805.03662.
[41] G.H. Low and N. Wiebe, 2018, “Hamiltonian Simulation in the Interaction Picture,” preprint arXiv:1805.00675.
[42] D.W. Berry, M. Kieferová, A. Scherer, Y.R. Sanders, G.H. Low, N. Wiebe, C. Gidney, and R. Babbush, 2018, Improved techniques for preparing eigenstates of fermionic Hamiltonians, npj Quantum Information 4(1):22.
[43] D. Wecker, M. B. Hastings, N. Wiebe, B.K. Clark, C. Nayak, and M. Troyer, 2015, Solving strongly correlated electron models on a quantum computer, Physical Review A 92(6):062318.
[44] D. Poulin, M.B. Hastings, D. Wecker, N. Wiebe, A.C. Doherty, and M. Troyer, 2014, “The Trotter step size required for accurate quantum simulation of quantum chemistry,” arXiv preprint arXiv:1406.49.
[45] M.B. Hastings, D. Wecker, B. Bauer, and M. Troyer, 2014, “Improving Quantum Algorithms for Quantum Chemistry,” preprint arXiv:1403.1539.
[46] D. Poulin, A. Kitaev, D.S. Steiger, M.B. Hastings, and M. Troyer, 2018, Quantum algorithm for spectral measurement with a lower gate count, Physical Review Letters 121(1):010501.
[47] D. Wecker, B. Bauer, B.K. Clark, M.B.. Hastings, and M. Troyer, 2014, Gate-count estimates for performing quantum chemistry on small quantum computers, Physical Review A 90(2):022305.
[48] A.W. Harrow, A. Hassidim, and S. Lloyd, 2009, Quantum algorithm for linear systems of equations, Physical Review Letters 103(15):150502.
[49] A.M. Childs and W.V. Dam, 2010, Quantum algorithms for algebraic problems, Reviews of Modern Physics 82(1):1.
[50] D.W. Berry, A.M. Childs, A. Ostrander, and G. Wang, 2017, Quantum algorithm for linear differential equations with exponentially improved dependence on precision, Communications in Mathematical Physics 356(3):1057-1081.
[51] F.G.S.L. Brandao and K. Svore, 2017, “Quantum Speed-Ups for Semidefinite Programming,” https://arxiv.org/abs/1609.05537.
[52] I. Kerenidis and A. Prakash, 2016, “Quantum Recommendation Systems,” preprint arXiv:1603.08675.
[53] E. Tang, 2018, “A Quantum-Inspired Classical Algorithm for Recommendation Systems,” preprint arXiv:1807.04271.
[54] P.D. Johnson, J. Romero, J. Olson, Y. Cao, and A. Aspuru-Guzik, 2017, “QVECTOR: An Algorithm for Device-Tailored Quantum Error Correction,” preprint: arXiv:1711.02249.
[55] A. Kandala, K. Temme, A.D. Corcoles, A. Mezzacapo, J.M. Chow, and J.M. Gambetta, 2018, “Extending the Computational Reach of a Noisy Superconducting Quantum Processor,” arXiv:1805.04492.
[56] A.R. Calderbank and P.W. Shor, 1997, “Good quantum error-correcting codes exist,” Physical Review A, 54:1098-1106, arXiv:quant-ph/9512032.
[57] A. Steane, 1996, Simple quantum error correcting codes, Physical Review A 54:4741, arXiv:quant-ph/9605021.
[58] See, for example, E. Knill, 2005, Quantum computing with realistically noisy devices, Nature 434:39-44.
[59] P. Aliferis, D. Gottesman, and J. Preskill, 2006, Quantum accuracy threshold for concatenated distance-3 codes, Quantum Information and Computation 6:97-165, arXiv:quantph/0504218.
[60] W.K. Wootters and W.H. Zurek, 1982, A single quantum cannot be cloned, Nature 299(5886):802-803.
[61] M. Reiher, N. Wiebe, K.M. Svore, D. Wecker, and M. Troyer, 2017, Elucidating reaction mechanisms on quantum computers, Proceedings of the National Academy of the Sciences of the U.S.A. 114:7555-7560.
[62] A.G. Fowler, M. Mariantoni, J.M. Martinis, and A.N. Cleland, 2012, Surface codes: Towards practical large-scale quantum computation, Physical Review A 86:032324.
[63] For details on low-distance codes, see Y. Tomita and K.M. Svore, 2014, “Low-distance Surface Codes under Realistic Quantum Noise,” https://arxiv.org/pdf/1404.3747.pdf. For general replacement rules for the surface code, see, for example, A.G. Fowler, M. Mariantoni, J.M. Martinis, and A.N. Cleland, 2012, “Surface Codes: Towards Practical Large-Scale Quantum Computation, https://arxiv.org/abs/1208.0928. For concatenated and block codes, see, for example, P. Aliferis, D. Gottesman, and J. Preskill, 2005, “Quantum Accuracy Threshold for Concatenated Distance-3 Codes,” https://arxiv.org/abs/quant-ph/0504218, and K.M. Svore, D.P. DiVincenzo, and B.M. Terhal, 2006, “Noise Threshold for a Fault-Tolerant Two-Dimensional Lattice Architecture,” https://arxiv.org/abs/quant-ph/0604090.
[64] See, for example, M.B. Hastings, J. Haah, “Distillation with Sublogarithmic Overhead,” https://arxiv.org/abs/1709.03543;
J. Haah and M.B. Hastings, 2017, “Codes and Protocols for Distilling T, controlled S, and Toffoli Gates,” https://arxiv.org/abs/1709.02832;
J. Haah, M.B. Hastings, D. Poulin, and D. Wecker, 2017, “Magic State Distillation at Intermdediate Size,” https://arxiv.org/abs/1709.02789; and
J. Haah, M.B. Hastings, D. Poulin. and D. Wecker, 2017, “Magic State Distillation with Low Space Overhead and Optimal Asymptotic Input Count,” https://arxiv.org/abs/1703.07847.
[65] See, for example, Table II in M. Reiher, N. Wiebe, K.M. Svore, D. Wecker, and M. Troyer, 2017, “Elucidating Reaction Mechanisms on Quantum Computers,” https://arxiv.org/pdf/1605.03590.pdf, for detailed numbers on the cost of the T implementation for understanding reaction mechanisms on a quantum computer using Hamiltonian simulation.
[66] H. Bombin and M.A. Martin-Delgado, 2006, Topological quantum distillation, Physical Review Letters 97:180501, arXiv:quant-ph/0605138.
[67] See, for example, J.E. Moussa, 2016, Transversal Clifford gates on folded surface codes, Physical Review A 94:042316, arXiv:1603.02286;
C. Horsman, A. G. Fowler, S. Devitt, and R. Van Meter, 2012, Surface code quantum computing by lattice surgery, New Journal of Physics 14:123011, arXiv:1111.4022;
S. Bravyi and A. Cross, 2015, “Doubled Color Codes,” arXiv:1509.03239;
H. Bombin, 2015, Gauge color codes: Optimal transversal gates and gauge fixing in topological stabilizer codes, New Journal of Physics 17:083002, arXiv:1311.0879;
T.J. Yoder and I.H. Kim, 2017, The surface code with a twist, Quantum 1:2, arXiv:1612.04795.
[68] See, for example, S. Bravyi, M. Suchara, and A. Vargo, 2014, Efficient algorithms for maximum likelihood decoding in the surface code, Physical Review A 90:032326, arXiv:1405.4883;
G. Duclos-Cianci and D. Poulin, 2014, Fault-tolerant renormalization group decoder for abelian topological codes, Quantum Information and Computation 14:721-740, arXiv:!304.6100.
[69] J. Chiaverini, Di. Leibfried, T. Schaetz, M.D. Barrett, R.B. Blakestad, J. Britton, W.M. Itano, et al., 2004, Realization of quantum error correction, Nature 432(7017):602.
[70] D. Nigg, M. Mueller, E.A. Martinez, P. Schindler, M. Hennrich, T. Monz, M.A. Martin-Delgado, and R. Blatt, 2014, Quantum computations on a topologically encoded qubit, Science 1253742.
[71] S. Rosenblum, P. Reinhold, M. Mirrahimi, Liang Jiang, L. Frunzio, and R.J. Schoelkopf, 2018, “Fault-Tolerant Measurement of a Quantum Error Syndrome,” preprint arXiv:1803.00102.
[72] N.M. Linke, M. Gutierrez, K.A. Landsman, C. Figgatt, S. Debnath, K.R. Brown, and C. Monroe, 2017, Fault-tolerant quantum error detection, Science Advances 3(10):e1701074.
[73] R. Harper and S. Flammia, 2018, “Fault Tolerance in the IBM Q Experience,” preprint arXiv:1806.02359.
[74] A. Peruzzo, J.R. McClean, P. Shadbolt, M.-H. Yung, X.-Q. Zhou, P.J. Love, A. Aspuru-Guzik, and J.L. O’Brien, 2013, “A Variational Eigenvalue Solver on a Quantum Processor,” arXiv:1304.3061.
[75] D. Wecker, M.B. Hastings, and M. Troyer, 2015, Progress towards practical quantum variational algorithms, Physical Review A 92:042303.
[76] J.R. McClean, J. Romero, R. Babbush, and A. Aspuru-Guzik, 2016, The theory of variational hybrid quantum-classical algorithms, New Journal of Physics 18:023023.
[77] P.J.J. O’Malley, R. Babbush, I.D. Kivlichan, J. Romero, J.R. McClean, R. Barends, J. Kelly, et al., 2016, Scalable quantum simulation of molecular energies, Physical Review X 6:031007.
[78] R. Santagati, J. Wang, A.A. Gentile, S. Paesani, N. Wiebe, J.R. McClean, S.R. Short, et al., 2016, “Quantum Simulation of Hamiltonian Spectra on a Silicon Chip,” arXiv:1611.03511.
[79] G.G. Guerreschi and M. Smelyanskiy, 2017, “Practical Optimization for Hybrid Quantum-Classical Algorithms,” arXiv:1701.01450.
[80] J.R. McClean, M.E. Kimchi-Schwartz, J. Carter, and W.A. de Jong, 2017, Hybrid quantum-classical hierarchy for mitigation of decoherence and determination of excited states, Physical Review A 95:042308.
[81] J.R. Romero, R. Babbush, J.R. McClean, C. Hempel, P. Love, and A. Aspuru-Guzik, 2017, “Strategies for Quantum Computing Molecular Energies Using the Unitary Coupled Cluster Ansatz,” arXiv:1701.02691.
[82] Y. Shen, X. Zhang, S. Zhang, J.-N. Zhang, M.-H. Yung, and K. Kim, 2017, Quantum implementation of the unitary coupled cluster for simulating molecular electronic structure, Physical Review A 95:020501.
[83] See, for example, E. Farhi, J. Goldstone, and S. Gutmann, 2014, “A Quantum Approximate Optimization Algorithm,” arXiv:1411.4028;
E. Farhi, J. Goldstone, and S. Gutmann, 2014, “A Quantum Approximate Optimization Algorithm Applied to a Bounded Occurrence Constraint Problem,” arXiv:1412.6062;
E. Farhi and A.W. Harrow, 2016, “Quantum Supremacy through the Quantum Approximate Optimization Algorithm,” arXiv:1602.07674.
[84] J. Romero, J. Olson, and A. Aspuru-Guzik, 2017, Quantum autoencoders for efficient compression of quantum data, Quantum Science and Technology 2:045001.
[85] M. Benedetti, D. Garcia-Pintos, Y. Nam, and A. Perdomo-Ortiz, 2018, “A Generative Modeling Approach for Benchmarking and Training Shallow Quantum Circuits,” https://arxiv.org/abs/1801.07686.
[86] G. Verdon, M. Broughton, and J. Biamonte, 2017, “A Quantum Algorithm to Train Neural Networks Using Low-Depth Circuits,” arXiv:1712.05304.
[87] A. Peruzzo, J.R. McClean, P. Shadbolt, M.-H. Yung, X.-Q. Zhou, P.J. Love, A. Aspuru-Buzik, and J.L. O’Brien, 2013, “A Variational Eigenvalue Solver on a Quantum Processor,” arXiv:1304.3061.
[88] D. Wecker, M.B. Hastings, and M. Troyer, 2015, Progress towards practical quantum variational algorithms, Physical Review A 92:042303.
[89] J.R. McClean, J. Romero, R. Babbush, and A. Aspuru-Guzik, 2016, The theory of variational hybrid quantum-classical algorithms, New Journal of Physics 18:023023.
[90] P.J.J. O’Malley, R. Babbush, I.D. Kivlichan, J. Romero, J.R. McClean, R. Barends, J. Kelly, et al., 2016, Scalable quantum simulation of molecular energies, Physical Review X 6:031007.
[91] R. Santagati, J. Wang, A.A. Gentile, S. Paesani, N. Wiebe, J.R. McClean, S.R. Short, et al., 2016, “Quantum Simulation of Hamiltonian Spectra on a Silicon Chip,” arXiv:1611.03511.
[92] G.G. Guerreschi and M. Smelyanskiy, 2017, “Practical Optimization for Hybrid Quantum-Classical Algorithms,” arXiv:1701.01450.
[93] J.R. McClean, M.E. Kimchi-Schwartz, J. Carter, and W.A. de Jong, 2017, Hybrid quantum-classical hierarchy for mitigation of dechoherence and determination of excited states, Physical Review A 95:042308.
[94] J.R. Romero, R. Babbush, J.R. McClean, C. Hempel, P. Love, and A. Aspuru-Guzik, 2017, “Strategies for Quantum Computing Molecular Energies Using the Unitary Coupled Cluster Ansatz,” arXiv:1701.02691.
[95] Y. Shen, X. Zhang, S. Zhang, J.-N. Zhang, M.-H. Yung, and K. Kim, 2017, Quantum implementation of the unitary coupled cluster for simulating molecular electronic structure, Physical Review A 95:020501.
[96] P.-L. Dallaire-Demers, J. Romero, L. Veis, S. Sim, and A. Aspuru-Guzik, 2018, “Low-Depth Circuit Ansatz for Preparing Correlated Fermionic States on a Quantum Computer,” arXiv:1801.01053.
[97] E. Farhi, J. Goldstone, and S. Gutmann, 2014, “A Quantum Approximate Optimization Algorithm,” preprint arXiv:1411.4028.
[98] J. Smith, A. Lee, P. Richerme, B. Neyenhuis, P. W. Hess, P. Hauke, M. Heyl, D. A. Huse, and C. Monroe, 2015, “Many-Body Localization in a Quantum Simulator with Programmable Random Disorder,” arXiv:1508.07026.
[99] A. Mazurenko, C.S. Chiu, G. Ji, M.F. Parsons, M. Kanász-Nagy, R. Schmidt, F. Grusdt, E. Demler, D. Greif, and M. Greiner, 2017, A cold-atom Fermi-Hubbard antiferromagnet, Nature 545:462-466.
[100] R. Harris, Y. Sato, A. J. Berkley, M. Reis, F. Altomare, M.H. Amin, K. Boothby, et al., 2018, Phase transitions in a programmable quantum spin glass simulator, Science 361(6398):162-165.
[101] A.D. King, J. Carrasquilla, J. Raymond, I. Ozfidan, E. Andriyash, A. Berkley, M. Reis, et al., 2018, Observation of topological phenomena in a programmable lattice of 1,800 qubits, Nature 560(7719):456.
[102] D. Aharonov, W. van Dam, J. Kempe, Z. Landau, S. Lloyd, and O. Regev, 2004, “Adiabatic Quantum Computation is Equivalent to Standard Quantum Computation,” arXiv:quant-ph/0405098.
[103] T. Kadowaki and H. Nishimori, 1998, Quantum annealing in the transverse Ising model, Physical Review E 58(5):5355.
[104] T. Albash and D.A. Lidar, 2016, “Adiabatic Quantum Computing,” preprint arXiv:1611.04471.
[105] E. Farhi, J. Goldstone, S. Gutmann, J. Lapan, A. Lundgren, and D. Preda, 2001, A quantum adiabatic evolution algorithm applied to random instances of an NP-complete problem, Science 292(5516):472-475.
[106] W. Van Dam, M. Mosca, and U. Vazirani, 2001, “How Powerful Is Adiabatic Quantum Computation?,” pp. 279-287 in 42nd IEEE Symposium on Foundations of Computer Science, 2001 Proceedings, https://ieeexplore.ieee.org.
[107] A.P. Young, S. Knysh, and V.N. Smelyanskiy, 2008, Size dependence of the minimum excitation gap in the quantum adiabatic algorithm, Physical Review Letters 101(17):170503.
[108] See, for example, A. Selby, http://www.archduke.org/stuff/d-wave-comment-oncomparison-with-classical-computers/;
S. Boixo, T.F. Rønnow, S.V. Isakov, Z. Wang, D. Wecker, D.A. Lidar, J.M. Martinis and M. Troyer, 2014, Evidence for quantum annealing with more than one hundred qubits, Nature Physics 10:218-224;
T.F. Rønnow, Z. Wang, J. Job, S. Boixo, S.V. Isakov, D. Wecker, J.M. Martinis, D.A. Lidar, M. Troyer, 2014, Defining and detecting quantum speedup, Science 345:420;
J. King, S. Yarkoni, M.M. Nevisi, J.P. Hilton, and C.C. McGeoch, “Benchmarking a Quantum Annealing Processor with the Time-to-Target Metric,” https://arxiv.org/abs/1508.05087;
I. Hen, J. Job, T. Albash, T.F. Rønnow, M. Troyer, and D.A. Lidar, 2015, Probing for quantum speedup in spin-glass problems with planted solutions, Physical Review A 92:042325;
S. Mandrà, Z. Zhu, W. Wang, A. Perdomo-Ortiz, and H.G. Katzgraber, 2016, Strengths and weaknesses of weak-strong cluster problems: A detailed overview of state-of-the-art classical heuristics versus quantum approaches, Physical Review A 94:022337;
V.S. Denchev, S. Boixo, S.V. Isakov, N. Ding, R. Babbush, V. Smelyanskiy, J. Martinis, and H. Neven, 2016, What is the Computational Value of Finite-Range Tunneling?, Physical Review X 6:031015;
S. Mandrà, H.G. Katzgraber, and C. Thomas, 2017, The pitfalls of planar spin-glass benchmarks: Raising the bar for quantum annealers (again), Quantum Science and Technology 2(3);
J. King, S. Yarkoni, J. Raymond, I. Ozfidan, A.D. King, M.M. Nevisi, J.P. Hilton, and C.C. McGeoch, 2017, “Quantum Annealing amid Local Ruggedness and Global Frustration,” https://arxiv.org/abs/1701.04579;
S. Mandrà and H.G. Katzgraber, 2018, A deceptive step towards quantum speedup detection, Quantum Science and Technology 3:04LT01;
T. Albash and D.A. Lidar, 2018, Demonstration of a scaling advantage for a quantum annealer over simulated annealing, Physical Review X 8:031016.
[109] T. Albash, V. Martin-Mayor, and I. Hen, 2017, Temperature scaling law for quantum annealing optimizers, Physical Review Letters 119(11):110502.
[110] T. Albash, V. Martin-Mayor, and I. Hen, 2018, “Analog Errors in Ising Machines,” preprint arXiv:1806.03744.
[111] S. Jordan, 2018, “Algebraic and Number Theoretic Algorithms,” National Institute of Standards and Technology, last updated January 18, 2018, http://math.nist.gov/quantum/zoo/.
[112] A.W. Harrow and A. Montanaro, 2017, Quantum computational supremacy, Nature 549(7671):203.
[113] S. Aaronson and A. Arkhipov, 2011, “The Computational Complexity of Linear Optics,” pp. 333-342 in Proceedings of the Forty-Third Annual ACM Symposium on Theory of Computing, https://dl.acm.org/proceedings.cfm.
[114] M.J. Bremner, R. Jozsa, and D.J. Shepherd, 2010, Classical simulation of commuting quantum computations implies collapse of the polynomial hierarchy, Proceedings of the Royal Society of London A 467(2126):rspa20100301.
[115] B.M. Terhal and D.P. DiVincenzo, 2001, “Classical Simulation of NoninteractingFermion Quantum Circuits,” arXiv:quant-ph/0108010.
[116] J. Carolan, C. Harrold, C. Sparrow, E. Martín-López, N.J. Russell, J.W. Silverstone, P.J. Shadbolt, et al., 2015, Universal linear optics, Science 349(6249):711-716.
[117] P. Clifford and R. Clifford, 2018, “The Classical Complexity of Boson Sampling,” pp. 146-155 in Proceedings of the Twenty-Ninth Annual ACM-SIAM Symposium on Discrete Algorithms, https://www.siam.org/Conferences/About-SIAM-Conferences/Proceedings.
[118] S. Boixo, S.V. Isakov, V.N. Smelyanskiy, R. Babbush, N. Ding, Z. Jiang, M.J. Bremner, J.M. Martinis, and H. Neven, 2017, “Characterizing Quantum Supremacy in Near-Term Devices,” arXiv:1608.00263.
[119] A. Bouland, B. Fefferman, C. Nirkhe, and U. Vazirani, 2018, “Quantum Supremacy and the Complexity of Random Circuit Sampling,” arXiv:1803.04402.
[120] S. Boixo, S.V. Isakov, V.N. Smelyanskiy, R. Babbush, N. Ding, Z. Jiang, M.J. Bremner, J.M. Martinis, and H. Neven, 2017, “Characterizing Quantum Supremacy in Near-Term Devices,” arXiv:1608.00263.
[121] A. Bouland, B. Fefferman, C. Nirkhe, and U. Vazirani, 2018, “Quantum Supremacy and the Complexity of Random Circuit Sampling,” arXiv:1803.04402.
[122] S. Aaronson and L. Chen, 2017, “Complexity-Theoretic Foundations of Quantum Supremacy Experiments,” pp. 22:1-22:67 in 32nd Computational Complexity Conference, CCC 2017 (R. O’Donnell, ed.), Volume 79 of LIPIcs, Schloss Dagstuhl—Leibniz-Zentrum für Informatik.
[123] A. Bouland, B. Fefferman, C. Nirkhe, and U. Vazirani, 2018, “Quantum Supremacy and the Complexity of Random Circuit Sampling,” arXiv:1803.04402.
[124] C. Neill, P. Roushan, K. Kechedzhi, S. Boixo, S.V. Isakov, V. Smelyanskiy, R. Barends, et al., 2017, “A Blueprint for Demonstrating Quantum Supremacy with Superconducting Qubits,” arXiv:1709.06678.
[125] Z. Brakerski, P. Christiano, U. Mahadev, U. Vazirani, and T. Vidick, 2018, “Certifiable Randomness from a Single Quantum Device,” arXiv:1804.00640.
[126] K. Bourzac, 2017, Chemistry is quantum computing’s killer app, Chemical and Engineering News 95(43):27-31.
[127] D.A. Lidar and H. Wang, 1999, Calculating the thermal rate constant with exponential speedup on a quantum computer, Physical Review E 59(2):2429.






































