Semantic Matrices
G.PATRICK MEREDITH
ABSTRACT. The semantic matrix is a grap hical device for plotting in a standard conventional form whatever precise elements of meaning have been ascertained from the semantic analysis of a concept.
The intended use of the device is to provide standard descriptions of the structure of conceptual stimuli in order to facilitate the comparison and replication of researches on concept-formation, communication, and comprehension.
The device may thus be compared with the standard Cartesian graph-convention for translating algebraic functions into geometrical forms The. notion may be regarded as a development of the “matrix-function” introduced by Whitehead and Russell in the Principia Mathematica. This was conceived as an array of propositions. The semantic matrix is a generalization of this.
Any array of symbols having determinate meanings whose interrelations are expressed by spatial positions may be said to constitute a semantic matrix. Pascal’s triangle of binomial coefficients is an example. But we are not restricted to numerical elements. The elements, however, must be clearly defined, both as regards semantic content and as regards syntactic function. This approach to the meaning of conceptual words reveals that the comprehension of such words often entails the grasp of a considerable wealth of essential implications. The semantic analysis may result in a hierarchy of conceptual elements, analogous to the Fourier series resulting from the analysis of a complex wave-form. This richness of meaning is described as “benign ambiguity.”
The formal theory developed in the present paper defines the referential elements, the syntactic functions, the matrical structure, and the principal variables in the design of semantic matrices. An inductive theory can be developed from a survey of existing graphic devices but this will demand prolonged research. A constructive theory is here presented in which certain arbitrary conventions are set up and their use is indicated.
In the field of scientific communication we have to deal not only with communication between experts or communication between the expert and the public (i.e., popularization) but also between experts in different fields, unfamiliar with one another’s concepts. In an age of interdisciplinary projects this last type of communication is of especial importance. The Cartesian graph provides one invaluable medium of interdisciplinary communication, but it is restricted to certain types of meaning only. The
G.PATRICK MEREDITH Department of Psychology, The University, Leeds, England.
constructive theory here offered deals first with some of the contextual problems arising in the analysis of concepts and goes on to establish logical conventions for the construction of matrices.
When logic is transposed from the context of philosophical discrimination to one of practical communication, new insights appear. In particular the traditional subject-predicate dichotomy is found to have a new psychological and linguistic significance. Again the class-calculus, Euler’s circles, and the theory of sets, when stripped of non-essentials, yield a simple graphical device very similar to a Cartesian graph in which an unlimited range of syntactic forms can be expressed, once the conventions are grasped. Each of these forms reveals a certain “inferential potential” which is of direct importance in comprehension and communication.
The conventions used here are based on a system of logical forms constituting a logical calculus designed for the analytical problems arising in research on the comprehensibility of scientific and technical reports and published in a separate paper (1).
The control of ambiguity
CONCEPTUAL AND INSTRUMENTAL FORMS
The concept of the semantic matrix is a development of the logical matrix as originally presented by Whitehead and Russell in Principia Mathematica. Quoting from the Introduction to the First Edition, 1910:
When something is asserted or denied about all possible values or about some [undetermined] possible values of a variable, that variable is called apparent, after Peano. The presence of the words all or some in a proposition indicates the presence of an apparent variable; but often an apparent variable is really present where language does not at once indicate its presence. Thus for example “A is mortal” means “there is a time at which A will die.” Thus a variable time occurs as apparent variable.
Whatever may be the instances of propositions not containing apparent variables, it is obvious that prepositional functions whose values do not contain apparent variables are the source of propositions containing apparent variables, in the sense in which the function φx is the source of the proposition (x) · φx. For the values for φx do not contain the apparent variable x, which appears in (x) φx; if they contain an apparent variable y, this can be similarly eliminated, and so on. This process must come to an end, since no proposition which we can apprehend can contain more than a finite number of apparent variables, on the ground that whatever we can apprehend must be of finite complexity. Thus we must arrive at last at a function of as many variables as there have been stages in reaching it from our original proposition, and this function will be such that its values contain no apparent variables. We may call this function the matrix of our original proposition and of any other propositions and functions to be obtained by turning some of the arguments to the function into apparent variables. Thus, for example, if we have a matrix-function whose values are φ (x,y), we shall derive from it
(y) · φ (x>y), which is a function of x,
(x) · φ (x,y), which is a function of y,
(x,y) · φ (x,y), meaning “φ (x,y) is true with all possible values of x and y.” This last is a proposition containing no real variable, i.e., no variable except apparent variables.
It is thus plain that all possible propositions and functions are obtainable from matrices by the process of turning the arguments to the matrices into apparent variables.
There are two points to note about this account. The first is that the matrix is conceived as a source of propositions. It is a condensed symbolism from which, by following certain rules, a series of consequential propositions may be obtained deductively. We may compare it with an algebraic matrix, say
A=aij
from which, by giving i and j respectively all the values from 1 to m and 1 to n, we obtain the extended form

The second point is that whereas in algebra the presentation in the extended form is often deemed essential, the prepositional matrix is nowhere presented in extended form in the Principia. I shall distinguish these two ways of using matrices as the “conceptual use” (non-extended) and the “instrumental use” (extended). For it is by spreading the elements of the matrix out in space that we are enabled to develop the consequences of their mutual relations. The spatial extension functions as an instrument of thought.
Later authorities on logic have indeed made some small use of extensional forms, the most obvious example being the truth tables introduced by Wittgenstein. This is a clear illustration of the fruitfulness of extended matrices as instruments of thought, for these tables enable the truth or falsity to be determined for logical propositions involving combinations of logical constants to any degree of complexity.
An extension of this technique is given by Bochenski (6) in a conveniently succinct notation for the logical constants. For example implication is symbolised thus:
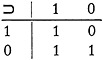
Here the truth-values in the lower right-hand quadrant are each a sort of
product of the values in the row and column headings. It is as if we said:
|
1×1=1 |
1×0=0 |
|
0×1=1 |
0×0=1 |
(This is the peculiar arithmetic of “material implication.” For the proposition “p implies q” is false only for the case when p is true and q is false, i.e., 1×0= 0.)
OPERATIONAL USE OF SPATIAL RELATIONS
The purpose of these examples is to stress the instrumental value of the spatial extension of symbols. From this point of view we may regard Descartes and Cayley as being complementary influences in the history of mathematics. For whereas Descartes related quantity and space through “algebraic geometry,” we might say that Cayley completed the relation by inventing what is essentially a “geometric algebra.” Many mathematical expressions, e.g., Pascal’s triangle, gain in significance when we perceive that the spatial arrangement-endows the geometric relations of the elements with a specific operational connotation. For consider the first few rows of the triangle:

The rule is that the sum of any two adjoining elements yields the element on the next line under the point midway between them. Clearly we are free to attach any rule we please to any spatial relation. We can thus generate an indefinite variety of extended symbolic forms. The algorithms for the four fundamental operations of arithmetic can be viewed in this light, as can the rules for vulgar fractions. There is, in fact, a kind of tacit spatial grammar at work throughout the whole of mathematical symbolism. We do not need to go into two dimensions to appreciate this. The simple algebraic symbolism for a product, xy, is a tacit use of linear juxtaposition to symbolize an operation. But of course the power of the matrix notation lies in the greater range of spatial relations which are opened up by a two-dimensional arrangement.
GENERALIZATION OF STATUS
But whereas in algebra the elements of a matrix are, in general, deemed to be quantities of some type or other, or at any rate quantitative operators (such as differentials), the propositional matrix of the Principia points to a much more general concept. The elements need not be quantitative. They can have any logical status whatever. And the spatial relations between elements can be associated with any rules of operation to suit our convenience. It should be
evident that we have here a symbolic device of exceptional generality and power awaiting precise development. For insofar as any concept has a logical structure which can be made articulate, i.e., expressed as a group of logically related elements, it can be represented as a matrix. And by the fact of possessing a defined logical status, the matrix can enter into the operations of a logical calculus. It is to this general concept that I have assigned the name “Semantic Matrix.”
COMMUNICATION OF SCIENTIFIC CONCEPTS
On the mathematical side a development analogous to that of the tensor calculus may be envisaged for these functions. But in view of the endless variability in the logical status of their elements (and hence in each type of matrix as a whole) some pragmatic criteria may be desirable in order to ensure that the development does not become a trivial proliferation of pretty patterns. “Pragmatic” can here be taken in two senses, viz., (1) criteria of relevance to the systematic development of symbolic logic or (2) criteria of relevance to the manipulation of concrete concepts such as those occurring in science. Both developments are desirable, but in this paper I shall pursue the second since the concept of the semantic matrix did, in fact, arise in a context of practical research on the communication of scientific concepts.1 A word or two on this problem will indicate the need for such a technique as that provided by the semantic matrix.
It is popularly supposed that the main reason for the difficulties encountered by the non-specialist seeking to understand a scientific document is the scientist’s use of “jargon.” Now it is true that scientists whose daily preoccupation is with physical problems do not always display the same facility with words as some of their colleagues for whom words are the stock-in-trade. But this is surely only a minor and remediable source of difficulty. The major source lies in the inherent complexity of the concepts to be communicated. Often an explanation in simple words, whilst theoretically possible, can be achieved only at the price of such prolixity as to defeat the ends of the explanation. (The analysis of a single word often occupies, for example, a paper of five to ten thousand words in the Proceedings of the Aristotelian Society.)
ANALOGY WITH RADIO COMMUNICATION
Any attempt to achieve an adequate solution of the problem of communicating scientific concepts through mere verbal simplification must in the long run prove abortive. I found a more radical approach imperative. If we con-
sider the partially analogous problem of radio communication we get some hint of a possible solution. The solution was in two stages: (1) the understanding of the nature, structure and control of electromagnetic radiation, and (2) the design of transmitters and receivers to permit resonance in the latter to the controlled emissions of the former.
In our problem we have, corresponding with the flow of radiation, a flow of scientific concepts emanating from the scientific journals. Our first task is therefore to understand the nature, structure, and control of this flow. For this we need something analogous to Clerk Maxwell’s equations. The analogy may here be pursued even more closely (bearing in mind the dangers in all analogy).
The inseparability of electric and magnetic occurrences and the curiously reciprocal relations between them formed the substance of Faraday’s fundamental discoveries and were subsequently formalized by Clerk Maxwell. There is likewise a duality in every scientific concept. On the one side it refers to concrete experiences and on the other to logical categories. Indeed this is true of ordinary words in a sentence. Every word has a “meaning” to convey and every word likewise exerts some grammatical function in the sentence. And these two, though different, are inseparable, except through a process of abstraction. Through abstraction logic can deal with the functional aspect of words apart from their meanings, and semantics can deal with their concrete references. But if either discipline strays too far from the other it tends towards triviality. At the same time we have as yet no adequate “logic of intensions” by which the two can be functionally joined, and logicians display an understandable reluctance to sacrifice their freedom in the realm of abstraction in the interests of concrete interpretations. Approaching the duality from the other side, viz., from the problem of communicating concepts I see in Russell’s propositional matrix the first hint of a functional bridge between logic and semantics. The semantic matrix represents an underpinning of this bridge to permit the passage of traffic.
THE CONTROL OF AMBIGUITY
Ambiguity plays a little-understood role in scientific communications. It may take two forms, “benign” or “malignant.” In the benign form it adds to the overt meaning of a term a succession of underlying layers of meaning which amplify and enrich the overt meaning. The depth of meaning to which any individual reader can penetrate is a function of his own conceptual equipment. Malignant ambiguity is the more usually understood sense of the term. Here a confused choice between alternative and independent or even incompatible meanings confronts the reader. When a concept can be expressed as a semantic matrix the malignant ambiguity is minimised and the benign ambiguity is given overt expression.
Again using analogy we may compare Fourier’s approach to the flow of heat2 in which earlier attempts by Lagrange and Dirichlet to express functions as sums of sinusoidal components were superseded by a quite general theorem thereby establishing the so-called “Fourier series” now in universal use. In our present terminology the coefficients of a Fourier series may be regarded as the overt expression of the benign ambiguity latent in the original function. What we seek in the semantic matrix is the equivalent in logical categories of the expression of successive refinements of algebraic “meaning” in a complex function.
Formal theory of semantic matrices
THE ELEMENTS
Definitions
-
A semantic matrix is a display of referential elements.
-
A referential element is a material sign conveying a meaning to a human respondent.
-
A display is an arrangement of elements in a spatial framework according to some ordering principle.
-
Semantic matrices develop functional properties in so far as their elements are assigned characteristic syntactic functions.
-
The syntactic function of a sign is a rule of usage whereby the sign enters into characteristic relations with other signs to establish a matrical structure of signs.
-
The matrical structure of a semantic matrix enables it to enter into inter-matrical relations with other semantic matrices.
Examples
-
An ordinary grammatical sentence is a semantic matrix. The words are the referential elements. The parts of speech are the syntactic functions. The linear arrangement is the display. The ordering principle is determined by the rules of grammar.
-
Maxwell’s colour triangle is also a semantic matrix. Here the referential elements are points either on the periphery or within the interior. These points may or may not bear labels. They refer to colours formed by mixing three primary hues in differing proportions. The syntactic functions of all the points may be described as “adjectival” since each refers to a colour-quality. The triangular arrangement is the display. The ordering principle is the relation between position and proportion.
Comparison of examples
-
The first display is a linear array; the second is two-dimensional. The first set of elements exhibits a mixture of syntactic functions—it may be called “hetero-typic.” The second contains elements all identical in function: it is “homo-typic.” In the first the ordering principle is grammatical. In the second it is mathematical.
Further examples
-
The Periodic Table of Elements. A family tree. A paradigm for the declension of a Latin noun. A determinant.
Comment
-
It will be seen that semantic matrices vary over a wide range of instances. But in every instance we have a display of meanings compactly expressed and arranged in such a way as to exhibit systematic relations. The properties of such displays, both formal and functional, merit a thorough analysis. Such an analysis would provide a basis for a general grammar of sign-systems. It would also facilitate the consistent treatment of many problems of communication. The above examples concern matrical structures only, not inter-matrical relations. The latter cannot be discussed profitably until we have formalized intra-matrical syntax.
PRINCIPAL VARIABLES
Definitions
-
Every semantic matrix has four characteristics:
-
Constitution, i.e., the visual appearance of the constituent elements,
-
Structure, i.e., the spatial arrangement of the elements,
-
Functional Character, i.e., the totality of syntactic functions exhibited.
-
Reference, i.e., the field of meanings involved.
-
Prescription
-
Since the matrix is a spatial display the primary character of the elements is visual. Whenever possible every element is to be assigned a phonetic rendering to facilitate communication. In the translation suitable cues to spatial structure are to be provided.
Example
-
x5 is a simple visual matrix. The same, read aloud as “ex to the fifth” is
-
the phonic counterpart. The words “to the” give the cue to the position of “5.”
Prescription
-
The visual elements may take any form whatever—pictorial, hieroglyphic, lexical, symbolic, geometrical, including mere points. A reason should always be given for the choice of form.
Prescription
-
In the spatial arrangement of the elements the geometric relations should be correlated with the logical relations between the elements. This applies not only to juxtaposed elements but ideally to any two elements.
Example
-
A family tree well illustrates the exact correlation of geometric with logical relations. The systematic family connexion between any two persons in the tree is immediately deducible from the sequence of vertical and horizontal steps. But it must be observed that such deductions are not solely a matter of geometry. The sex and marital status of each person are involved in the deduction.
Prescription
-
Elements are not, in general, mere points having nothing but geometrical relations with one another. They are symbols having not only semantic reference but a certain syntactic function.
Discussion
-
The theory can develop in two directions: (i) towards a systematic analysis of existing usage, and (ii) towards a system of rules for constructing semantic matrices for specified purposes. Since we are working towards a novel conception, viz., a geometrical syntax, whose working is not easy to anticipate, it is advisable to work empirically at first. Innumerable examples of tabular and other non-linear arrangements of words and symbols already exist. Grammarians have attended exclusively to the linear arrangement of words in sentences. This conventional grammar must now be regarded as a particular case of a very much more extensive system, just as Aristotelian logic has turned out to be a special case of the much wider system of symbolic logic. The richness of the field to be explored can be illustrated by the Periodic Table of Chemical Elements. The power of this visual display in generating systematic inferences concerning relations between its constituents indicates the latent potentiality of our nascent geometrical syntax.
Application of the principles
We come now to what is perhaps the central principle in the theory of semantic matrices. It must be borne in mind that their primary function is to facilitate understanding. To understand a concept is to apprehend correctly all the relations which determine its structure. This means not only grasping the fact that certain relations hold between certain terms but also seeing that the nature of the terms permits those relations to hold and that the global character of the concept determines their occurrence. For example, to understand the ecology of a hedgerow we have to understand that a whole system of predatory, parasitic, nutritive, and other relations hold between the various species of organisms in the hedgerow; that the nature of these organisms permit these relations and that the size, situation, and climatic exposure of the hedgerow determine the persistence of these relations, so that an ecological balance is maintained. This is a familiar enough concept for the trained biologist, but the function of semantic matrices is to analyse the problem of the learner faced with unfamiliar concepts.
A caterpillar, a hawthorn, a bird, a micro-organism, such may be the familiar subject-matter. But how familiar are they? Each has thousands of genes conspiring to produce innumerable characters. Through these characters the organism enters into relations with other organisms. To be “familiar” with a caterpillar may be no more than to recognize it at sight. To understand its role in an ecological system demands more than this. We cannot simply express the relation between two organisms, as the logicians do, by “x R y.” We have to find expression for what it is in x and in y which enables R to hold between them. We are not concerned with merely asserting a relation but with communicating an understanding of how the relation comes to hold. This demands that the meanings of x and y be expanded sufficiently to indicate the basis of the relation. The function of the semantic matrix is to supply this expansion of meaning.
As already indicated we can regard any visual expression of meanings as a semantic matrix but obviously some are much more explicit than others in their representation of meaning and structure. The position, then, is that countless semantic matrices already exist, though unnamed as such, but their geometric syntax (i.e., the logical relations expressed in the relative spatial dispositions of the elements) is commonly unstated and unexplored. The reason for this neglect is not far to seek. This is not a problem in pure mathematics, or in grammar, or in logic. It is one which necessarily draws upon all three and more besides. A new and even more resourceful George Boole is needed
to delineate the cartography of this new domain of logic. It had better be a young man for much fresh thinking is needed and the territory will need a lifetime to explore.
In a short introduction I can only indicate what seem to me the two main directions which developments must take. I shall call these the inductive theory and the constructive theory, respectively. The first sets out to explore the existing forms of semantic matrices and to establish what may be called their “natural history.” From this may be derived an empirical taxonomy. Thence the inquiry will branch into two directions. One will seek to formulate the principles of geometric syntax implicitly and intuitively employed by the authors of the existing matrices, and to separate those which do display logical order from those which do not. The other, taking the matrices as communicative devices which have to be perceived, interpreted, and comprehended, will investigate, by the methods of experimental psychology, the cognitive processes by which these matrices convey their meanings. We know something of the perception of geometric forms and something of the psychology of reading, but what hidden principles are at work in the interpretation of symbolic forms spread out in geometric arrangements? Such will be the quest in the inductive theory.
In the constructive theory we shall start not from existing forms of representation but from logical forms. Portions of knowledge to be communicated are translated into these logical forms and then arranged geometrically according to certain arbitrary but systematic codes. The knowledge is also expressed in conventional textual fashion. Experiments in comprehension are then carried out. The method, briefly, is as follows: a sufficiently large group of suitable readers is split in half. The topic to be communicated is expressed both conventionally and in a document based on analysis by semantic matrices. Both versions are split in half. One version is presented to one half-group of readers, the other version to the other half-group. For the second half of the topic the versions are changed over so that each half-group is “exposed” to both types of version. The tests of comprehension and the methods of scoring are both of unusual design, specially adapted to yield the information desired.
Briefly the information we seek in these experiments is this: which kinds of knowledge are more readily communicated conventionally and which kinds by documents derived from semantic matrices? There are, of course, many kinds of textual expression and many kinds of geometric arrangement and hence an extensive programme of experimentation is required. In the end we have to compare the best we can do in textual expression with the best in semantic matrices before deciding that one or other is superior, and even then
this superiority refers to the communication of only certain kinds of knowledge.
The motivation of this development lies in the need to improve our methods of communicating scientific knowledge, whether in education, in technology, in scientific journalism or in research. The impact of automation and its associated developments on our patterns of occupation and social organization is so forceful that unless quite radical changes in our methods of communication can be introduced only a technocratic dictatorship will be able to hold society together. This is not a matter of improving our technical media of communication, indeed it is these which are setting the pace. It is in the processes of interpretation and comprehension that our problem lies. It is useless to step up the bombardment of the human organism by pellets of information unless the pellets are so organized as to be capable of faster assimilation.
We have hitherto failed to correlate two fundamentally distinct modes of apprehension, viz., the linear reception of linguistic information in time and the two-dimensional reception of structural information on a surface. The fact that scanning-processes can convert the latter into the former must not blind us to the essential differences between the two modes of perception. It may well be that linear information, after reception in time, becomes spread out in cerebral space. It is true that given a well-learnt diagram we can wander about in it mentally building up our understanding by detecting its internal relationships. We can even reconstruct such a diagram from verbal descriptions. But are these processes efficient? Every shift of the focus of attention demands a fresh effort of recall. It is not in the nature of the brain substance to keep all the parts of a cognitive pattern simultaneously at the same level of vividness. But ink on paper preserves its sharpness indefinitely.
The above indicates the limitations of purely oral exposition. In a somewhat lesser degree it applies to verbal expositions presented textually. For although a printed page is two-dimensional, the printed language is normally presented in lines of type. It is true that very expert readers are able to take in the sense of a paragraph or even a whole page apparently at a glance, but this accomplishment is not widespread among those most in need of aids to comprehension. It is probably effective only with relatively familiar subject-matter and is not likely, for example, to operate for a physicist seeking a rapid grasp of the principles of genetics. And today many of the acutest problems of communication arise in the fields of inter-disciplinary research.
The development of semantic matrices is necessarily based on mathematical analogies. A caution is needed here. Analogies are notoriously liable to misuse. Yet the whole development of science and mathematics has rested on the triumphant exploitation of analogy. We shall be dealing with qualitative
variables akin to the terms of symbolic logic (but with an intensional reference) more often than with the quantitative variables of elementary algebra. But we shall speak of functions, and here it should be pointed out that for many purposes, even in algebra, functions are dealt with without any guarantee that their equations are known. We must not identify the function with its equation. A function expresses a certain distribution of values. The equation specifies the exact relation of dependence between the dependent and independent variables. The function exists as an empirical fact whether we can write down its equation or not. Thus in speaking of functions we are referring to patterns of values of variables without having to commit ourselves to the possibility of algebraic treatment. Indeed for many of the problems of communication the latter would be irrelevant. But it also follows that in any mathematical analogy we may use we must guard each step against any illicit importation of purely algebraic implications. What we seek to follow here are the strategies by which the great algebraists of the 19th century, Galois, Hermite, Kronecker, Cayley, Sylvester, Hilbert, and the rest, transformed their science, by attention to topological and other non-quantitative relations. And since we are dealing with problems in the mapping of knowledge, we shall also draw upon the geometric insight of Riemann and the automorphic functions of Poincaré.
Semantic matrices form part of a wider discipline, viz., the modular calculus which deals with the mathematical problems of epistemic communication (1). An outline of the concepts which have guided these developments is needed here in order to indicate the reason for the special character of semantic matrices.
The standard situation from which we start is that of a reader studying a scientific document. What are the factors determining his understanding? The document, in general, is about certain objects, organisms, instruments, etc., and may give an account of certain phenomena associated with these objects, certain laws, principles and theories, and the vocabulary and symbols required for the exposition. Some of the material of the document must be familiar to the reader, otherwise he has no foothold, e.g., certain common properties of objects and some of the vocabulary. On this basis of familiarity (the “subject-matter”) the writer has to construct unfamiliar concepts (the “predicate-matter”). Obviously there is no problem of comprehension unless some of the material is unfamiliar. For example the subject-matter might be a set of radio-components and the predicate-matter might be a radio circuit.
We assume that the reading is purposive. The reader wants to master the predicate-matter, either in order to construct the radio-set or to improve his knowledge of radio-theory, or both. To determine whether the document is
successful in fulfilling its communicative function we must therefore submit the reader to a practical test or a written test or both. Obviously his understanding may vary considerably in both depth and extent. Our design of the test will be an expression of the kind of understanding we want for him.
This whole situation is schematized in “The Square of Communication,” Fig. 1, presented in a symposium on semantics at the British Association for the
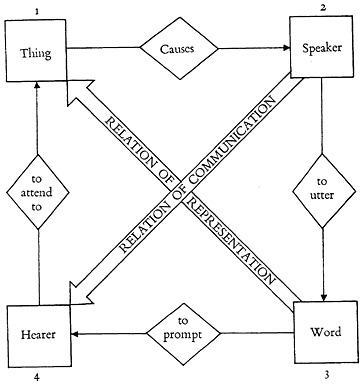
FIGURE 1. The square of communication.
Advancement of Science, Bristol, 1955 (2). For our present purpose the square may be elaborated and modified a little (Fig. 2). The original square was a development from the famous triangle of Ogden and Richards (3).
Now it has been assumed that the writer of the document is also the investigator or inventor of the original predicate-matter. But often this is not the case and, in general, it is better to introduce another agent into the situation. For the specialist who investigates a given field is not necessarily the best person to explain his discovery to the non-specialist. If he is a good research-worker his whole heart should be in the job and it would be a distraction to have to consider the linguistic and psychological problems of communication. So we introduce a “communicator” whose function is first to understand the original report of the scientist, couched in the latter’s own jargon and often
well-nigh incomprehensible style, and second to translate this into a form adapted to the needs of the reader.
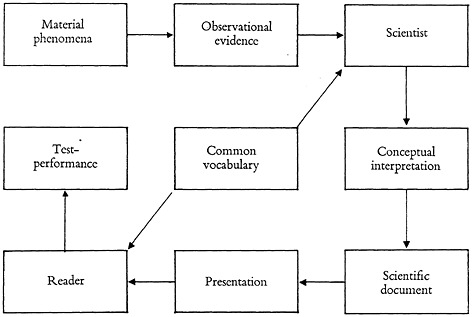
FIGURE 2. Documentary communication.
Now this situation provides us with four patterns of information to which we shall give distinctive names since they are fundamental in the whole development:
-
The pattern of information in the familiar subject-matter, called the Corpus.
-
The pattern of information in the novel predicate-matter, called the Scriptum.
-
The pattern of information in the communicator’s document, called the Modus.
-
The pattern of information in the test-results, called the Modulus.
The modular calculus is a system of logical variables and rules of operation by which any given pattern of information can be expressed in symbolic form. The pattern thus constitutes a map. The structure of the variables in such a map will be called a map-function. We thus have four types of function, the C-function (Corpus), the S-function (Scriptum), the D-function (Modus) and the L-function (Modulus).
Before considering the variables themselves and the matrices in which their meanings are expanded, we need to give some indication of the way in which these concepts work together to throw light on communication. Each of our
four patterns may be envisaged as occupying a screen. From each screen to the next is a kind of optical projection process. But this has to pass through a kind of medium in which the projection pattern undergoes, or may undergo, various modifications. These may be (i) losses, (ii) distortions, (iii) gains. Thus, in general, no two of the patterns are identical, but they will have, or should have, a good deal in common. In addition to the map-functions we therefore have a series of projection-functions, representing the action of the medium in modifying the map-functions.
We have already said that the Corpus represents the body of material information with which the reader is assumed to be familiar and on which the communication of the novel information is to be based. An epistemological point arises here. This information is derived from previous experience which the reader is assumed to have had. It is this experience which provides our first projection-function. The directly experienced field of material objects is called Z. It is non-linguistic and cannot be incorporated in a document. The variables in which it is expressed in the document are called “types” in the modular calculus. The variables of Z are called “sub-typical” variables. The process by which sub-typical variables give rise to types is deemed to be the concern of epistemology. The field of epistemic communication is a homogeneous documentary field. Thus the first projection-function by which Z gives rise to C is the business of epistemology and is outside our present province. The modular calculus provides formal definitions of its types in terms of the symbols for sub-typical variables but is not concerned with determining the nature of the latter.
In most documents the Corpus and the Scriptum are rolled into one. The familiar subject-matter and the unfamiliar predicate-matter are intertwined. This is almost a necessity of language, which requires both nouns and verbs in its sentences, and this probably has a good psychological reason. But for our purposes the two must be sorted out and it is part of the business of epistemic analysis to separate the information of the Corpus from the information of the Scriptum. This is not just a matter of separating nouns from verbs, however. It is rather a matter of deciding which aspects of the document are to be assumed familiar and which aspects unfamiliar. For in any document the familiar concepts provide the material out of which the unfamiliar concepts are constructed. A document containing nothing but unfamiliar concepts would be incomprehensible. A document containing nothing but familiar concepts would be banal. Communication depends upon the skilful blending of the two. (This epistemic principle is somewhat analogous to the concept of redundancy in information theory.)
Thus the projection-function from C to S represents the process by which
the predicate-matter of the Scriptum is constructed out of the subject-matter of the Corpus. The Corpus expressed familiar experience of material things. Latent in that experience are certain unnoticed potentialities out of which new knowledge can be generated. These are made explicit in the Scriptum. In general the actual process of generation demands experimentation. This determines which of the potentialities are in fact realizable. But it does not of itself make them comprehensible. The scientist himself is not satisfied with discovering a law by experiment. He wants to show how the law must have been predetermined in the properties of his materials. The experiment concerns the truth of the law, not its explanation.
It is at this point that the imagination of the scientist injects into the familiar knowledge of materials certain conceptual elements or “intervening variables” by which to relate what is familiar to what is novel. Thus the C → S projection function adds certain elements to the pattern of information in the Corpus in order to give a coherent Scriptum. The Scriptum is by this much richer than the Corpus.
It should now be evident that in a scientific document in which, as is often the case, there is a description of instruments and of the evidence they yield, together with a theoretical interpretation of that evidence, the reader is presented with concepts of several different orders. The mind of the scientist moves about easily among his own concepts whatever their type, but the reader, to whom they are unfamiliar, may well get lost among different levels of abstraction, particularly if there is nothing in the typography or design of the document to differentiate the levels.
It is thus the duty of the communicator to anticipate these difficulties by making these differentiations himself and by making them explicit in his design of the document. The primary function of the theory of semantic matrices is to provide him with a technique of analysing concepts. The principles underlying the translation of these insights into documentary factors and forms are a separate issue to be dealt with in another publication. The immediate need is to provide a constructive theory of semantic matrices.
Constructive theory
In order to keep the development of semantic matrices from spreading out uncontrolledly, we confine ourselves to four carefully defined types. These have some affinity with logical categories but are designed as semantic elements referring to different “modes of diversification” to use Whitehead’s term (4). Given any typical physical environment, Z, e.g., a river in which all kinds of events are taking place, we can divide it up in four principal modes: (i) accord-
ing to the material objects (e.g., pebbles, water, weeds, fish) constituting Z; (ii) according to the distributions of various properties (e.g., temperature, colour, acidity, hardness) characterizing Z; (iii) according to the functional activities of the various objects one upon another (e.g., erosion, consumption, transport) maintaining the dynamic character of Z; (iv) according to the connexions and mutual dispositions of the various objects by virtue of which Z forms a connected whole.
The above four types of element are called, X, K, F, and R respectively. Although these bear some resemblance to logical individuals, classes, predicates, and relations, respectively, they are not to be identified with these. Anyone who has attempted to work simultaneously on the semantic level of physical reference and the logical level of formal inference will know of the pitfalls which logic offers. Roughly speaking logic has become a game for logicians free from the trammels of semantic reference. In semantic analysis we must feel equally free to define our categories in accordance with the demands of physical meanings. Admittedly we must not fall foul of any of the truths of logic, but logic is a system of conventions as well as of truths, and there is nothing mandatory about conventions. It is the conventions with regard to logical “types” which present the semanticist with such difficulties. The attempts (5) of Russell, Zermelo, Skolem, Quine, von Neumann, and Bernays to formulate workable systems of types are, perhaps, to be regarded as experiments in system-building rather than as studies in logical necessity, even though inspired by the necessity to eliminate contradictions. Physical reasoning finds an occasional toleration of contradictions not merely unescapable but even fruitful.
Various graphical devices have been used for representing the relations of inclusion, overlapping, etc., which occur in logical calculi, e.g., the circles of Euler and the squares of Gonseth (6). Their function is to provide intuitive visual evidence for relations otherwise expressed purely symbolically. One curious feature of these devices is their use of areas, which are two-dimensional, to represent sets, which are one-dimensional. A linear symbolism will be adopted here for these representations thus setting the second dimension free for the representation of differences between the sets themselves.
The importance of developing an adequate system of representation for these relations between sets is that it is these relations which give rise to equations, and equations are the ultimate and most precise expression of scientific concepts. If we had a completely unified science we can suppose the total range of its variables to constitute a multidimensional manifold or N-space. This can be sliced up in various ways into 2-spaces. To express relations involving more than two variables we can arrange two or more of these 2-spaces
side by side with suitable connexions. In this way a mapping of concepts from the N-space on to a two-dimensional graphic framework can be achieved. For very simple relations a single semantic matrix may suffice. For more complex concepts we shall, in general, need an array of matrices. Thus a semantic matrix is a 2-space in which variables are displayed so as to indicate scientific assertions. We now have to establish conventions for these displays.
Conventions for semantic matrices
We distinguish between (i) G-matrices (i.e., general) which may be of any existing forms and for which general conventions either do not exist or have no systematic relations to one another, and (ii) Y-matrices (i.e., types) which represent one or other of the four “modular types,” X, K, F, R. It is these latter that concern us here.
It has been shown (1) that physical concepts of a concrete character can be mapped on to a framework having X, K, F, and R as coordinates. Given such a mapping we first construct matrices for all the types identified in the analysis. These matrices display the physical meanings embodied in the types, i.e., their entailments. But the document is more than the sum of its separate type-meanings. Each type is “syntactically oriented” towards one or more other types by important relations. These syntactic orientations are determined by inspection and each is then represented by an appropriate matrix. Assuming that the document possesses a certain semantic unity, we should next search for relations by which the succession of orientations can be seen to cohere into a logical sequence. These coherences in turn will be expressed in one or more matrices.
Thus the full analysis of the document will be represented by three sets of matrices: (i) entailment-matrices, (ii) orientation-matrices, (iii) coherence-matrices. These three roughly correspond with the semantic structures of words, or sentences, and of paragraphs, but the analysis may not adhere at all closely to these linguistic divisions because idiom and style may obscure underlying structure.
For the sake of exposition we will posit a fictitious encyclopaedic store in which all the variables known to science are listed, and all the values of these variables, qualitative or quantitative, are identified and codified. The whole store, though large, is taken to be finite and discrete. Each variable constitutes a taxonomic range, i.e., a set of discrete entities sharing some common character.
In the modular calculus (1) we have distinguished between two kinds of analysis of knowledge, viz., epistemological analysis, in which philosophical considerations predominate, and epistemic analysis which is concerned with scien-
tific meanings and the problems of communicating them. Our four modular types X, K, F, R are epistemic categories in whose definition certain experimential data are assumed. It is left for epistemologists to determine the status and provenance of these data. The data assumed are as follows:
|
1. |
Environments |
En |
|
2. |
Locations |
Lo |
|
3. |
Events |
ξ |
|
4. |
Structural factors |
(hikτ) |
|
5. |
Connexity |
ρ |
The predictable recurrence of an event ξc, having a particular character, gives us a property φc. A location Lo is the volume of space occupied by a material object in its various positions through space-time. We define objects X in terms of locations and properties, i.e., as a set of properties associated with a given location. The K-type (which corresponds with the class in logic) is defined as the distribution of a given property over a set of locations. Briefly,
The R-type is the expression of a connexity ρ between two structural factors. What this means is that we do not define relations as holding between objects as such since two objects may present an indefinite number of relations. But every object, by reason of its position in the environment, its orientation, momentum, etc. (any aspect of which is called a “structural factor”), exhibits mutual dependence or connexion with other objects. A relation R is defined as any one such connexion. (This is not an exhaustive definition. Relations of higher degree are defined separately.)
Functions F express the behavioral dominance of one object over other objects. A river erodes a river-bed. A fish eats an insect. A bird builds a nest. In all such cases we have an event ξ initiated in one location producing changes in other locations. The causal connexion ρ is taken as given. Thus R and F are briefly defined as follows
R=(hik τ)1ρ (hik τ)2
F=Lo1ξ ρ (ΔLo 2,3…n)3
The changes are themselves events. Thus a function may be regarded as one event which dominates a set of further events. We can therefore reformulate the definition:
F=Lo1ξ1ρ (Σξ2…n Lo2…n)
In order to achieve the maximum syntactic power from the matrix-arrangement we adopt a standard convention. Every matrix is a rectangular array of
positions. Each position has two coordinates. A semantic element in the matrix is represented by a small circle occupying a particular position. In general only a fraction of the total available positions are occupied. Each circle is numbered for identification. Its meaning is determined by its two coordinates. These are defined, in principle, by reference to the encyclopaedic store, but in practice by ad hoc descriptions (until the world decides to establish such a store). Lines can be drawn connecting pairs or sequences of elements.
Since the coordinates represent variables in the store, i.e., taxonomic ranges, every element represents the intersection of two such ranges. Thus an element is a pair of values of two variables associated together. We now have to examine the grammar of this convention.
Traditional logic adopted the subject-predicate form for the structure of a proposition, “S is P.” There has always been something both compelling and unsatisfactory about this. The confusion can be dispelled if we distinguish clearly between the purposes of logic and the purposes of communication. Communication which gives real information says something new. But it must say it in a vocabulary which is familiar to the recipient, otherwise no communication occurs. Thus looking at a sentence analytically he sees nothing unfamiliar in it. But apprehending the sentence as a complete structure he gets information. For example “The meteor contains nickel” consists of familiar words. Their juxtaposition in that order yields information.
The formula “S is P” misleads us completely on this. To call “the meteor” the “subject” and “contains nickel” the “predicate” is purely arbitrary. The subject is the set of words the, meteor, contains, nickel The predicate is the whole sentence. Thus the predicate is the information yielded by the arrangement and separate meanings of the words. Thus the predicate is always implicit. Hence the actual communication of the predicate depends as much on the recipient as on the communicator. Unless the recipient relates the given words together to yield the information in his own mind the communication fails. We may say that the communicator presents the subject and the recipient constructs the predicate.
Having grasped the predicate as a unified meaning, i.e., a concept, the recipient may anchor it by giving it a name, or a formula or some other label, e.g., “nickeliferous meteor.” This then becomes a new term in the vocabulary. It may then, in a later communication, play the role of a subject-term, e.g., “nickeliferous meteors are found in outer space.” This process by which implicit predicates are translated into explicit subject-terms represents the consolidation of science. Every new discovery is ushered in linguistically as a predicate. It is then converted into a subject-term to play its part in the expression of further discoveries.
This view of the subject-predicate relation underlies the grammar of semantic matrices. Every element in a matrix is a meeting of two variables. The latter constitute the subject. Their association constitutes the predicate. Then in the same matrix a number of other elements are presented, each representing a two-term predicate. Each such element, by being labelled, becomes a potential subject-term. The association of all the elements in the matrix constitutes a single complex predicate. The structure of this predicate is determined by their mutual dispositions in accordance with the conventions of the matrix. The matrix as a whole can then be given a label. It can, in turn, be associated with other matrices to yield a still more complex predicate. Whether this can be taken in as a whole or built up from the partial associations of pairs of matrices will depend partly on the insight of the recipient and partly on the character of the meaning to be communicated.
Reverting now to the one-dimensional representation of a class we find that this immediately yields a very powerful method for expressing class relations. And since every matrix can be regarded as a system of intersections of ranges of variables, i.e., classes, the method gives a clear interpretation of all the spatial relations in the matrix. Its “geometric grammar” is thus fixed and any implicit spatial assertion can immediately be translated into a proposition in the calculus of classes. This consequence will be called the “inferential potential” of the structure.
The convention is extremely simple. Individuals, here called “locations,” are represented by transverse lines across the matrix. Properties (or other qualifying factors) are represented by lines running from top to bottom. Any selection of individuals and of properties can be represented but, in general, they constitute a “universe.” Every instance of a property occurring at a location (i.e., every individual member of the class defined by that property) is denoted by a small circle at the point of intersection of the appropriate lines.
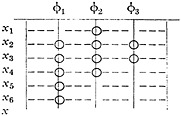
Let
α=x φ1(x)
β=x φ2(x)
γ=x φ3(x)
In this example we see that
x2, x3, x4, x5, x6=membership of α
x1, x2, x3, x4=membership of β
x2, x3=membership of γ
Further,
x2, x3, x4=α∩β, i.e., product of α and β
x1, x2, x3, x4, x5, x6=α∪β, i.e., sum of α and β
Also, since the extension of γ, viz., x2, x3, forms part of the extensions of both α and β, we have
γ⊂α and γ⊂β
Further inferences are:
i.e., α has members not shared by β.
and so on.
In the above representation we are committed to indicating the actual number of members in each class. If we wish to assert certain class-relations without making the extensions explicit we can replace the columns of circles by straight lines thus:
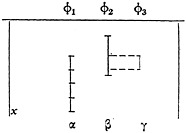
Here exactly the same relations are exhibited but with no necessity to specify-the number of members in any class. The relations of inclusion, overlap etc. can be shown by parallel projection. As an example γ⊂β is indicated. The dotted lines show that the projection of γ on β is contained within β.
There is a certain advantage in translating a matrix of discrete elements into one of line-ranges since the latter shows up the space-relations more clearly. But there is a second way in which this can be done. We can draw the lines transversely. A quite new set of relations then emerges. Our attention is switched from classes to the properties of individuals and the latter’s resemblances and differences.
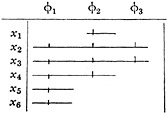
Here the range of individuals is necessarily taken to be discrete. The range of properties may or may not be discrete, e.g., it could represent the colours in
the spectrum. But there must be points of differentiation whereby one φ is distinguished from the next.
We again have relations of overlap and inclusion, seen by parallel projection. But these give the following interpretations (all of which, of course, are valid only for the universe prescribed by the data):
-
The individual x1 has a single property φ2.
-
The individual x5 has a single property φ1.
-
The individual x6 has a single property φ1.
-
The individual x4 has two properties, φ1 and φ2.
-
The individual x2 has three properties, φ1, φ2, and φ3.
-
The individual x3 has three properties, φ1, φ2, and φ3.
Thus
-
x1 is partly similar to x2, x3, x4.
-
x2 is distinguishable from x3 only by its location.
-
x4 is partly similar to x2, x3, x5, x6.
-
x5 is distinguishable from x6 only by its location.
-
By virtue of these similarities and partial similarities a new class-structure can be discerned.
This last point is a further indication of “inferential potential.” We can define new classes thus:
A=the class of individuals having a single property (viz., x1, x5, x6).
B=the class of individuals having two properties (viz., x4).
C=the class of individuals having all three properties (viz., x2, x3).
D=the class of individuals having one common property only, but here we have a relation which as formulated is indeterminate.
For example x2 and x3 both have the same common property with x1 but a different common property with x5 and x6, whilst they have three common properties with each other. This example illustrates clearly the ambiguities of verbal formulation. The matrix representation is entirely unequivocal.
It may here be noted that these matrices are formally identical with the answer-pattern obtained from the administration of tests and examinations in which answers are scored as either right or wrong. The treatment of rows or columns as lines used to be achieved by means of aluminium slats with small cavities to take ball-bearings. These could be transferred to an orthogonal framework of slats by superimposing the latter and inverting. This device is known as a “scalogram” (7). In our example we have considered numbers small enough for individual consideration but the pattern can obviously be regarded also as a statistical distribution.
The purpose of the matrix is to exhibit information in a form amenable to the extraction of inferences. The kind of inference to be extracted will depend on the purpose in hand. Since the concept of semantic matrices arose in a context of communications-research in which the problem concerned the comprehensibility of documents we shall naturally stress those inferences which contribute to comprehension. Or putting the matter otherwise the matrix presents us with an array of possible inferences any of which may be selected as defining what we are going to mean by “comprehension.” In other words the matrix contains implicitly all the relations needed for the construction of a test of comprehension. Whatever arbitrariness there may be in the selection of relations for the test it will be a manifest arbitrariness which can be defined in relation to a population of potential test items. The selection can thus be made to follow the principle of what Egon Brunswik (8) called “representative design.” Given a total population of inferences which collectively determine “full comprehension” we can suppose this population to be stratified into ranges of inference of different types. We then see to it that each range is sampled in the test by a number of items proportional to the frequency of inferences in the range. The possibility of weighting in accordance with some criterion of relative importance must be allowed for, since there may be key-inferences whose effect is paramount though they are few in number.
One caution is needed here. Although testing of this kind has many parallels with psychometric testing there are fundamental differences which render any analogies between the two dangerous. In psychometrics the object is to measure the abilities of individual persons and the distribution of abilities in populations. In epistemic communication research we are measuring the comprehensibility of documents. Many of the concepts involved are radically different from those of psychometrics. In particular the aim is to ascertain
those factors in the design of a document which make for difficulty and for comprehension respectively. We can then hope to redesign the document so as to maximize the latter and minimize the former factors. The psychometricians do not hope to redesign their human subjects.
THE FOUR TYPES OF Y-MATRIX
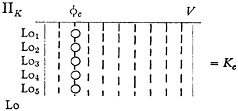
Class-matrix K
A property φc is distributed over a number of locations.
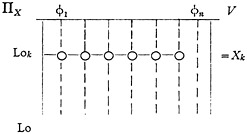
Object-matrix X
A number of properties φ1−n are associated at a single location Lok.
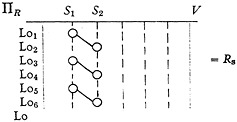
Relation-matrix R
A specific connexion exists between pairs of structural factors, S1, S2 associated with pairs of localities, Lok1, Lok2.
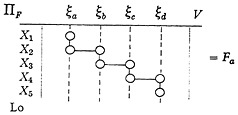
Function-matrix F
A dominant event ξa at X1 involving X2 initiates a sequence of other events ξb, ξc, ξd · · ·.
In analysing the document we aim at expressing all its primary factual content in terms of these four matrix-types, singly or in combination. In other
words, every datum is interpreted as the occurrence of a variable V at a location Lo or a combination of such occurrences.
But the document, in general, expresses more than a sum of factual data. We next have to look at the connexions between these data. The varieties of connexion are very numerous. Our programme includes their eventual reduction to expressions in terms of the same four types X, K, F, R but of “higher degree” and involving an analytical policy in respect of the use of language. Pending the completion of this programme we rely on a descriptive formulation of the semantic and syntactic connexions between primary matrices and give these “syntactic orientations” a verbal formulation, together with an appropriate symbol.
Regarding the document as initially a sequence of factual concepts expressible as modular types Y1, Y2, · · ·, Yn we note that the sequences of these concepts is partly determined by semantic connexions and partly by idiosyncrasy, style, expository needs, etc. Thus the juxtaposition of two concepts does not necessitate the recognition of any important connexion between them. Connexions may exist between concepts which are widely separated in the document. Thus we now need a means of expression by which any important connexion may be revealed. For this purpose we construct a matrix of syntactic orientations.
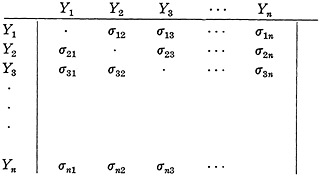
We here determine by conceptual inspection which of these orientations is important and express their logical or other sense in a suitable verbal formulation. Obviously many of the σ’s will be left blank.
Certain types of syntactic orientation will be found to recur. We can ideally envisage a complete system of such connexions, of which a small sample is manifested in any one document. If we symbolize these type-connexions by σa, σb, σc, etc., these may be regarded as constituting a range of relations whose field consists of the matrices Y1, Y2, · · ·, Yn. We can then express the whole syntactic pattern of the document by means of an R-matrix. This would appear something like this:
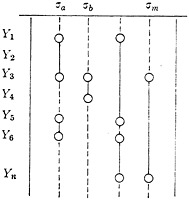
The meaning of this matrix is that an important and definable connexion between concepts Y1 and Y2, and again between Y5 and Y6 is manifested in the document, another between Y3 and Y4, and so on.
How much further we go depends partly on the level of understanding which we deem to be appropriate for the given document and for the recipients in view. Some documents would not lend themselves to further analysis. Some have such an inner coherence that connexions of a high order of abstraction can be discerned and identified. To arrive at these we repeat the foregoing procedure, but this time we seek for connexions between the σ’s. In other words we ask what considerations of theoretical coherence led the author to connect his concepts in such-and-such a way. Here we may well find three or more σ’s bound together by some logical, stylistic, or expository tie. The author uses his concepts functionally in order to achieve a certain result. Such connexions may be of decisive importance in the design of the document and are thus highly relevant to our research. Indeed in the light of the large number of experiments on “Transfer of Training” (9) over the past 50 years we may well look to these abstract elements as highly important factors in the determination of comprehension. Thus our analysis goes on to some such form as this:
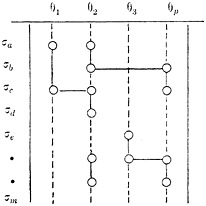
This would mean that σc enters into a theoretical coherence, θ1, with σa and another coherence θ2 with σd; that σb enters into coherence θ2 with σd and θp with σc, and so on.
We can even envisage an ideal document in which a single unifying concept bears significant relations to every other concept in the document.
Conclusion
These methods for the analysis and display of the concepts in scientific documents are initially designed for the use of research-workers in the field of comprehensibility. We are a long way from understanding the factors of documentary design which make for efficient communication, though we have some clues. In such a field as this one of the prime requisites is to secure the conditions for the replication of experiments. One of these conditions is a standard methodology and terminology. In semantic matrices and in the modular calculus a beginning has been made towards satisfying this condition. A further requisite is a standard system of non-parametric statistics for the analysis of experimental results. Here the recent work of Siegel (10) is proving an invaluable guide. For experimental work on the psychology of visual displays see ref. 11 on “Planned Seeing.”
In view of the frightening discrepancy between the advanced state of knowledge of a comparative handful of scientists and the low level of understanding not only of the population in general but particularly of administrators and statesmen, and even of scientists outside their own special fields it would seem that research on the comprehensibility of scientific documents is a matter of high urgency. Documentary communication is not, of course, the only medium, nor today is it the most popular. But it is important to appreciate that all the other media, graphic, filmic, radio, television, etc., all start from a script, i.e., a document. Unless the concepts and intentions of this document are clear, the translation is vitiated from the outset. Thus documentary research is fundamental to all studies in communication.
REFERENCES
1. G.PATRICK MEREDITH, Epistemic Communication Research, Modular Calculus, Part I. Proceedings of the Leeds Philosophical and Literary Society, 1958.
2. G.PATRICK MEREDITH, Semantics in Relation to Psychology. Archivum Linguisticum, Vol. VIII, Fasc. 1, 1956.
3. C.K.OGDEN and I.A.RICHARDS, The Meaning of Meaning. 1923.
4. A.N.WHITEHEAD, An Enquiry Concerning the Principles of Natural Knowledge, 1919.
5. W.V.O.QUINE, Mathematical Logic, 1951.
6. I.M.BOCHENSKI, Précis de Logique Mathématique, 1948.
7. L.GUTTMANN, “The Cornell Technique for Scale and Intensity Analysis.” Educational and Psychological Measurements, Vol. 7, No. 2, 1947.
8. EGON BRUNSWIK, Perception and the Representative Design of Psychological Experiments, 1956.
9. G.PATRICK MEREDITH, The Transfer of Training. Occupational Psychology, April 1941.
10. SIDNEY SIEGEL: Non-parametric Statistics, 1956.
11. SIR F.BARTLETT and N.H.MACKWORTH, Planned Seeing, H.M.S.O., 1950.






























