The Structure of Information Retrieval Systems
B.C.VICKERY
Four basic operations in the effective use of graphic records (documents), to store information and make it available, have been listed by Hyslop: A, recording information in documents; B, storing recorded information—documentary items; C, identifying items containing information relevant to a given problem, situation, or subject; D, providing the identified items from storage. Information storage and retrieval in the wide sense covers all these operations. In the narrow sense used in this paper, information retrieval means only C, identifying documentary items by subject.
An information retrieval system is therefore defined here as any device which aids access to documents specified by subject, and the operations associated with it. The documents can be books, journals, reports, atlases, or other records of thought, or any parts of such records—articles, chapters, sections, tables, diagrams, or even particular words. The retrieval devices can range from a bare list of contents to a large digital computer and its accessories. The operations can range from simple visual scanning to the most detailed programming.
A retrieval system stores units of information. Each unit is linked in the system to specifications of one or more documents or parts of documents—I will call them items. The user specifies particular units of information—specific subjects—and the system is designed to provide him with a knowledge of all relevant items recorded in the system.
A retrieval system can be studied at three levels:
-
The way in which units of information, and relevant relations between them, are defined in the system. This is the semantic level of subject analysis.
-
The general structural features of the system considered as a network of units of information linked to each other and to documentary items. This may be called structural analysis.
-
The physical mechanisms (hardware) in which the structure is embodied.
A general theory of information retrieval would cover (a) principles of sub-
B.C.VICKERY Imperial Chemical Industries Limited, Welwyn, England.
ject analysis, (b) a general study of structure, and perhaps (c) general experimental conclusions about the use of certain hardware. For two reasons, the present paper is restricted to (b). Firstly, problems (a) and (c) seem properly to belong to Areas 5 and 4, respectively, of the Conference. Secondly, the technique of subject analysis, on the one hand, and the experimental study of physical mechanisms, on the other, do not appear yet to have advanced sufficiently for firmly based general conclusions to be drawn.
This paper, then, deals only with the general structural features of retrieval systems.
The characteristics of specific subjects
Specific subjects are products of thought, and are typically in language or some other expressive symbolism. The units of meaning in such symbolism I will call terms. Without adducing formal proof, the following characteristics of specific subjects can be stated as facts of observation:
-
Each specific subject is symbolised by a single term or a combination of terms (simple and compound subjects respectively).
-
The same combination of terms can have more than one meaning, e.g., “the destruction of bacteria by dyestuffs” and “the destruction of dyestuffs by bacteria,” in other words, the terms within a specific subject are interrelated in certain ways.
-
Terms are also related to each other in at least two other ways: (a) by one term having a meaning which includes that of another term (generic relation) and (b) by both terms having meanings which are included in that of a third term (coordinate relation).
-
Specific subjects are consequently related to each other in at least three ways: (a) by each containing the same term or combination of terms, (b) by one specific subject containing a term which is generic to a term in another, and (c) by one containing a term which is coordinate with a term in another.
If T1, T2, T3, and T4 are terms, subject S1 is said to include subject S2 (i) when S1=T1 · T2 and S2=T1 · T2 · T3, or (ii) when S1=T1 · T2 and S2=T4 · T2, where T1 is generic to T4.
The information lattice
An information retrieval system includes a store of units of information, specific subjects. The assembly of specific subjects so stored may incorporate all the relations mentioned above. Between terms in each specific subject and
between specific subjects, semantic links exist. An intricate network of links is thus formed, a lattice of units of information.
The links in the lattice are of three general kinds: (a) between terms in each specific subject there are interlocking relations, which may be represented by dots in the lattice, thus T1 · T2, or by the multiplication sign, thus T1×T2; (b) between specific subjects there are firstly inclusion relations, which may be represented by solid lines in the lattice, thus S1—S2, or by the inequality sign, thus S1>S2; and (c) between specific subjects there are also coordinate relations, which may be represented by broken lines in the lattice, thus S1- - -S2, or by the equality sign, thus S1=S2.
We can now state what is meant by items “relevant” to a particular sought subject. The limits of relevance can be varied at the discretion of the designer of the retrieval system. The system can be made to retrieve items recorded for the subject sought, and, in addition, items recorded for subjects (1) which include the subject sought, (2) which are included by the subject sought, and (3) which are coordinate with the subject sought.
Let us consider a small sample retrieval system. It uses six terms, words, which we can represent as the capitals A to F. Of these, C, D, and F are independent, E and A are included in F, and B is included in E. The lattice for these relations is as follows—by convention, a solid line leads downwards from the inclusive to the included term.
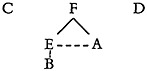
From these elements, ten specific subjects are derived. I will assume here that each subject coincides with a single documentary item, although this need not necessarily be the case. Each item is represented by a roman numeral.
|
Item |
Subject |
Item |
Subject |
|
I |
B · C · D |
VI |
A · C · D |
|
II |
C · D · F |
VII |
A · D · E |
|
III |
B · C |
VIII |
D · E |
|
IV |
C · E · D |
IX |
A · B |
|
V |
A · C · E |
X |
A · D |
The information lattice may now be extended to include these subjects, as in Figure 1. The complexity of even this small lattice (in which not all the coordinate relations have been drawn) is very evident.
Such a lattice is the structural basis for the store of an information retrieval system. The use of such a three-dimensional network as a retrieval system is, however, quite impracticable. The system must be simplified by breaking
many of the links and reducing the lattice to a two-dimensional or linear structure. This simplification may be made outright, without taking any compensating action, in which case relations within the system, represented as links in the lattice, are lost. The result is that the complexity of retrieval is reduced, the scope of possible “relevance,” as defined earlier, is narrowed. Alternatively, transformation to a system of fewer dimensions may be accompanied by compensating marking which preserves the lattice relations intact.
The information matrix
The first transformation may be to convert the lattice into a two-dimensional matrix, the coordinates of which are items and terms (Table 1).
TABLE 1.
|
|
Items |
|||||||||
|
Terms |
I |
II |
III |
IV |
V |
VI |
VII |
VIII |
IX |
X |
|
A (<F,=E) |
|
x |
x |
x |
|
x |
x |
|||
|
B (<E) |
x |
|
x |
|
x |
|
||||
|
C |
x |
x |
x |
|
x |
x |
|
|||
|
D |
x |
x |
|
x |
|
x |
x |
x |
|
x |
|
E (<F,=A,>B) |
|
|
x |
|
x |
x |
|
|||
|
F (>E, A) |
|
x |
|
|||||||
The terms A to F are listed alphabetically, and the links between them are thus broken. In compensation, against each term its inclusion and coordinate relations must be shown. Thus A is included in F and is coordinate with E, so the solid line A—F is replaced by A<F, and the dashed line A- - -E is replaced by A=E. All these lattice relations between terms are thus preserved.
The remaining inclusion and coordinate relations are represented by the postings (here, crosses) in the body of the matrix. Consider subject A · C · D (item VI). Subjects which include it are derived by suppressing terms one by one: A · C, A · D, C · D, A, C, D. Search of the matrix reveals that only one of these subjects (A · D) refers to a documentary item (X) which may be retrieved.
Coordinate subjects are derived by replacing each term in turn, and search retrieves items I(B · C · D), II(C · D · F), IV(C · E · D), V(A · C · E), and VII(A· D · E). Since A=E, then A · C · D=E · C · D, so that item IV is again on a subject coordinate with that of item VI. Since A<F, then A · C · D<F · C · D, and the subject of item II includes that of item VI.
Lastly, there is the problem of interlocking relations within subjects. In the sample matrix it is assumed that these are only significant in one item, IV. Here, the subject in the lattice, C · E · D, is considered to differ in meaning from a subject in which C and E are not interlocked, i.e., C · D · E. In all other three-termed subjects, it is assumed that no significant interlocking occurs. The link
between C and E in item IV must be recreated in the matrix by modifying the postings (here, doubling the crosses).
Having thus preserved all the lattice relations, the information matrix can in principle be used as a two-dimensional retrieval system. However, if a large number of terms and/or items were covered, the matrix would be intolerably large, a very high proportion of it would be wasted empty space, and the system would be very inefficient. The matrix must be further transformed.
The next transformation may be to partition the matrix either horizontally or vertically into units which can be inscribed on individual entries or tallies. Horizontal partition produces entries each bearing a single term and its associated items. Vertical partition produces entries each referring to a single item, bearing the terms associated with it. Partition into units greater than a single row or column is possible, and indeed necessary in certain cases.
The two-dimensional matrix is thus broken down into a series of units of the following types:
-
Term entry: A(<F,=E): V, VI, VII, IX, X
-
Item entry: I: B(<E), C, D
-
Interlocked term entry: C×E(<F,=A,>B): IV
-
Combined item entry: II+III: B(<E), C, D, F(>E, A)
The fourth type will not be further discussed.
The entries are inscribed with marks symbolising the terms and items. Information retrieval is the operation of selecting entries which bear marks for certain terms, and reading off their item specifications. The selection process thus operates on the term symbols.
The entries can be stored in the system in an order which is not related to the term symbols they bear, an arrangement which will be described as entries free. The selection of entries bearing a given term symbol can then only take place if the entire index is inspected. Systems so designed are described by Fairthorne as scanning systems. Alternatively, the entries can be stored in an order dictated by the ordinal values of the term symbols inscribed on them. Selection can then proceed by successive steps of “distillation,” and all entries need not be inspected. Such arrangements will be described as entries fixed, the result being a segregation system (Fairthorne).
Term entry systems
A series of term entries derived from the previously tabulated matrix is as follows; the word heading referring to the combination of term symbols on each entry.

The only lattice relation which has been broken by partition is the interlocking between C and E in item IV. The relation can be restored by including in Index No. 1 an interlocked term entry, C×E(<F,=A,>B): IV. Search operations can then proceed as described for the matrix.
The construction of Index No. 1 requires only the following schedule:
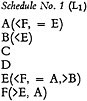
The system thus consists of Index No. 1 (N1) and Schedule No. 1 (L1). The operations of construction are (1) look up words in L1 to ascertain cross references, (2) inscribe headings on entries, (3) add interlocked term entries. The search operations are (1) consult sought words in N1 (e.g., A, C, and D), (2) compare items to find those which are on all three entries (none are), (3) move to related entries by suppressing terms (A · C, A · D, etc.) and as indicated by cross references (e.g., F · C · D includes A · C · D) and repeat comparison in each case.
In this system, the marks symbolising terms are words, and inclusion and coordinate relations are expressed as verbal cross references. These features have two disadvantages: (a) Words may be long, far longer than is necessary to distinguish between them; if the schedule covers N terms, and r separate marks are available, then the symbol length need not exceed n=log N/log r marks. (b) The use of words leads to alphabetical scattering of related terms, thus the coordinate terms A and E are separated, as is F from its subordinate A. This leads to complication of the search operation in systems with entries fixed. To overcome these disadvantages, other means of representing terms and relations may be adopted, leading to other schedules, indexes, and systems.
The simplest transformation is to replace the words A to F by random code symbols U to Z, which are no less “alphabetically scattered,” but which are reduced to the minimum length needed to distinguish them. The resulting Index
No. 2 is identical with N1, except that A to F become U to Z. A different schedule must be used in constructing the system.

The second transformation is to minimise the distance between related terms. It is accomplished by a transformation into linear form of the lattice of relations between terms, and the allocation of class numbers, as shown in the following schedules.

In L3, the independence of the three terms C, F, D is shown by their standing vertically in line, at the left of the schedule. Inclusion relations (F—E, E—B, F—A) are shown by indentation, coordinate relation (E- - -A) by vertically lining up. The class numbers simply fix the order of the terms, they are purely ordinal. In L4, the independence of C, F, and D is shown by their being represented by unitary class numbers (1, 2, 3). Any term (e.g., B, 211) is included in any other term whose symbol can be derived by suppressing marks from the right-hand end of B, thus 21,E and 2,F. Coordinate relation is shown by two terms (E,21 and A,22) having common initial marks (2). As well as having an ordinal function, such class numbers are hierarchical.
From such schedules, indexes such as the following can be constructed.

In order to construct and use such indexes, a further schedule is needed, to
lead from the words of the subjects indexed and sought to the symbols used in the system, thus:

The use of ordinal class symbols is possible only in systems with entries fixed, and is further restricted to systems which can indicate relations by structural features other than the symbolism, as by indentation in N3. Typical examples of such static indexes are the conventional card catalogue or the printed bibliography, in which purely ordinal symbolism is thus possible.
On the other hand, if the only device for indicating relations is the symbolism itself, the class numbers must be hierarchical. Such hierarchical class symbols have a function also in scanning systems with entries free. Although they do not then have the effect of juxtaposing related entries, yet they may be a simpler device for following up inclusion and coordinate relations than the original cross-references.
Item entry systems
An index of item entries derived directly from the previously tabulated matrix is as follows:
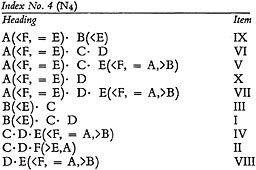
Such an index can be constructed from Schedule No. 1. Once again, the only lattice relation lost is the interlocking between C and E in item IV. The relation can be restored if the terms in each heading are cited, not in a random or (as here) alphabetical fashion, but in an interlocking order. Thus the heading for
item IV should become C · E(<F,=A,>B) · D. The heading as given in the index represents a subject significantly different in meaning. Such a solution is only possible in a system in which the terms occupy fixed relative positions in the entry, an arrangement which may be called terms fixed.
It is possible, however, to take a further step in transforming the original lattice, and to break the interlocking relations between terms (represented by dots in C · E · D). The positioning of terms on an entry then becomes random (e.g., they may be superimposed), an arrangement which may be called terms free. Two ways of restoring interlocking relations seem possible. (a) Thet firs is to include in the heading, not only the individual terms C, D, and E, but also a new compound CE. (b) The second is to modify the interlocked terms by the addition of symbols which indicate their linkage, thus C★, D, E★. For a system with terms free, therefore, N4 must be modified in one of these two ways.
Further transformations of N4 may be made exactly analogous to those of N1, replacing the words A to F with random code symbols, to give N5 (identical with N4 except that A to F become U to Z), or with ordinal or hierarchical class numbers, as follows:

Once again, the inclusion and coordinate relations must be shown by a non-symbolic feature (indentation) with ordinal class numbers, which are therefore only applicable in a system with entries fixed. Moreover, ordinal class numbers can only carry out the function of ordering related entries if the individual symbols in each heading (e.g., 1, 2, and 6 in item II) are taken in a fixed order, i.e., if the system has terms fixed as well as entries.
Hierarchical class symbols in a system with entries and terms fixed serve the same function, without the need for indentation. If the entries are free, the symbols cannot do this, but serve to indicate inclusion and coordinate relations. If the terms are also free, an interlocking device such as the asterisk must be added.
Access to item entry systems with entries and terms free is direct. Either the
sought word, say D, its corresponding random code symbol derived from S2(X), or the hierarchical symbol from S4(3), is matched against the index entries. Since terms are randomly arranged in the headings, the whole of each heading must be scanned.
Access to item entry systems with entries and terms fixed is not so direct. In each heading, the order of terms is fixed, and direct access is only through the primary term. Thus direct entry to N4 with D would yield only item VIII, and would not retrieve items VI, X, VII, I, IV, and II, in which D also figures. Access to fixed item entries therefore requires one of the following two alternative devices: (a) The entry may be partitioned into mutually exclusive fields, and any given term is always inscribed in a particular field. The entries can still be arranged so as to juxtapose related headings, but a search for all entries bearing a given term necessitates scanning the appropriate field in every heading. (b) No fields may be used, but an auxiliary chain index may be constructed in which each of the secondary terms in each heading is given a leading place in turn. Thus for index N4 the chain index would be as follows:
Chain Index No. 1
|
B·A see A·B |
D·C·B see B·C·D |
|
C·A see A·C |
E·C·A see A·C·E |
|
C·B see B·C |
E·D see D·E |
|
D·A see A·D |
E·D·A see A·D·E |
|
D·C see C·D |
E·D·C see C·D·E |
|
D·C·A see A·C·D |
F·D·C see C·D·F |
For N5, symbols U to Z would replace A to F after “see” in each line. For N6, the following would be constructed.

Structural criteria
The preceding analysis suggests a number of criteria which may be used in describing the structure of retrieval systems, as follows.
-
The lattice relations incorporated, whether a search for term T can also retrieve as “relevant” terms (a) included in T, (b) including T, (c) coordinate with T. The traditional hierarchical classification incorporates all these relations; a system using unique descriptors incorporates none of them; a cross-referenced alphabetical index may incorporate them partially. Measures of the “dimensionality” of a system are needed, the average length of inclusion chains, the size of coordinate arrays.
-
The type of subject indexed, simple or compound. Simple (single-term) subjects are typical of the purely enumerative classification, but most retrieval systems index compound subjects. The “connectivity,” maximum and average numbers of terms in a compound, would be characteristic of a system. The capacity to form interlocked compounds in subjects is also a characteristic feature.
-
The form of entry, by term or by item. Typical item entry systems are library catalogues, and term entry systems have been devised by Batten, Taube, and others.
-
The relationship of entries to each other, fixed or free. The typical fixed entry system is again a library catalogue, while punched card systems usually have entries free.
-
The arrangement of terms in term entries, fixed, free, or in fields. A composite subject heading is typically fixed; superimposed coding on cards has terms free; other punched cards use fields.
-
The symbolism used for terms, verbal, random code, ordinal class, or hierarchical class symbols.
-
The presence or absence of a chain index, a feature which arises from characteristic (5).
-
The type of search operations which can be conducted, logical sums, products, differences, and combinations of these. This feature has not been explicitly considered here, as it is now familiar in retrieval theory.
By permuting these eight sets of characteristics, a large variety of different retrieval systems can be designed, even though not all the characteristics are independent. The list of criteria is of course not intended to be exhaustive, it includes only abstract structural features of the system, and does not necessarily cover all the possibilities even in this sphere. Once the physical mechanisms and operation of a retrieval system are included, a whole host of other criteria arises,
and many of these have been listed in the “Proposed definitive statement of the scope of area 4.” These may be excluded from consideration in a study of general structure.
Operational Efficiency
The formulation of criteria by which to describe the structure of a retrieval system is not an end in itself. It is only a necessary preliminary to discovering which structural features lead to the highest operational efficiency of the system. The next step is to analyse the operations associated with the various structural features. The operations are of several kinds. First to be considered are operations needed to design the system:
-
Constructing a lattice of units of information. This is a semantic problem and involves the formulation of postulates as to the kinds of terms and relations to be used, and the subject analysis of the chosen field in the light of these principles.
-
Constructing schedules (L1 to L5) by appropriate transformations of the lattice, and the required coding. Next there are operations needed to construct the index:
-
Analysing the subject matter of each item into appropriate lattice units, terms.
-
Consulting schedules (L1, L2, L5) to ascertain coding.
-
Inscribing index entries with term symbols and item specifications.
-
Filing index entries.
-
Constructing chain index entries.
Lastly there are operations needed in using the system:
-
Naming the subject sought in appropriate terms.
-
Consulting schedules (L2 and L5) to ascertain coding.
-
Consulting chain index.
-
Inscribing search entries.
-
Matching search entries with index entries.
-
Moving to related index entries.
-
Inspecting matched and related index entries and recording inscribed item specifications.
Of these fourteen operations (which are, of course, subject to more detailed breakdown), numbers 1, 2, 3, and 8 must be performed by human agents. For the same indexed material and search questions, they will vary almost entirely in accordance with variations in the lattice. For all systems using the same lattice, these operations will be almost identical. Operations 12, 13, and 14 are purely clerical operations within the indexing system, and will vary widely
according to the physical mechanisms involved. The remaining operations, 4, 5, 6, 7, 9, 10, and 11, are also clerical. As listed above, a human clerk is assumed to be consulting, inscribing, filing and chain indexing, but all these operations could be carried out by a suitably instructed machine, and would then vary, not only in accordance with the physical nature of the index entries but also in accordance with their own mechanical nature.
The relative efficiency of different ways of carrying out these operations, therefore, cannot be discussed without reference to (a) the semantic problems of lattice construction, and (b) the physical mechanisms or clerical hardware. Neither of these subjects can be considered in this paper. Nevertheless, it is useful to conclude this study of the general structure of retrieval systems by examining some meanings of the word “efficiency.”
Two aspects of efficiency must be distinguished. There is first the retrieval efficiency, i.e., the degree to which a system actually retrieves from its store those item specifications which are in fact relevant to the search question. There is secondly the economic efficiency, i.e., the cost in labour, materials, time, and money of achieving a given retrieval efficiency. The economic efficiency will be a function of all the factors so far discussed: the semantic nature of the lattice, the structural criteria of the system, and the clerical hardware. It can be assessed by economic studies of existing complete retrieval systems, and by partial studies of particular, relatively self-contained operations within such systems.
The retrieval efficiency is dependent on fewer factors. The different forms of clerical hardware are only different ways of physically embodying certain structural characteristics. These in turn are alternative ways of transforming a given matrix and lattice. In principle, every retrieval system based upon a given lattice should have the same retrieval efficiency. Any variations should be introduced only as engineering noise, e.g., mistakes in coding by human agents, errors in machine operation, or “false sorts” deliberately allowed in the design of the system.
Perry and his associates have suggested several measures of retrieval efficiency, e.g., the noise, factor (the fraction of retrieved items not relevant to the subject sought) and the omission factor (the fraction of actually relevant items in the system which are not retrieved). These factors could be determined by examining, respectively, the retrieved items and the whole collection of items indexed. It is necessary to consider the relation of these factors to the meaning of relevance identified earlier.
If items are retrieved whose entries actually bear the sought combination of terms, but which prove to be irrelevant, then we are dealing only with engineering noise, a mistake has been made either by the indexer or the searcher. True semantic noise occurs only when an entry bearing terms related to the
sought terms is found not to be relevant. This may mean that in designing the system and constructing the lattice, the relevance limits have been made too wide, too great a selection of inclusive, including, or coordinate subjects has been linked to the sought subject. Or it may mean that in this particular search, the relevance limits have been made too wide, though in other searches they may not be wide enough, in which cases there will be significant omission factors.
The implications of tests of the retrieval efficiency of a system are therefore clear. A persistently and inconveniently high noise factor implies that the relevance limits should be narrowed; a persistently high omission factor, that they should be widened. In each case, detailed analysis is necessary to decide the inclusion or coordinate relations which need to be amended. If some tests on a system give a high noise factor, and others a high omission factor, the implication is that the system should be redesigned to permit variations in the relevance limits according to the search required.
Acknowledgments
Since this paper has been written in very general terms, it has not been found necessary to refer to many other writers. Nevertheless, much is clearly owed to those workers in information retrieval whose work I have tried to generalise.
It is no accident that of the few names cited one should be R.A.Fairthorne, from whom both the lattice and matrix concepts have been drawn. An exposition of a retrieval system as a lattice is found, for example, in his paper on “The patterns of retrieval,” American Documentation, 7 (1956), 65–70, and a brief account of a talk on the matrix in Classification Research Group Bulletin, 1957, no. 3.
The reference for measures of retrieval efficiency is to J.W.Perry, A Kent, and M.M.Berry, Machine Literature Searching (Interscience, 1956), which also contains an extended account of searching operations in terms of products, sums, and differences. The reference to M.R.Hyslop is to her chapter in J. H.Shera, A.Kent, and J.W.Perry, Documentation in action (Reinhold, 1956).
The concept of interlocking is implicit in the indexing system of J.E.L. Farradane, J. Documentation, 6 (1950), 83–99, and explicit in the paper of C.N. Mooers, “Information retrieval on structured content,” in Information theory (C.Cherry, editor, Butterworths, 1956). It is also implicit in the “role indicators” of Perry (loc. cit.) and the “interfixes” of D.D.Andrews and S.M.Newman, Storage and retrieval of contents of technical literature, nonchemical information (U.S. Patent Office, Research & Development Report, 15 May 1956).
The problems of term symbolism have been dealt with by many writers, but
the work of E.J.Coates is of particular value: see Classification Research Group Bulletin, 1956, no. 1; 1957, no. 2. S.R.Ranganathan has written copiously on symbolism, citation order of interlocked terms, chain indexing, and other problems. Four of his books may be cited: Classification, coding and machinery for search (Unesco, 1950), Classification and communication (Delhi University, 1951), Philosophy of library classification (Copenhagen, Munksgaard, 1951), and Prolegomena to library classification (London, Library Association, 1957).
Reference may also be made to B.C.Vickery, Classification and Indexing in Science (Butterworths, London, 1958) and to papers cited therein; and to the Classification Research Group memorandum, “The need for a faceted classification as the basis of all methods of information retrieval,” reprinted in Proceedings of International Study Conference on Classification for Information Retrieval (Aslib, 1957).
Note: Term entries have also been called “aspect” or “feature” entries. “Unit cards” are term entries which are further broken down so that each bears only a single item specification.
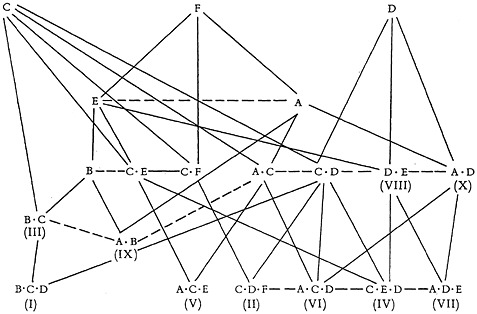
FIGURE 1. An information lattice showing inclusion (F—E), coordinate (E – – – A) and interlocking (B · C) relations between subjects.
















