A Mathematical Theory of Language Symbols in Retrieval1
CALVIN N.MOOERS
ABSTRACT. A mathematical model is presented which relates the language symbols of retrieval to the documents retrieved. The model is applied to three families of retrieval systems: those using for language symbols (1) descriptors, (2) characters with hierarchy, and (3) characters with logic. Most information retrieval systems now in use are variations of one of these systems. The similarities and differences between the three systems are displayed by the model. According to the model, a retrieval prescription is represented by a point in a space P. This space can be generated by taking the cardinal product of a repertory of simple partially ordered systems. The output of the retrieval system is a subset of documents, and each of these subsets can be represented by a point in a space L. The retrieval operation is represented by a transformation from a point in space P to a point in space L. Two different retrieval transformations are defined. Future elaborations and extensions of the model are outlined.
Most of the mathematical work which has been done toward developing a theory of information retrieval has been directed to studies of machine mathematics or coding mathematics, or to discussions of the gross statistics of retrieval efficiency. Comparatively little work has been done with the theory of the verbal symbols themselves or the way they operate in retrieval. The purpose of this paper is to lay the foundations for a unified mathematical theory for the language symbols of retrieval and to present a mathematical model based on the theory. It will study the algebras or the modes of combination of language symbols, and it will study the way such symbols are related to the subsets of documents which contain the desired information.
In present day writings about retrieval systems and their methodology, there is a confusing variety both in terminology and method with respect to (a) the verbal language symbols used, (b) the restrictions that are imposed upon the symbols, (c) the modes of combination that are permitted between the symbols, and (d) the manner in which the symbols or groups of symbols are re-
CALVIN N.MOOERS Zator Company, Cambridge, Massachusetts.
lated to the documents. Without any unifying theory to cover this variety of terminology and methodology, it is difficult to relate and compare one retrieval system with another, or to relate their individual theories with any of the well-established branches of mathematics or logic whose concepts, results, and theorems would be of assistance to the further development of a general retrieval theory.
This paper presents a mathematical model for the study of retrieval systems. According to this unifying theoretical scheme, it is possible to start from simple postulates and elements and, by systematic procedures, to generate the underlying framework of many of the present retrieval systems. It demonstrates in detail the mode of use of their verbal systems and exhibits the algebra of their symbol combinations and the ways in which the symbol combinations are related to the pertinent subsets in the document collection.
There are a number of important reasons for developing a mathematical model of this kind. It provides a neutral language by means of which the features of a great variety of retrieval systems can be discussed. Since the scheme which is presented can generate the theoretical framework of many different retrieval systems, starting from very simple postulates, it permits easy study of the effect of varying these postulates. We can see how one recognized kind of retrieval system changes into another when even a relatively simple change is made in the elementary combining elements. From this viewpoint, the various retrieval systems are actually special cases generated by the unifying mathematical model and therefore are easily placed in perspective with each other. Because the theoretical scheme described in this paper is based upon well-known mathematical concepts, it has the advantage that it will enable us to relate information retrieval theories to some of the established results from various branches of mathematics and perhaps to extend our theories as a result of that contact.
In this paper, attention is restricted entirely to the verbal symbols, their combinations, and to how they provide retrieval with respect to subsets of documents chosen from a document collection. The paper is not concerned with the details of the retrieval machine or its coding. It presumes that some retrieval machine does exist which is capable of performing the various tasks required by the verbal symbols. We are safe in making this presumption because the general purpose computing machines now available are so versatile and capable that any of the tasks of retrieval described here can be performed on such a machine. For this reason we know that there is at least one class of machine which can do the job. However, the use of these very expensive and complex machines is usually wasteful for performing simple retrieval tasks. Generally, much simpler special purpose machines will be used for retrieval.
Plan of attack
A customer desiring to use an information retrieval system actuates it by presenting a “prescription” for the information that he wants. The retrieval system responds to this prescription by indicating to the customer a set of documents from the collection which presumably will furnish the information he desires. In other words, an information retrieval system translates or transforms the customer’s prescription into a set of documents.
In all the retrieval systems now in use, the prescription is not given in ordinary English language, but rather in a special language of appropriately chosen retrieval words. These are the “language symbols” with which this paper is concerned. The customer’s retrieval prescription is ordinarily never stated in terms of only a single language symbol. It usually is composed of a complex of several symbols taken together. In the same way, the customer is seldom interested in a single document chosen from the collection. His needs are better answered by a small group of documents, that is, a subset of documents chosen from the collection.
For this reason, in studying retrieval systems, our main attention should be focused not upon single symbols nor upon single documents. It should be focused upon the complex of symbols taken together which form a prescription and upon the relationship of this prescription to the subsets of documents that can be chosen from the collection as a whole.
It is helpful to have a convenient way of picturing this relationship (see Fig. 1). The balloon at the left marked P represents, in the mathematical sense, a
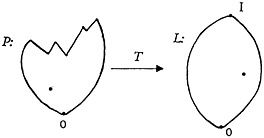
FIGURE 1. The space P of all possible retrieval prescriptions, the space L of all possible document subsets, and the retrieval transformation T associating points of P with points of L.
“space” in which each point represents a possible combination of language symbols useful in retrieval. The characteristics of this space will be developed in detail as we proceed. For the moment, we should realize that every possible point in the space represents a retrieval prescription, and conversely that every possible retrieval prescription is represented by a point in this space.
The balloon at the right marked L is another “space.” Each point in space L represents a subset of documents that can be formed by choosing documents from the entire collection in a library, and every set of documents that can be formed from the entire collection is represented by a point in this space. This space has a very large number of points. If there are N documents in the library, there are 2N subsets that can be formed on the documents in the collection (including the subset having no documents and the subset having all the documents). For example, if the library has 1,000,000 documents, the number of subsets is 21,000,000 or 10310,000.
There is a point in the space L representing any choice of documents that could be taken from the library. A moment’s reflection will show that most of the points in L represent heterogeneous sets of documents with no unifying similarities in their subject content; such sets are not a useful output to any input retrieval prescription. The sets that are a useful output are a very tiny fraction of the total points in L. On the basis of some rather reasonable presumptions about the variety of input prescriptions, I have computed that less than 1075 of the points in a typical space L for a collection of 1,000,000 would ever be used. Thus, in a relative sense, “almost all” the points in L are not useful for output. This fact constitutes the central problem of information retrieval. It is how to find the few useful subsets of documents when almost all the subsets that might be chosen in the collection are not useful.
The purpose of any retrieval system is to receive as an input a prescription which can be represented by a point in P, and to convert this input to an output which consists of a citation to, or a set of copies from, some subset of documents taken from the collection represented by a point in L. In other words, in terms of the diagram in Fig. 1, if we choose any point in P as a prescription, the retrieval system is to emit an output which is represented by some point in L. There is a fixed relationship or association between each and every one of the points in P to some of the points in L. A mathematician calls such an association a “transformation.” The retrieval transformation T is represented in Fig. 1 symbolically by the arrow directed from P to L.
If the information in the retrieval system depends upon some machine searching device, or other mechanization, the machine performs the transformation T. We should keep clearly in mind that the machine, when it is performing the transformation T, is only carrying out the intellectual design of a retrieval system which is represented by the two spaces P and L and the retrieval association from the one space to the other. If the design of the language symbol aspect of a retrieval system, as in Fig. 1, is ill-conceived, then no machine, however good, can overcome the poor intellectual design. For this reason, we must first pay attention to the way the language symbols operate
in retrieval. Only after we are sure that the language symbols perform the way we want them to, should we try to mechanize the system with some machine.
Many details are yet to be filled in before Fig. 1 is really meaningful. The structures of the two spaces have not been worked out, nor has the basis of the transformation been described. I shall begin by considering the space L. A mathematician would call this a “finite Boolean algebra.” (1, p. 159; 2, p. 318). What this really means is that the relationship between the points of the space L are just the relationships that will be found between the various subsets that can be formed on any aggregate of N objects, where each subset corresponds to a point of the space. Given a set of N objects, these are some of the operations and relationships: we can form subsets of the objects; we can combine or add any two of the subsets; we can take the intersection or the common members of any two of the subsets; and, upon comparing their membership, we can find that some of the subsets are included within others. Since the number N of objects is finite, the number of subsets is finite and thus we have a finite algebra. When we have a familiarity with these elementary operations upon subsets, we know some of the most important properties of a finite Boolean algebra and thus of the space L (cf. 2, p. 311).
Space P of the retrieval prescriptions is much more complicated than L, and we shall have to study it in more detail. Part of its complication results from the many differences between one retrieval system and another in the basic methodology of language symbols. However, it is difficult to study differences in methodology if we confine our attention only to the large and complicated space P. The problem becomes much simpler if we have some way to decompose P into simpler components. Fortunately, there is an easy way to do this.
We start with the repertory R consisting of a finite number of simple structures, as indicated in Fig. 2. Each of these structures, represented by one of the
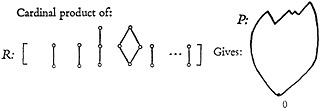
FIGURE 2. The repertory R of simple structures whose cardinal product is the space P of all possible retrieval prescriptions.
little diagrams enclosed in the brackets, stands for a simple retrieval element such as a descriptor or some other kind of term which I shall call a “character.” These simple structures can be combined or multiplied together to give a
“cardinal product” or a “direct product.” The cardinal product is also a structure, but it is more complicated than any of its factors. By combining the simple structures by the cardinal product, we actually can generate the space P with all its properties. Therefore, in order to get the answers to many of our questions about P, we can sometimes do it more easily by going back to the repertory R with its simple, easily understood elements.
This viewpoint has a number of advantages. We can see exactly how space P is built up or generated. We can more easily see the effect of employing different kinds of characters in the repertory. We can better understand exactly what we do when we make a prescription for retrieval or when we analyze a document to put it into the system. By a better understanding of P, we can also better understand the nature of the retrieval transformation T between the space P and space L.
However, before we can continue our investigation into the detailed features of retrieval systems, it will be necessary to introduce a number of mathematical tools and concepts that we will need in the exposition to follow.
Concepts employed
The first concept concerns the language elements which prescribe retrieval. In this paper I shall be primarily concerned with the class of language elements which I have called “characters.” I define a character as a verbal symbol which (a) can be independently manipulated in prescribing a retrieval selection, (b) does not decompose into two or more such independent symbols, (c) has a definite meaning or interpretation, and (d) comes from a finite repertory.
A string of Arabic numerals making up a decimal classification number, e.g., 512.3, is a character: it is complete in itself; it cannot be broken into two or more parts; it has a definite meaning; and it is taken from a repertory which is finite and not rapidly changing.
A descriptor (3) is a character because it clearly satisfies each of the four required points: it can be independently manipulated; it cannot be split up; it is precisely defined by a scope note; and it comes from a finite and actually quite small repertory.
A subject heading may or may not be a character, depending upon the care with which it is defined and used. Sometimes subject headings are used without scope notes or any other careful definition of meaning. Sometimes they are permitted to be generated ad lib without any particular limitation or control. Whenever these situations prevail, subject headings are defective characters.
“Uniterms” as introduced by Taube (4) have been used in a great variety of
ways and without very much standardization. Since they often tend to be words merely taken from text, they are likely to be defective as characters because they have no controlled meaning. The typical repertory of Uniterms is also indefinite and “open-ended,” and it is questionable if such a repertory can be called “finite” in the sense that any finite upper bound can be put on the total number of Uniterms for a system. If Uniterms were made more precise, by using scope notes, and if their number and their proliferation were controlled, they would fall within the definition of characters.
The next concept is that of a “partially ordered system” (1, p. 1; 2, p. 326). A very simple example of a partially ordered system is the hierarchy of people working in an office. The partial ordering relation is based upon who may receive orders from whom. If two people in the office are from different departments, neither may receive orders from the other. However, if they are both in the same “line of authority,” then one of them must take orders from the other. An organization chart is actually a diagram of this partially ordered system. It shows who takes orders from whom. Note that this is called a “partially ordered,” rather than a “totally ordered,” system in order specifically to indicate that the ordering relation is true of only certain pairs of people, and not of all pairs that can be formed.
More abstractly, a partially ordered system is a set of elements together with a specific ordering relationship such that, given any two elements x and y from the set, it is possible to say of them that x precedes y, or y precedes x, or that neither precedes the other. When x precedes y, it is signified by x≦y. (Where Birkhoff uses “included,” I have used the word “precedes” because of the possible confusion that might arise over the possible meanings of inclusion in discussing some other problems of retrieval.)
As an example of a partially ordered system in retrieval, we can take the points in the space L. Each of these points represents a subset of documents. If the partially ordered relationship is that of “being included within,” some of the subsets are included within some of the others. For other pairs of subsets, neither subset is completely included within the other, and therefore neither precedes the other in the partially ordered system.
A partially ordered system can be diagramed. This has been done in Fig. 3 for several simple systems. The individual elements of the partially ordered system are represented by small circles. The partial orderings are shown by the connecting lines. If element x precedes element y, x is below y, and it is possible to trace a continuously descending path with no up-and-down zigzags from element y down to element x. The path from element y to element x may pass through several other elements, or x and y may be adjacent. No horizontal lines are allowed in a diagram of this kind.
Some partially ordered systems have a “greatest element,” or a “least element,” or both. Referring to Fig. 3, element 5 of system (A) or element 8 of (D) are the greatest elements of these partially ordered systems. In the same
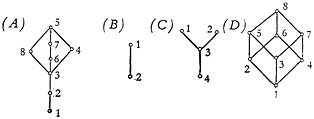
FIGURE 3. Four examples of simple partially ordered systems.
fashion, element 1 of (A) or element 4 of (C) are least elements of their systems. By convention, the greatest element of a partially ordered system is usually denoted by I, and the least element by 0. Not all partially ordered systems have a greatest or least element. The partially ordered system (C) has a least element, but it has no unique greatest element.
The concept of “level” is useful in the discussion of partially ordered systems (cf. 1, p. 11); however, Birkhoff uses the terms “dimension” or “height.” Referring to Fig. 3, the partially ordered system (C) has two distinguishable levels above the bottom element. To determine the level number for an element, we give the least element in the partially ordered system level number 0, and we count the number of elements as we move up in the diagram to the element whose level number is desired. Thus in the partially ordered system (D), element 5 is at level 2 and element 8 is at level 3. In many partially ordered systems, however, the concept of level does not have any meaning. If the system has no least element, or if there are several paths up to the given element, along different paths giving different counts, then the concept of level cannot be employed. For example, in the system (A) no consistent level can be assigned to the point 5. Sometimes it is useful to speak of levels counting down from the top, and this is done in a similar fashion but with the directions reversed.
The concept of cardinal or direct product between partially ordered systems plays a central role in the systematic method of generating the basic structures of retrieval systems. Given two partially ordered systems X and Y, whose typical elements are denoted by x and y, the cardinal product XY is also a partially ordered system. It is composed of all couples of the form (x,y), and it is partially ordered by the rule that (x,y) precedes (x′,y′) whenever x precedes x′ in X, and y precedes y′ in Y. The formation of the cardinal product can be diagramed. In Fig. 4 are shown two partially ordered systems along
with their cardinal product. The individual elements of each of the original systems are numbered so that it is possible to see how the cardinal product partially ordered system is formed from the couples, and how the ordering relation follows from the definition. This cardinal product partially ordered system of Fig. 4 is very simple, since it is formed from systems having relatively
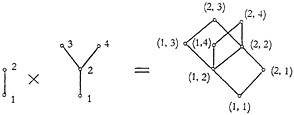
FIGURE 4. Illustration of the formation of the cardinal product of the two systems shown at the left.
few elements. When the starting systems are more complicated, the cardinal product becomes very complex.
The cardinal product of three or more partially ordered systems can also be formed. We merely multiply two of the partially ordered systems together, getting a product, and then multiply the next system into the product. This is permissible because the cardinal product is associative. Thus we can take the cardinal product of all the partially ordered systems in a repertory R, as in Fig. 2. As we shall see, this cardinal product system actually is the partially ordered system P, whose elements constitute the space in which retrieval systems are formulated.
According to another useful concept, we consider any two elements x and y in a partially ordered system, and we wish to identify the largest element z which precedes both x and y. In terms of the diagram for a partially ordered system, z would be the highest element in the diagram from which one can draw ascending lines to both of the elements x and y. Such an element z is a lower bound to both x and y; in fact, it is a “greatest lower bound” or “g.l.b.” The element z is also called the “cap” of the two elements, and this is denoted by x∩y=z. In Fig. 3 (D) the cap of elements 5 and 7 is the element 3.
In the same manner we can speak of upper bounds. We define the “least upper bound” or “l.u.b.” w of two elements x and y in a partially ordered system as the smallest element which is preceded by both x and y. The least upper bound w of two elements is often called their “cup,” and this is denoted by x∪y=w. The cup of elements 5 and 4 in (D) of Fig. 3 is the element 8. It should be noted that cup and cap do not always exist in partially ordered systems. In system (C), the cap of element 1 and 2 exists, but not their cup. In many situations, particularly when dealing with subsets formed upon an ag-
gregate of objects, cap is associated with the logical product or the intersecting part of the subsets.
We are now able to introduce the concept of a “lattice.” (1, p. 16; 2, p. 328). Fairthorne was perhaps the first to point out the value of lattices for gaining an insight into retrieval systems (5, 6). A lattice is defined as a partially ordered system in which every pair of elements from the system have both a cup and a cap. For example, the partially ordered systems (A), (B), and (D) of Fig. 3 are all lattices. The system (C) is not a lattice because cup does not exist for all pairs of elements.
One of the most important examples of a lattice is the partially ordered system composed of all the subsets formed upon a finite aggregate of N objects. Thus the document subsets that can be formed from a library collection form a lattice. Actually, it is a very special kind of a lattice, and it is called a Boolean algebra or Boolean lattice. Since the subsets of the documents do form a lattice, the space of these subsets in Fig. 1 is denoted by L. However, the document prescriptions do not always form a lattice, although they do usually form a partially ordered system. For this reason the space of document prescriptions is denoted by P.
We now have the main conceptual tools which will enable us to study the theory of a variety of information retrieval systems.
Retrieval systems based upon descriptors
Descriptors are perhaps the simplest form of characters, and thus the kind of retrieval system based upon them is simpler than any of the others. The following are the important facts about descriptor retrieval systems (3). When a document is analyzed to be entered into a descriptor retrieval system, the message of the document is tested against each of the descriptors in the repertory. The descriptors whose meanings provide retrieval clues to the message of the document are then associated with the document. Thus for each document in the collection, there is a delineating subset of descriptors. A retrieval prescription is given also in terms of a subset of descriptors. When the retrieval operation is performed, the prescribing subset will be included within some of the document subsets, and it will not be included within some of the others. This provides the criterion of selection. The output of the retrieval system consists of citations to those documents whose delineating subsets include the prescribing descriptor subset. Thus a document will be retrieved if the delineating subset of the document contains each and every one of the descriptors in the prescribing subset. If the document subset has additional descriptors, the document is still retrieved.
Let us now examine the descriptor retrieval system from the standpoint of the mathematical model sketched in Fig. 1. The space L of the document sets is a Boolean algebra typified by the subsets formed on a finite aggregate. It poses no problems. The space P of the retrieval prescriptions does demand our attention.
The space P is the cardinal product of all the two-element partially ordered systems in the repertory, where each of these partially ordered systems represents the behavior of a single descriptor. This is diagramed in Fig. 5. The partially ordered system for an individual descriptor is diagramed in Fig. 6.
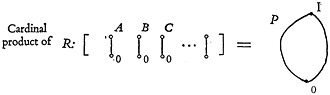
FIGURE 5. For descriptor systems, the partially ordered system P is the cardinal product of simple two-element partially ordered systems.
Let a hypothetical descriptor, which might have the meaning of “red” or “airplane” or “low temperature,” be designated by A. In either delineation of the document during an analysis, or prescription of it for retrieval, a descriptor can behave in only two ways. On the one hand, the descriptor A may be asserted
FIGURE 6. The partially ordered system for a single descriptor.
about the document as providing a clue to the message in the document. When this is the case, we represent it by the upper point in the diagram of Fig. 6. The other possibility is that no assertion one way or the other is made about the descriptor A. This situation is represented by the lower point marked 0 in the diagram of Fig. 6. These two possibilities, represented by the two points, are partially ordered by the partial ordering relationship: “being included within as a special case.” The assertion of A is certainly “included within as a special case” of 0, which is the lack of any assertion. This is the sense in which any descriptor and its behavior are quite well represented by this kind of simple, two-element partial ordered system.
The formation of the cardinal product for the partially ordered systems of several descriptors is shown in Fig. 7. Here the repertory has three descriptors. The complete cardinal product is shown at the right in the figure, and the meaning of each element is written out. For example, the element marked AB
means that both descriptors A and B are asserted. This figure also shows the way the notation is related to the definition of the couples which define the cardinal product. For example, taking element A in the cardinal product we have: ((A,0),0)=(A,0,0)=A. A similar relationship holds for the other elements in the cardinal product system.
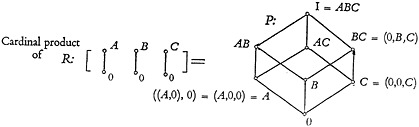
FIGURE 7. This shows the formation of the cardinal product for three descriptors. Each of these partially ordered systems is a Boolean lattice.
The space P of the retrieval prescriptions for a retrieval system based upon descriptors is a Boolean lattice. The easiest way to see this is to observe that the system P can also be built up by forming all of the possible subsets of the descriptors in the repertory. As has been mentioned before, any partially ordered system of all the subsets of a finite aggregate is a Boolean lattice.
It should be observed that the assertion of any subset of descriptors from the repertory is equivalent, for these descriptors, to taking the upper points in Fig. 5, and for the descriptors which are not asserted, to taking the lower points. Thus, in a way, we take an action upon each of the descriptors in the repertory. As is illustrated in Fig. 7, any such action asserting a subset of descriptors from the repertory is equivalent to asserting a single point in the lattice P. This demonstrates, for retrieval systems based upon descriptors, that every delineation of a document in terms of a descriptor set, or every prescription for retrieval in terms of a descriptor set, is represented by a single point in the space P.
We can now describe the retrieval transformations from points in the space P to the points in the space L. The first transformation T1 is the easiest to describe, but it is not the most useful in actual retrieval systems. Although it is not used at all in descriptor systems, I mention it here because it will be used for comparison purposes. Each document in the collection has a subset of descriptors assigned to it, i.e., each document is associated with some particular point of P. Looking now to a typical document subset, such as represented by any point in the space L, it is evident that the individual documents in such a subset will usually be associated with a wide variety of points in the space P. There will be some points in L which are unusual in that they represent the largest set of documents such that all the documents associated with the set
shown by the point will have the same set of descriptors. In other words, all the documents of such a point of L will have descriptors corresponding to the same point of P. Each of these points in P therefore has a unique association with a corresponding point in L (different from the 0 element). On the other hand, many of the combinations of descriptors, represented by other points of P, will not be assigned to any of the documents in the collection. Such points correspond to the set having no documents whatsoever, that is, such points of P correspond to the null set of documents represented by the point 0 in the diagram of L. Thus it is possible to associate every point of P with some point of L, though not every point in L is associated with a point of P. This association between the points of P and some of the points of L provides the definition of the transformation T1. Given any point in P, the transformation T1 then names a point in L.
In considering the retrieval properties of the transformation T1, we see that when we make a retrieval prescription by naming a single point in P, the transformation T1 gives us a subset of documents all which possess exactly the set of descriptors corresponding to the retrieval prescription point. For many purposes, this is not the best kind of selection for retrieval. The difficulty with this kind of selection is that when we name a set of descriptors to prescribe a search, we are interested not only in the documents which have exactly the prescribed set of descriptors, but also in any other documents having any additional descriptors which may not be specified. The transformation T1, when used for selective purposes, will exclude all such documents having descriptors other than those in the descriptor subset corresponding to the prescribing point of P. To remedy this defect, we must go to a slightly more complicated transformation, which I have designated T2.
The transformation T2 is the basis of selection in actual descriptor retrieval systems. Although the transformation T2 has already been described at the beginning of this section, we now want to describe it in terms of the points in spaces P and L. Given any point x in the space P, there is a large family X of other points in P which are preceded by the point x. As shown in Fig. 8, all these points lie above the point x in the partial ordering diagram. Looking now to the document collection, there are many documents whose assigned subset of descriptors is one of the points in the family X. We can then consider the largest set of documents such that each document in the set has a subset of descriptors represented by some point in X. Let this set of documents be represented by a point x★ in L. We can now define the point x★ in L to be the transformation according to T2 of the point x in P.
From this definition of T2, each of the points in P has a corresponding image point in L. On the other hand, not all the points of L are images of such a
transform, in fact, only a very few of them are. It is useful to designate the points of L which are the images of the points in P, through the transformation T2, by the designation L★. Then every point in P is associated by T2 with
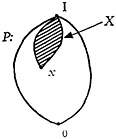
FIGURE 8. The class of points X in the system P consists of all the points which are preceded by the prescribing point x.
some point in L★, and every point in L★ is associated (through the inverse of the transformation T2) with some point in P. If we were to give a characterization of the partially ordered system L★, we could well call it the “retrieval skeleton of the system of document sets of the collection.” This name is appropriate because the system L★, although containing only a very small part of the system L, contains all the points of L which are of primary interest for the retrieval.
It is enlightening to make some comparisons between the transformations T1 and T2. One interesting comparison is based upon observing the transform of an ascending path drawn through space P. (Refer to Fig. 9.) By an ascending path, is meant a path drawn from 0 at the bottom, through one point after
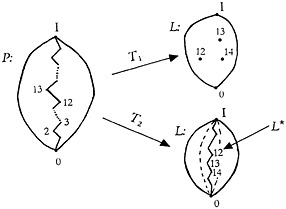
FIGURE 9. A continuously ascending line drawn in P transforms by T1 into points in L representing non-overlapping subsets. The transformation of the line by T2 is a descending line in L. The lattice L★ is the set of all the image points of P by the transformation T2.
another, going continuously upward through a selection of points, until the topmost point I is reached. Such a path represents in the space P what happens when we first start out with no descriptors at all in a prescription, then take one descriptor, then add another descriptor to it, then add a third descriptor to those we have, and so on until our accumulation of descriptors finally includes all the descriptors in the repertory, bringing us to the point I. When the accumulation has k descriptors in it, the set of descriptors is represented in P by a point at level k in the diagram.
If we apply the transformation T1 to the individual points along such a path, this is what happens. For the first several descriptors (k small), all the points transform into point 0 of L because most documents will always have more than only one, two, or three descriptors. Next, there will be some first point, such as at level 12, for which there are some documents having the corresponding set of descriptors. The point in L for this document set is at some point in the interior of L. There may also be documents corresponding to the next point on the line, at level 13. The transform of this next point will also be somewhere in the interior of space L. However, these two points will not be ordered with respect to each other in space L because they represent mutually exclusive sets of documents. Neither of these image points can precede the other according to the partial ordering relationship of set inclusion that prevails in the system L.
Thus we have the interesting situation in which the point at level 12 does precede the point at level 13 in space P, but the transforms of these points according to T1 are points which have no ordering relationship in L.
At a sufficiently high level in P along the ascending line, that is, for sets of a sufficiently large number of descriptors, there will be no corresponding documents in the collection. For these points in P, the transform according to T1 will again be the point 0 in L.
Thus the points along a continuously ascending line in P transform according to T1 as follows: first, into the point 0 of L, then into a scattering of (non-ordered) points in the interior of L, and finally, again into the point 0 of L.
This behavior may be contrasted with the transform according to T2 of the same points along the line. Referring again to Fig. 9, the point 0 of P goes over into I of L. This is because a prescription involving no descriptors will allow all the documents in the collection to be selected. Conversely, the point I of P goes over into the point 0 of L, because none of the documents in the collection will be associated with all the descriptors. Moreover, the transform of each of the points on the ascending line drawn in P is some point in L lying between I and 0 (or including I and 0). The points near the top of the line in P all go into the 0 element of L, since there are no documents having
this many descriptors. However, the transform of the first point above the 0 element P is not a point I in L, because the restriction imposed even by a single descriptor will prevent the entire collection (represented by I) from being selected. As we go up from point to point along the line in P, the transforms of the points are located in descending positions in L (and are in adjacent descending positions in L★). Moreover, the image points in L of the points of the line in P are all ordered with respect to each other. (None of the sets are mutually exclusive.) Where the point at level 12 in P precedes the point at level 13, the image point in L of the point 13 precedes that of point 12. Note that the direction of the partial ordering is inverted by the transformation T2.
In terms of the practical operation of an information retrieval system, what I have diagramed is the well-known fact that as one adds more and more descriptors to a retrieval prescription, the set of retrieved documents becomes smaller and smaller, and that each of the smaller sets of documents is included within the larger set which is obtained with fewer descriptors in a prescription.
It should be noted that some of the important machine systems and their codes for operation according to the descriptor retrieval system do not reproduce the transformation T2 exactly. For instance, the Zatocoding system, which uses code patterns of a random nature and which superimposes these patterns into the coding matrix, is one of these coding systems (3, 7). Such a method of coding will produce only a close approximation to the transformation T2. By suitable design of the coding any degree of accuracy in reproducing T2 can be achieved. All the desirable properties of the transformation T2 are preserved except for the addition of a negligibly small amount of “noise” which can be controlled. However, a discussion of machines and their coding systems is beyond the scope of this paper.
The points of the space P form a lattice, and therefore the operations cup and cap are always defined. For any points x and y, x∪y=z. However, by T2, each of the points x, y, and z has its transform point in L. Where the transform of x is indicated by x★ (and so on, for the other elements), we have, in the lattice L★, the relationship x★∩y★=z★. However, this relationship does not hold in the lattice L.
Similarly, for any three elements in P related by the cap operation, their corresponding transform points in L★ are related by the cup operation. Again, the cup relationship between the transformed points does not hold in L. These results may be compared to those of the transformation T1, for which neither the cup nor the cap operation on elements in P has any valid relationship to the cup and cap operations in L.
From these remarks we see that algebraic operations involving cup and cap operations in P are valid in L★, although the cup and cap are interchanged;
while these operations in P have no corresponding operations in L according to either T1 or T2. In practical retrieval system operation, the preservation of the operations cup and cap through the transformation T2 into the lattice L★ mirrors the way in which the descriptor combinations are related to the selected sets of documents. With these observations, we go on to the next type of retrieval system considered.
Retrieval systems based upon characters with hierarchy
The language symbols of retrieval employed in a hierarchical classification system are called “characters with hierarchy.” There are a number of examples of retrieval systems employing such characters. Very familiar are the Library of Congress and the Dewey Decimal classification systems. Slightly different in basic organization is the U.S. Patent Office classification system. Also falling within this category are the characters in the technique of interlocking sets of descriptors for the representation of structure (8). The Colon Classification of Ranganathan also uses characters with hierarchy (9).
There is a certain difficulty in studying characters with hierarchy because some of the systems have become so familiar to us with long use that we ordinarily do not think about their basic structure. Thus, although several of the examples named may seem to be the same in many respects, they have quite different postulates. One of the purposes of this section is to display which postulates are similar and which are different for the systems.
As an example of the behavior of characters with hierarchy, consider the two retrieval characters “shoes” and “clothing.” Because shoes are a kind of clothing, these two retrieval characters are not independent. When we are talking about shoes, we mean a specific kind of clothing. Also, when we are talking about clothing, we often intend to include shoes within the compass of our discussion.
These two characters do not behave like descriptors because, when we take the two of them together, i.e., “shoes—clothing,” one of them loses its purpose in any retrieval operation. If the two characters taken together are intended to cover all the ground mentioned by either of them, then their meaning is covered by the single character “clothing.” On the other hand, if the two characters taken together are intended to refine and to narrow the meaning of each other, then their meaning is completely covered by “shoes.” Ordinarily the second of these two possibilities is intended, and we shall make that interpretation in the discussion which follows.
Since some characters with hierarchy absorb others, they evidently are partially ordered. The diagram of the partially ordered system for the charac-
ters “shoes” and “clothing” is shown in Fig. 10. In explanation of this diagram, consider the delineation of the documents as they are analyzed to be placed into the retrieval system. If we make no assertion whatsoever about shoes or

FIGURE 10. The partially ordered system based upon two characters with hierarchy.
clothing, this is represented by the null element 0. The simplest factual assertion that can be made in delineation is “clothing,” represented by (a). A more exact assertion is “shoes,” but this character, during delineation of the document, must also carry along with it the meaning “clothing.” For this reason, “shoes” is considered to be a refinement of “clothing,” and is represented by (ab).
In the notation which I have adopted, the letters a and b without the parentheses around them are not characters. I shall call such letters “simple elements” or merely “elements.” The purpose of the elements is to represent the logical structure of characters with hierarchy. The elements cannot be used independently for retrieval operations; only characters can be so used. To indicate when an element, or a string of elements, becomes a character, I shall enclose the letters or string of letters in parentheses. Although we might say that element b of Fig. 10 has the meaning “shoes—irrespective of clothing,” this kind of analysis has not generally been used in hierarchical classification systems. I shall avoid it here. Only characters will have meanings usable in retrieval.
According to the logical structure of a hierarchical classification system, when we delineate a document with the character “shoes,” we also intend the assertion to include the assertion “clothing.” In another example, if a book or document is delineated by the character 512.3 from the Dewey Decimal Classification system, we also mean that this same document is delineated by the characters 512.–, 51–.–, and 5– –.–. In general, if the elemental representation of a typical character is (abcd), we intend that any document delineated by this character is also, by implication, delineated by any of the characters which can be formed by successively crossing off elements from the right-hand end of the representation. In another way of looking at this matter, we
refer to the partially ordered space P of Fig. 11, in which each point of the space represents a possible delineation of the document. Then, if the document is delineated by a character at point x, by implication, it is also delineated by all the points preceding x, as shown by the shaded area of Fig. 11.
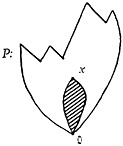
FIGURE 11. In a system P of characters with hierarchy, if a document is delineated by a point x, it is by implication delineated by all the points preceding x, as shown in the shaded area.
This brings out an interesting dual aspect of a hierarchical classification system. On the one hand, the characters are ordered in a hierarchy, and sometimes this ordering of characters alone seems to be an end in itself. On the other hand, the delineation of a document by one character implies its simultaneous delineation by all the characters that precede it in the hierarchical scheme. This has practical retrieval consequences. However, we should remember that this multiple delineation is only implicit. The degree to which it is actually made use of for practical retrieval purposes differs greatly from system to system.
The cardinal product can generate the retrieval language system for characters with hierarchy. This occurs when the cardinal product of a repertory of simple partially ordered systems is formed. In the case of characters with hierarchy, the simple partially ordered systems of the repertory are such as those shown in Fig. 10. Each partially ordered system of the repertory is a chain; that is, it is a single line of characters, with the most particular one at the top, descending down through several levels to the 0 element. In Fig. 12 at the left are shown two such chains. Their cardinal product is shown in the center. However, this cardinal product must be considerably simplified before it is really meaningful. For instance, the character (a,a) might be crudely interpreted as “clothing-clothing.” This is nonsense. What is really meant is merely “clothing.” Therefore such symbols as (a,a) must be reduced to (a). In the same way, the other symbols in the cardinal product must be simplified as follows. The commas are dropped out. Letters which repeat other letters are eliminated. If there are any letters other than 0, the 0 is eliminated. The
remaining letters are put in alphabetical order. The result is the elemental representation of the character. This simplification applied to the center diagram produces the upper right-hand diagram of Fig. 12.
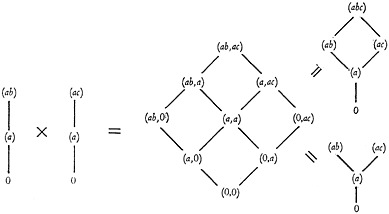
FIGURE 12. The cardinal product of the two partially ordered systems shown at the left has been taken, the intermediate product is shown at the center, and after the appropriate reductions have been performed, the final products are shown at the right. At top right is the system with weak hierarchy, at lower right is the system with strong hierarchy.
The new character (abc), which has appeared as a result of the cardinal product, needs some interpretation. If character (ab) has the same meaning as in Fig. 10, and if character (ac) is given the meaning “trousers,” then we can interpret the character (abc) as meaning “shoes and trousers integral in one garment of clothing.”
There are systems of hierarchical characters which do not permit the formation of systems of the type shown in the upper right-hand diagram of Fig. 12. In general, these systems do not permit a character to be preceded immediately by two other characters. For such systems, the manner of reduction must be supplemented so that the cardinal product of the original character systems is reduced to the form as shown in the diagram at the lower right-hand corner of Fig. 12.
The two situations illustrated at the right in Fig. 12 must be distinguished. Systems which do permit some characters to be preceded by more than one character, I call “systems with weak hierarchy.” The system of classification used in the U.S. Patent Office has weak hierarchy. Systems which do not permit any character to be preceded immediately by more than one character, I call “systems with strong hierarchy.” The Dewey Decimal Classification has strong hierarchy. The diagram of a strong hierarchical system is called a “tree” because none of the lines ever rejoins as you trace upwards in the diagram. In
my opinion, systems with weak hierarchy tend to be more versatile in retrieval.
We shall now consider postulational treatment of characters with hierarchy, based upon properties assigned to the elements.
1. There is an ordered sequence (alphabet) of simple elements, e.g., a, b, c,· · ·, etc.
2. Each character is represented by a string of simple elements taken from the sequence, and the elements in the string are arranged in the same order as in the sequence.
3. Strong hierarchy: In a system of characters with a strong hierarchy, each element in the sequence has a unique predecessor element in the sequence. When any element occurs in any string, it is always immediately preceded by its predecessor element. Elements which have the null element as a predecessor may begin a string.
4. Weak hierarchy: In a system of characters with weak hierarchy, each element in the sequence has one or more predecessor elements (including the null element), and it may also have one or more co-predecessor elements. When an element occurs in any string, it must always be preceded immediately by all its predecessor elements except when a co-predecessor element is in the string, in which case the co-predecessors may come between the element and its predecessors.
The operation of these postulates for characters with strong hierarchy is shown by example in the table of Fig. 13. Typical strings of elements forming
|
Element |
Predecessor |
Character formed |
|
a |
Null |
(a) |
|
b |
a |
(ab) |
|
c |
b |
(abc) |
|
d |
b |
(abd) |
|
e |
d |
(abde) |
FIGURE 13. Illustration of the application of the postulates to characters with strong hierarchy. Note that the combinations (ac), (ad), (abcd), or (ace) cannot represent characters.
characters are shown. Also listed are the elements and their predecessors. We notice that strings such as (ac) are not allowed because element c must always be preceded by element b.
The application of these postulates to the formation of characters with weak hierarchy is shown by example in the table of Fig. 14. We notice that element e must always be preceded by b, c, and d. Element d must be preceded by a, and d may or may not be preceded by b and c. Thus, characters formed according to weak hierarchy have a great deal more variety, because of the fewer restrictions, than characters with strong hierarchy.
From these examples, and by the postulates, we can see that the system of characters in the upper right-hand corner of Fig. 12 is compatible with weak hierarchy, while the system in the lower right-hand corner is compatible with strong hierarchy.
|
Element |
Predecessors |
Co-predecessors |
Character formed |
|
a |
Null |
|
(a) |
|
b |
a |
|
(ab) |
|
c |
a |
|
(ac) |
|
d |
a |
b, c |
(abd), (acd), (abcd), (ad) |
|
e |
b, c, d |
|
(abcde) |
FIGURE 14. Illustration of the application of the postulates to characters with weak hierarchy. Note that combinations (ade), (bc), or (ae) are among those that cannot represent characters.
In any system of characters with weak hierarchy, the system becomes more and more versatile as the different elements are allowed to have more and more co-predecessors, and also as the requirements for predecessors are removed. If this process is carried out to the limit, we have a situation in which the elements have no required predecessors (other than the null element), and they may have any other element as co-predecessors. When this happens, we can form characters by selecting any set of elements from the alphabet and listing them in order to form a string making up a character. With such a string, we can form a new character by deleting any element from the string. A moment’s reflection will show that, when the postulates are relaxed to this extent, we have a system of characters which is almost identical with the descriptor system. The elements behave as descriptors, and the strings of elements forming characters correspond to sets of descriptors.
This comparison provides an explicit demonstration of how our mathematical model can relate, through use of appropriate common terminology, two different kinds of retrieval systems which are ordinarily thought to be quite different.
In order to generate the partially ordered system of characters P, we must take the cardinal product of the set of partially ordered systems in the repertory. As yet, these partially ordered systems of the repertory have not been defined. Therefore, we require the following additional postulates in order to define the systems making up the repertory R.
5. The partially ordered systems of characters in the repertory are chains. The top character in each chain is called the “dominant character,” and it is represented by a string of elements.
6. For characters with strong hierarchy, there exists a dominant character
for each element which is not a predecessor element to any other element. This dominant character is represented by a string of elements ending in the element which is not a predecessor. (Thus there are as many dominant characters as there are elements which are not predecessors.) Each of the characters in the chain preceding a dominant character is formed by deleting one after another of the elements at the right end of the string of elements which designates the dominant character.
7a. For characters with weak hierarchy, there is a dominant character for each element which is not a predecessor of some other element, and such a dominant character is represented by a string of elements beginning at the right with the non-predecessor element and preceded by its predecessor elements only, the co-predecessor elements being systematically omitted.
7b. The characters in a chain which precede each dominant character are represented by strings in which successive elements are crossed off one after the other from the right-hand end. As this crossing off proceeds, certain elements in the string which were predecessors suddenly convert to co-predecessors. When this happens, such elements are eliminated as a group.
7c. A dominant character is then formed for each of these converted co-predecessors, with the co-predecessor element beginning the right end of a string which is built up of predecessor elements again. The characters in the chain preceding such new dominant characters are again formed by crossing off from the right.
7d. This process is continued until all of the dominant characters and their strings have been formed.
In order to illustrate the principles of postulates 1, 2, 3, 5, and 6, the system of characters with strong hierarchy described by the table in Fig. 13 has been diagramed in Fig. 15. To the left is the repertory consisting of two chains,
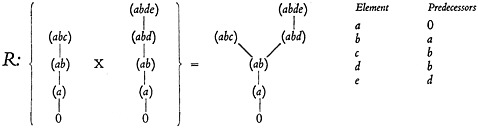
FIGURE 15. Diagram illustrating the cardinal product and reductions according to postulates for strong hierarchy.
each headed by a dominant character. The cardinal product of these chains, after all the reductions, is shown by the diagram in the center. Since we are dealing with strong hierarchy, none of the paths of such a diagram, once they
are separated, will ever join again as we go upwards. The diagram is a tree. At the right in Fig. 15 is a table giving the predecessors to each of the elements.
The system of characters with weak hierarchy from the table in Fig. 14 is diagramed in Fig. 16. At the left are three chains, each headed by a dominant
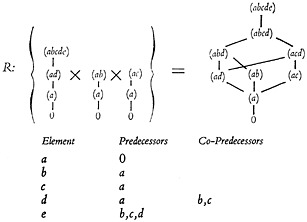
FIGURE 16. Diagram illustrating the cardinal product and reductions according to postulates for weak hierarchy. (Note. Although the same letters are used to represent the elements as in the system shown in FIG. 15, no relationship between the two systems is intended.)
character, which are found according to postulate 7. The cardinal product of these three chains, after all the reductions, is shown at the right. The table giving the predecessors and co-predecessors for each element is at the bottom. Careful study of Fig. 16 will demonstrate the application of postulates 1, 2, 4, 5, and 7.
At this point, I wish to mention the Colon Classification developed by S.R. Ranganathan of India (9). This ingenious classification provides somewhat greater freedom than the conventional methods of decimal classification. It can be described in terms of our terminology and postulates as a hierarchical system of characters in which the repertory of chains of characters is partitioned into several sub-repertories. Within any sub-repertory, the characters have strong hierarchy. However, between one sub-repertory and another, the characters have weak hierarchy. This is illustrated in Fig. 17, where the repertory at the left is symbolically separated into three sub-repertories. The table at the bottom exhibits the strong hierarchy within any sub-repertory, and the weak hierarchy between the sub-repertories.
Actually, between the sub-repertories, Ranganathan’s Colon Classification scheme behaves like a descriptor system. The cardinal product within any sub-repertory forms a tree, similar to that in Fig. 15, but when the cardinal
product is taken of the whole repertory to get P, the tree character disappears. However, P is not a lattice, because the cardinal product partially ordered system P does not have any maximum element.
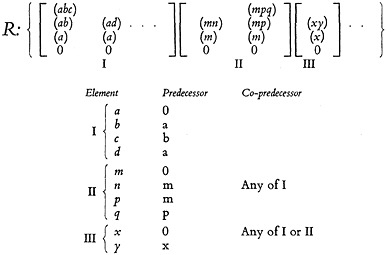
FIGURE 17. The system of characters with hierarchy devised by Ranganathan effectively has the repertory divided into sections, and the characters have strong hierarchy within any sub-repertory, while they have weak hierarchy from one section to another. This is also shown in the table at the bottom.
In the preceding discussion, we have subjected various varieties of systems of characters with hierarchy to analysis. We have set forth the postulates for finding the repertory of partially ordered systems whose cardinal product becomes the space P. Although we have done this for a variety of systems, there are so many permutations and variations which can be taken on characters of this kind that there are surely more kinds of characters with hierarchy than have been described here. However, I believe that I have established the main outlines for the analysis of their language systems into the space P. This brings us to the discussion of the retrieval transformations from space P to space L of the document subsets.
When each document is entered into the collection, its subject content is analyzed and is delineated by a single point in the partially ordered system of characters P. Certain of the points in L represent subsets of documents which are all delineated by the same point of P. Thus, each point of P is represented by some largest subset of documents (including the null set). What is the same thing, each point of P is associated with a point of L. This association between the points of P and some of the points of L defines the transformation T1.
One example of the retrieval transformation T1 is in the method of classifying and storing patent specifications in the U.S. Patent Office. This method can be fully characterized as a system of characters with weak hierarchy employing the transformation T1 for retrieval. It uses transformation T1 because, for each point in P, there is actually a “pigeonhole” containing the specifications for that particular character. (I am omitting consideration of the important use of cross-reference specifications which are filed in various other pigeonholes to assist retrieval.)
For any mechanical retrieval system, the transformation T2 is to be preferred. It can be defined in much the same fashion as was done for descriptors. Referring to Fig. 18, for any character x we find the class X of all characters
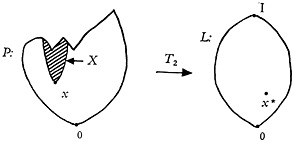
FIGURE 18. Illustration of the transformation T2 for characters with hierarchy. The class of points X are all the points in P which are preceded by the prescribing point x, while the point x★ in L is the largest set of documents all of which are delineated by some point in X.
which are preceded by x. This class X is indicated by the shaded portion of P. We then find the largest subset of documents such that all the documents in the subset are associated with a point in the class X. This subset of documents is represented by the point x★ in the lattice of document subsets L. The point x of P is associated with point x★ of L, and this association defines the transformation T2. We may again observe that the class of all image points such as x★ does not exhaust all of the points of L. As is the case with descriptors, the fraction of the points of L that actually are image points is negligibly small. Again we can call this class of image points L★.
Consider now the behavior of transformations T1 and T2 with respect to an ascending line drawn in the partially ordered system P. Such an ascending line corresponds to starting out with the very broad or general retrieval prescription, and then refining it step by step until we have a very narrow prescription. As before, the image points of transformation T1 are scattered points in L. They represent mutually exclusive subsets (except for the case in which the image points transform into the null element in L). Also as before, the
transformation according to T2 of an ascending line in P becomes a descending line in L. The line in L starts from the point I and goes down step by step until the characters in P become so narrow that there are no further documents, and then the image points are the 0 element of L.
Consider the transformations of cup and cap in P. If the system is one with strong hierarchy, the cup operation has no meaning in P because the structure of the partially ordered system P is that of a tree. Cap, however, is always defined. With weak hierarchy, cup is sometimes defined. When cup is defined, the cup and cap operations do transform by T2 over into L★, although with an interchange of cup and cap in L★. As before, the cup and cap operations in L★ will generally give different elements than the cup and cap operations in L. A vivid illustration of this is shown in Fig. 19. With this observation, I shall end our discussion of characters with hierarchy.
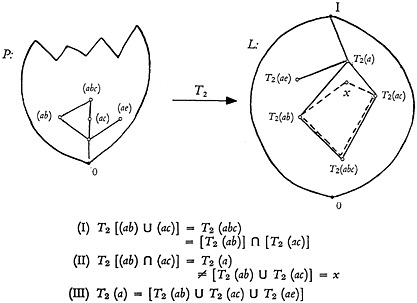
FIGURE 19. Illustration showing that the cup operation in P is preserved by T2, with cup going over into cap. However, the cap operation in P is not preserved by T2 in L, though it is preserved in L★. The dotted lines show the cup and cap operations in the lattice L.
Retrieval systems based upon characters with logic
By “characters with logic,” I mean characters which are combined for the purposes of retrieval prescription by the so-called logical operations AND, OR, and NOT. These operations are respectively illustrated by the following possibilities: The AND operation upon the characters A and B, for a retrieval pre-
scription, requires that the selected document be delineated by both the characters A and B. The OR operation on the characters A and B, for retrieval prescription, requires that the selected document be delineated by either A or B. The operation NOT upon a character A, for retrieval prescription, requires that the selected document be delineated by the character which is the negative of character A.
The application of characters with logic to problems related to retrieval is very old, going back to 1884 in work on selection by Hollerith (10), and is closely related to the theories set forth in 1847 and 1854 by Boole (11), yet the matter still has some confusing aspects. Some of these have been discussed by Birkhoff (1, first edition, pp. 122–126). The application of characters with logic to problems of information retrieval has never been too well defined. There are many fuzzy edges. In this discussion, I can only point out what I think is a reasonable way to make use of characters with logic.
I wish to stress that one should not be overly impressed with retrieval systems based upon characters with logic merely because of the word “logic.” This word is used only because the characters of this method are combined in the same fashion as are the propositions in symbolic logic. We should remember that symbolic logic is a stylized view of things, and that the symbolism or method which is found useful in that discipline need not necessarily be the most appropriate symbolism or method for information retrieval. At all stages, we have to examine very carefully the retrieval interpretations placed upon any operations or symbols.
In order to bring systems of characters with logic into the framework of this discussion, we shall assume a partially ordered system, and we shall identify the operation AND with cup, the operation OR with cap and the operation NOT with the complement of an element. The operation of complementation needs defining. The complement of a character A, when it exists, is represented by −A, and is an element such that both A∪−A=I and A∩−A=0. These can be respectively interpreted as “the least upper bound of a character and its complement is equal to I,” and “the greatest lower bound is equal to 0.” The complement behaves somewhat like the negative or inverse of the element. We shall presume that, for every character, there is a complementary character.
We can combine the characters and their complements by cups and caps to get “polynomials” such as [A∪(B∩C∩−D)]∪[A∩D]. The set of all such polynomials, which includes all the characters individually and their complements, and also the 0 and the I elements, forms a Boolean lattice. This lattice is the partially ordered system P in which each point (each polynomial)
represents a possible retrieval prescription. Also, all possible prescriptions are represented somewhere in P.
An example of such a Boolean lattice, formed on the characters A and B, is shown in Fig. 20. All the possible retrieval prescribing polynomials that can be formed upon these two characters can be reduced to one of the forms shown in Fig. 20, and each is represented by a point in the diagram. Since this lattice is a Boolean lattice, its diagram is identical to, or isomorphic to, the lattice of the subsets of an aggregate. In the case shown in Fig. 20, it is identical to the lattice formed upon the subsets of an aggregate of four objects. Those objects correspond to the elements diagramed at the first level. Therefore, any point in the lattice can be attained by using the cup operation upon some set of the simple polynomials represented at the first level of Fig. 20. For this reason, such polynomials are called “minimal polynomials.” (2, p. 322) Any possible Boolean polynomial can be formed by the cup operation upon one or more of such minimal polynomials.
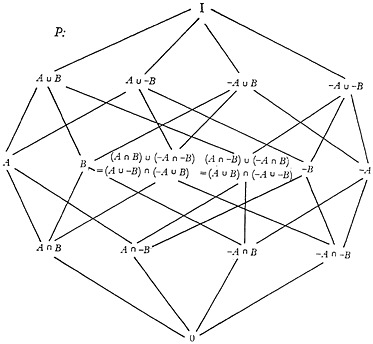
FIGURE 20. The Boolean lattice built upon the two characters A and B, by means of the operations cup, cap, and complement.
The lattice P can be generated as the cardinal product of simpler partially ordered systems. While there are a number of ways to factor P, the way that is the most interesting depends upon the use of the minimal polynomials. If
there are N different characters in the system, a minimal polynomial is an expression like A∩B∩−C· · ·∩−G involving each of the N characters or its complement, all joined by a cap operation. No character is repeated or left out. There are 2N such polynomials for N characters.
The repertory of simple partially ordered systems based upon minimal polynomials, whose cardinal product gives the lattice shown in Fig. 20, is shown in Fig. 21. The very close relationship between minimal polynomials and descriptors is obvious from this factorization.
Before going any further in the discussion of retrieval prescription, we must consider the problems involved in delineation by a single character. If the character A has the meaning “red,” and if a document describes something that is red, we use the character A to delineate the subject content of the document. If the object described is blue, then presumably we can use the character −A, meaning “not red.” If the document describes something for which the notion of color has no meaning, we are in a bit of a quandary. Presumably we should be able to sidestep the color delineation of the subject content. To do this, we would not use any of the color characters or their complements. If this is a valid viewpoint, a character can be asserted in delineation of the subject matter of a document only if the character is relevant to the document, and then only if it is determinable whether the character or its complement applies.
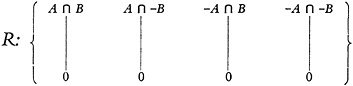
FIGURE 21. The repertory of minimal polynomials, whose cardinal product is the lattice shown in Fig. 20.
It is conceivable that a character may be relevant to the subject matter of a document although it is impossible to determine whether the character or its complement should be used in delineating the subject content. Then what do we do? Or, at the time of analyzing the document for delineation, it may not be known that a character is relevant although sometime later the character’s relevance for this subject matter may be well established.
Problems of this general kind have never been properly faced by those who wish to employ characters with logic for retrieval. In what follows, I shall avoid these questions by presuming that at all times, it is evident whether or not a character is relevant, and if the character is relevant, then it is possible to tell whether the character or its complement should be used in delineating the document.
Consider now the operations AND and OR upon two typical characters A and B with respect to document delineation. The AND operation upon A and B is represented by A∪B. This is a lattice polynomial. In delineation, it must be given the interpretation that both character A and character B are relevant to, and are descriptive of the subject matter of the document. (It should be noted that this is the way descriptors are used to delineate documents.) So far, so good.
However, the use of the OR operation in delineation is questionable. If two characters A and B are associated by the OR operation for delineation, they must be interpreted as saying that either one or the other character, or perhaps both, delineate the subject content. This is ridiculous. If a document is to be delineated, it should be delineated with precision, and not on the basis of such alternatives. For example, to delineate something by saying that it is “either red or square” (and this is easily possible with the use of the operation OR) is to be just a little precious, and not very helpful to a later customer of the retrieval system. For this reason, I do not believe that characters, or polynomials of characters, should be combined by the OR operation, or its equivalent, the cap, to form delineating polynomials.
According to this viewpoint, the only characters, or polynomials of characters, that may be used in delineation are: the null element 0, individual characters and their complements such as A, B, −C, and finally, polynomials of characters and their complements built up by use of the cup operation only. Thus, if the space P, as shown in Fig. 22, is the space of all possible
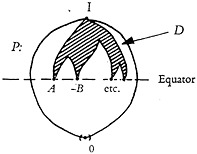
FIGURE 22. In a system of characters with logic, the points in the delineation space D (with the exception of 0) lie on the equator, or above the equator of P. D is a lattice, but it is not a sublattice of lattice P, even though the points of D are a subset of the points of P.
polynomials, then (with the exception of the null element) all the points which may delineate lie either at the “equator” or above it. Reference to the simple case in Fig. 20 shows that not even all of the points at the equator are allowed in delineation. Not all the points above the equator are allowed either, since
many of these points represent polynomials making use of the cap operation.
Let us call the set of all the allowed points, each representing an allowed polynomial, the delineation space D. The delineation space is a subset of P or is “embedded” in P. It is represented symbolically by the shaded area in Fig. 22. The D space of the lattice P in Fig. 20 is drawn out in full in Fig. 23. We should remember that the space D always includes the points 0 and I of P.
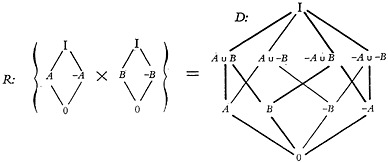
FIGURE 23. For characters with logic, the delineating space D is quite different from the prescribing space P. This diagram shows how the delineating lattice for two characters is generated. Note that lattice D is contained in lattice P of Fig. 20, but that D is not a sublattice.
Space D is a lattice, but it is not a sublattice of P because the cup and cap operations on the same elements give different results in D and P. Also, the lattice D does not have the same structure as the descriptor lattices, either for the case where there are as many descriptors as there are characters, or for the case where there are as many descriptors as there are characters and complements. Comparison of Fig. 23 with Fig. 7 will make this difference clear. The system D is not a Boolean lattice; it neither has unique complements, nor is distributive (1).
The lattice D can be factored into simpler partially ordered systems which, when combined by the cardinal product, give the lattice D. Such factors are shown at the left in Fig. 23 for the polynomial system of Fig. 20. Larger systems D, for a larger number of characters, can be generated by taking the cardinal product of a larger repertory of simple lattices of the same kind as shown in Fig. 23.
If the total number of characters is N, then the delineation of the content of the document may be according to any expression involving cup which has up to N different characters. Any such expression must never contain both a character and its complement.
If neither the character nor its complement is found in the polynomial of delineation, this means that either (a) the character is not relevant, or (b) it is
impossible to determine whether the character or its complement is the appropriate delineation.
Although the content of a document can be delineated only by a point in the space D which is a subset of P, the retrieval prescription can be framed in terms of any of the points of P. This means that we can build up any combination of requirements involving OR, AND, and NOT. For retrieval, we can meaningfully ask for things that are either “red OR square.” As another possibility, we can ask for those things that are “red AND square, or, if not that, are NOT long.” This can be signified by (A∪B)∩−C.
This leads us directly into the discussion of the retrieval transformations for characters with hierarchy. The retrieval transformation T1 is not very interesting; this is the transformation which associates each point x of D with a point x★ of L representing the largest subset of documents such that all the documents of the subset are delineated by the same point in D. Note that by T1, the only permitted retrieval prescriptions are points in D. The image points in L will be much the same as in the previous examples. In particular, the non-null image points in L will represent mutually exclusive document subsets. The rest of the features of the transformation T1 are also the same as they were for the other retrieval systems.
The retrieval transformation T2 is more interesting and useful. Any point x in P may be a retrieval prescription. For any prescribing point x, we define the class X of points in D each of which is preceded by the point x. Then we look to L, and find the largest subset such that every document associated with the subset is delineated by one of the points in X. Let this subset be represented by x★. Thus, for every point x in P, there is an associated point x★ in L, and this association defines the retrieval transformation T2.
A retrieval system based upon delineation according to a point in D, prescription according to a point in P, and the retrieval transformation T2, can be a very useful system. However, the problems of relevance and indeterminancy of the characters still requires further study. Also the interpretation of the complement holds a number of hazards. In particular, if character A or its complement has not been used to delineate a document, this document should not be selected by the prescription NOT A merely because A is absent. Yet there have been proposals for retrieval systems in which such selection was intended.
For some purposes, we might consider a retrieval system in which both delineation and prescription would be formulated in terms of descriptors based on the minimal polynomials. The scope of meaning for each descriptor would be defined to be compatible with the alternatives given by one of the minimal polynomials. For most practical purposes, a retrieval system designed on this
basis would not be too helpful. It would, for example, allow delineation of objects by “red OR square.” However, if such delineations were allowable in a retrieval system, minimal polynomials could be used as descriptors. If this were done, the “logical” operations would effectively disappear because the whole system would behave like a descriptor system. Such a system uses only set combination (cup) and inclusion (partial ordering); it does not use the notions of OR, AND, and NOT.
In concluding our discussion of characters with logic, let us consider the behavior of cup and cap under the transformation T2. As with the previous retrieval systems, the image points of the points of P, under the transformation T2, will be only a small fraction of the points in L. Designate by L★ the set of image points in L. This system L★ is a lattice, and the cup and cap operations in the system P go over into cup and cap operations on corresponding elements in L★. The relation between P and L★ is not an isomorphism, even though most of the structure is preserved, but is a homomorphism (1, p. vii; 2, pp. 155, 349).
Again the lattice L★ is not a sublattice of L. For example, the set T2 [(A∪B) ∩(A∪−B)]=T2 [A∪(B∩−B)]=T2[A] will contain elements delineated by only A, while neither of the sets T2 [A∪B] or T2 [A∪−B] will do so. Therefore the cup operation in lattice L★ does not conform to the cup operation on the same elements in L. This exhibits another peculiarity about systems of characters with logic. The behavior during reduction of the polynomials in P does not conform to what seem to be common-sense requirements. Let a retrieval prescription be: (red AND round) OR (red AND not-round). Implicit in this prescription is the requirement that geometric shape is relevant. However, after reduction in the lattice P, this prescription reduces to mere (red). According to the original retrieval prescription, documents on red geometric shapes would be produced, but not all the documents concerned with the color red. By the reduced polynomial in P, documents on red shapes, red spectral lines, red pigments, and others, would all be produced. Evidently, this is another aspect of systems of characters with logic which will require clarification.
Concluding remarks
This paper has presented a mathematical model for the theory of language symbols in retrieval and has applied the model to three different families of retrieval systems. I believe that almost all the retrieval systems now used in practice lie within the compass of these three families and their variations. In
making this statement, I have in mind the great variety of actual physical methods and mechanisms which are used to instrument each of these families. Although this model, with its method of generating the inner details of retrieval systems, can represent most of the present retrieval systems, our theoretical task is not ended. So far, only the foundations have been laid. I am well aware that there still remain some chinks, yet to be filled, in these foundations. Nevertheless, these foundations are a basis for a program of further theoretical development, and I now want to discuss some of the topics that must be dealt with in the future.
The model as developed here does not incorporate certain statistical information about information retrieval systems that must be used in their design. For example, it is important to know the frequency with which each of the various characters are used. In our model, we can attach a “scalar” to each character in the repertory R, where the scalar is a number giving the relative incidence or frequency of usage of this character upon the documents in the collection. Also, in much the same way, each of the points in the system P is related by T1 or T2 to a certain number of documents in the collection. Thus, each point of P has two scalars associated with it, one according to T1 and the other according to T2. In the actual design of a retrieval system, we would like these scalar values on the points of P to be somewhat comparable at the same level in P, and to decrease in an orderly fashion as the level in P increases.
In the lattice L, there are also several important statistical features to be described. We have already mentioned one number of interest: the ratio of the number of points in L★ to the number of points in L. This ratio tells us the fraction of possible subsets that are actually used in information retrieval. Another statistic of L depends upon the fact that most of the lattice L★ is concentrated toward the bottom of the diagram of L. This means that most of the document subsets of actual use in retrieval are small. For system design, it is useful to know how the size of these subsets is distributed. A precise way of formulating this is to ask for the distribution of the number of points of L★ for each level of L. Another closely related kind of information has to do with the fact that sometimes a very simple prescription for information will produce the same number of documents as some other quite complicated prescription. This means that a simple prescription, represented by a point low in P, will transform into a point in L at the same level as some other point of P which is at a much higher level in P. Thus we are interested in a measure of the dispersion of the levels of P as a function of the level in L.
All the transformations of this mathematical model have presumed that the
associated machines and codings are exact. However, certain coding schemes are not exact, and therefore we shall have to consider transformations such as T3 which are based upon a probabilistic approach.
The elaboration of this mathematical model need not be restricted to mere embellishment of the diagrams with statistical information. Another very important virtue of this model is that it provides a method of generating the detailed structure of new language systems of retrieval by the use of cardinal products on partially ordered systems. By changing the partially ordered systems that go into the repertory, we can come out with quite different retrieval systems. For example, in our discussion of characters with logic, we avoided consideration of indeterminancies due to relevance, or to the applicability of a character or its complement. However, in the practical use of characters, we must always make allowance for all kinds of lack of information, ignorance, and error. When we do this, my study seems to indicate that each of the simple partially ordered systems of the repertory shown at the left in Fig. 23 takes on the character of the system shown in Fig. 24. The cardinal
FIGURE 24. In a system of characters with logic, the relevance of a character may be in doubt, or it may be impossible to tell whether to apply the character or its complement in delineation. Also, errors may be made in delineation. In order to take into account these situations, the basic repertory lattice for a character and its complement apparently takes this form.
product of a repertory consisting of such systems will result in a delineating system D which is much more complicated than the one shown at the right in Fig. 23. All complications of this kind need to be investigated. In a similar manner, repertories involving other simple diagrams can be set up. Such diagrams can express various useful properties of the characters employed.
In regard to any program of generating new retrieval systems, we should remind ourselves that the discussion in this paper has dealt only with systems of characters which combine by formation of sets and classes. All such characters are commutative. With commutative characters, the order in which we
make statements does not matter: AB means the same as BA. Commutative systems operate very well when we are dealing with objects in which no particular ordering or structure of the subject matter is involved, but this is not always true. The subject matter may be structured, either in a linear fashion, or in some form of a network.
If the information in a document is structured in linear sequence, the ideas are not commutative. It may then be useful to use characters in delineation and retrieval which themselves are not commutative. We may say that such characters combine by concatenation. As soon as we permit non-commutative characters, the partially ordered system of characters takes on an infinite number of levels, even though the number of different characters is finite.
Characters of still another kind are combined in a network fashion. We can say that these characters combine by reticulation, and such characters are used in chemical ciphering methods.
Another line of development involves the treatment of “super lattices.” This technique seems to be called for when a document describes a number of different topics, and each topic is delineated by a separate point in the lattice P. The document as a whole should not be represented merely by the greatest lower bound or the least upper bound of these points. Instead, we should somehow be able to form a new kind of a representative point which keeps these various points of P distinct. The way to do this is to use the entire set of points of P as an aggregate of objects upon which a lattice is built by the formation of subsets from this aggregate. This defines the super lattice. Any document of however many different topics can then be fully represented in terms of a point in this super lattice.
Thanks are given to Mr. Russell A.Kirsch, of the National Bureau of Standards, for his specific encouragement in the development of this mathematical model of language systems of retrieval.
REFERENCES
1. BIRKHOFF, GARRETT, Lattice Theory, revised edition, New York, American Mathematical Society, 1948.
2. BIRKHOFF, GARRETT, and MACLANE, SAUNDERS, A Survey of Modern Algebra, New York, The Macmillan Company, 1941.
3. MOOERS, C.N., Zatocoding and Developments in Information Retrieval, ASLIB Proc., 8, 3–22 (February 1956).
4. TAUBE, MORTIMER, and ASSOCIATES, Studies in Coordinate Indexing, Washington, D.C., Documentation Inc., 1953.
5. FAIRTHORNE, R.A., The Mathematics of Classification, Proc. British Society of International Bibliography, 9 [4], 1947.
6. FAIRTHORNE, R.A., The Patterns of Retrieval, American Documentation, 7, 65–75 (April 1956).
7. MOOERS, C.N., Zatocoding Applied to Mechanical Organization of Knowledge, The XVIIth Conference, Federation Internationale de Documentation, Rome, 1951; American Documentation, 2, 20–32 (January 1951).
8. MOOERS, C.N., Information Retrieval on Structured Content, paper published in the proceedings, Information Theory—Third London Symposium, edited by Colin Cherry, pp. 121–134, London, Butterworth’s Scientific Publications, 1956. The full paper as presented at the meeting is published as Zator Technical Bulletin No. 102, Cambridge, Mass., Zator Company, 1955.
9. RANGANATHAN, S.R., “Colon Classification and Its Approach to Documentation,” pp. 94–105 of Bibliographic Classification, edited by J.H. Shera and M.E. Egan, Chicago, University of Chicago Press, 1951.
10. HOLLERITH, HERMAN, “Art of Compiling Statistics” U. S. Patent No. 395,782 dated January 8, 1889, original application filed September 23, 1884; also “Apparatus for Compiling Statistics,” U.S. Patent No. 395,783, same dates.
11. BOOLE, G., The Mathematical Analysis of Logic, Cambridge, 1847; An Investigation into the Laws of Thought, London, 1854 (New York, Dover Publications).






































