Prime Obsession: Bernhard Riemann and the Greatest Unsolved Problem in Mathematics (2003)

I. In 1930 David Hilbert attained his 68th birthday. In conformity with the regulations of Göttingen University, he retired. Honors poured in. Among them was a resolution by the authorities of Königsberg to award the keys of the city to this eminent native son. The presentation was to be made at the opening session of a conference scheduled for that fall, a meeting of the Society of German Scientists and Physicians. The occasion naturally required a speech. Thus, on September 8, 1930, in Königsberg, Hilbert delivered the second great public speech of his career.

The title of the speech was “Logic and the Understanding of Nature.” Hilbert’s purpose was to express some opinions about the relationship between our inner lives—our mental processes, including those that help us to create and prove mathematical truths—and the physical universe. This was, of course, a topic with a long philosophical pedigree, one in which the name of another of Königsberg’s native sons, the eighteenth-century philosopher Immanuel Kant, has particular prominence. It is one to which the modern understanding of the Riemann Hypothesis is, as it happens, rather especially perti-

nent, as I shall show in Chapter 20. This was not known at the time of Hilbert’s Königsberg address, though.

It had been arranged that, following the speech, Hilbert would give a shorter version of the address over the radio—at that time, of course, a very new thing. That shorter version was recorded and was actually released as a 78 R.P.M. gramophone record. (“Celebrity mathematician” was apparently not an oxymoron in Weimar Germany.) It can now be found on the Internet. With very little effort you can now hear spoken, in Hilbert’s own voice, the six words for which he is best remembered, and which appear on his memorial stone at the cemetery in Göttingen. Those words are the last in his Königsberg address.

Hilbert believed firmly in the unbounded power of the human mind to uncover the truths of Nature and mathematics. In his youth, the rather pessimistic theories of the French philosopher Emil duBois-Reymond had been very popular. DuBois-Reymond maintained that certain things—the nature of matter and of human consciousness, for example—are intrinsically unknowable. He coined the apothegm ignoramus et ignorabimus—“we are ignorant and we shall remain ignorant.” Hilbert had never liked this gloomy philosophy. Now, with all the world (or at any rate the scientific-mathematical part of it) listening, he gave it a last resounding kick.

Those last six words—in German, Wir müssen wissen, wir werden wissen—are the most famous that Hilbert ever spoke, and among the most famous in the history of science. They express a strong optimism, all the more remarkable from a man who was heading into

retirement and was furthermore unwell. (Hilbert had for some years been suffering from pernicious anemia, a disease that in the 1920s was only just beginning to yield to treatment.) Those words make a happy contrast with the rather gloomy solipsism of Hardy’s Apology—written 10 years later when Hardy was 63, five years younger than was Hilbert at the time of the Königsberg address.

II. A happy contrast too—though now we are in the realm of hindsight—with the horrors that were soon to engulf Germany. When Hilbert retired from his professorship in 1930, Göttingen was still what it had been for 80 years, a great center of mathematical research and study, probably the greatest in the world at that point. Four years later it was an empty shell, from which the greatest minds had fled, or been driven out.

The principal events here were of course those that took place in the early months of 1933: Adolf Hitler’s swearing-in as Chancellor on January 30, the Reichstag fire on February 27, the elections of March 5, in which the Nazis won 44 percent of the votes (a plurality), and the Enabling Act of March 23, which transferred key constitutional powers from legislature to executive. By April the Nazis had almost total control of Germany.

One of their first decrees, on April 7, was intended to bring about the dismissal of all Jews from the civil service. I say “was intended” because the old Field Marshal, Paul von Hindenburg, was still president of the German Republic and had to be deferred to. He insisted that there be two categories of exemption to the April 7 decree: first, any Jew who had performed military service in World War I, and second, any who had already held a civil service position before August 1914, when that war began.

University professors were civil servants and so came under the scope of the decree. Of the five professors teaching mathematics at

Göttingen, three—Edmund Landau, Richard Courant, and Felix Bernstein—were Jewish. A fourth, Hermann Weyl (who had succeeded to Hilbert’s chair), had a Jewish wife. Only Gustav Herglotz was racially uncompromised. As a matter of fact, the April 7 decree did not apply to Landau or Courant, since they fell within the Hindenburg exemptions. Landau had been appointed to his professorship in 1909; Courant had performed valiant war service on the Western Front.⁸⁶

It was not the way of the Nazis to stick to the letter of the law in such matters, though. It did not help that Göttingen at large was rather strong for Hitler. This was true of both “town” and “gown.” In the 1930 elections, Göttingen had delivered twice as many votes to Hitler’s party as the national average; and the Nazis had a majority in the university’s student congress as far back as 1926. (That grand house of which Edmund Landau was so proud had been defaced with a painting of a gallows in 1931.) On April 26 the town newspaper, Göttinger Tageblatt, which was keenly pro-Nazi,⁸⁷ printed an announcement that six professors at the university were being placed on indefinite leave. The announcement came as a surprise to the six professors; they had not been notified.

Between April and November that year, Göttingen as a mathematical center was gutted. Not only Jewish faculty were involved; anyone thought to have leftist leanings came under suspicion. The mathematicians fled—most eventually finding their way to the United States. Altogether 18 faculty members left or were dismissed from the Mathematics Institute at Göttingen.

One holdout was Edmund Landau (the only Göttingen math professor, by the way, who was a member of the town’s synagogue). Relying on the integrity of the law, Landau attempted to resume his calculus classes in November 1933, but the Science Students’ Council learned of his intention and organized a boycott. Uniformed storm troopers prevented Landau’s students from entering the lecture hall. With singular courage, Landau asked the Council leader, a 20-year-

old student named Oswald Teichmüller, to write out as a letter his reasons for organizing the boycott. Teichmüller did so, and the letter somehow survived.

Teichmüller was a very intelligent man and in fact became a fine mathematician.⁸⁸ It is clear from his letter that his motivation for the boycott was ideological. He believed, wholeheartedly and sincerely, in the Nazi doctrines, including the racial ones, and felt it improper that German students should be taught by Jews. We are accustomed to think of Nazi activists as thugs, low-lifes, opportunists, and failed artists of one sort or another, which indeed most of them were. It is salutary to be reminded that they also included in their ranks some people of the highest intelligence.⁸⁹

Landau himself then left Göttingen, brokenhearted. He went back to the family home in Berlin. There were a few overseas lecturing trips, which seemed to give him great pleasure, but he would not leave his native land to live permanently abroad and died from natural causes at his Berlin home in 1938.

Hilbert himself died in wartime Göttingen on February 14, 1943, three weeks after his 81st birthday, from complications following a fall in the street. No more than a dozen people attended the funeral service. Only two of them had much claim to mathematical honors: the physicist Arnold Sommerfeld, who had been an old friend of Hilbert’s, and the above-mentioned Gustav Herglotz. Hilbert’s home city of Königsberg was flattened in the war; it is now the Russian city of Kaliningrad. Göttingen is now a rather ordinary provincial German university with a strong math department.

III. Those years of the early 1930s, before the darkness fell, brought forth one of the most romantic episodes in the history of the Riemann Hypothesis, the discovery of the Riemann-Siegel formula.

Carl Ludwig Siegel, the son of a Berlin letter carrier, was a lecturer at the University of Frankfurt. An accomplished number theo-

rist, he understood very well, as any mathematician who reads it must, that Riemann’s 1859 paper was only, to employ the terminology of Erving Goffman that I introduced in Chapter 4.ii, a “front” display— a summary for formal presentation of what must have been a far greater amount of “back” work. Siegel spent such time as he could spare at Göttingen, going through Riemann’s private mathematical papers from the period, to see if he could gain any insight into the activity of Riemann’s mind when he was constructing the paper.

Siegel was by no means the first to attempt this. The papers had been deposited at the university library in 1895 by Heinrich Weber, following his second edition of Riemann’s collected works. When Siegel arrived, they had been sitting there in the Göttingen archives (where they still sit—see Chapter 22.i) for 30 years. Several researchers had investigated them, but all had been defeated by the fragmentary and disorganized style of Riemann’s jottings, or else they lacked the mathematical skills needed to understand them.

Siegel was made of sterner stuff. He persevered with the piles of scribbled sheets, and made an astonishing discovery, which he published in 1932 in a paper titled “Of Riemann’s Nachlass⁹⁰ as It Relates to Analytic Number Theory.” This is one of the key papers in the story of the Riemann Hypothesis. To explain the nature of Siegel’s discovery, I shall have to return to the computational thread in my narrative—that is, to the effort to actually calculate the zeros of the zeta function and to verify the Riemann Hypothesis experimentally.

IV. I left the computational thread in Chapter 12 with Jørgen Gram’s publication of the first 15 non-trivial zeros in 1903. Further work in this direction has continued down to the present day. At the 1996 Seattle conference on the Riemann Hypothesis, Andrew Odlyzko presented the history shown in Table 16-1.

Van de Lune went on to carry his investigation to 5 billion zeros at the end of 2000, and to 10 billion by October 2001. In the mean-

time, in August 2001, Sebastian Wedeniwski, using idle time on 550 office PCs at IBM Corp., Germany, began a project to advance computation yet further. The latest result posted by Wedeniwski is dated August 1, 2002, and reports that the number of non-trivial zeros with real part one-half has now been carried to 100 billion.

There are actually a number of different things going on here, and it is important to keep them distinct in one’s mind.

First, there is the confusion between (a) height up the critical line, and (b) number of zeros. “Height” here just means the imaginary part of a complex number; the height of 3 + 7i is 7. In discussions of the zeta zeros, it is now customary to refer to this height as t or T. (Since we know that the zeros are symmetrical about the real axis, we only bother with positive t, by the way.) We have a formula for the number of zeros up to height T.

This is actually a very good formula—the first two terms are Riemann’s—giving excellent approximations even for quite low val-

ues of T. Ignoring the big oh term,⁹¹ for T equal to 100, 1,000, and 10,000, it gives 28.127, 647.741, and 10,142.090. The actual numbers of zeros up to these heights are 29, 649 and 10,142. To get a value of N(T) equal to Wedeniwski’s 100 billion, you need T to be 29,538,618,432.236 … , and that is the height Wedeniwski has carried his work to.

And then there is the confusion about what is actually being calculated. It should not be assumed that Wedeniwski can show us all 50 billion of those zeros, to a high (or even medium) degree of accuracy. The aim of most of this kind of work is to confirm the Riemann Hypothesis, and this can be done without very precise computations of the zeros. There is a piece of theory that lets you compute how many zeros are in the critical strip between heights T₁ and T₂—that is, inside a rectangle whose bottom and top edges are imaginary T₁ and T₂, and whose left and right edges are real 0 and 1, as illustrated in Figure 16-1. There is another piece of theory that lets you compute how many zeros are on the critical line between these heights.⁹² If the two computations give the same result, you have confirmed the Riemann Hypothesis in that range. You can do this with only a rough knowledge of where the zeros actually are. Most of the work in Table 16-1 is of this kind.

What about tabulation of the actual precise values of the zeros? Surprisingly little of this has been done, except incidentally to the other effort (i.e., verifying the Hypothesis). So far as I am aware, the first published table of this kind to any length was by Brian Haselgrove. In 1960, working on second-generation mainframe computers at the universities of Cambridge and Manchester, in England, Haselgrove and his colleagues tabulated the first 1,600 zeros, accurate to six decimal places, and published the table.

Andrew Odlyzko told me that when he began his work on the zeta zeros in the late 1970s, Haselgrove’s tables were the only ones he knew of, though he thinks that Lehman, as part of his 1966 work, might have done accurate computation of more zeros. Andrew himself has a table (on computer disk, not printed) of the first two mil-

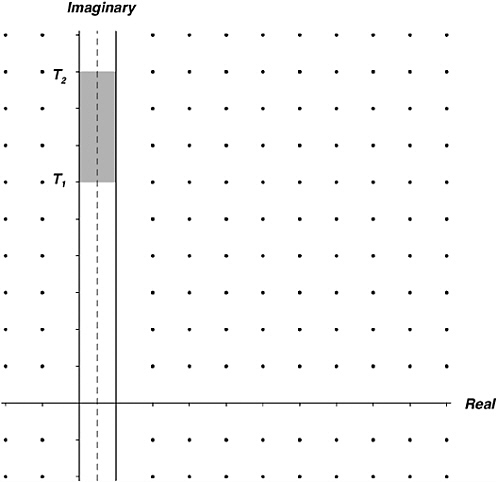
FIGURE 16-1 Heights T₁ and T₂ up the critical strip.

lion zeros, accurate to nine decimal places. At the time of writing, that is the largest known table of zeros.

All of the above work is concerned with the first N zeros. Andrew Odlyzko has also leapt ahead to examine small, isolated ranges very high up. He has published the highest non-trivial zero of the zeta function known to date, the 10,000,000,000,000,000,010,000-th. It is at argument , to five places of decimals in the imaginary part. Andrew has also computed the

first 100 zeros to 1,000 decimal places each.⁹³ The first zero (I mean, of course, its imaginary part) begins

V. There are stories behind Table 16-1. That A.M. Turing, for example, is the very same Alan Turing who worked in mathematical logic, developing the idea of the Turing Test (a way of deciding whether a computer or its program is intelligent), and of the Turing machine (a very general, theoretical type of computer, a thought experiment used to tackle certain problems in mathematical logic). There is a Turing Prize for achievement in computer science, awarded annually since 1966 by the Association for Computing Machinery, equivalent to a Fields Medal⁹⁴ in mathematics, or to a Nobel Prize in other sciences.

Turing was fascinated by the Riemann Hypothesis. By 1937 (his 26th year) he had made up his mind that the Hypothesis was false and conceived the idea of constructing a mechanical computing device with which to generate a counterexample—a zero off the critical line. He applied to the Royal Society for a grant to cover the cost of construction and actually cut some of the gear wheels himself, at the engineering department of King’s College, Cambridge, where he was lecturing.

Turing’s work on the “zeta function machine” stopped abruptly in 1939, when World War II broke out. He joined the Government Code and Cypher School at Bletchley Park and spent the war years breaking enemy codes. Some of the gear wheels survived, however,

and were found among his effects when he died, probably from suicide, on June 7, 1954.

As sad and strange as Turing’s death was—he ate an apple coated, by himself, with cyanide—he enjoyed posthumous good fortune in the matter of biographers. Andrew Hodges wrote a beautiful book about him (Alan Turing: The Enigma, 1983), and then Hugh Whitemore made a fascinating play based on the book (Breaking the Code, 1986).

I have no space here to go into the details of Turing’s life. I refer the reader to Hodges’s fine biography, from which I shall just quote the following.

Turing was to be tried on March 31 on 12 charges of “gross indecency,” consensual homosexual acts being at that time criminal offenses in Britain. In the event he did not go to prison. He was found guilty but placed on probation, with the condition that he undergo medical treatment. “There was,” notes Hodges, “no concept of a right to sexual expression in the Britain of 1952.”

There are other stories, too. Edward Titchmarsh, who had been a student of Hardy’s (as, by the way, had Turing), worked through his 1,041 zeros⁹⁵ using punched-card machines on loan from the British Admiralty, which used them for compiling tide tables. He went on to write a classic mathematical text on the zeta function.⁹⁶ All this mechanical work came to an end with the advent of electronic computers after World War II, of course.

Other stories, too … but I have strayed too far from my course.⁹⁷ I was going to finish telling you about the Riemann-Siegel formula.

VI. The first three entries in Table 16-1—the contributions of Gram, Backlund, and Hutchinson—all consisted of work done painstakingly with paper, pencil, and books of mathematical tables. This was computational hard labor; values of the zeta function are not easy to compute. The basic technique was one named “Euler-Maclaurin summation,” developed around 1740 by Leonhard Euler and the Scottish mathematician Colin Maclaurin, working independently. It involves the approximation of integrals by long and complicated sums. Though arduous, it was the best method anyone could come up with. Gram himself tried several others, over a period of years, with very little success.

The essence of Carl Siegel’s discovery, from his researches into Riemann’s Nachlass at the Göttingen library, was this: Bernhard Riemann, in the background work for his 1859 paper, had developed a much better method for working out the zeros—and had actually implemented it and computed the first three zeros for himself! None of this was revealed in the 1859 paper. It was all hidden away in the Nachlass.

Says Harold Edwards: “Riemann was in fact in possession of the means to compute with amazing accuracy.”⁹⁸ Riemann satisfied himself with rough calculations, however, precise knowledge of the location of the zeros not being essential for his work. He got the imaginary part of the first zero (see above) as 14.1386 and confirmed that it is the first; he computed the second and third to within a percentage point or two of accuracy.

The discovery of Riemann’s formula, fine-tuned and published by Siegel to become the Riemann-Siegel formula, made work on the zeros much easier. All significant research depended on it up to the mid-1980s. Andrew Odlyzko’s classic 1987 paper, “On the Distribution of Spacings Between Zeros of the Zeta Function,” for example, which I shall have more to say about in Chapter 18.v, used Riemann-Siegel. Stimulated by this work, Odlyzko and Arnold Schönhage then

developed and implemented some improved algorithms, but everything is built on Riemann-Siegel.

Carl Siegel, by the way, was not Jewish and was not directly affected by the restrictive laws of the early Nazi period. He detested the Nazis, though, and left Germany in 1940 to work at the Institute for Advanced Study in Princeton. He returned to Germany in 1951, finishing his career as a professor at that same Göttingen where, 20 years before, the archives had yielded up to him a glimpse of the astonishing powers of mind that dwelt behind Bernard Riemann’s quiet diffidence.