Prime Obsession: Bernhard Riemann and the Greatest Unsolved Problem in Mathematics (2003)

I. Supposing, as I have tried to persuade you, that complex numbers are a perfectly straightforward extension of ordinary real numbers, obeying all the normal rules of arithmetic with the single extra one that i ² =–1; and recalling that a function just turns one range of numbers—its domain—into another; is there any reason there should not be functions of complex numbers? No reason at all.

The squaring function, for example, works just fine for complex numbers, following the rule for multiplication. The square of –4 + 7i, for example, is (–4 + 7i) × (–4 + 7i), which is 16 – 28i – 28i + 49i², i.e., –33 – 56i. Table 13-1 shows a sample of the squaring function for some random complex numbers.⁶⁷

It may be hard to believe at this point, but the study of “functions of a complex variable” is one of the most elegant and beautiful branches of higher mathematics. All the familiar functions of high school math can easily have their domains extended to cover all, or most, of the complex numbers. For example, Table 13-2 gives a glimpse of the exponential function for some complex numbers.

Note that, just as before, when I choose the arguments to go up by addition—as of course I do, in this case adding 1 + i each time— the function values go up by multiplication, in this case by 1.46869 + 2.28736i. If I had picked the arguments to go up by adding 1 each time, then of course the values would have multiplied by e. Note also that I slipped into this table one of the most beautiful identities in all of math.

Gauss is supposed to have said—and I wouldn’t put it past him—that if this was not immediately apparent to you on being told it, you would never be a first-class mathematician.

How on earth is it possible to define a complex power for e, or any other number? By a series, that’s how. Expression 13-1 shows the actual definition of e^z for any number z whatsoever, real or complex.

Expression 13-1

Miraculously (it seems to me) this infinite sum converges for every number. The denominators grow so fast they eventually swamp any power of any number. Equally miraculously, if z is a natural number, the infinite sum works out to exactly what the basic meaning of “power” would lead you to expect, though from just looking at Expression 13-1, there is no obvious reason why it should. If z is 4, it works out to exactly the same as e × e × e × e, which is what e⁴ is supposed to mean.

Let me just feed π i into Expression 13-1, to show how it converges. If z is π i, then z² is –π ², z³ is –π ³i, z⁴ is π ⁴, z⁵ is π ⁵i, and so on. Feeding these into the infinite sum, and calculating the actual powers of π (to just six decimal places for simplicity’s sake), the sum is

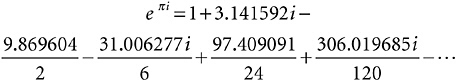
If you add up the first 10 terms of this, you have –1.001829104 + 0.006925270i. If you add up the first 20, you have –0.9999999999243491 – 0.000000000528919i. Sure enough, it is converging on –1. The real part is closing in on –1, and the imaginary part is disappearing.

Can the log function be extended to complex numbers, too? Yes, it can. It is, of course, just the inverse of the exponential function. If e^z = w, then w = log z. Unfortunately, as with square roots, you run into the many-valued function quicksand unless you take precautions. This is because, in the complex world, the exponential function sometimes gives the same value for different arguments. The cube of –1, for example, is, by the rule of signs, –1; so if you cube both sides of e^{π i} =–1, you get e^{3π i} =–1; so the arguments π i and 3π i both yield the same function value of –1, just as –2 and +2 both yield value 4 under the squaring function. So what is log(–1)? Is it π i? Or 3π i?

It’s π i. To stay out of trouble, we restrict the imaginary part of the function value to between –π , exclusive, and π , inclusive. Then every non-zero complex number has a log, and log(–1) = π i. In fact,

in the symbols I introduced in Chapter 11.v, log z = log |z|+iAm(z), with Am(z) measured in radians, of course. Table 13-3 is a sample of the log function, using six decimal places.

Here the arguments go up by multiplication (each row is 1 + i times the previous row) while the function values go up by addition (of 0.346574 + 0.785398i each time). So, it’s a log function. The only wrinkle is, when the imaginary part of the function value gets bigger than π , as it does in going from argument –4 to argument –4 – 4i, you have to subtract 2 π i to keep it in range, 2 π radians being 360 degrees. (Recall from Chapter 11.v that radians are just mathematicians’ favorite way to measure angles.) This doesn’t cause any problems in practice.

II. Since there is an exponential function for complex numbers, and a log function, there doesn’t seem to be any reason we can’t raise any complex number to any complex power. By Power Rule 8 in Chapter 5.ii, any real number a is just e^{log a}, so by Power Rule 3, a^x is just e^{x log a}. Can’t we just extend this idea into the realm of complex numbers, and say that for any two complex numbers z and w, z^w just means e^{w log z}?

We certainly can, and do. If you wanted to raise –4 + 7i to the power of 2 – 3i, you’d first calculate the log of –4 + 7i, which turns out to be around 2.08719 + 2.08994i. Then you’d multiply that by 2 – 3i, getting answer 10.4442 – 2.08169i. Then you’d raise e to that power, giving final result –16793.46 – 29959.40i. So

Piece of cake. As another example, since e^{π i} =–1, taking the square root of both sides gives . If you now raise both sides to the power of i, remembering Power Rule 3 again, you get . Note that this is a real number, equal to 0.2078795763….

Since I can raise any complex number to the power of any complex number, it should be easy to raise a real number to a complex power. Given a complex number z, I can, therefore, calculate 2^z, 3^z, 4^z, and so on. You can see where this is leading. Can we extend the domain of the zeta function

into the world of complex numbers? Of course we can. I tell you, with complex numbers you can do anything.

III. Since the formula for zeta is still an infinite sum, the question of convergence arises. It turns out that the sum converges for any complex number whose real part is greater than one. Mathematicians say “in the half-plane Re(s) > 1,” where Re(s) is understood to mean “the real part of s.”

As with the zeta function for real arguments, though, mathematical tricks can be used to extend the domain of the zeta function back into regions where the infinite sum doesn’t converge. After applying those tricks, you have the complete zeta function, whose domain is all

the complex numbers, with a single exception at s = 1. There, just as I started out showing with that deck of cards in Chapter 1, the zeta function has no value. Everywhere else, it has a single, definite value. There are some places, of course, where that value is zero. We already know that. Those graphs in Chapter 9.iv show the zeta function taking the value zero at all the negative even numbers –2, –4, –6, –8, …. I have already dismissed these arguments as not being very important. They are the trivial zeros of the zeta function. Could it be that there are some complex arguments for which the value of the zeta function is zero? And that these are the non-trivial zeros mentioned in the Hypothesis? You bet; but I am getting a little ahead of the story.

IV. Forty years ago the brilliant but eccentric Theodor Estermann⁶⁸ wrote a textbook titled Complex Numbers and Functions, which contains just two diagrams. “I … have avoided any appeal to geometric intuition,” announced the author in his preface. There has been a small number of kindred spirits, but the generality of mathematicians do not follow Estermann’s approach. They tackle the theory of complex functions in a strongly visual way. Most of us feel that complex functions are easier to get to grips with if you have some visual aids.

How then can complex functions be visualized? Let’s take the simplest non-trivial complex function, the squaring function. Is there any way to get a handle on what it looks like?

In the first place, ordinary graphs are no help. In the world of real numbers you can graph a function like this. Draw a line to represent the arguments (remember the real numbers live on a line). Draw another line at right angles to represent the function values. To represent the fact that this function turns the number x into the number y, go east from argument zero a distance x (west if x is negative); then go north from value zero a distance y (south if y is negative). Mark the spot. Repeat for as many function values as you care to compute. This gives you a graph of the function. Figure 13-1 shows an example.

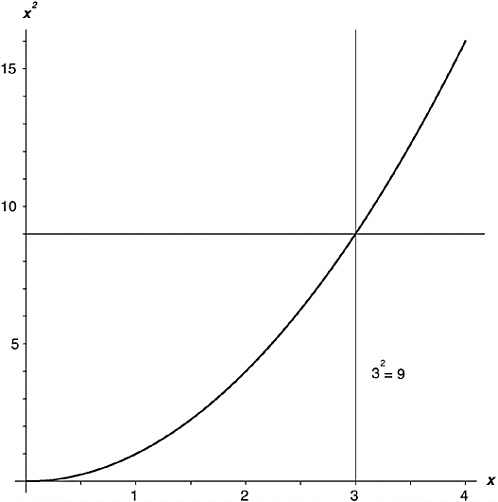
FIGURE 13-1 The function x².

This can’t be made to work for complex functions. The arguments need a two-dimensional plane to be laid out on. The function values need another two-dimensional plane. So to get a graph, you need four dimensions of space to draw it in: two for the argument, two for the function value. (In four dimensions of space, believe it or not, two flat two-dimensional planes can intersect in a single point. Compare the fact, utterly inconceivable to the inhabitants of a two-dimensional universe, that in three dimensions, two non-parallel straight lines need not intersect at all.)

To compensate us for this disappointment, there are things you can do to make pictures of complex functions. Remember the basic thing about a function; it turns one number (the argument) into an-

other number (the value). Well, the argument number is a point somewhere on the complex plane; and the function value is some other point. So a complex function sends all the points in its domain to a bunch of other points. You can just pick some points and see where they go.

Figure 13-2, for example, shows some numbers forming the sides of a square in the complex plane. I’ve marked the corners a, b, c, and d. They are actually the complex numbers –0.2 + 1.2i, 0.8 + 1.2i, 0.8 + 2.2i, and –0.2 + 2.2i. What happens to these numbers if I apply the squaring function? If you multiply –0.2 + 1.2i by itself, you get –1.4 – 0.48i; so that’s the function value for a. Squaring b, c, and d gives you values for the other corners—I have marked them as A, B, C, and D. If you repeat this for all the points along the sides of the square, and the points making up the grid inside, you get the distorted square I have shown in Figure 13-2.

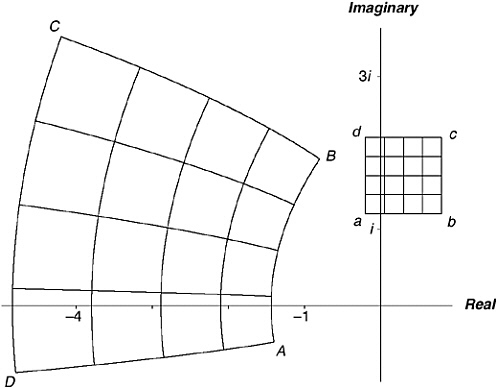
FIGURE 13-2 The function z² applied to a square.

V. It helps with complex functions to think of the complex plane as an infinitely stretchable sheet of rubber and ask what a function does to this sheet. You can see from Figure 13-2 that the squaring function stretches the sheet counter-clockwise round the zero point, while simultaneously stretching it outward from that point for the numbers I’ve shown. The number 2i, for example, whose natural home is on the positive-imaginary (north) axis, when you square it, goes to –4, which is on the negative-real (west) axis, and twice as far from the zero point. In turn, –4, when you square it, gets stretched round to 16, on the positive-real (east) axis, and even further from zero. By the rule of signs, –2i, down on the negative-imaginary (south) axis, gets winched all the way round to –4. Because of the rule of signs, in fact, every function value turns up twice, from two arguments. Remember that –4 is not only the square of 2i, it is also the square of –2i.

Bernhard Riemann, who seems to have had a very powerful visual imagination, conceived of the matter like this. Take the entire complex plane. Make a cut along the negative real (west) axis, stopping at the zero point. Now grab the top half of that cut and pull it round counter-clockwise, using the zero point as a hinge. Stretch it right round through 360 degrees. Now it’s over the stretched sheet, with the other side of the cut under the sheet. Pass it through the sheet (you have to imagine that the complex plane is not only infinitely stretchable, but also is made of a sort of misty substance that can pass through itself) and rejoin the original cut. Your mental picture now looks something like Figure 13-3. That is what the squaring function does to the complex plane.

This is not a fanciful or trivial exercise. From it, Riemann developed a whole theory, called the theory of Riemann surfaces. It contains some powerful results and gives deep insights into the behavior of complex functions. It also yokes function theory to algebra and topology, two key growth areas of twentieth-century math. It is, in fact, a typical product of Riemann’s bold, fearless, and ever-original imagination—a fruit of one of the greatest minds that ever existed.

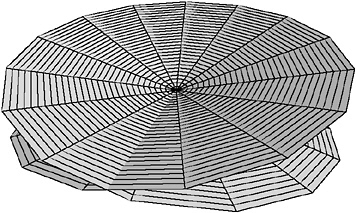
FIGURE 13-3 The Riemann surface corresponding to the function z².

VI. I am going to take a much simpler approach to illustrating complex functions. I’d like you to meet my pal the argument ant, shown in Figure 13-4.

FIGURE 13-4 The argument ant.

The argument ant is awfully hard to see, because he is infinitesimal in size. If you could see him, however, he would look just like a regular ant—a Camponotus japonicus worker, to be precise—with the regulation number of appendages, antennae, etc. In one of the frontmost appendages, which for convenience we may call a “hand,” the argument ant holds a small gadget rather like a beeper, or a mobile telephone, or one of those global positioning devices that can tell you

exactly where you are. This gadget (Figure 13-5) has three displays. The first display, labeled “Function,” shows the name of some function: z², log z, or whatever the gadget might be set to. The second display, labeled “Argument,” shows the point—the complex number—the argument ant is currently standing on. The third display, labeled “Function value,” shows the value of the function at that argument. So the argument ant always knows exactly where he is; and, for any given function, he knows where the point he’s standing on gets sent to by the function.

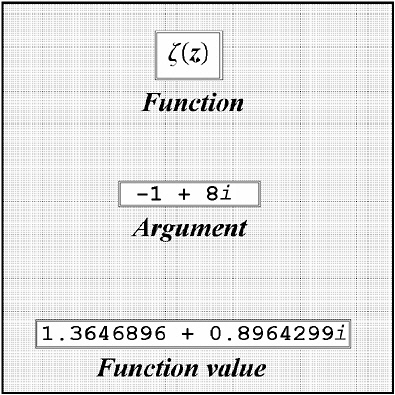
FIGURE 13-5 The ant’s gadget.

I have set the gadget to show the zeta function, and I am going to let the argument ant wander freely over the complex plane. When “Function value” shows zero, he will be standing on a point (“Argument”) that is a zero of the zeta function. I can have him mark those points for us with a magic marker he carries in a small pouch under

his thorax. Then we shall know where the zeros of the zeta function are.

In fact, I am going to have the argument ant do a little bit more work than that. I am going to have him mark all arguments that give a pure-real or pure-imaginary function value. An argument whose value is 2 or –2, or 2i or –2i, will be marked; a point whose value is 3 – 7i will not. To put it another way, all those points that zeta will send to the real line or the imaginary line will be marked. And, of course, since the real line and the imaginary line cross at zero, the arguments where these lines cross, will be zeros of the zeta function. In this way, I can get some kind of picture of the zeta function.

Figure 13-6 shows the result of this little odyssey. The straight lines in it show the real and imaginary axes and the critical strip. All the curved lines are made up of points that are sent to either the real or imaginary axis. At the point where each curve leaves the diagram at left or right, I have written in the function value corresponding to that point.

Trying to imagine what the zeta function does to the complex plane—in the sense of Figure 13-3, which shows what the squaring function does to it—is a rather demanding mental exercise. While the squaring function wraps the plane over itself into the double-sheeted surface of Figure 13-3, the zeta function does the equivalent thing an infinite number of times, to give an infinite-sheeted surface. If you find this difficult to visualize, don’t feel bad about it. You need long practice over several years to get an intuitive feel for these functions. As I said, I shall take a simpler approach here.

The argument ant has marked up the complex plane to give the patterns of Figure 13-6. Now I shall set him to wandering along some of those curves. Let’s suppose he starts out standing on the point –2. Since this is a zero of the zeta function—one of the trivial zeros—the “Function value” display reads 0. Now he starts heading west along the real axis. The function value begins to creep up from zero.

Shortly after he passes the point –2.717262829, heading west, “Function value” reaches the number 0.009159890…. Then it starts

to decline back down to zero again. Since you have read Chapter 9, you can guess what is going to happen. The function value will decline all the way down to zero, which it will reach at argument –4.

That wasn’t very interesting. Let’s start again. From –2, with the function value reading 0, the argument ant heads west to that point where the function value maxed. Instead of continuing west to –4, he makes a sharp right turn and heads north along the top half of that parabola shape. Now the function value will go on increasing, past 0.01, then past 0.1, reaching 0.5 shortly after he crosses the imaginary axis. As he heads out east on that upper arm of the parabola, it continues to increase. As he leaves the page, heading pretty much directly due east now, the display reads 0.9990286. It is still increasing, but awfully slowly, and he has to walk all the way out to infinity before it shows 1.

Since the argument ant now finds himself at infinity, he may as well turn round and come back. Instead of coming back along the same path, though, I’ll have him come back along the positive real axis. (Don’t think about this too much. For these purposes, there is really only one “point at infinity,” so whenever you find yourself there, you can head back into the realm of actual finite numbers from any direction at all.) The “Function value” display increases now, showing 1.0009945751 … as he re-enters the diagram, 1.644934066848 … as he passes 2 (remember the Basel problem?) and then really soaring as he approaches 1.

As he steps on the number 1, a buzzer goes off in the gadget he is holding, and the “Function value” display shows a big bright red flashing infinity sign, “∞.” If he looks more closely at the display, the argument ant will notice a curious thing. At the right of the infinity sign, a small letter “i” is flickering on and off very fast. Simultaneously, to the left of the infinity a minus sign is flickering on and off, also very fast, and out of sync with the flickering “i.” It is as if the display were trying to show four different values all at the same time: ∞, –∞, ∞i, and –∞i. Curious!

The reason is that the argument ant now has three choices (other than to go back the way he came). If he just goes forward, heading west along the real axis until he comes home to the zero at argument –2, he will see the function values turn into large negative numbers, like minus 1 trillion, then rise very fast to moderate-sized negative numbers (minus 1,000, minus 100) eventually coming up to –1, then to –0.5 as he steps on the zero point (because ζ (0) =–0.5), and eventually back to zero at argument –2.

If, on the other hand, he takes a sharp right turn northwards at 1 and traverses the top half of that oval shape around the zero point, he will find from the display that the function values are ascending the negative imaginary axis, from numbers like –1,000,000i, up through –1,000i to –10i, –5i, –2i, then to –i. Shortly before he crosses the imaginary axis the display reads –0.5i. Then, as he heads to the zero at –2, the function value rises to, of course, zero.

Just to help you keep your bearings, and to anchor this firmly in the world of functions (which I first introduced in Chapter 3 by way of tables),Table 13-4 shows that last walk, counterclockwise round the top of the oval shape. I have picked the arguments for this table to have the following amplitudes (in degrees, not radians): 0°, 30°, 60°, 90°, 120°, 150°, and 180°. All numbers are rounded to four decimal places in Table 13-4.

If the ant had taken a left turn at 1, the function values would have come back to zero down the positive imaginary axis instead, through 1.8273i, 0.7998i, and so on.

VII. The argument ant can start his walk from any other zero of the function. I have shown them all in Figure 13-6 with teeny circles. To help the ant know where he is going, I have shown the actual values that are on the “Function value” display at the moment he leaves the diagram along any particular line. (To save space, I have written “m” for “million” in these values. “i,” of course, just means i.) Notice the pattern as he goes up the left-hand edge of the diagram, that is, through arguments whose real part is –10. The first line to leave the diagram at this edge is one that maps into the negative real axis. The next maps into the positive imaginary axis; the next, into the positive real axis; the next, into the negative imaginary axis, … and so on, this pattern repeating itself.

The lines that leave the diagram on the right-hand edge, by contrast, are all mapping into the positive real axis. To the right of the critical strip, in fact, this is a pretty dull function. This whole vast eastern region maps into a tiny area around the 1 point. It is not as “busy” as the left-hand western region; and that western region is not as interesting as the critical strip. With the zeta function, all the interesting stuff happens in the critical strip. (For another illustration of this general truth, see my account of the Lindelöf Hypothesis in the Appendix.)

Figure 13-6 is really the heart of this book. There you actually see the Riemann zeta function, as well as a complex function can be seen. I urge you to spend some time in silent contemplation of this diagram, and to venture out on a few of those ant-walk exercises. The functions of higher mathematics are very wonderful things. They don’t yield up their secrets easily. Some, like this one, can offer a lifetime of study. I can by no means claim to be an expert on the zeta

function. I don’t have a comprehensive collection of zeta-function literature, having relied mainly on university libraries and personal acquaintances for the facts in this book. Still, even without trying hard, I seem to have acquired my own copies of E.C. Titchmarsh’s The Theory of the Riemann Zeta-function (412 pages), S.J. Patterson’s An Introduction to the Theory of the Riemann Zeta-Function (156 pages), and Harold Edwards’s indispensable Riemann’s Zeta Function (316 pages, and I have three copies of this one—that’s a long story), as well as a thick folder of photocopied articles from various journals and periodicals. There must be a score of other full-length books plumbing the mysteries of this function, and thousands of articles. This is serious math.

And, best of all, you can see in that diagram the Riemann Hypothesis shining clear. Look!—the non-trivial zeros actually do all lie on the critical line. I have not shown the critical line in Figure 13-6, but obviously it lies halfway down the critical strip, like a highway median.

VIII. Before leaving the topic of visualizing zeta, just a couple more pictures. First, note that the general pattern you see in Figure 13-6 continues all the way up, for as far as we know.

To illustrate this, Figure 13-7 shows a block of zeros up around . You will notice that they are packed closer together than the ones in Figure 13-6. In fact the average spacing between the eight zeros shown here is 2.096673119…. For the five zeros shown in Figure 13-6, the average spacing was 4.7000841…. So up here around 100i on the imaginary axis, the zeros are packed more than twice as densely as down around 20i.

There is in fact a rule for the average spacing of zeros at height T in the critical strip. It is ~ 2 π/ log(T / 2 π ). If T is 20 this works out to 5.4265725.… If T is 100 it is 2.270516724.… You can see that the rule is not very precise, though, as the twiddle sign tells you, it gets better

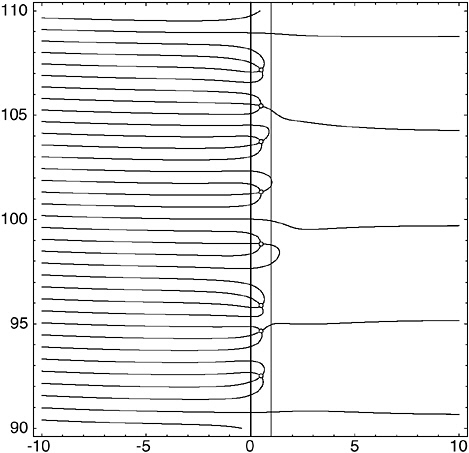
FIGURE 13-7 A higher region of the argument plane.

for bigger numbers. Andrew Odlyzko has published a list of 10,000 zeros up in the neighborhood of . In that neck of the woods, 2 π/ log(T / 2π ) is worth about 0.13416467. The actual average of the 9,999 spaces is 0.13417894…. Not bad.

Next, note a point that will be of some importance later in the book. There is a certain symmetry about the real (i.e., east-west) axis. If I extended Figure 13-6 down south of the real axis, the lines would be mirror images of what they are north of it. The only difference is that while the real numbers I have written in on Figure 13-6 are just the same south as they are north, the imaginary numbers have their signs flipped. To put it mathematically, if ζ (a + bi) = u + vi, then ζ (a – bi) = u – vi. In proper complex-number symbols, .

The important thing that follows is: If a + bi is a zero of the zeta function, then so is a – bi.

IX. Finally, a pictorial representation of the Riemann Hypothesis— or at any rate, of the fact that there are lots of zeros on the critical line.

To understand Figure 13-8, you should remember that Figures 13-6 and 13-7 were pictures of the argument plane. A function of a complex variable sends one set of complex numbers, the arguments, to another set, the values. Since the complex numbers can be laid out as points on a plane, you can think of a function as sending points of one plane, the argument plane, to points of another plane, the value plane. The zeta function sends the point in the argument plane to the point 0 in the value plane. Look back at Figure 13-2. There I showed both the argument plane and the value plane together, as if they were transparencies, one laid on top of the other.

Figures 13-6 and 13-7 are pictures of the argument plane, showing which arguments are sent to interesting values. The argument ant lives on the argument plane—whence his name. I had him wandering over the argument plane, noting where the argument points are sent to by the zeta function. I actually had him wandering along strange curves and loops, made up of points that are sent to (i.e., whose function values are equal to) pure real or pure imaginary numbers. I shall call these “‘sent to’ pictures of the argument plane.”

An alternative way to show a function is with a “comes from” picture of the value plane.⁶⁹ Instead of showing, as I did in Figures 13-6 and 13-7, which arguments are sent to interesting values (in those cases, pure-real and pure-imaginary numbers), I can present a picture of the value plane, showing which value points come from interesting arguments.

Let us imagine that the argument ant has a twin brother who lives on the value plane. This brother is, of course, the value ant. Let’s further suppose that the two brothers are in instantaneous radio com-

munication; and that by this means they synchronize their movements, so that whichever argument the argument ant is standing on at any moment, the value ant is standing on the corresponding value in the value plane. If the argument ant is standing on , for example, with his gadget set to the zeta function, then the value ant is standing on 0 in his plane, the value plane.

Now suppose that the argument ant, instead of following those fancy loops and whorls in Figure 13-6 (which send the value ant on dull hikes up and down the real and imaginary axes), takes a walk straight up the critical line, heading due north from argument . What path will the value ant follow? Figure 13-8 shows you. His path starts out at , which, as I showed in Chapter 9.v, is –1.4603545088095…. Then he does a sort of half-circle counter-clockwise below the zero point, then turns and loops clockwise

FIGURE 13-8 The value plane, showing points that come from the critical line.

around 1. He heads to zero and passes through it (that’s the first zero—the argument ant has just passed ). Then he keeps going round in clockwise loops, passing through the zero point every so often—whenever his twin on the argument plane steps on a zero of the zeta function. I stopped his walk when the argument ant reached , because that’s as far as Figure 13-6 goes. By that point, the curve has passed through zero five times, corresponding to the five non-trivial zeros in Figure 13-6. Notice that points on the critical line have a strong tendency to map to points with positive real part.

Once again, Figure 13-8 shows the value plane. It is not a “sent to” diagram like Figures 13-6 and 13-7; it is a “comes from” diagram, showing what the zeta function does to the critical line, just as Figure 13-2 showed what the squaring function does to that little checkered box. If you want to be properly mathematical about it, that looping curve in Figure 13-8 is ζ (critical line), the set of all points that come from points on the critical line. The curves in Figures 13-6 and 13-7 are ζ ^–1(real and imaginary axes), the set of all points that are sent to the real and imaginary axes. The notation “ζ (critical line)” means “all zeta function values for arguments on the critical line.” Conversely, “ζ ^–1(real and imaginary axes)” means “all arguments whose zeta function values are on the real or imaginary axis.” Note that the expression “ζ ^–1” is used here in the special function-theory sense of “inverse function.” Don’t confuse it with a^–1 as in Power Rule 8, which has the meaning 1 / a, the arithmetic reciprocal of a. This is a different usage—another case of overloading math symbols, like the use of π for both 3.14159… and the prime counting function.

Speaking very generally, “sent to” pictures of the argument plane are better tools for understanding a function in its broad properties (e.g., where its zeros are). “Comes from” pictures of the value plane are more useful for exploring particular aspects or curious features of the function.⁷⁰

The Riemann Hypothesis states that all the non-trivial zeros of the zeta function lie on the critical line—the line of complex num-

bers with real part one-half. All the non-trivial zeros I have shown in this chapter do indeed lie on that line, as you can see from Figures 13-6, 13-7, and 13-8. Of course, that doesn’t prove anything. The zeta function has an infinite number of non-trivial zeros, and no diagram could show them all. How do we know that the trillionth one, or the trillion trillionth, or the trillion trillion trillion trillion trillion trillionth lies on the critical line? We don’t, not from drawing diagrams anyway. What’s it all got to do with prime numbers? To answer that, I shall have to turn the Golden Key.